Heliconical smectic phases with transversal polar order

Abstract

Liquid crystalline (LC) materials integrating polar order and mirror symmetry-broken helical superstructures are of growing interest for advanced applications. We report a new series of achiral bent-core LCs based on 4-cyanoresorcinol bis-terephthalate cores with end-chains ranging from OC₂H₅ to OC₂₀H₂₃. For chains ≥OC₆H₁₃, all compounds form smectic phases which exhibit a paraelectric-to-(anti)ferroelectric transition with Curie–Weiss type divergence, accompanied by an onset of molecular tilt leading to a SmA–SmC phase transition. Increasing chain length induces a tilt correlation crossover from anticlinic (alternating, SmC_a) to synclinic (uniform, SmC_s) ordering. Notably, a stable heliconical smectic phase with a helical axis perpendicular to the polar layers (Sm(CP)^hel) emerges near this crossover. Application of an alternating electric field further expands the Sm(CP)^hel stability range, replacing the SmC_s phase and vanishing near SmC_a. The helical superstructure – spanning C₁₀ to C₂₀ chains and a temperature range up to 80 K – is attributed to synergistic effects of the polar cyano apex, weak molecular bending, and transient helicity. These transversely polarized heliconical phases complement the recently reported longitudinally polarized analogues, offering new pathways for designing chiral LCs from achiral molecules.

---

1. Introduction

Liquid crystalline (LC) materials^1–3 are omnipresent in numerous technological applications as for example in optical, electrooptical, chiroptical and nonlinear optical devices,^4,5 for biomedical sensing,^1a,6 as photoconductive and charge carrier mobility materials,^1d and many others.^7,8 Prof. H. Ringsdorf contributed in different fields to the development of LC research, including polymeric LCs,^1b photoconducting discotic LCs,^1d amphotropic LCs,^1a and donor–acceptor systems.^1c Especially his landmark review from 1988^1a provided a broader view on this field as a state of matter combining order and chaos, leading to their capability to respond to external stimuli and being of basic importance for new materials as well as for the functionality of biologically relevant structures. Besides their switchability due to the unique combination of long-range order with molecular mobility,^1a the capability of formation of helical superstructures,^5,9–13 and the development of long-range polar order (ferroelectricity and antiferroelectricity) are of special contemporary relevance for their applications.^2,14

Bent-core LCs (BCLCs, banana-shaped LC, Fig. 1a, middle) were the first materials showing polar order due to the restriction of molecular rotation around their long axes (steric induced polar order).^9,15–17 For these compounds the polarization direction is transversal to the layer normal (Fig. 2a).

Fig. 1 (a) Modes of polar order in achiral rod-like and bent-core liquid crystals and (b) structure of the 4-cyanoresorcinol derived LCs under discussion.

Fig. 2 (a) Notations of the polar tilted smectic (SmC type) LC phases of bent core molecules; SmC_S = synclinic tilt (identical tilt direction) and SmC_a = anticlinic tilt (alternating tilt direction);^16b dots and crosses indicate the polar direction being oriented into or out of the plane, respectively; (b) and (c) schematic sketches of the heliconical organizations (b) of bent-core mesogens in a heliconical phase with transversal polarization and (c) of polar rod-like molecules (black arrows) in a heliconical phase with longitudinal polarization; note that the heliconical pitch is not drawn in scale; while the helix in (b) is actually shorter, in (c) it is much longer; moreover only one sign of helicity is shown.

In recent years polar LC phases with longitudinal polarization, i.e. along the molecular long axis, were surprisingly also found for achiral rod-like molecules without any bend, where the spontaneous parallel alignment of the molecular dipoles¹⁸ leads to ferroelectric versions of the apolar lamellar (SmA, SmC)^19–21 and nematic (N) phases (see Fig. 1a, left).^22–25 These fluid longitudinal ferroelectric LCs,²⁶ formed by molecules with highly polar end-groups like NO₂ or multiple fluorines, show polarization values exceeding any other ferroelectric LC, reaching and even exceeding the values of related inorganic solid-state materials.²⁷

However, in soft matter systems the electrostatic energy of polar ordered states often induces a polarization splay leading to a helical twist, which then gives rise to a helical organization and spontaneous mirror symmetry breaking.⁹ Thus, for these polar phases helical superstructures (Fig. 2b and c) can often be found. The helix sense is uniform for chiral molecules,¹⁴ while for achiral molecules both signs of helicity coexist (ambidextrous chirality).^28–31 The developing helix can distort and modulate the layers, leading to isotropic mesophases.^9,32 However, if the helix axis is parallel to the layer normal, then flat layers are retained in the resulting heliconical smectic phases. The first heliconical smectic phase formed by achiral molecules was discovered for 4-cyanoresorcinol based bent-core molecules 1/n with two n-alkyl end-chains, shown in Fig. 1b and abbreviated as Sm(CP)^hel (also SmC_sP^hel_F or SmCP_α were used previously).^33–38 For these compounds with a polar CN group at the apex, the polar direction of the layers rotates transversal to the layer normal (=transversal polarization, see Fig. 2b). In the meanwhile, also a nonpolar version of this heliconical phase was reported for achiral bent mesogenic dimers (SmC_TB).³⁹ More recently, longitudinal polar versions with the polar axis rotating on a cone around the layer normal (SmC^hel_F, SmC^H_P, see Fig. 2c)²⁹ were also reported for achiral polar rod-like molecules. Table 1 summarizes the (to the best of our knowledge) presently known mirror-symmetry broken, nematic^40,41 smectic^32,42–44 and isotropic⁴⁵ mesophases of achiral rod-like and bent molecules with their abbreviations and main characteristics.

Table 1 Spontaneously mirror symmetry broken fluids formed by achiral molecules, ordered according to their discovery^a

LC phase	Molecule type	Polarization	Layers	Tilt	Year	Ref.
a Only fluid mesophases without fixed positions of individual molecules and without in-plane periodicity are considered, soft crystalline (B4, HNF, HNC, etc.)^9d,f,11–13 and columnar phases are not included. Abbreviations: N = nematic, SmC = tilted smectic LC phase; for the abbreviations of polar phases of bent molecules, see Fig. 2a. [*] and DC (“dark conglomerate”) = chiral conglomerates in isotropic or low birefringent mesophases, observable by POM; hel, H, HC = helical/heliconical superstructures; TB = twist-bend phases; molecule types: BC = bent-core; BD = bent dimesogen; PR = polar rod; polarization modes: L = longitudinal and T = transversal direction of polarization.b folded and twisted layers leading to an amorphous and isotropic sponge-like structure.
DC^[*^]	BC	T	√^b	√	2000	32
N^[*^]	BC	—	—	—	2002	40
NTB (NPT, NX)	BD, BC	—	—	—	2010	41
Iso^[*^]	Polycatenar	—	—	—	2014	45
Sm(CP)^hel (SmCSP^helF, SmCPα)	BC	T	√	√	2016	33
SmCTB	BD	—	√	√	2018	39
NF^[*^]	PR	L	—	—	2023	31
N^helF (^HCNF, NTBF)	PR	L	—	—	2024	28
SmC^helF (SmC^HP)	PR	L	√	√	2024	29

---

As noted above, the heliconical smectic phase with transversal polarization (Sm(CP)^hel) was discovered for the n-alkyl substituted bent-core compounds 1/n (Fig. 1b), suggesting that the polar CN group at the apex plays a critical role in formation of this phase. Notably, no other BCLC lacking the 4-cyanoresorcinol core has exhibited such phase. However, the two previously known compounds 1/O8 and 1/O12 with alkyloxy instead of alkyl chains (Fig. 1b) were reported to form only nonpolar and polar orthogonal smectic phases (SmA and SmAP_A),^46,47 This discrepancy prompted us to reinvestigate these two compounds and to complete this series (1/On, n = 2 to 20) to elucidate the chain-length dependence of the Sm(CP)^hel phase formation, and the effect of the ether oxygens on Sm(CP)^hel formation.

Here we demonstrate that indeed compounds 1/On (including 1/O12) can exhibit stable heliconical Sm(CP)^hel phases, while those of the series 1/n are only metastable. Furthermore, treatment with an alternating electric field substantially enhances the thermal stability range of the Sm(CP)^hel phase by suppressing competing phases, including 3D modulated phases (M1/M2) and non-helical synclinic SmC_sP_A phases. This leads to remarkably broad chain length and temperature ranges for the Sm(CP)^hel phases, significantly wider than those observed in the series 1/n. Interestingly, the transition to the anticlinic SmC_aP_A phase removes Sm(CP)^hel, it even cannot be field induced in this phase range. The formation of this helical superstructure is attributed to synergistic effects of the polar and electron withdrawing CN apex,⁴⁸ weak molecular bending,⁴⁹ and transient molecular helicity.^12a,50 The complete 1/On series is discussed in relation to related molecules. Based on the investigations, general conditions for the heliconical phase formation are proposed.

2. Materials and methods

2.1 Synthesis

Compounds 1/On with n = 2, 4, 10, 11, 12 and 16–20 were synthesized according to Scheme 1 by acylation of 4-cyanoresorcinol C⁴⁹ with 4-[4-n-alkyloxyphenoxycarbonyl]benzoic acids A/n, which were obtained by acylation of 4-alkyoxyphenols with 4-formylbenzoic acid followed by oxidation of CHO to COOH.⁵¹ The detailed synthetic procedures and analytical data are reported in the ESI.† Compounds 1/O8 and 1/O12 have been reported previously by Weissflog et al.⁴⁶ and their phase sequences have been reinvestigated, corrected and updated. The homologs 1/O6⁵² and 1/O14⁵³ have been reported in previous communications and are included here for comparison, but not discussed in more detail.

Scheme 1 Synthetic route to the bent-core mesogens 1/On.

2.2. Investigation methods

The self-assembly of compounds 1/On was studied by polarizing optical microscopy (POM), differential scanning calorimetry (DSC), X-ray scattering (XRS, small-angle scattering and wide-angle scattering, SAXS and WAXS), electro-optical investigations and some of them by dielectric studies, second harmonic generation (SHG) and in free-standing films by the methods and the equipment described in the ESI.†

3. Results and discussion

The transition temperatures and the associated enthalpies for the 1/On compounds are summarized in Table 2 and the data on cooling are shown graphically in Fig. 3. In principle the compounds can be divided into three groups, the short-chain compounds 1/O2–1/O8 forming nematic (N) and smectic phases with emerging anticlinic tilt and polar order (SmA, SmAP_R, SmC_aP_A). The second group of medium chain compounds 1/O10–1/O14 is characterized by a transition to synclinic tilt (SmC_SP_A) and emergence of heliconical phases (Sm(CP)^hel), while for the long chain compounds 1/O16–1/O20 the synclinic tilt becomes more dominant at higher temperature and is replaced by anticlinic tilt at lower temperature (SmC_aP_A), and the heliconical phases can only be field-induced. For the two latter groups, additional 3D modulated mesophases M1/M2 can be observed (Fig. 3). In the following the development of soft self-assembly across these three groups will be discussed step-by-step.

Table 2 Phase transitions of compounds 1/On upon heating (→) and cooling (←) and after treatment with an alternating electric field (E)^a

Comp.	T (°C) [ΔH (kJ mol^−1)]
a Peak temperatures from second DSC heating/cooling scans (10 K min^−1). Curie temperatures are in bold. Arrows indicate heating (→) and cooling (←), E = phase sequence observed upon cooling after application of few cycles of an alternating E-field (on–off switching of a DC field). Transitions without enthalpy were determined by POM or other investigations; abbreviations: Cr = crystalline solid, Iso = isotropic liquid, NCybA = nematic phase with cybotactic clusters of the SmA-type, SmA = uniaxial lamellar phase; SmAPR = high permittivity paraelectric SmA phase range showing ferroelectric-like switching with only one broad polarization current peak per half-period of an applied E-field; SmAPAR = high permittivity paraelectric SmA phase showing two broad polarization current peaks; SmCaPR = high permittivity paraelectric SmCa phase showing ferroelectric-like switching; Sm(CP)^hel = heliconical polar smectic phase; SmCsPA = antiferroelectric switching polar synclinic tilted SmC phase; SmCaPA = antiferroelectric switching polar anticlinic tilted SmC phase; M1 = birefringent and highly viscous mesophase with mosaic texture and unknown structure; M2 = modulated lamellar phase with low birefringence, high viscosity and still unknown precise structure; the M1/M2 ranges were determined by POM investigation of homeotropic samples. The Curie temperatures and heliconical phases are indicated in bold.b First heating scan.c SmCaPA is observed in planar cells and M1 in homeotropic alignment and in free-standing films.d This compound was investigated previously, for details see ref. 52.e This compound was reported in ref. 46 and the original sample was reinvestigated herein, the previously reported SmAPA range turned out to represent SmCaPA and SmAPAR phases; the small differences in transition temeratures result from using DSC data instead of optical.f This compound was reported in ref. 46 and was resynthesized; the DSC transitions are close to those reported previously, while the phase sequence turned out to be different due to the presence of Sm(CP)^hel and weakly tilted smectic phases which were previously interpreted as nontilted phases.g This compound was reported in ref. 53, the initially proposed SmCaPA range below 110 °C tuned out to represent SmCsPA; the pristine Sm(CP)^hel phase was named SmCPα, but the field induced Sm(CP)^hel phase was previously not recognized and this has lead to the initial interpretation as an anticlinic tilted phase. For DSC traces, see Fig. S9 (ESI), for XRD data, see Fig. S10–S25 and Tables S1–S13 (ESI).
1/O2	→ Cr 154[32.3] NCybA 194[0.8] Iso →
	← Cr 86[14.9] NCybA 192[0.8] Iso ←
1/O4	→ Cr 126[28.8] SmCa 129[1.5] SmA 165[1.2] NCybA 170[0.8] Iso →
	← Cr 85[18.9] SmCa 127[1.7] SmA 164[1.3] NCybA 168[1.0] Iso ←
1/O6^d	→ Cr 103[18.6] SmCaPA 144[1.6] SmAPAR 150[−] SmAPR → SmA 179[6.2] Iso →
	← Cr 74[13.8] SmCaPA 142[1.5] SmAPAR 148[−] SmAPR ← SmA 177[6.2] Iso ←
1/O8^e	→ Cr 112[32.0]^b SmCaPA 141[0.9] SmAPR→ SmA 189[8.2] Iso →
	← Cr 65[13.0] SmCaPA 139[1.0] SmAPR ← SmA 186[8.2] Iso ←
1/O10	→ Cr 96[19.3] SmCSPA 122[−] SmCaPA ∼134 SmCaPA/M1^c 139[0.7] SmCaPR ∼145[−] SmAPR → SmA 189[9.0] Iso →
	← Cr 65[13.7] SmCSPA 110[−] SmCaPA ∼130 SmCaPA/M1^c 138[0.8] SmCaPR ∼143[−] SmAPR ← SmA 186[9.2] Iso ←
	E: Cr 65 Sm(CP)^hel ∼ 95 SmCaPA 138 SmCaPR ← SmAPR ← SmA 186 Iso ←
1/O11	→ Cr 93[18.7] SmCSPA 134[−] Sm(CP)^hel 136[1.0] SmCaPR 139[−] SmAPR → SmA 189[9.3] Iso →
	← Cr 61[12.9] SmCSPA 126[−] Sm(CP)^hel 131[−] M1 135[1.0] SmCaPR 138[−] SmAPR ← SmA 187[9.6] Iso ←
	E: Cr 61 Sm(CP)^hel 135 SmCaPR ←SmAPR ← SmA 187 Iso ←
1/O12^f	→ Cr 111[36.8] SmCSPA 136[1.2] SmCaPR 143[−] SmAPR → SmA 191[9.3] Iso →
	← Cr 60 [26.2] SmCSPA 106 [−] Sm(CP)^hel 133[1.2] SmCaPR 143[−] SmAPR ← SmA 190 [9.7]Iso ←
	E: Cr 60 Sm(CP)^hel 133 SmCaPR 143 SmAPR ← SmA 190 Iso ←
1/O14^g	→ Cr 104[36.6] SmCSPA (125[−] Sm(CP)^hel/M1) 136[1.7] SmCPR 146[−] SmA 192[9.3] Iso →
	← Cr 65[29.7] SmCSPA (115[−] Sm(CP)^hel/M1) 133[1.7] SmCPR 145[−] SmA 190[9.7] Iso ←
	E: Cr 65 Sm(CP)^hel 133 SmCPR 145 SmA 190 Iso ←
1/O16	→ Cr 91[41.7] SmCaPA ∼ 90[−] SmCSPA 117 M2 129[1.4] SmCSPR154[−] SmA 185[8.7] Iso →
	← Cr 68[35.4] SmCaPA ∼ 90[−] SmCSPA 115 M2 127[1.3] SmCSPR 152[−] SmA 183[8.8] Iso ←
	E: Cr 68 Sm(CP)^hel 127 SmCSPR 152 SmA 183 Iso ←
1/O18	→ Cr 98[60.5] SmCSPA/M2 128[1.3] SmCSPR → SmCS 158[−] SmA 183[8.3] Iso →
	← Cr 79[49.7] SmCaPA ∼ 85[−] SmCSPA/M2 126[1.4] SmCSPR ← SmCS 156 [−] SmA 180[8.2] Iso ←
	E: Cr 79 SmCaPA ∼ 85 Sm(CP)^hel 126 SmCSPR ← SmCs 156 SmA 180 Iso ←
1/O20	→ Cr 102[81.0] SmCSPA/M2 124[1.4] SmCSPR → SmCS 155[−] SmA 181 [7.2] Iso →
	← Cr 87[53.6] SmCaPA 90–100[−] SmCSPA/M2 122[1.4] SmCSPR ← SmCS 153[−] SmA 178[7.1] Iso ←
	E: Cr 87 SmCaPA ∼90 Sm(CP)^hel 122 SmCSPR ← SmCS 153 SmA 178 Iso ←

---

Fig. 3 Bar diagram of compounds 1/On showing the development of the LC phases on cooling and depending on chain length (see Table 2 for abbreviations and numerical values). ^a E indicates transitions after treatment with few cycles of an alternating electric field; the dashed white line indicates the approximate chain-length dependence of the Curie temperatures of the paraelectric–ferroelectric transition.

3.1. Compounds 1/O2–1/O8 – cybotactic nematic phases and transition to smectic phases

Compounds 1/O2 and 1/O4 (Fig. 3) with the shortest terminal chains form an enantiotropic nematic phase upon cooling from the isotropic liquid state (Fig. 4c). The XRD pattern of a magnetically oriented sample (B ≈ 1 T, see Fig. 4a and b) of the nematic phase of 1/O4 shows a diffuse WAXS with a maximum at d = 0.48 nm located on the equator and a diffuse SAXS with a single maximum at d = 3.58 nm on the meridian, being comparable with the molecular length L_mol = 4.0 nm (determined for a Λ-shaped conformation with 120° bending angle and stretched alkyl chains). This diffraction pattern, indicates a nematic phase composed of cybotactic SmA clusters (N_CybA).^44a,54 It is noted that this type of nematic phase is rare as most nematic phases of bent-core LCs are composed of tilted cybotactic SmC clusters (N_CybC).^55,56

Fig. 4 Data of compound 1/O4 upon cooling. Left and middle column: XRD patterns of a magnetically aligned sample (B = 1 T); (a), (d), (g) and (j) show the complete patterns after subtraction of the scattering in the isotropic liquid state at 172 °C; (b), (e), (h) and (k) show the small angle patterns; (c), (f), (i) and (l) show the POM textures between two non-treated glass plates in the different LC phases at the indicated temperatures; in (c) optically isotropic areas are homeotropic aligned areas, homeotropic alignment is retained in (f), (i) and (l); white arrows in (a) show the direction of the applied magnetic field (B) and in (f) the directions of polarizer (P) and analyzer (A); for textures in planar cells and polarization current curves, see Fig. S27 (ESI†), for textures of 1/O2, see Fig: S26 (ESI†).

Upon cooling, the nematic phase of 1/O4 the diffuse SAXS condenses into a sharp layer reflection with d = 3.66 nm and its second order on the meridian (Fig. 4e) indicating the transition to a smectic phase. The layer reflection remains perpendicular to the maximum of the diffuse WAXS on the equator (Fig. 4d), as typical for a non-tilted SmA phase. However, the layer reflections are elongated parallel to the equator, indicating some orientational order distribution in this SmA phase. Optical investigations under a polarizing microscope confirm the nematic phase which easily aligns completely homeotropic (Fig. 4c). The optically isotropic (black) appearance in the homeotropic alignment is retained across the N-SmA transition (Fig. 4f) and at the next transition at T = 127 °C a birefringent schlieren texture emerges which increases in birefringence on further cooling (Fig. 4i and l). This indicates the onset of phase biaxiality at the transition at 127 °C, due to a transition from random to uniform tilt in the layers. A slight decrease of the layer spacing can be observed at this transition (Fig. S12, ESI†), suggesting a small increase of a molecular tilt in the layers. The striped texture (Fig. 4i) of the homeotropic sample and the horizontally (parallel to the equator) expanded layer reflection (Fig. 4h and k) are in line with an anticlinic tilted SmC_a phase with a small tilt angle.⁵⁷ There is no visible response upon application of an electric field in the SmA as well in the SmC_a range; therefore, we consider both phases as apolar or weakly paraelectric (Fig. S27, please note that the small broad peak is already observed in the Iso phase and could be due to a dielectric response or a conductivity, ESI†).

3.2. Compounds 1/O6 and 1/O8 – emergence of polar order

For the following compounds 1/On with n = 6–20 the nematic phase is removed, and exclusively lamellar phases can be observed (Fig. 3). For example, upon cooling compound 1/O8,⁴⁶ an optical uniaxial smectic phase (SmA) is formed at 189 °C (Fig. 5a, b and Fig. S28a, ESI†) which shows a broad single current peak in each half period of an applied triangular electric wave field (Fig. 5c). Close to the Iso-SmA transition it is very weak and grows on cooling, meaning that the SmA phase is paraelectric and small ferroelectric grains grow in size with lowering temperature (Fig. S28a, ESI†), thus leading to a high permittivity (“superparaelectric”) range of the SmA phase (below ∼150 °C), designated as SmAP_R.⁵⁸ On further cooling the texture of the homeotropic sample becomes birefringent at the phase transition around 139 °C (Fig. 5f and Fig. S9c, ESI†), indicating emerging phase biaxiality due to the onset of an anticlinic tilt. Simultaneously, the broad polarization current peak vanishes, and two sharp current peaks appear (Fig. 5g), indicating the transition to an antiferroelectric switching anticlinic tilted smectic phase (SmC_aP_A). The spontaneous polarization is about 500–700 nC cm⁻², representing typical values for bent-core mesogens. The switching in this SmC_aP_A phase takes place by rotation of the molecules around their long axis (SmC_aP_A ↔ SmC_aP_F),⁵⁹ as typically observed for the weakly bent 4-cyanoresorcinol based mesogens.^37,49 Therefore, the switching process cannot be detected optically by a rotation of the dark extinction crosses, but only by slight textural and birefringence colour changes (Fig. 5d, e and Fig. S28c, ESI†).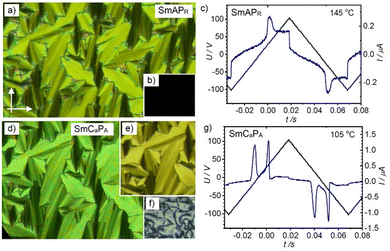

Fig. 5 POM textures (left) and polarization current response curves (right) of compound 1/O8: (a)–(c) in the SmAP_R phase at 145 °C and (d)–(g) in the SmC_aP_A phase at 105 °C, (a) and (d) showing planar textures (PI coated ITO cell 6 μm) in (a) and (d) without applied field and in (e) under an applied field of +10 V μm⁻¹; (b) and (f) show the homeotropic textures without applied field, for additional data, see Fig. S28 (ESI†).

The development of polar order was previously studied in detail for compound 1/O6.⁵² For this compound an additional high permittivity SmAP_AR range, appears between SmAP_R at higher and SmC_aP_A at lower temperature. In the SmAP_AR range the broad single polarization current peak of SmAP_R splits into two broad peaks,⁶⁰ leading to the phase sequence SmA → SmAP_R → SmAP_AR → SmC_aP_A (Fig. 3 and Table 2). While in SmAP_AR the correlation between ferroelectric grains is antipolar, in SmAP_R it is synpolar (ferroelectric).⁵² This means that upon lowering temperature only for 1/O6 antipolar correlation sets in already before macroscopic polar order evolves, while for 1/O8 it coincides with this transition. The removal of SmAP_AR at the transition from 1/O6 to 1/O8 indicates an increasing tendency towards synpolar correlation with growing chain length. For both compounds the anticlinic tilt develops together with the onset of macroscopic polarization at the transition from the high permittivity paraelectric phase to SmC_aP_A.

Compounds 1/O6 and 1/O8 and all following homologues show similar DSC curves having only one lambda-shaped peak with a relatively small enthalpy around ΔH ∼ 1 kJ mol⁻¹ in the whole LC temperature range (see Fig. 6a and Fig. S9, ESI†). In all cases this peak is associated with the onset of macroscopic polar order at the paraelectric–(anti)ferroelectric transition, as confirmed by the dielectric investigations described further below.

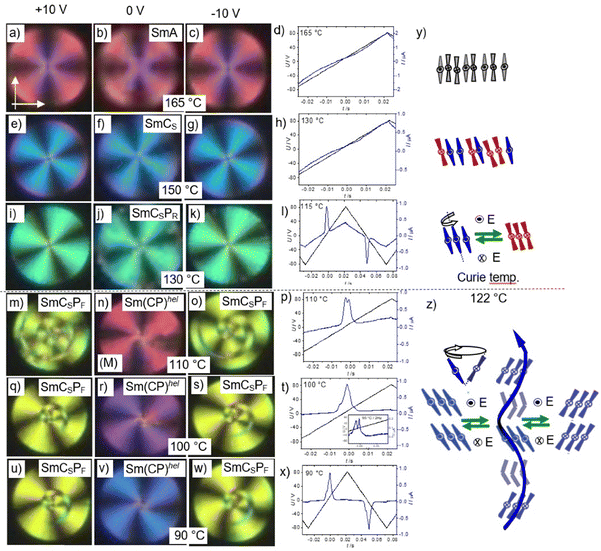
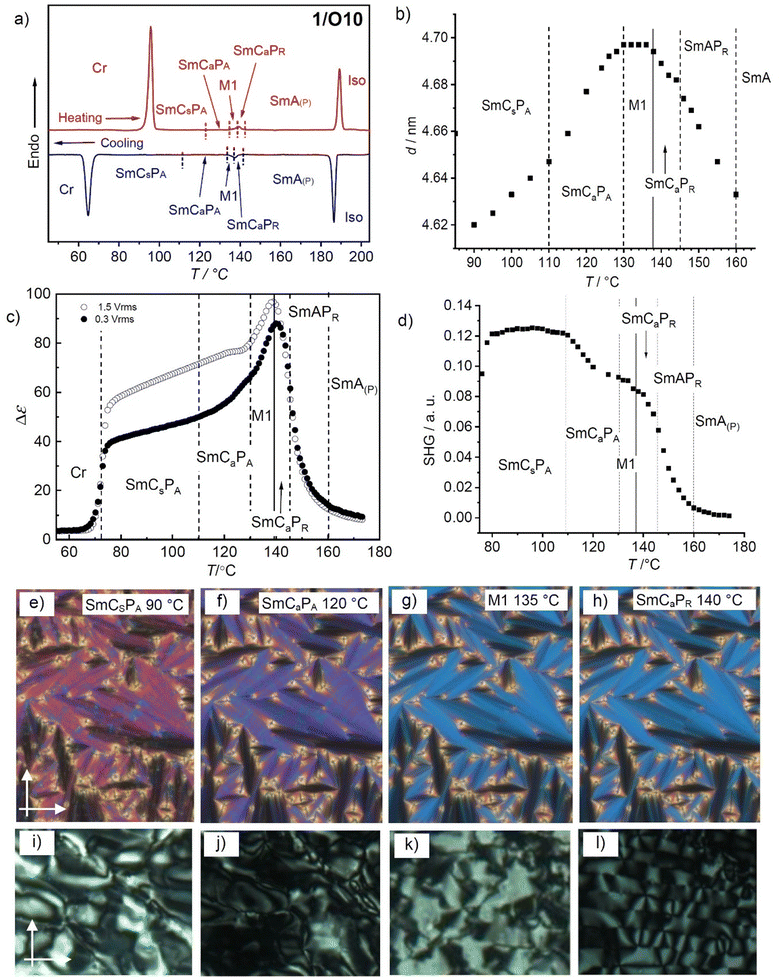Fig. 6 Data of compound 1/O10. (a) DSC heating and cooling traces at 10 K min⁻¹; (b) temperature dependence of the layer spacing, (c) plot of the dielectric relaxation strength (Δε) as a function of temperature; (d) temperature dependence of the SHG activity in a 6 μm ITO cell under an applied field of 12.5 V μm⁻¹ (for field dependence, see Fig. S29, ESI†); (e)–(h) show the fan-like POM textures (planar alignment) and (i)–(l) the POM textures in homeotropic alignment in the different phases at the indicated temperatures; for additional textures, see Fig. S30 (ESI†).

3.3. Compound 1/O10 – development of synclinic tilt, leading to layer modulation and field-induced heliconical twist

3.3.1. Optic and electrooptic investigations. For compound 1/O10 anticlinic tilt sets in already at T = 143 °C, i.e. before long-range polar order starts developing at the transition at 138 °C, associated with the small DSC peak (Fig. 6a). The onset of tilt is indicated by the development of phase biaxiality in a homeotropic cell upon cooling from the uniaxial SmA phase (Fig. 6l). In a planar cell the fan-shaped textures of the SmA phase does not change, i.e. the dark extinctions remain parallel to polarizer and analyser, meaning that the tilt is anticlinic (Fig. 6h). Upon applying an electric field in this temperature range a broad single polarization peak is recorded (Fig. 7c, the small sharper peak C is attributed to conductivity) which means that relatively large polar domains with synpolar correlation grow under the applied electric field, as typical for the high permittivity phase ranges. However, for 1/O10 the high permittivity phase range between 143 and 138 °C is anticlinic tilted and hence designated as SmC_aP_R (see Fig. 3 and Table 2). Here anticlinic tilt develop before long range polar order is achieved.

Fig. 7 Optical micrographs of the POM textures observed for the different LC phases of compound 1/O10 in a PI coated 6 μm ITO cell in planar alignment, (a), (d) and (g) without applied electric field, (b), (e) and (h) after application of 6 V DC field, and (c), (f) and (i) polarization current response curves in the same cell at the indicated temperatures; in (c) C indicates the conductivity peak; all data were recorded on cooling.

At the phase transition at T = 138 °C the texture in the homeotropic cell becomes mosaic-like, consisting of birefringent platelets and the viscosity of the LC phase increases significantly, indicating the transition to a modulated LC phase (M1 phase, Fig. 6k). On further cooling the homeotropic sample to about 130 °C restores a fluid schlieren texture, though without the stripe pattern (Fig. 6j) and with gradually increasing birefringence on further cooling (Fig. 6i). However, in the planar fan texture no change takes place in the M1 phase region (Fig. 6h and g). This means that either a layer modulation develops only in homeotropic alignment where the molecules are organized with the layer planes parallel to the interfaces, while in planar alignment with the molecules parallel to the surfaces this modulation is suppressed, or the layer modulation has for any reason no effect on the planar texture. Under a triangular wave field two sharp polarization peaks per half period can be observed (Fig. 7f). This double peak confirms an antiferroelectric switching below 138 °C, in the range of the M1 phase as well as in the SmC_aP_A range. Because no change of the orientation of the extinctions is observed this switching takes place by rotation around the long axis between SmC_aP_A and SmC_aP_F, (Fig. 7d and e).

At 110–100 °C the birefringence of the hometropic sample increases (Fig. 6i), while in the planar fan texture the dark extinction parallel to the polarizers become gradually birefringent due to a transition from anticlinic to synclinic tilt correlation between the layers (Fig. 6f and e). In the synclinic phase below 100 °C there are still two polarization current peaks (Fig. 7i), so that this low temperature phase is SmC_SP_A. Under the applied electric field a stripe pattern develops on the fans, as typical for field induced SmC_sP_F states with opposite tilt (Fig. 7h). However, after switching off the applied field the extinctions parallel to polarizer and analyser become completely dark (Fig. 7g), indicating a smectic phase with the optical axis perpendicular to the layers (Fig. 7g). This observation is explained further below for compound 1/O11 as example.

3.3.2. X-ray scattering. The SAXS patterns of 1/O10 confirm a layer structure with a spacing of d = 4.6 to 4.7 nm (Fig. 6b) in all LC phases. There is an increase in d-spacing between 160 °C and the phase transition at 138 °C, in line with an increasing packing density due to the growing orientational order parameter. No further change of d-spacing and no extra scattering peaks can be found beside the layer reflection in the M1 range, even by using a synchrotron source (Fig. S16, ESI†). At the transition to the polar smectic phases d starts decreasing, in line with an increasing tilt, but without visible discontinuity in the d-value change at the anticlinic–synclinic transition (see Fig. 6b). In all LC phases discussed herein the WAXS is diffuse with a maximum around 0.48–0.50 nm at highest and 0.46–0.48 nm at lowest temperature, confirming fluid LC phases without fixed positions of individual molecules (see for example Fig. S13, ESI†).

3.3.3. Dielectric investigation. Dielectric spectroscopy of 1/O10 was performed in the frequency range between 1 Hz and 10 MHz (Fig. S44, ESI†) using the Havriliak–Negami equation to fit the data. Fig. 6c shows the temperature dependence of dielectric strength and relaxation frequency. On cooling the sample from the isotropic phase, the dielectric strength δε increases in the paraelectric LC range (SmA → SmAP_R → SmC_aP_R) due to the growth of the ferroelectric grains and reaches a maximum at the phase transition at 138 °C, when the ferroelectric grains fuse to almost infinite polar layers. Thus, the δε maximum at the phase transition around 138 °C can be attributed to the paraelectric–ferroelectric transition with Curie–Weiss-type divergence.⁶¹ Below 138 °C, δε decreases, but still remains high in magnitude, meaning that the electrostatic energy of the developing ferroelectric layers is reduced by polarization splay, leading to the modulated M1 phase. The transition to the antipolar SmC_aP_A phase is associated with a decrease of the slope of the δε curve. Further, δε continuously decreases until crystallization at 60 °C, which is attributed to the strengthening of the antipolar correlation between the polar layers with lowering temperature. There is no indication for any change of the dielectric strength around the synclinic-anticlinic transition at ∼110 °C. Similar δε = f(T) curves were recorded for 1/O12 and 1/O16 (see Fig. S43a–c, ESI†).

3.3.4. SHG investigations. Development of polar order was additionally confirmed by measuring second harmonic generation (SHG) in PI coated 6 μm ITO cells. No SHG signal was observed in all LC phases in the field-free state. The temperature dependence of the field-induced SHG signal under a low frequent (10 Hz) rectangular waveform voltage of 25 V_pp μm⁻¹ is shown in Fig. 6d. Very weak field-induced SHG could be detected already in the SmA range confirming its paraelectric nature. The SHG signal continuously increases with increasing electric field strength and lowering temperature. It considerably rises below ca. 160 °C in the SmAP_R and SmC_aP_R ranges, where the SHG signal shows a field-dependent saturation as typically observed for clusters of molecules whose dipoles cooperatively reorient (Fig. S42c, ESI†). The character of the SHG field dependence shows a sharp step below 138 °C, as indicative of an antiferroelectric switching (Fig. S42d, ESI†). The sharp step remains in the investigated temperature range down to 80 °C (Fig. S42e and f, ESI†) with an increase of the SHG intensity until the transition from SmC_aP_A to SmC_sP_A at 110 °C (Fig. 6d). Hence, the SHG studies confirm the conclusions drawn from the dielectric studies, especially assigning the phase transition with small ΔH in the LC range (Fig. 6a) to the Curie temperature of the paraelectric–ferroelectric transition. The almost linear decrease of the temperature of this transition with growing chain length is indicated in Fig. 3 by a dashed white line across the bars.

3.3.5. Freely suspended films. The rich variety of polar and tilted LC phases of 1/O10 makes it a very interesting system to study in freely suspended films. The character of polarity and tilt correlations can often be better determined in thin films rather than in the bulk, though some phase transition temperatures can be significantly shifted to higher temperatures compared to the bulk samples and thus need to be cross-checked and adjusted. For example, the SmA-Iso transition is shifted by 15 K up to 204 °C. The films were prepared in the SmAP_R phase range at 150 °C. The isotropic extinct texture is uniaxial with the optical axis aligned perpendicular to the smectic plane. The transition into the biaxial smectic phase (SmC_aP_R) is accompanied by the development of a Schlieren texture (Fig. 8a). Applying an in-plane electric field in the SmC_aP_R range at 145 °C, we could test the polar character of the molecular order. The director field readily responses to the DC and AC electric fields in the frequencies range DC – 1 kHz. The AC response is dominated by the dielectric reorientation; the slow bow axis aligns perpendicular to the electric field (Fig. 8b–d). This suggests that the effective dielectric anisotropy within the film plane is negative (Fig. 8e).

Fig. 8 (a)–(d) POM textures of a 1.9 μm thick freely suspended film in the SmC_aP_R phase of 1/O10 at T = 145 °C, (a) in the field-free state, (b) and (c) under an electric field of opposite polarity; (d) image with the λ-wave-plate; the width of the images is 700 μm. (e) and (f) The sketches demonstrate (e) negative dielectric anisotropy: the slow axis (γ, red arrows) is aligning perpendicular to the applied electric field direction (E) and (f) positive dielectric anisotropy where γ and E are parallel; see also Fig. S50 (ESI†).

However, under a DC field the situation is different. The slow axis aligns parallel to the field (Fig. 8f) and the response has a clear polar character suggesting the presence of the spontaneous polarisation in the film. This is particularly well seen in the presence of the topological defects of the topological strength +1 as shown in Fig. 8a–d. The polar director forms tangential loops around the defect core. In Fig. 8b, an electric field favours the director orientation in the bottom left quarter, while in Fig. 8c, the opposite polarity favours the top right quarter. The spontaneous polarisation could be estimated from the field dependence of the widths ξ of the inversion walls and accounts for approx. 140 nC cm⁻². The inversion wall is proportional to E^−1/2 in concord with the polar (vs. dielectric) coupling (Fig. S49, ESI†). The static DC field obviously supports the growth and fusion of the ferroelectric grains to larger polar domains.

The transition from SmC_aP_R to M1 phase is accompanied by “freezing” of the Schlieren texture and its transformation into a mosaic-type polymorphic texture composed of small stripe-like domains with typical widths of about 5–10 μm (Fig. 9a). This texture shows no response on an electric field (1 V mm⁻¹). A drastic textural transformation occurs on rapid heating from the SmC_aP_A phase below the M1 phase, when a finger-like structures nucleates, which elongates and bifurcates resulting in quasi-1D periodic striped texture (Fig. 9b–d). This indicates the emergence of a layer modulation force at this temperature, which is likely to be caused by the increasing polar coherence length.

Fig. 9 (a) Growth of the labyrinthine texture (a) at the transition from the SmC_aP_R phase on cooling and (b)–(d) at the transition from the SmC_aP_A to the M1 phase upon rapid heating; (a)–(c) as observed between crossed polariser and (d) with a full-wave plate in a freely suspended film of 1/O10; (e) and (f) show the transition from the (e) SmC_aP_A phase at 128 °C to (f) the SmC_sP_A phase at 104 °C. The film thickness is 740 nm in (a)–(d) and >1000 nm in (e) and (f).

There are two additional tilted phases occurring below the modulated M1 phase. On cooling, the labyrinth texture melts into the Schlieren pattern containing a large number of concentric inversion walls which slowly relax with time. This texture suggests a tilted SmC-type phase without spontaneous polarization (Fig. 9e). Examining the film under oblique incidence, we found no asymmetry in the transmission change on the tilting, confirming that the phase is of anticlinic structure (SmC_aP_A). The inversion walls represent alternating regions of splay and bend deformations of the c-director.

At T = 114 °C another transition takes place, but the texture remains SmC-type Schlieren (Fig. 9f). The transition is marked by nucleation of circular domains enclosed by dislocation lines. The analysis of the optical transmittance under oblique incidence confirms that the structure of the phase is synclinic. Bend and splay inversion walls appear to be of the same width suggesting that K_s ≈ K_b (Fig. S49, ESI†). This transition corresponds to the SmC_aP_A–SmC_sP_A transition occurring in the bulk sample at ∼110–100 °C on cooling and 122 °C on heating. Thus, thin film investigations fully confirm the proposed phase sequence of 1/O10.

3.4. Compounds 1/O11–1/O14 – emergence of the heliconical Sm(CP)^hel phase

3.4.1. Compound 1/O11. For compound 1/O11 upon approaching the Curie temperature the polar order develops in the same way (SmA → SmAP_R → SmC_aP_R) and in the homeotropic aligned sample the low birefringent schlieren texture (Fig. 10a) turns at the Curie temperature (DSC peak at 135 °C, Fig. S9d, ESI†) into a highly birefringent mosaic-like texture (M1 phase, Fig. 10b), similar as found for 1/O10. However, for 1/O11 the M1 range is very short and the homeotropic sample becomes pseudoisotropic at 133 °C (Fig. 10c) at the transition to a uniaxial smectic phase. The d-spacing decreases in the M1 phase and in the uniaxial phase (see Fig. S17b, ESI†), confirming a growing tilt. In planar alignment the fan texture with extinctions parallel to polarizer and analyser is retained in this temperature range, additionally confirming a uniaxial phase (Fig. 10f–h). This combination of tilted organization and uniaxiality is a first indication of a short-pitch heliconical phase (Sm(CP)^hel). The heliconical superstructure was unambiguously proven for the alkyl substituted compounds 1/14³⁶ by soft resonant X-ray scattering at the carbon-13 edge. It was found to represents an incommensurate helix with a pitch length of ∼3 molecules.³⁴ Based on this direct proof, typical features of the Sm(CP)^hel phase were identified, which allow the identification and confirmation of this heliconical phase (see Section S6 of the ESI†). One of them is the development of a regular stripe pattern on the fans (“tiger stripes”,³⁴ see Fig. 10l) under an applied DC field due to partial unwinding of the heliconical twist. At sufficiently high field strength the helix is completely unwound and then a tilt-domain texture is formed (Fig. 10m–o). At the field induced transition to SmC_sP_F states with opposite tilt direction. The stripe pattern is formed immediately below the Curie temperature in the ranges of the M1 and the uniaxial smectic phase and with decreasing temperature the field strength required for the transition from the tiger stripes to the tilt domain texture decreases. This means that a helical twist is already involved in the M1 phase and that the helical twisting power becomes smaller at lower temperature. (see Fig. 10l, m and Fig. S32a, ESI†). Another typical feature of the Sm(CP)^hel phase is the occurrence of two peaks in the polarization current curves, both positioned around 0 V-crossing with the peak before 0 V being splitted into two close peaks, in most cases only indicated by a shoulder or a significant peak broadening (“ferrielectric switching”, Fig. 10r and s).^36,37,53

Fig. 10 Optical micrographs of the textures observed for the different LC phases of compound 1/O11. (a)–(e) In a homeotropic cell, the insets show the planar alignment in PI coated 6 μm ITO cell before applying any field; (k)–(o) under an applied DC field and (f)–(j) after switching off the electric field, recorded at the indicated temperatures; (p)–(t) show the corresponding polarization current response curves at the indicated temperatures; for related data of 1/O12–1/O18, see Fig. S33–S41 (ESI†).

The field induced textures (Fig. 10h–j and m–o) and the shape of the polarization current curves do not change on further cooling down to crystallization, (Fig. 10r–t), meaning that the Sm(CP)^hel phase is retained once an electric field has been applied. However, in the pristine sample, before application of an electric field there is a change of the fan texture at 126 °C where the dark extinctions become birefringent (insets in Fig. 10c–e), due to the transition from Sm(CP)^hel to a synclinic tilted phase (SmC_sP_A) at this temperature. In addition, the uniaxial homeotropic sample becomes birefringent, confirming the transition to a biaxial SmC_SP_A phase (Fig. 10c–e). This means that in the pristine material before any field treatment there is the sequence SmA – SmAP_R – SmC_aP_R – M1 – SmC_sP^hel_F – SmC_SP_A on cooling. Upon heating the SmC_SP_A range is expanded up to 134 °C, replacing the M1 phase completely and reducing SmC_sP^hel_F to a small range between 134 and 136 °C (Table 2). However, after treatment under an electric field the M1 phase as well as the SmC_SP_A phase are completely suppressed and only the heliconical phase is observed between the crystalline state and the Curie temperature, i.e. there is a direct transition between Sm(CP)^hel and SmC_aP_R, leading to the field-induced sequence SmA – SmAP_R – SmC_aP_R – SmC_sP^hel_F (Table 2 and Fig. 3). The field induced transition from SmC_SP_A to Sm(CP)^hel is also found in the SmC_SP_A range of the shorter homologue 1/O10 (see previous section), and it is observed in the SmC_SP_A ranges of all following homologs with n ≥ 10 (Fig. 3).

3.4.2. Compound 1/O12. For the next homologue 1/O12 the same phase sequence is observed with the difference that no M1 phase can be found and the Sm(CP)^hel range of the pristine sample is larger and expanded down to 106 °C on cooling. However, upon heating neither the M1 phase nor the Sm(CP)^hel phase were detected and a direct transition from SmC_SP_A to SmC_aP_R takes place at the Curie temperature. Also in this case the SmC_SP_A phase is completely replaced by Sm(CP)^hel under an alternating electric field (see Table 2 and Fig. 3, Fig. S32b–S34, ESI†).

For this compound the induction of a heliconical superstructure was additionally confirmed in homeotropic alignment by application of an in-plane field (Fig. 11). The relatively small birefringence of the SmC_SP_A phase suggests that some distortion (due to splay director modulation or twist) is already involved in the ground state (Fig. 11a). Upon application of the in-plane field in the SmC_SP_A range at 105 °C (Fig. 11a–d) the birefringence first increases between the electrodes by alignment of the molecules and removal or reduction of the above-mentioned distortions (Fig. 11a and b) and transformation of the SmC_SP_A phase into a structure with a larger contribution of synpolar aligned layers (see (b and f) in Fig. 11i). At a certain threshold field strength, the area between the electrodes becomes isotropic (i.e. the phase becomes uniaxial) due to the induction of a short pitch helix (Fig. 11b and c). On further increasing field strength the helix is unwound to give the birefringent field-induced polar SmC_SP_F state (Fig. 11d).

Fig. 11 (a)–(h) POM textures of 1/O12 in an 8 μm homeotropic cell at the indicated temperatures under the given applied in-plane fields; (a)–(d) in the SmC_aP_A temperature range and (e)–(h) in the Sm(CP)^hel range; the gap between the electrodes is 180 μm. (i) Shows the schematic energy profile and schematics of the molecular reorganization during the field induced transitions; see Fig. S35 (ESI†) for relaxation experiments and for related data of 1/O10 and 1/O18, see Fig. S29 and S41 (ESI†).

Interestingly, in the temperature range of the Sm(CP)^hel phase (at 127 °C, see Fig. 11e–h) the birefringence is first induced under the field before it disappears again. This means that the helix is first partly unwounded or deformed before an optical uniaxial field induced state is formed at higher field strength (Fig. 11e–g). This field induced uniaxial state can represent a 90° twisted 4-layer state related to the α-phase⁶² or any short-pitch heliconical state which might be slightly different from the Sm(CP)^hel ground state structure, for example by different pitch lengths or degree of commensurability with the layer periodicity. In the temperature range of the SmC_sP_A phase the field-induced Sm(CP)^hel state (which again might be identical or slightly different from the initial ground state) appears to be metastable (at least in homeotropic cells), as it slowly relaxes (within several minutes to hours) back to a birefringent texture (see Fig. S35, ESI†).

3.4.3. Compound 1/O14. While for compounds 1/O10–1/O12 the polarization randomized phase above the Curie temperature is an aniclinic tilted SmC_aP_R phase, for compound 1/O14⁵³ the tilt becomes synclinic, though the synclinic layer coupling appears to be still very weak in this case (therefore we use SmCP_R instead of SmC_SP_R). The modulated M1 phase, the heliconical Sm(CP)^hel and the SmC_sP_A phase compete with each other below the Curie temperature as reported previously.⁵³ However, in contrast to the previous report we found that below ∼115 °C on cooling only the SmC_sP_A phase is formed which on heating is stable to ∼125 °C. Upon field treatment the SmC_sP_A and M1 phases are removed thus expanding the Sm(CP)^hel phase range from the Curie temperature down to crystallization. It is noted that in ref. 53 the SmC_SP_A range was mistakenly assigned as SmC_aP_A, because the field-induced Sm(CP)^hel phase formation was not recognized at that time; the updated phase sequences are given in Fig. 3 and Table 2.

3.5. Compounds 1/O16–1/O20 – dominance of synclinic tilt

3.5.1. Optical and electrooptical investigations. For all compounds with n = 16–20 there is a well-developed synclinic tilt in the high permittivity smectic phase range (SmC_sP_R). Only for 1/O16 a direct SmA–SmC_sP_R transition takes place, while for compounds with longer chains synclinic tilt is formed (SmC_S) before SmC_sP_R develops and the SmC_sP_R range shrinks with growing chain length (see Fig. 3), i.e. development of polar coherence starts only after the onset of uniform synclinic tilt. The textures of the ground state LC phases of compound 1/O20, as an example, show a transition from the uniaxial SmA phase (Fig. 12a and f) at highest temperature via a uniformly tilted smectic phase range involving SmC_S and SmC_SP_A (Fig. 12b–d, g and h) to an anticlinic SmC_aP_A phase at lowest temperature (birefringent homeotropic texture + extinctions parallel to the polarizers in planar alignment, see Fig. 12e and j).

Fig. 12 Textures of pristine compound 1/O20, (a)–(e) in homeotropic alignment and (f)–(j) in planar alignment in the LC phases at the indicated temperatures. for DSC-traces, see Fig. S9h (ESI†).

Remarkably, there is a low birefringent, but not completely dark state for the homeotropic texture below the Curie temperature at 122 °C (Fig. 12b–e) showing the absence of the uniaxial Sm(CP)^hel and the highly birefrngent M1 phases. The reorientation of the extinction crosses in a circular domain in Fig. 13 clearly shows the switching mechanisms in the distinct LC phases, together with the field induced structures. There is no change of the orientation of the extinction crosses under the applied E-field in the non-polar and paralelectric SmA (Fig. 13a–c) and SmC ranges (Fig. 13e–g), while only a slight increase of birefringence can be identified for the field-induced texture in the SmC_SP_R range (bluish green vs. green, see Fig. 13i–k), as typical for Langevin type paraelectric reorganization of polar clusters by rotation of the molecules around their long axes (Fig. 13y, bottom). Below the Curie temperature the extinctions become aligned parallel to the polarizers at 0 V, in line with the induction of a heliconical Sm(CP)^hel state by the applied alternating E-field (Fig. 13n). Under an applied positive or negative electric field, the extinctions rotate to the left or right (Fig. 13m and o), due to the removal of the helix by transition to the field induced SmC_SP_F states with opposite tilt direction. Because of insetting crystallization, we were unable to study the SmC_aP_A phase below 90 °C.

Fig. 13 (a)–(x) Switching in the smectic phases of compound 1/O20 (6 μm non-coated ITO cell). The three left columns show circular domain as observed by POM upon cooling, from left to right at +10 V, after switching off the applied voltage, and at −10 V; the right column show the corresponding polarization current curves (160 V_pp, 10 Hz); (y) and (z) show sketches of molecular reorganization for the distinct switching processes.

The polarization current response curves show the absence of polar switching in SmA and SmC_s (Fig. 13d and h), a ferroelectric-like relatively broad single peak in SmC_SP_R and a broad feature in SmC_SP_A (Fig. 13p and t). Applying a lower frequency (2 Hz) leads to a splitting into a broad and a sharper peak, as typical for the ferrielectric-like switching in the field induced Sm(CP)^hel state (Fig. 13t, inset). They merge to a single peak on further cooling (Fig. 13x), which is interpreted as a result of slowing down of the switching due to the increasing sample viscosity and the insetting partial crystallization.

3.5.2. M2 phases. For all three compounds 1/O16–1/O20 in homeotropic alignment, a decrease of birefringence takes place immediately below the Curie temperature, though these samples never become completely isotropic (Fig. 12c). In this low birefringent temperature range the viscosity of the sample is significantly enhanced. This temperature range is designated as M2 to distinguish it from the highly birefringent M1 phase of the shorter homologs 1/O10–1/O14 (Fig. 10b). The reduced birefringence is most probably due to the presence of a helical twist, while the increased viscosity suggests that not a simple heliconical phase is formed, but a polarization and chirality modulated mesophase with more complex structure evolves. It is likely that the formation of the birefringent M1 phase (n = 10–14) is associated with a certain tendency towards anticlinic tilt correlation, while the low birefringent M2 phase (n = 16–20) requires a sufficiently strong preference of synclinic tilt. As for M1, also in M2 there is no extra SAXS scattering besides the layer reflections (Fig. S20, S21 and S23) and a birefringent texture is found in planar alignment (Fig. 12h). The phase becomes fluid upon cooling to the phase range designated as SmC_SP_A, without visible change of the planar texture at this “transition”. As observed for the M1 phase of compounds 1/O10–1/O14, under an alternating E-field the Sm(CP)^hel phase is induced in the M2 range, too, which once formed remains stable in the whole M2 and also in the SmC_SP_A range down to the crystallization or transition to the SmC_aP_A phase.

3.5.3. Freely suspended films. For 1/O16, as example for the long chain compounds, the phase sequence was investigated in a freely suspended film. The SmC phase above the Curie temperature is indicated as synclinic by the optical transmission around the +1 defect in Fig. 14a. Upon transition to the M2 phase the Schlieren texture of the SmC_SP_R phase evolves into a polymorphic texture characterized by fine ripples overlaying the original Schlieren pattern (M2 phase, Fig. 14b). As the temperature changes further, these ripples gradually smooth out (Fig. 14c and d). The rippled texture reflects a periodic, smectic-like modulation on a submicrometer scale within the film plane. This modulation likely arises from splay director modulation in the ferroelectric phase or from a frustrated helical structure due to film confinement. Such periodic modulation significantly increases the material's viscosity and enhances the film's elasticity. The observed flattening of the texture suggests that the modulation periodicity becomes smaller than the optical resolution, resulting in a texture typical of smectic phases in a bookshelf geometry.

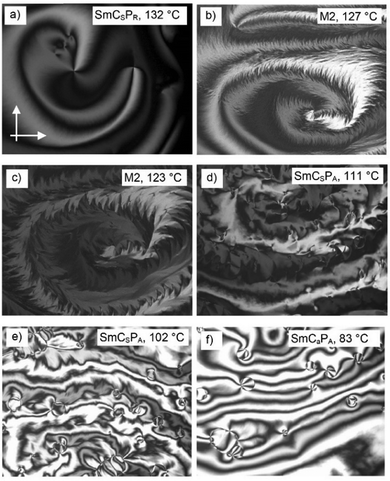Fig. 14 (a–f) POM textures of a freely suspended film (2.6 μm) of 1/O16 as observed at the indicated temperature on cooling; the image width is 700 μm.

Upon further cooling, the texture “melts” into a nematic-like Schlieren texture, indicating the dissolution of the periodic structure and the re-establishment of the nematic-like in-plane order of the c-director (Fig. 14e). In case of oblique incidence, the films appear to have regions with two distinct tilt states confirming the synclinic character of the SmC phase (SmC_SP_A). The regions of opposite tilt are marked by the circular domains. The contrast between the domains of opposite tilt diminishes upon the next phase transition. This results from the anticlinic order of the tilt in the SmC_aP_A phase at lowest temperature. Here circular domains with the phase mismatch of the alternating tilt are separated by the domain walls (Fig. 14f). Thus, the investigation of thin films confirms the phase sequence deduced from the other investigations (see Table 2 and Fig. 3; for thin films investigations of 1/O20, see Fig. S51 and S52, ESI†).

3.6 Discussion of structure–property relations

3.6.1. Phase sequence depending on chain length and temperature. For all compounds 1/On with n = 6–20 (Fig. 3) there is a paraelectric-(anti)ferroelectric transition with Curie–Weiss type divergence (see Fig. 6c and Fig. S43, ESI†). In the high permittivity paraelectric ranges above the Curie temperature the polar order is restricted to local domains, while long range polar order develops at the Curie temperature. In the high permittivity ranges shortly above the Curie temperature chain elongation leads to a transition from the non-tilted (or randomly tilted) SmAP_AR phase (n = 6) via SmAP_R (n = 8) to an anticlinic tilted SmC_aP_R phase range (n = 10–12), which becomes synclinic for n = 14 (SmCP_R) and the synclinic tilt correlation is strengthened upon further chain elongation (SmC_SP_R). In the polar smectic phases below the Curie temperature the layer correlation changes with growing chain length n from anticlinic (n = 6–10, SmC_aP_A) via heliconical (Sm(CP)^hel) for n = 11 → 14 to synclinic for all following compounds with n = 11–20 (SmC_SP_A, see Fig. 3). Thus, the Sm(CP)^hel phase is an intermediate phase involving polar layers and occurring at the anticlinic–synclinic transition, accompanied by (and competing with) the M1 and M2 phases, having more complex and not yet solved helical or splay modulated structures. As synclinic tilt becomes more dominant, the Sm(CP)^hel phase is removed as pristine ground state structure, and M1 is replaced by M2 at the transition from n = 14 to 16 (Fig. 3). For all compounds with n ≥ 11 the Sm(CP)^hel is expanded and replaces the complete SmC_SP_A range after treatment with a few cycles of an alternating electric field; in most cases only one switching cycle is required.

3.6.2. Comparison of series 1/n and 1/On – the effect of the ether linkages. In Fig. 15 the LC phase ranges of the previously reported alkyl substituted compounds 1/n are shown, which could be compared with those of the alkoxysubstituted compounds 1/On, shown in Fig. 3. As expected, all LC phase transition temperatures, including the Curie temperatures (100–115 °C for 1/n³⁷ and 120–140 °C for 1/On, dotted white lines in Fig. 3 and 15), are a bit higher for the series 1/On with alkyloxy chains, while the phase types and phase sequences are quite similar. Remarkably, all compounds 1/On have their Curie temperature above the melting point and thus form stable enantiotropic polar heliconical phases, whereas for all compounds of the previous series 1/n they were only monotropic, i.e. metastable and only observable on cooling. In both series there is a transition from a N_CybA phase (n = 2, 4) to a SmA/SmC dimorphism with a transition from anticlinic to synclinic tilt in the SmC phases by chain elongation and an increasing polar coherence length with lowering temperature.

Fig. 15 Bar diagram of compounds 1/n showing the development of the LC phases on cooling and depending on chain length;^{37 a} Phase transitions before applying an external electric field and ^b after application of a few cycles of an AC field (E); the dashed white line indicates the approximate chain-length dependence of the Curie temperatures starting with 1/8. Note that also for 1/8 there is a short SmAP_AR range between SmC_aP_A and SmA. Reproduced with permission from ref. 37, copyright 2020, Wiely.

A major difference between these two series is the stronger tendency of series 1/On to assume synclinic instead of anticlinic tilt. Therefore, in this series the SmC_aP_A–SmC_SP_A transition already takes place for n = 10, while n = 18 is required for series 1/n. Though the region of Sm(CP)^hel phase formation in the ground state is comparable in both series (n = 12–16 for 1/On and n = 11–14 for 1/n), the field-induced Sm(CP)^hel phase is much more prominent in series 1/On and can be found already for n = 10 while n = 18 is required for compounds 1/n (Fig. 3 and 15). Moreover, the layer modulated M1/M2 phases are missing in the series 1/n, which might indicate a stronger helical twisting power provided by compounds 1/On.

Though there is no measurable difference of the optical tilt between compounds 1/n and 1/On with the same chain length (ca. 20° in SmC_R and ca. 30° in SmCP_A), the synclinic tilt appears to be more robust in the series 1/On. This might be an effect of introduction of the two ether linkages providing slightly different molecular conformations and conformational mobilities (different rotational barriers around the Ph-CH₂CH₂- and Ph-OCH₂- bonds),⁶³ thus modifying the molecular helicity^12a,50 and the interlayer end-to-end interactions between the molecules.⁶⁴ It appears that in the pristine samples of compounds 1/On the Sm(CP)^hel formation is disfavourd in the anticlinic SmC_aP_A range and favoured in the synclinic SmC_SP_A range, while in the series 1/n it is just the other way around (Fig. 3 and 15). Consequently, in the series 1/n the pristine Sm(CP)^hel phase is derived from the SmC_aP_A phase just before transition to SmC_SP_A while in series 1/On it is derived from SmC_SP_A and removed upon SmC_aP_A phase formation. However, in both series the field induced Sm(CP)^hel phase can only be obtained in the SmC_SP_A phase range (Fig. 16, right), while in SmC_aP_A the switching takes place by rotation around the long axis between SmC_aP_A and SmC_aP_F (Fig. 16, left). For compounds 1/On the Sm(CP)^hel phase is field induced in the complete SmC_SP_A ranges, while for most of the compounds of series 1/n, with exception of 1/18, it is only formed in a small part of the SmC_SP_A phase (compare Fig. 3 and 15). In addition, different low temperature phases can be observed in the two series; for compounds 1/n there is a re-entrance of an SmA phase, in this case showing ferroelectric switching (SmA′P_F) for n = 16–20,^37,65 partly or completely replacing the SmC_aP_A phase of compounds 1/On with the same chain length.

Fig. 16 Switching modes in the tilted smectic LC phases of the series 1/n and 1/On; the dotted lines indicate spontaneous reorganizations without applied field.

There are also differences in the switching process (Fig. 16). In both series application of an electric field to the Sm(CP)^hel phase unwinds the helix and leads to a field induced SmC_SP_F state, which then relaxes back to Sm(CP)^hel after releasing the field (Fig. 11i and 16, right side). In the SmC_SP_A phase range of both series at first Sm(CP)^hel, and then the SmC_SP_F state is induced under an increasing applied field. However, in the SmC_aP_A phase of compounds 1/On no helix can be induced and the switching takes place by collective rotation around the long axis, leading to the field-induced SmC_aP_F state which in the same way relaxes back to SmC_aP_A after switching off the applied field (Fig. 16, left side). Hence, no Sm(CP)^hel phase can be induced as soon as the SmC_SP_A phase is replaced by SmC_aP_A (compounds 1/O6–1/O10 and 1/O18–1/O20, see for example Fig. S29, ESI†). Therefore, we observe for compound 1/O10 the induced Sm(CP)^hel phase not directly below the Curie temperature, as found in all other cases, but at much lower temperature after the transition from SmC_aP_A to SmC_SP_A.

For compounds 1/On there is also a slightly larger tendency towards synpolar (“ferroelectric”) layer correlation above the Curie temperature, i.e. there is only one compound with an antipolar SmC_aP_AR phase (1/O6) compared to two for the series 1/n (n = 6, 8), and the SmC_SP_AR phase of 1/20 is missing for 1/O20. On the other hand, in the series 1/n a non-tilted ferroelectric SmA′P_F is observed for n = 16–20⁶⁵ which is replaced by an anticlinic and antiferroelectric SmC_aP_A phase for the same chain length in the series 1/On. Nevertheless, dielectric investigations show for these long chain compounds of series 1/On an increase of δε in the low temperature range of the SmC_sP_A phases of compounds 1/O16–1/O20 (Fig. S43b–d, ESI†) which could be interpreted as a growing tendency towards ferroelectric polar order. This is supported by the temperature dependence of the d-spacing in the SAXS patterns (Fig. 17). While for compounds 1/O10–1/O11 there is a continuous decrease of the d-spacing below the Curie temperature due to the growing tilt (see also Fig. 6b and Fig. S17b, ESI†), for 1/O12 and 1/O14 an increase of the d-value starts within the SmC_sP_A range (see also Fig. S18 and S19, ESI†) while for the long chain compounds 1/O16–1/O20 there is a continuous increase of the layer spacing (despite of the tilt) with lowering temperature in the whole LC range (see also Fig. S20b, S22c and S24c, ESI†). This means that increasing packing density, coupled with an alkyl chain stretching, becomes dominating for the layer spacing. Because crystallization sets in around the SmC_SP_A–SmC_aP_A transition we cannot state with certainty if any ferroelectric phase is formed in the monotropic phase range of compounds 1/O16–1/O20.

Fig. 17 Comparison of the d = f(T) curves of the layer spacing of compounds 1/O4–1/O20 (see Fig. S25 for more explanations, the individual curves are shown in Section S4 of the ESI†).

3.6.3. Effects of core-structure – the direction of the COO groups. The influence of the direction of the outer COO groups on the LC phase sequences is shown in Table 3 for the compounds with OC₁₂H₂₅ chains at both ends. From this comparison it can be concluded that the orientation of the linking groups X and Y (OOC vs. COO) is of major importance for development of tilt and polar order. Compound 1/O12 with two electron deficit terephthalate wings (T, T) shows the highest transition temperature of the LC phases and the highest Curie temperature. The combination of two electron deficit wings obviously increases the attractive core-core interactions between the molecules. This allows a dense packing and easy development of polar order. The relatively small tilt, thus leading to the presence of a SmA–SmC transition, the limited molecular bend, the dense packing providing the development of polar order close to the synclinic–anticlinic transition,^66,67 all together support the formation of the polar heliconical smectic (Sm(CP)^hel) phase.

Table 3 Phase transitions of isomeric 4-cyanoresorcinol based bent-core LCs depending on the directions of the outer COO groups

Comp.	X	Y	Phase sequence (T/°C)	Ref.
Abbreviations: T = terephthalate based wing; B = benzoyloxybenzoate wing.
1/O12	OOC (T)	COO (T)	→ Cr 111 SmCSPA 136 SmCaPR 143 SmAPR → SmA 191 Iso
			← Cr 60 SmCSPA 106 Sm(CP)^hel 133 SmCaPR 143 SmAPR ← SmA 190 Iso
2/O12	COO (B)	COO (T)	→ Cr 119 SmAPR → SmA 163 Iso	36
			← Cr 103 SmAPR ← SmA 162 Iso
3/O12	OOC (T)	OOC (B)	→ Cr 114 (SmCSPA 106) SmCsPAR 116 SmCSPR^[*^] 148 Iso	36
			← Cr <20 SmCSPA 104 SmCsPAR 115 SmCSPR^[*^] 147 Iso
4/O12	COO (B)	OOC (B)	→ Cr 103 (SmCSPA 94) SmC 109 NcybC 129 Iso	46

---

In contrast, compound 4/O12 with two electron-rich phenylbenzoate wings (B, B) has the lowest LC phase stability, it is the only compound in Table 3 forming a nematic phase and all LC phases have a strong synclinic tilt (35–45°).^46,56 The looser packing between the electron rich wings requires a stronger tilt to achieve layer formation and polar order. In this case no heliconical smectic phase is found.

The two compounds 2/O12 and 3/O12 with mixed terephthalate and benzoate wings (B, T and T, B), and thus intermediate average electron density of the wings, show LC phase stabilities being intermediate between the two symmetric compounds.³⁶ The comparison between these two compounds shows the influence of the direction of the COO group Y with respect to the direction of the CN group. The tilt is removed (2/O12) or reduced (1/O12) if the terephthalate wing is at the side of the CN group (Y = COO), while the benzoate wings (Y = OOC) at this side induces an especially strong preference for tilted organization (3/O12 and 4/O12). The phenyl benzoate wing at the opposite side to the CN group (X = COO) reduces the polar order, while a terephthalate wing at this side apparently supports the formation of helical phases (SmC_SP_R^[*^] for 3/O12 and Sm(CP)^hel for 1/O12). Overall, compound 1/O12 represents the best compound in this series with respect to mesophase stability and with the highest tendency towards formation of heliconical phases. It appears that 1/O12 provides the strongest transient molecular helicity (conformational chirality)⁵⁰ caused by the twisting of the properly arranged COO groups.^9b The distinct contributions of electrostatic effects and molecular conformations to heliconical self-assembly require DFT calculations being planned for future work.

4. Conclusions

A series of 4-cyanoresorcinol bisterephthalates 1/On terminated with alkoxy chains having variable lengths ranging from 2 to 20 was synthesized, and their LC self-assembly was investigated in detail. The main observations are summarized schematically in Fig. 18.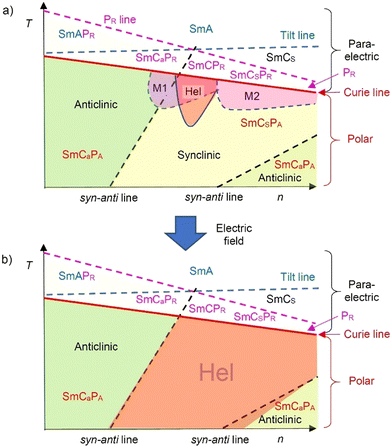

Fig. 18 Sketch of the development of tilt, polar order and helicity in the smectic LC phases of the bent-core molecules 1/On depending on temperature and alkyl chain length (n = 8–20): (a) in the pristine material and (b) after applying a short AC sequence; Hel = heliconical Sm(CP)^hel phase, for other abbreviations, see Table 2.

All compounds with n ≥ 6 show a transition with Curie Weiss type divergence from nonpolar via paraelectric and high permittivity paraelectric (superparaelectric, polarization radomized, P_R) to polar smectic phases (P_F/P_A) accompanied by an onset of a relatively small tilt (Fig. 18). While for the short chain compounds (n = 6–10) the anticlinic tilt correlation is dominating (SmC_aP_A) it becomes synclinic (SmC_SP_A) at the transition to n = 11 and around this cross-over modulated (M1, M2) and heliconical smectic phases (Sm(CP)^hel) with helical twist between polar SmCP_F layers occur below the Curie temperature (Fig. 18). Induction of the heliconical phase is geneally observed in the synclinic SmC_sP_A range of these compounds and this leads to wide ranges of the field-induced Sm(CP)^hel phases (n = 10–20). The highly polar and electron withdrawing lateral CN group is considered to play a crucial role for the development of polar order, emergence of helical twist and distinct tilt modes.

Recent advances in highly polar rod-like LCs have achieved large polarization values in phases with longitudinal polarization (Fig. 1a, left; Table 1), where heliconical phases (though with larger pitch) also emerge. This report provides fundamental insights into the synergistic roles of electrostatic energy, transient molecular helicity, and phase structure in controlling heliconical twist formation – advancing both the design of functional soft materials and the understanding of complexity and symmetry breaking in condensed matter systems.

To enhance transversal polarization, strategic molecular design – such as the introduction of lateral polar groups via targeted fluorination^21b – could yield “facial polar” bent-core mesogens (Fig. 1a, right). Although these systems may exhibit shorter conjugation pathways, their directed cooperative bend alignment could enable transversal polarizations approaching those of longitudinal ferroelectrics. Such high-polarization transversal ferroelectrics would offer distinct advantages over their longitudinal counterparts, particularly for fast-switching optical and chiroptical devices.^68–70

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Deutsche Forschungsgemeinschaft (424355983 – AL2378/1-2, 436494874 – RTG 2670). We thank Prof. W. Weissflog (Martin Luther University Halle-Wittenberg) for providing samples of 1/O8 and 1/O12.

References

1. (a) H. Ringsdorf, B. Schlarb and J. Venzmer, Angew. Chem., Int. Ed. Engl., 1988, 27, 113; (b) H. Finkelmann, H. Ringsdorf and J. H. Wendorff, Makromol. Chem., 1978, 179, 273; (c) H. Bengs, O. Karthaus and H. Ringsdorf, Liq. Cryst., 1991, 10, 161; (d) D. Adam, P. Schuhmacher, J. Simmerer, L. Häussling, K. Siemensmeyer, K. H. Etzbach, H. Ringsdorf and D. Haarer, Nature, 1994, 371, 141.
2. Handbook of Liquid Crystals, ed. J. W. Goodby, J. P. Collings, T. Kato, C. Tschierske, H. F. Gleeson and P. Raynes, Wiley-VCH, Weinheim, 2nd edn, 2014.
3. C. Tschierske, Angew. Chem., Int. Ed., 2013, 52, 8828.
4. J. Uchida, B. Soberats, M. Gupta and T. Kato, Adv. Mater., 2022, 34, 2109063.
5. H. K. Bisoyi and Q. Li, Chem. Rev., 2022, 122, 4887.
6. Y.-K. Kim, X. Wang, P. Mondkar, E. Bukusoglu and N. L. Abbott, Nature, 2018, 557, 539.
7. E.-K. Fleischmann and R. Zentel, Angew. Chem., Int. Ed., 2013, 52, 8810.
8. S. Sergeyev, W. Pisula and Y. H. Geerts, Chem. Soc. Rev., 2007, 36, 1902.
9. (a) R. A. Reddy and C. Tschierske, J. Mater. Chem., 2006, 16, 907; (b) H. Takezoe, Top. Curr. Chem., 2012, 318, 303; (c) M. Nagaraj, Liq. Cryst., 2016, 43, 2244; (d) K. V. Le, H. Takezoe and F. Araoka, Adv. Mater., 2017, 1602737; (e) C. Tschierske, Liq. Cryst., 2018, 45, 2221; (f) A. Yoshizawa, Crystals, 2024, 14, 97.
10. T. Buhse, J.-M. Cruz, M. E. Noble-Teran, D. Hochberg, J. M. Ribo, J. Crusats and J.-C. Micheau, Chem. Rev., 2021, 121, 2147.
11. T. Sekine, T. Niori, J. Watanabe, T. Furukawa, S.-W. Choi and H. Takezoe, J. Mater. Chem., 1997, 7, 1307.
12. (a) M. Alaasar, M. Prehm, M. Brautzsch and C. Tschierske, Soft Matter, 2014, 10, 7285; (b) M. Alaasar, M. Prehm and C. Tschierske, Chem. – Eur. J., 2016, 22, 6583; (c) M. Alaasar, A. F. Darweesh, Y. Cao, K. Iakoubovskii and M. Yoshio, J. Mater. Chem. C, 2024, 12, 1523.
13. A. Gowda, S. Kumar Pathak, G. A. R. Rohaley, G. Acharjee, A. Oprandi, R. Williams, M. E. Prevot and T. Hegmann, Mater. Horiz., 2024, 11, 316.
14. (a) S. T. Lagerwall, Ferroelectrics, 2004, 301, 15; (b) A. Fukuda, Y. Takanishi, T. Isozaki, K. Ishikawa and H. Takezoe, J. Mater. Chem., 1994, 4, 997; (c) A. Yoshizawa, Crystals, 2024, 14, 350.
15. (a) T. Niori, T. Sekine, J. Watanabe, T. Furukawa and H. Takezoe, J. Mater. Chem., 1996, 6, 1231; (b) D. R. Link, G. Natale, R. Shao, J. E. Maclennan, N. A. Clark, E. Korblova and D. M. Walba, Science, 1997, 278, 1924; (c) D. M. Walba, E. Korblova, R. Shao, J. E. Maclennan, M. A. Glaser and N. A. Clark, Science, 2000, 288, 2181.
16. (a) G. Pelz, S. Diele and W. Weissflog, Adv. Mater., 1999, 11, 707; (b) A. Eremin and A. Jákli, Soft Matter, 2013, 9, 615; (c) M. Alaasar, Liq. Cryst., 2016, 43, 2208; (d) H. Takezoe and A. Eremin, Bent-shaped Liquid Crystals, Taylor and Francis, Boca Rotan FL, 2017.
17. R. A. Reddy, C. Zhu, R. Shao, E. Korblova, T. Gong, Y. Shen, E. Garcia, M. A. Glaser, J. E. Maclennan and D. M. Walba, Science, 2011, 332, 72.
18. M. Born, Sitzungsber. K. Preuss. Akad. Wiss., 1916, 30, 614.
19. (a) Y. Song, M. Deng, Z. Wang, J. Li, H. Lei, Z. Wan, R. Xia, S. Aya and M. Huang, J. Phys. Chem. Lett., 2022, 13, 9983; (b) H. Kikuchi, H. Matsukizono, K. Iwamatsu, S. Endo, S. Anan and Y. Okumura, Adv. Sci., 2022, 9, 2202048; (c) X. Chen, V. Martinez, P. Nacke, E. Korblova, A. Manabe, M. Klasen-Memmer, G. Freychet, M. Zhernenkov, M. A. Glaser, L. Radzihovsky, J. E. Maclennan, D. M. Walba, M. Bremer, F. Giesselmann and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2210062119.
20. (a) J. Hobbs, C. J. Gibb, D. Pociecha, J. Szydłowska, E. Górecka and R. J. Mandle, Angew. Chem., Int. Ed., 2025, 64, e202416545; (b) H. Kikuchi, H. Nishikawa, H. Matsukizono, S. Iino, T. Sugiyama, T. Ishioka and Y. Okumura, Adv. Sci., 2024, 11, 2409827.
21. (a) G. J. Strachan, E. Gorecka, J. Szydlowska, A. Makal and D. Pociecha, Adv. Sci., 2025, 12, 2409754; (b) G. J. Strachan, E. Górecka, J. Hobbs and D. Pociecha, J. Am. Chem. Soc., 2025, 147, 6058.
22. (a) R. J. Mandle, S. J. Cowling and J. W. Goodby, Phys. Chem. Chem. Phys., 2017, 19, 11429; (b) R. J. Mandle, S. J. Cowling and J. W. Goodby, Chem. – Eur. J., 2017, 23, 14554.
23. H. Nishikawa, K. Shiroshita, H. Higuchi, Y. Okumura, Y. Haseba, S. Yamamoto, K. Sago and H. A. Kikuchi, Adv. Mater., 2017, 29, 1702354.
24. X. Chen, E. Korblova, D. Dong, X. Wei, R. Shao, L. Radzihovsky, M. A. Glaser, J. E. Maclennan, D. Bedrov, D. M. Walba and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14021.
25. S. Brown, E. Cruickshank, J. M. D. Storey, C. T. Imrie, D. Pociecha, M. Majewska, A. Makal and E. Gorecka, ChemPhysChem, 2021, 22, 2506.
26. First attempts towards longitudinal ferroelectrics: F. Tournilhac, L. M. Blinov, J. Simon and S. V. Yablonsky, Nature, 1992, 359, 621.
27. Y. Song, S. Aya and M. Huang, Giant, 2024, 19, 100318.
28. (a) P. Kumari, B. Basnet, M. O. Lavrentovich and O. D. Lavrentovich, Science, 2024, 383, 1364; (b) J. Karcz, J. Herman, N. Rychłowicz, P. Kula, E. Gorecka, J. Szydlowska, P. W. Majewski and D. Pociecha, Science, 2024, 384, 1096; (c) H. Nishikawa, D. Okada, D. Kwaria, A. Nihonyanagi, M. Kuwayama, M. Hoshino and F. Araoka, Adv. Sci., 2024, 11, 2405718.
29. C. J. Gibb, J. Hobbs, D. I. Nikolova, T. Raistrick, S. R. Berrow, A. Mertelj, N. Osterman, N. Sebastián, H. F. Gleeson and R. J. Mandle, Nat. Commun., 2024, 15, 5845.
30. J. Hobbs, C. J. Gibb and R. J. Mandle, Small Sci, 2024, 4, 2400189.
31. N. Yadav, Y. P. Panarin, W. Jiang, G. H. Mehl and J. K. Vij, Phys. Chem. Chem. Phys., 2023, 25, 9083.
32. (a) J. Thisayukta, Y. Nakayama, S. Kawauchi, H. Takezoe and J. Watanabe, J. Am. Chem. Soc., 2000, 122, 7441; (b) G. Dantlgraber, A. Eremin, S. Diele, A. Hauser, H. Kresse, G. Pelzl and C. Tschierske, Angew. Chem., Int. Ed., 2002, 41, 2408.
33. S. P. Sreenilayam, Y. P. Panarin, J. K. Vij, V. P. Panov, A. Lehmann, M. Poppe, M. Prehm and C. Tschierske, Nat. Commun., 2016, 7, 11369.
34. A. A. S. Green, M. R. Tuchband, R. Shao, Y. Shen, R. Visvanathan, A. E. Duncan, A. Lehmann, C. Tschierske, E. D. Carlson, E. Guzman, M. Kolber, D. M. Walba, C. S. Park, M. A. Glaser, J. E. Maclennan and N. A. Clark, Phys. Rev. Lett., 2019, 122, 107801.
35. (a) J. K. Vij, Y. P. Panarin, S. Sreenilayam, M. Alaasar and C. Tschierske, Phys. Rev. Mater., 2019, 3, 045603; (b) S. Sreenilayam, Y. P. Panarin, J. K. Vij, A. Lehmann, M. Poppe and C. Tschierske, Phys. Rev. Mater., 2017, 1, 045603.
36. M. Poppe, M. Alaasar, A. Lehman, S. Poppe, M.-G. Tamba, M. Kurachkina, A. Eremin, M. Nagaraj, J. K. Vij, X. Cai, F. Liu and C. Tschierske, J. Mater. Chem. C, 2020, 8, 3316.
37. A. Lehmann, M. Alaasar, M. Poppe, S. Poppe, M. Prehm, M. Nagaraj, S. P. Sreenilayam, Y. P. Panarin, J. K. Vij and C. Tschierske, Chem. – Eur. J., 2020, 26, 4714.
38. C. Tschierske, Liq. Cryst., 2022, 49, 1043.
39. J. P. Abberley, R. Killah, R. Walker, J. M. D. Storey, C. T. Imrie, M. Salamończyk, C. Zhu, E. Gorecka and D. Pociecha, Nat. Commun., 2018, 9, 228.
40. G. Pelzl, A. Eremin, S. Diele, H. Kresse and W. Weissflog, J. Mater. Chem., 2002, 12, 2591.
41. (a) V. P. Panov, M. Nagaraj, J. K. Vij, Y. P. Panarin, A. Kohlmeier, M. G. Tamba, R. A. Lewis and G. H. Mehl, Phys. Rev. Lett., 2010, 105, 167801; (b) M. Cestari, S. Diez-Berart, D. A. Dunmur, M. R. Ferrarini, M. R. de la Fuente, D. J. B. Jackson, D. O. Lopez, G. R. Luckhurst, M. A. Perez-Jubindo and R. M. Richardson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031704.
42. R. A. Reddy and B. K. Sadashiva, J. Mater. Chem., 2002, 12, 2627.
43. (a) M. Alaasar, M. Prehm, M. Nagaraj, J. K. Vij and C. Tschierske, Adv. Mater., 2013, 25, 2186; (b) M. Alaasar, M. Prehm, K. May, A. Eremin and C. Tschierske, Adv. Funct. Mater., 2014, 24, 1703.
44. (a) M. Alaasar, M. Prehm, S. Poppe and C. Tschierske, Chem. – Eur. J., 2017, 23, 5541; (b) M. Alaasar, M. Prehm, M.-G. Tamba, N. Sebastian, A. Eremin and C. Tschierske, ChemPhysChem, 2016, 17, 278; (c) M. Alaasar, M. Prehm, S. Belau, N. Sebastián, M. Kurachkina, A. Eremin, C. Chen, F. Liu and C. Tschierske, Chem. – Eur. J., 2019, 25, 6362.
45. C. Dressel, T. Reppe, M. Prehm, M. Brautzsch and C. Tschierske, Nat. Chem., 2014, 6, 971.
46. L. Kovalenko, M. W. Schröder, R. A. Reddy, S. Diele, G. Pelzl and W. Weissflog, Liq. Cryst., 2005, 32, 857.
47. A. Eremin, S. Diele, G. Pelzl, H. Nádasi, W. Weissflog, J. Salfetnikova and H. Kresse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 051707.
48. G. W. C. Kayne and T. H. Laby, Tables of Physical & Chemical Constants, 16th edn, 1995.
49. I. Wirth, S. Diele, A. Eremin, G. Pelzl, S. Grande, L. Kovalenko, N. Pancenko and W. Weissflog, J. Mater. Chem., 2001, 11, 1642.
50. C. Tschierske and G. Ungar, ChemPhysChem, 2016, 17, 9.
51. G. S. Lee, Y.-J. Lee, S. Y. Choi, Y. S. Park and K. B. Yoon, J. Am. Chem. Soc., 2000, 122, 12151.
52. N. Sebastian, S. Belau, A. Eremin, M. Alaasar, M. Prehm and C. Tschierske, Phys. Chem. Chem. Phys., 2017, 19, 5895.
53. M. Alaasar, M. Prehm, M. Poppe, M. Nagaraj, J. K. Vij and C. Tschierske, Soft Matter, 2014, 10, 5003.
54. (a) M. Majumdar, P. Salamon, A. Jákli, J. T. Gleeson and S. Sprunt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 031701; (b) G. Shanker, M. Prehm, M. Nagaraj, J. K. Vij and C. Tschierske, J. Mater. Chem., 2011, 21, 18711; (c) S. Kumar and A. N. Gowda, Liq. Cryst. Rev., 2015, 3, 99.
55. (a) O. Francescangeli, F. Vita, C. Ferrero, T. Dingemans and E. T. Samulski, Soft Matter, 2011, 7, 895; (b) M. Alaasar, M. Prehm and C. Tschierske, Liq. Cryst., 2014, 41, 126; (c) M. Alaasar, S. Poppe and C. Tschierske, Liq. Cryst., 2017, 44, 729.
56. (a) C. Keith, A. Lehmann, U. Baumeister, M. Prehm and C. Tschierske, Soft Matter, 2010, 6, 1704; (b) M. Alaasar, S. Poppe, C. Kerzig, C. Klopp, A. Eremin and C. Tschierske, J. Mater. Chem. C, 2017, 5, 8454.
57. (a) T. Hegmann, J. Kain, S. Diele, G. Pelzl and C. Tschierske, Angew. Chem., Int. Ed., 2001, 40, 887; (b) C. V. Yelamaggad, I. S. Shashikala, V. P. Tamilenthi, D. S. Shanker Rao, G. G. Nair and S. K. Prasad, J. Mater. Chem., 2008, 18, 2096; (c) R. Pratibha, N. V. Madhusudana and B. K. Sadashiva, Europhys. Lett, 2007, 80, 46001.
58. (a) D. Pociecha, M. Cepic, E. Gorecka and J. Mieczkowski, Phys. Rev. Lett., 2003, 91, 185501; (b) Y. Shimbo, E. Gorecka, D. Pociecha, F. Araoka, M. Goto, Y. Tankanishi, K. Ishikawa, J. Mieczkowski, K. Gomola and H. Takezoe, Phys. Rev. Lett., 2006, 97, 113901.
59. M. Nakata, R.-F. Shao, J. E. Maclennan, W. Weissflog and N. A. Clark, Phys. Rev. Lett., 2006, 96, 067802.
60. K. Gomola, L. Guo, D. Pociecha, F. Araoka, K. Ishikawa and H. Takezoe, J. Mater. Chem., 2010, 20, 7944.
61. (a) A. Eremin, H. Nadasi, G. Pelzl, S. Diele, H. Kresse, W. Weissflog and S. Grande, Phys. Chem. Chem. Phys., 2004, 6, 1290; (b) D. Pociecha, E. Gorecka, M. Cepic, N. Vaupotic, K. Gomola and J. Mieczkowski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 060701(R); (c) D. Pociecha, E. Gorecka, M. Cepic, N. Vaupotic and W. Weissflog, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021702.
62. (a) Y. P. Panarin, M. Nagaraj, S. Sreenilayam, J. K. Vij, A. Lehmann and C. Tschierske, Phys. Rev. Lett., 2011, 107, 247801; (b) S. Sreenilayam, M. Nagaraj, Y. P. Panarin, J. K. Vij, A. Lehmann and C. Tschierske, Mol. Cryst. Liq. Cryst, 2012, 553, 140.
63. J. L. Hobbs, C. J. Gibb, E. Cruickshank, R. Walker and R. J. Mandle, Liq. Cryst., 2024, 51, 1022.
64. K. Kumazawa, M. Nakata, F. Araoka, Y. Takanishi, K. Ishikawa, J. Watanabe and H. Takezoe, J. Mater. Chem., 2004, 14, 157.
65. Y. P. Panarin, S. P. Sreenilayam, V. Swaminathan, C. Tschierske and J. K. Vij, Phys. Rev. Res., 2020, 2, 013118.
66. (a) D. Malkar, B. K. Sadashiva and A. Roy, Soft Matter, 2016, 12, 4960; (b) D. Malkar and A. Roy, Liq. Cryst., 2022, 49, 1147.
67. J. Svoboda, V. Kozmık, K. Bajzıkova, M. Kohout, V. Novotna, N. Podoliak, D. Pociecha and E. Gorecka, J. Mater. Chem. C, 2024, 12, 10903.
68. (a) C. Keith, M. Prehm and C. Tschierske, Chem. Commun., 2010, 46, 3702; (b) M. Nagaraj, Y. P. Panarin, J. K. Vij, C. Keith and C. Tschierske, Appl. Phys. Lett., 2010, 97, 213505; (c) Y. P. Panarin, M. Nagaraj, J. K. Vij, C. Keith and C. Tschierske, Europhys. Lett, 2010, 92, 26002; (d) Y. P. Panarin, S. Sreenilayam, J. K. Vij, A. Lehmann and C. Tschierske, J. Mater. Chem. C, 2017, 5, 12585.
69. (a) A. S. Amrutha, A. S. Achalkumar and Q. Li, in Photoactive Functional Soft Materials: Preparation, Properties, and Applications, ed. Q. Li, Wiley-VCH, Weinheim, Germany, 2019, pp. 227–283; (b) H. K. Bisoyi, T. J. Bunning and Q. Li, Adv. Mater., 2018, 30, 1706512.
70. K. Yin, E.-L. Hsiang, J. Zou, Y. Li, Z. Yang, Q. Yang, P.-C. Lai, C.-L. Lin and S.-T. Wu, Light: Sci. Appl., 2022, 11, 161.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5tc01109d

---