Theory and modeling of nematic disclination branching under capillary confinement
Abstract
Defects in nematic liquid crystals under controlled confinement serve as a useful tool to characterize material properties as well as to reveal texture stability and pattern formation mechanisms in anisotropic soft matter. In particular, nematics inside micro-capillaries can exhibit a large variety of textures with point defects, line defects and loop defects, whose stability is dictated by factors such as geometry and temperature. In this paper we present a theoretical model, scaling, and simulation of a texture transition between two commonly observed patterns (planar polar and radial), through the uniform translation of a shape-invariant disclination branch point in generic calamitic nematic liquid crystals under capillary confinement and strong radial anchoring. Using the “nematic elastica” model derived from the Q-tensor Landau–de Gennes and n-vector Frank–Oseen equations, the geometry, stability, and energetics of disclination branching of a straight high order +1 disclination into a pair of curved +1/2 disclinations under capillary confinement are fully characterized, including the branch angle, the curvature and final separation of the +1/2 lines, and the scaling of these quantities with the capillary radius (R). It is found that the branching and disclination shapes adjust to the capillary confinement by regulating their tension-to-bending stiffness ratio in such a way that the resulting branch angle is close to π/3, the branch curvature is 3/R and the final disclination distance is 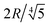 . These new findings based on the “nematic elastica” are also useful to predict other novel structures that arise in conical and toroidal geometries of current interest and can be used to assess the Frank elasticity of nematic liquid crystals.
. These new findings based on the “nematic elastica” are also useful to predict other novel structures that arise in conical and toroidal geometries of current interest and can be used to assess the Frank elasticity of nematic liquid crystals.


 Please wait while we load your content...
Please wait while we load your content...