Marginally compact hyperbranched polymer trees

Abstract

Assuming Gaussian chain statistics along the chain contour, we generate by means of a proper fractal generator hyperbranched polymer trees which are marginally compact. Static and dynamical properties, such as the radial intrachain pair density distribution ρ_pair(r) or the shear-stress relaxation modulus G(t), are investigated theoretically and by means of computer simulations. We emphasize that albeit the self-contact density 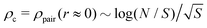diverges logarithmically with the total mass N, this effect becomes rapidly irrelevant with increasing spacer length S. In addition to this it is seen that the standard Rouse analysis must necessarily become inappropriate for compact objects for which the relaxation time τ_p of mode p must scale as τ_p ∼ (N/p)^5/3 rather than the usual square power law for linear chains.