Anomalous diffusion, aging, and nonergodicity of scaled Brownian motion with fractional Gaussian noise: overview of related experimental observations and models
Abstract
How does a systematic time-dependence of the diffusion coefficient D(t) affect the ergodic and statistical characteristics of fractional Brownian motion (FBM)? Here, we answer this question via studying the characteristics of a set of standard statistical quantifiers relevant to single-particle-tracking (SPT) experiments. We examine, for instance, how the behavior of the ensemble- and time-averaged mean-squared displacements—denoted as the standard MSD 〈x2(Δ)〉 and TAMSD 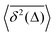 quantifiers—of FBM featuring
quantifiers—of FBM featuring 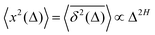 (where H is the Hurst exponent and Δ is the [lag] time) changes in the presence of a power-law deterministically varying diffusivity Dα(t) ∝ tα−1—germane to the process of scaled Brownian motion (SBM)—determining the strength of fractional Gaussian noise. The resulting compound “scaled-fractional” Brownian motion or FBM–SBM is found to be nonergodic, with 〈x2(Δ)〉 ∝ Δα+2H−1 and
(where H is the Hurst exponent and Δ is the [lag] time) changes in the presence of a power-law deterministically varying diffusivity Dα(t) ∝ tα−1—germane to the process of scaled Brownian motion (SBM)—determining the strength of fractional Gaussian noise. The resulting compound “scaled-fractional” Brownian motion or FBM–SBM is found to be nonergodic, with 〈x2(Δ)〉 ∝ Δα+2H−1 and 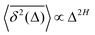 . We also detect a stalling behavior of the MSDs for very subdiffusive SBM and FBM, when α + 2H − 1 < 0. The distribution of particle displacements for FBM–SBM remains Gaussian, as that for the parent processes of FBM and SBM, in the entire region of scaling exponents (0 < α < 2 and 0 < H < 1). The FBM–SBM process is aging in a manner similar to SBM. The velocity autocorrelation function (ACF) of particle increments of FBM–SBM exhibits a dip when the parent FBM process is subdiffusive. Both for sub- and superdiffusive FBM contributions to the FBM–SBM process, the SBM exponent affects the long-time decay exponent of the ACF. Applications of the FBM–SBM-amalgamated process to the analysis of SPT data are discussed. A comparative tabulated overview of recent experimental (mainly SPT) and computational datasets amenable for interpretation in terms of FBM-, SBM-, and FBM–SBM-like models of diffusion culminates the presentation. The statistical aspects of the dynamics of a wide range of biological systems is compared in the table, from nanosized beads in living cells, to chromosomal loci, to water diffusion in the brain, and, finally, to patterns of animal movements.
. We also detect a stalling behavior of the MSDs for very subdiffusive SBM and FBM, when α + 2H − 1 < 0. The distribution of particle displacements for FBM–SBM remains Gaussian, as that for the parent processes of FBM and SBM, in the entire region of scaling exponents (0 < α < 2 and 0 < H < 1). The FBM–SBM process is aging in a manner similar to SBM. The velocity autocorrelation function (ACF) of particle increments of FBM–SBM exhibits a dip when the parent FBM process is subdiffusive. Both for sub- and superdiffusive FBM contributions to the FBM–SBM process, the SBM exponent affects the long-time decay exponent of the ACF. Applications of the FBM–SBM-amalgamated process to the analysis of SPT data are discussed. A comparative tabulated overview of recent experimental (mainly SPT) and computational datasets amenable for interpretation in terms of FBM-, SBM-, and FBM–SBM-like models of diffusion culminates the presentation. The statistical aspects of the dynamics of a wide range of biological systems is compared in the table, from nanosized beads in living cells, to chromosomal loci, to water diffusion in the brain, and, finally, to patterns of animal movements.

- This article is part of the themed collection: 2022 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...