Characterising local environments in high energy density Li-ion battery cathodes: a combined NMR and first principles study of LiFexCo1−xPO4†
Fiona C.
Strobridge
a,
Derek S.
Middlemiss‡
a,
Andrew J.
Pell§
b,
Michal
Leskes
a,
Raphaële J.
Clément
a,
Frédérique
Pourpoint¶
a,
Zhouguang
Lu
c,
John V.
Hanna
d,
Guido
Pintacuda
b,
Lyndon
Emsley
b,
Ago
Samoson
de and
Clare P.
Grey
*af
aDepartment of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK. E-mail: cpg27@cam.ac.uk; Fax: +44 (0)1223 336539; Tel: +44 (0)1223 336509
bCentre de RMN à Très Hauts Champs, UMR 5280 CNRS/Ecole Normale Supérieure de Lyon/UCB Lyon 1, 69100 Villeurbanne, France
cLaboratory of Green and Renewable Energy Materials, Department of Materials Science and Engineering, South University of Science and Technology of China, 1088 Tangchang Blvd., Nanshan District, Shenzhen, Guangdong 518055, China
dDepartment of Physics, University of Warwick, Gibbet Hill Road, Coventry, CV4 7AL, UK
eTehnomeedikum, Tallinn University of Technology, Tallinn, Estonia
fDepartment of Chemistry, SUNY Stony Brook, Stony Brook, New York 11794-3400, USA
First published on 9th June 2014
Abstract
Olivine-type LiCoPO4 (LCP) is a high energy density lithium ion battery cathode material due to the high voltage of the Co2+/Co3+ redox reaction. However, it displays a significantly poorer electrochemical performance than its more widely investigated isostructural analogue LiFePO4 (LFP). The co-substituted LiFexCo1−xPO4 olivines combine many of the positive attributes of each end member compound and are promising next-generation cathode materials. Here, the fully lithiated x = 0, 0.25, 0.5, 0.75 and 1 samples are extensively studied using 31P solid-state nuclear magnetic resonance (NMR). Practical approaches to broadband excitation and for the resolution of the isotropic resonances are described. First principles hybrid density functional calculations are performed on the Fermi contact shift (FCS) contributions of individual M–O–P pathways in the end members LFP and LCP and compared with the fitted values extracted from the LiFexCo1−xPO4 experimental data. Combining both data sets, the FCS for the range of local P environments expected in LiFexCo1−xPO4 have been calculated and used to assign the NMR spectra. Due to the additional unpaired electron in d6 Fe2+ as compared with d7 Co2+ (both high spin), LFP is expected to have larger Fermi contact shifts than LCP. However, two of the Co–O–P pathways in LCP give rise to noticeably larger shifts and the unexpected appearance of peaks outside the range delimited by the pure LFP and LCP 31P shifts. This behaviour contrasts with that observed previously in LiFexMn1−xPO4, where all 31P shifts lay within the LiMnPO4–LFP range. Although there are 24 distinct local P environments in LiFexCo1−xPO4, these group into seven resonances in the NMR spectra, due to significant overlap of the isotropic shifts. The local environments that give rise to the largest contributions to the spectral intensity are identified and used to simplify the assignment. This provides a tool for future studies of the electrochemically-cycled samples, which would otherwise be challenging to interpret.
1. Introduction
The widespread goal to reduce greenhouse gas emissions, specifically CO2, has engaged the scientific community in efforts to develop lithium ion batteries (LIBs) for use in all-electric, hybrid and plug-in hybrid electric vehicles and in grid storage.1 The layered oxide cathode material LixCoO2 (ref. 2) is in widespread use in the portable communications industry; however, it is unstable towards O2 loss for x > 0.5 (ref. 3) and is deemed unsuitable for the electrification of automobiles. Padhi et al.4 studied olivine-type LiFePO4 (LFP) in 1997, leading to widespread interest owing to its high stability, long cycle life, fast charge rates in nano-particulate form, high reversible theoretical capacity (170 mA h g−1 as compared with 140 mA h g−1 in LiCoO2) and safe operating voltage (3.45 V vs. Li+/Li). However, the low operating voltage also constitutes its main disadvantage, leading to a low energy density (580 W h kg−1).The LiMPO4 (M = Mn, Co or Ni) phases all adopt the olivine structure and have higher operating voltages compared to LFP, at 4.1 V, 4.8 V and 5.0 V vs. Li+/Li,4–8 respectively, and thus have been explored as a method to increase the energy density. However, they have more sluggish kinetics and are more difficult to charge and discharge fully. An alternative strategy is to substitute the Fe2+ ions in LFP with one or more of these transition metals (TMs) to form a solid solution on the M site.4,9 This paper focuses on the binary olivine LiFexCo1−xPO4 as a potential next generation cathode material, combining the high theoretical energy density of LiCoPO4 (LCP) at 800 W h kg−1 with the superior electrochemical performance of the Fe phase.10 Upon charging, the lower oxidation potential of Fe2+ implies that Fe2+ oxidises to Fe3+ first, followed by oxidation of the Co2+ sites. Kim et al.11 have proposed that the potential associated with the higher voltage Co2+/Co3+ couple is sensitive to the nature of the nearby TM ions, where Co2+ neighbouring Fe3+ sites are thought to react preferentially over Co2+ adjoining other Co2+ sites. In order to test this hypothesis and understand the basis for the improved electrochemical performance in this class of high energy density materials, the local structure must be probed across the range of electrochemical conditions encountered in battery operation. Here we address the first step of this process, seeking to fully characterise the local structure in the as-synthesized (i.e. fully lithiated) materials.
X-ray diffraction is an important characterisation technique, providing information on long-range structural order and particle size and strain. In contrast, nuclear magnetic resonance (NMR) spectroscopy gives direct insight into the local coordination environment of the nucleus under observation and is particularly suited to study disordered materials. LiFexCo1−xPO4, like many cathode materials, is paramagnetic at room temperature, containing the high spin 3d6 (t42ge2g) Fe2+ and 3d7 (t52ge2g) Co2+. The nuclear spins (here, the 31P sites) interact with the time-averaged magnetic moments of the paramagnetic ions, which are of the order 103 times greater than the nuclear magnetic moments, resulting in hyperfine interactions that dominate the NMR response. These occur via through-space (dipolar) and through-bond (Fermi contact) interactions, and their magnitudes scale linearly with the field strength for magnetic moments below their saturation values. The dipolar interactions typically result in large spinning sideband manifolds under magic angle spinning (MAS), which, when originating from multiple local environments, can result in a series of overlapping peaks. Meanwhile, the Fermi contact shift (FCS) dominates the 31P NMR spectra of LiMPO4 compounds.12 The FCS arises out of the transfer of unpaired electron spin density from the M2+ sites through an intervening bond network into an s-orbital of the NMR observed nucleus. If the magnetic susceptibility of the material is anisotropic, the dipolar interaction also contributes an additional pseudocontact shift (PCS); however, in the present study, the FCS is significantly larger and the PCS is assumed to be negligible.13 The interaction of the nuclei with the anisotropic moment can result in inhomogeneous line broadening which is significant in this system. Despite the inherent challenges these phenomena lead to, the use of paramagnetic solid-state NMR has led to a detailed understanding of the local structures arising in LIB materials.14–16
31P is the most useful nucleus for studying the local structure in LiFexCo1−xPO4 on account of its high natural abundance (100%), a nuclear spin quantum number I = 1/2 ruling out quadrupolar interactions, and isotropic shifts exhibiting greater spectral dispersion than in 6,7Li spectra.17 However, it is challenging to obtain high-resolution 31P NMR spectra, due to the high 31P gyromagnetic ratio and the strong covalency of the P–O bonds, resulting in large hyperfine shifts. Spectra can be collected in low fields, so as to reduce the size of the broadening (in frequency units), which, in combination with fast MAS speeds, moves the sidebands outside the region of interest. However, this must be balanced against the desire to use higher fields to increase the sensitivity. At higher fields, however, the spinning sideband separation decreases on the ppm scale and pulse sequences that separate the sidebands from the isotropic peaks and permit for large excitation bandwidths may be required. Two commonly used experiments are the magic angle turning (MAT)18,19 and the phase adjusted sideband separation (PASS)20–22 sequences. In order to excite the entire region of interest, short high-power adiabatic pulses (SHAPs)23 or very short radio frequency (RF) pulses must be employed. The adiabatic MAT (aMAT) sequence was first applied in the paramagnetic LiFexMn1−xPO4 system and uses a series of SHAPs in a modified MAT-type experiment, successfully isolating the isotropic shifts.24 The MATPASS sequence uses short RF pulses and benefits from the fewer increments in the PASS experiment and has shown promising results in other paramagnetic cathode materials.25 We use both methods in the following.
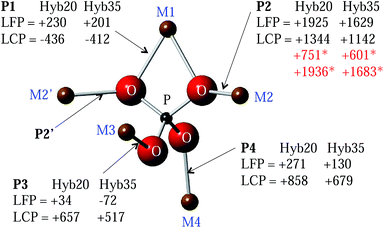
Transfer of spin density via the Fermi contact interaction depends strongly on the geometry of the bond network linking the paramagnetic species with the observed nucleus, reflecting the overlap of orbitals on the paramagnetic ion, oxygen and phosphorus sites. Fig. 1 shows the local structure of a P atom in LiMPO4 compounds. One crystallographically distinct P site is present, each with 5 neighbouring M cations bridged by O. Two of these M sites are equivalent (M2), resulting in four distinct M–O–P pathways. M1 is linked to P by two P1 pathways, each with equal bond angles of 94.3° and 93.9° in LFP and LCP, respectively, whereas pathways P2, P3 and P4 have bond angles in the range 120–130° (128.1°, 120.0° and 123.7°, respectively in LFP and 127.5°, 122.9° and 126.2°, respectively in LCP), as shown in the ESI.† Here, the bond angles and distances are obtained from the first principles structural optimizations of LFP and LCP performed by Middlemiss et al.26 While the net spin transfer through M–O–P pathways at angles 90° and 180° may be reasonably well rationalised within the Goodenough–Kanamori model,27,28 intermediate angles present a formidable problem, necessitating the use of electronic structure calculations of varying degrees of sophistication.14,29
The assignment of solid-state NMR spectra can be very challenging. Pioneering work by Mauri et al.30 made possible the calculation of shielding tensors for solid-state diamagnetic systems within a linear response formalism. Carlier et al. calculated the spin densities in paramagnetic systems within the density functional theory (DFT) + U approach, applying the results to the interpretation of experimental spectra in an indirect fashion via the use of integrated atomic magnetic moments31 and more recently directly via the use of the full-potential LAPW method within the WIEN2k package.32,33 Other methods by Mali et al. using DFT/Projector Augmented-Wave approaches have also been employed to calculate contact shifts in the Li2FeSiO4.34
Kim et al. calculated hyperfine shifts in a variety of Fe(III)-phosphates using periodic hybrid DFT methods.29 Two hybrid exchange–correlations were used: the B3LYP functional, containing 20% Hartree–Fock (HF) exchange (Hyb20) and a 35% HF hybrid (Hyb35). The experimental NMR shifts were found to fall within the range of values bounded by the Hyb20 and Hyb35 results. More recently, Middlemiss et al. used Hyb20 and Hyb35 functionals to calculate P hyperfine shifts in LiMPO4 and MPO4 (M = Fe, Mn and Co) compounds.26 In this work, the spin at one of the M sites in the first coordination shell of P is flipped, and the FCS contribution of the inverted M–O–P spin density transfer pathway is obtained as half of the difference between the P hyperfine shift in the flipped and the initial fully aligned spin configurations. Here, we extend this ‘spin-flipping’ approach, previously applied to the LiFe1−xMnxPO4 solid solution,24 making use of the FCS contributions already obtained for the M–O–P pathways in LFP and LCP as shown in Fig. 1 for both the Hyb20 and Hyb35 functionals. As discussed previously, Fe and Co ions are randomly distributed on the 5 M sites around P, giving rise to 32 local P environments (24 of which are distinct, due to the mirror plane located on the P group (resulting in M2 = M2′) reducing the number of inequivalent environments). The hyperfine shifts of all of these environments are calculated using the LFP and LCP end member pathways and used to fit and then assign the experimental NMR spectra. We also explore the effectiveness of different NMR methods to acquire 31P spectra in strongly paramagnetic phases.
2. Experimental section
2.1. Synthesis and characterisation
The carbon-coated LiFexCo1−xPO4 (x = 1, 0.75, 0.5, 0.25, 0) series were synthesized via the solid-state method using iron oxalate, cobalt oxalate, lithium carbonate, ammonium dihydrogen phosphate and carbon precursors in stoichiometric mixtures. After high-energy ball milling for 20 minutes, the reaction mixture was pelletized and heated to 600 °C under flowing argon. The LFP precursors were heated for 6 h.35 For LiFe0.75Co0.25PO4, they were heated for 6 h, then cooled and reheated for a further 11 h. For LiFexCo1−xPO4 (x = 0.5, 0.25, 0), the precursors were heated for 6 h, cooled and reheated for 11 h twice, before a final 24 h heating step. The additional heating and cooling steps were employed to remove trace impurities.The X-ray diffraction (XRD) patterns were obtained using a PANalytical Empyrean X-ray diffractometer with a Cu Kα source. The data for LiFexCo1−xPO4 (x = 1, 0.5, 0.25 and 0) were collected for a total scan time of 9 h and 52 minutes using a step size of 0.017° over a 2θ range of 5–140°. The data for LiFe0.75Co0.25PO4 was collected for a total scan time of 1 h and 41 minutes using a step size of 0.017° over a 2θ range of 5–120°. Rietveld refinements were performed within the TOPAS software.36
2.2. Nuclear magnetic resonance
The 31P Hahn echo NMR experiments performed on a 2.35 T Oxford Spectrospin spectrometer (100 MHz for 1H) at a Larmor frequency of approximately 40.5 MHz were carried out using a 1.3 mm MAS Samoson probe. The Hahn echo pulse sequence was synchronized to two rotor periods, at a spinning speed of 55 kHz, to prevent ringing. A 90° pulse width of 1.1 μs and a recycle delay of 0.02 s were used.Corresponding 31P MATPASS spectra were collected on a Bruker 200 Avance III spectrometer (4.7 T) at a Larmor frequency of 81 MHz, using a 1.8 mm MAS Samoson probe. A series of five 90° pulses with a pulse width of 1.6 μs were employed, and rotor synchronised to a spinning frequency of 40 kHz.24 The recycle delay was 0.015 s. The decay time constant of the Hahn echo/MAT sequence, T′2, was obtained at 4.7 T for LFP and LCP using a series of Hahn echoes where τ, the delay separating the centres of the 90° and 180° pulses, was varied between 50 μs and 10 ms in 8 increments. The signal decay was then fitted with an exponential function. The T′2 values obtained for LFP and LCP were 367 and 1199 μs, respectively.
Additional 31P aMAT data were acquired on a Bruker 500 Avance III spectrometer at a Larmor frequency of 202 MHz, using a 1.3 mm HX Bruker probe. The data were collected using tanh/tan SHAPs,23,37 sweeping through 5 MHz in 50 μs with a RF amplitude of 417 kHz. The evolution time was set to seven rotor periods (116.67 μs), excluding the lengths of the SHAPs. The recycle delay was set to 100 ms. The spectra of the pure LCP and LFP phases were acquired with a spectral width in the indirect dimension of 147.7 kHz and 32 complex increments, with 9216 scans per increment. The spectra of the co-substituted phases were acquired with a spectral width in the indirect dimension of 1177 kHz and 256 complex increments. The number of scans per increment was 1568, 4224 and 4096, for LiFexCo1−xPO4x = 0.25, 0.5 and 0.75, respectively. The complex increments were acquired and processed using the echo/anti-echo scheme. All experiments were carried out at a sample temperature estimated at 320 K (elevated from room temperature due to MAS-induced frictional heating).
Testing of the excitation efficiency and separation of the sidebands was carried out on a Bruker 700 Avance III spectrometer (16.45 T) at a Larmor frequency of 283.5 MHz, using a 1.3 mm Bruker probe. The 90° pulse width was 1.42 μs, the recycle delay was 0.015 s and the spinning speed was 60 kHz. Both the SHAP echo and the aMAT data were collected using tanh/tan SHAPs, sweeping through 5 MHz in 50 μs with a RF amplitude of 175.5 kHz. The evolution time in the aMAT sequence was set to seven rotor periods, excluding the length of the SHAPs. 256 complex increments were acquired and processed using the echo/antiecho scheme.
At all fields the 31P data were referenced to an 85 wt% H3PO4 solution at 0 ppm.
2.3. Hybrid density functional theory
The Fermi contact contributions for the Fe–O–P and Co–O–P pathways in LFP and LCP, respectively, were taken from the values calculated by Middlemiss et al.26 For the ‘distortion’ analysis, in which Fe was placed in the previously optimised LCP structure, and Co, in the previously optimised LFP structure, the Fermi contact contributions were obtained using the same bulk magnetic parameters as for Fe and Co in their native LFP and LCP structures, respectively,24,26 and neglecting further geometry changes in response to the substitutions, so that the distortions might be regarded as limiting cases. In brief, the first principles solid-state DFT calculations were performed within the CRYSTAL09 linear combinations of atomic orbitals code.38 Two hybrid functionals were used: the B3LYP functional with 20% Hartree–Fock (HF) exchange (Hyb20)39 and a related 35% HF Becke-LYP hybrid (Hyb35).40–42 The Fermi contact contribution to the hyperfine shift was computed directly from the spin density at the 31P nuclear position in the ferromagnetic state and subsequently scaled to a value consistent with the paramagnetic state, as described previously by Middlemiss et al. and Clément et al.24,26 The bulk magnetic parameters defining the temperature dependent paramagnetic susceptibilities of LFP and LCP were as in the previous study.26 M–O–P bond pathway decompositions of total 31P hyperfine shifts were performed by flipping selected M spins in Li8M8(PO4)8 supercells, where the variations in 31P contact shifts due to the flip directly yield the symmetry distinct pathway contributions.263. Results and discussion
3.1. X-ray diffraction
LiFexCo1−xPO4 (x = 1, 0.75, 0.5, 0.25 and 0) were characterised and confirmed as phase pure using XRD. Rietveld refinements of the XRD patterns and analysis of the cell parameters (ESI†) show a linear decrease in the cell volume as the Co content increases, which is consistent with the smaller ionic radius of Co2+ in comparison with that of Fe2+ (88.5 and 92 pm,43 respectively for the high spin six-fold co-ordinated crystal radii). The linear relationship of the cell parameters with Co content is consistent with Vegard-type behaviour (Fig. 2 and ESI†) and is indicative of a solid solution of Fe and Co on the M site. This is in agreement with the conclusions of the neutron diffraction study of Nytén et al.44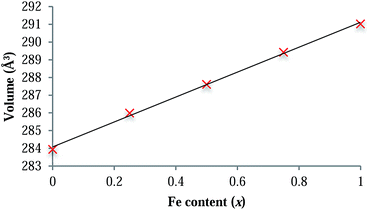 | ||
| Fig. 2 Plot showing the dependence of the unit cell volume on Fe content across the LiFexCo1−xPO4 series. The linear correlation (R2 = 0.9983) follows Vegard's law. | ||
3.2. Nuclear magnetic resonance
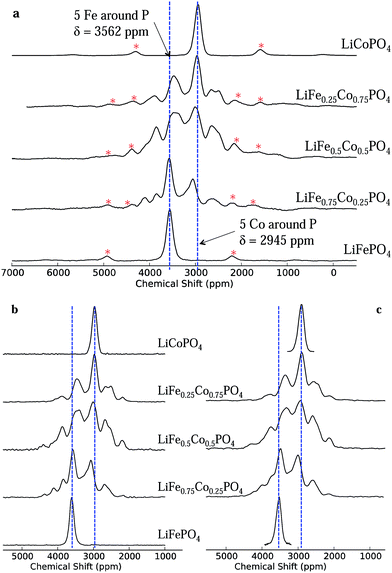
The one-dimensional NMR spectra of LiFexCo1−xPO4 (x = 1, 0.75, 0.5, 0.25 and 0) acquired at a low magnetic field strength of 2.35 T and a fast spinning frequency of 55 kHz are shown in Fig. 3a. The isotropic shift (δiso) of LFP is higher than that of LCP (3562 and 2954 ppm, respectively), but the linewidths are similar, with a full width at half maximum (FWHM) of 6.3 kHz/170 ppm. The NMR spectra of the co-substituted olivines contain two resonances near those of the two end members compounds, but they also contain resonances lying outside the bounds of these two shifts. This is surprising, as it is intuitive to expect the resonances for the intermediate LiFexCo1−xPO4 (0 < x < 1) stoichiometries to lie between the all-Fe and all-Co shifts, as was the case in our prior study of the LiFe1−xMnxPO4 solid solutions.24The short pulse widths and low magnetic field strength enable us to excite the whole region of interest in the NMR spectra (additional experiments showing this are presented in the ESI†) while the fast MAS frequencies successfully remove the spinning sidebands of the two most intense peaks in all the spectra (shown by a red asterisk) from the region of the isotropic resonances. Spectra recorded at a lower spinning frequency (40 kHz) and at twice the magnetic field strength (4.7 T; presented in ESI†) show strong peak overlap due to the greater number of sidebands, rendering it virtually impossible to distinguish the different 31P isotropic resonances from their sidebands.
The isotropic 1D spectra extracted from the 2D MATPASS and aMAT pulse sequences, recorded at 200 and 500 MHz (4.7 and 11.75 T), respectively, are shown in Fig. 3b and (c). They show good agreement with each other, and with the low magnetic field 1D data, in respect of peak positions and relative intensities, proving that the excitation bandwidth is sufficiently broad at all three fields strengths. Additionally the removal of the sidebands in the aMAT and MATPASS spectra confirms the assignment of the isotropic resonances in the 1D data. The most notable difference in the spectra arises in the slightly larger linewidth and consequent poorer resolution of the peaks in the 500 MHz data. This is ascribed to a larger temperature gradient and broader distribution in shifts (due to the strong temperature dependence of the hyperfine shift). A series of further experiments (presented in the ESI†) confirm that this broadening is unrelated to the magnetic field strength and the pulse sequence.
Additional experiments were carried out to explore the efficiencies of excitation of the aMAT and MATPASS pulse sequences using a physical mixture of LiFePO4, LiCoPO4 and LiNiPO4 (the 31P site in LiNiPO4 resonating at 1800 ppm). The experiments were carried out at a high magnetic field strength (700 MHz/16.45 T), where the isotropic peaks and their spinning sideband manifolds span an extremely large frequency range, of more than 1 MHz in width. In order to test the excitation window of the two pulse sequences, a 1D stimulated echo (consisting of 90° pulses) was compared with a 1D SHAP echo, which employs adiabatic pulses, 90° and adiabatic pulses being employed in the MATPASS and aMAT experiments, respectively, to obtain the broadband excitation. The spectra were compared with a ‘model spectrum’ (representative of perfect excitation), constructed by summing the three Hahn echo spectra,45 acquired with carrier frequencies centred at 1500, 2500 and 3500 ppm (presented in the ESI†). When the carrier frequency was placed in the middle of the spectra, both pulse sequences successfully excited the entire range. However, the SHAP echo proved to have a larger excitation window: when the carrier was moved off centre by 0.28 MHz the bandwidths for the stimulated echo and the SHAP echo were 1 MHz and 1.3 MHz, respectively. Both the aMAT and MATPASS experiments successfully separated the sidebands from the isotropic peaks, resulting in spectra with peaks arising only from the unique 31P local environments. Since the aMAT pulse sequence is longer than the MATPASS (the former is synchronised to seven rotor periods, the latter to one), it is more susceptible to T′2 dephasing effects, i.e., a loss of intensity due to signal decay prior to acquisition. However, the intensities seen here seem to agree well between the aMAT and the MATPASS spectra, and we assume the effect is negligible in this system.
In summary, the results of all three NMR experiments show good agreement, confirming that they are robust techniques for the study of paramagnetic materials. The further spectral analysis detailed below will be performed with the 200 MHz MATPASS data, given poorer peak resolution in the 500 MHz spectra, while, in the 100 MHz data, although the sidebands of the most intense peaks are moved beyond the region of interest, this is not the case for some of the sidebands associated with the weaker peaks.
3.3. Density functional theory calculations
The FCS contributions, δP, for each of the M–O–P pathways (P) in LFP and LCP acquired from spin-flipping calculations26 within the Hyb20 and Hyb35 functionals are shown in Fig. 1. Since the FCS contributions are additive to a good approximation,26 the overall 31P hyperfine shifts in LiFexCo1−xPO4 (0 < x < 1) were calculated by placing Fe and Co on the five M sites (resulting in 32 configurations) and by summing over the FCS contributions for the five relevant M–O–P pathways. Further calculations have shown that we only need to consider the first coordination shell of M around P, because the more distant M shells have less than a 2% contribution to the FCS (ESI†).Since the bond pathway shift contributions were calculated within the LFP and LCP end member structures, there has been no consideration of the local and longer-range distortions induced by Fe and Co co-substitution into the olivine lattice. For example, we know that the cell parameters vary smoothly across the entire stoichiometric range, which might reasonably be expected to be associated with changes in local structure. We explored this effect by calculating the bond pathway contributions when Co and Fe cations were substituted into the fixed LFP and LCP structures, respectively (denoted as Co@LFP and Fe@LCP), Table 1.
| Fe@LFP, ppm | Fe@LCP, ppm | Co@LCP, ppm | Co@LFP, ppm | |||||
|---|---|---|---|---|---|---|---|---|
| Hyb20 | Hyb35 | Hyb20 | Hyb35 | Hyb20 | Hyb35 | Hyb20 | Hyb35 | |
| δ P1 | 230 | 201 | 666 | 577 | −436 | −412 | −436 | −394 |
| δ P2 | 1925 | 1629 | 1944 | 1640 | 1344 | 1142 | 1287 | 1108 |
| δ P3 | 34 | −72 | 404 | 245 | 657 | 517 | 211 | 127 |
| δ P4 | 271 | 130 | 828 | 627 | 858 | 679 | 585 | 442 |
The differences in pathway contributions, ΔδP, are examined, where, for example, ΔδP1 is the difference δP1(Fe–O–P) − δP1(Co–O–P). A reasonable bounding range for the effects of local distortions in the co-substituted olivine may be derived by comparing the differences in bond pathway contributions obtained for TM species in their native environments (Fe@LFP & Co@LCP) versus those obtained from the cross-substituted case (Fe@LCP & Co@LFP), and the two intermediate cases (Fe@LFP & Co@LFP; and Fe@LCP & Co@LCP). We have calculated the averages, ranges and standard deviations for the ΔδP values obtained in these four cases (Table 2); and take this as representative of the shifts in LiFexCo1−xPO4. The range of ΔδP2 is less than 80 ppm, which may be neglected given that the FWHM of the peaks is 170 ppm. However the distortion-induced ranges of ΔδP3 and ΔδP4 are significant, at greater than 700 ppm. The findings are consistent with the fact that the P2 bond angles are similar in the LFP and LCP structure (differing by 0.6°), while the P3 and P4 bond angles differ by more than 2.5° in the two structures.
| Differences in pathway contributions δP(Fe–O–P) − δP(Co–O–P), ppm | ||||||
|---|---|---|---|---|---|---|
| Average | Standard deviation | Range | ||||
| Hyb20 | Hyb35 | Hyb20 | Hyb35 | Hyb20 | Hyb35 | |
| ΔδP1 | 898 | 792 | 252 | 217 | 463 | 394 |
| ΔδP2 | 620 | 510 | 35 | 21 | 76 | 46 |
| ΔδP3 | −215 | −236 | 335 | 290 | 816 | 707 |
| ΔδP4 | −172 | −182 | 358 | 318 | 830 | 734 |
It is easier to rationalise the transfer of electron density for the 90° (P1) pathway, than for the 120° (P2–P4) pathway, as discussed by Grey et al.14 Using the same model for the P1 pathway (∼90°) in LFP as described for lithium manganates, the doubly occupied O 2pz orbital can transfer some “down” spin density into a singly occupied Fe2+ t2g orbital and some “up” spin density into the P 4s orbital (as shown in the ESI†). This results in the P having a positive shift, as is seen for the P1 pathway in Fe@LFP.
A simplistic analysis might suggest that Co2+ should induce a smaller FCS than Fe2+, purely on the basis that the Fe2+ has one more unpaired electron than Co2+. A corresponding trend is observed in the LiFexMn1−xPO4 materials, where Fe2+ induces a smaller FCS than Mn2+ (3d5).24 However, it is challenging to rationalise the large negative shift for Co in the P1 pathway. As this large shift is present for Co2+ in both the LCP and LFP structures we infer that the electron transfer mechanism is more sensitive to the TM species involved than to the pathway geometry. The results of our earlier study show that there is also a negative FCS for the P1 pathway in the MnPO4, FePO4 and CoPO4 materials.26 As the TM ion decreases in size, the δP1 becomes progressively more negative. A linear relationship between the δP1 and the M radii (ESI†) is observed, and when the size of the ion is <90 pm the δP1 becomes negative. Thus, there is clearly a competing mechanism that result in negative shifts, this mechanism dominating for shorter (more covalent) M–O bonds. The results in Table 1 suggest that for P3 and P4 the transfer of spin density is dominated by pathway geometries, rather than by the number of unpaired electrons in the system, as δP3 and δP4 are both significantly larger when Co or Fe is in the LCP structure. Tentatively, this is ascribed to the better orbital overlap along the M–O–P P3 and P4 pathways in the LCP structure, owing to shorter bond lengths compared with the LFP structure (3.647 and 3.633 Å, for P3 and P4, respectively, in LCP and 3.72, 3.652 Å, for P3 and P4, respectively, in LFP).
It is clear that the causes of the shifts are complex with multiple competing mechanisms, the orientation of the singly occupied orbitals at each TM site being sensitive to the details of the local anion coordination; the bond pathway contributions are then sensitive to both this orbital orientation and to the geometry of the M–O–P bond network. The results of the distortion analysis suggest that a deviation of the experimentally measured FCS in the LiFexCo1−xPO4 series from the ideal pathway contributions calculated for Fe@LFP and Co@LCP might reasonably be expected, especially for the P3 and P4 pathways. We therefore proceed by applying a fitting routine to the isotropic NMR spectra to extract the ΔδP values providing the best fit with the experimental data, as described by Clément et al.24 From the XRD analysis, there is evidence of a solid solution of Fe and Co on the olivine M sublattice,44 and so the relative probabilities of the 32 configurations occurring in LiFexCo1−xPO4 (x = 0.25, 0.5 and 0.75) are calculated using a random model determined by the ratio of Fe to Co in the lattice:
| probability = fa × cb |
The results from the fit taking the Hyb35 data as initial ΔδP values are shown in Fig. 4 (the numbering of the 32 local P environments is shown in the ESI†). The fitted spectra show good agreement with the experimental data. The minor changes in the geometry of the P environments between the materials, is likely to be one source of the slight discrepancies between the experimental and the fitted data; any differences in the T′2 values for the different environments from those calculated using our simple model are also likely to be important. When the Hyb20 data was used as the initial values for the fit, there was poor agreement with the NMR spectra (ESI†) suggesting that the Hyb35 starting values are a better model for the LiFexCo1−xPO4 materials. The outputs of the ΔδP obtained in the fits with the Hyb35 initial values are shown in Table 3. The ΔδP2 resulted in a small change from the starting values (65 ppm), whereas the ΔδP3 and ΔδP4 changed by 110 and 255 ppm, respectively, which is in good agreement with the distortion analysis (Table 2).
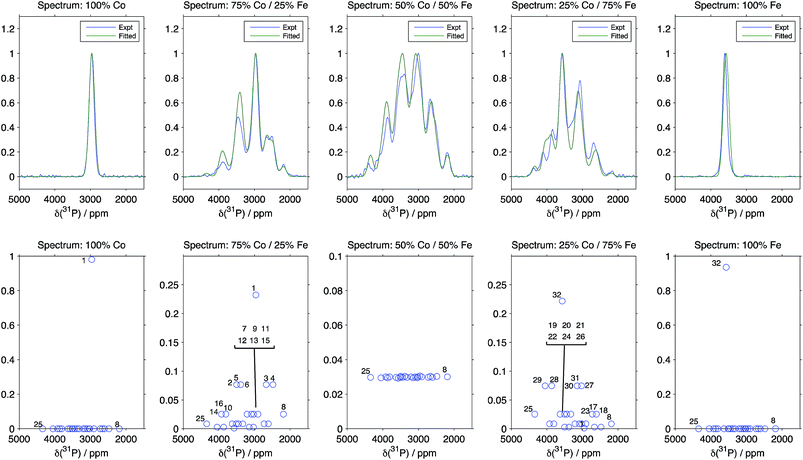 | ||
| Fig. 4 Comparison between the experimental spectra, and the results of fitting the pathway contribution differences using the Hyb35 calculations as starting values and fixing the isotropic shifts of the 32 possible Fe/Co configurations around P (the numbering of the 32 local P environments is shown in the ESI†). R2 is 0.9822, 0.9396, 0.9524, 0.9411 and 0.8320 for LiFexCo1−xPO4 for x = 1, 0.75, 0.5, 0.25 and 0, respectively. | ||
| ΔδP, ppm | Fitted output (Fitted) | Initial value: Fe@LFP–Co@LCP Hyb35 calculations |
|---|---|---|
| ΔδP1 | 539 | 613 |
| ΔδP2 | 422 | 487 |
| ΔδP3 | −479 | −589 |
| ΔδP4 | −294 | −549 |
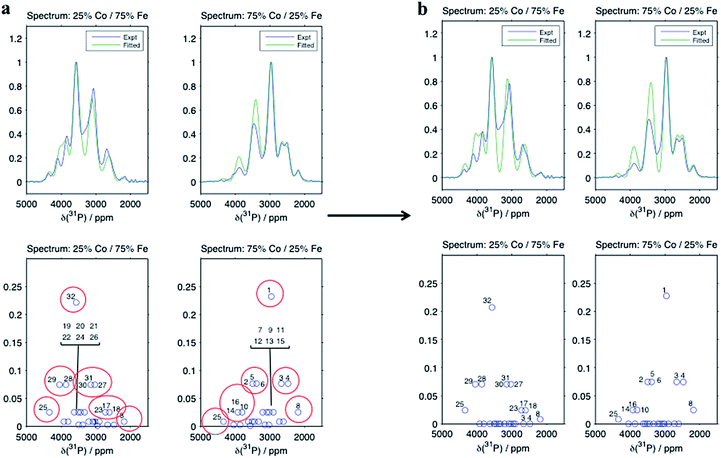
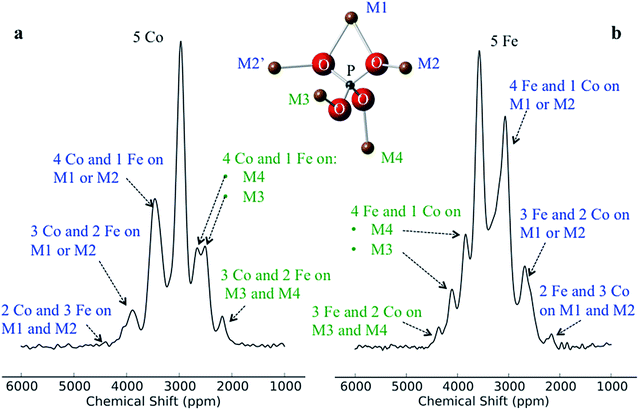
Despite there being 32 P environments (24 of which are distinct because M2 = M2′), there are at most seven distinguishable peaks in the spectra of the co-substituted materials. Examining the intensities of the configurations that fall within each of these peaks for LiFe0.25Co0.75PO4 and LiFe0.75Co0.25PO4, dominant configurations with a significant contribution to the intensity are always clearly evident (circled in Fig. 5a). The output from the Hyb35 fits was re-plotted including only the main contributions to each of the resonances (Fig. 5b). The fitted data still capture the main features of the spectra and result in a good fit (R2 = 0.8684 and 0.8712 for LiFe0.75Co0.25PO4 and LiFe0.25Co0.75PO4, respectively, compared with R2 = 0.9396 and 0.9411 for LiFe0.75Co0.25PO4 and LiFe0.25Co0.75PO4, respectively, when all of the contributions are included). The most notable differences appear to be around the “all-Fe” and “all-Co” peaks, configurations 32 and 1 respectively, indicating that the lower intensity peaks are most significant in this region. Using the results in Fig. 5 we are able to assign the peaks that are observable in the NMR spectra to a set of dominant configurations (Fig. 6). Importantly, we can make a definitive assignment concerning the number of Fe and Co ions in the local coordination shell. This is what is important for understanding the electrochemistry of these systems in subsequent studies.
In the LiFe0.25Co0.75PO4 and LiFe0.75Co0.25PO4 spectra, we observe that when the majority TM is exchanged on the M3 or M4 site by the minority TM, the shift for that P environment moves beyond the isotropic shift of the pure majority metal phase (i.e. to above 3600 ppm for LFP and to below 3000 ppm for LCP). This is due to δP3 and δP4 being larger in LCP as compared with LFP. Thus, Co on the M1 and/or M2 sites results in a lower shift for that environment, while Co on the M3 and/or M4 sites leads to higher shifts. Therefore we have been able to rationalise the appearance of peaks outside the range of the all-Fe and all-Co P environments by the calculation and use of individual M–O–P bond pathway shift contributions. If, as might initially be thought, Fe should always display a larger FCS contribution than Co due its additional unpaired electron, the P shifts in the mixed TM systems would all appear within the bounds of the LFP and LCP peaks, as observed for the LiFexMn1−xPO4 system.24
4. Conclusions
We have carried out a comprehensive study using solid-state NMR and hybrid DFT calculations of the high energy density LiFexCo1−xPO4 paramagnetic cathode materials for 0 ≤ x ≤ 1, arriving at a detailed understanding of the NMR spectra. Three different experimental NMR methods for broadband excitation and sideband separation have been employed, allowing for the collection of spectra containing only the isotropic peaks. The adiabatic pulses employed in the aMAT sequence resulted in the largest bandwidth (of greater than 1 MHz). The data acquired at a low magnetic field strength and with fast spinning did not require a 2D pulse sequence, and represents the most trivial of the NMR techniques, however there may be a small overlap between the sidebands of the lower intensity peaks and some of the isotropic peaks. This issue is avoided in the 2D experiments.First principles hybrid DFT calculations on LFP and LCP have provided us with a tool to calculate the 31P hyperfine shifts in LiFexCo1−xPO4. Using a minimisation fitting routine we assigned the 32 P environments in the co-substituted olivine. Lacking the DFT calculations, it would have proved impossible to rationalise the assignment of the spectra because the majority of the peaks fall beyond the all-Co and all-Fe 31P shifts. The origin of this phenomenon comes from the differences in the FCS in two M–O–P pathways (δP3 and δP4) being greater in LCP than LFP. This contradicts the admittedly simple notion that Fe2+ should transfer more electron density onto P than Co2+, owing to its greater number of unpaired electrons, and instead suggests that more subtle effects such as the variation of bond lengths and angles in the local shells around the two ions are the source of the effect. In order to render our findings more immediately applicable to future NMR studies of the electrochemical cycling of such materials, we have identified the local configurations that give rise to the dominant experimental peaks, and provide definitive assignments of the resonances in terms of the numbers of Fe and Co ions in the local coordination shell, clearly distinguishing two groups of resonances depending on whether the ions are connected to the phosphate ions via M1/M2–O–P or the M3/M4–O–P pathways.
Acknowledgements
We thank Ben Zhu for his help with the NMR and thoughtful discussions. We also thank the UK EPSRC for a DTA award (FCS) the US DOE for support via NECCES, an Energy Frontier Research Center (DE-SC0001294) (CPG) and the EU ERC for financial support and a Marie Curie intra-European fellowship (ML). AJP, GP and LE were supported by the LABEX iMUST (ANR-10-LABX-0064) of the Université de Lyon, within the program “Investissements d'Avenir” (ANR-11- IDEX-0007) operated by the Agence Nationale de la Recherche (ANR). JVH thanks the EPSRC and the University of Warwick for partial funding of the solid-state NMR infrastructure at Warwick, and acknowledges additional support for this infrastructure obtained through Birmingham Science City: Innovative Uses for Advanced Materials in the Modern World (West Midlands Centre for Advanced Materials Projects 1 and 2), with support from Advantage West Midlands (AWM) and partial funding by the European Regional Development Fund (ERDF).Notes and references
- J.-M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS PubMed
.
- K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Mater. Res. Bull., 1980, 15, 783–789 CrossRef CAS
.
- J. N. Reimers and J. R. Dahn, J. Electrochem. Soc., 1992, 139, 2091–2097 CrossRef CAS PubMed
.
- A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 1188–1194 CrossRef CAS PubMed
.
- K. Amine, H. Yasuda and M. Yamachi, Electrochem. Solid-State Lett., 2000, 3, 178–179 CrossRef CAS PubMed
.
- F. Zhou, M. Cococcioni, K. Kang and G. Ceder, Electrochem. Commun., 2004, 6, 1144–1148 CrossRef CAS PubMed
.
- S. Okada, S. Sawa, M. Egashire, J.-I. Yamaki, M. Tabuchi, H. Kageyama, T. Konishi and A. Yoshino, J. Power Sources, 2001, 97-98, 430–432 CrossRef CAS
.
- J. Yang and J. J. Xu, J. Electrochem. Soc., 2006, 153, A716 CrossRef CAS PubMed
.
- J. Wolfenstine and J. Allen, J. Power Sources, 2004, 136, 150–153 CrossRef CAS PubMed
.
- D.-W. Han, Y.-M. Kang, R.-Z. Yin, M.-S. Song and H.-S. Kwon, Electrochem. Commun., 2009, 11, 137–140 CrossRef CAS PubMed
.
- J. Kim, D.-H. Seo, S.-W. Kim, Y.-U. Park and K. Kang, Chem. Commun., 2010, 46, 1305 RSC
.
- J. Cabana, J. Shirakawa, G. Chen, T. J. Richardson and C. P. Grey, Chem. Mater., 2010, 22, 1249–1262 CrossRef CAS
.
- T. Pennanen and J. Vaara, Phys. Rev. Lett., 2008, 100, 133002 CrossRef
.
- C. P. Grey and N. Dupré, Chem. Rev., 2004, 104, 4493–4512 CrossRef CAS
.
- L. J. M. Davis, I. Heinmaa, B. L. Ellis, L. F. Nazar and G. R. Goward, Phys. Chem. Chem. Phys., 2011, 13, 5171 RSC
.
- L. Zhou, M. Leskes, A. J. Ilott, N. M. Trease and C. P. Grey, J. Magn. Reson., 2013, 234, 44–57 CrossRef CAS PubMed
.
- M. C. Tucker, M. M. Doeff, T. J. Richardson, R. Fiñones, E. J. Cairns and J. A. Reimer, J. Am. Chem. Soc., 2002, 124, 3832–3833 CrossRef CAS PubMed
.
- S. L. Gann, J. H. Baltisberger and A. Pines, Chem. Phys. Lett., 1993, 210, 405–410 CrossRef CAS
.
- J. Z. Hu, D. W. Alderman, C. Ye, R. J. Pugmire and D. M. Grant, J. Magn. Reson., 1993, 105, 82–87 CrossRef CAS
.
- W. T. Dixon, J. Magn. Reson., 1981, 44, 220–223 CAS
.
- W. T. Dixon, J. Chem. Phys., 1982, 77, 1800 CrossRef CAS PubMed
.
- O. N. Antzutkin, S. C. Shekar and M. H. Levitt, J. Magn. Reson., 1995, 115, 7–15 CrossRef CAS
.
- G. Kervern, G. Pintacuda and L. Emsley, Chem. Phys. Lett., 2007, 435, 157–162 CrossRef CAS PubMed
.
- R. J. Clément, A. J. Pell, D. S. Middlemiss, F. C. Strobridge, J. K. Miller, M. S. Whittingham, L. Emsley, C. P. Grey and G. Pintacuda, J. Am. Chem. Soc., 2012, 134, 17178–17185 CrossRef PubMed
.
- I. Hung, L. Zhou, F. Pourpoint, C. P. Grey and Z. Gan, J. Am. Chem. Soc., 2012, 134, 1898–1901 CrossRef CAS PubMed
.
- D. S. Middlemiss, A. J. Ilott, R. J. Clément, F. C. Strobridge and C. P. Grey, Chem. Mater., 2013, 25, 1723–1734 CrossRef CAS
.
- J. B. Goodenough, J. Phys. Chem. Solids, 1958, 6, 287–297 CrossRef CAS
.
- J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98 CrossRef CAS
.
- J. Kim, D. S. Middlemiss, N. A. Chernova, B. Y. X. Zhu, C. Masquelier and C. P. Grey, J. Am. Chem. Soc., 2010, 132, 16825–16840 CrossRef CAS PubMed
.
- J. Yates, C. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401 CrossRef
.
- A. Castets, D. Carlier, Y. Zhang, F. Boucher and M. Ménétrier, J. Phys. Chem. C, 2012, 116, 18002–18014 CAS
.
- Y. Zhang, A. Castets, D. Carlier, M. Ménétrier and F. Boucher, J. Phys. Chem. C, 2012, 116, 17393–17402 CAS
.
- A. Castets, D. Carlier, Y. Zhang, F. Boucher, N. Marx, R. Gautier, E. Le Fur, L. Le Pollès, L. Croguennec and M. Ménétrier, Solid State Nucl. Magn. Reson., 2012, 42, 42–50 CrossRef CAS PubMed
.
- G. Mali, C. Sirisopanaporn, C. Masquelier, D. Hanzel and R. Dominko, Chem. Mater., 2011, 23, 2735–2744 CrossRef CAS
.
- G. Kobayashi, S.-I. Nishimura, M.-S. Park, R. Kanno, M. Yashima, T. Ida and A. Yamada, Adv. Funct. Mater., 2009, 19, 395–403 CrossRef CAS
.
- A. A. Coelho, Acta Crystallogr., Sect. A: Found. Crystallogr., 2007, 63, 400–406 CrossRef CAS PubMed
.
- T.-L. Hwang, P. C. M. van Zijil and M. Garwood, J. Magn. Reson., 1998, 133, 200–203 CrossRef CAS PubMed
.
- R. Dovesi, R. Orlando, B. Civalleri, C. Roetti, V. R. Saunders and C. M. Ziovich-Wilson, Z. Kristallogr., 2005, 571–573 CAS
.
- J. Muscat, A. Wander and N. M. Harrison, Chem. Phys. Lett., 2001, 342, 397–401 CrossRef CAS
.
- X. Feng and N. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 092402 CrossRef
.
- D. S. Middlemiss, L. M. Lawton and C. C. Wilson, J. Phys.: Condens. Matter, 2008, 20, 335231 CrossRef
.
- I. de P. R. Moreira, F. Illas and R. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155102 CrossRef
.
- R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767 CrossRef
.
- A. Nytén and J. O. Thomas, Solid State Ionics, 2006, 177, 1327–1330 CrossRef PubMed
.
- A. J. Pell, R. J. Clément, C. P. Grey, L. Emsley and G. Pintacuda, J. Chem. Phys., 2013, 138, 114201 CrossRef PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: LFP and LCP M–O–P pathway bond lengths and angles, XRD patterns and refinements, experiment to test the excitation window at a magnetic field strength of 100 MHz, comparison of the Hahn echo and the MATPASS pulse sequence at a magnetic field strength of 200 MHz, the Hahn echo, stimulated echo, SHAP echo, aMAT and MATPASS pulse sequences, the LiNiPO4 synthesis, spectra of a mixture of LiNiPO4, LFP and LCP at a magnetic field strength of 700 MHz comparing the excitation width for the 90° and adiabatic pulses, the FCS contributions of the second co-ordination shell in LFP and LCP for the Hyb20 and Hyb35 calculations, an electron transfer process in a 90° M–O–P pathway, the δP1 plotted as a function of the size of the transition metal for LiMnPO4, LFP, LCP, MnPO4, FePO4 and CoPO4, the T′2 values used for different Fe/Co ratios around P, the labelling of the 32 configurations of Fe and Co around P in the olivine structure and the results from the fitting using the Hyb20 results as input values. See DOI: 10.1039/c4ta00934g |
| ‡ Current address: Department of Chemistry, University of Warwick, Gibbet Hill Road, Coventry, CV4 7AL, UK. |
| § Current address: Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1 EW, UK. |
| ¶ Current address: Université Lille Nord de France, CNRS, UMR 8181 UCCS, ENSCL, Université de Lille 1, 59652 Villeneuve d'Ascq, France. |
| This journal is © The Royal Society of Chemistry 2014 |