Open Access Article
Open Access ArticleChemical looping of metal nitride catalysts: low-pressure ammonia synthesis for energy storage†
R.
Michalsky
*abc,
A. M.
Avram‡
a,
B. A.
Peterson§
a,
P. H.
Pfromm
a and
A. A.
Peterson
b
aDepartment of Chemical Engineering, Kansas State University, 1005 Durland Hall, Manhattan, Kansas 66506, USA. E-mail: michalskyr@ethz.ch; Tel: +41-44-6338383
bSchool of Engineering, Brown University, 184 Hope Street, Providence, Rhode Island 02912, USA
cDepartment of Mechanical and Process Engineering, ETH Zürich, 8092 Zürich, Switzerland
First published on 1st May 2015
Abstract
The activity of many heterogeneous catalysts is limited by strong correlations between activation energies and adsorption energies of reaction intermediates. Although the reaction is thermodynamically favourable at ambient temperature and pressure, the catalytic synthesis of ammonia (NH3), a fertilizer and chemical fuel, from N2 and H2 requires some of the most extreme conditions of the chemical industry. We demonstrate how ammonia can be produced at ambient pressure from air, water, and concentrated sunlight as renewable source of process heat via nitrogen reduction with a looped metal nitride, followed by separate hydrogenation of the lattice nitrogen into ammonia. Separating ammonia synthesis into two reaction steps introduces an additional degree of freedom when designing catalysts with desirable activation and adsorption energies. We discuss the hydrogenation of alkali and alkaline earth metal nitrides and the reduction of transition metal nitrides to outline a promoting role of lattice hydrogen in ammonia evolution. This is rationalized via electronic structure calculations with the activity of nitrogen vacancies controlling the redox-intercalation of hydrogen and the formation and hydrogenation of adsorbed nitrogen species. The predicted trends are confirmed experimentally with evolution of 56.3, 80.7, and 128 μmol NH3 per mol metal per min at 1 bar and above 550 °C via reduction of Mn6N2.58 to Mn4N and hydrogenation of Ca3N2 and Sr2N to Ca2NH and SrH2, respectively.
1. Introduction
Ammonia is one of the most important synthetic chemicals in today's economy. With an annual production of about 162 million metric tons,1 NH3 is irreplaceable as a fertilizer, responsible for growing the food for approximately half of the world's population.2,3 However, the catalytic synthesis of NH3 from N2 and H2 is realized at some of the most severe process conditions of the chemical industry, i.e., about 300 bar and 400–500 °C (ref. 4 and 5) (the Haber–Bosch process), and consumes energy at 28–166 GJ per ton NH3 (ref. 1 and 5) in the form of natural gas, coal, or Naphtha;1 this is 1–2% of the world's annual energy production.6 About 15% of these net energy requirements are consumed for the technologically sophisticated high-pressure operations alone.1 The fossil-fuel dependence links food security to natural gas price fluctuations and results in net CO2 emissions of 1.9 tons (H2 generation via steam reforming of natural gas) to 16.7 tons (H2 generation via partial oxidation of coal) per ton NH3.1 Economies of scale dictate the need for large facilities producing typically 1000–3000 tons NH3 per day,1 which requires a highly developed infrastructure for production and distribution.2 The conceivable development of a catalyst for a low-pressure and low-temperature Haber–Bosch process could theoretically alleviate these conditions. Although thermodynamically favorable at ambient temperature and pressure, no catalyst has been found that establishes reasonable reaction rates at these conditions,7 which has been rationalized with the scaling of the activation energy for the N2 dissociation and the adsorption energy of nitrogen at the catalyst surface.7–9Beyond its irreplaceable use in agriculture, the use of NH3 as a fuel is an attractive proposition since it is easily liquefied, rendering it a stable one-way hydrogen carrier and one of the most energy-dense zero-carbon fuels10,11 that can be used as a direct substitute for fossil fuels in internal combustion engines.12 This, and the prospect of zero-CO2-emission vehicles, have motivated the development of the “AmVeh” car prototype fueled by a 70% NH3/30% gasoline blend.13 Current combustion research is focused on increasing the energy substitution by NH3 and improving the exhaust treatment for removing un-combusted NH3.13,14 Additionally, NH3 can be used in alkaline fuel cells that decompose NH3 into N2 and H2 fuel15 for direct electricity generation.16 The development of the electrocatalysts and the cell design are currently limiting the costs and efficiency of this technology.16 The synthesis of ammonia as a “solar fuel”,17 could conceivably be deployed beginning with the electrolysis of water with photovoltaic electricity18 (the generated H2, however, would require massive investments into infrastructure for compression, storage and transport, hindering its direct use). Instead, H2 could be employed for the synthesis of more practical liquid ammonia-based fuels via the conventional Haber–Bosch process. However, this technology requires sophisticated multi-step high-pressure and high-temperature unit operations and high-value electricity to operate these units due to the limited activity of the employed heterogeneous catalysts.1,2,19
One proposed means to circumvent the high-pressure and high-temperature requirements of the Haber–Bosch process is the electrochemical reduction of N2 to synthesize NH3 with solar-derived photovoltaic electricity at ambient pressure and temperature.20–22 NH3 evolution at the cathode becomes thermodynamically favorable at an equilibrium potential of 0.1 V vs. the reversible hydrogen electrode, RHE,20,21 and electronic structure calculations have suggested materials may be found that would liberate NH3 at about −0.5 V vs. RHE.21,23,24 However, no suitable electrocatalyst has been identified experimentally for these potentials – the observed rates of NH3 evolution are low and the best reported Faradaic efficiencies are in the order of 0.2–2%,20,25 while more negative (stronger) potentials decrease the Faradaic efficiency further due to the competing hydrogen evolution reaction.
This article introduces an alternative approach: splitting of a catalytic reaction into two separate reaction steps that are facilitated with a looped metal compound catalyst. We demonstrate this approach with looped metal nitride catalysts for solar-driven low-pressure synthesis of ammonia. Solar-driven thermochemical N2 reduction could circumvent the high-pressure requirements of the Haber–Bosch process and the energetic deficiencies of the electrochemical N2 reduction. This approach separates the NH3 synthesis into two reaction steps:26–29 first, N2 is reduced, typically, with a metal oxide and concentrated sunlight at elevated temperatures yielding a metal nitride. In a second step, the metal nitride is oxidized with H2O to yield NH3 and the restored metal oxide at lower temperatures. On paper, the optimization of the reactive materials30,31 and of the solar radiation receiver-reactor technology32 could allow us to approach solar-to-fuel energy conversion efficiencies of 70–75%, for solar radiation concentrated 5000-fold to 800–1500 °C.33 However, while NH3 can be formed at 1 bar and 200–500 °C by the oxidation of certain metal nitrides with H2O,27,34,35 recycling the metal oxide requires either a chemical reducing agent, such as biomass and/or syngas, or temperatures above 1500 °C.26–29
We propose production of NH3 and O2 from H2O and N2, without a sacrificial reducing agent and at moderate temperatures, via solar-driven cleavage of H2O into H2 and O2 (ref. 30 and 31) and subsequent fixation and hydrogenation of N2 with H2 into NH3 at 1 bar and up to 800 °C using a looped metal nitride catalyst and concentrated solar energy. Looped metal nitrides may decouple scaling of the nitrogen adsorption energy with the activation energy for N2 dissociation that typically limits the activity of Haber–Bosch catalysts,7 since the chemical potential of a metal nitride can be utilized in a low-temperature oxidation liberating NH3, while N2 can be reduced via recycling the metal nitride at elevated temperatures. At the process scale, this approach does neither require electricity for NH3 formation nor the infrastructure for supplying natural gas or coal and the know-how and technology for high-pressure operations. As indicated by our previous net-present value analysis of solar-driven NH3 synthesis via metal nitride hydrolysis,26 such a process can be economically more attractive in geographically, economically, or politically isolated regions than NH3 from large-scale Haber–Bosch plants.
In a broader context, looped nitride catalysis is analogous to looped oxide catalysis with reduced metal oxides that provide oxygen vacancies for the abstraction of oxygen from, for instance, bio-oils upgraded with H2 into hydrocarbons.36 Looped nitride catalysts provide active lattice nitrogen that is converted with H2 into NH3 and nitrogen vacancies, with ideally high selectivity for NH3 and no formation of N2 and N2H4. This is in contrast to the activity of redox materials, for instance, for solar-driven splitting of CO2 and H2O with total selectivity for CO, H2, and O2.33,37 In turn, established computational tools for the rational design of heterogeneous catalysts and electrocatalysts, such as free energy minimization to determine reaction paths,38,39 can be utilized to develop reducible metal nitride catalysts. In the following two Sections we employ electronic structure theory to determine and describe limiting reaction energetics for metal nitrides. Comparable to chemical looping applications, the oxygen vacancies of a looped oxide may be regenerated at high temperatures with concentrated solar energy, while the nitrogen vacancies of a looped nitride are refilled via solar-driven N2 reduction. While we discuss trends in the bond strength of nitrogen adsorbates and lattice nitrogen, the presented principles are expected to apply analogously to the bond strength of oxygen, that governs the adsorption of oxygen at electrocatalysts for the oxygen reduction and evolution reactions (ORR/OER),40,41 the reversible oxygen vacancy formation at metal oxide surfaces for selective deoxygenation,42 and the oxygen exchange capacity of metal oxide redox materials for solar-driven CO2 and H2O splitting.31,33,37,43 The discussed metal nitrides form a bridge between materials with weak metal–nitrogen bonds for nitrogen activation44–46 and materials with strong metal–nitrogen bonds for hydrogen storage,10,11,47,48 such as certain Li-based compounds which may reversibly release H2 at reasonable pressures and temperatures (e.g., 0.4–20 bar and 195–285 °C for Li3N/Li2NH)47 and that ideally do not liberate NH3.49
In this article we suggest design principles – which we derive from both electronic structure calculations and experiments – that can inform the design of a metal nitride for solar-driven ammonia synthesis. Section 2.1 outlines the ammonia-synthesis potential of metal nitrides that facilitate the incorporation of hydrogen into the bulk crystal lattice. This is rationalized in Section 2.2 via electronic structure calculations that describe how nitrogen vacancies control NH3 evolution at the atomic scale. Sections 2.3 and 2.4 quantify the reaction kinetics of NH3 evolution and experimentally demonstrate the augmented conversion of lattice nitrogen via hydrogenation of metal nitrides relative to the reduction of metal nitrides.
2. Results and discussion
2.1 Thermochemical reactivity of metal nitride catalysts
We start by using literature data to provide basic reactivity principles for nitrides and to outline the pressure and temperature conditions of the proposed ammonia production via chemical looping of metal nitride catalysts. Similar to the Sabatier principle in catalysis,7,21,45 producing NH3 from N2 and H2via looping of a metal nitride catalyst should have an optimum stability of the metal–nitrogen bond. At one extreme, thermally unstable nitrides – such as Co3Mo3N, Ni3N, Cu3N and Zn3N2 – have been shown to yield much NH3via denitridation with H2 at about 250–400 °C.44,46 However, the latter three materials are too unstable to be regenerated with N2 at 1 bar46 and a completely reversible recycling of Co3Mo3N from the formed Co6Mo6N requires long-time heating for 4 h in H2/N2.44 On the other extreme, some more stable metal nitrides, when reacted with H2, absorb hydrogen reversibly yielding mixtures of metal imide, amide and hydride (e.g., Li2NH, LiNH2 and LiH from the reaction of Li3N with H2), rather than being selective to NH3.47,48 These nitrides can liberate some NH3 at elevated temperatures in the presence of H2, e.g., from LiNH2 above 300 °C (ref. 47) and from Ca3N2 above 600 °C.50 Ideally, an intermediate metal–nitrogen bond strength would balance these effects.In principle, the reduction of a metal nitride yields NH3 and a lower nitride phase:
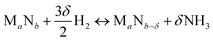 | (1) |
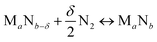 | (2) |
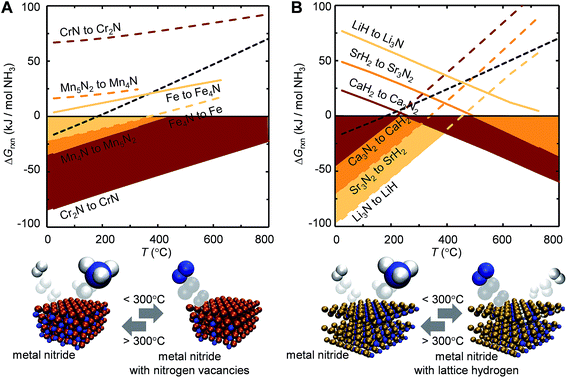
Ideally, both reactions would have an exergonic region of temperature space, such that NH3 is synthesized via a temperature-swing operation. Fig. 1A shows thermodynamic calculations of both reactions as functions of temperature for some representative systems. Unfortunately, none of these reactions exhibits this characteristic; instead, this figure generally identifies NH3 evolution to be endergonic and N2 reduction to be exergonic, except for Fe4N and Co3N (ESI†) with reversed reaction energetics. This can be understood due to the low thermal stability of Fe4N and Co3N.
 | ||
| Fig. 1 Ammonia synthesis at 1 bar and up to 800 °C (computed from tabulated free energy data)51via (A) metal nitride reduction with H2 (eqn (1), dashed lines) and N2 reduction with reduced metal nitrides (eqn (2), solid lines) and (B) metal nitride hydrogenation (eqn (3), dashed line) and N2 reduction with metal hydrides (eqn (4), solid line). Shaded regions mark exergonic reactions. The equilibrium of NH3 with 3/2H2 and 1/2N2 is shown as reference at 1 bar (dotted line; negative values corresponding to NH3 evolution). | ||
To understand these trends, Fig. 2A shows the free energy of NH3 evolution vs. the product of the number of d-electrons in the metal ground state, Nd, and the energy of these electrons, Ed. The analysis suggests increasing NH3 evolution and decreasing stability of the metal–nitrogen bond with increasing occupancy of the d-states, which indicates their antibonding character. This phenomena is well known from the interaction of adsorbates at transition-metal surfaces.52 While we did not include Ni3N, Cu3N and Zn3N2 in this analysis due to limited thermodynamic data, the high NH3 yields with these unstable metal nitrides46 can be understood due to an even higher number of d-electrons, relative to Fe4N. We suggest that the trade-off between NH3 evolution and N2 reduction may be optimized for doped transition-metal nitrides by targeting properties intermediate to those of Mn and Fe, that is, an NdEd of about −50 eV. Since the correlation of d-state occupancy and nitride reactivity is linked through the stability of the metal–nitrogen bond, for a ternary system NdEd may be defined in first approximation as the arithmetic average of the value for the metals that form metal–nitrogen bonds.
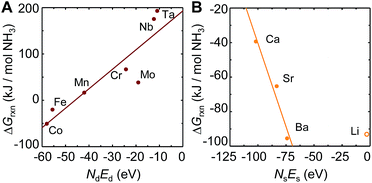 | ||
| Fig. 2 Scaling of the free energy of the NH3 evolution at 25 °C (computed from tabulated free energy data as described in Section 3.1) via metal nitride (A) reduction and (B) hydrogenation with the product of the number of electrons in the metal ground state, N, and the energy of these electrons, E, in the (A) d-states and (B) s-states. The metal marks the metallic constituent of the composition given with ESI.† Solid lines are fits to the data shown with solid symbols. | ||
Instead, the yield of NH3 could be increased with a material that facilitates exergonic NH3 evolution via metal nitride oxidation at low temperatures and exergonic N2 reduction at higher temperatures. We suggest that this can be achieved by partially substituting the lattice nitrogen with hydrogen, as we examine for the reaction:
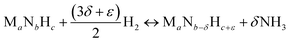 | (3) |
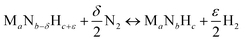 | (4) |
2.2 Formation of nitrogen vacancies vs. lattice hydrogen
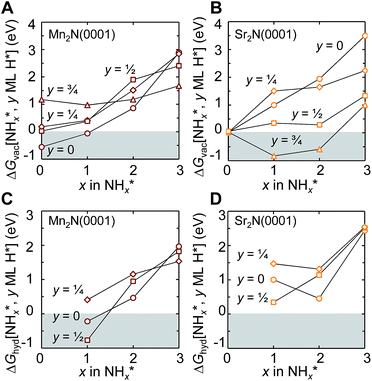
This Section uses electronic structure calculations to outline how nitrogen vacancies control the intercalation of hydrogen and the evolution of NH3, focusing on the (0001) surfaces of Mn2N and Sr2N. To quantify the reactivity of these materials, Table 1 shows free energy changes for key vacancy and surface reactions. We can see a net-energy penalty for forming surface and bulk nitrogen vacancies that is by more than 1 eV higher for Sr2N(0001) than for Mn2N(0001). The energy penalty for the nitrogen vacancy migration into the bulk, i.e., ΔGvac, bulk − ΔGvac, is about equal. This suggests that the nitrogen vacancies of Sr2N(0001) require more energy to be formed and are more reactive than those of Mn2N(0001). This is a first indicator for the trend of surface adsorbates such as H* to fill vacancies. The strong hydrogen binding indicates that in the presence of H2 both surfaces are expectedly covered with H*.| Energy (eV) | Reactiona | Mn2N | Sr2N |
|---|---|---|---|
| a Lat, s, and ss mark the lattice nitrogen, surface and subsurface. b Dissociative hydrogen adsorption at increased surface coverage of 1/2 ML H*. c H2O dissociated to OH* and H*. | |||
| ΔGvac |
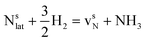
|
0.50 | 1.52 |
| ΔGvac, bulk |
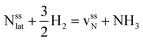
|
0.82 | 1.88 |
| ΔGads[H*] |
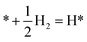
|
−0.79 | −0.45 |
| ΔGads[2H*]b | 2* + H2 = 2H* | −1.30 | −1.10 |
| ΔGads[H2O*] | * + H2O = H2O* | —c | −0.64 |
| ΔGads[OH*] |
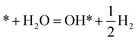
|
−1.47 | −2.20 |
| ΔGads[OH*, H*] | 2* + H2O = OH* + H* | −1.81 | −2.73 |
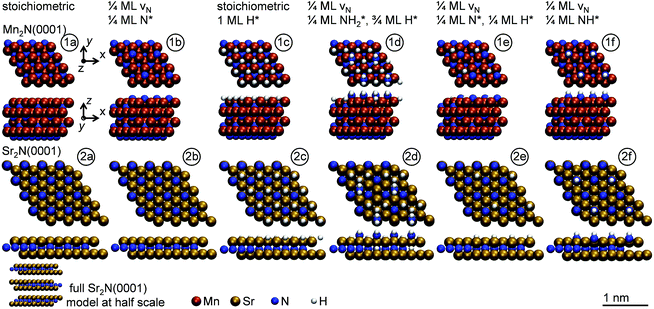
To understand the reaction mechanism of the lattice nitrogen with surface hydrogen, Fig. 3A and B show the energetics of forming 1/4 ML vN at Mn2N(0001) and Sr2N(0001) yielding NH*x (x = 0, 1, 2 or 3) from surface hydrogen (and partly H2 gas, in cases where 1 ML H* does not supply enough hydrogen to yield a specific H*/NH*x surface coverage). The analysis points out a few general trends: the conversion of lattice nitrogen into vN and N* is exergonic at Mn2N(0001) in the absence of H* and increasingly complicated in the presence of an increasing H* coverage. That is, H* appears to act as a surface “poison” for the adsorption of N* or NH* at Mn2N(0001). Second, while 1/4 ML N* is not formed on Sr2N(0001) with 1/4 ML vN, which is independent of the H* coverage (±0.04 eV), the formation of vN at Sr2N(0001) is more favorable if the lattice nitrogen yields NH* or NH*2 in presence of 1/2–3/4 ML H* relative to 0–1/4 ML H*. That is, H* prevents the filling of vN at Sr2N(0001) by surface nitrogen. Such energetic promotion of the vacancy formation by H* co-adsorbates is absent at Mn2N(0001) where H* mostly hinders formation of NH*x with x = 0, 1 or 2. We note the endergonic formation of NH*3 that is stabilized by H* at both surfaces indicates that the direct formation of 1/4 ML NH*3 from lattice nitrogen and 3/4 ML H* is unlikely. Furthermore, departures and “crossover” from these free energy trends are due to the source of the hydrogen and the rearrangement of adsorbates (ESI†).
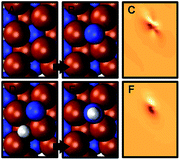
Fig. 3C and D show the energy required to hydrogenate adsorbed nitrogen, which indicates a similar trend: the higher the degree of under-coordination of the adsorbed nitrogen at the surface the easier it is to hydrogenate the nitrogen, which involves breaking surface-nitrogen bonds. Fig. 4 shows that these bonds are favorably formed at three-fold metal sites with charge localization between the adsorbate and the nitrogen vacancy. This is opposed, for instance, to three clearly defined metal–carbon bonds for C* adsorbates at Mo2C(001).9 The most notable exception from this trend is the highly unfavorable hydrogenation of N* to NH* at low H* coverage on Sr2N(0001) which is discussed in the following.
The optimized adsorption geometries are given with Fig. 5. The figure shows intercalation of hydrogen at Sr2N(0001) that is not observed at Mn2N(0001). In absence of surface hydrogen, the strong Sr–N bonds result in unstable 1/4 ML N* that is filling the vacancies at Sr2N(0001), which is visualized by the identical geometries shown with panels (2a and 2b) of Fig. 5, while Mn2N(0001) yields a stable 1/4 ML N* surface coverage (Fig. 5, panels 1a and 1b). In presence of surface hydrogen, Fig. 5 shows that the energetic promotion of forming 1/4 ML vN and NH* or NH2* at high H* coverage at Sr2N(0001) but not at Mn2N(0001) (shown with Fig. 3A and B) is due to filling of vN by H* yielding lattice hydrogen at Sr2N(0001) (Fig. 5, panels 2c and 2d vs. 1c and 1d). These calculations show hydrogen intercalating at the surface. The tendency of this lattice hydrogen to diffuse further into the bulk leading to formation of hydrides is outlined in Section 2.1. Finally, hydrogenating 1/4 ML N* with H* to NH* is energetically demanding at Sr2N(0001) relative to Mn2N(0001) (Fig. 3C and D) since it requires formation of 1/4 ML vN at Sr2N(0001) (Fig. 5, panels 2e and 2f vs. 1e and 1f).
In summary, the lattice nitrogen activity was outlined to control the formation and hydrogenation of adsorbed nitrogen and the formation of lattice hydrogen. These trends are analogous to the reactivity of the bulk metal nitrides.
2.3 Ammonia from partial reduction of metal nitrides
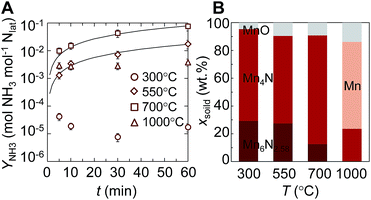
In the following two Sections we study the role of nitrogen vacancies experimentally by comparing the reactivity of Mn-based transition-metal nitrides to the reactivity of Ca- and Sr-based alkaline earth metal nitrides. This Section characterizes the NH3 evolution via the reduction of manganese nitride.Fig. 6A shows the evolution of ammonia from the reaction of manganese nitride with H2. The yield of NH3 relative to the lattice nitrogen available for the reaction was at maximum ∼8 mol% NH3 after 60 min at 700 °C. The location of the optimum at an intermediate temperature is presumably due to slow reaction kinetics at lower temperatures and thermal decomposition of NH3 at higher temperatures. At low NH3 yields we observe decreasing NH3 yields with time, which is presumably due to partial stripping of NH3 with the H2 routed through the liquid absorbent. Since we observe this effect only for NH3 yields between 10−5 to 3 × 10−3, NH3 stripping is assumed to not significantly affect NH3 evolution with higher yields above 300 °C. More important, the ammonia evolution at 550 and 700 °C is described best by a reaction- or gas diffusion-limited kinetic model with an activation energy estimated from an Arrhenius plot of 98 ± 7 kJ mol−1. This indicates that the kinetics of the NH3 formation with H2 are more sensitive to temperature than the steam hydrolysis of Mn4N with an activation energy of 63 kJ mol−1, where oxygen intercalation fills the nitrogen vacancies.34
Fig. 6B shows the composition of the solid after the reaction with H2. Increasing temperature decreases the fraction of Mn6N2.58 and yields a maximum Mn4N fraction near 700 °C. This suggests that NH3 is formed through the reduction of a higher nitride into a lower nitride phase that contains less nitrogen and that decomposes thermally at 1000 °C to Mn and N2.51 The thickness of the reaction front through a particle with constant volume (i.e., L = XNρnitride−1ABET−1, where ρnitride is the density of the reacting nitride and XN is the fraction of liberated lattice nitrogen), can be estimated based on a nitrogen mass balance to be 54 nm or 46 nm for NH3 evolution at 700 °C from Mn6N2.58 or Mn4N, respectively. Fig. 6 suggests that this bulk reaction is limited at the surface: by gas-phase diffusion or the surface reaction, that is by the formation of nitrogen vacancies and the hydrogenation of surface nitrogen. We note, attempting to control the lattice nitrogen reactivity via doping Mn4N with Fe did not increase the NH3 evolution at 700 °C (ESI†), which may be due to the catalytic activity of Fe in establishing the chemical equilibrium in NH3, N2 and H2 gas mixtures.4
For comparison, some metal nitrides that cannot be regenerated with 1 bar N2 may yield significant quantities of NH3. Ni3N, Cu3N, Zn3N2 and Ta3N5 may liberate 30, 25, 23, and 13 mol% of their lattice nitrogen as NH3 when reacted for at least 30 min at 250, 250, 400, and 700 °C, respectively.46 Ammonia yields decrease when reacting H2 with more stable nitrides: such as to 8 mol% with Co3Mo3N for 60 min at 400 °C.44 Manganese nitrides can be formed from N2 at 1 bar, as shown with Fig. 1A, and spent iron-doped manganese nitrides can be regenerated with N2, as shown for three consecutive cycles with Fig. S3.† However, stable performance and long-term stability of metal nitrides, in form of pellets or porous structures for instance,31,33,37 have to be assessed in the future.
2.4 Ammonia from formation of hydrogenated metal nitrides
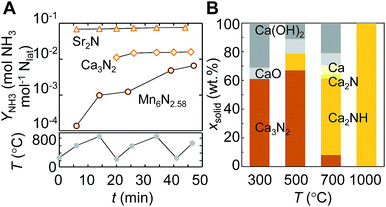
Some alkali and alkaline earth metal nitrides may yield ammonia exergonically from the reaction with H2 due to the intercalation of hydrogen, as discussed in Section 2.1. The electronic structure calculations reported in Section 2.2 outline how the reactivity of the bulk metal nitrides correlates with the activity of the nitrogen vacancies. With the experimental results in this Section we show the ready evolution of ammonia and the corresponding hydrogenated metal compounds from the nitrides of Ca and Sr under H2.The liberation of the lattice nitrogen of Ca3N2 and Sr2N as NH3 may be limited kinetically at the low temperatures that are favored thermodynamically, as was shown with Fig. 1. Therefore, Ca3N2 and Sr2N, as well as Mn6N2.58 as reference, were reacted with H2 at 1 bar and a range of temperatures including the low and high end of the spectrum, 220–850 °C. Fig. 7A shows the NH3 yield over the course of three heating cycles. Sr2N liberates NH3 nearly instantaneously during the initial heating period, which is followed by a continuous and comparably slight increase of the NH3 yield. The absolute NH3 yield from Ca3N2 is lower than that from Sr2N, but both alkaline earth metal nitrides liberate NH3 faster and in significantly larger quantities than the transition-metal nitride.
The minimum apparent reaction rates of hydrogenating lattice nitrogen with H2 into NH3 are estimated with 0.9 ± 0.2, 1.3 ± 0.4 and 2.1 ± 0.2 μmol NH3 (mol metal × s)−1 for Mn6N2.58, Ca3N2 and Sr2N respectively. Since OH and H2O adsorb strongly at alkaline earth metal nitrides (Table 1), this is accounting for partial nitride hydrolysis by traces of adsorbed water, although neither Sr2N nor Ca3N2 appeared visually oxidized after the reaction. These reaction rates of Ca3N2 and Sr2N and significant formation of up to 12 mol% NH3 from Ca3N2 that we observed with a late onset between 30–60 min heating at various H2 flow rates (ESI†) indicate that NH3 is formed from the reaction of lattice nitrogen and H2. For comparison, these yields are higher than the previously reported 1 mol% NH3 from Ca3N2 heated for 120 min at 800 °C in H2, which can be understood due to the unfavorable NH3–N2/H2 equilibrium that is established during these early studies by F. Haber, et al.50
The intercalation of hydrogen can be observed for Ca3N2 yielding mainly Ca2NH and Sr2N yielding SrH2: Fig. 7B shows the composition of Ca3N2, determined via XRD, after the reaction with H2. Increasing temperature increases the formation of Ca2NH, with nominally 25 mol% lattice hydrogen. From the yield of Ca2NH, the activation energy of the NH3 evolution is about 42 ± 7 kJ mol−1. However, the different surface morphologies, shown with Fig. 8, and the slightly different BET surface areas, given with Table S1 (ESI†), of the nitrides indicate that this value of the activation energy cannot be compared directly to the activation energy of the NH3 evolution from manganese nitride, given in Section 2.3. The lower activation energy of Ca3N2 is, however, qualitatively in agreement with the higher NH3 evolution rate with Ca3N2, relative to Mn6N2.58. Furthermore, a 58% higher NH3 evolution rate from Sr2N with a 16% lower specific surface area relative to Ca3N2 indicates that the reported results are not solely due to the available surface area. These results confirm that the intercalation of the two alkaline earth metal nitrides by hydrogen promotes the ammonia evolution from the lattice nitrogen at the surface.
3. Methods
3.1 Thermochemical equilibrium calculations
To guide the design of looped metal nitride catalysts, the thermochemical equilibrium of various bulk metal nitrides, H2, and their reaction products was determined at 1 bar and as a function of temperature from tabulated free energy data.51 Per convention, negative free energy differences mark exergonic reactions.3.2 Electronic structure calculations
To determine the NH3-evolution-controlling mechanism at the atomic scale, hexagonal ζ-Mn2N and trigonal Sr2N were modeled via density functional theory (DFT), performed with the open-source planewave pseudopotential periodic electronic-structure code DACAPO.53–55 Atomic manipulations were handled in the Atomic Simulation Environment (ASE)56 and exchange–correlation interactions were treated by the revised Perdew–Burke–Ernzerhof (RPBE) functional of Hammer, Hansen, and Nørskov57 derived in the generalized gradient approximation (GGA). A k-point sampling of 4 × 4 × 4 for bulk and 4 × 4 × 1 for surface calculations was used for sampling of the Brillouin zone in the x, y and z directions, with the z direction orthogonal to the surface slab. A Fermi-Dirac smearing of 0.1 eV was used to achieve convergence and results were extrapolated to 0 K. The linesearch BFGS algorithm was employed for relaxing atomic geometries until the maximum force on any unconstrained atom was less than 0.05 eV Å−1. To avoid reminiscent stress in the calculations, the lattice constants were chosen as the DFT-calculated lattice constants (i.e., (a, c) = (2.81, 4.44) Å for Mn2N, and (3.90, 21.15) Å for Sr2N), which are within 2.2% of the experimental values (i.e., (a, c) = (2.84, 4.51) Å for Mn2N,58 and (3.86, 20.70) Å for Sr2N59). Calculations for Mn2N were spin-polarized. All surface calculations were performed for the (0001) facet with 2 × 2 × 4 or 2 × 2 × 6 metal atoms in the x, y and z directions of the Mn2N or Sr2N slab. The surfaces were modeled with 10 Å of vacuum perpendicular to the surface with the lower layers of the slab constrained to the bulk geometry while the atoms in the upper two layers were always optimized to zero-force positions. The interaction between the dipole moments of surfaces was decoupled via introduction of a dipole layer in the vacuum.The correlated electronic structure of certain metal oxides is not well described with simple GGA methods. This is sometimes addressed by the inclusion of an empirical Hubbard U term that accounts for on-site Coulomb repulsion and exchange interactions, thereby correcting self-interaction errors, when modeling certain metal oxides,60–62 while other metal oxides have been modeled well without the additional U parameter63 (and references therein). The value of U can be determined self-consistently,62 however, commonly it is chosen by fitting the experimental band gap60 or reaction energetics (resulting in a consistent offset of the free energy of reaction with varying U).64 Introducing nitrogen into a transition metal lattice may lead to partial electron localization with a minor increase in the metal oxidation state, compared to the presence of lattice oxygen.65 Hence, transition metal nitrides, including Mn2N, are typically modeled without a Hubbard U correction.23,66 Verifying this and assessing the use of GGA + U methods for metal nitride surfaces is an important point. In a prospective article, we will show how adsorption energies respond to the value of U only for metal compounds that possess a (pseudo) band gap. While Sr2N and Mn2N are metallic conductors,58,59 Sr2N exhibits localized N 2p states.67 Thus, whether GGA + U methods may improve the accuracy of DFT-computed adsorption energies at Sr2N surfaces deserves further study.
To aid in our description of nitride activity from first principles, four free-energies are defined. First, ΔGvac is the free energy required to form a nitrogen vacancy, vN, at the surface:
| ΔGvac ≡ Gs[vN] − (Gs − GrN) | (5) |
Next, ΔGads[A*] is the adsorption energy of the adsorbate(s) A (an asterisk indicates an adsorbed species):
| ΔGads[A*] ≡ Gs[A*] − (Gs + GrA) | (6) |
Third, ΔGvac[NH*x, yH*] is the free energy change to create adsorbed NHx species while creating nitrogen vacancies and leaving y adsorbed H's at the surface; that is to form 1/4 ML vN at a surface with z ML H* (z = 0, 1/4, 1/2, 3/4 or 1) yielding 1/4 ML NH*x (x = 0, 1, 2 or 3, corresponding to 0, 1/4, 1/2 or 3/4 ML H*) and y ML H* remaining at the surface (y = 0, 1/4, 1/2 or 3/4):
| ΔGvac[NH*x, yH*] ≡ Gs[vN, NH*x, yH*] − (Gs[zH*] + (x + y − z)GrH) | (7) |
Finally, ΔGhyd[NH*x, yH*] is the energy for hydrogenating NH*x−1 with (y + 1) pre-adsorbed H*, leaving NH*x and yH*:
| ΔGhyd[NH*x, yH*] ≡ Gs[vN, NH*x, yH*] − Gs[vN, NH*x−1, (y + 1)H*] | (8) |
Details on the local optimization procedures, references energies, conversion of electronic energies to free energies, and adsorption energetics in presence of OH and H2O and at oxynitride surfaces are given with ESI.†
3.3 Metal nitride preparation
Manganese was nitridated34 by heating 2 g Mn in N2 under two different thermal conditions; first, for 120 min at 700 °C which yielded 59–67 wt% ε-Mn4N and 25–34 wt% ζ-Mn6N2.58 (denoted as Mn4N), and second, for 240 min at 750 °C which yielded 91–94 wt% ζ-Mn6N2.58 (denoted as Mn6N2.58). We note ζ-phase manganese nitride ranges from 28.6–33.3 mol% lattice nitrogen including Mn5N2, Mn6N2.58, and Mn2N.58 The nitride characterization is summarized with Table S1 (ESI†). Fe-doped Mn nitride, Fe/Mn4N, was prepared by heating 2 g of an equimolar mixture Mn and Fe powder for 120 min in N2 yielding 26 ± 1 wt% ε-Mn4N and 16 ± 1 wt% ζ-Mn6N2.58. All Mn-containing powders were pretreated at 60 °C for 10 min in air to remove water. Ca3N2 and Sr2N34,68 were prepared by heating 4.4 g metal pieces for 240 min (Ca) or 420 min (Sr) in N2 and milling for about 5 min with mortar and pestle. The fraction of hydroxides formed when handling Ca3N2 or Sr2N during the X-ray diffraction (XRD) analysis in air were disregarded in NH3 yield calculations since these materials were otherwise handled in Ar. All N2 flows were 1.9 ± 0.1 L(STP) N2 min−1.3.4 Reduction of Mn4N and Mn6N2.58 with H2
To probe the reactivity of manganese nitride, 651 ± 2 mg Mn4N containing 3.01 ± 0.01 mmol lattice nitrogen was heated in a quartz boat with a tube furnace at ambient pressure. The tube furnace was a HTF55347C model, Lindberg/Blue, with a quartz tube that was purged before each experiment for 10 min with N2 to remove residual O2 and H2O. The temperature was ramped from 100 to 300 °C or from 400 to 550, 700 and 1000 °C respectively. H2 was supplied at 0.5 ± 0.1 L(STP) H2 min−1 and final temperatures were held for 60 min. The gas leaving the furnace was routed through a liquid absorbent consisting of 50 ± 5 mL(STP) 10 mM HCl, chilled with ice-cold H2O. Five mL samples were taken at 0, 5, 10, 30 and 60 ± 0.5 min after the reaction temperature was reached. These samples were analyzed for NH3 as described below. After 60 min the furnace was cooled to below 100 °C. Solids were stored at 4 °C. All liquids were stored at room temperature. Additionally, the NH3 evolution from Fe-doped Mn4N was quantified (ESI†).3.5 Hydrogenation of Ca3N2 and Sr2N with H2
The optimum temperature for reacting Ca3N2 with 0.5 ± 0.1 L(STP) H2 min−1 was determined using the experimental setup described in Section 3.4 without the absorption vessel. The powder (476 ± 170 mg, i.e., 6 ± 2 mmol lattice nitrogen) was held for 60 min at 300, 500, 700 and 1000 °C and analyzed for the loss of lattice nitrogen. All Ca-containing solids were stored under Ar at 4 °C. The effect of the H2 flow rate on the NH3 yield from Ca3N2 was tested (ESI†). To compare the NH3 evolution kinetics between metal nitride reduction (Mn6N2.58) and hydrogenation (Ca3N2 and Sr2N), 519 ± 18 mg metal nitride (2.8–7.0 mmol lattice nitrogen) were heated in 0.5 ± 0.1 L(STP) H2 min−1 from 220 to 850 ± 5 °C. After holding temperatures for 2 min, the furnace was cooled to 250 °C. The temperature change was repeated in triplicate. Liquid samples were taken at 250, 550 and 850 °C while the solids were analyzed after three cycles, reintroduced into the furnace, heated for 120 min at 750 °C in 1.9 ± 0.1 L(STP) N2 min−1 and analyzed anew.3.6 Analytical
Solids were weighed (AE260 DeltaRange balance, ±0.1 mg, Mettler) and analyzed via XRD (Miniflex II diffractometer, Cu-target X-ray tube, Rigaku, 5–80° 2θ range, 1 or 10° 2θ per min scan speed, PDXL Software Version 1.6.0.0 for quantitative solid phase analysis). The XRD analysis was in air which explains minor metal oxide and hydroxide fractions. To confirm N2 reduction energy-dispersive X-ray spectroscopy (EDS) was employed using a S-3500N scanning electron microscope (SEM, 20 keV, Hitachi; Link Pentafet 7021 X-ray detector and Inca Energy X-ray analysis software, both Oxford Instruments). The specific BET surface area, ABET, was analyzed using N2 at NanoScale Inc., Manhattan, KS. NH3 was quantified with an NH3 Ion Selective Electrode and a pH/ISE Controller model 270 (both Denver Instrument). The concentration of dissolved NH3 was estimated with zeroing for the signal from pure water. As estimated from the pH change, the formation of N2H4 was negligible relative to NH3 formation in all reported experiments. The outlet of the absorption vessel was equipped with an NH3 gas detection tube (0.25–3 or 5–70 ppm NH3 detection range, Dräger). Ammonia yield, YNH3, is reported as the molar ratio of NH3 captured by the absorbent at a given time relative to the lattice nitrogen stored in the solid initially. The data is fitted to a kinetic model limited by the reaction or gas phase diffusion (ESI†).3.7 Chemicals
Mn (99.9%, −325 mesh) and Fe (99.9%, −325 mesh) were from Noah Technologies, Ca (99%, granular) and NH4Cl (99.5%) were from Acros, Sr (99%, pieces) was from MP Biomedicals and NaOH (99.6%, pellets) and HCl (12.1 N) were from Fisher Scientific. H2O was deionized (Direct-Q 3 UV, Millipore) and degassed with Ar. H2, N2 and Ar (all UHP Zero grade) were from Linweld.4. Conclusions
We have introduced chemical looping of metal nitride catalysts for solar-driven synthesis of ammonia at ambient pressure from overall, water, N2, and concentrated sunlight as source of renewable process heat. Augmented NH3 evolution due to the formation of lattice hydrogen was correlated to the exergonic character of the hydrogenation of alkali and alkaline earth metal nitrides vs. endergonic reduction of transition-metal nitrides. These trends were confirmed experimentally and rationalized via electronic structure calculations which showed that the lattice nitrogen activity controls hydrogen intercalation and the energetics of forming and hydrogenating adsorbed nitrogen. The energy of the metal d-states was discussed as a quantitative descriptor for the design of ternary metal nitrides with reactivities between those of Fe- and Mn-based nitrides, while the energy of the metal s-states may guide the design of, for instance Li-doped, alkaline earth metal nitrides for an NH3 evolution promoted by the intercalation of surface hydrogen. Stable NH3 evolution and long-term mechanical stability of metal nitride catalysts, in form of pellets or porous ceramics for instance, have to be assessed in the future.Acknowledgements
Kent E. Hampton is acknowledged for his technical assistance. All glass and quartz ware manufactured at Kansas State University was from James R. Hodgson. The experimental components are based upon work supported by National Science Foundation Grant # 0903701: “Integrating the Socioeconomic, Technical, and Agricultural Aspects of Renewable and Sustainable Biorefining Program, awarded to Kansas State University.” Funding by the Center for Sustainable Energy, Kansas State University is kindly acknowledged. The theoretical calculations and analysis were supported by the Office of Naval Research (Young Investigator Award N00014-12-1-0851). Electronic structure calculations were conducted at the Center for Computation and Visualization, Brown University.Notes and references
- I. Rafiqul, C. Weber, B. Lehmann and A. Voss, Energy, 2005, 30, 2487–2504 CrossRef CAS PubMed
.
-
V. Smil, Enriching the Earth: Fritz Haber, Carl Bosch, and the Transformation of World Food Production, The MIT Press, Cambridge, Massachusetts, 2004 Search PubMed
.
- V. Smil, Nature, 1999, 400, 415 CrossRef CAS
.
- G. Ertl, Angew. Chem., Int. Ed., 2008, 47, 3524–3535 CrossRef CAS PubMed
.
- Z. Kirova-Yordanova, Energy, 2004, 29, 2373–2384 CrossRef CAS PubMed
.
- S. K. Ritter, Chem. Eng. News, 2008, 86, 53 Search PubMed
.
- A. Vojvodic, A. J. Medford, F. Studt, F. Abild-Pedersen, T. S. Khan, T. Bligaard and J. K. Nørskov, Chem. Phys. Lett., 2014, 598, 108–112 CrossRef CAS PubMed
.
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105 CrossRef CAS
.
- R. Michalsky, Y.-J. Zhang, A. J. Medford and A. A. Peterson, J. Phys. Chem. C, 2014, 118, 13026–13034 CAS
.
- A. Klerke, C. H. Christensen, J. K. Nørskov and T. Vegge, J. Mater. Chem., 2008, 18, 2304–2310 RSC
.
- C. H. Christensen, T. Johannessen, R. Z. Sørensen and J. K. Nørskov, Catal. Today, 2006, 111, 140–144 CrossRef CAS PubMed
.
- C. W. Gross and S. C. Kong, Fuel, 2013, 103, 1069–1079 CrossRef CAS PubMed
.
- http://nh3fuelassociation.org/2013/06/20/the-amveh-an-ammonia-fueled-car-from-south-korea/(retrieved%205/2/14) .
- A. J. Reiter and S.-C. Kong, Energy Fuels, 2008, 22, 2963–2971 CrossRef CAS
.
- F. Vitse, M. Cooper and G. G. Botte, J. Power Sources, 2005, 142, 18–26 CrossRef CAS PubMed
.
- J. C. Ganley, J. Power Sources, 2008, 178, 44–47 CrossRef CAS PubMed
.
- S. Dahl and I. Chorkendorff, Nat. Mater., 2012, 11, 100–101 CrossRef CAS PubMed
.
- M. Carmo, D. L. Fritz, J. Merge and D. Stolten, Int. J. Hydrogen Energy, 2013, 38, 4901–4934 CrossRef CAS PubMed
.
- G. P. Van der Laan and A. Beenackers, Catal. Rev.: Sci. Eng., 1999, 41, 255–318 CAS
.
- V. Kordali, G. Kyriacou and C. Lambrou, Chem. Commun., 2000, 1673–1674 RSC
.
- E. Skúlason, T. Bligaard, S. Gudmundsdóttir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2012, 14, 1235–1245 RSC
.
- G. Marnellos and M. Stoukides, Science, 1998, 282, 98–100 CrossRef CAS
.
- J. G. Howalt and T. Vegge, Phys. Chem. Chem. Phys., 2013, 15, 20957–20965 RSC
.
- Y. Abghoui, A. L. Garden, V. F. Hlynsson, S. Björgvinsdóttir, H. Ólafsdóttir and E. Skúlason, Phys. Chem. Chem. Phys., 2015, 17, 4909–4918 RSC
.
- R. Lan, J. T. S. Irvine and S. W. Tao, Sci. Rep., 2013, 3, 1145 Search PubMed
.
- R. Michalsky, B. J. Parman, V. Amanor-Boadu and P. H. Pfromm, Energy, 2012, 42, 251–260 CrossRef CAS PubMed
.
- M. E. Gálvez, A. Frei, M. Halmann and A. Steinfeld, Ind. Eng. Chem. Res., 2007, 46, 2047–2053 CrossRef
.
- R. Michalsky and P. H. Pfromm, AIChE J., 2012, 58, 3203–3213 CrossRef CAS PubMed
.
- R. Michalsky and P. H. Pfromm, Sol. Energy, 2011, 85, 2642–2654 CrossRef CAS PubMed
.
- K. M. Allen, N. Auyeung, N. Rahmatian, J. F. Klausner and E. N. Coker, JOM, 2013, 65, 1682–1693 CrossRef CAS
.
- P. Furler, J. Scheffe, M. Gorbar, L. Moes, U. Vogt and A. Steinfeld, Energy Fuels, 2012, 26, 7051–7059 CAS
.
- W. Villasmil, M. Brkic, D. Wuillemin, A. Meier and A. Steinfeld, J. Sol. Energy Eng., 2014, 136, 011017 CrossRef
.
- M. Romero and A. Steinfeld, Energy Environ. Sci., 2012, 5, 9234–9245 CAS
.
- R. Michalsky and P. H. Pfromm, J. Phys. Chem. C, 2012, 116, 23243–23251 CAS
.
- M. H. Yang, A. J. Allen, M. T. Nguyen, W. T. Ralston, M. J. MacLeod and F. J. DiSalvo, J. Solid State Chem., 2013, 205, 49–56 CrossRef CAS PubMed
.
- C. Hargus, R. Michalsky and A. A. Peterson, Energy Environ. Sci., 2014, 7, 3122–3134 CAS
.
- W. C. Chueh, C. Falter, M. Abbott, D. Scipio, P. Furler, S. M. Haile and A. Steinfeld, Science, 2010, 330, 1797–1801 CrossRef CAS PubMed
.
- W. L. Zhu, R. Michalsky, O. Metin, H. F. Lv, S. J. Guo, C. J. Wright, X. L. Sun, A. A. Peterson and S. H. Sun, J. Am. Chem. Soc., 2013, 135, 16833–16836 CrossRef CAS PubMed
.
- A. A. Peterson and J. K. Nørskov, J. Phys. Chem. Lett., 2012, 3, 251–258 CrossRef CAS
.
- D. Friebel, V. Viswanathan, D. J. Miller, T. Anniyev, H. Ogasawara, A. H. Larsen, C. P. O'Grady, J. K. Nørskov and A. Nilsson, J. Am. Chem. Soc., 2012, 134, 9664–9671 CrossRef CAS PubMed
.
- N. M. Marković and P. N. Ross, Surf. Sci. Rep., 2002, 45, 117–229 CrossRef
.
- C. Doornkamp and V. Ponec, J. Mol. Catal. A: Chem., 2000, 162, 19–32 CrossRef CAS
.
- C. L. Muhich, B. W. Evanko, K. C. Weston, P. Lichty, X. H. Liang, J. Martinek, C. B. Musgrave and A. W. Weimer, Science, 2013, 341, 540–542 CrossRef CAS PubMed
.
- S. M. Hunter, D. McKay, R. J. Smith, J. S. J. Hargreaves and D. H. Gregory, Chem. Mater., 2010, 22, 2898–2907 CrossRef CAS
.
- C. J. H. Jacobsen, S. Dahl, B. S. Clausen, S. Bahn, A. Logadottir and J. K. Nørskov, J. Am. Chem. Soc., 2001, 123, 8404–8405 CrossRef CAS
.
- A. M. Alexander, J. S. J. Hargreaves and C. Mitchell, Top. Catal., 2012, 55, 1046–1053 CrossRef CAS
.
- P. Chen, Z. T. Xiong, J. Z. Luo, J. Y. Lin and K. L. Tan, Nature, 2002, 420, 302–304 CrossRef CAS PubMed
.
- U. Ash-Kurlander, G. E. Shter, S. Kababya, A. Schmidt and G. S. Grader, J. Phys. Chem. C, 2013, 117, 1237–1246 CAS
.
- D. E. Demirocak, S. S. Srinivasan, M. K. Ram, J. N. Kuhn, R. Muralidharan, X. Li, D. Y. Goswami and E. K. Stefanakos, Int. J. Hydrogen Energy, 2013, 38, 10039–10049 CrossRef CAS PubMed
.
- F. Haber and G. van Oordt, Z. Anorg. Chem., 1905, 44, 341–378 CrossRef PubMed
.
-
I. Barin, Thermochemical Data of Pure Substances, VCH Verlagsgesellschaft mbH, Weinheim, Federal Republic of Germany, 1993, 0–6940 Search PubMed
.
- B. Hammer and J. K. Nørskov, Surf. Sci., 1995, 343, 211–220 CrossRef CAS
.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef
.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66 CrossRef CAS
.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef
.
- Y. J. Liu, L. M. Xu, X. Y. Li, P. Hu and S. W. Li, J. Appl. Phys., 2010, 107, 103914 CrossRef PubMed
.
- N. E. Brese and M. O'Keeffe, J. Solid State Chem., 1990, 87, 134–140 CrossRef CAS
.
- Y. L. Lee, J. Kleis, J. Rossmeisl and D. Morgan, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 224101 CrossRef
.
- H. J. Kulik and N. Marzari, J. Chem. Phys., 2011, 134, 094103 CrossRef PubMed
.
- M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef
.
- R. Michalsky, A. Steinfeld, V. Botu, C. M. Hargus and A. A. Peterson, Adv. Energy Mater., 2014, 4, 1401082 Search PubMed
.
- M. García-Mota, M. Bajdich, V. Viswanathan, A. Vojvodic, A. T. Bell and J. K. Nørskov, J. Phys. Chem. C, 2012, 116, 21077–21082 Search PubMed
.
- A.-M. Alexander and J. S. J. Hargreaves, Chem. Soc. Rev., 2010, 39, 4388–4401 RSC
.
- X. P. Du, V. C. Lo and Y. X. Wang, J. Comput. Chem., 2012, 33, 18–24 CrossRef CAS PubMed
.
- C. M. Fang, G. A. de Wijs, R. A. de Groot, H. T. Hintzen and G. de With, Chem. Mater., 2000, 12, 1847–1852 CrossRef CAS
.
- R. Chemnitzer, G. Auffermann, D. M. Többens and R. Kniep, Z. Anorg. Allg. Chem., 2005, 631, 1813–1817 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental and computational details, free energy plots for the NH3 evolution and N2 reduction with Co3N/Co, Fe4N/Fe, Mn5N2/Mn4N, Mo2N/Mo, CrN/Cr2N, TaN/Ta2N, NbN/Nb2N, Li3N/LiH, Ba3N2/BaH2, Sr3N2/SrH2, and Ca3N2/CaH2, surface oxidation energetics, ΔGvac[NH*x, yH*] based on gas phase H2 as hydrogen source, NH3 evolution with Fe-doped Mn4N, NH3 evolution with Mn6N2.58, Ca3N2 and Sr2N after correcting for partial nitride hydrolysis, NH3 yield from Ca3N2vs. time and H2 gas flow rate. See DOI: 10.1039/c5sc00789e |
| ‡ Present address: College of Engineering, 4183 Bell Engineering Center, University of Arkansas, Fayetteville, Arkansas 72701, USA. |
| § Present address: Department of Chemical and Biological Engineering, Missouri University of Science and Technology, 143 Schrenk Hall, Rolla, Missouri 65409, USA. |
| This journal is © The Royal Society of Chemistry 2015 |