Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Deciphering conformational transitions of proteins by small angle X-ray scattering and normal mode analysis
Alejandro
Panjkovich
 and
Dmitri I.
Svergun
*
and
Dmitri I.
Svergun
*
European Molecular Biology Laboratory, Hamburg Outstation, EMBL c/o DESY, Notkestr. 85, Geb. 25a, 22607 Hamburg, Germany. E-mail: svergun@embl-hamburg.de
First published on 16th November 2015
Abstract
Structural flexibility and conformational rearrangements are often related to important functions of biological macromolecules, but the experimental characterization of such transitions with high-resolution techniques is challenging. At a lower resolution, small angle X-ray scattering (SAXS) can be used to obtain information on biomolecular shapes and transitions in solution. Here, we present SREFLEX, a hybrid modeling approach that uses normal mode analysis (NMA) to explore the conformational space of high-resolution models and refine the structure guided by the agreement with the experimental SAXS data. The method starts from a given conformation of the protein (which does not agree with the SAXS data). The structure is partitioned into pseudo-domains either using structural classification databases or automatically from the protein dynamics as predicted by the NMA. The algorithm proceeds hierarchically employing NMA to first probe large rearrangements and progresses into smaller and more localized movements. At the large rearrangements stage the pseudo-domains stay as rigid bodies allowing one to avoid structural disruptions inherent to the earlier NMA-based algorithms. To validate the approach, we compiled a representative benchmark set of 88 conformational states known experimentally at high resolution. The performance of the algorithm is demonstrated in the simulated data on the benchmark set and also in a number of experimental examples. SREFLEX is included into the ATSAS program package freely available to the academic users, both for download and in the on-line mode.
1 Introduction
Biological macromolecules and their assemblies may undergo conformational changes as part of their functions inside the living cell. A deep understanding of these phenomena can have profound implications in medical and biotechnological research. Nevertheless, characterization of these events at the molecular level remains a difficult task in spite of the major progress in structural biology during the last decades. Macromolecular X-ray crystallography (MX) can deliver high-resolution information, but requires a crystalline sample that limits the conformational space explored by the macromolecule compared to the native state. Nuclear magnetic resonance (NMR) is better positioned to characterize such transitions in solution, but it is limited by the molecular weight of the entities under study. Partially overcoming some of the limitations, small-angle X-ray scattering (SAXS) provides information on conformational states, multimerization and transitions at low resolution (∼10 Å) for macromolecular assemblies in solution.1 The method provides overall shapes ab initio but also hybrid models can be obtained by using the crystallographic models of the entire macromolecule or its partial structures (domains) as building blocks. Given the static nature of the conformational snapshots obtained through MX and the typically less-physiological conditions of the crystallization process, MX structures often represent a biased sampling of the conformational space explored by the macromolecule in solution. In such cases (or when studying homologous proteins), the crystalline and solution conformations may differ, which is reflected in a disagreement between experimental SAXS data and theoretical intensities calculated from the MX structure. The latter may still constitute a good starting point for the interpretation of SAXS data and the initial disagreement may even be exploited to provide insight into the structural rearrangements of the system under study. These concepts will be illustrated in this work as we present a new methodology that computationally explores the conformational space of high-resolution models to find conformations that are consistent with SAXS experimental information.High resolution in silico sampling of conformational space at atomic level is traditionally achieved through molecular dynamics.2 However, when working with lower resolution SAXS data, a coarse-grained approach may provide sufficient precision for a fraction of the computational cost. For example, normal mode analysis (NMA) is a well established coarse-grained methodology used to study protein conformational transitions.3–5 Despite its multiple approximations, NMA based on the elastic network model6 has been shown to predict conformational changes surprisingly well in comparison with more complex approaches.7,8 The interpretation of SAXS experiments aided by NMA of known crystallographic models has been proposed previously. For instance, Winkler et al. not only discarded possible changes in the oligomerization state of blue-light-regulated phosphodiesterase 1 based on SAXS experiments, but also combined SAXS data with NMA-generated conformational states of the protein to characterize its light-exposure structural rearrangements.9
Besides ad-hoc applications, systematic approaches combining SAXS and NMA have been developed independently by the groups of Florence Tama and Wenjun Zheng.10,11 These methodologies differ in their approach to overcome the structural deformation that follows from the direct application of normal modes to generate structural models. The distortion of stereochemistry originates from the fact that normal modes represent harmonic and linear motions, while conformational changes in biological macromolecules are nonlinear and anharmonic.10,12 To generate less distorted models, Tama's group developed an ‘iterative’ NMA approach, where only small deformations are applied to the atomic coordinates and NMA is recalculated on each step to avoid severe deformation of the structure.10 Zheng and Tekpinar implemented a different approach, based on modifying the elastic network model by adding pseudoenergy terms to maintain pseudobonds and secondary structure while penalizing steric collisions. In the same article, both methods were compared on a set of five known protein conformational changes, with the modified elastic network model showing better performance.11
Here, we present a new hierarchical refinement approach that combines SAXS and NMA, while expanding the validation by means of a systematically compiled benchmark dataset that contains 88 conformational changes (44 representative proteins available in two distinct conformational states). A key step of the methodology presented here consists in partitioning the input model coordinates into a set of ‘pseudo-domains’ that maintain their internal distances constant during the initial low-resolution probing of the conformational space. Such a partition allows one to reduce the search space,13,14 and to diminish unphysical deformation of the structure by treating pseudo-domains as rigid bodies. Knowledge on domains derived from evolutionary conservation and structural classification databases (e.g. SCOP,15 CATH16) can be used as guidelines to partition the macromolecule under study. However, to avoid this segmenting information to become a sine qua non requirement or limitation of the procedure, we also implemented an automatic partitioning scheme based on protein dynamics.
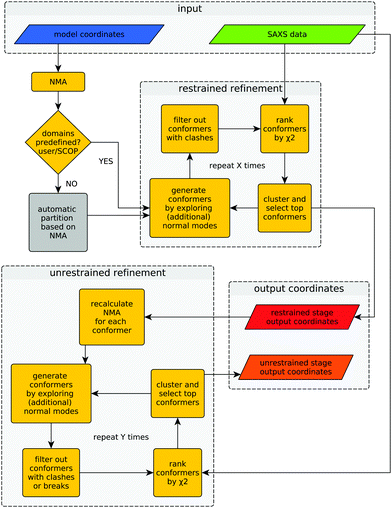
Once the structure has been partitioned into pseudo-domains, the method proceeds hierarchically by probing large global rearrangements (using rigid-body restraints) and progresses into smaller and more localized movements (unrestrained) to improve the agreement with the SAXS profile. This hierarchical refinement approach, together with the initial automatic partitioning, markedly distinguish the hybrid modeling methodology presented here from previous methods that systematically combine SAXS and NMA.10,11 The complete procedure (partitioning + restrained and unrestrained refinement) has been implemented in a program called SREFLEX. The method and the program are described below, together with application cases, benchmarking results and comparisons with the other available method.
2 Theory and methods
We developed a hybrid modeling methodology to study conformational change in macromolecules by combining small angle X-ray scattering (SAXS) and normal mode analysis (NMA) of high-resolution structures. As explained in the introduction, the method is aimed at solving cases where the available high-resolution model is not consistent with the experimental SAXS profile. Next, we will briefly revisit the theoretical background and then describe the methodology in further detail.2.1 Small angle X-ray scattering
Small angle X-ray scattering (SAXS) can be used to obtain shape and size information of biological macromolecules in solution.1 Briefly, scattering intensities I(s) of X-rays after irradiating a biological sample are recorded as a function of angle, or momentum transfer s: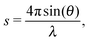 | (1) |
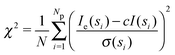 | (2) |
2.2 Normal mode analysis
Normal mode analysis (NMA) is a well established coarse-grained approach to study macromolecular conformational changes.3–5 Here, NMA was applied on structural coordinates using the implementation by Sanejouand and coworkers,18 particularly the PDBMAT and DIAGRTB programs.Briefly, a Hessian (H) of the potential energy function V is calculated for a given set of atomic coordinates (Cα) and then diagonalized to obtain eigenvectors that correspond to the molecule's vibrational normal modes. The potential energy V is described by Tirion's elastic network model6 as a set of harmonic springs of equal strength k, that link Cα atoms within an Euclidean distance of Rc of each other:
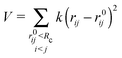 | (3) |
Normal modes are ordered according to their vibrational frequencies, starting with lower-frequency normal modes that correspond to global rearrangements of the structure, while higher-frequency normal modes describe smaller and more localized movements.
Note that the first six lowest-frequency normal modes do not deform the structure, as they correspond to translations and rotations of the molecule as a whole. Thus, the first six normal modes will be ignored throughout this work, as only structure-deforming normal modes will be considered (i.e. starting from number 7).
2.3 Generation of alternative conformational states: unrestrained conformers
Given an initial conformational state and its corresponding normal modes, Cα atoms can be displaced in Cartesian space following a given normal mode (or a combination of multiple normal modes) to generate a new conformational state or ‘conformer’. These displacements can be of different magnitude, which we measured in terms of root-mean-square deviation (Cα RMSD or from now on simply: RMSD) from the initial conformational state. For example, one conformer is generated at 1.5 Å RMSD from the initial configuration while another conformer is created using larger displacements to reach 4.5 Å RMSD. During the structural search, conformers are generated by combining normal modes at different displacement magnitudes. Conformers generated by this approach are ‘unrestrained’ when compared to the ‘domain-based’ or ‘restrained’ conformers that will be described below. Unrestrained conformers (UC) may display a distorted stereochemistry and in many cases a loss of recognizable secondary structure, as expected from direct projection of normal modes on atomic coordinates.122.4 Generation of alternative conformational states: restrained conformers
The domains defined by the user or equivalent ‘pseudo-domains’ defined automatically as explained below, will be treated as rigid-bodies during the first stage of conformational search, i.e. their internal distances will be kept constant. For this, an unrestrained conformer (UC) is initially created as described above from a given set of normal modes and displacement magnitudes. Then, each of the previously defined ‘pseudo-domains’ of the original model are superimposed as rigid-bodies on the corresponding region of the UC to generate a restrained conformer (RC). This superimposition step allows to explore large domain movements without disrupting inter-atomic distances within ‘pseudo-domains’, i.e. stereochemistry and secondary structure of the macromolecule is conserved within the pseudo-domains. Only the stereochemistry of peptide bonds at the hinges connecting pseudo-domains may become distorted in the RC model.2.5 Structural checks to filter conformational states
To minimize the amount of stereochemical distortion in the models generated during refinement, two criteria were used:• Clashes: Cα–Cα distances below 2.5 Å are counted as steric clashes and conformers with more than five clashes are discarded.
• Breaks: if the shortest Euclidean distance between a subset of Cα atoms and the rest of the structure is larger than 4.5 Å, the conformer is considered ‘disconnected’ and discarded.
To accelerate these calculations, an algorithm based on k–d trees was implemented.19 By default, breaks are allowed only for restrained conformers (i.e. only in the hinge regions).
2.6 Automatic partitioning of model coordinates into ‘pseudo-domains’
A key step of the methodology presented here consists in partitioning the input model coordinates into a set of ‘pseudo-domains’. The user can provide domain definitions to partition the structure, but the method is able to define pseudo-domains automatically based on predicted protein dynamics using NMA. In brief, this procedure finds a set of residues or ‘hinges’ that divide the structure into segments which are continuous in sequence and move in a concerted manner according to NMA.At the very first step, the procedure starts by dividing the protein chain into two (pseudo-) domains which, according to NMA, can move with relative independence of each other. The same process is repeated and the structure is further divided into subgroups until a certain threshold is met. The algorithm is described in more detail below.
| Sj = RMSDhsi − RMSDhsi+j | (4) |
2.7 Conformational search protocol
Provided with an experimental SAXS profile and a related high-resolution model, the method explores the conformational space of the given structure to improve its consistency with the experimental SAXS profile. A graphical representation of the algorithm is shown in Fig. 1.The difference between both refinement stages lies in the way conformers are generated. During the first (restrained) refinement stage, large global structural rearrangements are explored by generating ‘restrained-conformers’, for which pseudo-domains are treated as rigid bodies, as described above. The top ranking conformers generated during the restrained refinement stage are made available to the user as part of the output, but also serve as the starting point for the ‘unrestrained’ stage that follows after recalculation of normal modes for each conformer. Besides the selected restrained conformers, the initial structure supplied by the user is also forwarded to the unrestrained stage as yet another starting point. This is useful in cases where all the conformers generated during the restrained stage would fail the breaks filter or when the structural partitioning was not helpful. During the unrestrained refinement stage, pseudo-domain restraints are discarded and each residue is allowed to move independently according to a given combination of normal modes, to model smaller and more localized features of conformational change. By default, conformers with more than five clashes are discarded during both stages, but breaks are only taken into account as a filtering criterion during the unrestrained refinement stage. This is done to partially compensate the fact that structural distortions accumulate faster during the unrestrained refinement stage. The application of filters at different stages can be modified by the user through the corresponding program arguments. Finally, the output contains full-atom structures of the top-ranking conformers (in terms of χ2) of both refinement stages.
For the benchmark presented below, we limited the structural exploration to the ten lowest-frequency normal modes (7th to 16th), as it has been done previously.7,20 This parameter can be changed by the user if an extended sampling of conformational space is required in a particular case.
2.8 Benchmark set
To systematically evaluate the performance of the approach, we compiled a benchmark set of proteins that undergo conformational change and for which at least two distinct conformational states are available as MX or NMR structures. We started by querying the Protein Data Bank (PDB21) in the search of proteins for which more than one conformational state is available (sequence similarity >95% and RMSD > 5.0 Å) in a similar way as previously described.22 To reduce the complexity of the analysis, we clustered the dataset in terms of sequence identity, retaining highest resolution structures that had been assigned two SCOP domains as representatives.15 In total, the benchmark set contains 44 distinct proteins, which account for 88 cases when the direction of conformational change is taken into account: (1) once as ‘opening’, i.e. starting from the more compact structure (smaller radius of gyration) into to the more extended conformation and in (2) the opposite direction of conformational change, or ‘closing’.We simulated SAXS data for each of the 88 conformational states available in the benchmark set, which during benchmarking would serve to ‘guide’ the conformational sampling, mimicking real application cases. The initial step to simulate SAXS data from a high-resolution structure is to calculate expected solution scattering intensities using CRYSOL. Special attention was given to generate a more realistic benchmark, by introducing statistical variations to the simulated data based on the variation information obtained from real data, as recently described.23
3 Results
3.1 Program evaluation
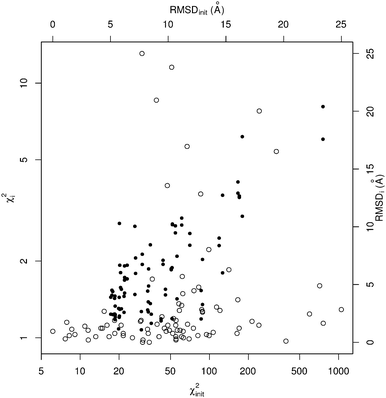
The overall methodology described in the Methods section has been implemented in a program called SREFLEX, as in ‘SAXS REFinement through FLEXibility’. The performance of SREFLEX was evaluated as follows: For each of the 88 cases in the benchmark set described above, the initial RMSD (RMSDinit) between the starting conformational state (startcoords) and the other known conformational state (targetcoords) is calculated. As mentioned above, RMSD values are calculated by taking into consideration all Cα atoms. Then, SREFLEX is executed on each benchmark case, while the actual input is restricted to (a) startcoords and (b) simulated SAXS data for the other known conformational state (targetintensities) of the same protein. Once the program finishes execution, it writes a set of ten different solutions as output coordinates i (outputcoordsi), and these solutions are then evaluated for benchmarking purposes using the following measures:(1) χ2i values are calculated to measure the consistency between targetintensities and outputcoordsi. χ2i values below 2.0 were considered as satisfactory, while the lowest initial χ2 values (χ2init) are above 6.1 in the benchmark set (average = 99.3).
(2) RMSDi is obtained between outputcoordsi and targetcoords after superposition considering all Cα atoms.24 We consider the complete superposition, and not only equivalent or ‘optimally aligned’ Cα positions as routinely done when reporting RMSD values,25 to account for distorted positions which are relevant in our case. When the resulting RMSDi is <5.0, we consider that the target conformation has been found, i.e. the solution is ‘correct’. It is important to note that all RMSDinit values were higher than 5.0 Å in the benchmark set, with an average value of 9.1 Å.
(3) ΔRMSDi measures the variation in terms of RMSD (RMSDinit − RMSDi) for each solution structure i. This measure is useful because in many cases the target conformation is not reached, but only approached. A positive ΔRMSDi value indicates that the solution coordinates i are closer to the target than the starting conformational state.
The results of this benchmarking procedure on the default version of SREFLEX (i.e. SREFLEXauto) are shown Table 1 and Fig. 2. The benchmarking procedure was applied also to different variations of SREFLEX, and the results are summarized in Table 2 and explained below.
| PDB id 1 | PDB id 2 | RMSDinit | RMSDi | χ 2init | χ 2 i | |||
|---|---|---|---|---|---|---|---|---|
| Closing | Opening | Closing | Opening | Closing | Opening | |||
| 4jhaL | 1b6dB | 8.3 | 3.5 | 2.6 | 67.7 | 54.9 | 1.1 | 1.1 |
| 4hqqL | 3h0tA | 5.9 | 2.9 | 4.6 | 59.3 | 56.4 | 1.1 | 1.1 |
| 4hanA | 3vkmB | 6.2 | 5.4 | 6.6 | 49.0 | 52.0 | 1.1 | 1.0 |
| 1lcfA | 1cb6A | 6.4 | 6.7 | 5.5 | 67.2 | 61.0 | 5.6 | 1.3 |
| 4fw1B | 1c0mC | 14.4 | 8.4 | 9.0 | 163.6 | 113.6 | 1.0 | 1.3 |
| 8ohmA | 3kqnA | 5.8 | 2.3 | 10.3 | 241.6 | 243.1 | 1.1 | 7.8 |
| 3uv5A | 1eqfA | 10.8 | 7.5 | 3.8 | 1049.6 | 713.4 | 1.3 | 1.6 |
| 1aivA | 1ovtA | 7.2 | 7.3 | 6.0 | 36.1 | 30.1 | 1.7 | 13.1 |
| 1mceA | 2mcg1 | 12.8 | 2.0 | 4.5 | 95.0 | 88.4 | 1.0 | 1.3 |
| 1ngzB | 1ngwB | 5.2 | 4.4 | 2.4 | 47.7 | 61.7 | 1.1 | 1.7 |
| 1yywA | 2nugA | 11.9 | 9.4 | 8.4 | 55.1 | 82.6 | 1.0 | 1.6 |
| 1fguA | 1jmcA | 8.3 | 6.3 | 4.9 | 85.6 | 87.2 | 3.7 | 1.3 |
| 4fq1L | 4fqcL | 9.8 | 4.1 | 4.6 | 75.2 | 58.6 | 1.1 | 1.3 |
| 3kygB | 2rdeA | 9.6 | 6.8 | 7.1 | 75.9 | 62.2 | 1.5 | 1.5 |
| 2h6bB | 3e6cC | 16.2 | 12.7 | 12.5 | 391.2 | 141.5 | 1.0 | 1.9 |
| 1gafH | 1aj7H | 5.4 | 2.0 | 4.0 | 33.6 | 39.4 | 1.0 | 1.1 |
| 2ombB | 2omnA | 10.3 | 2.0 | 6.5 | 62.6 | 58.0 | 1.1 | 1.4 |
| 3rfzD | 3jwnH | 14.7 | 12.7 | 6.0 | 120.7 | 99.0 | 1.3 | 2.2 |
| 4d8kA | 1x27D | 10.6 | 9.5 | 10.1 | 30.4 | 29.6 | 1.0 | 1.2 |
| 4bjlB | 1bjmA | 13.0 | 3.3 | 7.2 | 99.5 | 88.3 | 1.0 | 1.3 |
| 3muhL | 3u2sB | 7.7 | 1.1 | 2.7 | 20.7 | 16.7 | 1.1 | 1.0 |
| 3fweB | 4hzfA | 11.2 | 10.2 | 10.8 | 21.6 | 18.4 | 1.0 | 1.2 |
| 2wvdB | 2wvfA | 7.8 | 6.7 | 7.6 | 6.1 | 7.7 | 1.1 | 1.0 |
| 1k1qB | 4nlgA | 5.9 | 4.7 | 6.0 | 14.4 | 15.3 | 1.1 | 1.3 |
| 3u7yL | 3ngbF | 5.8 | 3.9 | 2.2 | 55.0 | 55.2 | 1.0 | 1.2 |
| 4avxA | 3zyqA | 5.0 | 3.9 | 2.4 | 8.2 | 8.6 | 1.0 | 1.1 |
| 4akeA | 1akeA | 7.1 | 4.1 | 10.0 | 107.0 | 42.9 | 1.1 | 1.2 |
| 1jvkA | 1lhzB | 9.4 | 2.0 | 1.9 | 44.8 | 40.8 | 1.1 | 1.0 |
| 2havA | 4h0wA | 6.2 | 4.3 | 5.6 | 46.3 | 38.9 | 1.1 | 8.6 |
| 1um5L | 2rcsL | 5.4 | 2.4 | 2.2 | 14.9 | 11.6 | 1.1 | 1.0 |
| 1ooaA | 1nfkA | 5.3 | 2.5 | 3.8 | 9.1 | 7.9 | 1.0 | 1.1 |
| 1nfiA | 2ramA | 10.4 | 10.2 | 10.2 | 52.7 | 51.0 | 1.2 | 11.5 |
| 2vkxB | 2vkwA | 8.5 | 2.4 | 1.6 | 40.7 | 34.2 | 1.0 | 1.0 |
| 2w9nA | 3b08A | 10.3 | 6.3 | 6.4 | 213.7 | 169.9 | 1.2 | 1.1 |
| 1p7hL | 1a02N | 16.4 | 17.8 | 10.9 | 760.5 | 595.4 | 1.1 | 1.2 |
| 3fdsA | 2jejA | 16.0 | 12.9 | 13.9 | 329.7 | 166.0 | 5.4 | 1.4 |
| 1st4B | 1st0A | 8.4 | 3.4 | 8.4 | 62.9 | 47.2 | 1.0 | 4.0 |
| 1nc2A | 1sm3L | 6.2 | 2.6 | 4.0 | 33.2 | 29.3 | 1.1 | 1.2 |
| 2g75A | 2dd8H | 5.4 | 2.4 | 3.1 | 25.4 | 30.6 | 1.0 | 1.0 |
| 2uylA | 3baeL | 5.8 | 6.7 | 2.9 | 10.9 | 11.5 | 1.1 | 1.1 |
| 3h42L | 4d9lN | 8.2 | 4.4 | 2.8 | 81.5 | 69.7 | 1.0 | 1.0 |
| 1d5iH | 1d5bB | 5.1 | 4.1 | 4.5 | 55.2 | 60.9 | 1.0 | 1.0 |
| 4amvA | 3oojA | 23.4 | 20.4 | 17.6 | 18.5 | 21.5 | 1.0 | 1.0 |
| 3mj9L | 3mj8A | 5.7 | 1.2 | 2.9 | 16.1 | 13.2 | 1.1 | 1.0 |
| Evaluation movement | χ 2 i < 2.0 | ΔRMSDi > 1.0 Å | RMSDi < 5.0 Å | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Closing | Opening | Total | Closing | Opening | Total | Closing | Opening | Total | |
| SREFLEXauto | 93.2 | 86.4 | 89.8 | 84.1 | 72.7 | 78.4 | 56.8 | 47.7 | 52.3 |
| SREFLEXscop | 93.2 | 86.4 | 89.8 | 79.5 | 72.7 | 76.1 | 63.6 | 52.3 | 58.0 |
| Restrained | 88.6 | 84.1 | 86.4 | 77.3 | 65.9 | 71.6 | 54.5 | 40.9 | 47.7 |
| Unrestrained | 29.5 | 18.2 | 23.9 | 70.5 | 59.1 | 64.8 | 27.3 | 29.5 | 28.4 |
• SREFLEXauto is based on the automatic structure partition procedure that is described in the Methods section.
• SREFLEXscop uses structural protein domain definitions based on experts' knowledge as available in SCOP.15
When considering the output χ2i values (which illustrate the consistency between output coordinates and input SAXS data), SREFLEX produces good fits independently of the domain definition used, as shown by the high percentage of cases (89.8%) in the benchmark set where good χ2i values (<2.0) are obtained, as displayed in Table 2. In most cases, even large χ2init values can be improved to final χ2i values that are close to 1.0, as shown in Fig. 2 for SREFLEXauto. A detailed version of these results are shown in Table 1 for each of the PDB entries in the benchmark set.
Since in this benchmark we know the coordinates of the target structure (even though the program only ‘sees’ the target SAXS profile), we can measure if the output structures are closer to the target in comparison to the starting conformation by at least 1.0 Å RMSD (ΔRMSDi > 1.0 Å), which is the case for over 70% of the benchmark set. A stricter evaluation is to measure the final RMSD of solution coordinates against the target structure, considering results below 5.0 Å RMSD to be satisfactory (RMSDi < 5.0 Å). The distribution of black dots in Fig. 2 shows that in general, better results can be expected when the initial RMSD is smaller, but some exceptional cases where the starting RMSD is above 10.0 Å and the final RMSD is below 3.0 Å can be observed as well. Under the RMSD-criterion, SREFLEXscop performs better than SREFLEXauto (summarized in Table 2), as expected given the additional information and curation involved in SCOP domain classifications.
Independently of the domain assignment used, ‘opening’ cases seem to be more difficult than ‘closing’ cases (i.e. it is easier for the program to go from an extended conformational state to a more compact one). This is to be expected given that the interdomain distances are smaller in closed conformations and thus more interdomain contacts exist, which hinder the ability of the method to ‘move’ the substructures apart from each other (opening). Interdomain contacts may also hinder the NMA-based automatic partition scheme, because there may be a lower chance of identifying substructures as separate entities in the more compact or ‘closed’ conformation.
Details regarding the differences between the restrained and unrestrained refinement stages output are further explained using the examples below.
3.2 Application examples
In this section we describe several SREFLEX applications in more detail to illustrate both the possibilities and limitations of the method. The first two examples (adenylate kinase and DNA-binding domain) are based on simulated SAXS data to show how the different refinement stages and domain assignments may affect the results. The third example (calmodulin), also based on simulated SAXS profiles, illustrates the limitations of the algorithm. The two last cases (MurA and Josephin domain) demonstrate the practical application of SREFLEX using experimental SAXS data.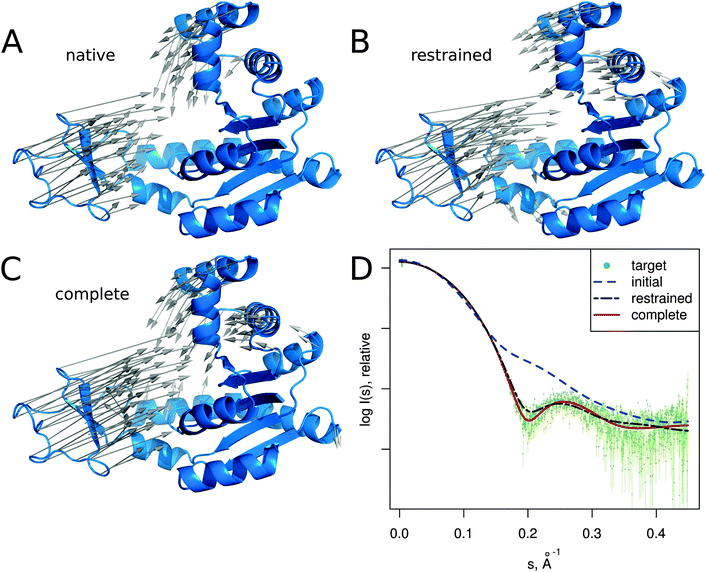 | ||
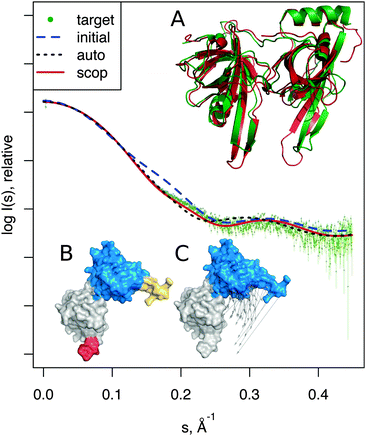
| Fig. 3 Adenylate kinase conformational change modeled by SREFLEXauto through the refinement of the initial conformation based on the target SAXS profile. (A) The native conformational change that adenylate kinase undergoes upon catalytic activity. Vectors have been drawn connecting equivalent residues from the open or unliganded state in blue (PDB:4ake) of a single protein chain to the liganded or closed conformation (PDB:1ake), of which the structure is not shown to improve clarity. (B) An intermediate step of the refinement, where the conformational change displayed is the outcome of the first refinement stage (restrained movement) of SREFLEX based on the initial conformation, its automatic partitioning and the target SAXS profile. (C) The complete SREFLEXauto simulated movement, after both refinement stages (i.e. restrained + unrestrained) have been completed as explained in the text. (D) Corresponding theoretical SAXS profiles, where the improved consistency can be observed against the simulated data (dots). | ||
It is interesting to note that in this case, a user familiar with the structural features of adenylate kinase may improve the results obtained in the restrained stage by further splitting the protein into three structural domains (LID, NMP and CORE) a priori, instead of two as it is done automatically or with SCOP (i.e. NMP-CORE and LID). Partitioning adenylate kinase in three domains allows SREFLEX to produce a better fit to the SAXS profile and to the target structure in terms of RMSD during the initial restrained refinement stage. However, when the unrestrained refinement stage is applied on the outcome of the different pseudo-domain definitions, the final models are almost identical.
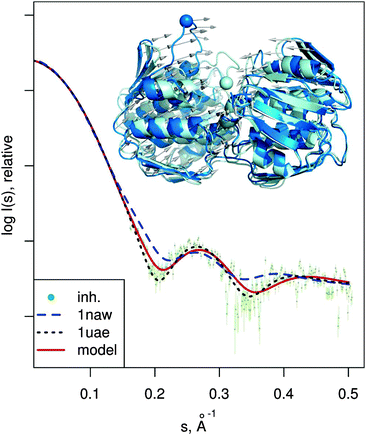 | ||
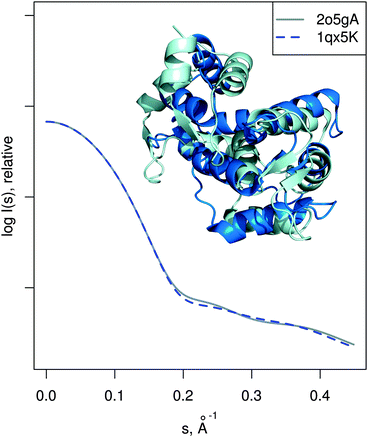
| Fig. 6 MurA structures of the open (PDB:1naw, blue) and closed (PDB:1uae, cyan) conformation are shown superimposed. The catalytic residue Cys115 is marked with a sphere. Vectors show the transition modeled by SREFLEXauto, starting from the open conformation and guided by the experimental SAXS profile of the inhibited protein (dots). Theoretical SAXS curves for the mentioned structures are shown as well. | ||
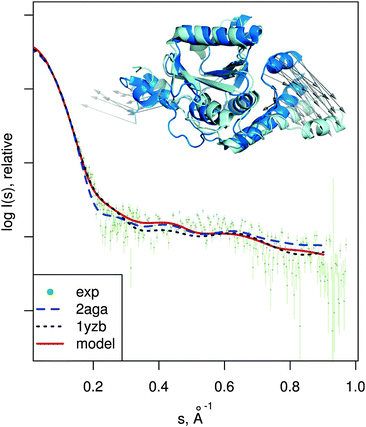 | ||
| Fig. 7 Josephin domain of ataxin-3. PDB entries corresponding to two different conformations are shown superimposed (PDB:2aga in blue, PDB:1yzb in cyan). Vectors show the conformational change modeled by SREFLEXauto when starting from PDB:2aga and guided by experimental SAXS profile of the protein (dots). Theoretical SAXS intensities for the mentioned structures are plotted as well. | ||
3.3 Execution times and technical remarks
The execution times of SREFLEX depend on multiple parameters, in particular on the speed of χ2 convergence, which is hard to predict from the protein size or shape. For the benchmark set, the average running time using a single processor core (Intel Core i7-3770) was 21 minutes, with the shortest calculations finishing in 5 minutes and the longest in 2.5 hours. Running time of the NMA component increases exponentially with the amount of residues in the input coordinates, but this calculation is performed only once at the beginning of each refinement stage and thus requires a small part of CPU time. Most of calculation time is spend predicting theoretical scattering profiles of conformer coordinates for their scoring against the SAXS profile. To accelerate the process, this task can run in parallel threads, taking advantage of multi-core or multi-CPU processors. For example, when using 8 cores, the running time of the adenylate kinase example (214 residues) is 2 minutes, while 7 minutes are needed with a single core. Better running times are expected once the other sections of the program are parallelized (e.g. filtering and NMA). Even though NMA, filtering and superpositions are computed using Cα atoms, conformers for scoring against SAXS data and output structures are generated using all non-hydrogen atoms available (i.e. rotations and translations are applied on a per-residue basis). Technically, the program can handle multiple protein chains and nucleotide residues as well, but these features were not tested thoroughly.4 Discussion
The approach presented in this work is aimed to aid in cases where only one conformational state is known from the crystallographic structure or model and this model does not match the corresponding SAXS data. Thus, an ideal benchmark set would contain crystallographic structures and corresponding experimental SAXS data in relative disagreement. Given the obvious fundamental difficulties in obtaining such information for a large number of distinct proteins, we simulated SAXS profiles for the 88 conformational states present in the benchmark set. Simulated SAXS profiles have been used previously to benchmark a hybrid modeling procedure based on NMA and SAXS, but using smaller number of benchmarking cases (7 pairs) and a stricter RMSD threshold (2 to 3 Å).11All cases in our benchmark set start with large conformational differences above 5.0 Å RMSD, and given that the resolution of SAXS is not better than 10 Å, obtaining solution models below 5.0 Å RMSD of the target structure is a positive outcome. Even though the 5.0 Å RMSD threshold could be considered permissive, the benchmark used in this work is challenging, and this can be emphasized by using as a reference the alternative method ‘FlexFitSaxs’.11 FlexFitSaxs is also based on NMA and uses a modified version of the elastic network model to flexibly fit a structure to a SAXS profile. In their article, the authors evaluated the performance of FlexFitSaxs on a handful of cases and compared it to another related approach by the group of Florence Tama,10 showing comparatively better performance for FlexFitSaxs. When we execute FlexFitSaxs on the benchmark set, it is able to generate a solution within 5.0 Å RMSD of the target structure for 29.6% of the cases. It is important to note that FlexFitSaxs does not partition the structure or exploit explicit domain information, and so it is comparable to a testing version of SREFLEX where only the unrestrained refinement stage is used (28.4%). These results indicate that the hierarchical refinement based on pseudo-domains plays an important role. Besides probably mimicking better certain protein conformational changes of modular nature, the rigid-body approach also reduces the conformational search space, as previously described.13,14 As indicated in Table 2, SREFLEX performs considerably better by combining both restrained and unrestrained refinement (52.3%), and the results are further improved by incorporating SCOP domain definitions (58%), as these include experts' curation of protein structures into the process. For compatibility with the previous publications, we did also compile the refinement statistics for the stricter threshold of 3.0 Å RMSD. The percentage of ‘successful’ reconstructions is expectedly lower (27.3% of cases for both SREFLEXauto and SREFLEXscop). FlexFitSaxs fulfils this threshold in 9.1% cases.
Information on biological domains may not always be available, and databases like SCOP may not subdivide the structure, as in the above cases of MurA and the Josephin domain. In such cases, the automatic partitioning procedure is useful, even at the expense of a slightly lower performance, as shown in Table 2 and by the SSB example (Fig. 4). Approaches to divide a macromolecule into subdomains based on normal modes have been suggested and implemented previously.12,33 Shudler and Niv calculated the correlation among normal modes to partition protein kinase structures into subdomains.33 We followed a somewhat different path by splitting the input structure into a set of pseudo-domains for which internal distances are barely modified by low-frequency normal modes. This works well on a variety of protein folds checked (i.e. particularly difficult cases with large rotations of closely attached domains). On 77% of the benchmark set, the automatic procedure returns the same amount of domains as SCOP, while the remaining structures were divided into a larger number of pseudo-domains. One such cases is shown in Fig. 4. We did not test the automatic partitioning procedure extensively, and work is ongoing to further improve its performance, in particular for the domains comprising more than one continuous sequence of residues, and for loops, N/C-terminus tails, or other regions with low connectivity to the rest of the structure.
Other limitations in SREFLEX are related to the nature of both NMA and SAXS. NMA is a coarse-grained approach to describe protein flexibility and, despite its good results in predicting dynamics and conformational change,8 a more complete simulation of atomic interactions, using for example molecular dynamics (MD) may improve the overall results.34,35 MD can also be incorporated into the prediction of theoretical scattering, in terms of explicit solvent and atomic fluctuations, as recently described.36 As expected, these calculations require considerably more computational work and the current SREFLEX running times in the order of minutes would be extended to many hours or days. Nevertheless, relaxing stereochemical considerations may still be useful, as illustrated by the SSB example shown in Fig. 4A, where the peptidic chain is broken during the restrained refinement as a shortcut to provide a meaningful model. Even if using MD could be beneficial, other limitations would still apply. For example, different conformational states may present similar shapes that are hard to distinguish from the SAXS profile.37 Actually, the difference between the benchmark results for the evaluation criterion related to χ2 (consistency between model coordinates and SAXS profile) and the criteria that take the target coordinates into consideration (RMSD values) shown in Table 2, illustrates that the conformational states differing considerably in terms of RMSD may still display the same ‘shape’ defining the SAXS profile.38 A concrete example of such ambiguity is calmodulin case in Fig. 5. It must also be noted that, as seen in the results obtained for the MurA example when using the isolated unrestrained refinement stage, improvements in RMSD may not always correlate with better consistency to the SAXS experiment. Furthermore, the benchmark dataset of conformational change used in this work was build based on pairs of conformational states, representing a selected subset of the variety of conformations that a protein may explore. Thus, some of the conformational states found by the programs tested may exist in reality, even if not matching the particular structural snapshot that we used as a target for evaluation.
Obviously, SREFLEX will be sensitive to the quality of SAXS data used, meaning that errors in buffer subtraction, radiation damage and other issues that decrease the quality of experimental SAXS data will limit the performance of the approach. In this respect, the restraints implemented (checks for breaks and clashes) are very important to prevent the program from creation of unrealistic models that fit low quality data. When using experimental SAXS data of good quality, very reasonable results may be reached by SREFLEXauto, as illustrated by the MurA and Josephin domain examples presented above.
5 Concluding remarks
The hybrid modeling procedure presented here integrates different sources of information: high-resolution structures are used as a starting point, NMA predicts accessible conformational changes, domain assignments reduce the search space and the experimental SAXS profile guides the hierarchical conformational sampling to construct full-atom models that should correspond better to the conformation of the macromolecule in solution. Very importantly, the procedure provides direct insight about the conformational changes.The complete approach has been implemented as a C++ computer program called SREFLEX, which is available to the scientific community for download as part of the ATSAS package39 at http://www.embl-hamburg.de/biosaxs/download.html and also as a web-server at http://www.embl-hamburg.de/biosaxs/online.html. Given its performance, speed and ease-of-use, we expect SREFLEX to aid structural biologists in the interpretation of experiments combining SAXS and high-resolution models.
Acknowledgements
We thank Wenjun Zheng for providing the FlexFitSaxs program that was used for comparison. We also want to thank Daniel Franke for providing the scripts to simulate experimental errors on theoretical SAXS profiles and the rest of the bioSAXS group at EMBL Hamburg for useful suggestions and discussion, particularly Haydyn Mertens, Maxim Petoukhov and Gundolf Schenk. This work was supported by the European Commission, BioStruct-X grant 283570. AP acknowledges Marie Curie Actions for the EMBL Interdisciplinary Postdoc (EIPOD) fellowship.References
-
D. I. Svergun, M. H. J. Koch, P. A. Timmins and R. P. May, Small angle X-ray and neutron scattering from solutions of biological macromolecules, Oxford University Press, 1st edn, 2013, vol. 19, IUCr Texts on Crystallography Search PubMed
.
- M. Karplus and J. A. McCammon, Nat. Struct. Biol., 2002, 9, 646–652 CrossRef CAS PubMed
.
- T. Noguti and N. Go, Nature, 1982, 296, 776–778 CrossRef CAS PubMed
.
- B. Brooks and M. Karplus, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 4995–4999 CrossRef CAS
.
- S. Mahajan and Y.-H. Sanejouand, Arch. Biochem. Biophys., 2015, 567C, 59–65 CrossRef PubMed
.
- M. M. Tirion, Phys. Rev. Lett., 1996, 77, 1905–1908 CrossRef CAS PubMed
.
- F. Tama and Y. H. Sanejouand, Protein Eng., 2001, 14, 1–6 CrossRef CAS PubMed
.
- M. Delarue and Y.-H. Sanejouand, J. Mol. Biol., 2002, 320, 1011–1024 CrossRef CAS PubMed
.
- A. Winkler, A. Udvarhelyi, E. Hartmann, J. Reinstein, A. Menzel, R. L. Shoeman and I. Schlichting, J. Mol. Biol., 2014, 426, 853–868 CrossRef CAS PubMed
.
- C. Gorba, O. Miyashita and F. Tama, Biophys. J., 2008, 94, 1589–1599 CrossRef CAS PubMed
.
- W. Zheng and M. Tekpinar, Biophys. J., 2011, 101, 2981–2991 CrossRef CAS PubMed
.
- K. Hinsen, Proteins, 1998, 33, 417–429 CrossRef CAS
.
- M. V. Petoukhov and D. I. Svergun, Biophys. J., 2005, 89, 1237–1250 CrossRef CAS PubMed
.
- F. Förster, B. Webb, K. A. Krukenberg, H. Tsuruta, D. A. Agard and A. Sali, J. Mol. Biol., 2008, 382, 1089–1106 CrossRef PubMed
.
- A. Andreeva, D. Howorth, C. Chothia, E. Kulesha and A. G. Murzin, Nucleic Acids Res., 2014, 42, D310–D314 CrossRef CAS PubMed
.
- I. Sillitoe, T. E. Lewis, A. Cuff, S. Das, P. Ashford, N. L. Dawson, N. Furnham, R. A. Laskowski, D. Lee, J. G. Lees, S. Lehtinen, R. A. Studer, J. Thornton and C. A. Orengo, Nucleic Acids Res., 2015, 43, D376–D381 CrossRef PubMed
.
- D. Svergun, C. Barberato and M. H. J. Koch, J. Appl. Crystallogr., 1995, 28, 768–773 CrossRef CAS
.
- F. Tama, F. X. Gadea, O. Marques and Y. H. Sanejouand, Proteins, 2000, 41, 1–7 CrossRef CAS
.
- J. L. Bentley, Commun. ACM, 1975, 18, 509–517 CrossRef
.
- M. Delarue and P. Dumas, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 6957–6962 CrossRef CAS PubMed
.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed
.
- V. Alexandrov, U. Lehnert, N. Echols, D. Milburn, D. Engelman and M. Gerstein, Protein Sci., 2005, 14, 633–643 CrossRef CAS PubMed
.
- D. Franke, C. M. Jeffries and D. I. Svergun, Nat. Methods, 2015, 12, 419–422 CrossRef CAS PubMed
.
- W. Kabsch, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 922–923 CrossRef
.
- A. R. Ortiz, C. E. M. Strauss and O. Olmea, Protein Sci., 2002, 11, 2606–2621 CrossRef CAS PubMed
.
- C. W. Müller, G. J. Schlauderer, J. Reinstein and G. E. Schulz, Structure, 1996, 4, 147–156 CrossRef
.
- A. Bochkarev, R. A. Pfuetzner, A. M. Edwards and L. Frappier, Nature, 1997, 385, 176–181 CrossRef CAS PubMed
.
- C. B. Marshall, T. Nishikawa, M. Osawa, P. B. Stathopulos and M. Ikura, Biochem. Biophys. Res. Commun., 2015, 460, 5–21 CrossRef PubMed
.
- E. Schönbrunn, D. I. Svergun, N. Amrhein and M. H. Koch, Eur. J. Biochem., 1998, 253, 406–412 Search PubMed
.
- G. Nicastro, R. P. Menon, L. Masino, P. P. Knowles, N. Q. McDonald and A. Pastore, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10493–10498 CrossRef CAS PubMed
.
- Y. Mao, F. Senic-Matuglia, P. P. D. Fiore, S. Polo, M. E. Hodsdon and P. D. Camilli, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 12700–12705 CrossRef CAS PubMed
.
- G. Nicastro, M. Habeck, L. Masino, D. I. Svergun and A. Pastore, J. Biomol. NMR, 2006, 36, 267–277 CrossRef CAS PubMed
.
- M. Shudler and M. Y. Niv, J. Phys. Chem. A, 2009, 113, 7528–7534 CrossRef CAS PubMed
.
- B. Wen, J. Peng, X. Zuo, Q. Gong and Z. Zhang, Biophys. J., 2014, 107, 956–964 CrossRef CAS PubMed
.
- L. Boldon, F. Laliberte and L. Liu, Nano Rev., 2015, 6, 25661 Search PubMed
.
- P.-C. Chen and J. S. Hub, Biophys. J., 2015, 108, 2573–2584 CrossRef CAS PubMed
.
- V. V. Volkov and D. I. Svergun, J. Appl. Crystallogr., 2003, 36, 860–864 CrossRef CAS
.
- M. V. Petoukhov and D. I. Svergun, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2015, 71, 1051–1058 CAS
.
- M. V. Petoukhov, D. Franke, A. V. Shkumatov, G. Tria, A. G. Kikhney, M. Gajda, C. Gorba, H. D. T. Mertens, P. V. Konarev and D. I. Svergun, J. Appl. Crystallogr., 2012, 45, 342–350 CAS
.
| This journal is © the Owner Societies 2016 |