Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Compositional control of pore geometry in multivariate metal–organic frameworks: an experimental and computational study†
Laura K.
Cadman
,
Jessica K.
Bristow
,
Naomi E.
Stubbs
,
Davide
Tiana
,
Mary F.
Mahon
*,
Aron
Walsh
* and
Andrew D.
Burrows
*
Department of Chemistry, University of Bath, Claverton Down, Bath BA2 7AY, UK. E-mail: a.d.burrows@bath.ac.uk
First published on 14th December 2015
Abstract
A new approach is reported for tailoring the pore geometry in five series of multivariate metal–organic frameworks (MOFs) based on the structure [Zn2(bdc)2(dabco)] (bdc = 1,4-benzenedicarboxylate, dabco = 1,8-diazabicyclooctane), DMOF-1. A doping procedure has been adopted to form series of MOFs containing varying linker ratios. The series under investigation are [Zn2(bdc)2–x(bdc-Br)x(dabco)]·nDMF 1 (bdc-Br = 2-bromo-1,4-benzenedicarboxylate), [Zn2(bdc)2–x(bdc-I)x(dabco)]·nDMF 2 (bdc-I = 2-iodo-1,4-benzenedicarboxylate), [Zn2(bdc)2–x(bdc-NO2)x(dabco)]·nDMF 3 (bdc-NO2 = 2-nitro-1,4-benzenedicarboxylate), [Zn2(bdc)2–x(bdc-NH2)x(dabco)]·nDMF 4 (bdc-NH2 = 2-amino-1,4-benzenedicarboxylate) and [Zn2(bdc-Br)2–x(bdc-I)x(dabco)]·nDMF 5. Series 1–3 demonstrate a functionality-dependent pore geometry transition from the square, open pores of DMOF-1 to rhomboidal, narrow pores with increasing proportion of the 2-substituted bdc linker, with the rhomboidal-pore MOFs also showing a temperature-dependent phase change. In contrast, all members of series 4 and 5 have uniform pore geometries. In series 4 this is a square pore topology, whilst series 5 exhibits the rhomboidal pore form. Computational analyses reveal that the pore size and shape in systems 1 and 2 is altered through non-covalent interactions between the organic linkers within the framework, and that this can be controlled by the ligand functionality and ratio. This approach affords the potential to tailor pore geometry and shape within MOFs through judicious choice of ligand ratios.
Introduction
Metal–organic frameworks (MOFs) have structures that contain extended co-ordination networks of metal centres connected by bridging organic ligands.1,2 Materials chemistry has seen a rapid growth in the study of MOFs in recent years due largely to their potential for porosity and the extensive range of applications, such as gas storage,3 separations4 and drug delivery,5 that derive from this.Making changes to the structure and geometry of the bridging ligand is a powerful route to optimising pore size and shape.6 The IRMOF series, for example, consists of MOFs of the general formula [Zn4OL3] where L is a linear dicarboxylate.7 The pore size of the MOF can be increased through extension of L, or decreased by introducing a substituent onto L that projects into the pores. To illustrate the utility of this, analysis of the IRMOF series allowed identification of the MOF with optimum pore size for methane adsorption.7 The lengthening of organic linkers can lead to less stable frameworks and on some occasions result in different topologies or interpenetration.
Multivariate MOFs (MTV-MOFs), mixed-component MOFs in which two or more linkers play the same structural role, allow for the incorporation of multiple functionalities into the structure whilst maintaining the framework topology.8–10 Here we present a route to the tuning of pore geometry in DMOF-1 type structures of the general formula [Zn2L2(dabco)] (L = dicarboxylate, dabco = 1,8-diazabicyclooctane) in which two linkers of the same length, but differing in the functional groups attached to the aromatic ring, are used in the synthesis.
DMOF-1 is a zinc-based pillared MOF of the form [Zn2(bdc)2(dabco)] (bdc = 1,4-benzenedicarboxylate).11,12 The as-synthesised form of the MOF contains a cubic framework with square pores in which the bdc linkers are bent away slightly from the square grid, and solvent molecules (DMF, H2O) are present as guests within the pores. The framework geometry is maintained upon removal of the included solvent, though the activated MOF contains linear bdc linkers and a regular square grid. The framework also displays guest-induced flexibility, resulting in a compressed structure upon the inclusion of benzene into the pores.
Flexible MOFs have received increasing attention due to their interesting properties.13,14 For example, they often display reversible structural alterations in response to solvent changes, temperature or pressure. Several studies have shown that replacing the bdc ligands in DMOF-1 with another dicarboxylate can result in alterations of the pore size and shape, similar to the guest-induced behaviour (Fig. 1).6,15–17
Given the success in replacing the bdc linker in DMOF-1 with structurally similar dicarboxylate ligands,15,18,19 a synthetic strategy was developed to investigate the potential for forming mixed-ligand frameworks related to this material. Multivariate analogues of DMOF-1 have been prepared previously, either through use of mixtures of dicarboxylic acids in the synthesis6,12 or incomplete post-synthetic modification of [Zn(bdc-NH2)2(dabco)] (bdc-NH2 = 2-amino-1,4-benzenedicarboxylate).15 However, the effect of the linker ratio on the pore geometry has, to the best of our knowledge, not previously been studied. Here we report a systematic approach through which pore compression can be enhanced and pore size control can be achieved. A multivariate approach is adopted to fine tune the structures and properties of several series of MOFs relating to the DMOF-1 framework. A second dicarboxylic acid which is functionally substituted at the ortho-position on the benzene ring, referred to generically as H2bdc-X, was introduced into the reaction mixture in varying ratios of H2bdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2bdc-X. By employing this doping procedure, MOF libraries of the form [Zn2(bdc)2–x(bdc-Br)x(dabco)]·nDMF 1 (bdc-Br = 2-bromo-1,4-benzenedicarboxylate), [Zn2(bdc)2–x(bdc-I)x(dabco)]·nDMF 2 (bdc-I = 2-iodo-1,4-benzenedicarboxylate), [Zn2(bdc)2–x(bdc-NO2)x(dabco)]·nDMF (bdc-NO2 = 2-nitro-1,4-benzenedicarboxylate) 3 and [Zn2(bdc)2–x(bdc-NH2)x(dabco)]·nDMF 4 were prepared and characterised. In a similar manner, the series [Zn2(bdc-Br)2–x(bdc-I)x(dabco)]·nDMF 5 was prepared through the use of different ratios of H2bdc-Br and H2bdc-I in the reaction mixture.
H2bdc-X. By employing this doping procedure, MOF libraries of the form [Zn2(bdc)2–x(bdc-Br)x(dabco)]·nDMF 1 (bdc-Br = 2-bromo-1,4-benzenedicarboxylate), [Zn2(bdc)2–x(bdc-I)x(dabco)]·nDMF 2 (bdc-I = 2-iodo-1,4-benzenedicarboxylate), [Zn2(bdc)2–x(bdc-NO2)x(dabco)]·nDMF (bdc-NO2 = 2-nitro-1,4-benzenedicarboxylate) 3 and [Zn2(bdc)2–x(bdc-NH2)x(dabco)]·nDMF 4 were prepared and characterised. In a similar manner, the series [Zn2(bdc-Br)2–x(bdc-I)x(dabco)]·nDMF 5 was prepared through the use of different ratios of H2bdc-Br and H2bdc-I in the reaction mixture.
Results and discussion
Synthesis and composition
The reaction of Zn(NO3)2·6H2O with dabco and mixtures of dicarboxylic acids in varying ratios in DMF at 120 °C for 3 days afforded crystalline products for all members of series 1–5. All products were formed in good yields of approximately 60–80%. For members of series 1, 3 and 5, colourless block crystals were produced, whereas the compounds in series 2 yielded colourless needles and those in series 4 gave orange-brown block crystals. The composition of all compounds in series 1–5 were determined using 1H NMR spectroscopy on acid-digested samples of the dried MOFs. In addition to studying bulk samples, NMR spectra were also recorded on one individual acid-digested crystal for select members of series 1, 3, 4 and 5. These 1H NMR spectra showed the presence of both bdc and bdc-X ligands in each sample, demonstrating the successful formation of multivariate MOFs as opposed to physical mixtures containing two discrete phases.The integral analyses from the spectra taken of both bulk and individual crystal samples of series 1, 3 and 4 showed that all members of these series had a ligand ratio composition similar to that present in the reaction mixture, thus demonstrating that there were no significant ligand preferences and that the composition can be controlled through the relative reactant concentrations. This is in contrast to observations on the IRMOF system, for which there were significant differences between the ratios of linkers used in the reaction mixture and those observed in the products.9,10
Series 1, 3 and 4 showed little compositional variation within the bulk phase itself, with a comparison of the integrals from individual crystal samples to those of the bulk products indicating only small variations between samples from the same batch (<3% of the mean value quoted).
In contrast, analysis of the integrals in the 1H NMR spectra of series 2 and 5 revealed evidence of strong ligand preferences. In both of these series the bdc-I ligand is preferentially excluded in favour of the other dicarboxylate. In series 2 this resulted in an incorporation of up to 20% more bdc into the framework than was present in the reaction mixture, and in series 5 there was up to 24% more bdc-Br in the framework than was expected from the reaction mixture (Fig. 2).
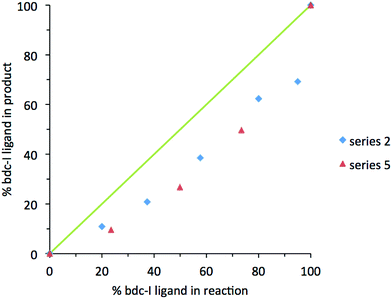 | ||
| Fig. 2 The percentage inclusion of bdc-I into [Zn2(bdc)2–x(bdc-I)x(dabco)]·nDMF 2 and [Zn2(bdc-Br)2–x(bdc-I)x(dabco)]·nDMF 5, plotted against the percentage bdc-I in the reaction mixture. | ||
X-ray diffraction analysis of [Zn2(bdc)2–x(bdc-Br)x(dabco)]·nDMF 1
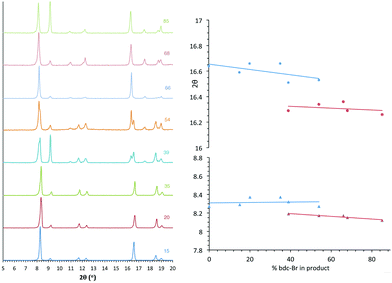
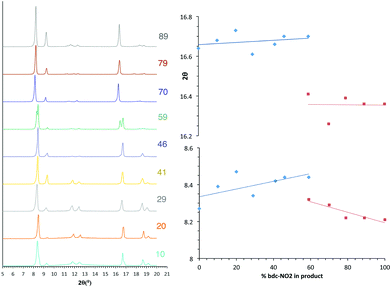
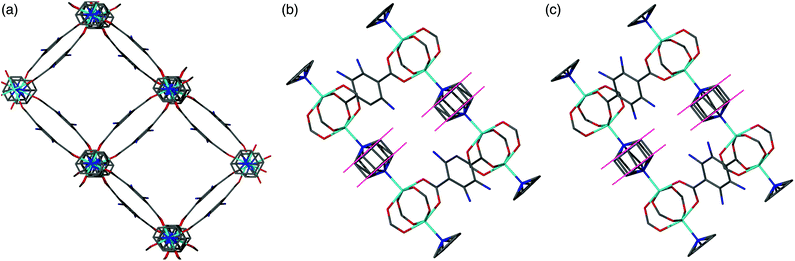
All members of series 1 gave powder XRD patterns containing the same general features, suggesting all compounds possess similar framework topologies. A closer inspection revealed the presence of two unique phases, which can be identified in the PXRD patterns through differences in their peak positions (Fig. 3). Above a bdc-Br content of 54%, peaks at 2θ 8.4° and 16.7° shift to lower values. These subtle alterations in the PXRD patterns suggest that the products with a higher bdc-Br content contain structural differences (concurrent with altered unit cell parameters) to those with lower bdc-Br content. The PXRD patterns from the samples with 39% and 54% bdc-Br show elements of the traces from both pore types (Fig. 3), suggesting that both phases are present in these samples.Four of the ligand ratios used yielded crystals that were suitable for single crystal X-ray diffraction, and these compounds were structurally characterised as [Zn2(bdc)(bdc-Br)(dabco)]·DMF 1a, [Zn2(bdc)0.8(bdc-Br)1.2(dabco)]·DMF 1b, [Zn2(bdc)0.4(bdc-Br)1.6(dabco)] 1c and [Zn2(bdc)0.3(bdc-Br)1.7(dabco)] 1d. The crystal structures of all contain the expected DMOF-1 framework topology, consistent with PXRD results. Thus the structures all contain paddlewheel units formed from two Zn(II) centres bridged by four carboxylate groups and with nitrogen donors from dabco ligands occupying the axial sites. The bridging dicarboxylate and dabco ligands link these secondary building units (SBUs) into three-dimensional networks. In all four structures, the bromine atoms exhibited positional disorder over the four available positions of the benzene ring.
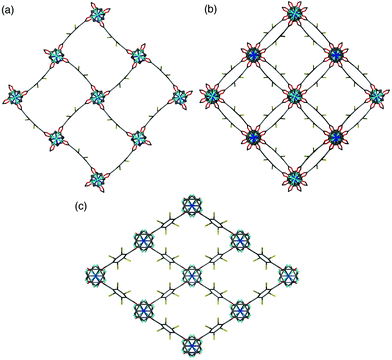
A clear difference in the crystal structures is observed between the lower bdc-Br content structures 1a and 1b and the higher bdc-Br content structures 1c and 1d. Compounds 1a and 1b crystallise in a tetragonal space group and display a distorted square grid topology (Fig. 4a), similar to that observed in the solvated DMOF-1 structure. For both of these structures the dicarboxylate linker is bent, arching away from a linear arrangement and causing a distortion to the regular square grid topology of the framework. These distortions alternate into and out of the pore between each layer of the framework leading to square channels throughout the structure (Fig. 4b).
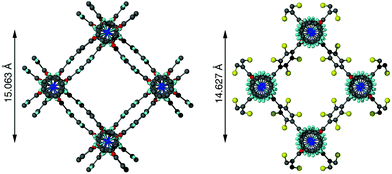
In contrast to 1a and 1b, compounds 1c and 1d crystallise in an orthorhombic space group and display pores of a rhomboidal, narrow geometry (Fig. 4c). A comparison of the frameworks of 1c and 1d to that of [Zn2(bdc-Br)2(dabco)]19 show that the pores in the mixed-ligand structures are compressed to a higher degree than in the single ligand parent (Table 1).
| Structure | Pore shape | Shortest pore diagonal Zn⋯Zn (Å) |
|---|---|---|
| [Zn2(bdc)2(dabco)]·4DMF·0.5H2O (DMOF-1)11 | Distorted square | 15.063 |
| [Zn2(bdc)(bdc-Br)(dabco)]·DMF 1a | Distorted square | 14.988 |
| [Zn2(bdc)0.8(bdc-Br)1.2(dabco)]·DMF 1b | Distorted square | 14.976 |
| [Zn2(bdc)0.4(bdc-Br)1.6(dabco)] 1c | Rhomboidal | 12.759 |
| [Zn2(bdc)0.3(bdc-Br)1.7(dabco)] 1d | Rhomboidal | 12.858 |
| [Zn2(bdc)0.48(bdc-Br)1.52(dabco)] 1c′ | Rhomboidal | 14.229 |
| [Zn2(bdc-Br)2(dabco)]19 | Rhomboidal | 14.627 |
The change in pore size and shape in series 1 with increased bdc-Br content is accompanied by a loss of the dicarboxylate distortion shown in 1a and 1b. The subtle changes observed in the experimental PXRD patterns from low to high bdc-Br content reflect changes in the unit cell parameters that occur with the change in pore geometry. Further analysis of these structures has been addressed by a computational study (vide infra).
In contrast to most of the MOFs in this paper, the experimental powder X-ray diffraction patterns of 1c and 1d showed a number of differences in the positions of the peaks to those in the X-ray powder diffraction patterns simulated from the single crystal studies. These differences were suspected of being related to the difference in temperature at which the diffraction patterns were generated – the experimental pattern was collected at ambient temperature whereas the single crystal X-ray diffraction data were collected at 150 K. To test this theory, the single crystal data for 1c was re-collected at ambient temperature (1c′). While the overall topology of 1c′ is similar to that of 1c, crystallising in an orthorhombic space group and presenting rhomboidal pores, significant changes in the unit cell parameters were observed. The compression of the pores is more acute in 1c than in 1c′ (Table 1) accounting for the changes in unit cell parameters observed. After the room temperature data collection, the crystal of 1c′ was cooled to 150 K and the unit cell parameters collected at that temperature matched those of 1c. The reversible unit cell parameter shift from 1c to 1c′ leads to a movement of peaks in the generated diffraction pattern, and the experimental patterns recorded for the bulk samples of 1c and 1d at room temperature match well to that simulated from the single crystal structure of 1c′ (Fig. S24†). The slight difference in bdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) bdc-Br ratio between 1c and 1c′ is insignificant, and a consequence of different crystals being used in the analyses and the softness in determining site occupancy factors against a backdrop of the disorder noted.
bdc-Br ratio between 1c and 1c′ is insignificant, and a consequence of different crystals being used in the analyses and the softness in determining site occupancy factors against a backdrop of the disorder noted.
X-ray analysis of [Zn2(bdc)2–x(bdc-I)x(dabco)]·nDMF 2
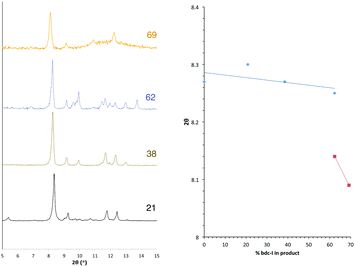
Similar structural trends to those found in series 1 are observed in [Zn2(bdc)2–x(bdc-I)x(dabco)]·nDMF 2. All members of series 2 display powder diffraction patterns with the same gross features as those in DMOF-1, suggesting all multivariate species are isoreticular. As with series 1 there is a transition point within the PXRD patterns indicating a change from one crystal system to another (Fig. 5). This transition is characterised through peak position shifts similar to those observed in the brominated series and can therefore be identified as a change in the pore geometry of the framework from square to rhomboidal.The bdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) bdc-I ratio in the products of series 2 were determined by bulk NMR spectroscopy. Integral analysis shows a clear preference for bdc inclusion into the product framework at the expense of the bdc-I ligand, and is consistent for all products of series 2. Due to the strong ligand preferences observed, the square pore to rhomboidal pore transition does not occur until loadings of approximately 90% in the reaction mixture; equivalent to 60% bdc-I in the MOF. Taking the ratio of bdc
bdc-I ratio in the products of series 2 were determined by bulk NMR spectroscopy. Integral analysis shows a clear preference for bdc inclusion into the product framework at the expense of the bdc-I ligand, and is consistent for all products of series 2. Due to the strong ligand preferences observed, the square pore to rhomboidal pore transition does not occur until loadings of approximately 90% in the reaction mixture; equivalent to 60% bdc-I in the MOF. Taking the ratio of bdc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) bdc-I in the framework into account, the shift from square to rhomboidal pore geometries occurs at approximately the same product stoichiometry for series 1 and series 2. The small size and needle-like nature of the crystals from series 2 meant that single crystal X-ray diffraction was not possible for any of the compounds in this series.
bdc-I in the framework into account, the shift from square to rhomboidal pore geometries occurs at approximately the same product stoichiometry for series 1 and series 2. The small size and needle-like nature of the crystals from series 2 meant that single crystal X-ray diffraction was not possible for any of the compounds in this series.
X-ray diffraction analysis of [Zn2(bdc)2–x(bdc-NO2)x(dabco)]·nDMF 3
The PXRD patterns from [Zn2(bdc)2–x(bdc-NO2)x(dabco)]·nDMF 3 show a similar trend to those observed in the bdc-Br and bdc-I analogues, 1 and 2. Products which contain a stoichiometry of >60% bdc-NO2 give diffraction patterns with a shift of peaks along with the loss and appearance of others (Fig. 6) when compared with those with low bdc-NO2 content.These changes are consistent with the premise that a change in the pore geometries and lattice parameters are occurring. In the sample containing 59% bdc-NO2, the PXRD pattern clearly shows the presence of both square-pore and rhomboidal-pore phases of the MOF (Fig. 6).
Single crystal X-ray analysis was carried out on [Zn2(bdc)1.2(bdc-NO2)0.8(dabco)]·2.5DMF 3a confirming this compound contains a distorted square pore framework (Fig. 7), similar to those of 1a and 1b and consistent with the PXRD data. Single crystal X-ray diffraction of compound [Zn2(bdc)0.6(bdc-NO2)1.4(dabco)]·nDMF 3b was also carried out and it showed unit cell parameters similar to those for 1c and 1d, indicating that the rhomboidal pore form of this species is accessible. As data quality for 3b were poor, with disorder precluding any additional insight into the factors affecting pore geometry, this crystal structure has not been presented herein (see ESI†).
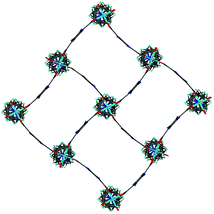 | ||
| Fig. 7 Structure of the network in [Zn2(bdc)1.2(bdc-NO2)0.8(dabco)]·2.5DMF 3a showing a view of one layer of the framework as viewed along the c-axis, demonstrating the distorted bdc linkers. | ||
In contrast to series 1 and 2, a second transition in series 3 is observed at 100% bdc-NO2 content i.e. [Zn2(bdc-NO2)2(dabco)] which crystallises in a tetragonal crystal lattice with square pore geometry.18 This means that rhomboidal pores with bdc-NO2 are only possible in a multivariate system, and furthermore the multivariate approach allows the attainment of pore geometries containing particular functional groups that cannot otherwise be accessed.
X-ray diffraction analysis of [Zn2(bdc)2–x(bdc-NH2)x(dabco)]·nDMF 4
In contrast to series 1–3, the PXRD patterns for compounds of series [Zn2(bdc)2–x(bdc-NH2)x(dabco)]·nDMF 4 show no evidence for a transition between structures containing square and rhomboidal pores (Fig. S19†). Instead, all of the frameworks display powder diffraction patterns that correspond to the square pore form. Further evidence is provided by single crystal analyses completed upon [Zn2(bdc)1.6(bdc-NH2)0.4(dabco)]·2.6DMF 4a and [Zn2(bdc)0.2(bdc-NH2)1.8(dabco)]·1.5DMF 4b. Both of these MOFs show similar connectivity and topology to that of DMOF-1, and display distorted square pores, despite significantly different loadings of the bdc-NH2 ligand in the framework.Whilst a comparison to series 1–3 might lead to the assumption that both 4a and 4b would crystallise in tetragonal settings, there is a change in space group from tetragonal in the case of 4a to monoclinic in the case of 4b. The structure of 4b is overall very similar to that of 4a but shows a minor deviation in the alignment of the crystal sheets as viewed along the b-axis causing a distortion of the neighbouring dabco units (Fig. 8). This corresponds in the β angle shifting away from the required 90° of the tetragonal species, to 94.727(2)°.
X-ray diffraction analysis of [Zn2(bdc-Br)2–x(bdc-I)x(dabco)]·nDMF 5
The series [Zn2(bdc-Br)2–x(bdc-I)x(dabco)]·nDMF 5 was formed through varying the ratios of the two substituted ligands bdc-Br and bdc-I. As with series 1–4, the formations of the multivariate products were identified through 1H NMR spectroscopy. PXRD analysis of the products showed similarities to that of DMOF-1, indicating that isoreticular structures had been formed. No evidence for a transition between structural types was observed (Fig. S20†).The products from a reaction mixture ratio of 50% H2bdc-Br and H2bdc-I yielded crystals suitable for single crystal X-ray diffraction. The crystal structure was solved in an orthorhombic space group and identified as [Zn2(bdc-Br)1.4(bdc-I)0.6(dabco)]·2.6DMF 5a. The structure shows the presence of rhomboidal pores, similar to those observed in 1c and 1d. Unlike the mixed bdc/bdc-Br and bdc/bdc-I series, 1 and 2 respectively, the compounds in series 5 always contain 100% halogenated ligands, but with varying ratios of bdc-Br and bdc-I. The lack of any changes in the peak positions within the PXRD patterns of 5 suggests that all species from this series crystallise in the rhomboidal pore form. This is consistent with findings from compounds with high loadings of bdc-Br and bdc-I from series 1 and 2.
Materials modelling
Given the changes observed in pore geometry with composition in compounds from series 1–3 and the contrasting lack of changes observed in series 4 and 5, atomistic simulations were undertaken in order to gain insight into these observations.Further to assessing the energy difference between different phases, we also probed potential transitions between the structures in order to gain insight into the dynamic stability. Solid-state nudged elastic band (SS-NEB) calculations between symmetry representative structures were performed using VASP at the DFT/PBEsol level of theory.20–24 The saddle point in potential energy obtained between two stable polymorphs (within SS-NEB) can be used to predict the activation energy associated with the possible structural transformation. Full computational details can be found in the ESI.†
Two different 100% halogenated structures were modelled for series 1 and 2. The first halogenated model has Br/I substituted alternatively on each side of neighbouring aromatic rings (A), resulting in 50% of the halogens within each neighbouring pore. The second model has halogen substitution with the same overall concentration but with the halogens on neighbouring rings located within the same pore (S) (Fig. 9). These models allow us to assess the effect of local halogen orientation and concentration, which may influence the phase stability.
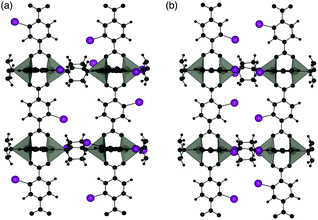 | ||
| Fig. 9 Halogen substitution positions modelled in DMOF-1. (a) Substitution within alternating pores (A) and (b) substitution in the same pore (S), with the halogen atoms shown in purple. | ||
Three pore topologies were considered: perfect square, distorted square and rhomboid for each halogen substituent and un-substituted (100% bdc) framework. The relative energies of each topology with respect to the distorted pore structures are given in Table 2, with calculated activation energies between each phase.
| Ligand | Perfect square pore | Distorted square pore | Rhomboidal pore | E act(1)/kJ mol−1 | E act(2)/kJ mol−1 | E act(3)/kJ mol−1 |
|---|---|---|---|---|---|---|
| bdc | 52.1 | 0 | −8.2 | 18.5 | −0.1 | — |
| bdc-Br (A) | −34.8 | 0 | −10.8 | 42.7 | −0.2 | 37.8 |
| bdc-Br (S) | −29.4 | 0 | −68.5 | 37.4 | — | 14.6 |
| bdc-I (A) | −65.7 | 0 | −32.6 | 49.2 | 2.1 | 67.0 |
| bdc-I (S) | 23.0 | 0 | −51.8 | 69.2 | 3.1 | 22.0 |
Calculated relative energies (Table 2) of the structures support the observed behaviours of the frameworks with higher concentrations of halogenated-bdc (i.e. in series 1 and 2). In particular, the relative energy between the square and rhomboidal pore structures is lowest for the 100% bdc structure whereas the perfect square pore structure becomes less accessible with increasing halogen content, supporting the experimental observation that with increasing halogen content the square pore structure is not formed.
When considering the relative energies between square and rhomboid structures with 100% bdc, 100% bdc-Br (A) or 100% bdc-I (A), the rhomboid form is the higher energy configuration. In contrast, for either the 100% bdc-Br (S) or 100% bdc-I (S), where there is a high concentration of Br in half of the pores, the rhomboidal form is more stable. This observation suggests that above a certain concentration of halogen within a pore, there is a thermodynamic driving force for the formation of the narrow, rhomboidal pore framework.
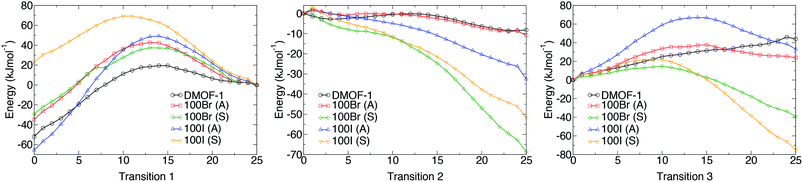
Potential energy profiles showing the activation energies between structures (as given in Table 2) for the three hypothetical structural transformations are depicted in Fig. 10 to further evaluate the thermodynamic stabilities of each structure. Three structural transitions were considered:
Transition 1: ‘Distorted square’ to ‘square’ pore structure. This defines activation energy Eact(1) required to remove the structural distortion following solvent evacuation.
Transition 2: ‘Distorted square’ to ‘rhomboid’ pore structure. This defines activation energy Eact(2) for the compression of the pores observed in some mixed-ligand structures.
Transition 3: ‘Perfect square’ to ‘rhomboid’ pore structure. This defines activation energy Eact(3) associated with compressing the structure from a higher symmetry square pore form. It is also associated with MOF ‘breathing’ and structural flexibility.
The energy profiles further support the observed behaviour of the frameworks. Each structure is locally stable and dynamic conversion between pore topologies would not be possible for structures with halogen substituents. Interestingly, for the 100% bdc structure, no activation barrier between square and rhomboid pore topology is evident. This supports the capability of the 100% bdc structure to ‘breathe’ with applied external stimulus such as a temperature or pressure.
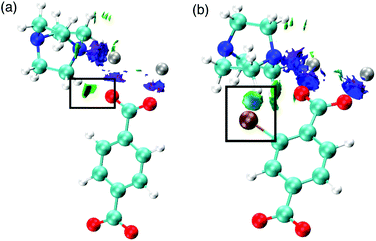
We also consider the change in chemical interactions with increasing halogen concentration within the pore. Non-covalent interaction (NCI) analysis allows the visualisation of charge density within a chemical system that is not attributed to formal covalent bonding.25–28 Two interactions were found to be of importance for the structural behaviour of DMOF-1. Firstly, attractive dispersive interactions between the carboxylate oxygen atoms and the hydrogen atoms on the dabco ligand are present. This interaction is present regardless of the substituent on the bdc ligand and could be a driving force for the COO–Zn–COO angle to change in DMOF-1, subsequently contributing to reversible structural ‘breathing’. We show here that the relative energies of the different pore topologies are consistent with experimental observations. The calculated activation energies confirm that the structures are not interconvertible and a single pore topology is thermodynamically favorable for all systems, supporting the X-ray analyses.
Secondly, the preference for a rhomboidal pore structure for the halogenated mixed-ligand DMOF-1 structures can be explained by the dispersive interactions between the halogen atom and the hydrogen atom on the dabco ligand. Fig. 11 depicts this interaction between Br and H in the 100% bdc-Br (S) system. With increasing concentration of halogen, the number of these interactions increases and this provides the thermodynamic driving force for the observed behaviour. As the halogen–halogen distances within the pore are greater than 6 Å in series 1, this rules out halogen–halogen interactions as a contributing factor to pore compression. Indeed, these interactions were also not evident in the NCI analysis. Further support can be found in series 3 and 4, with NO2 and NH2 groups as substituents on the bdc ligand. At 100% concentration of substituent on each aromatic ring these structures do not collapse into rhomboidal geometry, but remain in a square pore topology. For the amino-containing framework 4, H(NH2)–H(dabco) only weak interactions are present that would not provide enough attractive force to drive the structure to collapse. For the case of series 3, the analysis of observed pore topologies is more complex. During geometry optimisation, a rotation of the NO2 substituent renders the non-covalent interactions diffuse and weak due to the lone pair repulsion between the O(NO2)–O(carboxylate). The relative energies of pore topologies with high concentration of NO2 are sensitive to the extent of rotation and are therefore not reported.
Structural stability of series 1–5
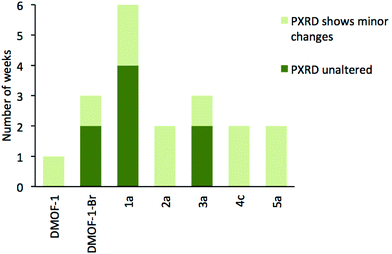
Previous reports have shown that the DMOF-1 structure is susceptible to hydrolysis from atmospheric water leading to the collapse of the framework over time.29 Studies were therefore undertaken on selected members of series 1–5 to determine if the addition of a second bdc-X ligand affected the stability in air. A similar protocol has been used to assess the structural stability of MOF-177.30Compounds [Zn2(bdc)(bdc-Br)(dabco)]·DMF 1a, [Zn2(bdc)1.5(bdc-I)0.5(dabco)]·nDMF 2a, [Zn2(bdc)1.2(bdc-NO2)0.8(dabco)]·2.5DMF 3a, [Zn2(bdc)1.16(bdc-NH2)0.84(dabco)]·nDMF 4c and [Zn2(bdc-Br)1.4(bdc-I)0.6(dabco)]·2.6DMF 5a were monitored by powder X-ray diffraction at one week intervals over several weeks. DMOF-1 was also monitored under the same conditions as a control sample. Compounds 2a, 4c and 5a showed slightly increased framework stabilities in air relative to DMOF-1, with all three compounds showing significant structural changes after one week and a total collapse in crystallinity after 2–3 weeks.
Powder X-ray diffraction of 3a showed no change in the structure of the framework after one week. As with 2a and 4c, this represents an increase in stability compared to DMOF-1, although complete loss of crystallinity in 3a was observed after three weeks of air exposure. In contrast, the diffraction pattern of compound 1a remained unchanged for over four weeks of air exposure, suggesting that the framework has considerably greater structural stability in air than the parent DMOF-1. Although powder X-ray diffraction studies will not reveal the presence of amorphous decomposition phases, the similar signal to noise ratios in the PXRD patterns of 1a over time suggest the possibility of the bulk of the material decomposing to an amorphous product leaving only a small amount of crystalline product is unlikely.
The stability of [Zn2(bdc-Br)2(dabco)] was similarly monitored for comparison. Although the framework stability of this compound was greater than that of DMOF-1 with no alterations to the diffraction pattern for up to two weeks, it is significantly lower than 1a. Multivariate MOFs, such as 1a, therefore can allow access to more air- or moisture-stable structures than those of the single-linker structures. These results are summarized graphically in Fig. 12.
Experimental
All chemicals used were commercially sourced (Sigma-Aldrich) unless otherwise stated, and were used without purification. DMOF-1 and its multivariate analogues were prepared using similar syntheses to that previously reported with modifications to the dicarboxylic acid ratios as detailed in the ESI.† The synthetic procedure for compounds in series 1–4 involved the combination of H2bdc and H2bdc-X along with dabco and Zn(NO3)2·6H2O in DMF. Each reaction mixture was sonicated to aid dissolution before being sealed and heated at 120 °C for 3 days. For each of series 1, 3 and 4, nine compounds were synthesised by varying the compositional factor, x in [Zn2(bdc)2–x(bdc-X)x(dabco)]. Series 2 contained four compounds and series 5 contained three compounds. Characterisation was carried out using 1H NMR spectroscopy, powder X-ray diffraction and single crystal X-ray crystallography (see ESI†).Individual crystal samples for 1H NMR spectroscopy used only one signal crystal of the compound, with the sample prepared in a similar manner to the bulk samples. The bulk samples were first dried at 120 °C before being digested using an acid-based digestion solution of DMSO-d6 and DCl (see ESI†). Individual crystal samples were air dried prior to being digested.
Single crystal X-ray analysis were carried out on compounds 1a–d, 1c′, 3a, 4a, 4b and 5a with details of the data collections and refinements given in Table 3. Further details of these analyses are provided in the ESI.†
| Compound | 1a | 1b | 1c | 1d | 1c′ | 3a | 4a | 4b | 5a |
|---|---|---|---|---|---|---|---|---|---|
| Chemical formula | C25H26O9N3BrZn2 | C25H25.8O9N3Br1.2Zn2 | C22H18.4O8N2Br1.6Zn2 | C22H18.4O8N2Br1.6Zn2 | C22H18.48O8N2Br1.52Zn2 | C29.5H36.7O12.1N5.3Zn2 | C29.8H38.6O10.6N5Zn2 | C22H21.8O8N3.8Zn2 | C29.8H36.2O10.6N4.6I0.6Br1.4Zn2 |
| Formula Mass | 723.14 | 738.92 | 697.38 | 705.27 | 691.07 | 789.88 | 767.19 | 598.17 | 947.19 |
| Temperature/K | 150(2) | 150(2) | 150(2) | 150(2) | 298(2) | 150(2) | 150(2) | 150(2) | 150(2) |
| Crystal system | Tetragonal | Tetragonal | Orthorhombic | Orthorhombic | Orthorhombic | Tetragonal | Tetragonal | Monoclinic | Orthorhombic |
| Space group | P4/ncc | P4/ncc | Ammm | Ammm | Ammm | I4/mcm | P4/ncc | I2/a | Pncb |
| a/Å | 14.9880(4) | 14.9760(4) | 9.6280(2) | 9.6230(3) | 9.6342(14) | 15.0210(4) | 14.9813(3) | 15.3434(4) | 9.6270(3) |
| b/Å | 14.9880(4) | 14.9760(4) | 12.7590(2) | 12.8580(6) | 16.488(3) | 15.0210(4) | 14.9813(3) | 14.7669(3) | 13.2670(4) |
| c/Å | 19.2400(5) | 19.2380(6) | 17.5720(3) | 17.4800(8) | 14.229(3) | 19.2220(8) | 19.2011(6) | 19.2363(4) | 17.2190(5) |
| α/° | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 |
| β/° | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 94.7265(19) | 90 |
| γ/° | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 |
| Unit cell volume/Å3 | 4322.1(3) | 4314.7(3) | 2158.61(7) | 2162.84(16) | 2260.2(8) | 4337.1(3) | 4309.5(2) | 4343.63(17) | 2199.24(11) |
| No. of formula units per unit cell, Z | 4 | 4 | 2 | 2 | 2 | 4 | 4 | 4 | 2 |
| No. of reflections measured | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 851 851 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056 056 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 984 984 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 147 147 |
2827 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 254 254 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 611 611 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 630 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 992 992 |
| No. of independent reflections | 1901 | 1904 | 1399 | 1403 | 1229 | 1356 | 2088 | 4259 | 1953 |
| R int | 0.0967 | 0.0561 | 0.0437 | 0.0752 | 0.0532 | 0.1208 | 0.0789 | 0.0526 | 0.0996 |
| Final R1 values (I > 2σ(I)) | 0.0917 | 0.0967 | 0.0653 | 0.0735 | 0.0905 | 0.0529 | 0.0650 | 0.0523 | 0.0950 |
| Final wR(F2) values (I > 2σ(I)) | 0.2620 | 0.2472 | 0.1840 | 0.2074 | 0.2471 | 0.1299 | 0.1891 | 0.1624 | 0.2457 |
| Final R1 values (all data) | 0.1212 | 0.1109 | 0.0697 | 0.0786 | 0.0981 | 0.0806 | 0.0810 | 0.0595 | 0.1186 |
| Final wR(F2) values (all data) | 0.2795 | 0.2558 | 0.1897 | 0.2131 | 0.2562 | 0.1483 | 0.2081 | 0.1702 | 0.2667 |
Representative samples from series 1–5 were selected for framework stability experiments. The samples were air dried and kept open to the atmosphere under ambient conditions. Monitoring of the framework crystallinity was conducted using powder X-ray diffraction at one week intervals over a period of six weeks.
Computational methods, based on density functional theory (DFT), are detailed in the ESI.†
Conclusions
Multivariate MOFs based on the structure of DMOF-1 and containing varying ratios of different dicarboxylate ligands have been successfully synthesised and characterised. The series [Zn2(bdc)2–x(bdc-Br)x(dabco)]·nDMF 1, [Zn2(bdc)2–x(bdc-NO2)x(dabco)]·nDMF 3 and [Zn2(bdc)2–x(bdc-NH2)x(dabco)]·nDMF 4 show the incorporation of ligands into the product framework in the same ratio as that present in the reaction mixture. Both series [Zn2(bdc)2–x(bdc-I)x(dabco)]·nDMF 2 and [Zn2(bdc-Br)2–x(bdc-I)x(dabco)]·nDMF 5 demonstrate a strong ligand preference with the bdc-I ligand being preferentially excluded during framework formation.The systematic approach to mixed-ligand MOF formation has demonstrated that by variation of dicarboxylic acid ratios in the reaction mixture the pore topology of the framework can be controlled. Computational studies on series [Zn2(bdc)2–x(bdc-Br)x(dabco)]·nDMF 1 have shown that above a certain halogen concentration there is a thermodynamic driving force for pore compression. However, at very high concentrations of halogen within the pore, the activation energy for this transition is lowered. These results support the experimental findings of a lower pore compression in [Zn2(bdc-Br)2(dabco)] than in the multivariate MOFs. The correlation of pore geometry to the ligand ratio opens up the possibility of pore size and shape tuning through reaction stoichiometry control. Pore geometries which may only otherwise be accessed via solvent changes or complete substitution of the ligand can therefore be formed through the use of a multivariate approach.
This approach allows the potential for pore shape alterations without the loss of desirable properties introduced through ligand choices. These pore transitions are dependent upon the functionality of the substituent, as demonstrated by series [Zn2(bdc)2–x(bdc-NH2)x(dabco)]·nDMF 4 and [Zn2(bdc-Br)2–x(bdc-I)x(dabco)]·nDMF 5 which show no pore transitions.
The multivariate MOFs of series 1, 2, 3 and 4 are more stable to air than DMOF-1. In the specific case of [Zn2(bdc)(bdc-Br)(dabco)]·DMF 1a, the compound shows enhanced stability over both [Zn2(bdc)2(dabco)] and [Zn2(bdc-Br)2(dabco)], demonstrating that multivariate species can have properties which extend beyond the combination of the corresponding single ligand systems.
Acknowledgements
L.K.C. is funded by an EPSRC studentship. J.K.B. is funded by the EPRSC Doctoral Training Centre for Sustainable Chemical Technologies at the University of Bath (Grant No. EP/G03768X/1). D.T. was funded under ERC starting grant 277757. A.W. acknowledges support from the Royal Society and EPSRC Grant No. EP/K004956/1. The work benefits from the high performance computing facility at the University of Bath. Access to ARCHER supercomputer was facilitated through membership of the HPC materials Chemistry Consortium (EPSRC Grant No. EP/L000202). The authors thank Dr A. Otero de la Roza for useful discussions and Dr J. Lowe for NMR spectroscopic advice.Notes and references
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed
.
- S. Horike, S. Shimomura and S. Kitagawa, Nat. Chem., 2009, 1, 695 CrossRef CAS PubMed
.
- M. P. Suh, H. J. Park, T. K. Prasad and D.-W. Lim, Chem. Rev., 2012, 112, 782 CrossRef CAS PubMed
.
- J.-R. Li, J. Sculley and H.-C. Zhou, Chem. Rev., 2012, 112, 869 CrossRef CAS PubMed
.
- P. Horcajada, R. Gref, T. Baati, P. K. Allan, G. Maurin, P. Couvreur, G. Férey, R. E. Morris and C. Serre, Chem. Rev., 2012, 112, 1232 CrossRef CAS PubMed
.
- S. Henke, A. Schneemann, A. Wütscher and R. A. Fischer, J. Am. Chem. Soc., 2012, 134, 9464 CrossRef CAS PubMed
.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469 CrossRef CAS PubMed
.
- A. D. Burrows, CrystEngComm, 2011, 13, 3623 RSC
.
- H. Deng, C. J. Doonan, H. Furukawa, R. B. Ferreira, J. Towne, C. B. Knobler, B. Wang and O. M. Yaghi, Science, 2010, 327, 846 CrossRef CAS PubMed
.
- A. D. Burrows, L. C. Fisher, C. Richardson and S. P. Rigby, Chem. Commun., 2011, 47, 3380 RSC
.
- D. N. Dybtsev, H. Chun and K. Kim, Angew. Chem., Int. Ed., 2004, 43, 5033 CrossRef CAS PubMed
.
- H. Chun, D. N. Dybtsev, H. Kim and K. Kim, Chem. – Eur. J., 2005, 11, 3521 CrossRef CAS PubMed
.
- T. Loiseau, C. Serre, C. Huguenard, G. Fink, F. Taulelle, M. Henry, T. Bataille and G. Férey, Chem. – Eur. J., 2004, 10, 1373 CrossRef CAS PubMed
.
- P. Horcajada, F. Salles, S. Wuttke, T. Devic, D. Heurtaux, G. Maurin, A. Vimont, M. Daturi, O. David, E. Magnier, N. Stock, Y. Filinchuk, D. Popov, C. Riekel, G. Férey and C. Serre, J. Am. Chem. Soc., 2011, 133, 17839 CrossRef CAS PubMed
.
- Z. Wang and S. M. Cohen, J. Am. Chem. Soc., 2009, 131, 16675 CrossRef CAS PubMed
.
- S. Henke, D. C. F. Wieland, M. Meilikhov, M. Paulus, C. Sternemann, K. Yusenko and R. A. Fischer, CrystEngComm, 2011, 13, 6399 RSC
.
- S. Henke, A. Schneemann, S. Kapoor, R. Winter and R. A. Fischer, J. Mater. Chem., 2012, 22, 909 RSC
.
- K. Uemura, F. Onishi, Y. Yamasaki and H. Kita, J. Solid State Chem., 2009, 182, 2852 CrossRef CAS
.
- K. Uemura, Y. Yamasaki, F. Onishi, H. Kita and M. Ebihara, Inorg. Chem., 2010, 49, 10133 CrossRef CAS PubMed
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953 CrossRef
.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978 CrossRef CAS
.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- K. J. Caspersen and E. A. Carter, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6738 CrossRef CAS PubMed
.
- J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625 CrossRef CAS PubMed
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS PubMed
.
- A. Otero de la Roza, M. A. Blanco, A. M. Pendás and V. Luaña, Comput. Phys. Commun., 2009, 180, 157 CrossRef CAS
.
- A. Otero de la Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007 CrossRef CAS
.
- H. Jasuja, N. C. Burtch, Y.-G. Huang, Y. Cai and K. S. Walton, Langmuir, 2013, 29, 633 CrossRef CAS PubMed
.
- D. Saha and S. Deng, J. Phys. Chem. Lett., 2010, 1, 73 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Syntheses, characterisation and computational details. CCDC 1401468–1401475 and 1431185. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt04045k |
| This journal is © The Royal Society of Chemistry 2016 |