Open Access Article
Open Access ArticleBenchmarking nanoparticulate metal oxide electrocatalysts for the alkaline water oxidation reaction†
Suho
Jung
*a,
Charles C. L.
McCrory
*a,
Ivonne M.
Ferrer
ab,
Jonas C.
Peters
*ab and
Thomas F.
Jaramillo
*ac
aJoint Center for Artificial Photosynthesis, California Institute of Technology, Pasadena, CA 91125, USA. E-mail: benchmarking@solarfuelshub.org
bDivision of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, CA 91125, USA
cDepartment of Chemical Engineering, Stanford University, Stanford, CA 94305, USA
First published on 27th November 2015
Abstract
Nanoparticulate metal-oxide catalysts are among the most prevalent systems for alkaline water oxidation. However, comparisons of the electrochemical performance of these materials have been challenging due to the different methods of attachment, catalyst loadings, and electrochemical test conditions reported in the literature. Herein, we have leveraged a conventional drop-casting method that allows for the successful adhesion of a wide range of nanoparticulate catalysts to glassy-carbon electrode surfaces. We have applied this adhesion method to prepare catalyst films from 16 crystalline metal-oxide nanoparticles with a constant loading of 0.8 mg cm−2, and evaluated the resulting nanoparticulate films for the oxygen evolution reaction under conditions relevant to an integrated solar fuels device. In general, the activities of the adhered nanoparticulate films are similar to those of thin-film catalysts prepared by electrodeposition or sputtering, achieving 10 mA cm−2 current densities per geometric area at overpotentials of ∼0.35–0.5 V.
Introduction
The storage of solar energy in the form of chemical bonds using integrated artificial photosynthetic devices comprised of earth-abundant materials is a promising approach to generate clean and sustainable chemical fuels.1–14 The development of such solar fuel devices requires the identification of efficient electrocatalysts for the water-splitting reactions. However, a lack of standardization in the measurement and reporting of water-splitting materials has made it difficult to compare the performance of electrocatalytic water-splitting systems under identical conditions. This lack of standardization in performance evaluation for electrocatalytic systems frustrates efforts to identify both the most promising catalysts for device integration and the technological gaps still to be overcome through the design of new materials and systems.To establish a standardized protocol for catalyst measurement and reporting, we previously proposed a methodology for evaluating the activity and short-term stability of electrodeposited and sputtered electrocatalysts for the oxygen evolution reaction (OER)15,16 and the hydrogen evolution reaction (HER)15 in aqueous alkaline and acidic solutions. As part of this benchmarking protocol, we identified a relevant primary figure of merit as the overpotential necessary to achieve 10 mA cmgeo−2 (geometric area) current density, ηj=10 mA cmgeo−2, the approximate current density expected in a 10% efficient integrated solar-to-fuels device under 1 sun illumination.11,17,18 Uniform application of this benchmarking methodology to dozens of HER and OER electrocatalytic films allowed us to identify several key trends in catalyst performance, but of particular interest is that most of the active OER catalysts showed similar activity in alkaline solution, achieving 10 mA cmgeo−2 current densities at overpotentials of ηj=10 mA cmgeo−2 = 0.35–0.6 V,15,16 lending support to the theorized existence of a minimum “thermodynamic overpotential” of ∼0.4 V for OER at planar metal-oxide surfaces.19,20
Nanoparticulate electrocatalysts for artificial photosynthetic devices are also of considerable interest because (i) their active surface areas can be controlled by controlling the nanoparticle size, suggesting that nanoparticles and other nanostructured materials may allow for very high surface area systems at relatively small catalyst loading per geometric area,21,22 (ii) they offer ease of control in synthesizing and characterizing material phases (composition and crystallinity) compared to deposited film syntheses,23 and (iii) the particle size and shape also may impact light scattering behavior in the solar-fuel devices.24 However, despite the numerous reports on particulate electrocatalysts for the OER, there is no standard method to evaluate particulate catalyst performances using consistent deposition methods and electrochemical test conditions.
Herein, we report a testing protocol for evaluating particulate electrocatalysts and use it to study a series of metal oxide nanoparticles for the OER under conditions relevant to an integrated solar-fuels device operating in alkaline solution.
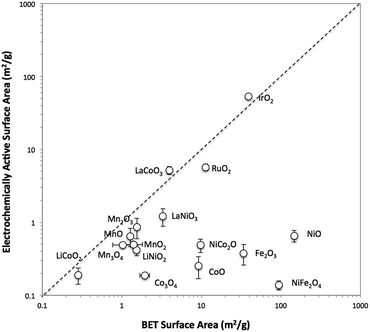
Catalyst films are formed using a simple drop-cast method for the attachment of a wide range of particle catalysts onto glassy carbon working electrode substrates using a thin Nafion binder.25 This attachment strategy is conceptually similar to those previously reported for the immobilization of nanoparticulate electrocatalysts for the oxygen reduction reaction (ORR)26–29 and the OER.25,30,31 Note that minimizing the thickness of the Nafion binder film is crucial to reduce oxygen transport resistance.29 We have applied this attachment method to study the OER performance of drop-casted electrocatalyst particles for 16 crystalline metal oxides (Table 1) selected due to their frequent use as OER electrocatalysts. The phase of the oxide materials are identified by X-ray powder diffraction, and images of the drop-casted particles are obtained by scanning electron microscopy (SEM). The surface areas of the metal oxide particles are estimated by two methods: (i) Brunauer–Emmett–Teller (BET) gas adsorption of the catalyst particles, and (ii) electrochemically active surface area (ECSA) based on cyclic voltammetry measurements. Comparisons of the two surface area measurements are provided, and the appropriateness of each method for estimating electrocatalyst surface area is discussed. The activity and stability of each system is tested in alkaline solution (1 M NaOH), and the performances of the oxide catalysts are compared.
| Oxide | Crystal structure | BET SA (m2 g−1) | ECSA (m2 g−1) |
|---|---|---|---|
| CoO | Rock salt | 9.20 ± 0.30 | 0.25 ± 0.17 |
| Co3O4 | Spinel | 1.95 ± 0.50 | 0.19 ± 0.03 |
| NiO-(i) | Rock salt | 147.06 ± 11.30 | 0.65 ± 0.23 |
| NiCoO2 | Rock salt | 9.78 ± 0.30 | 0.49 ± 0.20 |
| NiFe2O4 | Spinel | 94.28 ± 1.60 | 0.14 ± 0.04 |
| Fe2O3 | Spinel | 34.10 ± 1.20 | 0.38 ± 0.24 |
| IrO2-(i) | Rutile | 39.02 ± 2.10 | 52.98 ± 3.04 |
| RuO2 | Rutile | 11.38 ± 0.10 | 5.69 ± 1.22 |
| LiCoO2 | ABO2 layered | 0.28 ± 0.01 | 0.19 ± 0.10 |
| LiNiO2 | ABO2 layered | 1.53 ± 0.01 | 0.42 ± 0.14 |
| LaCoO3 | ABO3 perovskite | 1.27 ± 0.10 | 0.65 ± 0.37 |
| LaNiO3 | ABO3 perovskite | 3.96 ± 0.30 | 5.19 ± 1.28 |
| Mn2O3 | Scandium oxide | 3.28 ± 0.10 | 1.21 ± 0.65 |
| MnO | Rock salt | 1.54 ± 0.10 | 0.86 ± 0.54 |
| MnO2 | Rutile | 1.40 ± 0.80 | 0.50 ± 0.03 |
| Mn3O4 | Spinel | 1.02 ± 0.50 | 0.49 ± 0.02 |
| Glassy carbon | N/A | N/A | N/A |
Experimental section
Materials
All materials were used as received. The following nanoparticles used in this study were purchased from commercial vendors in specified grade: ruthenium(IV) oxide (RuO2, 99.9%), nickel(II) oxide (NiO-(i), nanopowder, <50 nm particle size, 99.8%), nickel(II) oxide (NiO-(ii), powder and chunks, 99.99%), cobalt(II) oxide (CoO, ≥99.99%), nickel(II) cobalt(II) oxide ((NiO)(CoO), nanopowder, <150 nm, 99%), cobalt(II,III) oxide (Co3O4, nanopowder, <50 nm), iron(III) oxide (Fe2O3, <5 μm), lithium cobalt(III) oxide (LiCoO2, 99.8%), lithium nickel(II) oxide (LiNiO2, ≥98%), manganese(II) oxide (MnO, ≥99.99%), manganese(IV) oxide (MnO2, ≥99.99%), manganese(III) oxide (Mn2O3, ≥99.99%), manganese(II,III) oxide (Mn3O4, 97%), and iridium(IV) oxide (IrO2-(ii), 99.9%, >20 μm) were purchased from Sigma Aldrich; iridium(II) oxide powder (IrO2-(i), 20–32 m2 g−1 BET surface area according to the supplier) was purchased from Premetek; and nickel(II) iron(III) oxide (NiFe2O4, nanopowder, 30 nm, 99.5%) was purchased from MTI Corporation.In addition, lanthanum(III) nitrate hexahydrate (La(NO3)3·6H2O, 99.999%), cobalt(II) nitrate hexahydrate (Co(NO3)2·6H2O, 99.999%), nickel(II) nitrate hexahydrate (Ni(NO3)2·6H2O, 99.999%), tetramethylammonium hydroxide pentahydrate (TMAH, (CH3)4N(OH)·5H2O, ≥97%), nickel(II) nitrate hexahydrate (Ni(NO3)2·6H2O, 99.999%), ammonium hydroxide (NH4OH, BioUltra), sodium hydroxide (NaOH, BioUltra), sodium phosphate monobasic dihydrate (NaH2PO4·2H2O, BioUltra), and ammonium perchlorate (NH4ClO4, 99.999%) were purchased from Sigma Aldrich. Puratronic grade cobalt(II) sulfate heptahydrate (CoSO4·7H2O, 99.999%) was purchased from Alfa-Aesar. 2-Propanol (ACS grade) was obtained from BDH, and 5 wt% Nafion 117 solution in a mixture of lower aliphatic alcohols and water was purchased from Sigma-Aldrich. Oxygen cylinders (O2, Alphagaz-1 grade 99.999%) were purchased from Air Liquide. All water used was purified using a Thermo Scientific Barnstead Nanopure water purification system (18.2 MΩ cm resistivity).
Perovskite oxide synthesis
Lanthanum cobalt(III) oxide (LaCoO3) and lanthanum nickel(III) oxide (LaNiO3) were prepared by modifying literature methods.32–34 For both oxides, 0.2 M of La(NO3)3·6H2O and either Co(NO3)2·6H2O or Ni(NO3)2·6H2O were mixed with 1.2 M TMAH to form a total of 250 mL solution. The mixtures were stirred overnight, and then washed with water at least 5 times using filter paper. The washed particles were then dried overnight in a gravity convection oven at 60 °C. The dried powders were collected and ground using mortar and pestle. The resulting powders were then calcined on a ceramic boat in a 1 inch diameter quartz tube using a three-zone tube furnace (Mellen, SV Series Split furnace) in which all three zones were set to the same temperature as follows: LaCoO3 was calcined at 1000 °C for 5 hours in dry air with a flow rate of ∼9 slm (standard liters per minute), and LaNiO3 was calcined in O2 at 800 °C for 5 hours in O2 at a flow rate of ∼9 slm. Finally the calcined powders were ground again using mortar and pestle.Analytical equipment
Electrochemical measurements were conducted with a Bio-Logic VMP3 multichannel potentiostat/galvanostat with a built-in EIS analyzer. The working electrodes were 5 mm diameter disk electrodes with a surface area of 0.196 cm2, mounted into a Pine Instrument Company E6-series ChangeDisk RDE assembly and affixed to an MSR rotator. Reference electrodes were commercial saturated calomel electrodes (SCE) (CH Instruments) externally referenced to a solution of ferrocenecarboxylic acid (Sigma-Aldrich) in 0.2 M phosphate buffer at pH 7 (0.284 V vs. SCE)35 prior to each set of experiments, and the auxiliary electrodes were carbon rods (99.999%, Strem Chemicals). All data were recorded using the BioLogic EC-Lab software package (v.10.23).The phases of the oxide materials were identified by powder X-ray diffraction (XRD). A tabletop X-ray diffractometer (Bruker D2 Phaser) with Cu-Kα as the radiation source was used to generate X-ray at the power of 30 kV/10 mA. Peak matching was performed with Bruker DIFFRAC.EVA software. The BET (Brunauer–Emmett–Teller) surface areas of the oxide materials were estimated from nitrogen adsorption/desorption isotherms in powder forms using a surface area analyzer (Micromeritics Tristar II). The powder samples were de-gassed using a gentle flow of nitrogen at 150 °C for 5–10 hours, then immediately transferred to the sample tube for the measurements after weighing them.
The drop-casted nanoparticle images were obtained from scanning electron microscopy (SEM) using a Nova NanoSEM 450 FEI with a 15 kV of accelerating voltage and a through-the-lens detector (TLD). Some oxides required a stage bias of ∼400 V due to charging effects caused by low electrical conductivities.
Working electrode preparation
5 mm diameter-glassy carbon disks (4 mm thick, Sigradur G, HTW Hochtemperatur-Werkstoff GmbH) were used as working electrode substrates. The disks were lapped with silicon carbide abrasive papers (CarbiMet 2, 600/P1200, Buehler), followed by sequential polishing with diamond abrasive slurries (MetaDi Supreme, Buehler) in an order of 9 μm, 6 μm, 3 μm, 1 μm, and 0.1 μm diameter particle based slurries (1 min polishing each), to obtain mirror surfaces. Synthetic nap based polishing pads (MD Floc, Struers) were used for diamond polishing. The lapping and polishing were performed using a LaboSystem (LaboPol-5 and LaboForce-1, Struers) with 5 psi of applied pressure per disk, 8 rpm of the head speed and 200 rpm of the platen speed. To clean the polished disks, they were sonicated sequentially in pure water, acetone, and 2-propanol for 10 minutes each. The cleaned disks were then sonicated again in water for 10 minutes prior to use.The dropcasting protocol reported here is modified from a literature protocol.25 Powder-based inks for each catalyst were made using 3.8 mL water, 1.0 mL 2-propanol, 40 μL of 5% Nafion 117 solution, and 80 mg of the oxide powder. Note that the powders used contained only the native oxide and were not supported on conductive media such as carbon black. The inks were sonicated for 10 minutes, and then 10 μL of the inks were drop-casted onto mirror-polished glassy carbon disks using a micro-pipetter, followed by drying in an oven at 60 °C for 10 minutes.
Note that although the sulfonic acid sites in Nafion are very acidic, we do not believe the Nafion imparts significant catalyst degradation in the ink. This is because only a very small concentration of Nafion is used in the catalyst inks (∼1.2 mg L−1). Taking into account the equivalent weight of Nafion 117 (∼1100 g per sulfonic acid group), the resulting total concentration of acidic sites is ∼1 μM. This suggests the overall pH of the ink should be near neutral, and many of the Nafion sites will likely be deprotonated in the ink. pH measurements were conducted on several of the catalyst inks, and in general most had pH ≥ 7.
Electrodepositions of both nickel and cobalt onto glassy carbon electrodes were conducted in a 100 mL cell with 40 mL of an aqueous deposition solution. The metallic cobalt film was cathodically deposited onto a 5 mm diameter glassy carbon disk from a solution of 0.202 g CoSO4·7H2O and 0.164 g NH4ClO4 (pH adjusted to 6.8 with NH4OH) at −50 mA cmgeo−2 for 30 seconds with the working electrode rotated at 200 rpm. The metallic nickel film was cathodically deposited in a solution of 1.047 g Ni(NO3)2·6H2O at −16 mA cmgeo−2 for 10 seconds with the working electrode rotated at 800 rpm. The carbon auxiliary electrode was separated from the glassy carbon working electrode and SCE reference electrodes using a fine-porosity glass frit (BioAnalytical systems, Inc.). pH measurements were conducted with a VWR Symphony multiparameter meter with a Thermo Scientific Orion refillable Ag/AgCl pH electrode filled with Orion Ag/AgCl reference electrode filling solution.
In addition, metallic nickel, iridium, and ruthenium films were deposited onto glassy carbon disks via a reactive sputtering method based on a previously reported procedure.15,36 The glassy carbon disks were affixed to a glass slide using double-sided Kapton tape, and then the iridium and ruthenium were sputtered onto the electrode surface from an RF source at 200 W at 300 °C for 30 min under a constant flow of 3.0/3.0 sccm (standard cubic centimeters per minute) Ar/O2 for iridium, 4.5/0.5 sccm Ar/O2 for ruthenium, using Ir and Ru targets, respectively (≥99.9% from AJA International). The nickel film was sputtered from an RF source at 150 W at room temperature under a constant flow of 20 sccm Ar while maintaining an overall pressure of 8.5 mtorr for 35 min using a Ni target (99.95%, ACI alloys).
Electrochemical measurements
The electrocatalyst-modified electrodes were mounted in the RDE assembly, and activity, stability, and surface area measurements were conducted in a 2-chamber U-cell as previously described.15,16 Briefly, the first chamber held the working and reference electrodes in ∼120 mL of 1 M NaOH solution, and the second chamber held the auxiliary electrode in ∼15 mL of 1 M NaOH solution. Prior to each set of electrochemical tests, the electrolyte solution was bubbled with O2 for at least 30 minutes. During cyclic voltammetry (CV) measurements, the solution in the first chamber was blanketed under O2. During rotating disk electrode voltammetry (RDEV), chronoamperometry (CA), and chronopotentiometry (CP) measurements, the solution in the first chamber was continuously bubbled with O2. The uncompensated solution resistance (Ru) was measured with a high-frequency single-point impedance measurement at 100 kHz with a 20 mV amplitude about the open-circuit potential (OCP), and RDEV and CA measurements were corrected for IR drop at 85% through positive feedback using the Bio-Logic EC-Lab software. CP measurements were manually corrected for IR drop. Our typical electrochemical setup resulted in Ru = ∼10 Ω in 1 M NaOH.Double layer capacitance was estimated in order to determine electrochemically active surface areas (ECSA) as previously described.15,16 In brief, a potential range in which there is minimal faradaic current response was estimated by CV. All measured current in this region is assumed to be a charging current due to double-layer charging. CV measurements were conducted in quiescent solution by sweeping the potential across this non-faradaic region from the more positive to negative potential and back at 8 different scan rates: 5, 10, 25, 50, 100, 200, 400, and 800 mV s−1. The working electrode was held at each potential vertex for 10 s before beginning the next sweep.15,16,37 Plotting the charging current as a function of the scan rate yields a straight line with the slope equal to the double-layer capacitance. The ECSA of the system is then calculated by dividing the double-layer capacitance by a general specific capacitance of 0.040 mF cm−2, a typical value reported for a metal electrode in an aqueous NaOH solution.16
Results and discussion
Materials characterization
The phases of all the oxide materials were confirmed by powder diffraction patterns. As shown in Fig. S1–S6† and summarized in Table S1,† most of the oxide materials studied have rock salt, spinel, rutile, layered, and perovskite structures. The rock salt and spinel structures are primarily the oxides from the first-row transition metals that are based on the cubic system (CoO, NiO, and NiCoO2 for rock salt; and Fe2O3, Co3O4, and NiFe2O4 for spinel). Catalysts with the rutile structure, based on the tetragonal system, include the noble-metal oxides IrO2 and RuO2 which are known to have high activity for the OER with relatively high stability in aqueous solutions at various pH.10,11,15,38,39 LiNiO2 and LiCoO2 are probably most well-known as lithium-ion battery cathode materials with a layered rhombohedral structure, although recently these layered ABO2 type oxides have been used for alkaline OER.40–43 Lastly, ABO3-type perovskite-structured oxides, including LaCoO3 and LaNiO3, have been attracting increased interest due to their comparatively efficient OER activities, high electrical conductivities, and large composition spaces for doping A and B sites.32,44–48 In addition to the above systems, four manganese oxides, all with different crystal structures, were also explored for this benchmarking study. Crystalline and amorphous Mn-based oxide materials have shown promise as bifunctional catalysts for the OER and ORR.18,49,50The qualitative particle size and shape were examined by SEM, which are shown in Fig. S7–S12.† The images of the immobilized oxide particles overall do not show signs of thick Nafion film covering the particle layers. This suggests that the small amount of Nafion efficiently bind particles together and to the glassy carbon substrate without embedding the particles in a thick polymer film. The micrographs suggest that there is a wide range of particle size and shape when comparing the various nanopowders, ranging in size from ∼10 nm nanoparticles up to 10 μm aggregates.
Surface area measurements
The surface area of each particle was characterized with two different methods, BET gas adsorption and ECSA. The BET surface area (BET SA) was measured ex situ using the raw powder form of the particle by evaluating nitrogen adsorption/desorption isotherms, whereas the ECSA was measured for the particle immobilized onto a glassy carbon disk in 1 M NaOH. A direct comparison of the BET SA and ECSA of all 16 oxide particles is shown in Fig. 1. For convenience, ECSA has been converted from units of cm2 to units of m2 g−1 by dividing the ECSA area by the constant catalyst loading used in this study (0.8 mg cm−2). In general, the two methods of surface area determination do not give similar values. Most of the ECSA values are clustered in a narrow range between 0.1 and 1 m2 g−1, whereas BET SA values range from 0.1 to 1000 m2 g−1. Some exceptions include IrO2-(i), RuO2, LaCoO3, and LaNiO3 which show comparable BET SA and ECSA values greater than 1 m2 g−1.To better probe the general discrepancy between the two methods, we compared the BET SA and ECSA of relatively high surface area, small particles of IrO2-(i) and NiO-(i) to lower-surface area, large particles and aggregates of IrO2-(ii) and NiO-(ii). The phase of IrO2-(i) and NiO-(i) are equivalent to that of IrO2-(ii) and NiO-(ii), respectively, as measured by XRD, but the latter materials appear much coarser in SEM images as seen in Fig. S7 and S9.† The BET SA and ECSA of these four materials were measured and are compared in insets of Fig. S13.† The BET SA of the coarser IrO2-(ii) and NiO-(ii) particles are 8–20 times lower compared to those of the IrO2-(i) and NiO-(i) particles as expected. However, while a similar decrease in ECSA is observed when comparing IrO2-(ii) to IrO2-(i) particles, both the low-surface area NiO-(ii) and high-surface area NiO-(i) shows nearly equivalent ECSA values.
To test whether ECSA or BET SA is a better way of measuring the surface area relevant to catalysis for both IrO2 and NiO systems, the OER activity was measured using rotating disk electrode voltammetry (RDEV). The resulting voltammograms for the OER activity per geometric area (mA cmgeo−2) for the two NiO and IrO2 systems are shown in Fig. S13.† In the case of IrO2, the activity per geometric areas of IrO2-(i) is significantly higher than that of IrO2-(ii). This is consistent with IrO2-(i) having a significantly higher surface area as suggested by both ECSA and BET measurements. In the case of NiO, the NiO-(i) activity is significantly higher than that of NiO-(ii), again suggesting that NiO-(i) has a higher catalytically-relevant surface area. This higher surface area for NiO-(i) is captured in the BET measurements, but is not evident from the ECSA measurements, suggesting that the BET area is a better descriptor of the catalytically-relevant surface area for NiO.
The inaccuracy of the ECSA measurements for NiO-(i) and NiO-(ii) may result from inaccurate measurements of double layer capacitance. In particular, we propose that more-insulating oxides such as NiO and CoO may provide additional capacitance during the ECSA measurements due to their dielectric behavior, a phenomenon not expected for more-metallic oxides such as IrO2 and RuO2.38 This oxide capacitance for insulating oxides is likely small compared to the double layer capacitance, especially for high surface area systems. Because the small oxide capacitance and double layer capacitance are in series in the equivalent circuit, the overall capacitance measured from charging currents may more accurately reflect the smaller oxide capacitance as opposed to the larger double-layer capacitance.
A list of reported electrical conductivities for several of the oxides in this study is shown in Table S2.† We caution that the conductivities in the table were compiled from reports that use various sample types and do not necessarily reflect the actual conductivities of the materials under study here, but they still provide a qualitative guide that may be useful in establishing trends. For instance, metallic-like oxides with high conductivity such as the rutile oxides IrO2 and RuO2 and the perovskite oxides LaNiO3 and LaCoO3 all show similar BET SA and ECSA measurements. However, most of the other oxide particle studied show lower conductivities attributed to insulators and semiconductors. Most of these low-conductivity systems show similar ECSA < 1 m2 g−1 regardless of their BET surface area, suggesting that perhaps the capacitance measured for these systems is influenced or dominated by the oxide capacitance.
Note that there are also several other factors that may be contributing to inaccuracy in the double layer capacitance determinations. In particular, pseudocapacitance due to surface coordination of ions and ion intercalation, chemical capacitance due to the population of trap states, and capacitance from any residual charge-transfer processes in the putative non-faradaic region may all also influence the measured capacitance, and therefore the estimated ECSA.
These overall observations highlight the differences between ECSA and BET surface area measurements. In general, BET is a more well-defined empirical measurement that, in most cases, leads to an accurate description of the total surface area. However, the BET SA can potentially overestimate the catalytically-active surface area, as active sites are a subset of the total surface sites. Thus, normalization of activity data by BET SA leads to a conservative estimate of specific activity. By comparison, ECSA could in principle provide a more accurate description of the catalytically-active surface area. However, due to the difficulties in determining ECSA highlighted above, it may underestimate or overestimate the catalytically-active area. Ultimately, it is unclear whether ECSA or BET is more appropriate for estimating the catalytically-active surface area and depends greatly on the particular sample. Therefore, a recommended practice is to report both ECSA and BET SA so that the full range of possible surface areas and specific activities can be considered.
Activity and stability measurements
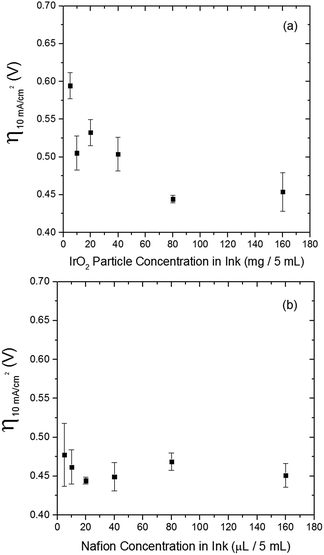
The electrocatalytic activity and short-term stability of each system was measured using a protocol we have previously described with the primary figure of merit being the overpotential necessary to achieve 10 mA cmgeo−2 (geometric area).15 The choice of the loading of particles and Nafion binder used in this study is based on a loading optimization study for a state-of-the-art catalyst, IrO2-(i). Fig. 2 shows the activity of IrO2-(i) for the OER as a function of increasing concentrations of particles and Nafion in the drop-cast inks. The operating overpotential ηj=10 mA cmgeo−2 for particle films decreases with increasing particle concentration in the deposition inks for concentrations <80 mg/5 mL ink, whereas the OER activity of IrO2-(i) drop-cast from solutions with concentrations of 80 mg/5 mL ink is identical to that at twice the loading of 160 mg/5 mL ink. The Nafion concentration of the deposition solution does not appear to appreciably influence the activity of the drop-casted IrO2-(i). Based on these measurements, an optimal particle concentration of 80 mg mL−1 ink and Nafion concentration of 40 μL Nafion/5 mL ink were identified for IrO2, which corresponds to a catalyst loading of ∼0.8 mg cm−2 in a ∼0.2 μm thick Nafion film. This loading was then used for each catalyst film for consistency in the comparative activity measurements.Representative RDEVs at 1600 rpm and 2 h stability measurements for each catalyst investigated are shown in Fig. S14,† and their relevant activity and stability parameters are summarized in Table 2. Tafel plots for each system were constructed from the steady-state chronoamperometric and chronopotentiometric data at 1600 rpm, and representative curves for each catalyst are shown in Fig. S15–S21,† and the linear region of the Tafel plots for each catalyst are summarized in Fig. 3. Tafel slopes were determined from the curves in Fig. 3 and are also shown in Table 2. Although Tafel slopes are related to catalytic mechanism and materials with different Tafel slopes often operate with different mechanisms or rate-determining steps, they can be difficult to interpret for multi-electron reactions involving many possible intermediates with different rates of formation that may change with applied potential, such as the OER.11,51–53 Tafel slopes here are provided for comparison, but in-depth mechanistic analysis is beyond the scope and intent of this manuscript.
| Oxide | η j=10 mA cmgeo−2,t=0 (V) | η j=10 mA cmgeo−2,t=2 h (V) | j s,η=0.35 V,geo (mA cmgeo−2) | j s,η=0.35 V,BET (mA cmBET−2) | j s,η=0.35 V,ECSA (mA cmECSA−2) | Tafel slope (mV dec−1) |
|---|---|---|---|---|---|---|
| a The specific current densities and Tafel slopes of Fe2O3 and NiFe2O4 were not obtained, as they degraded during steady-state measurements. b From ref. 16. | ||||||
| CoO | 0.45 ± 0.01 | 0.58 ± 0.01 | 0.25 ± 0.09 | 0.003 ± 0.001 | 0.120 ± 0.043 | 39.8 |
| Co3O4 | 0.50 ± 0.01 | 0.52 ± 0.03 | 0.06 ± 0.02 | 0.038 ± 0.001 | 0.039 ± 0.013 | 60.9 |
| NiO-(i) | 0.43 ± 0.01 | 0.42 ± 0.03 | 1.77 ± 0.89 | 0.002 ± 0.001 | 0.331 ± 0.166 | 62.4 |
| NiCoO2 | 0.39 ± 0.02 | 0.44 ± 0.05 | 2.25 ± 1.08 | 0.028 ± 0.010 | 0.565 ± 0.271 | 52.5 |
| NiFe2O4 | 0.51 ± 0.01 | 1.27 ± 0.01 | —a | —a | —a | —a |
| Fe2O3 | 1.24 ± 0.04 | 1.28 ± 0.01 | —a | —a | —a | —a |
| IrO2-(i) | 0.38 ± 0.01 | 0.43 ± 0.01 | 2.23 ± 1.15 | 0.007 ± 0.003 | 0.005 ± 0.003 | 47.7 |
| RuO2 | 0.38 ± 0.02 | 0.43 ± 0.02 | 3.63 ± 1.50 | 0.039 ± 0.020 | 0.078 ± 0.032 | 64.6 |
| LiCoO2 | 0.47 ± 0.01 | 0.50 ± 0.02 | 0.12 ± 0.08 | 0.053 ± 0.030 | 0.078 ± 0.052 | 44.5 |
| LiNiO2 | 0.41 ± 0.01 | 0.39 ± 0.01 | 1.09 ± 0.10 | 0.088 ± 0.008 | 0.318 ± 0.029 | 42.7 |
| LaCoO3 | 0.55 ± 0.02 | 0.69 ± 0.09 | 0.11 ± 0.05 | 0.011 ± 0.004 | 0.021 ± 0.009 | 64.7 |
| LaNiO3 | 0.45 ± 0.02 | 0.55 ± 0.02 | 0.70 ± 0.31 | 0.022 ± 0.001 | 0.016 ± 0.007 | 66.6 |
| Mn2O3 | 0.53 ± 0.04 | 0.52 ± 0.01 | 0.16 ± 0.03 | 0.006 ± 0.001 | 0.016 ± 0.003 | 69.1 |
| MnO | 0.51 ± 0.04 | 0.49 ± 0.01 | 0.22 ± 0.18 | 0.018 ± 0.010 | 0.031 ± 0.025 | 88.3 |
| MnO2 | 0.50 ± 0.03 | 0.50 ± 0.05 | 0.41 ± 0.35 | 0.036 ± 0.030 | 0.100 ± 0.086 | 84.7 |
| Mn3O4 | 0.43 ± 0.02 | 0.42 ± 0.01 | 0.72 ± 0.49 | 0.087 ± 0.060 | 0.180 ± 0.122 | 60.9 |
| Glassy carbon | 1.21 ± 0.04b | 1.25 ± 0.01b | N/A | N/A | N/A | N/A |
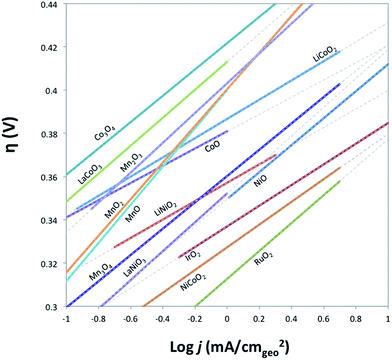 | ||
| Fig. 3 Comparison of Tafel plots of various crystalline metal oxides in their linear regions. Solid lines indicate where the linear region of Tafel curve is obtained from, and the dashed lines show the extensions of the linear region. Raw Tafel curves are shown in Fig. S15–S21.† The iridium oxide and nickel oxide shown in this figure are IrO2-(i) and NiO-(i), respectively. Tafel plots for Fe2O3 and NiFe2O4 oxides are not available as the oxides degrade on the timescale of the steady-state measurements used to generate the plots. | ||
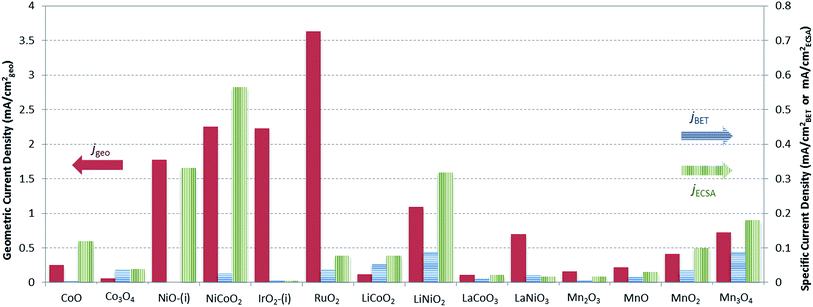
A graphical representation of the activity, stability, and surface area of each catalyst investigated is shown in Fig. 4. The advantage of this comparative plot is that it facilitates the comparison of activity, 2 h stability, and surface area for every catalyst investigated, and allows for the identification of trends in activity. As we have previously observed,15,16 the majority of the oxide materials examined here show similar activities, achieving 10 mA cmgeo−2 current densities with overpotentials of η = 0.35–0.60 V. It is also noted that this is somewhat expected since we purposely chose to investigate systems known to be electrocatalytically active for OER. In addition, to facilitate the comparison of the specific activity of each system, the geometric activity, specific activity per ECSA, and specific activity per BET SA are shown in Fig. 5.
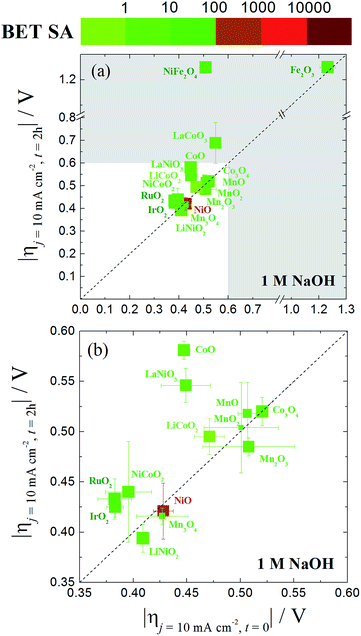 | ||
| Fig. 4 (a) A comparative plot of catalyst activity, stability and BET surface area for nanoparticle OER electrocatalysts in 1 M NaOH. The x-axis is the overpotential required to achieve 10 mA cmgeo−2 per geometric area at time = 0. The y-axis is the overpotential required to achieve 10 mA cmgeo−2 per geometric area at time = 2 h. The dashed diagonal line indicates where the stable catalysts would lie on. The color of the each data point represents the BET surface area of the oxide catalyst with a bin size of one order of magnitude. Here the BET surface area is used because it provides an upper bound for the catalytically-active surface area. The size of each data point is inversely proportional to the standard deviation in the BET measurement reported in Table 1. The region of interest for benchmarking is the unshaded white region of the plot where the overpotential required to achieve 10 mA cmgeo−2 per geometric area at time = 0 and t = 2 h is less than 0.6 V. An inset of this area is expanded in (b). The iridium oxide and nickel oxide shown in this figure are IrO2-(i) and NiO-(i), respectively. | ||
Although many of the electrocatalysts investigated here have approximately similar activity, it is still possible to identify a few systems with promising comparative electrocatalytic performance. Of the catalysts investigated, IrO2-(i), RuO2, and NiCoO2 showed the highest activity, achieving 10 mA cmgeo−2 current densities at overpotentials of η = 0.38–0.39 V. Of the three systems, note that NiCoO2 and RuO2 have significantly lower BET SA and ECSA than IrO2-(i) and therefore they show larger comparative specific current densities as shown in Fig. 5. Other particularly active catalyst include LiNiO2, Mn3O4, and NiO, each showing promising activity and stability with operating overpotentials of ηt=0 ∼ ηt=2 h ∼ 0.42 V. Note that LiNiO2 and Mn3O4 operate with higher specific current densities per BET SA of 90 μA cmBET−2 at 0.35 V overpotential, compared to all other systems, suggesting that their inherent catalytic activities may be higher than the others.
Conclusions
The OER performance of 16 different crystalline metal oxides, all deposited with the same method and loading, were evaluated and compared under identical alkaline conditions relevant to an integrated artificial photosynthetic device under 1 sun illumination. The surface areas of the particulate materials were determined with both BET and ECSA methods, but there was not a strict correlation between the resulting surface areas measured with both methods. BET surface area measurements like provide an upper bound to the active surface area, providing a more conservative estimate of specific activity. However, it is unclear whether BET or ECSA is a more accurate estimate of the true active sites of the system. Because specific activity is often used to differentiate between catalyst activity of particulate systems, and because it is unclear whether BET or ECSA is a more accurate measurement for catalytically-active surface area, we suggest that both be reported for particulate electrocatalysts. Using both ECSA and BET surface areas provides a limiting range of specific activities that allows researchers to better compare the performance of particulate OER materials.The activity and stability of each system were evaluated using a standard benchmarking protocol,15 and the activity, stability, and surface area of the catalysts were summarized in a graphical representation to facilitate the comparison of catalyst performance. In particular, all the OER materials investigated operate with similar activity, achieving 10 mA cmgeo−2 current densities with overpotentials of η = 0.35–0.60 V. Including this report and some of our previous studies,15,16,54 we have now shown that over 50 of the most well-known and/or active systems for the OER operate with similar activity when measured under identical conditions in alkaline solution.
Note that while all of the materials in this study operated within a narrow activity range owing to our choice of OER electrocatalysts known to be comparatively efficient, some materials did show better OER performance than their peers. In particular, NiCoO2 showed similar activity to that of RuO2 and IrO2 with an operating overpotential of η = 0.39 V. Other systems of interest include Mn3O4 and LiNiO2. While these systems operated with slightly higher overpotentials than RuO2, IrO2, and NiCoO2 at 10 mA cmgeo−2 per geometric area, they achieved large current densities per BET SA of js = 0.09 mA cmBET−2 at η = 0.35 V, nearly 2–3 times that of any other catalyst investigated. This suggests that Mn3O4 and LiNiO2 are promising candidates for further studies to increase their surface area, and therefore their OER activity per geometric area, either by decreasing the catalyst particle size or through the formation of porous, nanostructured materials.
Acknowledgements
This material is based upon work performed by the Joint Center for Artificial Photosynthesis, a DOE Energy Innovation Hub, supported through the Office of Science of the U.S. Department of Energy under Award Number DE-SC0004993. We would like to acknowledge much assistance in BET measurements by Kurt M. Van Allsburg.Notes and references
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed
.
- M. Graetzel, Acc. Chem. Res., 1981, 14, 376–384 CrossRef CAS
.
- A. J. Bard and M. A. Fox, Acc. Chem. Res., 1995, 28, 141–145 CrossRef CAS
.
- O. Khaselev and J. A. Turner, Science, 1998, 280, 425–427 CrossRef CAS PubMed
.
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS PubMed
.
- P. V. Kamat, J. Phys. Chem. C, 2007, 111, 2834–2860 CAS
.
- G. W. Crabtree and M. S. Dresselhaus, MRS Bull., 2008, 33, 421–428 CrossRef CAS
.
- R. van de Krol, Y. Liang and J. Schoonman, J. Mater. Chem., 2008, 18, 2311–2320 RSC
.
- H. B. Gray, Nat. Chem., 2009, 1, 7 CrossRef CAS PubMed
.
- T. R. Cook, D. K. Dogutan, S. Y. Reece, Y. Surendranath, T. S. Teets and D. G. Nocera, Chem. Rev., 2010, 110, 6474–6502 CrossRef CAS PubMed
.
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS PubMed
.
- Y. Tachibana, L. Vayssieres and J. R. Durrant, Nat. Photonics, 2012, 6, 511–518 CrossRef CAS
.
- F. E. Osterloh, Chem. Soc. Rev., 2013, 42, 2294–2320 RSC
.
- Z. Li, W. Luo, M. Zhang, J. Feng and Z. Zou, Energy Environ. Sci., 2013, 6, 347–370 CAS
.
- C. C. L. McCrory, S. Jung, I. M. Ferrer, S. M. Chatman, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2015, 137, 4347–4357 CrossRef CAS PubMed
.
- C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef CAS PubMed
.
- M. F. Weber and M. J. Dignam, J. Electrochem. Soc., 1984, 131, 1258–1265 CrossRef CAS
.
- Y. Gorlin and T. F. Jaramillo, J. Am. Chem. Soc., 2010, 132, 13612–13614 CrossRef CAS PubMed
.
- M. T. M. Koper, J. Electroanal. Chem., 2011, 660, 254–260 CrossRef CAS
.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS
.
- A. J. Esswein, M. J. McMurdo, P. N. Ross, A. T. Bell and T. D. Tilley, J. Phys. Chem. C, 2009, 113, 15068–15072 CAS
.
- E. A. Paoli, F. Masini, R. Frydendal, D. Deiana, C. Schlaup, M. Malizia, T. W. Hansen, S. Horch, I. E. L. Stephens and I. Chorkendorff, Chem. Sci., 2015, 6, 190–196 RSC
.
-
C. M. Sanchez-Sanchez, J. Solla-Gullon and V. Montiel, in Electrochemistry: Volume 11-Nanosystems Electrochemistry, The Royal Society of Chemistry, 2013, vol. 11, pp. 34–70 Search PubMed
.
-
J. McKone and N. Lewis, in Photoelectrochemical Water Splitting: Materials, Processes and Architectures, The Royal Society of Chemistry, 2013, pp. 52–82, 10.1039/9781849737739-00052
.
- T. Reier, M. Oezaslan and P. Strasser, ACS Catal., 2012, 2, 1765–1772 CrossRef CAS
.
- F. Gloaguen, F. Andolfatto, R. Durand and P. Ozil, J. Appl. Electrochem., 1994, 24, 863–869 CrossRef CAS
.
- U. A. Paulus, T. J. Schmidt, H. A. Gasteiger and R. J. Behm, J. Electroanal. Chem., 2001, 495, 134–145 CrossRef CAS
.
- T. J. Schmidt, H. A. Gasteiger, G. D. Stäb, P. M. Urban, D. M. Kolb and R. J. Behm, J. Electrochem. Soc., 1998, 145, 2354–2358 CrossRef CAS
.
- J. Suntivich, H. A. Gasteiger, N. Yabuuchi and Y. Shao-Horn, J. Electrochem. Soc., 2010, 157, B1263–B1268 CrossRef CAS
.
- A. Grimaud, K. J. May, C. E. Carlton, Y.-L. Lee, M. Risch, W. T. Hong, J. Zhou and Y. Shao-Horn, Nat. Commun., 2013, 4, 2439 Search PubMed
.
- X. Lu and C. Zhao, J. Mater. Chem. A, 2013, 1, 12053–12059 CAS
.
- J. O. M. Bockris and T. Otagawa, J. Electrochem. Soc., 1984, 131, 290–302 CrossRef CAS
.
- B. Seyfi, M. Baghalha and H. Kazemian, Chem. Eng. J., 2009, 148, 306–311 CrossRef CAS
.
- J. Suntivich, H. A. Gasteiger, N. Yabuuchi, H. Nakanishi, J. B. Goodenough and Y. Shao-Horn, Nat. Chem., 2011, 3, 546–550 CrossRef CAS PubMed
.
- E. Liaudet, F. Battaglini and E. J. Calvo, J. Electroanal. Chem., 1990, 293, 55–68 CrossRef CAS
.
- J. M. Spurgeon, J. M. Velazquez and M. T. McDowell, Phys. Chem. Chem. Phys., 2014, 16, 3623–3631 RSC
.
- J. D. Benck, B. A. Pinaud, Y. Gorlin and T. F. Jaramillo, PLoS One, 2014, 9, e107942 Search PubMed
.
- Y. Matsumoto and E. Sato, Mater. Chem. Phys., 1986, 14, 397–426 CrossRef CAS
.
- S. Trasatti, Electrochim. Acta, 1984, 29, 1503–1512 CrossRef CAS
.
- G. P. Gardner, Y. B. Go, D. M. Robinson, P. F. Smith, J. Hadermann, A. Abakumov, M. Greenblatt and G. C. Dismukes, Angew. Chem., Int. Ed., 2012, 51, 1616–1619 CrossRef CAS PubMed
.
- S. W. Lee, C. Carlton, M. Risch, Y. Surendranath, S. Chen, S. Furutsuki, A. Yamada, D. G. Nocera and Y. Shao-Horn, J. Am. Chem. Soc., 2012, 134, 16959–16962 CrossRef CAS PubMed
.
- N. Li, J. Li, L. Yang, H. Gao, S. Li and B. Lin, Electrochim. Acta, 2001, 46, 717–722 CrossRef
.
- T. Maiyalagan, K. R. Chemelewski and A. Manthiram, ACS Catal., 2014, 4, 421–425 CrossRef CAS
.
- A. Costa, M. E. M. Jorge, M. D. Carvalho, A. Gomes and M. I. da Silva Pereira, J. Solid State Electrochem., 2013, 17, 2311–2318 CrossRef CAS
.
- E. M. Garcia, H. A. Tarôco, T. Matencio, R. Z. Domingues and J. A. F. dos Santos, Int. J. Hydrogen Energy, 2012, 37, 6400–6406 CrossRef CAS
.
- R. N. Singh and B. Lal, Int. J. Hydrogen Energy, 2002, 27, 45–55 CrossRef CAS
.
- J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, Science, 2011, 334, 1383–1385 CrossRef CAS PubMed
.
- A. Vojvodic and J. K. Nørskov, Science, 2011, 334, 1355–1356 CrossRef CAS PubMed
.
- Y. Meng, W. Song, H. Huang, Z. Ren, S.-Y. Chen and S. L. Suib, J. Am. Chem. Soc., 2014, 136, 11452–11464 CrossRef CAS PubMed
.
- H.-Y. Su, Y. Gorlin, I. C. Man, F. Calle-Vallejo, J. K. Norskov, T. F. Jaramillo and J. Rossmeisl, Phys. Chem. Chem. Phys., 2012, 14, 14010–14022 RSC
.
-
A. J. Bard and L. R. Faulkner, Electrochemical Methods, Wiley, New York, 2nd edn, 2001 Search PubMed
.
- J. O. M. Bockris, J. Chem. Phys., 1956, 24, 817–827 CrossRef CAS
.
- J. O. Bockris and T. Otagawa, J. Phys. Chem., 1983, 87, 2960–2971 CrossRef CAS
.
- S. Suseno, C. C. L. McCrory, R. Tran, S. Gul, J. Yano and T. Agapie, Chem.–Eur. J., 2015, 21, 13420–13430 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Powder diffraction patterns; SEM images of drop-casted particles; electrical conductivity of metal oxides; activity and stability of metal oxides; Tafel plots; comparisons of OER activity for particulate films and other deposited films. See DOI: 10.1039/c5ta07586f |
| This journal is © The Royal Society of Chemistry 2016 |