Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Anionic and cationic Hofmeister effects are non-additive for guanidinium salts†
V.
Balos
,
M.
Bonn
 and
J.
Hunger
and
J.
Hunger
 *
*
Max Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: hunger@mpip-mainz.mpg.de
First published on 24th March 2017
Abstract
To understand specific ion effects on a molecular level we explore the effect of salts on the rotational mobility of a model amide using dielectric spectroscopy. Based on our previous studies on the effect of strong denaturing anions or cations, here we study the additivity of the anionic and cationic effect. Using salts consisting of denaturing spherical anions and spherical cations we find such salts to affect the amide according to what one expects based on the additive activity of the individual ions. The guanidinium (Gdm+) cation appears to be a notable exception, as our results suggest that GdmI (and accordingly GdmSCN) is less efficient in hindering the rotation of the amide than KI or GdmCl.
Understanding the fundamentals of specific ion effect on the stability of proteins is a longstanding enigma in biophysical chemistry.1–3 The first systematic study on the effect of ions on biomolecules dates back to 1888, when Hofmeister ordered different salts according to their efficiency to stabilize or denature proteins.4 From these experiments it was concluded that salts containing cations with a high surface charge density and/or anions with a low surface charge density tend to destabilize proteins in solution.5,6 Experimentally several other macroscopic properties, e.g. the stability of colloids in solution,7 the surface propensity of ions8 and the surface potential of charged surfaces in contact with a salt solution,9 have been shown to follow trends according to the Hofmeister series. This intriguing observation has inspired many physico-chemical studies to explore the molecular-level origins of these specific ion-effects,10–15 since specific ion effects are commonly used in biotechnological and pharmaceutical applications to reversibly un-fold and fold proteins.16 However, despite the seminal work of Hofmeister describing the effect of salts, the overall effect is often separated into individual contributions from the anion and cation, as anionic and cationic Hofmeisters series, though it has remained unexplored whether specific ion effects can be attributed to the properties to individual ions or are characteristic to a salt, i.e. an anion–cation pair.
In recent years increasing evidence has emerged that specific ion effects on biomolecules originate from direct interaction between ions and proteins.10–12,17,18 The most prominent interaction site for binding of ions to proteins is the amide backbone, the main structural motif common to all proteins. Various – predominantly spectroscopic studies – have shown that interaction of ions with amide groups follow the Hofmeister series13,19–21 and it has thus been concluded that ion–amide interaction explains part of the observed destabilization of proteins. We have recently shown that the rotational mobility of a model amide, N-methylacetamide (NMA) is a very sensitive reporter of the interaction of ions with amide groups.19–21 Importantly, the rotational mobility can probe the interaction of the amide with both anions and cations – as opposed to other techniques that probe either cationic or anionic interaction sites.21 Consequently, using the sensitivity to both ions allows us to address the question if the interaction of the anion and the cation with NMA is additive. In the present study we explore the effect of salts, for which both the anion and the cation tend to denature proteins, on the rotational mobility of NMA. Comparison to our earlier results focusing on either the cationic or anionic effects (by choosing a non- or weakly interacting counter-ion) allows determining whether Hofmeister effects are specific ion effects or specific salt effects.
To investigate additivity of anionic and cationic specific ion effects, we use aqueous mixtures with a constant concentration of NMA (2 mol L−1) with an increasing concentration of salt, csalt = 0 to 2 mol L−1. Here we chose a series of salts that consist of ions with both anion and cation reducing the rotational mobility of NMA: the monovalent salts NaBr, NaI, bivalent MgI2 together with two guanidinium (Gdm+) salts GdmI and GdmSCN and compare these to our earlier results where we used the weakly interacting K+ and Cl− as counter-ions.19–21
To quantify the interaction of the salts with NMA we use dielectric relaxation spectroscopy (DRS) at frequencies ranging from 0.8 to 1600 GHz21 (for experimental details see ESI†). DRS probes the polarization of a sample as a response to an oscillating electric field with field frequency ν. At the frequencies of this study the polarization of liquid samples predominantly stems from the rotation of dipolar molecules in the externally applied field. The polarization is measured in terms of the complex permittivity ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) (ν) = ε′(ν) − iε′′(ν), with the real part ε′ being the dielectric permittivity and the imaginary part ε′′ the dielectric loss. In Fig. 1a we show the dielectric spectra (corrected for the conductivity of the solutions) for a series of ternary solutions consisting of water + NMA + GdmI. Spectra for other salts are shown in the ESI,† Fig. S1. All spectra exhibit a broad dispersion in ε′ and a corresponding peak in ε′′ at ∼10 GHz, which is due to the rotation of both dipolar NMA and water molecules. With increasing salt concentration the static permittivity of the samples (the limiting value of ε′ at low frequencies) decreases and simultaneously the amplitude of the dielectric loss peak (the overall dielectric strength) decreases: addition of salt leads to depolarization of the sample.
(ν) = ε′(ν) − iε′′(ν), with the real part ε′ being the dielectric permittivity and the imaginary part ε′′ the dielectric loss. In Fig. 1a we show the dielectric spectra (corrected for the conductivity of the solutions) for a series of ternary solutions consisting of water + NMA + GdmI. Spectra for other salts are shown in the ESI,† Fig. S1. All spectra exhibit a broad dispersion in ε′ and a corresponding peak in ε′′ at ∼10 GHz, which is due to the rotation of both dipolar NMA and water molecules. With increasing salt concentration the static permittivity of the samples (the limiting value of ε′ at low frequencies) decreases and simultaneously the amplitude of the dielectric loss peak (the overall dielectric strength) decreases: addition of salt leads to depolarization of the sample.
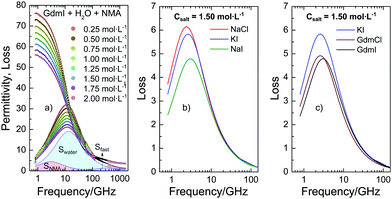 | ||
| Fig. 1 (a) Complex permittivity spectra of binary mixtures of water and NMA (2 mol L−1) with increasing GdmI concentration. The shaded areas correspond to contributions of bulk water, NMA, and fast water to the dielectric loss for csalt = 2 mol L−1 GdmI. The symbols correspond to the experimental data, while the solid lines to fits with eqn (1). The Ohmic loss (last term of eqn (1)) has been subtracted for visual clarity. (b and c) Dielectric loss due to NMA as obtained from fitting eqn (1) to the experimental spectra (imaginary part of the first term of eqn (1)) for samples containing 2 mol L−1 NMA and csalt = 1.5 mol L−1 salt for different salts. Data for NaCl, KI, and GdmCl were taken from ref. 19–21. | ||
As discussed in our earlier studies,19–21 this depolarization has three different molecular-level origins: (i) reduction of the molar concentration of water, (ii) formation of rigid solvation shells around ions, and (iii) kinetic depolarization (KD). While (i) can be readily accounted for by using the reduced water concentration in our analysis and (ii) has only significant contributions for Na+ and Mg2+ ions (see below and details of the analysis in the ESI†), KD (iii) is relevant to all samples and dominates the observed depolarization for the present samples. KD results from the coupling between the translation of an ion with the rotation of a dipole in the external electric field. According to the first description of KD by Hubbard and Onsager,22 the magnitude of the depolarization scales with the medium's conductivity (ionic mobility) and the dipolar relaxation time. More recent studies on KD have indicated that at high concentrations of salt the magnitude of KD may deviate from this simple scaling due to screening of the ionic charges.23 In addition to these purely electrostatic considerations for kinetic depolarization, we have recently demonstrated that for aqueous solutions of NMA the depolarization is also ion-specific:19–21 The reduction of the static permittivity not only depends on the concentration of the salt and the mobility of the ions (conductivity) but also depends on the chemical identity of the ions: in line with the Hofmeister series, ions with an increasing protein denaturation tendency also increasingly depolarize aqueous NMA solutions. This ion specificity can be explained from the increasing proximity of these ions to NMA, as KD of NMA results in a larger depolarization as compared to KD of water.19
To explore whether these specific effects of anions and cations on the depolarization – and thus the interaction between anions and cations with NMA – are additive, we quantify the depolarization using a dielectric relaxation model to describe the experimental spectra. In-line with our previous studies,19–21 we fit a combination of three relaxation modes to the experimental spectra. The rotational diffusion of NMA centred at ∼4 GHz is modelled with a Debye relaxation,24 the orientational relaxation of the hydrogen-bonded water network at ∼20 GHz is modelled with a symmetrically broadened (as compared to a Debye relaxation) Cole–Cole relaxation,25 and the small amplitude, fast relaxation mode at ∼200 GHz attributed to a small angular motion of water26 is described with a Debye type relaxation mode:
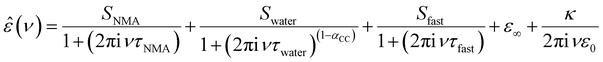 | (1) |
In order to disentangle the closely overlapping relaxations due to NMA (∼4 GHz) and water (∼20 GHz), we reduce the number of parameters in fitting eqn (1) to the spectra. As water is the prevailing molecular species in all samples, we fix Swater to what would be expected for an ideal solution (accounting for the reduced water concentration in the samples upon addition of salt, the KD for random distribution of the ions in the solution, and full hydration of Na+ and Mg2+; for details see ESI†).27,28 This constrained model describes the experimental spectra very well (solid lines in Fig. 1a and Fig. S1, ESI†) and the contributions of the NMA relaxation, the water relaxation, and the fast water relaxation to the dielectric loss are indicated as shaded areas in Fig. 1a.
Both, the parameters describing the fast water relaxation and the relaxation time of water vary with salt concentration as reported previously: τwater decreases with increasing salt concentration (Fig. S5a, ESI†) – a common observation for aqueous electrolytes,19–21,25 while the relaxation time of the fast water mode is largely unaffected by addition of salt (Fig. S5c, ESI†). The amplitude of the fast water mode somewhat increases with increasing csalt as seen in Fig. S4c (ESI†). This increase in Sfast is a common observation upon addition of salt and can be related to an increasing angular mobility of water in the hydration shells of ions.19–21 More relevant to the ion-specific effects discussed above are the parameters of the NMA relaxation (first term of eqn (1)). As can be seen from Fig. 1b and c, the contribution of NMA to the dielectric loss (the imaginary part of the first term of eqn (1)) strongly depends on the nature of the added salt: both the amplitude and the position vary with varying salt. The somewhat different center positions (i.e. values of τNMA) of the peaks have been shown to correlate with the solution viscosity,19 evidencing that the rotational relaxation of NMA is consistent with diffusive rotation of NMA. Additionally, we observe a very pronounced variation of the relaxation amplitude (peak intensity) of the NMA relaxation (Fig. 1b and c) when changing the chemical identity of the salt. Comparing this relaxation strength for variation of an individual cation/anion with keeping the counterion (anion/cation) the same, the observed variation follows the Hofmeister series: for instance the NMA relaxation amplitude is lower for NaI compared to NaCl or KI (Fig. 1b). Hence, ions with increasing protein denaturation tendency increasingly reduce the relaxation strength. In other words: our results indicate that denaturing salts reduce the rotational mobility of NMA. Interestingly, the relaxation amplitude for GdmCl and GdmI are similar (Fig. 1c), though I− tends to destabilize proteins in contrast to Cl−, which gives a first indication of non-additivity of the individual ion-properties.
To quantify the reduction of the rotational mobility due to the different salts, we relate the relaxation strength of NMA (SNMA) to the concentration of free NMA – the molar concentration of NMA that is not affected by the salt, cNMA,free. Since for diffusive rotation as the underlying molecular mechanism of the observed relaxation, the relaxation amplitude is proportional to the molar concentration of the dipolar species and their squared effective electrical dipole moment (see eqn (S2), ESI†), we extract cNMA,free by assuming the effective dipole moment of NMA to be constant.‡ In turn, (2 mol L−1–cNMA,free), is a measure for the effective concentration of NMA molecules that are rotationally hindered. The thus obtained values of (2 mol L−1–cNMA,free), are displayed in Fig. 2 for the investigated salts. In general, for all studied salts the number of affected NMA molecules is increasing with increasing salt concentration, with MgI2 showing the largest effect. The trends follow the Hofmeister series and – in line with our previous study21 – variation of the cation has a more pronounced effect on cNMA,free than substitution of the anion.
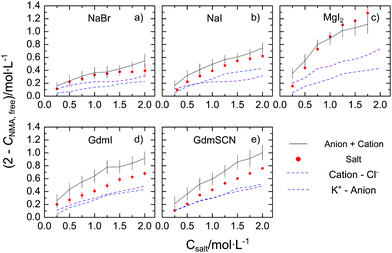 | ||
| Fig. 2 Concentration of rotationally-affected NMA molecules (2 mol L−1–cNMA,free) with increasing salt concentration for (a) NaBr, (b) NaI, (c) MgI2, (d) GdmI and (e) GdmSCN. The red solid data points correspond to the values for the salts (see text) and error bars correspond to standard deviation within six independent measurements. The grey solid lines show the sum of the contribution from the cation (purple dashed line) and the anions (blue dashed line), which were taken from our earlier results using the corresponding Cl− and K+ salts of the corresponding ions.19–21 The errors for this estimation, shown as vertical bars, are based on additive error propagation. | ||
To explore whether the effects of the studied salts on cNMA,free can be explained by the additive effect of the anion and of the cation, we compare the present values of (2 mol L−1–cNMA,free) to the value that would be expected from the cation and the anion individually. The effect of the ‘individual’ ions we take from our earlier studies on the K+ salt and the Cl− salts, as cNMA,free has remained virtually constant at cNMA,free = 2 mol L−1 upon addition of KCl.19,20 As can be seen from Fig. 2a–c the values of (2 mol L−1–cNMA,free) observed for NaBr, NaI, and MgI2 agree within the experimental uncertainty well with the sum of the affected NMA concentration of the corresponding K+ and Cl− salt: within the error bars the red symbols and the black solid lines in Fig. 2a–c coincide. Hence, our results suggest that the observed reduction of the rotational mobility of NMA is the average, additive effect of both the anion and the cation. This notion however does not hold for the salts containing the Gdm+ cation: in Fig. 2d and e we show the same comparison for GdmSCN/GdmI, where the observed reduction of the rotational mobility of NMA is lower than the sum of GdmCl and KSCN/KI, respectively. Hence, our results provide evidence for non-additivity for guanidinium salts.
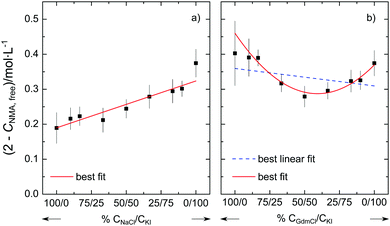
To provide further evidence for the non-additivity for Gdm+ salts, we perform two additional series of experiments at csalt = 1.5 mol L−1. In one series we vary the molar ratio of the salt from neat NaCl to neat KI. In line with the additivity of the individual effects of Na+ and I− described above, we find that (2 mol L−1–cNMA,free) varies linearly with the salt composition (Fig. 3a). Conversely, when varying the molar ratio of the salt from neat GdmCl to neat KI, the variation of (2 mol L−1–cNMA,free) cannot be described well by a linear relation (dashed blue line in Fig. 3b). Rather, our results indicate that the number of affected NMA molecules shows a minimum for the equimolar GdmCl/KI mixture: In the presence of 0.75 mol L−1 GdmCl and 0.75 mol L−1 KI the number of NMA molecules with reduced rotational mobility is lower than for solutions containing 1.5 mol L−1 GdmCl or 1.5 mol L−1 KI. This non-linear behavior for GdmCl/KI mixtures thus further supports the notion that the effect of GdmI cannot be described by the independent interaction of the Gdm+ cation and the I− anion with NMA.
Thus our results suggest that the additivity of the ion-amide interaction depends on the identity of the ions. For the simple spherical cations K+, Na+, and Mg2+ and the corresponding spherical halide anions Cl−, Br−, and I− our results suggest that their ability to reduce the rotational mobility of NMA can be explained from the sum of the individual interaction of the anion and the cation with NMA. Hence, the cation and the anion interact (on average) independently with the amide and – despite the long-range electrostatic interactions – there is no need to invoke any cooperativity. In contrast, our experiments provide evidence that such additivity does not hold for salts containing the guanidinium cation. For the guanidinium salts GdmI and GdmSCN we find less NMA molecules to be affected in their rotational mobility than what would be expected based on the individual effect of Gdm+ and the anions I− or SCN−. It may be significant that the minimum in Fig. 3b is located close to the equimolar composition, which points towards a competitive interaction for Gdm− and I−.
In general there are two plausible explanations for such competitive interaction: (i) the Gdm+ cation binds preferentially to the I− or SCN− anion and thus the cation–anion interaction is competing with the ion–NMA interaction. However, such a scenario appears unlikely, since the tendency of Gdm+ to associate with anions in solution (i.e. to form ion-pairs) is rather low and comparable to the ion-pair association of the corresponding sodium salts.29,30 Additionally, the dielectric spectra of the aqueous solutions of GdmI and GdmSCN (see ESI,† Fig. S2) do not exhibit any indications for contributions due to long-lived ion-pairs. As ion-pairs can in principle be readily detected with DRS via a separate ion-pair relaxation due to their intrinsically large electrical dipole moment,31 the absence of a contribution due to long-lived ion-pairs renders scenario (i) rather unlikely. Alternatively, (ii) the origins of the competitive behavior may be a result of competitive interaction with NMA: if Gdm+ and I−/SCN− reduce the rotational mobility of NMA via association to the same binding site at NMA, a similar dependency of the affected NMA molecules as shown in Fig. 3b would be expected, as at the equimolar composition the anions and the cations compete with a limited number of NMA binding sites. This notion might in fact be crucial for the high denaturation efficiency of the Gdm+ cation, as in general the disruption of proteins by anions – i.e. binding to anionic binding sites – more effectively denatures proteins, as compared to spherical cations.18
Conclusions
In the present work we study for a range of salts the additivity of anionic and cationic interaction with the model amide NMA in aqueous solutions. We determine the reduction of the rotational mobility of NMA due to the presence of these salts via the rotational relaxation of NMA that contributes to the dielectric spectra of the samples. For the spherical, monovalent salts NaI, NaBr, and the bivalent MgI2, we find that the reduction of rotationally mobile NMA molecules is consistent with the additive effect of the individual anions and cations. Salts containing the strongly denaturing guanidinium cation deviate from additivity and we find that GdmI (and similarly GdmSCN) interacts to a lesser extent with NMA than the sum of the interaction of its individual ions (Gdm+ and I−). This non-additive behaviour is likely related to competitive interaction for the Gdm+ cation and the I− or SCN− anion. Overall, our results indicate that separating the Hofmeister series into separate series for anions and cation is largely justified, with the notable exception of guanidinium salts.Acknowledgements
We thank Heejae Kim and Natalia Martin Sabanés for fruitful discussions. This work was funded by the German Science foundation (Deutsche Forschungsgemeinschaft, HU1860/4). Open Access funding provided by the Max Planck Society.Notes and references
- P. Jungwirth and B. Winter, Annu. Rev. Phys. Chem., 2008, 59, 343–366 CrossRef CAS PubMed.
- P. Jungwirth and P. S. Cremer, Nat. Chem., 2014, 6, 261–263 CrossRef CAS PubMed.
- W. Kunz, Specific Ion Effects, World Scientific Publishing, Toh Tuck Link, Singapore, 2009 Search PubMed.
- F. Hofmeister, Arch. Exp. Pathol. Pharmakol., 1888, 24, 247–260 Search PubMed.
- K. D. Collins and M. W. Washabaugh, Q. Rev. Biophys., 1985, 18, 323–422 CrossRef CAS PubMed.
- W. Kunz, J. Henle and B. W. Ninham, Curr. Opin. Colloid Interface Sci., 2004, 9, 19–37 CrossRef CAS.
- A. Salis and B. W. Ninham, Chem. Soc. Rev., 2014, 43, 7358–7377 RSC.
- L. Piatkowski, Z. Zhang, E. H. G. Backus, H. J. Bakker and M. Bonn, Nat. Commun., 2014, 5, 4083 CAS.
- A. P. dos Santos, A. Diehl and Y. Levin, Langmuir, 2010, 26, 10778–10783 CrossRef CAS PubMed.
- E. P. O’Brien, R. I. Dima, B. Brooks and D. Thirumalai, J. Am. Chem. Soc., 2007, 129, 7346–7353 CrossRef PubMed.
- R. Godawat, S. N. Jamadagni and S. Garde, J. Phys. Chem. B, 2010, 114, 2246–2254 CrossRef CAS PubMed.
- J. Hladílková, J. Heyda, K. B. Rembert, H. I. Okur, Y. Kurra, W. R. Liu, C. Hilty, P. S. Cremer and P. Jungwirth, J. Phys. Chem. Lett., 2013, 4, 4069–4073 CrossRef PubMed.
- H. I. Okur, J. Kherb and P. S. Cremer, J. Am. Chem. Soc., 2013, 135, 5062–5067 CrossRef CAS PubMed.
- J. Paterová, K. B. Rembert, J. Heyda, Y. Kurra, H. I. Okur, W. R. Liu, C. Hilty, P. S. Cremer and P. Jungwirth, J. Phys. Chem. B, 2013, 117, 8150–8158 CrossRef PubMed.
- H. Meuzelaar, M. R. Panman and S. Woutersen, Angew. Chem., Int. Ed., 2015, 54, 15255–15259 CrossRef CAS PubMed.
- T. Svedberg, Nature, 1937, 139, 1051 CrossRef CAS.
- A. Kubíčková, T. Křížek, P. Coufal, E. Wernersson, J. Heyda and P. Jungwirth, J. Phys. Chem. Lett., 2011, 2, 1387–1389 CrossRef.
- Y. Zhang and P. S. Cremer, Annu. Rev. Phys. Chem., 2010, 61, 63–83 CrossRef CAS PubMed.
- V. Balos, M. Bonn and J. Hunger, Phys. Chem. Chem. Phys., 2015, 17, 28539–28543 RSC.
- V. Balos, M. Bonn and J. Hunger, Phys. Chem. Chem. Phys., 2016, 18, 1346–1347 RSC.
- V. Balos, H. Kim, M. Bonn and J. Hunger, Angew. Chem., Int. Ed., 2016, 55, 8125–8128 CrossRef CAS PubMed.
- J. B. Hubbard, L. Onsager, W. M. van Beek and M. Mandel, Proc. Natl. Acad. Sci. U. S. A., 1977, 74, 401–404 CrossRef CAS.
- M. Sega, S. Kantorovich and A. Arnold, Phys. Chem. Chem. Phys., 2015, 17, 130–133 RSC.
- U. Kaatze, H. Gerke and R. Pottel, J. Phys. Chem., 1986, 90, 5464–5469 CrossRef CAS.
- W. Wachter, W. Kunz, R. Buchner and G. Hefter, J. Phys. Chem. A, 2005, 109, 8675–8683 CrossRef CAS PubMed.
- T. Fukasawa, T. Sato, J. Watanabe, Y. Hama, W. Kunz and R. Buchner, Phys. Rev. Lett., 2005, 95, 197802 CrossRef PubMed.
- R. Buchner, G. T. Hefter and P. M. May, J. Phys. Chem. A, 1999, 103, 1–9 CrossRef CAS.
- R. Buchner, T. Chen and G. Hefter, J. Phys. Chem. B, 2004, 108, 2365–2375 CrossRef CAS.
- J. Hunger, S. Niedermayer, R. Buchner and G. Hefter, J. Phys. Chem. B, 2010, 114, 13617–13627 CrossRef CAS PubMed.
- J. Hunger, R. Neueder, R. Buchner and A. Apelblat, J. Phys. Chem. B, 2013, 117, 615–622 CrossRef CAS PubMed.
- R. Buchner, Pure Appl. Chem., 2008, 80, 1239–1252 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp00790f |
| ‡ Note that the used effective dipole moment values may contain medium effects (e.g. molecular polarizability) and dipolar correlations. Given the similar static permittivities and ranges of ionic strengths for each studied salt (except Mg2+ salts), screening effects and thus dipolar correlations are expected to be similar as only the nature of the cation is changed. |
| This journal is © the Owner Societies 2017 |