Thermodynamic and first-principles biomolecular simulations applied to synthetic biology: promoter and aptamer designs
Kristin V.
Presnell
a and
Hal S.
Alper
 *ab
*ab
aMcKetta Department of Chemical Engineering, The University of Texas at Austin, 200 E Dean Keeton St. Stop C0400, Austin, Texas 78712, USA. E-mail: halper@che.utexas.edu; Fax: +(512) 471 7060; Tel: +(512) 471 4417
bInstitute for Cellular and Molecular Biology, The University of Texas at Austin, 2500 Speedway Avenue, Austin, Texas 78712, USA
First published on 30th November 2017
Abstract
A major challenge in the field of metabolic engineering and synthetic biology is the design of DNA elements, most often promoters, that achieve precisely targeted levels of expression of a given protein. The most widely applied strategy for addressing this challenge includes making libraries of thousands of mutants, then screening and selecting each mutant in the hopes of finding a favorable change to the DNA of interest which yields the desired expression level. Even with rational approaches to the design of these mutants, this process is slow and labor-intensive and requires improvements in high throughput screening methods to improve discovery rates. Biomolecular models (designed from a combination of first-principles thermodynamics and empirical data) and solution of these models through simulation, bypass these approaches, enabling nucleotide and amino acid level resolution by carrying out screening processes in silico or allowing for a more rational method of design. This review examines recent advances in biomolecular simulations and methods of subsequent data analysis in their role of designing functional DNA, RNA, and protein elements. We provide an orienting introduction to design choices in biomolecular simulations then discuss major recent developments in simulation technology with a more intensive focus on promoter and aptamer design. We then conclude with both a forward-looking prospectus on the field as well as pitfalls and areas for further study.
Design, System, ApplicationThis review article highlights recent advances in the computational design of synthetic parts in cells. In particular, biological components (like promoters and aptamers) can be designed and optimized through simulations including molecular dynamic and Monte Carlo approaches. We highlight advances in this area as well as challenges with establishing force fields and samplings methods that are unique to biological, aqueous systems. |
1. Introduction
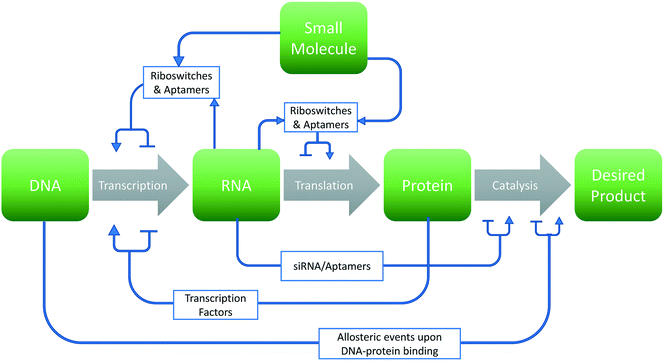
The past several decades have seen a growing interest in the harnessing of cellular potential for phenotypes such as chemical overproduction.1–3 Many of these advances are leveraged by the greener chemistry and more precise stereochemistry control afforded by cellular systems. However, optimizing biological systems involves many design choices at each level of the central dogma of biology (Fig. 1). This problem becomes even more daunting considering the sheer number of choices that exist within the 4n and 20n search-space found with canonical nucleic acids and amino acids, respectively. In this respect, synthetic biology has leveraged two options to traverse this space: high-throughput screening4–6 and model-based design.7–9 However, experimental approaches cannot exhaustively sample this space in any meaningful manner. Thus, computational approaches toward the de novo design and improvement of components and interactions in cells are gaining interest.The use of computational approaches and biomolecular modeling can address many experimental limitations. In this regard, in silico simulations of DNA mutations can replace the need to clone and screen large libraries in physicality. Likewise, the rational redesign of synthetic elements can theoretically preclude the need for trail-and-error methods. Indeed, such approaches can be applied at all levels (DNA, RNA, and protein) of the central dogma as well as to the interactions between these elements for biological design. These approaches can aid in a broad range of applications including synthetic biology,8 metabolic engineering,10 drug development,11 and biosensor technology.12
In this review, we provide a broad overview of applied computational design in biological systems with a focus on DNA and RNA systems. First, we provide an overview of the guiding principles and technologies available for biomolecular simulations to discuss the challenges and limitations. Next, we discuss progress and challenges for simulating DNA and RNA. Given the expanse of work in these fields, we focus this review primarily on examples encompassing DNA–protein interactions (with an emphasis on promoter design) and RNA folding/function simulations (with an emphasis on rational nucleic acid aptamer design). This review is meant to focus on advances within the past two to three years and readers are directed to many other reviews covering both older and alternative applications.13,14
2. An overview of biomolecular modeling
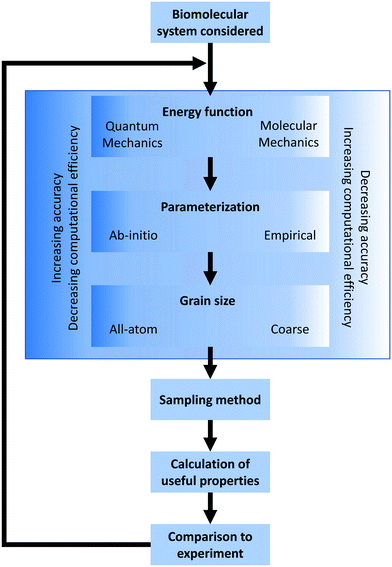
In the broadest sense, biomolecular modeling is the simulation of isolated or interacting biological components.15 In practice, this comprises solving systems of equations and parameters (that comprise the energy function) developed from combinations of theoretical understanding or empirical observations. This modeling effort results in simulations that can answer fundamental questions at the molecular level including estimations of kinetics/thermodynamics of protein folding, dynamics of proteins binding to DNA or RNA, or binding affinities between any of these three biomolecules and their substrates/ligands/targets. In this overview section, we briefly describe the formulation of energy equations and the methods of exploring or sampling the resultant potential energy surface, and the potential methods for analyzing results (Fig. 2). After this, we discuss approximations that can be made to reduce the necessary computational resources for these simulations as well as highlight popularly used simulation software. A variety of software options are highlighted in Table 1 with details of their operation and references.2.1 Defining the energy equation
Defining the energy function is a critical first step for simulations and ultimately determines the accuracy with which simulations can match in vitro and in vivo observations. These functions can either be based on molecular mechanics or quantum mechanics. For molecular mechanics, covalent bonds are treated as perfect harmonic springs with Coulomb's Law and Lennard-Jones potentials used to describe electrostatic and Van der Waals interactions, respectively.16,17 For quantum mechanical based calculations, electrons are considered independently of each atom and Schrödinger's equation is used to determine the electronic configuration energy of valence electrons. Further information for quantum mechanics-based simulations of biomolecules can be found in several recent reviews.18–20 Ultimately, the potential equation along with any necessary parameters (discussed below) define a multi-dimensional energy surface that is used to extract atomic positions, molecular confirmations, and associated thermodynamic energies for the given system.2.2 Parameterizing the energy equation
Energy equations for molecular mechanics simulations contain many different parameters such as spring constants, Lennard-Jones constants, and partial charges that seek to impart chemical specificity on a per-atom basis. Typically, these parameters are determined using empirical or semi-empirical methods.20 For example, constraints on equilibrium bond lengths and bond angles are generally determined empirically through X-ray crystallography data or NMR experiments.21 In this regard, an accurate crystal structure is crucial for accuracy of most biomolecular simulations. However, biological systems are highly responsive to environmental conditions. Thus, parameterization is conducted to reproduce a given set of experimental data (often the baseline condition) and thus can be very specific to these conditions (including temperature, pH, and salt concentration).22,23 Finally, it is possible to determine parameters for molecular mechanics simulations through ab initio quantum mechanical calculations.242.3 Exploring the potential energy surface
Biological systems (especially large macromolecules) have many potential atomic positions and conformations. Thus, the most popular application of a potential energy function is to determine the most probable individual configuration, corresponding to the lowest free energy.25 While this calculation amounts to a minimization of the potential energy surface, such a calculation is not trivial, especially due to multiple local energy minima. Therefore, a more comprehensive survey of the potential energy surface (in a way that is more independent of starting conformation) is necessary to identify a global minimum.26 To enable such searches, molecular dynamics (MD) and Monte Carlo (MC) simulations are two common approaches and we consider each in the sections below.In order to capture relevant atomic events such as bond vibration and rotation, these simulations require a minimum discrete time step on the order of femtoseconds. However, this timescale is not congruent with large-scale conformational changes such as protein or RNA folding or DNA looping that occur on the order of at least milliseconds.13,30 Therefore, it would be necessary to evaluate force equations for thousands of atoms 1012 times in order to carry out a single simulation of one of these events. Not surprisingly, reductions in computational demand (described later in this review) are an active area of research. Despite this drawback, MD simulations can measure time-dynamics of a molecule, thus enabling potential elucidation of kinetic events such as protein folding pathways,31 enzymatic mechanisms,14,32 and allosteric cause and effect events.33
2.4 The challenge of computational intensity
Levinthal's paradox50 notes that if a protein in the process of folding were to physically sample every possible conformation, it would require a time longer than the age of the universe to arrive at its correct native conformation. But in physicality, protein folding occurs spontaneously and on much shorter time scales than the age of the universe due to fast formation of local structural interactions.39,51 The identities of local structural interactions are determined by tradeoffs in energy and entropy in the protein/solvent system. The progression of a series of metastable partially folded structures, each at a local energy minima, form a funnel-shaped protein energy landscape. Essentially, protein folding can occur in one of several accessible folding trajectories progressing down the funnel, and the number of different conformations a protein could exist in at a given system energy decreases as the energy of the system decreases. This is to say that decreasing system energy down the protein folding funnel results in fewer energy states of non-negligible probability that the protein could occupy. This property is reflected in the Boltzmann distribution for a given folded protein species. This constriction greatly decreases the energy landscape sampling required by the protein, allowing it to fold within timescales much faster than the age of the universe.In silico sampling of the energy landscape requires even further reductions in the amount of sampling that must be done to make a given simulation computationally tractable (i.e. converge within a reasonable amount of time). Simulations of biomolecules can commonly take days or even weeks to converge. As such, reductions in computational resources are highly desirable. One method of reduction in sampling requirements is through the use of importance sampling, which biases simulation sampling toward a target distribution.52 Additional simplifying approximations used in defining a model and/or use of enhancement of sampling algorithms can serve to even greater alleviate computational intensity. Such reductions in computation time enable longer simulation timescales and therefore the ability to capture more interesting phenomena. However, each simplification makes an implicit trade-off in decrease in resolution and/or accuracy as described below.
All force fields will suffer from lack of transferability from the system for which they were defined to use in other systems. However, a major weakness of CG methods in particular is the lack of transferability of their force fields compared to that of atomistic ones, because, in reducing atomistic details, interactions between particles are averaged in ways that are especially dependent upon given conditions. As such, results of CG potentials are only reliable if used in simulation conditions strictly matching those for which the CG was made. For example, in the aforementioned MARTINI force field, the secondary structure of the protein is fixed throughout the simulation. Deviations of thermodynamic parameters away from those for which the secondary structure of the molecule was developed will result in unreliable simulation results.
More sophisticated CG fields have been produced through systematic derivation from all-atom simulations. Examples include CG fields developed specifically for DNA by Savelyev and Papoian,55 and CG models for lipid bilayers developed by Izvekov and Voth.56 Additional recent references on the topic of coarse-graining in biomolecular simulations are available.19,23,57
Within implicit solvent models, the change in free energy due to solvation is generally divided into two additive contributions: non-polar solvation and polar solvation. Non-polar solvation is generally a linear function of the surface area of the biomolecule in contact with the solvent, multiplied by a term describing surface tension of the solvent. With regard to polar solvation, the two broadest classes of implicit fields are those developed through generalized Born (GB) models63,64 and those developed through Poisson–Boltzmann (PB) distributions.65 Extensive reviews have been published elsewhere on the development of these polar solvent models.66 A recent study by Anandakrishnan et al. compares the performance of implicit vs. explicit solvent models on a collection of small and large-scale conformational changes in DNA and proteins.67
2.5 Interpreting the results
After running the various simulations described above, it is necessary to extract meaning out of the simulations. Results of these simulations are used in many different ways and many software packages are available for this task.73–77 Broadly, simulation trajectories can be used to gain insight into structural quantities, dynamic quantities, and thermodynamic quantities.78 For instance, root-mean-square deviation (RMSD) is a metric that can be used to quantify structural information by giving a measure of the deviation between structures of two biomolecules.79 Diffusion constants can be extracted from trajectory information to yield dynamic information about molecules within the simulation, and finally, free energy trajectories obtained during simulation can be used to find time averages, statistical error approximations, and relative free energy differences, ΔΔG, between different processes.80In another approach to data analysis, Markov state models (MSM)81 decompose the vast potential conformational space into states and rates of transition between these states. In doing so, this approach can provide kinetic as well as thermodynamic interpretation to the results. Additional references regarding the theory and usage of these models are available.82,83
Machine learning approaches84–87 provide a unique vehicle for analysis via empirical model-building using the results of these simulations. Outcomes from simulations, such degree of helix twist in a short segments of DNA, can be correlated to useful experimental properties, such as the ability of the segment to function as a transcription factor binding site, then used to predict properties for novel segments of DNA.88 These concepts are applicable to a variety of properties. Two major classes of machine learning are quantitative structure–activity relationships (QSAR) and support vector regression (SVR). QSAR methods relate a set of predictor variables to the potency of the response variable and have been used to predict ligand binding potential from RNA secondary motifs.89 Likewise, these methods have been applied to drug design challenges.90 In SVR, a support vector machine serves as a supervised learning model and has been used in applications such as determining DNA–protein binding affinity based on nucleotide sequence.91
Finally, visualization software have been developed to view the results of molecular dynamic simulations. Noteworthy visualization packages include VMD92 and UCSF Chimera.93 Docking software that seek to quantify binding affinity94 can likewise evaluate the potential of biomolecular interactions.90,95 Further information on docking approaches have been reviewed elsewhere94 with notable docking software listed in Table 2.
| Software | Docking algorithm | Biomolecule it was developed for (protein, DNA, RNA) | Reference |
|---|---|---|---|
| Zdock | Fast-Fourier transform methods (FFT) for grid matching | Protein–protein | 230 |
| Patchdock | Geometry-based | Protein–protein | 231 |
| Protein–small molecule | |||
| Autodock Vina | MC simulation-based | Macromolecules | 232 |
| HADDOCK | Data-driven/ bioinformatics based | Bio macromolecules | 233 |
| RosettaDock | MC simulation-based | Protein–protein | 234 |
| 3dRPC | FFT-based | RNA–protein | 235 |
| MDockPP | Hierarchal approach consisting of reduced FFT then knowledge-based refinement | Protein–protein | 236 |
| Dock 6 | Anchor-and-grow sampling algorithm + AMBER score | RNA | 237 |
This review is not meant to be an all-encompassing overview of the available methods of analysis of simulation data. The interested reader is referred elsewhere for more complete discussion of this area.96–99
2.6 Outlooks
It is important to note that the majority of molecular simulation methods are used as a method to obtain purely thermodynamic data at equilibrium. As a result, many 3D structures such as aptamers could disagree with in vivo observation if kinetic limitations are important. Finally, molecular simulations are still very limited in their ability to completely fold peptides, and only very small peptides can be considered in this process. Truly de novo prediction of structures for large biomolecules through simulation remains challenging, thus previously determined empirical/experimental crystal structures are typically a prerequisite for simulation of a given molecule. For this reason, simulations are often limited as supplemental techniques to experimental methods. Nevertheless, as computational techniques improve in both accuracy and speed, a higher number of larger biomolecules can be simulated, and simulations can be used in more truly de novo design. The remainder of this review covers case studies in advances in the simulation and design of various native and synthetic elements in cells.3. Computational modeling and simulations of DNA
3.1 Overview of DNA modeling and challenges
As the central code for the cell, there is a great interest to model the interactions and dynamics of DNA with itself, proteins such as histones and transcription factors, as well as the various catalytic processes involving DNA including repair and transcription. For the purposes of simulation, determining a force field that has been properly parameterized for DNA can be challenging. Many DNA modeling applications rely upon accurate empirical structures from crystal structures100 that usually are specific to the DNA–ligand pair. Moreover, the negatively charged backbone of DNA requires polarizable fields, as fixed-charge approximations have been shown to be inadequate for many aspects of DNA stability or binding.101,102Fixed-charge approximations embody a mean-field approximation. This means that polarization in dielectric mediums experienced due to charges are only described in an average way. In reality, the dielectric environment and polarization responses within the environment can vary widely across a biomolecular system, and do so dynamically.103 Polarizable fields58 can account for these variations in charge distribution that occur when a highly anionic DNA species is solvated in an aqueous medium, an important aspect of correctly capturing DNA conformations.104,105 Several modifications to force fields have been developed for polarizability while still balancing the need for computational resources.22,106–108
Among these advances in force fields developed for DNA is the recent emergence of the PARMBSC1 force field,109 which utilizes high-level quantum mechanics data in order to fit revised parameters for backbone degrees of freedom of DNA strands (sugar puckering, glycosidic torsion, and ε and ζ rotations). This force field was able to make progress in several of the most common limitations in DNA simulations. A few examples are reducing inaccuracies at terminal base pairs, and maintaining accurate DNA structures for longer time scales (such as microsecond-scale dynamics of the Drew–Dickerson dodecamer) than provided by preceding force fields.110 In addition to PARMBSC1, other force field parameterizations for DNA have been highly used in the field.111,112 Finally, a collection of enhanced sampling methods and coarse graining technologies specific to DNA have been explored.66,113–116
Overall, many promising advances have been made in development of simulation methods for nucleic acids. However, nucleic acid force fields still suffer from severe biases. These biases accumulate throughout the duration of the simulation, rendering even state-of-the-art simulations unable to access time scales greater than microseconds. Many biologically relevant events regarding nucleic acids take place on longer time scales, such as base pair opening (microseconds to milliseconds), and folding of nucleic acid structures (microseconds to multiple days).117 Continued advances are necessary within these fields to access and accurately predict structures within these time scales.
In the remainder of this section, we focus on simulations related to DNA–protein interactions published in the past few years as they mainly relate to promoter and transcription factor function. Additional references are available for other applications of DNA-based modeling.30,107,118–120
3.2 Modeling of DNA–protein interactions
Metabolic engineering and synthetic biology both require precise control of gene expression levels.121 In many instances, the binding affinity between the DNA sequence and protein regulatory transcriptional machinery correlates with promoter function.122 Given this correlation, there is substantial interest in simulating and designing this interaction. Mechanistically, DNA–protein binding events are marked by transience. The protein must first contact DNA and travel with loose binding to nonspecific nucleotides before binding to its cognate sequence123 with free energies limited to ∼−16 kcal mol−1 (ref. 124) to ensure binding reversibility. As such, conformational changes in both DNA and protein upon binding are responsible for highly specific DNA sequence binding motifs despite the narrow range of free energy of binding. Therefore, dynamic conformational changes of DNA must be carefully considered along with changes in binding energies.On the other side of the equation, transcription factors (TFs) are the proteins of interest (for most promoter applications) and must be considered as well. Current predictions of transcription factor binding sites (TFBSs) rely on statistical observations such as through position weight matrices (PWM).125 Experimental methods including binding assays and even systematic evolution of ligands by exponential enrichment (SELEX) methods provide a more time-intensive and iterative process to determine TF binding specificities.126,127 Alternatively, in silico evaluation of these elements allow for investigation of factors influencing binding affinity beyond just that of nucleotide identity and enable a precise quantification of conformation changes.
For the remainder of this section, we focus on recent progress for molecular modeling of DNA–protein interactions. This overview is not meant to be exhaustive and instead covers only select examples from recent years. A review of less recent work can be found in the literature.30,128Table 3 provides an overview summary of the software utilized by each of the examples described below.
| DNA–protein combination considered | Initial structure | Evaluation method and software | Force field/ parameterization | Solvation model | Ref. |
|---|---|---|---|---|---|
| ELK1 (human TF) | Protein–DNA complex: PDB entry | MD: Pmemd program of Amber 14 | DNA: parmbsc1 | TIP3P water molecules + 0.15 M KCl | 128 |
| Proteins: AMBER ff14sb | |||||
| GCM1 (human TF) | |||||
| MAX (human TF) | |||||
| PPR1 (S. cerevisiae TF) | |||||
| 70 nucleotide DNA chain | DNA constructed with Make-NA server (http://structure.usc.edu/make-na/server.html) | MD: software not available | DNA: AMBER parm99 + bsc0 | TIP4P-EW water molecules + 0.15 M NaCl | 129 |
| 20 individual amino acid residues, reduced to side chains only | |||||
| Amino acid side chins: AMBER ff99SB-ILDN f | |||||
| Training set of 2121 DNA fragments of 12–17 nucleotides | Custom-built canonical B-DNA with ideal structural features for each dinucleotide | Custom MC sampling | DNA: AMBER94 | Implicit solvent model by Rohs et al. 1999 | 130 |
| Training set of 136 unique DNA 12-mers | DNA constructed with nucgen module of Amber | MD: Amber 6 and 7 | DNA: parm99 + bsc0 modifications | TIP3P water molecules + 0.15 M KCl | 132 |
| SKN-1 (C. elegans TF) | Protein–DNA complex: PDB entry | MD: Amber 12 | DNA: parm99 + bsc0 modifications | SPC/E water molecules + 0.15 M KCl | 134 |
| ADAPT | |||||
| ARN (P. aeruginosa TF): monomer | ARN monomer structures: PDB entry. | Patchdock | Features inherent to Patchdock | 135 | |
| DNA built in Discovery Studio | |||||
| P53 | Protein–DNA complex: PDB entry | MD: Gromacs 4.5 with PLUMED for enhanced sampling | DNA: CHARMM27 | TIP3P water molecules + 0.15 M NaCl | 136 |
| Protein: CHARMM22/CMAP | |||||
| DNA loops of 21 (IN21) or 42 (IN42) nucleotides + 1KX5 (human nucleosome) | Protein–DNA complex: PDB entry. | MD: Gromacs 5 | DNA: parmbsc1 | SPC/E water molecules + 0.15 M KCl | 142 |
| Protein: Amber 99SB-ILDN | |||||
| Loops were manually constructed with help of JUMNA minimization | |||||
| Abf2p (S. cerevisiae mt-packinging protein) + mtDNA-derived fragments | Protein–DNA complex: X-ray crystal structures derived in this work | MD: Amber 14 | Amber14SB + parmbsc1 | TIP3P water molecules + 0.15 M NaCl | 143 |
| EcoRI (restriction enzyme) | Protein–DNA complex: PDB entry | MD: Gromacs 5 | DNA: PARMbsc1 | TIP3P water molecules | 145 |
| Protein: ff14SB | |||||
| TRF1 (human telomere-binding protein) | Protein–DNA complex: PDB entry | MD: Gromacs 4.5 and 5 | Amber 99sb-parmbsc0 | TIP3P water molecules + 0.154 M KCl | 148 |
| DNA modified to a 20 nucleotide periodic, effectively infinite model | |||||
| HUα2 dimer (bacterial architectural protein) | Protein: two different PDB entries, one for dimerization core and one for β-arms | CafeMol | DNA: 3SPN.2C | Not available | 150 |
| Protein: AICG2 + (both are coarse grained fields) | |||||
| DNA: 3DNA package | |||||
| PCNA (human clamp) | PCNA–DNA complex with 10 nucleotide DNA: PDB entry | MD: Gromacs 5 | parmbsc1 | TIP3P water molecules + 0.1 M NaCl | 151 |
| PCNA–DNA complex with 30 nucleotide DNA: PDB entry + COOT software to extend DNA | |||||
In another study, Andrews et al. quantified the binding affinities of single amino acid residues to single nucleotides within the binding site.130 Moreover, this study was particularly novel in its comparisons to both single-stranded DNA (ssDNA) and double-stranded DNA (dsDNA). To perform these studies, a 70-base pair DNA strand, containing all possible triplet sequences with only four repeating instances, was simulated in an aqueous NaCl solution as both dsDNA and ssDNA forms. Ten copies of 20 amino acid side chain analogs (200 individual amino acid molecules in total) were also placed into this simulation environment. Through repeated association and dissociation of these 200 molecules to the DNA molecules, it was possible to collect binding affinity data on all resides to all possible DNA triplicates in a single simulation run. These results show that, in general, amino acid residues interact more favorably with ssDNA than dsDNA, with the exception of positively charged residues. Likewise, a base-by-base analyses of ssDNA demonstrated that negatively charged residues and chloride ions preferentially bind to guanine nucleotides in ssDNA and positively charged residues and sodium ions preferentially bind to cytosine nucleotides in ssDNA. This finding provides a potential explanation for the lower salt dependence of DNA duplex stability in GC-rich sequences of DNA compared to AT-rich sequences.
The contribution of DNA structure itself to DNA–protein specificity has been a growing focus of research in recent years. In 2013, Zhou et al. presented a web server called “DNAshape”88 that uses a machine learning algorithm based on MC simulation data for 2121 different DNA pentamer fragments, resulting in the ability to predict the shape of new DNA sequences based on scores in various conformational categories. This machine learning algorithm catalogs structural feature information across four such conformational categories – minor groove width, propeller twist, roll, and helix twist – supplied by the Monte Carlo simulation at a single nucleotide level of resolution for each pentameter fragment. This data was then used to predict DNA shape features of arbitrary sequences. Importantly, this method does not require initial crystal structure data, only primary sequence information. Additionally, this method supports genome-wide studies for linking DNA shape to TFBS recognition. This high throughput method reportedly predicts DNA structural features of the entire yeast genome at nucleotide resolution on a single processor in less than one minute.
This method was validated in numerous ways, but perhaps most noteworthy was the use of all of the available experimental DNA structures from the Protein Data Bank.131 Designated ‘extreme structures’ with conformational shape scores outside of a normal range were omitted from the validation. X-ray bound PDB structures scored by the DNAshape program achieved Spearman's rank correlation coefficients between 0.54 and 0.67 across the four different conformational shape categories. However, X-ray unbound PDB structures only achieved Spearman coefficients between 0.29 and 0.55.
As a follow up to “DNAshape,” “DynaSeq”132 utilizes similar machine learning methods but is trained on MD simulations for 136 tetramer DNA sequences. Use of MD over the static MC alternative helps DynaSeq expand the number of DNA conformational categories quantified from four to thirteen. This technique was cross-validated on a set of 1312 known TFBSs and achieved very modest positive prediction scores when nucleotide positions within 200 base pairs of the TF consensus sequence (from positions −200 to 200) were tested. Scoring improved as the window of base pairs sampled was decreased from 200 base pairs away from the consensus site to only 15 base pairs downstream of the site (positions 0 to 15). The validation results were found to agree with DNAshape predictions where applicable. This validation study showed that the base-pair opening conformational category contributed the most to prediction of TFBS, and that binding site preference could potentially be detected by conformational changes up to 200 nucleotides away. However, it must be noted that the positive scores achieved by this method were very weak and improvements are left to be made upon this technology before it can be reliably used to predict novel TFBS's based on sequence alone.
Prior to these two approaches, ADAPT is another approach developed in 2000 to create generalizable sequence-structure relationships for DNA.133 ADAPT is a sequence-threading technique which uses internal coordinate molecular mechanics to reduce the computational demand of free energy calculations. Thus, ADAPT also enables genome-wide evaluation of sequence-based DNA conformation. Etheve et al. recently demonstrate the high-throughput capabilities of ADAPT by computationally generating a PWM for the 9 central base pairs of the TFBS for SKN-1 in Caenorhabditis elegans.134 This PWM was compared with experimentally obtained PWMs and resulting correlations show information loss in the simulation-based technique in comparison to the experimental technique, attributed to the fact that ADAPT only takes a singular snap-shot of the conformation of the binding site. Moreover, as SKN-1 contains a positively charged protein tail motif and MD simulations conducted in this same study show a time-averaged ensemble of four distinct conformational sub-states for the bound DNA–protein complex, involving two positively charged arginine residues in the tail motif of interest. Simulation times exceeding the 0.5 μs used can provide a more definitive conclusion of this binding effect.
Recent progress has also been made on investigating binding mechanisms between individual DNA–protein pairs. For example, simulations have been conducted with the ARN TF, which regulates expression of a Pseudomonas aeruginosa operon leading to virulent properties in immune-repressed patients. In this study,135 MD simulations were used to investigate the promoter-binding mechanism that was believed to require two monomeric subunits of ARN to bind to a Fe4S4 ligand prior to DNA binding. This study confirmed in silico the need for the Fe4S4 based dimerization, and further identified two positively charged Asp residues as mediators of this ligand binding. An additional Arg residue was found to be essential for DNA binding. The results of this simulation were corroborated through alanine mutagenesis at these residues and observing a subsequent destabilization of the protein complex. This study this provides a path forward for therapeutic strategies for ARN destabilization, and showcases use of in silico simulations as supplements to experiments.
Allostery is also an important regulatory mechanism studied through simulations. For example, Lambrughi et al. investigate how protein binding to DNA affects distal binding sites on tumor-suppressing protein p53.136 Enhanced sampling techniques (combined parallel tempering and metadynamics137,138), were employed to show binding to DNA induces a conformational change 3 nm away from the DNA binding site in p53. This conformational change traps p53 in a solvent-shielded conformation where it is no longer accessible to binding partners pertinent to its transcription-independent signaling properties. These observations were not accessible in MD simulations without enhanced sampling, suggesting there are large energy barriers associated with these conformation changes, and that they only occur on longer simulation time scales and with approaches that can model increasing sizes of these biomolecules (namely, DNA).
An additional long-range effect with DNA is packing and organization, especially with respect to nucleosomes. Specifically, the location of nucleosomes on the DNA strand determines which genes are down-regulated and can play a significant role in the performance of transcriptional control elements including promoters139 and terminators.140 It is suspected that DNA loops formed around histones influence controlled remodeling processes.141 To test this hypothesis, Pasi et al. performed atomistic MD simulations on the formation of these loops142 and revealed that localized DNA kinking enables their formation. Additionally, it was shown that mechanisms of loops involving the insertion of DNA into a native nucleosome reduced final loop lengths from 179 to 168 base pairs to 79 to 45 base pairs for small and large loops respectively, a result consistent with known controlled remodeling mechanisms.
Packing regulation also occurs in mitochondrial DNA (mt-DNA), which assembles into the less-understood DNA–protein complexed called nucleoids. Chakraborty et al. report the use of MD simulations to investigate mechanisms of mt-DNA packaging in S. cerevisiae.143 This study provides evidence supporting the formation of a DNA U-turn during binding with mitochondrial packing protein Abf2p. Simulations showed poly-adenosine tract (A-tract) sequences maintain the structure of unbound DNA during packaging events, thus providing evidence to support the crucial role of A-tract sequences in nucleoid positioning.
DNA kinks as described in packing above have also been implicated with other DNA–protein events including DNA–EcoRI binding,144 possibly due to interactions between cationic protein residues and backbone phosphates of DNA. To study this effect, Ramachandrakurup et al. used MD simulations to study the influence of three charged amino acid residues, a lysine, an arginine, and an aspartic acid, on kink formation.145 Each of the selected residues create a hydrogen-bond to a phosphate of the DNA in the binding sequence, but at a distance of 8–9 Å away from the kink site. After mutagenesis analysis in silico, it was concluded that positively charged residues have a propensity for long-range conformational changes in the DNA–EcoRI binding mechanism while negatively charged residues only impart local changes. Collectively, these studies demonstrate the influence of simulations on understanding protein binding events to DNA.
Proteins such as TRF1 bind telomeric tandem repeat regions of DNA, an interesting problem with respect to sequence specificity. Wieczór et al. used MD simulations to demonstrate that TRF1 uses two major mechanisms: (1) it can use its unstructured basic tail to sample DNA sequence at a distance when encountering telomeric tracts, and (2) it can dissociate to increase sampling speed at off-target sites.148 More importantly, this study shows that TRF1 contains both residues to increase affinity at target sequences and residues to decrease affinity at off-target sites. A broader analysis of proteins in the PDB database suggests this mechanism may also occur in other proteins with other DNA targets. Of final important note on this study, full agreement with crystal structures required 34 μs of simulations, far longer than the nanosecond timescales used for transient off-site intermediate complex formations.
HU is a broader, non-sequence specific protein responsible for transcription repression in Escherichia coli.149 To study the function of this protein, Tan et al. investigated the interplay between HU sliding and DNA bending mechanisms using MD trajectories.150 To establish these trajectories, dimensionless coordinates were assigned to short time scale dynamics and analyzed with respect to HU sliding and DNA bending. These results suggested that greater DNA bending correlates to greater protein binding. Moreover, HU pausing occurred with especially sharp DNA bending events, and this mechanism was shown to be generalizable to 6 additional DNA-binding proteins analyzed.
Finally, De March et al. used MD simulations to investigate the molecular mechanism of PCNA- the eukaryotic sliding clamp that recruits polymerases and other replisome proteins to DN.151 This simulation was used to corroborate previous experimental evidence of five key residues.152 In this study, it is shown that these residues take part in binding of PCNA to DNA, evidencing a potential mechanism where these key residues guide DNA through PCNA and into the clam loader to form a tight complex.
3.3 Outlooks for DNA–protein binding
As has been demonstrated, substantial progress has been made in recent years on the simulation of protein and DNA binding events. To this end, progress has allowed sequence-to-structure road maps for DNA–TF binding at the genome scale. These results demonstrate that positively charged amino acid residues serve as key mediators of binding and emphasize the importance of electrostatic interactions between these residues and negatively charged phosphate groups on their DNA binding partners. However, studies for the most part serve to showcase a concept, and are not yet suitable for de novo TFBS design or discovery, due to high rates of false positive detection. Continued progress towards more sophisticated DNA force field parameterizations could be key in making these predictions more reliable across wide varieties of DNA sequences.A reoccurring issue in the study of DNA–protein dynamics is the necessity of micro to millisecond-long MD simulation time spans. These time spans can be challenging to achieve, even with access to specialized computational hardware.153 However, approaches such as enhanced sampling methods136 can improve overall simulations. Additionally, despite the development of DNA-related force fields, balancing DNA–protein interaction terms adds a great deal of complexity to the parameterization process. As a result, the development of additional parameterization efforts to treat DNA–protein interfaces specifically could benefit this area.
4. Computational modeling and simulations of RNA
4.1 Overview of RNA modeling and challenges
RNA is an extremely versatile biopolymer and serves to convey information from DNA, catalyze reactions in the form of ribozymes, and bind small molecules or proteins. Likewise, RNA can serve as an important metabolic engineering lever through control of regulatory processes.154 As with DNA, determination of structure is rather important as RNA tends to have rather complex secondary and tertiary structures. Thus, the use of crystal structures are particularly helpful as starting points for accurate simulations among the other RNA-specific challenges described elsewhere.155–158 RNA-specific adaptations to more generic force fields and other additional approximation methods have been made and have been compared elsewhere.159–163 As a noteworthy example, Chen and Garcia reparametrized the RNA Amber-99 force field by calibrating these parameters against a wider range of experimental data.164 By adapting van der Waals parameters to RNA-specific values, use of this new force field resulted in more accurate base-stacking propensities, syn–anti glycosidic rotamers, and contact distances determined by dispersion-corrected quantum calculations.Specialty software and web-servers exist for the prediction of RNA structure (secondary or tertiary) based solely upon sequence information with many highlighted in Table 4. The performance and therefore the value of these web-servers varies depending on the individual server and intended use. For example, RNAComposer, upon validation, produced predicted tertiary structures with an average global RMSD of 5.5 Å when compared to known tertiary structures. ViennaRNA reports Matthews Correlation Coefficients of 0.763 when averaged across 1817 reference structures, omitting those with pseudoknots. Vfold is only able to predict tertiary structure as a function of individual secondary structural techniques, which is not always a valid predictor of tertiary structure. The accuracy of the results from these simulations are variable and depend on length of RNA examined (with shorter being more reliable) and presence of unanticipated complex secondary structure (such as pseudoknots). As such, the assumptions made in the energy equations in each web-server method must be taken with caution. Works comparing performances for several of these web-servers are provided.165
| Software | Secondary or tertiary structure | Reference |
|---|---|---|
| ViennaRNA | Secondary | 238 |
| Mfold | Secondary | 239 |
| Vfold | Secondary and tertiary | 240 |
| RNAComposer | Tertiary | 196 |
| Centroid-fold | Secondary | 241 |
| RNAstructure | Secondary | 242 |
| 3D-DART | Tertiary for double stranded DNA | 243 |
| MC-fold | Secondary | 244 |
| MC-Sym | Tertiary | 244 |
| NuPack | Secondary | 245 |
Docking software has been used to predict binding of RNA to small molecule or protein ligands. Much of the available docking software has been developed specifically for proteins. In contrast to proteins, RNA, like DNA, is a highly charged molecule by nature. Thus, challenges arise in developing of solvation models and handling of electrostatic effects, analogous to those presented in modeling of DNA. To address these issues, several modifications for RNA (and DNA) use in docking programs have already been released.166–168
In the remainder of this section, we focus on simulations related to single-strand RNAs binding to target ligands, with an emphasis on aptamers published in the past few years. Additional references are available for generic computational modeling of RNA,163,169 RNA–protein interactions.32,157,170–172
4.2 Modeling of RNA aptamers
RNA Aptamers are short, single-stranded nucleotide sequences that bind to a target ligand (both small molecules and larger proteins) with high affinity.173,174 Aptamers have successfully been designed for therapeutic,175 biosensor,176–178 diagnostics,179 biomarker discovery,176 and riboswitching applications.180–182 Experimentally, novel aptamers can be generated through SELEX in a process similar to that described above for DNA selections. These processes require very large (up to 1016) oligonucleotide libraries180 that highly depend on the starting library diversity183 as the process cannot screen all mutations comprehensively. Inherent to the SELEX procedure is the risk of getting stuck in a structural motif ‘local minima’. As evidence, the most common final products of SELEX consist only of simple stem-loop structures given this bias in the initial library.184 Computational approaches can certainly aid in the development of novel aptamers that bypass these limitations.For the remainder of this section, we focus on recent progress in simulation-aided aptamer design. While some of these approaches conduct screening in silico, others concentrate on pure ab initio design. As with the DNA section above, this overview is not meant to be exhaustive and instead covers only examples from recent years. A review of less recent work can be found in the literature.169 While the focus of this section is on RNA, we will also discuss some DNA aptamers as the challenges are the same. Table 5 provides an overview summary of the software utilized by each of the examples described below.
| Reference | Initial sequences | 2D structure software | 3D structure software | Docking software | Approach |
|---|---|---|---|---|---|
| 184 | Purely random nucleotide generation | ViennaRNA | Rosetta + AMBER10 for energy minimization | DOVIS package (contains AutoDock 4) | De novo design/virtual screening |
| 188 | Perl scripts for patterned libraries | ViennaRNA | Rosetta | AutoDock Vina | De novo design/virtual screening |
| 193 | Pre-existing aptamers from various literatures | Centroid-fold | RNAComposer | ZDOCK + ZRANK | Existing aptamer improvement/virtual screening |
| Rational mutation scheme to conserve essential motifs | |||||
| 198 | Pre-existing aptamers | RNAfold | RNAComposer | ZDOCK + ZRANK | Existing aptamer improvement/virtual screening |
| MATLAB genetic algorithm | |||||
| 200 | None | N/A | 3D-DART | MD with Amber10 in lieu of docking | Ab initio design |
| 201 | ERE DNA segments | MC-fold | MC-Sym | AutoDock Vina | Rational de novo design/ virtual screening |
| HADDOCK | |||||
| PatchDock | |||||
| 202 | Double-helix structural motifs for structural fragment | Not available | Not available | Dock 6.5 for trinucleotides | Rational de novo design/ virtual screening |
| 208 | Pre-existing PSMA aptamers A9 and A10 | Method presented by Cao et al.246 | Method presented by Cao et al.246 | MDockPP | Rational truncation |
| 209 | Pre-existing truncated A9 aptamer | Vfold2D | Vfold3D + Amber energy minimization | MDockPP | Rational truncation |
| 210 | Pre-existing Ang2 aptamers | Mfold | RNAComposer | ZDOCK | Rational truncation |
| 212 | Pre-existing theophylline aptamer | RNAfold | None | None | Riboswitch design using existing aptamer |
| 213 | Pre-existing tetracycline and streptavidin aptamers | RNAfold | None | None | Riboswitch design using existing aptamer |
While the work by Chushak et al. is novel with respect to 3D structure predictions, it is also highly computationally expensive. As such, most work has leveraged crystal structures or bypassed their need altogether. In one such application,190 an initial library containing 413 sequences was designed through exhaustive mutagenesis of a theophylline-binding aptamer scaffold191 while preserving nucleotides implicated in essential hydrogen bonding with theophylline. This library was in silico screened on the basis of propensity to form secondary structural motifs as quantified by ΔΔG measurements between mutant and original aptamer secondary structures using MD simulations. In doing so, 3D structure predictions were bypassed through the assumption that individual mutations did not change structure from the pre-existing theophylline aptamer–ligand crystal structure.192 In the end, the workflow produced one novel theophylline-binding aptamer sequence with a binding affinity two times greater than that of the original aptamer, and five novel aptamer sequences of commensurate binding affinities to the experimental analog.
In a similar fashion, Hu et al.193 also leveraged previously characterized aptamer sequences for Ang2, a protein involved in tumor angiogenesis.194,195 These simulations were used to evaluate nucleotides directly in contact with Ang2 through docking simulations.196 For one of the three original aptamer sequences mutated, one novel sequence was identified with higher relative binding affinity for Ang2, compared to one of the original sequences. However, it was noted that, in general, experimental quantification of binding was not always in agreement with docking simulations. Hu et al. suggest this is possibly due to differences in ionic strength and pH of buffer solutions between experiment and simulation. However, when the performance of the ZRANK algorithm is examined more closely, the RMSD of top-scoring structures out of 2000 predictions frequently reaches 20, to even 30 Å.197 While agreement between physical conditions of experiments and simulations is indeed important, understanding that scoring functions and free-energy calculations of docking algorithms are often highly approximate and error-prone is also critical.
Finally, in similar work by Hsieh et al., a genetic algorithm was applied to re-diversify a starting aptamer library based on secondary structure and docking simulation scores.198 This work starts with five sequences199 for prostate specific antigen (PSA), a protein with cancer diagnostic value, and generates only 20 new aptamer sequences. After 3D structure prediction and docking simulations, eight aptamers were tested experimentally. The four highest scoring aptamers in vitro were then used for iterative rounds of genetic algorithm based re-design. After two generations, a novel PSA aptamer was identified with three-fold higher binding affinity than its counterparts developed purely in vitro.
Additional examples demonstrate the potential of ab initio design. Ahirwar et al. used computational design to make an ERα-binding aptamer.201 The in silico binding affinity predictions predicted ERE-derived aptamers binding tighter to ERα than randomly generated aptamer sequences including a hairpin motif. The top 5 scoring aptamer sequences were evaluated experimentally relative to an ERα antibody control, and one of the selected aptamer sequences had a higher relative binding affinity. Likewise, Shcherbinin et al.202 designed a fragment-based approach203,204 for aptamer design. This approach considers aptamers in a modular fashion with one fragment serving to bind with the target ligand while the second fragment serves to stabilize the conformation of the RNA. The authors used this approach to design an aptamer to cytochrome p450, an anti-fungal drug target. Specifically, a three-nucleotide recognition sequence was developed by docking simulations. The best scoring trinucleotide sequences each formed a U-like structure which coincided with a hairpin structural motif. Ultimately, this methodology successfully generated a set of seven different cytochrome p450 aptamers with moderate binding ability to cytochrome p450 (on par with previously reported cytochrome p450 aptamers developed in vitro).
Beyond defining functional aptamers, in silico approaches have been used to reduce the length of aptamers, an approach that can enhance ligand binding affinity.205 Traditionally, these truncation studies require trial and error and systematic nucleotide removal.206,207 In contrast, Rockey et al.208 report rational truncation guided by RNA secondary structure models. In doing so, this study resulted in removal of nearly 30 nucleotides from a prostate-specific membrane aptamer while still retaining function. In a follow-up study,209 this same aptamer was further truncated utilizing 3D structural models and resulted in an aptamer that is being evaluated in preclinical trials, as the truncated aptamer size is short enough to allow for large-scale synthesis. Heiat et al. apply a similar work flow to single stranded DNA aptamers.210 Thus, these examples all demonstrate the potential of in silico modeling as aids to aptamer design.
4.3 Modeling of riboswitches
Riboswitches are closely related to aptamers and refer to short RNA sequences with the potential to control gene expression at transcriptional or translational levels. These sequences undergo structural changes upon ligand binding211 and have become a newfound set of synthetic tools for switchable, responsive gene regulation. Due to interest in these applications, these elements have also been designed in silico. For example, Wachsmuth et al. designed linker regions and terminator-imitating regions and tethered these to a known theophylline aptamer sequence in order to regulate expression at the transcriptional level in E. coli.212 In order to do so, random libraries of variable length were considered along with secondary structure analysis and free energy calculations. Of the eight riboswitch sequences chosen for experimental analysis, the design with the highest activation response to theophylline dosage was chosen for additional rational modification. Upon insertion of a 19-nucleotide spacer region between the U-stretch and Shine–Dalgarno sequence regions of the terminator, the resultant riboswitch enabled a 6.5-fold increase in gene expression upon theophylline dosing. In a later study with a similar approach,213 this technique was capable of creating a riboswitch with 3.4-fold increase in expression upon tetracycline dosing. However, this approach failed to create a streptavidin-responsive riboswitch. Collectively, this work demonstrates that other functional RNAs can be computationally designed.4.4 Outlooks for RNA modeling
As has been demonstrated, substantial progress has been made in recent years on the simulation of functional RNAs (especially as aptamers). Much of the success in the field hinges upon an accurate 3D structure prediction or measurement prior to applying MD or docking simulations. When successful, this approach can significantly reduce the overall experimental costs for large-scale screening applications such as SELEX. Yet, there is much work left to be done to refine 3D structure predictions and improve docking simulations (for RNA and DNA) so that they may properly capture the electrostatic interactions inherent to RNA. Likewise, ab initio design of aptamers is promising but highly specific to the individual ligand of interest and is rather far from generalizability at the moment. Additional cycles of design and test will be required to more fully evaluate the strengths and weaknesses of these approaches.On the other hand, in silico approaches have been quite successful in smaller-scale problems such as rational truncation of existing aptamers or successful tethering of aptamers to motifs. Much of this success is owed to the lack of reliance on 3D structure determination and docking simulations for these applications.
Overall, in silico approaches to RNA design are still quite error-prone and require experimental validation in order to be trusted, and as such, are limited to aides to reduce the burden of experimental-based design.
5. Computational design of proteins
While not a major focus of this review (due to brevity and the expanse of the field), we turn attention briefly to proteins. As the main functional element within cells (especially for engineering applications), the topic of protein modeling and design have been widely reviewed and explored for applications such as folding simulations,214–216 redesign of key structural motifs and key catalytic residues for drug design,217 modifications for metabolic engineering applications,218 and even de novo protein design.31,219As with RNA and DNA molecules, there are challenges with the potential energy landscape with respect to potential conformations of the protein. As such, strong sampling algorithms and approximations are used to alleviate computational intensity along with crystal structure information. Further complications arise in the area of modeling membrane proteins, given that traditional solvent models alone cannot be used to simulate this environment.220–222
Proteins have long been the subject of simulations. In fact, most biomolecular modeling software available was originally written for protein design or analysis in original intent. As such, modifications to force fields to adapt them for proteins are rarely necessary. In many aspects, simulations serve a similar role with proteins as with the DNA and RNA examples discussed above including large mutant screens and rational re-design for particular function.
6. Concluding remarks
The vast sequence space of 4n and 20n for canonical elements necessitates methods for in silico design and analysis. In this regard, computational design can help rewire biological molecules and test underlying hypotheses of function. Continued development of ab initio parameterizations is critical for improving simulation accuracy. As biomolecular simulations continue to grow more robust and accessible to the experimentalist, it will become increasingly possible to bypass costly and time-consuming experimentation as well as access currently inaccessible search spaces.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support from the Air Force Office of Scientific Research under Award No. FA9550-14-1-0089.References
- J. Sun and H. S. Alper, J. Ind. Microbiol. Biotechnol., 2015, 42, 423–436 CrossRef CAS PubMed
.
- L. T. Cordova and H. S. Alper, Curr. Opin. Chem. Biol., 2016, 35, 37–42 CrossRef CAS PubMed
.
- K. A. Curran and H. S. Alper, Metab. Eng., 2012, 14, 289–297 CrossRef CAS PubMed
.
- J. J. Agresti, E. Antipov, A. R. Abate, K. Ahn, A. C. Rowat, J.-C. Baret, M. Marquez, A. M. Klibanov, A. D. Griffiths and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4004–4009 CrossRef CAS PubMed
.
- D. A. Pereira and J. A. Williams, Br. J. Pharmacol., 2007, 152, 53–61 CrossRef CAS PubMed
.
- J.-L. Lin, J. M. Wagner and H. S. Alper, Biotechnol. Adv., 2017 DOI:10.1016/j.biotechadv.2017.07.005
.
- N. Crook and H. S. Alper, Chem. Eng. Sci., 2013, 103, 2–11 CrossRef CAS
.
- M. A. Marchisio and J. Stelling, Curr. Opin. Biotechnol., 2009, 20, 479–485 CrossRef CAS PubMed
.
- J. T. MacDonald, C. Barnes, R. I. Kitney, P. S. Freemont and G.-B. V. Stan, Integr. Biol., 2011, 3, 97 RSC
.
- W. B. Copeland, B. A. Bartley, D. Chandran, M. Galdzicki, K. H. Kim, S. C. Sleight, C. D. Maranas and H. M. Sauro, Metab. Eng., 2012, 14, 270–280 CrossRef CAS PubMed
.
-
D. C. Young, Computational drug design: a guide for computational and medicinal chemists, Wiley, 2009 Search PubMed
.
- L. L. Looger, M. A. Dwyer, J. J. Smith and H. W. Hellinga, Nature, 2003, 423, 185–190 CrossRef CAS PubMed
.
- Z. Fan, R. O. Dror, T. J. Mildorf, S. Piana, D. E. Shaw and D. E. S. Research, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 1–6 CrossRef
.
- W. Wang, O. Donini, C. M. Reyes and P. A. Kollman, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 211–243 CrossRef CAS PubMed
.
-
A. R. Leach, Molecular modelling: principles and applications, Prentice Hall, 2001 Search PubMed
.
-
P. Watkins, Molecular mechanics and modeling, Nova Science Publishers, Incorporated, 2015 Search PubMed
.
- G. Bao and S. Suresh, Nat. Mater., 2003, 2, 715–725 CrossRef CAS PubMed
.
-
J. Dreyer, G. Brancato, E. Ippoliti, V. Genna, M. De Vivo, P. Carloni and U. Rothlisberger, in Simulating Enzyme Reactivity, ed. A. Warshel and R. P. Bora, Royal Society of Chemistry, Cambridge, 2016, pp. 294–339 Search PubMed
.
- A. Gray, O. G. Harlen, S. A. Harris, S. Khalid, Y. M. Leung, R. Lonsdale, A. J. Mulholland, A. R. Pearson, D. J. Read and R. A. Richardson, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2015, 71, 162–172 CAS
.
- A. S. Christensen, T. Kubař, Q. Cui and M. Elstner, Chem. Rev., 2016, 116, 5301–5337 CrossRef CAS PubMed
.
- N. Pastor and C. Amero, Front. Plant Sci., 2015, 6, 306 Search PubMed
.
- J. A. Lemkul and A. D. Mackerell, J. Chem. Theory Comput., 2017, 13, 2053–2071 CrossRef CAS PubMed
.
- H. I. Ingolfsson, C. A. Lopez, J. J. Uusitalo, D. H. De Jong, S. M. Gopal, X. Periole and S. J. Marrink, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 225–248 CrossRef CAS PubMed
.
- G. A. Kaminski, H. A. Stern, B. J. Berne and R. A. Friesner, J. Phys. Chem. A, 2004, 108, 621–627 CrossRef CAS
.
- M. Karplus and J. A. McCammon, Nat. Struct. Biol., 2002, 9, 646–652 CrossRef CAS PubMed
.
-
C. A. Floudas and P. M. Pardalos, Optimization in computational chemistry and molecular biology: local and global approaches, Springer Science and Business Media, 2013 Search PubMed
.
-
J. M. Haile, Molecular Dynamics Simulation: Elementary Methods, John Wiley & Sons, Inc., 1997 Search PubMed
.
-
D. C. Rapaport, The art of molecular dynamics simulation, Cambridge University Press, 1997 Search PubMed
.
- N. Bou-Rabee, Entropy, 2014, 16, 138–162 CrossRef
.
- P. D. Dans, J. Rgen Walther, H. Gó Mez and M. Orozco, Curr. Opin. Struct. Biol., 2016, 37, 29–45 CrossRef CAS PubMed
.
- M. C. Childers and V. Daggett, Mol. Syst. Des. Eng., 2017, 2, 9–33 CAS
.
- M. T. Panteva, T. Dissanayake, H. Chen, B. K. Radak, E. R. Kuechler, G. M. Giambaşu, T.-S. Lee and D. M. York, Methods Enzymol., 2015, 553, 335–374 CAS
.
- V. A. Feher, J. D. Durrant, A. T. Van Wart and R. E. Amaro, Curr. Opin. Struct. Biol., 2014, 25, 98–103 CrossRef CAS PubMed
.
-
R. Y. Rubinstein and D. P. Kroese, Simulation and the Monte Carlo Method, John Wiley & Sons, Inc., New Jersey, 3rd edn, 2016 Search PubMed
.
-
T. Wilkinson, Computer Simulation of Biomolecular Systems: Theoretical and Experimental Applications, Springer Science and Business Media, 1997 Search PubMed
.
-
C. Z. Mooney, Monte Carlo simulation, Sage Publications, 1997 Search PubMed
.
- R. Zwanzig, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 9801–9804 CrossRef CAS
.
- J. Shimada and E. I. Shakhnovich, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 11175–11180 CrossRef CAS PubMed
.
- J. D. Bryngelson, J. N. Onuchic, N. D. Socci and P. G. Wolynes, Proteins: Struct., Funct., Genet., 1995, 21, 167–195 CrossRef CAS PubMed
.
- J. Shimada, E. Kussell and E. Shakhnovich, J. Mol. Biol., 2001, 308, 79–95 CrossRef CAS PubMed
.
- U. H. E. Hansmann, Chem. Phys. Lett., 1997, 281, 140–150 CrossRef CAS
.
- M. Luitz, R. Bomblies, K. Ostermeir and M. Zacharias, J. Phys.: Condens. Matter, 2015, 27, e323101 CrossRef PubMed
.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef CAS
.
- Y. Miao and J. A. McCammon, Mol. Simul., 2016, 42, 1046–1055 CrossRef CAS PubMed
.
- R. C. Bernardi, M. C. R. Melo and K. Schulten, Biochim. Biophys. Acta, Gen. Subj., 2015, 1850, 872–877 CrossRef CAS PubMed
.
- U. Doshi and D. Hamelberg, Biochim. Biophys. Acta, Gen. Subj., 2015, 1850, 878–888 CrossRef CAS PubMed
.
- D. M. Zuckerman, Annu. Rev. Biophys., 2011, 40, 41–62 CrossRef CAS PubMed
.
- T. Lelièvre, Eur. Phys. J.: Spec. Top., 2015, 224, 2429–2444 CrossRef
.
- A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843 CrossRef CAS
.
-
C. Levinthal, Mössbaun Spectrosc. Biol. Syst. Proc., Univ. Illinois Bull., 1969, vol. 67, pp. 22–24 Search PubMed
.
- H. S. Chan and K. A. Dill, Nat. Struct. Biol., 1997, 4, 10–19 CrossRef
.
- Z. Li and H. A. Scheraga, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 6611–6615 CrossRef CAS
.
- S. Riniker, J. R. Allison, W. F. van Gunsteren, S. J. Marrink, P. Carloni, S. J. Marrink, P. Gee, D. P. Geerke, A. Glättli, P. H. Hünenberger, M. A. Kastenholz, C. Oostenbrink, M. Schenk, D. Trzesniak, N. F. A. van der Vegt and H. B. Yu, Phys. Chem. Chem. Phys., 2012, 14, 12423 RSC
.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed
.
- A. Savelyev and G. A. Papoian, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20340–20345 CrossRef CAS PubMed
.
- S. Izvekov and G. A. Voth, J. Phys. Chem. B, 2005, 109, 2469–2473 CrossRef CAS PubMed
.
- S. Takada, R. Kanada, C. Tan, T. Terakawa, W. Li and H. Kenzaki, Acc. Chem. Res., 2015, 48, 3026–3035 CrossRef CAS PubMed
.
- P. Ren, J. Chun, D. G. Thomas, M. J. Schnieders, M. Marucho, J. Zhang and N. A. Baker, Q. Rev. Biophys., 2012, 45, 427–491 CrossRef PubMed
.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS
.
- T. E. Cheatham, J. L. Miller, T. Fox, T. A. Darden and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 4193–4194 CrossRef CAS
.
- D. J. Price and C. L. Brooks, J. Chem. Phys., 2004, 121, 10096–10103 CrossRef CAS PubMed
.
- M. Petukh and E. Alexov, Asian J. Phys., 2014, 23, 735–744 Search PubMed
.
- D. Bashford and D. A. Case, Annu. Rev. Phys. Chem., 2000, 51, 129–152 CrossRef CAS PubMed
.
- W. C. Still, A. Tempczyk, R. C. Hawley and T. Hendrickson, J. Am. Chem. Soc., 1990, 112, 6127–6129 CrossRef CAS
.
- F. Fogolari, A. Brigo and H. Molinari, J. Mol. Recognit., 2002, 15, 377–392 CrossRef CAS PubMed
.
- T. E. Cheatham and D. A. Case, Biopolymers, 2013, 99, 969–977 CAS
.
- R. Anandakrishnan, A. Drozdetski, R. C. Walker and A. V. Onufriev, Biophys. J., 2015, 108, 1153–1164 CrossRef CAS PubMed
.
- J. Zavadlav, R. Podgornik, M. N. Melo, S. J. Marrink and M. Praprotnik, Eur. Phys. J.: Spec. Top., 2016, 225, 1595–1607 CrossRef CAS
.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed
.
- A. Duster, C. Garza and H. Lin, Methods Enzymol., 2016, 577, 341–357 CAS
.
- R. B. Pandey, D. J. Jacobs and B. L. Farmer, J. Chem. Phys., 2017, 146, 195101 CrossRef CAS PubMed
.
- M. S. Lee, F. R. Salsbury and M. A. Olson, J. Comput. Chem., 2004, 25, 1967–1978 CrossRef CAS PubMed
.
- D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed
.
- R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernández, C. R. Schwantes, L.-P. Wang, T. J. Lane and V. S. Pande, Biophys. J., 2015, 109, 1528–1532 CrossRef CAS PubMed
.
- E. Chovancova, A. Pavelka, P. Benes, O. Strnad, J. Brezovsky, B. Kozlikova, A. Gora, V. Sustr, M. Klvana, P. Medek, L. Biedermannova, J. Sochor and J. Damborsky, PLoS Comput. Biol., 2012, 8, e1002708 CAS
.
- P. Schmidtke, A. Bidon-Chanal, F. J. Luque and X. Barril, Bioinformatics, 2011, 27, 3276–3285 CrossRef CAS PubMed
.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed
.
- A. P. Eichenberger, J. R. Allison, J. Zica Dolenc, D. P. Geerke, B. A. C. Horta, K. Meier, C. Oostenbrink, N. Schmid, D. Steiner, D. Wang, W. F. Van Gunsteren and J. Chem, J. Chem. Theory Comput., 2011, 7, 3379–3390 CrossRef CAS PubMed
.
- K. L. Damm and H. A. Carlson, Biophys. J., 2006, 90, 4558–4573 CrossRef CAS PubMed
.
- D. L. Mobley and M. K. Gilson, Annu. Rev. Biophys., 2017, 46, 531–558 CrossRef CAS PubMed
.
- F. Noé, J. Chem. Phys., 2008, 128, 244103 CrossRef PubMed
.
- V. S. Pande, K. Beauchamp and G. R. Bowman, Methods, 2010, 52, 99–105 CrossRef CAS PubMed
.
- C. R. Schwantes, R. T. McGibbon and V. S. Pande, J. Chem. Phys., 2014, 141, 90901 CrossRef CAS PubMed
.
- N. Berliner, J. Teyra, R. Çolak, S. Garcia Lopez and P. M. Kim, PLoS One, 2014, 9, e107353 Search PubMed
.
- D. S. Glazer, R. J. Radmer and R. B. Altman, Pac. Symp. Biocomput., 2008, 332–343 CAS
.
- M. M. Sultan, G. Kiss, D. Shukla and V. S. Pande, J. Chem. Theory Comput., 2014, 10, 5217–5223 CrossRef CAS PubMed
.
- Z. Li, J. R. Kermode and A. De Vita, Phys. Rev. Lett., 2015, 114, 96405 CrossRef PubMed
.
- T. Zhou, L. Yang, Y. Lu, I. Dror, A. C. Dantas Machado, T. Ghane, R. Di Felice and R. Rohs, Nucleic Acids Res., 2013, 41, W56–W62 CrossRef PubMed
.
- B. Musafia, R. Oren-Banaroya and S. Noiman, PLoS One, 2014, 9(5), e97696 Search PubMed
.
- A. Abdolmaleki, J. Ghasemi and F. Ghasemi, Curr. Drug Targets, 2017, 18, 556–575 CrossRef CAS PubMed
.
- A. V. Persikov and M. Singh, Nucleic Acids Res., 2014, 42, 97–108 CrossRef CAS PubMed
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed
, 27–8.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed
.
- S. F. Sousa, P. A. Fernandes and M. J. Ramos, Proteins: Struct., Funct., Bioinf., 2006, 65, 15–26 CrossRef CAS PubMed
.
- Z. Liu, M. Su, L. Han, J. Liu, Q. Yang, Y. Li and R. Wang, Acc. Chem. Res., 2017, 50, 302–309 CrossRef CAS PubMed
.
- D. A. Case, T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, K. M. Merz, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688 CrossRef CAS PubMed
.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed
.
- E. Lyman and D. M. Zuckerman, Biophys. J., 2006, 91, 164–172 CrossRef CAS PubMed
.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS
.
- S. S. Wijmenga and B. N. M. Van Buuren, Prog. Nucl. Magn. Reson. Spectrosc., 1998, 32, 287–387 CrossRef CAS
.
- K. Gkionis, H. Kruse, J. A. Platts and J. Koc, J. Chem. Theory Comput., 2014, 10, 1326–1340 CrossRef CAS PubMed
.
- N. Gresh, J. E. Sponer, M. Devereux, K. Gkionis, B. de Courcy, J.-P. Piquemal and J. Sponer, J. Phys. Chem. B, 2015, 119, 9477–9495 CrossRef CAS PubMed
.
- T. A. Halgren and W. Damm, Curr. Opin. Struct. Biol., 2001, 11, 236–242 CrossRef CAS PubMed
.
- P. E. M. Lopes, B. Roux and A. D. MacKerell, Theor. Chem. Acc., 2009, 124, 11–28 CrossRef CAS PubMed
.
- A. Savelyev and A. D. MacKerell, J. Comput. Chem., 2014, 35, 1219–1239 CrossRef CAS PubMed
.
- C. Liu, Y. Li, B.-Y. Han, L.-D. Gong, L.-N. Lu, Z.-Z. Yang, D.-X. Zhao and J. Chem, J. Chem. Theory Comput., 2017, 13, 2098–2111 CrossRef CAS PubMed
.
- A. van der Vaart, Biochim. Biophys. Acta, Gen. Subj., 2015, 1850, 1091–1098 CrossRef CAS PubMed
.
- C. M. Baker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 241–254 CrossRef CAS
.
- I. Ivani, P. D. Dans, A. Noy, A. Pérez, I. Faustino, A. Hospital, J. Walther, P. Andrio, R. Goñi, A. Balaceanu, G. Portella, F. Battistini, J. L. Gelpí, C. González, M. Vendruscolo, C. A. Laughton, S. A. Harris, D. A. Case and M. Orozco, Nat. Methods, 2016, 13, 55–58 CAS
.
- P. D. Dans, L. Danilāne, I. Ivani, T. Dršata, F. Lankaš, A. Hospital, J. Walther, R. I. Pujagut, F. Battistini, J. L. Gelpí, R. Lavery and M. Orozco, Nucleic Acids Res., 2016, 44, 4052–4066 CrossRef CAS PubMed
.
- M. Zgarbová, J. Šponer, M. Otyepka, T. E. Cheatham, R. Galindo-Murillo and P. Jurečka, J. Chem. Theory Comput., 2015, 11, 5723–5736 CrossRef PubMed
.
- K. Hart, N. Foloppe, C. M. Baker, E. J. Denning, L. Nilsson and A. D. MacKerell, J. Chem. Theory Comput., 2012, 8, 348–362 CrossRef CAS PubMed
.
- R. Galindo-Murillo, J. C. Robertson, M. Zgarbova Jir, M. Otyepka, P. Jurec and T. E. Cheatham, J. Chem. Theory Comput., 2016, 12, 4114–4127 CrossRef CAS PubMed
.
- G. S. Freeman, D. M. Hinckley, J. P. Lequieu, J. K. Whitmer and J. J. de Pablo, J. Chem. Phys., 2014, 141, 165103 CrossRef PubMed
.
- C. Maffeo, T. T. M. Ngo, T. Ha and A. Aksimentiev, J. Chem. Theory Comput., 2014, 10, 2891–2896 CrossRef CAS PubMed
.
- J. Sponer, P. Banas, P. Jurecka, M. Zgarbova, P. Kuhrova, M. Havrila, M. Krepl, P. Stadlbauer and M. Otyepka, J. Phys. Chem. Lett., 2014, 5, 1771–1782 CrossRef CAS PubMed
.
- T. E. Cheatham and M. A. Young, Biopolymers, 2000, 56, 232–256 CrossRef CAS PubMed
.
- T. Dršata and F. Lankaš, J. Phys.: Condens. Matter, 2015, 27, 323102 CrossRef PubMed
.
- A. Pérez, F. J. Luque and M. Orozco, Acc. Chem. Res., 2012, 45, 196–205 CrossRef PubMed
.
- S. Izadi, R. Anandakrishnan and A. V. Onufriev, J. Chem. Theory Comput., 2016, 12, 5946–5959 CrossRef CAS PubMed
.
- J. M. Leavitt and H. S. Alper, Curr. Opin. Biotechnol., 2015, 34, 98–104 CrossRef CAS PubMed
.
- M. Levo and E. Segal, Nat. Rev. Genet., 2014, 15, 453–468 CrossRef CAS PubMed
.
- R. Rohs, X. Jin, S. M. West, R. Joshi, B. Honig and R. S. Mann, Annu. Rev. Biochem., 2010, 79, 233–269 CrossRef CAS PubMed
.
- L. Jen-Jacobson, L. E. Engler, L. A. Jacobson, A. Sarai, H. Nakamura and H. M. Berman, Structure, 2000, 8, 1015–1023 CrossRef CAS PubMed
.
- G. D. Stormo, Bioinformatics, 2000, 16, 16–23 CrossRef CAS PubMed
.
- M. F. Berger, A. A. Philippakis, A. M. Qureshi, F. S. He, P. W. Estep and M. L. Bulyk, Nat. Biotechnol., 2006, 24, 1429–1435 CrossRef CAS PubMed
.
- A. Jolma, J. Yan, T. Whitington, J. Toivonen, K. R. Nitta, P. Rastas, E. Morgunova, M. Enge, M. Taipale, G. Wei, K. Palin, J. M. Vaquerizas, R. Vincentelli, N. M. Luscombe, T. R. Hughes, P. Lemaire, E. Ukkonen, T. Kivioja and J. Taipale, Cell, 2013, 152, 327–339 CrossRef CAS PubMed
.
- L. A. Liu and P. Bradley, Curr. Opin. Struct. Biol., 2012, 22, 397–405 CrossRef CAS PubMed
.
- M. Khabiri and P. L. Freddolino, J. Phys. Chem. B, 2017, 121, 5151–5161 CrossRef CAS PubMed
.
- C. T. Andrews, B. A. Campbell and A. H. Elcock, J. Chem. Theory Comput., 2017, 13, 1794–1811 CrossRef CAS PubMed
.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed
.
- M. Andrabi, A. P. Hutchins, D. Miranda-Saavedra, H. Kono, R. Nussinov, K. Mizuguchi and S. Ahmad, Sci. Rep., 2017, 7(1), 4071 CrossRef PubMed
.
- I. Lafontaine and R. Lavery, Biopolymers, 2000, 56, 292–310 CrossRef CAS PubMed
.
- L. Etheve, J. Martin and R. Lavery, Nucleic Acids Res., 2016, 44, 1440–1448 CrossRef CAS PubMed
.
- N. Chowdhury and A. Bagchi, Appl. Biochem. Biotechnol., 2017, 182, 1144–1157 CrossRef CAS PubMed
.
- M. Lambrughi, L. De Gioia, F. L. Gervasio, K. Lindorff-Larsen, R. Nussinov, C. Urani, M. Bruschi and E. Papaleo, Nucleic Acids Res., 2016, 44, 9096–9109 CAS
.
- M. Bonomi, A. Barducci and M. Parrinello, J. Comput. Chem., 2009, 30, 1615–1621 CrossRef CAS PubMed
.
- G. Bussi, F. L. Gervasio, A. Laio and M. Parrinello, J. Am. Chem. Soc., 2006, 128(41), 13435–13441 CrossRef CAS PubMed
.
- K. A. Curran, N. C. Crook, A. S. Karim, A. Gupta, A. M. Wagman and H. S. Alper, Nat. Commun., 2014, 5, 4002 CAS
.
- N. Morse, M. Gopal, J. Wagner and H. Alper, ACS Synth. Biol., 2017, 6(11), 2086–2095 CrossRef CAS PubMed
.
- Y. Zhang, C. L. Smith, A. Saha, S. W. Grill, S. Mihardja, S. B. Smith, B. R. Cairns, C. L. Peterson, C. Bustamante and C. Dekker, Mol. Cell, 2006, 24, 559–568 CrossRef CAS PubMed
.
- M. Pasi and R. Lavery, Nucleic Acids Res., 2016, 44, 5450–5456 CrossRef CAS PubMed
.
- A. Chakraborty, S. Lyonnais, F. Battistini, A. Hospital, G. Medici, R. Prohens, M. Orozco, J. Vilardell and M. Soì, Nucleic Acids Res., 2017, 45, 951–967 CrossRef PubMed
.
- D. R. Lesser, M. R. Kurpiewski, T. Waters, B. A. Connolly and L. Jen-Jacobson, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 7548–7552 CrossRef CAS
.
- S. Ramachandrakurup, S. Ammapalli, V. Ramakrishnan and R. H. Sarma, J. Biomol. Struct. Dyn., 2016 DOI:10.1080/07391102.2016.1261741
.
- A. Bhattacherjee, D. Krepel and Y. Levy, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 515–531 CrossRef CAS
.
- M. Slattery, T. Zhou, L. Yang, A. Carolina, D. Machado, R. Gordâ and R. Rohs, Trends Biochem. Sci., 2014, 39, 381–399 CrossRef CAS PubMed
.
- M. Wieczór and J. Czub, Nucleic Acids Res., 2017, 45, 7643–7654 CrossRef PubMed
.
- D. E. Lewis, M. Geanacopoulos and S. Adhya, Mol. Microbiol., 1999, 31, 451–461 CrossRef CAS PubMed
.
- C. Tan, T. Terakawa and S. Takada, J. Am. Chem. Soc., 2016, 138, 8512–8522 CrossRef CAS PubMed
.
- M. De March, N. Merino, S. Barrera-Vilarmau, R. Crehuet, S. Onesti, F. J. Blanco and A. De Biasio, Nat. Commun., 2017, 8, 13935 CrossRef CAS PubMed
.
- K. Fukuda, H. Morioka, S. Imajou, S. Ikeda, E. Ohtsuka and T. Tsurimoto, J. Biol. Chem., 1995, 270, 22527–22534 CrossRef CAS PubMed
.
- R. O. Dror, R. M. Dirks, J. P. Grossman, H. Xu and D. E. Shaw, Annu. Rev. Biophys., 2012, 41, 429–452 CrossRef CAS PubMed
.
- M. Mckeague, R. S. Wong and C. D. Smolke, Nucleic Acids Res., 2016, 44, 2987–2999 CrossRef CAS PubMed
.
- Q. Zhang, H. Lv, L. Wang, M. Chen, F. Li, C. Liang, Y. Yu, F. Jiang, A. Lu and G. Zhang, Int. J. Mol. Sci., 2016, 17, 2134 CrossRef PubMed
.
- J. A. Doudna, Nat. Struct. Biol., 2000, 7, 954–956 CrossRef CAS PubMed
.
- S. Jones, Biophys. Rev., 2016, 8, 359–367 CrossRef CAS PubMed
.
- D. K. Yadav and P. J. Lukavsky, Prog. Nucl. Magn. Reson. Spectrosc., 2016, 97, 57–81 CrossRef CAS PubMed
.
- A. Gil-Ley, S. Bottaro and G. Bussi, J. Chem. Theory Comput., 2016, 12, 2790–2798 CrossRef CAS PubMed
.
- C. Bergonzo, N. M. Henriksen, D. R. Roe and T. E. Cheatham Iii, RNA, 2015, 21, 1578–1590 CrossRef CAS PubMed
.
- S. Vangaveti, S. V. Ranganathan and A. A. Chen, Wiley Interdiscip. Rev.: RNA, 2017, 8, e1396 CrossRef PubMed
.
- W. K. Dawson, M. Maciejczyk, E. J. Jankowska and J. M. Bujnicki, Methods, 2016, 103, 138–156 CrossRef CAS PubMed
.
- S. E. McDowell, N. Špačková, J. Šponer and N. G. Walter, Biopolymers, 2007, 85, 169–184 CrossRef CAS PubMed
.
- A. A. Chen and A. E. García, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 16820–16825 CrossRef CAS PubMed
.
- P. P. Gardner and R. Giegerich, BMC Bioinf., 2004, 5, 140 CrossRef PubMed
.
- I. Banitt and H. J. Wolfson, Nucleic Acids Res., 2011, 39, e135 CrossRef CAS PubMed
.
- I. Tuszynska, M. Magnus, K. Jonak, W. Dawson and J. M. Bujnicki, Nucleic Acids Res., 2015, 43, W425–W430 CrossRef CAS PubMed
.
- P. Setny, R. P. Bahadur and M. Zacharias, BMC Bioinf., 2012, 13, 228 CrossRef CAS PubMed
.
- C. Laing and T. Schlick, Curr. Opin. Struct. Biol., 2011, 21, 306–318 CrossRef CAS PubMed
.
- D. Marchese, N. S. de Groot, N. Lorenzo Gotor, C. M. Livi and G. G. Tartaglia, Wiley Interdiscip. Rev.: RNA, 2016, 7, 793–810 CrossRef CAS PubMed
.
- I. Tuszynska, D. Matelska, M. Magnus, G. Chojnowski, J. M. Kasprzak, L. P. Kozlowski, S. Dunin-Horkawicz and J. M. Bujnicki, Methods, 2014, 65, 310–319 CrossRef CAS PubMed
.
- R. Li, L. Macnamara, J. Leuchter, R. Alexander and S. Cho, Int. J. Mol. Sci., 2015, 16, 15872–15902 CrossRef CAS PubMed
.
- A. D. Ellington and J. W. Szostak, Nature, 1990, 346, 818–822 CrossRef CAS PubMed
.
- C. Tuerk and L. Gold, Science, 1990, 249, 505–510 CAS
.
- A. D. Keefe, S. Pai and A. Ellington, Nat. Rev. Drug Discovery, 2010, 9, 537–550 CrossRef CAS PubMed
.
- T.-H. Ku, T. Zhang, H. Luo, T. M. Yen, P.-W. Chen, Y. Han and Y.-H. Lo, Sensors, 2015, 15, 16281–16313 CrossRef CAS PubMed
.
- K. Sefah, J. A. Phillips, X. Xiong, L. Meng, D. Van Simaeys, H. Chen, J. Martin and W. Tan, Analyst, 2009, 134, 1765 RSC
.
- J. Abatemarco, M. F. Sarhan, J. M. Wagner, J.-L. Lin, L. Liu, W. Hassouneh, S.-F. Yuan, H. S. Alper and A. R. Abate, Nat. Commun., 2017, 8, 332 CrossRef PubMed
.
- J. P. Dassie, X. Liu, G. S. Thomas, R. M. Whitaker, K. W. Thiel, K. R. Stockdale, D. K. Meyerholz, A. P. McCaffrey, J. O. McNamara and P. H. Giangrande, Nat. Biotechnol., 2009, 27, 839–846 CrossRef CAS PubMed
.
- M. You, Y. Chen, L. Peng, D. Han, B. Yin, B. Ye and W. Tan, Chem. Sci., 2011, 2, 1003 RSC
.
- M. Etzel and M. Mö, Biochemistry, 2017, 56, 1181–1198 CrossRef CAS PubMed
.
- K. Y. Sanbonmatsu, Biochim. Biophys. Acta, Gene Regul. Mech., 2014, 1839, 1046–1050 CrossRef CAS PubMed
.
- Y. X. Wu and Y. J. Kwon, Methods, 2016, 106, 21–28 CrossRef CAS PubMed
.
- Y. Chushak and M. O. Stone, Nucleic Acids Res., 2009, 37, e87 CrossRef PubMed
.
- J. M. Carothers, S. C. Oestreich and J. W. Szostak, J. Am. Chem. Soc., 2006, 24, 7929–7937 CrossRef PubMed
.
- R. Das and D. Baker, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 14664–14669 CrossRef CAS PubMed
.
- R. Das and D. Baker, Annu. Rev. Biochem., 2008, 77, 363–382 CrossRef CAS PubMed
.
- Y. G. Chushak, J. A. Martin, J. L. Chávez, N. Kelley-Loughnane and M. O. Stone, Methods Mol. Biol., 2014, 1111, 1–15 CAS
.
- K. M. Ruff, T. M. Snyder and D. R. Liu, J. Am. Chem. Soc., 2010, 132, 9453–9464 CrossRef CAS PubMed
.
- Q. Zhou, X. Xia, Z. Luo, H. Liang and E. Shakhnovich, J. Chem. Theory Comput., 2015, 11, 5939–5946 CrossRef CAS PubMed
.
- G. R. Zimmermann, C. L. Wick, T. P. Shields, R. D. Jenison and A. Pardi, RNA, 2000, 6, 659–667 CrossRef CAS PubMed
.
- G. M. Clore, J. Kuszewski and J. Am, J. Am. Chem. Soc., 2003, 125, 1518–1525 CrossRef CAS PubMed
.
- W.-P. Hu, J. V. Kumar, C.-J. Huang and W.-Y. Chen, BioMed Res. Int., 2015, 2015(2015), 658712 Search PubMed
.
- R. R. White, S. Shan, C. P. Rusconi, G. Shetty, M. W. Dewhirst, C. D. Kontos and B. A. Sullenger, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5028–5033 CrossRef CAS PubMed
.
- S. Sarraf-Yazdi, J. Mi, B. J. Moeller, X. Niu, R. R. White, C. D. Kontos, B. A. Sullenger, M. W. Dewhirst and B. M. Clary, J. Surg. Res., 2008, 146, 16–23 CrossRef CAS PubMed
.
- M. Popenda, M. Szachniuk, M. Antczak, K. J. Purzycka, P. Lukasiak, N. Bartol, J. Blazewicz and R. W. Adamiak, Nucleic Acids Res., 2012, 40, e112 CrossRef CAS PubMed
.
- B. Pierce and Z. Weng, Proteins: Struct., Funct., Bioinf., 2007, 67, 1078–1086 CrossRef CAS PubMed
.
- P.-C. Hsieh, H.-T. Lin, W.-Y. Chen, J.
J. P. Tsai and W.-P. Hu, BioMed Res. Int., 2017, 2017, 1–11 CrossRef PubMed
.
-
N. Savory, K. Abe, W. Yoshida and K. Ikebukuro, in Applications of Metaheuristics in Process Engineering, Springer International Publishing, Cham, 2014, pp. 271–288 Search PubMed
.
- C.-Y. Tseng, M. Ashrafuzzaman, J. Y. Mane, J. Kapty, J. R. Mercer and J. A. Tuszynski, Chem. Biol. Drug Des., 2011, 78, 1–13 CAS
.
- R. Ahirwar, S. Nahar, S. Aggarwal, S. Ramachandran, S. Maiti and P. Nahar, Sci. Rep., 2016, 6, 21285 CrossRef CAS PubMed
.
- D. S. Shcherbinin, O. V. Gnedenko, S. A. Khmeleva, S. A. Usanov, A. A. Gilep, A. V. Yantsevich, T. V. Shkel, I. V. Yushkevich, S. P. Radko, A. S. Ivanov, A. V. Veselovsky and A. I. Archakov, J. Struct. Biol., 2015, 191, 112–119 CrossRef CAS PubMed
.
- A. Kumar, A. Voet and K. Y. J. Zhang, Curr. Med. Chem., 2012, 19, 5128–5147 CrossRef CAS PubMed
.
- D. Joseph-McCarthy, A. J. Campbell, G. Kern and D. Moustakas, J. Chem. Inf. Model., 2014, 54, 693–704 CrossRef CAS PubMed
.
- T. T. Le, O. Chumphukam and A. E. G. Cass, RSC Adv., 2014, 4, 47227–47233 RSC
.
- J. Lee, K. H. Lee, J. Jeon, A. Dragulescu-Andrasi, F. Xiao and J. Rao, ACS Chem. Biol., 2010, 5, 1065–1074 CrossRef CAS PubMed
.
- S. E. Lupold, B. J. Hicke, Y. Lin and D. S. Coffey, Cancer Res., 2002, 62, 4029–4033 CAS
.
- W. M. Rockey, F. J. Hernandez, S.-Y. Huang, S. Cao, C. A. Howell, G. S. Thomas, X. Y. Liu, N. Lapteva, D. M. Spencer, J. O. Mcnamara Ii, X. Zou, S.-J. Chen and P. H. Giangrande, Nucleic Acid Ther., 2011, 21, 299–314 CrossRef CAS PubMed
.
- X. Xu, D. D. Dickey, S.-J. Chen and P. H. Giangrande, Methods, 2016, 103, 175–179 CrossRef CAS PubMed
.
- M. Heiat, A. Najafi, R. Ranjbar, A. M. Latifi and M. J. Rasaee, J. Biotechnol., 2016, 230, 34–39 CrossRef CAS PubMed
.
- M. Wieland and J. S. Hartig, ChemBioChem, 2008, 9, 1873–1878 CrossRef CAS PubMed
.
- M. Wachsmuth, S. Findeiss, N. Weissheimer, P. F. Stadler and M. Morl, Nucleic Acids Res., 2013, 41, 2541–2551 CrossRef CAS PubMed
.
- G. Domin, S. Findeiß, M. Wachsmuth, S. Will, P. F. Stadler and M. Mörl, Nucleic Acids Res., 2016, 45, 4108–4119 Search PubMed
.
- P. C. Whitford, J. N. Onuchic, A. Pastore and G. Wei, Curr. Opin. Struct. Biol., 2015, 30, 57–62 CrossRef CAS PubMed
.
- R. M. Abaskharon and F. Gai, Biophys. J., 2016, 110, 1924–1932 CrossRef CAS PubMed
.
- R. B. Best, Curr. Opin. Struct. Biol., 2012, 22, 52–61 CrossRef CAS PubMed
.
- S. Kuyucak and V. Kayser, Comput. Struct. Biotechnol. J., 2017, 15, 138–145 CrossRef CAS PubMed
.
- M. Bermudez, J. Mortier, C. Rakers, D. Sydow and G. Wolber, Drug Discovery Today, 2016, 21, 1799–1805 CrossRef CAS PubMed
.
- C. A. Rohl, C. E. M. Strauss, K. M. S. Misura and D. Baker, Methods Enzymol., 2004, 383, 66–93 CAS
.
- K. Pluhackova and R. A. Böckmann, J. Phys.: Condens. Matter, 2015, 27, 323103 CrossRef PubMed
.
- T. Baştuğ and S. Kuyucak, Biophys. Rev., 2012, 4, 271–282 CrossRef PubMed
.
- J. J. Madsen, A. V. Sinitskiy, J. Li and G. A. Voth, J. Chem. Theory Comput., 2017, 13, 935–944 CrossRef CAS PubMed
.
- R. Salomon-Ferrer, D. A. Case and R. C. Walker, WIREs Comput. Mol. Sci., 2013, 3(2), 198–210 CrossRef CAS
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 12, 19–25 CrossRef
.
- R. F. Alford, A. Leaver-Fay, J. R. Jeliazkov, M. J. O’Meara, F. P. DiMaio, H. Park, M. V. Shapovalov, P. D. Renfrew, V. K. Mulligan, K. Kappel, J. W. Labonte, M. S. Pacella, R. Bonneau, P. Bradley, R. L. Dunbrack, R. Das, D. Baker, B. Kuhlman, T. Kortemme and J. J. Gray, J. Chem. Theory Comput., 2017 DOI:10.1021/acs.jctc.7b00125
.
- K. W. Kaufmann, G. H. Lemmon, S. L. Deluca, J. H. Sheehan and J. Meiler, Biochemistry, 2010, 49, 2987–2998 CrossRef CAS PubMed
.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed
.
- H. Kenzaki, N. Koga, N. Hori, R. Kanada, W. Li, K. Okazaki, X.-Q. Yao, S. Takada and J. Chem, J. Chem. Theory Comput., 2011, 7, 1979–1989 CrossRef CAS PubMed
.
- W. R. P. Scott, P. H. Hünenberger, I. G. Tironi, A. E. Mark, S. R. Billeter, J. Fennen, A. E. Torda, T. Huber, P. Krüger and W. F. van Gunsteren, J. Phys. Chem., 1999, 103, 3596–3607 CrossRef CAS
.
- B. G. Pierce, K. Wiehe, H. Hwang, B.-H. Kim, T. Vreven and Z. Weng, Bioinformatics, 2014, 30, 1771–1773 CrossRef CAS PubMed
.
- D. Schneidman-Duhovny, Y. Inbar, R. Nussinov and H. J. Wolfson, Nucleic Acids Res., 2005, 33, W363–W367 CrossRef CAS PubMed
.
- O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31(2), 455–461 CAS
.
- S. J. de Vries, M. van Dijk and A. M. J. J. Bonvin, Nat. Protoc., 2010, 5, 883–897 CrossRef CAS PubMed
.
- S. Lyskov and J. J. Gray, Nucleic Acids Res., 2008, 36, W233–W238 CrossRef CAS PubMed
.
- Y. Huang, H. Li and Y. Xiao, Biophys. Rep., 2016, 2, 95–99 CrossRef PubMed
.
- S.-Y. Huang and X. Zou, Proteins: Struct., Funct., Bioinf., 2010, 78, 3096–3103 CrossRef CAS PubMed
.
- P. T. Lang, S. R. Brozell, S. Mukherjee, E. F. Pettersen, E. C. Meng, V. Thomas, R. C. Rizzo, D. A. Case, T. L. James and I. D. Kuntz, RNA, 2009, 15, 1219–1230 CrossRef CAS PubMed
.
- R. Lorenz, S. H. Bernhart, C. Höner zu Siederdissen, H. Tafer, C. Flamm, P. F. Stadler and I. L. Hofacker, Algorithms Mol. Biol., 2011, 6, 26 CrossRef PubMed
.
- M. Zuker, Nucleic Acids Res., 2003, 31, 3406–3415 CrossRef CAS PubMed
.
- X. Xu, P. Zhao and S.-J. Chen, PLoS One, 2014, 9, e107504 Search PubMed
.
- K. Sato, M. Hamada, K. Asai and T. Mituyama, Nucleic Acids Res., 2009, 37, W277–W280 CrossRef CAS PubMed
.
- J. S. Reuter and D. H. Mathews, BMC Bioinf., 2010, 11, 129 CrossRef PubMed
.
- M. van Dijk and A. M. J. J. Bonvin, Nucleic Acids Res., 2009, 37, W235–W239 CrossRef CAS PubMed
.
- M. Parisien and F. Major, Nature, 2008, 452, 51–55 CrossRef CAS PubMed
.
- J. N. Zadeh, C. D. Steenberg, J. S. Bois, B. R. Wolfe, M. B. Pierce, A. R. Khan, R. M. Dirks and N. A. Pierce, J. Comput. Chem., 2011, 32, 170–173 CrossRef CAS PubMed
.
- S. Cao and S.-J. Chen, J. Phys. Chem. B, 2011, 115, 4216–4226 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2018 |