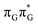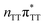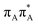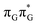Open Access Article
Open Access ArticleSequential electron transfer governs the UV-induced self-repair of DNA photolesions†
Rafał
Szabla
 *ab,
Holger
Kruse
*ab,
Holger
Kruse
 b,
Petr
Stadlbauer
bc,
Jiří
Šponer
b,
Petr
Stadlbauer
bc,
Jiří
Šponer
 b and
Andrzej L.
Sobolewski
a
b and
Andrzej L.
Sobolewski
a
aInstitute of Physics, Polish Academy of Sciences, Al. Lotników 32/46, PL-02668 Warsaw, Poland
bInstitute of Biophysics of the Czech Academy of Sciences, Královopolská 135, 61265 Brno, Czech Republic. E-mail: szabla@ibp.cz
cRegional Centre of Advanced Technologies and Materials, Department of Physical Chemistry, Faculty of Science, Palacký University, 17. Listopadu 1192/12, 77146 Olomouc, Czech Republic
First published on 22nd February 2018
Abstract
Cyclobutane pyrimidine dimers (CpDs) are among the most common DNA lesions occurring due to the interaction with ultraviolet light. While photolyases have been well known as external factors repairing CpDs, the intrinsic self-repairing capabilities of the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T DNA sequence were discovered only recently and are still largely obscure. Here, we elucidate the mechanistic details of this self-repair process by means of MD simulations and QM/MM computations involving the algebraic diagrammatic construction to the second order [ADC(2)] method. We show that local UV-excitation of guanine may be followed by up to three subsequent electron transfers, which may eventually enable efficient CpD ring opening when the negative charge resides on the T
T DNA sequence were discovered only recently and are still largely obscure. Here, we elucidate the mechanistic details of this self-repair process by means of MD simulations and QM/MM computations involving the algebraic diagrammatic construction to the second order [ADC(2)] method. We show that local UV-excitation of guanine may be followed by up to three subsequent electron transfers, which may eventually enable efficient CpD ring opening when the negative charge resides on the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer. Consequently, the molecular mechanism of GAT
T dimer. Consequently, the molecular mechanism of GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T self-repair can be envisaged as sequential electron transfer (SET) occurring downhill along the slope of the S1 potential energy surface. Even though the general features of the SET mechanism are retained in both of the studied stacked conformers, our optimizations of different S1/S0 state crossings revealed minor differences which could influence their self-repair efficiencies. We expect that such assessment of the availability and efficiency of the SET process in other DNA oligomers could hint towards other sequences exhibiting similar photochemical properties. Such explorations will be particularly fascinating in the context of the origins of biomolecules on Earth, owing to the lack of external repairing factors in the Archean age.
T self-repair can be envisaged as sequential electron transfer (SET) occurring downhill along the slope of the S1 potential energy surface. Even though the general features of the SET mechanism are retained in both of the studied stacked conformers, our optimizations of different S1/S0 state crossings revealed minor differences which could influence their self-repair efficiencies. We expect that such assessment of the availability and efficiency of the SET process in other DNA oligomers could hint towards other sequences exhibiting similar photochemical properties. Such explorations will be particularly fascinating in the context of the origins of biomolecules on Earth, owing to the lack of external repairing factors in the Archean age.
Introduction
Dimerization of DNA bases is one of the most detrimental phenomena occurring during the exposure of nucleic acid strands to UV-light.1 Cyclobutane pyrimidine dimers (CpDs) and (6-4) lesions can be classified among the most frequent photodimers and are responsible for mutagenic processes driven by hindered transcription and DNA replication.2 To protect living organisms from such UV-activated stress, nature developed sophisticated enzymes, i.e. photolyases, which selectively repair CpDs and (6-4) lesions via electron transfer or proton-coupled electron transfer processes.3,4 Despite the existence of repairing machinery, DNA photolesions are a common cause of skin cancer1,5–7 and the mechanistic details of their formation and repair have been attracting significant attention involving both experimental and theoretical studies.8–17The vulnerability of DNA and RNA to the harmful effects of UV-radiation is particularly intriguing in the context of the origins of life. First of all, it is reasonable to assume that the highly sophisticated photolyases were absent during the emergence of the first oligonucleotides. Furthermore, recent theoretical estimates showed that much higher amounts of UV-light were reaching the surface of the Archean Earth, owing to the lack of oxygen in the atmosphere and higher Sun activity in the ultraviolet spectral range.18–22 Interestingly, a recent work by Bucher et al.23 revealed that specific DNA sequences may promote very efficient self-repair driven by photoinduced electron transfer to the CpD lesion containing two dimerized thymine bases (T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T). This remarkable property was discovered for the GAT
T). This remarkable property was discovered for the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T sequence in single and double strands, while no repair was reported for the TAT
T sequence in single and double strands, while no repair was reported for the TAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T and AT
T and AT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T oligomers.23 The significant selectivity of this process implies that UV-light played an important role in the prebiotic selection of the most photochemically stable nucleic acid sequences.24
T oligomers.23 The significant selectivity of this process implies that UV-light played an important role in the prebiotic selection of the most photochemically stable nucleic acid sequences.24
Many fundamental aspects of the photochemistry of nucleic acid oligomers (such as GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T) are still obscure, including the relative contribution of locally-excited (LE) and delocalized excitations in DNA strands, the extent of the charge-transfer (CT) character of the latter, and the availability of different photorelaxation pathways in such assemblies.25,26 While some valuable insights into these processes were provided by time-resolved (TR) spectroscopic (e.g. transient absorption UV) techniques,27 it is generally difficult to study the clear origin of the long-lived states due to overlapping absorption features of different nucleobases.25 In addition, selective synthesis of specific photodamaged sequences is challenging. On the other hand, considerable system sizes often restrict the applications of theoretical simulations to methods such as Time-Dependent Density Functional Theory (TDDFT). Even though TDDFT was employed with some success in investigations of photochemical and photophysical properties of oligonucleotides,28,29 the applicability of this methodology to similar problems has been criticized because of often significant overstabilization of CT states.26,30,31 While range-separated functionals can alleviate this problem to some extent for vertical excitations, nonadiabatic molecular dynamics simulations of adenine with TDDFT failed to correctly describe the excited-state lifetimes and photodeactivation pathways.32
T) are still obscure, including the relative contribution of locally-excited (LE) and delocalized excitations in DNA strands, the extent of the charge-transfer (CT) character of the latter, and the availability of different photorelaxation pathways in such assemblies.25,26 While some valuable insights into these processes were provided by time-resolved (TR) spectroscopic (e.g. transient absorption UV) techniques,27 it is generally difficult to study the clear origin of the long-lived states due to overlapping absorption features of different nucleobases.25 In addition, selective synthesis of specific photodamaged sequences is challenging. On the other hand, considerable system sizes often restrict the applications of theoretical simulations to methods such as Time-Dependent Density Functional Theory (TDDFT). Even though TDDFT was employed with some success in investigations of photochemical and photophysical properties of oligonucleotides,28,29 the applicability of this methodology to similar problems has been criticized because of often significant overstabilization of CT states.26,30,31 While range-separated functionals can alleviate this problem to some extent for vertical excitations, nonadiabatic molecular dynamics simulations of adenine with TDDFT failed to correctly describe the excited-state lifetimes and photodeactivation pathways.32
In the light of the above discussion, characterization of photoinduced processes in oligonucleotides based on highly accurate quantum-chemical methods is urgently needed. In particular, a much more balanced description of the LE and CT states, even outside the Franck–Condon region, can be obtained with the algebraic diagrammatic construction to the second order [ADC(2)] method.33,34 The ADC(2) method was recently proved to provide reliable results in the investigations of the photochemistry of nucleic acids fragments within the QM/MM framework (referred to as ADC(2)/MM from here on).26,35–39 However, these simulations only involved the nucleobases treated at the ADC(2) level and the effects of the truncation of the QM region at the N-glycosidic bond are unclear. Moreover, previous studies did not consider optimizations of minimum-energy crossing points (MECPs) at the ADC(2)/MM level, which are crucial in understanding the reactivity of different electronic states participating in the photochemistry of oligonucleotides.
Our goal is to identify the possible mechanistic features and intermediate states that govern the sequence selective self-repair in nucleic acid fragments, first observed by Bucher et al.23 For this purpose, we employ the ADC(2)/MM protocol (nucleobases treated at the ADC(2) level) to optimize the minimum-energy geometries and compare the relative energies of different LE and delocalized states in the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T oligomer. We further discuss MECP optimizations and validate the energies of all stationary points by including the whole tetranucleotide in the QM region. This enables us to expose some of the potential pitfalls of the previous approaches, like often incorrect prediction of the relative energies of intermediate delocalized states. Based on these simulations we propose that the photochemical self-repair of the GAT
T oligomer. We further discuss MECP optimizations and validate the energies of all stationary points by including the whole tetranucleotide in the QM region. This enables us to expose some of the potential pitfalls of the previous approaches, like often incorrect prediction of the relative energies of intermediate delocalized states. Based on these simulations we propose that the photochemical self-repair of the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T sequence can be envisioned as a sequential electron transfer (SET) process which involves multiple changes of the orbital (diabatic) character of the S1 state occurring downhill along the slope of the S1 potential energy surface, after the local excitation of one of the purine bases.
T sequence can be envisioned as a sequential electron transfer (SET) process which involves multiple changes of the orbital (diabatic) character of the S1 state occurring downhill along the slope of the S1 potential energy surface, after the local excitation of one of the purine bases.
Computational methods
MD simulations
The initial geometry of the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T tetranucleotide was prepared in the B-DNA helical form. The T
T tetranucleotide was prepared in the B-DNA helical form. The T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T residue was prepared in the same way as the standard AMBER nucleotides.40 The torsion parameters for the cyclobutane ring in the T
T residue was prepared in the same way as the standard AMBER nucleotides.40 The torsion parameters for the cyclobutane ring in the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer given by the standard atomic types of the parmOL15 force field41–44 were found satisfactory according to our test simulation. MD simulations were carried out under the parmOL15 force field41–44 in an octahedral box of explicit water molecules (either SPC/E,45 or OPC model46) with 0.15 M excess KCl,47 using the AMBER software package.48 Each of these simulations was propagated for 10 μs. The trajectories were clustered by a custom modified algorithm49 of Rodriguez et al.,50 using the eRMSD metric.51 More details about the MD simulations are included in the ESI† to this article.
T dimer given by the standard atomic types of the parmOL15 force field41–44 were found satisfactory according to our test simulation. MD simulations were carried out under the parmOL15 force field41–44 in an octahedral box of explicit water molecules (either SPC/E,45 or OPC model46) with 0.15 M excess KCl,47 using the AMBER software package.48 Each of these simulations was propagated for 10 μs. The trajectories were clustered by a custom modified algorithm49 of Rodriguez et al.,50 using the eRMSD metric.51 More details about the MD simulations are included in the ESI† to this article.
QM/MM simulations
The geometries of selected (GA-anti and GA-syn) conformers obtained from the clustering procedure were further utilized in the QM/MM calculations. These geometries were solvated in a spherical droplet of SPC/E explicit water molecules, with a radius of 25 Å. The solvent was then equilibrated for 10 ps, in order to obtain a reasonable distribution of the water molecules within the sphere. We considered two different QM/MM setups: QMDNA/MM setup contained the whole tetranucleotide treated at the QM level, while only the nucleobases were included in the QM region of QMbases/MM setup (see Fig. 1, for the pictorial representation). In fact, QMbases/MM setup is the primarily used setting in many calculations considering the photochemistry and photophysics of nucleic acid fragments.52,53 The link hydrogen atom scheme was applied in QMbases/MM setup, where the boundary between the QM and MM regions bisected the covalent N-glycosidic bonds. The point charge of the MM link hydrogen atom was set to zero, to avoid overpolarization.54 These simulations were performed using a locally-modified QM/MM interface54 of the AMBER suite of programs48 to enable QM calculations employing the TURBOMOLE 7.1 program,55 within the electrostatic embedding framework.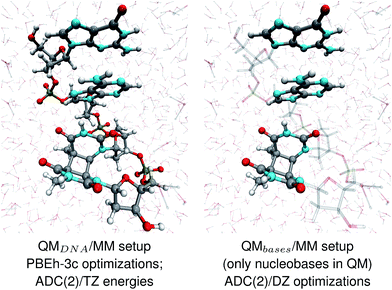 | ||
| Fig. 1 The two QM/MM setups applied to the energy calculations and structural optimizations performed in this work. | ||
The QM/MM optimizations of the ground-state equilibrium geometries were first performed using QMDNA/MM setup and the low-cost hybrid DFT composite scheme, PBEh-3c.56 The PBEh-3c method was recently shown to be particularly well suited for calculations of RNA tetranucleotides.57 The initial optimizations were performed for the whole QM/MM system using the internal AMBER48 optimizer and the limited-memory BFGS method. These geometries were reoptimized with tighter convergence criteria using a rational function and approximate normal coordinates scheme as implemented in the open-source optimizer XOPT.58–60 During the reoptimization procedure only the atom positions in an inner spherical region of the QM/MM system were relaxed, while the outer region was kept frozen. The inner region contained all the atoms within 11.5 Å of the most central atom of the GA-anti conformer and 12.5 Å of the most central atom of the GA-syn conformer. The inner region was in each case carefully selected to keep an appropriate solvation shell around the tetranucleotide. This approach was also applied in the excited-state calculations.
The algebraic diagrammatic construction to the second order [ADC(2)]33,34,61 method was used in all the excited-state calculations. The ADC(2) method was shown to yield a correct description of the excited-state potential energy surfaces of adenine and thymine outside the Franck–Condon region.32,62 The vertical excitation energies and oscillator strengths were calculated on top of the PBEh-3c geometries, using the QMbases/MM setup, ADC(2) method and the TZVP basis set. The QMbases/MM setup was also used in the ADC(2)/MM optimizations of the different minima on the PE surface of the S1 state and all the minimum-energy crossing points (MECPs). The TheoDORE 1.5.1 package was used to establish the charge transfer numbers and perform electron–hole population analysis.63,64 The molecular orbitals were generated using the IboView program.65 MECPs were optimized employing the approach of Levine, Coe and Martínez,66 which was recently shown to provide reliable S1(ππ*)/S0 conical intersection geometries in several biomolecular systems without the evaluation of nonadiabatic couplings.67,68 This scheme was included in the XOPT code to enable the optimization of state crossings within the QM/MM framework. Even though, it was indicated that the ADC(2)/MP2 methods may fail to correctly reproduce the topography of nπ*/S0 state crossings in nucleobases,68 all of the S1/S0 MECPs considered in this work involved ππ* excitations, and consequently we anticipate the corresponding MECP geometries to be reliable. To keep consistent geometries when comparing the energies of different excited state minima with the Franck–Condon region, the ground-state geometry was additionally optimized using QMbases/MM setup and MP2/MM approach. All of the ADC(2)/MM and MP2/MM optimizations were performed with the def2-SVP basis set. In addition, the energies of all the stationary points were recalculated using the QMDNA/MM setup (whole tetranucleotide in the QM region) the ADC(2) and MP2 methods and the larger TZVP basis set.
Results and discussion
MD simulations and conformational analysis
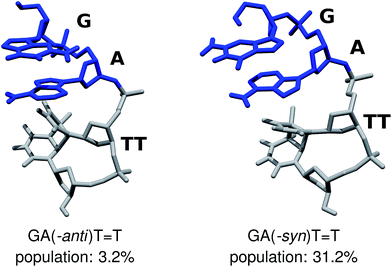
We performed Molecular Dynamics (MD) simulations of the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T tetranucleotide to explore its conformational space and asses the population of different structural arrangements. Our main goal was to establish the availability of different fully stacked conformations, which could readily assist in the sequential electron transfer process responsible for the self-repair of CpD lesions, as described by Bucher et al.23 Even though force-field based MD simulations of DNA and RNA tetramers frequently yield spurious populations of experimentally unconfirmed conformers,69–71 better agreement with experiments was obtained for r(GACC) and r(CCCC) by employing more accurate solvent models, like OPC.46,68,72 Consequently, we carried out 10 μs-long MD simulations employing one of the traditionally used 3-point water models SPC/E, and the conceivably more accurate 4-point water model OPC,46 for comparison. Both the SPC/E and OPC simulations yielded qualitatively consistent populations of the fully stacked conformations of the GAT
T tetranucleotide to explore its conformational space and asses the population of different structural arrangements. Our main goal was to establish the availability of different fully stacked conformations, which could readily assist in the sequential electron transfer process responsible for the self-repair of CpD lesions, as described by Bucher et al.23 Even though force-field based MD simulations of DNA and RNA tetramers frequently yield spurious populations of experimentally unconfirmed conformers,69–71 better agreement with experiments was obtained for r(GACC) and r(CCCC) by employing more accurate solvent models, like OPC.46,68,72 Consequently, we carried out 10 μs-long MD simulations employing one of the traditionally used 3-point water models SPC/E, and the conceivably more accurate 4-point water model OPC,46 for comparison. Both the SPC/E and OPC simulations yielded qualitatively consistent populations of the fully stacked conformations of the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T tetramer, i.e. 54.1% and 45.5% respectively. While some discrepancies between these two simulation runs are apparent, we focus on discussing the two conformers which could potentially have the largest contribution to the overall photochemistry either in the tetranucleotide or in longer DNA strands (cf.Fig. 2).
T tetramer, i.e. 54.1% and 45.5% respectively. While some discrepancies between these two simulation runs are apparent, we focus on discussing the two conformers which could potentially have the largest contribution to the overall photochemistry either in the tetranucleotide or in longer DNA strands (cf.Fig. 2).
The majority of the ADC(2)/MM calculations were performed for the GA-anti conformer, which has the anti orientation of the G and A bases and represents the spatial arrangement of the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T sequence in longer DNA strands. Since the population of the GA-anti conformer is relatively low (3.2% based on the OPC simulations), we additionally considered the GA-syn conformer having both the G and A bases in the syn orientation with respect to the sugar moieties. Both the SPC/E and OPC simulations indicate that the GA-syn conformer is the dominant molecular arrangement with the estimated populations of 47.0% and 31.2%, respectively. The ADC(2)/MM calculations performed for the GA-syn are shown in the ESI,† since the major conclusions regarding the self-repair mechanism remained unchanged in both studied cases. We also identified two other conformers which contributed to the ensemble of fully stacked geometries, namely the G-syn-A-anti and G-anti-A-syn substates, but were not examined in the further ADC(2)/MM calculations.
T sequence in longer DNA strands. Since the population of the GA-anti conformer is relatively low (3.2% based on the OPC simulations), we additionally considered the GA-syn conformer having both the G and A bases in the syn orientation with respect to the sugar moieties. Both the SPC/E and OPC simulations indicate that the GA-syn conformer is the dominant molecular arrangement with the estimated populations of 47.0% and 31.2%, respectively. The ADC(2)/MM calculations performed for the GA-syn are shown in the ESI,† since the major conclusions regarding the self-repair mechanism remained unchanged in both studied cases. We also identified two other conformers which contributed to the ensemble of fully stacked geometries, namely the G-syn-A-anti and G-anti-A-syn substates, but were not examined in the further ADC(2)/MM calculations.
Vertical excitation energies
The averaged OPC structures of the GA-syn and GA-anti conformers were further optimized using the QMDNA/MM setup (Fig. 1) and the PBEh-3c method. Based on these geometries we calculated the vertical excitation energies using the QMbases/MM setup and the ADC(2)/TZVP method (cf.Table 1 for the GA-anti conformer). As observed previously for other DNA oligomers,26,38 the lower-energy range of the spectrum is populated by locally excited states, while the lowest-lying CT of the GA-anti conformer state can be classified as the S10 state and is associated with an electron transferred from the A purine base to the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer. The lower part of the spectrum is essentially dominated by ππ* and nπ* excitations localized on the respective bases.
T dimer. The lower part of the spectrum is essentially dominated by ππ* and nπ* excitations localized on the respective bases.
The lowest-lying locally-excited 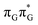 state on the G base has an excitation energy of 4.91 eV and is the lowest-energy excitation (S1) in the whole tetranucleotide. We expect that this state was predominantly populated in the experiments conducted by Bucher et al.,23 which involved photoexcitation in the UVB spectral range (λexc = 290 nm, 4.28 eV). The optically bright
state on the G base has an excitation energy of 4.91 eV and is the lowest-energy excitation (S1) in the whole tetranucleotide. We expect that this state was predominantly populated in the experiments conducted by Bucher et al.,23 which involved photoexcitation in the UVB spectral range (λexc = 290 nm, 4.28 eV). The optically bright 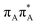 transitions associated with the A base correspond to the S3 and S4 states in the GAT
transitions associated with the A base correspond to the S3 and S4 states in the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T tetranucleotide and can be accessed at slightly higher excitation energies, i.e. 5.11 eV and 5.21 eV. The remaining states present in the lower energy range of the spectrum are nπ* excitations localized on the C4
T tetranucleotide and can be accessed at slightly higher excitation energies, i.e. 5.11 eV and 5.21 eV. The remaining states present in the lower energy range of the spectrum are nπ* excitations localized on the C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups of the T
O groups of the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer. These nπ* states were previously suggested to participate in the direct self-repair of the T
T dimer. These nπ* states were previously suggested to participate in the direct self-repair of the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimers. However, the MM solvent is represented by a point charge scheme and many electronic effects crucial for the dark nπ* are neglected in this approach. In fact, it was demonstrated that the inclusion of explicit QM water molecules results in considerable blue-shift of nOπ* states.73,74 Here, the consideration of all the neighbouring water molecules at the QM level is beyond our computational capabilities, albeit we expect that such blue-shift of these nOπ* states in the GAT
T dimers. However, the MM solvent is represented by a point charge scheme and many electronic effects crucial for the dark nπ* are neglected in this approach. In fact, it was demonstrated that the inclusion of explicit QM water molecules results in considerable blue-shift of nOπ* states.73,74 Here, the consideration of all the neighbouring water molecules at the QM level is beyond our computational capabilities, albeit we expect that such blue-shift of these nOπ* states in the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T tetranucleotide would significantly decrease their availability in the photochemical processes studied in this work. The ππ* excitations associated with the T
T tetranucleotide would significantly decrease their availability in the photochemical processes studied in this work. The ππ* excitations associated with the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer can be also found in higher energy range of the spectrum.
T dimer can be also found in higher energy range of the spectrum.
Sequential electron transfer
Assuming the initial population of the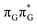 state, we expect all the subsequent photophysical and photochemical processes to occur on the S1 hypersurface. The near proximity of several chromophores enables the formation of exciplex states and occurrence of charge transfer events resulting in changes of the character of the S1 state. In fact, the multitude of possible excited-state phenomena makes the photochemistry of oligonucleotides much more complex when compared to isolated nucleobases. Here, we propose that the self-repair of the GAT
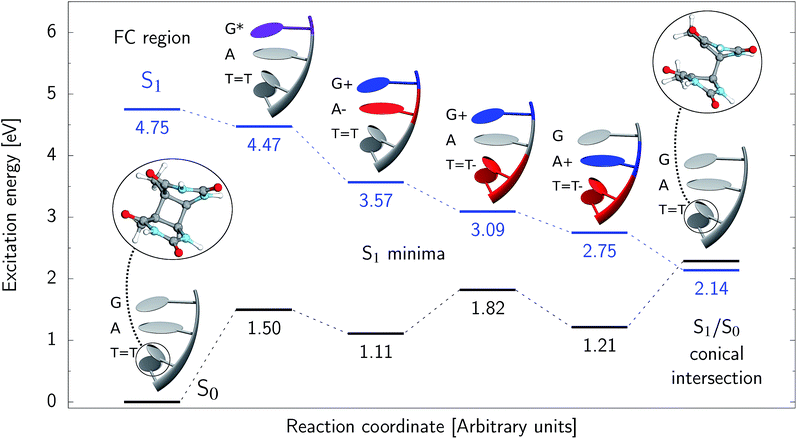
state, we expect all the subsequent photophysical and photochemical processes to occur on the S1 hypersurface. The near proximity of several chromophores enables the formation of exciplex states and occurrence of charge transfer events resulting in changes of the character of the S1 state. In fact, the multitude of possible excited-state phenomena makes the photochemistry of oligonucleotides much more complex when compared to isolated nucleobases. Here, we propose that the self-repair of the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T tetramer can be envisioned as a sequential electron transfer involving consecutive changes of the diabatic character of the S1 state. As shown in Fig. 3, each of the stationary points between the Franck–Condon region and the CpD ring-opening MECP corresponds to a local minimum associated with a different orbital character and the deduced mechanism operates downhill on the S1 hypersurface.
T tetramer can be envisioned as a sequential electron transfer involving consecutive changes of the diabatic character of the S1 state. As shown in Fig. 3, each of the stationary points between the Franck–Condon region and the CpD ring-opening MECP corresponds to a local minimum associated with a different orbital character and the deduced mechanism operates downhill on the S1 hypersurface.
Right after the photoexcitation, the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T tetranucleotide can undergo vibrational relaxation to the minimum of the
T tetranucleotide can undergo vibrational relaxation to the minimum of the 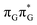 state (denoted as G* in Fig. 3) associated with moderate puckering of the guanine base. This ring puckering effect is most pronounced at the C4 and C5 atoms in the GA-anti conformer and the C2 carbon atom connected to the amino group in the case of the GA-syn conformer. From these
state (denoted as G* in Fig. 3) associated with moderate puckering of the guanine base. This ring puckering effect is most pronounced at the C4 and C5 atoms in the GA-anti conformer and the C2 carbon atom connected to the amino group in the case of the GA-syn conformer. From these 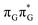 minima the system can reach the ππ*/S0 conical intersection described before as the dominant photodeactivation channel in isolated guanine.75,76 This state crossing in the GA-syn conformer is characterized by a more pronounced puckering of the C2 carbon atom and a slightly sloped topography, since it lies 0.15 eV above the
minima the system can reach the ππ*/S0 conical intersection described before as the dominant photodeactivation channel in isolated guanine.75,76 This state crossing in the GA-syn conformer is characterized by a more pronounced puckering of the C2 carbon atom and a slightly sloped topography, since it lies 0.15 eV above the 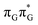 minimum. Based on analogous calculations and virtually identical results for isolated guanine, we anticipate that the photorelaxation of UV-excited guanine in the GA-syn conformer resembles the photodeactivation mechanisms reported in gas phase studies.75 In contrast, our optimizations of the
minimum. Based on analogous calculations and virtually identical results for isolated guanine, we anticipate that the photorelaxation of UV-excited guanine in the GA-syn conformer resembles the photodeactivation mechanisms reported in gas phase studies.75 In contrast, our optimizations of the 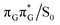 MECP in the GA-anti conformer yielded a C4-puckered geometry that lies 0.5 eV above the respective
MECP in the GA-anti conformer yielded a C4-puckered geometry that lies 0.5 eV above the respective 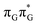 minimum. This suggests that some of the monomeric photodeactivation channels in oligonucleotides may be significantly hindered in selected conformers due to the interactions with neighbouring bases.
minimum. This suggests that some of the monomeric photodeactivation channels in oligonucleotides may be significantly hindered in selected conformers due to the interactions with neighbouring bases.
Alternatively, the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T tetranucleotide containing UV-excited guanine may follow a relaxation pathway on the S1 surface towards a further local minimum possibly associated with a CT or exciplex state. This scenario was previously hypothesized by Bucher et al.,23 who suggested that the G+˙A−˙ state could be the key intermediate state that precedes the electron transfer to the T
T tetranucleotide containing UV-excited guanine may follow a relaxation pathway on the S1 surface towards a further local minimum possibly associated with a CT or exciplex state. This scenario was previously hypothesized by Bucher et al.,23 who suggested that the G+˙A−˙ state could be the key intermediate state that precedes the electron transfer to the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer.23 Our ADC(2)/MM calculations reveal that even though the G+˙A−˙
T dimer.23 Our ADC(2)/MM calculations reveal that even though the G+˙A−˙ 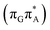 state lies above the S10 state in the Franck–Condon region of the GA-anti conformer, it is significantly red-shifted during the initial vibrational relaxation of the UV-excited guanine. In fact both the S2 and S3 excitations, computed on the
state lies above the S10 state in the Franck–Condon region of the GA-anti conformer, it is significantly red-shifted during the initial vibrational relaxation of the UV-excited guanine. In fact both the S2 and S3 excitations, computed on the 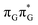 LE minimum-energy geometry, are delocalized states involving charge transfer between the G and A bases. In particular, the G+˙A−˙ state considered by Bucher et al.,23 lies merely 1.59 eV above the
LE minimum-energy geometry, are delocalized states involving charge transfer between the G and A bases. In particular, the G+˙A−˙ state considered by Bucher et al.,23 lies merely 1.59 eV above the 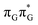 LE minimum and corresponds to the S3 state. Surprisingly, the S2 state lying 1.26 eV above the
LE minimum and corresponds to the S3 state. Surprisingly, the S2 state lying 1.26 eV above the 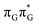 LE minimum is characterized by an opposite electron transfer from adenine to guanine. While we successfully optimized the S1 minimum corresponding to the G+˙A−˙ state, we could not locate the G−˙A+˙ minimum at the ADC(2)/MM level and we anticipate that this latter state is not involved in the photoreactivity of the GAT
LE minimum is characterized by an opposite electron transfer from adenine to guanine. While we successfully optimized the S1 minimum corresponding to the G+˙A−˙ state, we could not locate the G−˙A+˙ minimum at the ADC(2)/MM level and we anticipate that this latter state is not involved in the photoreactivity of the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T tetramer.
T tetramer.
The G+˙A−˙ minimum lies 0.9 eV below the 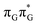 LE minimum and may become the direct precursor of the
LE minimum and may become the direct precursor of the 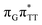 CT state which entails an electron transfer to the T
CT state which entails an electron transfer to the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer. In other words, the negatively charged adenine could readily transfer its excess electron to the T
T dimer. In other words, the negatively charged adenine could readily transfer its excess electron to the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer leading to the formation of the reactive state with self-repair propensity. This G+˙AT
T dimer leading to the formation of the reactive state with self-repair propensity. This G+˙AT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T−˙ minimum is again lower in energy than the preceding stationary point, by nearly 0.5 eV. In addition, we located another local minimum on the S1 surface containing the negatively charged CpD, namely the GA+˙T
T−˙ minimum is again lower in energy than the preceding stationary point, by nearly 0.5 eV. In addition, we located another local minimum on the S1 surface containing the negatively charged CpD, namely the GA+˙T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T−˙
T−˙ 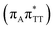 state. The ADC(2)/MM energies computed for the whole tetranucleotide reveal that the latter CT minimum having the positive charge localized on the A base is, in fact, the lowest-energy S1 minimum available in the GA-syn conformer and possibly the last link in the SET mechanism before the actual T
state. The ADC(2)/MM energies computed for the whole tetranucleotide reveal that the latter CT minimum having the positive charge localized on the A base is, in fact, the lowest-energy S1 minimum available in the GA-syn conformer and possibly the last link in the SET mechanism before the actual T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer repair.
T dimer repair.
Our optimizations of the S1/S0 MECP initiated from both the GA+˙T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T−˙ and G+˙AT
T−˙ and G+˙AT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T−˙ minimum-energy geometries converged to the same
T−˙ minimum-energy geometries converged to the same 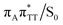 state crossing. This MECP is characterized by a partially opened cyclobutane ring with the C5–C5 bond being broken and the C6–C6 bond remaining the single covalent connection between the two thymine bases (cf.Fig. 3). We anticipate that this self-repair mechanism can operate from both the GA+˙T
state crossing. This MECP is characterized by a partially opened cyclobutane ring with the C5–C5 bond being broken and the C6–C6 bond remaining the single covalent connection between the two thymine bases (cf.Fig. 3). We anticipate that this self-repair mechanism can operate from both the GA+˙T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T−˙ and G+˙AT
T−˙ and G+˙AT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T−˙ minima, since the primary factor that enables the T
T−˙ minima, since the primary factor that enables the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer repair is the electron transfer to the photolesion and not the location of the hole (positive charge) in the system.
T dimer repair is the electron transfer to the photolesion and not the location of the hole (positive charge) in the system.
It is generally difficult to envisage the exact reaction coordinates leading to the transitions between the different stationary points presented in Fig. 3, owing to the large number of nuclear degrees of freedom in the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T tetramer. In other words, S1 hypersufaces of oligonucleotides are significantly more complex when compared to isolated nucleosides and nucleobases. However, we anticipate that the local minima constituting the SET mechanism are rather shallow and we expect the energy barriers separating the consecutive stages to be generally low. This is reflected by the high sensitivity of the excited-state optimizations to the initial guess geometry, i.e. sometimes small changes in the initial geometry may result in convergence to another local minimum on the S1 hypersurface. Another important factor which determines the efficiency of the transitions between the different minima is the availability of S1/S0 conical intersections from the intermediate states. As we have shown above, the high energy of the
T tetramer. In other words, S1 hypersufaces of oligonucleotides are significantly more complex when compared to isolated nucleosides and nucleobases. However, we anticipate that the local minima constituting the SET mechanism are rather shallow and we expect the energy barriers separating the consecutive stages to be generally low. This is reflected by the high sensitivity of the excited-state optimizations to the initial guess geometry, i.e. sometimes small changes in the initial geometry may result in convergence to another local minimum on the S1 hypersurface. Another important factor which determines the efficiency of the transitions between the different minima is the availability of S1/S0 conical intersections from the intermediate states. As we have shown above, the high energy of the 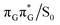 state crossing will facilitate the population of the G+˙A−˙ minimum. Limited accessibility of the
state crossing will facilitate the population of the G+˙A−˙ minimum. Limited accessibility of the 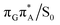 state crossings is discussed below. As pointed out by Lee and co-workers,16 the evaluation of diabatic coupling matrix elements (DCMEs) between the electronic states is crucial for proving the validity of a proposed photoreaction mechanism. Our estimates based on the generalized Mulliken Hush and Boys localization approaches,77,78 yielded DCMEs exceeding 0.1 eV between the consecutive electronic states. This implies that the electron transfer events in the GAT
state crossings is discussed below. As pointed out by Lee and co-workers,16 the evaluation of diabatic coupling matrix elements (DCMEs) between the electronic states is crucial for proving the validity of a proposed photoreaction mechanism. Our estimates based on the generalized Mulliken Hush and Boys localization approaches,77,78 yielded DCMEs exceeding 0.1 eV between the consecutive electronic states. This implies that the electron transfer events in the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T could be indeed very efficient. Nevertheless, our DCME estimates require a separate commentary, which can be found in the ESI.† A detailed and accurate description of the transition paths between the different stationary points in the SET mechanism could be inferred from nonadiabatic molecular dynamics simulations, but this approach is currently beyond our computational capabilities for systems of this size.
T could be indeed very efficient. Nevertheless, our DCME estimates require a separate commentary, which can be found in the ESI.† A detailed and accurate description of the transition paths between the different stationary points in the SET mechanism could be inferred from nonadiabatic molecular dynamics simulations, but this approach is currently beyond our computational capabilities for systems of this size.
The characteristics of the available intermediate states
Intermediate states with charge transfer character play a central role in driving the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T tetramer towards the S1/S0 conical intersection responsible for C5–C5 bond breaking of the CpD lesion. Therefore, understanding their most distinctive features is essential in finding the photoreaction pathway responsible for the self-repair of a given oligonucleotide. The molecular orbitals associated with each of the proposed intermediate states in the GA-anti conformer are presented in Fig. 4. The dominant π (occupied; blue and violet) and π* (virtual; green and yellow) molecular orbitals contributing in at least 88% to each of these excitations clearly demonstrate their CT character.
T tetramer towards the S1/S0 conical intersection responsible for C5–C5 bond breaking of the CpD lesion. Therefore, understanding their most distinctive features is essential in finding the photoreaction pathway responsible for the self-repair of a given oligonucleotide. The molecular orbitals associated with each of the proposed intermediate states in the GA-anti conformer are presented in Fig. 4. The dominant π (occupied; blue and violet) and π* (virtual; green and yellow) molecular orbitals contributing in at least 88% to each of these excitations clearly demonstrate their CT character.
Apart from the three CT states already mentioned in the SET mechanism, we also located one exciplex state shared between the G and A bases which does not have any notable CT character. The corresponding geometry of the GA-exciplex minimum is presented in the top left panel of Fig. 4. The ADC(2) optimizations performed using the QMbases/MM setup initially indicated that the GA-exciplex state could be the first intermediate reached from the 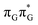 LE state. At the same time, the ADC(2) energy of the G+˙A−˙ minimum obtained using the QMbases/MM setup was higher than the
LE state. At the same time, the ADC(2) energy of the G+˙A−˙ minimum obtained using the QMbases/MM setup was higher than the 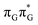 LE minimum. However, this picture is completely different when the ADC(2) energies are recalculated within the QMDNA/MM setup, i.e. when the sugar-phosphate backbone is included in the QM region. We presume that this unexpected behavior is the result of strong differences in the electric dipole moment direction and magnitude between the QMDNA/MM and QMbases/MM setups characteristic for these two particular states. In other words, the QMbases/MM setup is incapable of correctly reproducing the μ vectors of the G+˙A−˙ and GA-exciplex states, which substantially affects the relative energies of the states in the field of electrostatic point charges. The relative energies of the remaining intermediate states are not affected by the size of QM region in the qualitative sense. Nevertheless, the example of the GA-exciplex and G+˙A−˙ intermediate states shows that the truncation of the QM region at the N-glycosidic bond might result in deceptive results and considerable care needs to be taken during the prediction of relative energies of different electronic states in nucleic acids within the QM/MM framework.
LE minimum. However, this picture is completely different when the ADC(2) energies are recalculated within the QMDNA/MM setup, i.e. when the sugar-phosphate backbone is included in the QM region. We presume that this unexpected behavior is the result of strong differences in the electric dipole moment direction and magnitude between the QMDNA/MM and QMbases/MM setups characteristic for these two particular states. In other words, the QMbases/MM setup is incapable of correctly reproducing the μ vectors of the G+˙A−˙ and GA-exciplex states, which substantially affects the relative energies of the states in the field of electrostatic point charges. The relative energies of the remaining intermediate states are not affected by the size of QM region in the qualitative sense. Nevertheless, the example of the GA-exciplex and G+˙A−˙ intermediate states shows that the truncation of the QM region at the N-glycosidic bond might result in deceptive results and considerable care needs to be taken during the prediction of relative energies of different electronic states in nucleic acids within the QM/MM framework.
The electron–hole population analysis shows that the G+˙A−˙ state is associated with 0.57 and 0.45 electron transferred from guanine to adenine in the corresponding G+˙A−˙ S1 minima of the GA-anti and GA-anti conformers. The consecutive 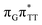 CT state accessed in the GA-anti conformer involves a transfer of 0.97 e− to the T
CT state accessed in the GA-anti conformer involves a transfer of 0.97 e− to the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer from the G and A bases, where 0.55 e− is transferred from G and 0.42 e− from A. In contrast, the corresponding
T dimer from the G and A bases, where 0.55 e− is transferred from G and 0.42 e− from A. In contrast, the corresponding 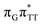 CT state found in the GA-syn conformer involves a transfer of 0.94 e− to the T
CT state found in the GA-syn conformer involves a transfer of 0.94 e− to the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer occurring exclusively from the G base. However, we denote this state as G+˙AT
T dimer occurring exclusively from the G base. However, we denote this state as G+˙AT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T−˙, to keep a uniform naming scheme for both studied conformers. Finally, the GA+˙T
T−˙, to keep a uniform naming scheme for both studied conformers. Finally, the GA+˙T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T−˙ minimum in the GA-anti conformer is associated with 0.96 e− transferred to the T
T−˙ minimum in the GA-anti conformer is associated with 0.96 e− transferred to the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer, where the majority of the hole (0.87) is located on the A base. These results confirm the previous suggestion that CT states could involve delocalization of the transferred charge over the neighbouring bases.25 However, we expect this feature to be dependent on the local arrangement of nucleobases, since it is present in only one of the studied conformers.
T dimer, where the majority of the hole (0.87) is located on the A base. These results confirm the previous suggestion that CT states could involve delocalization of the transferred charge over the neighbouring bases.25 However, we expect this feature to be dependent on the local arrangement of nucleobases, since it is present in only one of the studied conformers.
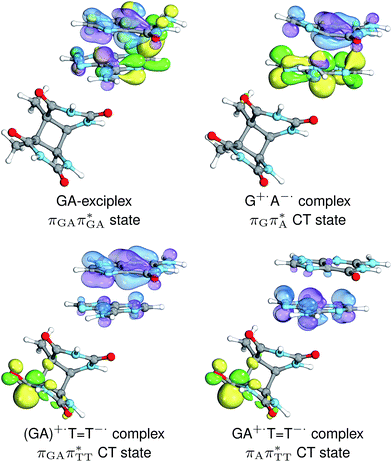
The charge transfer process occurring from guanine to adenine results in the formation of fascinating interactions between the two bases (cf.Fig. 5). In the case of the GA-anti conformer, a strong interaction is created between the C5 atom of guanine and the amino group of adenine associated with a C5⋯NH2 distance of 2.14 Å. On the contrary, the G+˙A−˙ state in the GA-syn conformer leads to the formation of an interaction between the C6 atom of guanine and the C6 atom of adenine with the equilibrium distance of 2.24 Å. Shortening of these two distances leads to 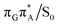 conical intersections and covalent bond formation between the two bases. The optimized
conical intersections and covalent bond formation between the two bases. The optimized 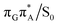 MECP lies 0.25 eV below the G+˙A−˙ minimum in the GA-anti conformer and these two points on the PES are separated by a modest energy barrier of ∼0.1 eV. Interestingly, the
MECP lies 0.25 eV below the G+˙A−˙ minimum in the GA-anti conformer and these two points on the PES are separated by a modest energy barrier of ∼0.1 eV. Interestingly, the 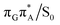 MECP located in the GA-syn conformer lies 0.42 eV above the corresponding local minimum, which indicates that this state crossing is much less available and the corresponding
MECP located in the GA-syn conformer lies 0.42 eV above the corresponding local minimum, which indicates that this state crossing is much less available and the corresponding 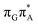 state is presumably long-lived, at least in this particular arrangement of the G and A bases. Indeed, Bucher et al. observed the existence of a charge-separated intermediate state with a lifetime of ∼300 ps, which is in excellent agreement with our picture.
state is presumably long-lived, at least in this particular arrangement of the G and A bases. Indeed, Bucher et al. observed the existence of a charge-separated intermediate state with a lifetime of ∼300 ps, which is in excellent agreement with our picture.
CpD ring opening and T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) T dimer repair
T dimer repair
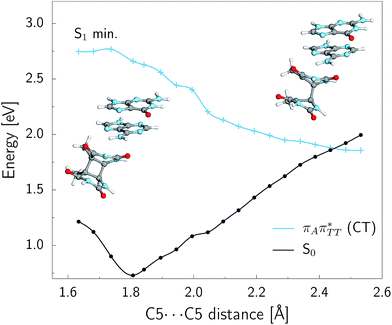
As we have already pointed out, the CpD ring opening is initiated in one of the CT states where the negative charge is located on the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer. According to our calculations, the opening of the C5–C5 bond between the two thymine bases is the first step during the actual CpD ring cleavage, and the GA+˙T
T dimer. According to our calculations, the opening of the C5–C5 bond between the two thymine bases is the first step during the actual CpD ring cleavage, and the GA+˙T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T−˙ minimum with closed CpD ring is very shallow. The relaxed scan in Fig. 6 demonstrates that stretching of the C5–C5 bond by merely 0.1 Å out of the equilibrium arrangement leads to the region of the PES where the partial CpD ring opening process occurs spontaneously. The C5⋯C5 distance at the
T−˙ minimum with closed CpD ring is very shallow. The relaxed scan in Fig. 6 demonstrates that stretching of the C5–C5 bond by merely 0.1 Å out of the equilibrium arrangement leads to the region of the PES where the partial CpD ring opening process occurs spontaneously. The C5⋯C5 distance at the 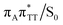 MECP amounts to 2.54 Å, while the C6–C6 bond length amounts to 1.58 Å and is nearly not affected at this stage. The peaked topography of this state crossing visible in Fig. 6 suggests that this crucial phase of the self-repair process efficiently drives the oligonucleotide to the electronic ground state with partially regenerated thymine bases.
MECP amounts to 2.54 Å, while the C6–C6 bond length amounts to 1.58 Å and is nearly not affected at this stage. The peaked topography of this state crossing visible in Fig. 6 suggests that this crucial phase of the self-repair process efficiently drives the oligonucleotide to the electronic ground state with partially regenerated thymine bases.
The T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer repair process can be eventually completed by C6–C6 bond cleavage in the vibrationally hot electronic ground state of the tetranucleotide, i.e. after the photorelaxation through the
T dimer repair process can be eventually completed by C6–C6 bond cleavage in the vibrationally hot electronic ground state of the tetranucleotide, i.e. after the photorelaxation through the 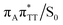 conical intersection. Such sequential and nearly barrierless CpD ring opening initiated at the C5–C5 site was also proposed based on DFT/MM simulations of the T
conical intersection. Such sequential and nearly barrierless CpD ring opening initiated at the C5–C5 site was also proposed based on DFT/MM simulations of the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer in the radical-anionic form.79 The optimization of the ground state geometry starting from the
T dimer in the radical-anionic form.79 The optimization of the ground state geometry starting from the 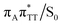 MECP shows that C6–C6 bond rupture occurs in a barrierless manner when at least weak restraints are imposed on the C5⋯C5 distance to prevent its closure. If no restraints are imposed, the C5–C5 bond is spontaneously reformed and the CpD structure can be recovered. Such bifurcation after passing through a S1/S0 conical intersection is typical for many fundamental photochemical reactions, and we anticipate that the dynamic system can yield either the repaired thymine bases or the CpD depending on the momentary arrangement of the surroundings when the discussed state crossing is reached. It is worth to note, that this stepwise mechanism was recently proposed to govern the UV-induced formation of T
MECP shows that C6–C6 bond rupture occurs in a barrierless manner when at least weak restraints are imposed on the C5⋯C5 distance to prevent its closure. If no restraints are imposed, the C5–C5 bond is spontaneously reformed and the CpD structure can be recovered. Such bifurcation after passing through a S1/S0 conical intersection is typical for many fundamental photochemical reactions, and we anticipate that the dynamic system can yield either the repaired thymine bases or the CpD depending on the momentary arrangement of the surroundings when the discussed state crossing is reached. It is worth to note, that this stepwise mechanism was recently proposed to govern the UV-induced formation of T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimers in the triplet manifold, which is the opposite reaction to the self-repair process described in this work.17
T dimers in the triplet manifold, which is the opposite reaction to the self-repair process described in this work.17
Conclusions
Based on the ADC(2)/MM calculations we propose that the self-repair of the CpD lesion in the GAT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T tetramer can be rationalized in terms of the sequential electron transfer (SET) mechanism. This process is initiated in one of the optically bright LE states of the tetranucleotide (e.g.
T tetramer can be rationalized in terms of the sequential electron transfer (SET) mechanism. This process is initiated in one of the optically bright LE states of the tetranucleotide (e.g.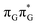 state) and is associated with consecutive electron transfer processes and changes of the orbital character occurring downhill in energy on the S1 hypersurface. The CpD repair process may be triggered in one of the lowest-lying S1 minima containing an excessive electron located on the T
state) and is associated with consecutive electron transfer processes and changes of the orbital character occurring downhill in energy on the S1 hypersurface. The CpD repair process may be triggered in one of the lowest-lying S1 minima containing an excessive electron located on the T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T dimer (either G+˙AT
T dimer (either G+˙AT![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T−˙ or GA+˙T
T−˙ or GA+˙T![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) T−˙). The CpD ring opening is then preferentially started at the C5–C5 site and leads to the S1/S0 conical intersection with virtually no barrier. The self-repair process is eventually completed by the C6–C6 bond rupture in the vibrationally hot ground state of the tetranucleotide.
T−˙). The CpD ring opening is then preferentially started at the C5–C5 site and leads to the S1/S0 conical intersection with virtually no barrier. The self-repair process is eventually completed by the C6–C6 bond rupture in the vibrationally hot ground state of the tetranucleotide.
The MECP optimizations enabled us to assign the long-lived state observed by Bucher et al., to the 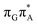 CT state (G+˙A−˙) in the GA-syn conformer. The experimental lifetime of 300 ps is clearly reflected by the presence of the sloped
CT state (G+˙A−˙) in the GA-syn conformer. The experimental lifetime of 300 ps is clearly reflected by the presence of the sloped 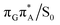 MECP which lies 0.42 eV above the G+˙A−˙ minimum.
MECP which lies 0.42 eV above the G+˙A−˙ minimum.
The qualitative features of the SET mechanisms are conserved in both studied conformers, but some specific differences are evident. For instance, the stacking pattern strongly differs in the syn/anti conformers, while retaining the same (formal) intermediate 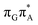 state (cf. the G+˙A−˙ minima in Fig. 5). The different interaction mode from the stacking variants leads to a significantly different energies of the S1/S0 state crossings in the G+˙A−˙ intermediate, resulting in different lifetimes and presumably conformer-dependent self-repair efficiency. This suggests that a more complete understanding of the photochemistry of short oligonucleotides requires conformational sampling.
state (cf. the G+˙A−˙ minima in Fig. 5). The different interaction mode from the stacking variants leads to a significantly different energies of the S1/S0 state crossings in the G+˙A−˙ intermediate, resulting in different lifetimes and presumably conformer-dependent self-repair efficiency. This suggests that a more complete understanding of the photochemistry of short oligonucleotides requires conformational sampling.
We propose the main criteria which could help in identifying these nucleic-acid sequences which could efficiently promote self-repair of CpD lesions:
(i) The CT states containing the excess electron residing on the CpD lesion should be available directly or indirectly from the LE states populated soon after the photoexcitation.
(ii) The CpD repairing state can be accessed indirectly via several local S1 minima corresponding to intermediate diabatic states, within the SET mechanism. An efficient SET mechanism operates downhill along the S1 hypersurface, the consecutive diabatic states should be strongly coupled and the local minima should be separated by rather low energy barriers.
(iii) The intermediate diabatic states should have sufficiently long excited-state lifetimes to prevent premature relaxation to the S0 state and enable efficient population of successive minima in the SET mechanism. This property can be deduced from the availability of S1/S0 conical intersections in the respective local S1 minima.
Such predictive capacity is critical for deciphering the yet unclear stages of abiogenesis, since the emergence of first oligonucleotides on our planet was presumably regulated by high UV fluxes and the lack of photolesion repair factors.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank prof. Wolfgang Zinth, Corinna Kufner, Dr Dominik Bucher and prof. Wolfgang Domcke for fruitful discussions. J. S. acknowledges support from the Praemium Academiae. This work was supported by a fellowship from the Simons Foundation (494188, R. S.), and Grant GA16-13721S from the Czech Science Foundation.References
- J. S. Taylor, Acc. Chem. Res., 1994, 27, 76–82 CrossRef CAS
.
- R. P. Sinha and D.-P. Häder, Photochem. Photobiol. Sci., 2002, 1, 225–236 CAS
.
- S. Weber, Biochim. Biophys. Acta, Bioenerg., 2005, 1707, 1–23 CrossRef CAS PubMed
.
- T. Todo, H. Takemori, H. Ryo, M. Lhara, T. Matsunaga, O. Nikaido, K. Sato and T. Nomura, Nature, 1993, 361, 371–374 CrossRef CAS PubMed
.
- J. E. Cleaver and E. Crowley, Front. Biosci., 2002, 7, d1024–1043 CAS
.
- B. A. Gilchrest, M. S. Eller, A. C. Geller and M. Yaar, N. Engl. J. Med., 1999, 340, 1341–1348 CrossRef CAS PubMed
.
- J. T. Reardon and A. Sancar, Genes Dev., 2003, 17, 2539–2551 CrossRef CAS PubMed
.
- S. Faraji, D. Zhong and A. Dreuw, Angew. Chem., Int. Ed., 2016, 55, 5175–5178 CrossRef CAS PubMed
.
- S. Faraji and A. Dreuw, Photochem. Photobiol., 2017, 93, 37–50 CrossRef CAS PubMed
.
- S. Faraji and A. Dreuw, Annu. Rev. Phys. Chem., 2014, 65, 275–292 CrossRef CAS PubMed
.
- W. J. Schreier, T. E. Schrader, F. O. Koller, P. Gilch, C. E. Crespo-Hernández, V. N. Swaminathan, T. Carell, W. Zinth and B. Kohler, Science, 2007, 315, 625–629 CrossRef CAS PubMed
.
- L. Liu, B. M. Pilles, J. Gontcharov, D. B. Bucher and W. Zinth, J. Phys. Chem. B, 2016, 120, 292–298 CrossRef CAS PubMed
.
- C. Rauer, J. J. Nogueira, P. Marquetand and L. González, J. Am. Chem. Soc., 2016, 138, 15911–15916 CrossRef CAS PubMed
.
- W. J. Schreier, J. Kubon, N. Regner, K. Haiser, T. E. Schrader, W. Zinth, P. Clivio and P. Gilch, J. Am. Chem. Soc., 2009, 131, 5038–5039 CrossRef CAS PubMed
.
- K. Haiser, B. P. Fingerhut, K. Heil, A. Glas, T. T. Herzog, B. M. Pilles, W. J. Schreier, W. Zinth, R. de Vivie-Riedle and T. Carell, Angew. Chem., Int. Ed., 2012, 51, 408–411 CrossRef CAS PubMed
.
- W. Lee, G. Kodali, R. J. Stanley and S. Matsika, Chem.–Eur. J., 2016, 22, 11371–11381 CrossRef CAS PubMed
.
- C. Rauer, J. J. Nogueira, P. Marquetand and L. González, Monatsh. Chem., 2018, 149, 1–9 CrossRef CAS PubMed
.
- S. Ranjan and D. D. Sasselov, Astrobiology, 2016, 16, 68–88 CrossRef CAS PubMed
.
- S. Ranjan and D. D. Sasselov, Astrobiology, 2017, 17, 169–204 CrossRef CAS PubMed
.
- C. S. Cockell and G. Horneck, Photochem. Photobiol., 2001, 73, 447–451 CrossRef CAS PubMed
.
- C. S. Cockell, Origins Life Evol. Biospheres, 2000, 30, 467–500 CrossRef CAS
.
- R. J. Rapf and V. Vaida, Phys. Chem. Chem. Phys., 2016, 18, 20067–20084 RSC
.
- D. B. Bucher, C. L. Kufner, A. Schlueter, T. Carell and W. Zinth, J. Am. Chem. Soc., 2016, 138, 186–190 CrossRef CAS PubMed
.
- A. A. Beckstead, Y. Zhang, M. S. d. Vries and B. Kohler, Phys. Chem. Chem. Phys., 2016, 18, 24228–24238 RSC
.
- D. B. Bucher, B. M. Pilles, T. Carell and W. Zinth, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 4369–4374 CrossRef CAS PubMed
.
- V. A. Spata and S. Matsika, Phys. Chem. Chem. Phys., 2015, 17, 31073–31083 RSC
.
- C. T. Middleton, K. d. L. Harpe, C. Su, Y. K. Law, C. E. Crespo-Hernández and B. Kohler, Annu. Rev. Phys. Chem., 2009, 60, 217–239 CrossRef CAS PubMed
.
- Y. Zhang, J. Dood, A. A. Beckstead, X.-B. Li, K. V. Nguyen, C. J. Burrows, R. Improta and B. Kohler, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 11612–11617 CrossRef CAS PubMed
.
- L. Martinez-Fernandez, Y. Zhang, K. d. L. Harpe, A. A. Beckstead, B. Kohler and R. Improta, Phys. Chem. Chem. Phys., 2016, 18, 21241–21245 RSC
.
- A. Dreuw and M. Head-Gordon, J. Am. Chem. Soc., 2004, 126, 4007–4016 CrossRef CAS PubMed
.
- N. T. Maitra, J. Phys.: Condens. Matter, 2017, 29, 423001 CrossRef PubMed
.
- F. Plasser, R. Crespo-Otero, M. Pederzoli, J. Pittner, H. Lischka and M. Barbatti, J. Chem. Theory Comput., 2014, 10, 1395–1405 CrossRef CAS PubMed
.
- A. B. Trofimov and J. Schirmer, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2299 CrossRef CAS
.
- A. Dreuw and M. Wormit, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 82–95 CrossRef CAS
.
- V. A. Spata and S. Matsika, J. Phys. Chem. A, 2014, 118, 12021–12030 CrossRef CAS PubMed
.
- V. A. Spata, W. Lee and S. Matsika, J. Phys. Chem. Lett., 2016, 7, 976–984 CrossRef CAS PubMed
.
- W. Lee and S. Matsika, Phys. Chem. Chem. Phys., 2015, 17, 9927–9935 RSC
.
- F. Plasser, A. J. A. Aquino, W. L. Hase and H. Lischka, J. Phys. Chem. A, 2012, 116, 11151–11160 CrossRef CAS PubMed
.
- F. Plasser and H. Lischka, Photochem. Photobiol. Sci., 2013, 12, 1440–1452 CAS
.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS
.
- A. Pérez, I. Marchán, D. Svozil, J. Sponer, T. E. I. Cheatham, C. A. Laughton and M. Orozco, Biophys. J., 2007, 92, 3817–3829 CrossRef PubMed
.
- M. Krepl, M. Zgarbová, P. Stadlbauer, M. Otyepka, P. Banáš, J. Koča, T. E. Cheatham, P. Jurečka and J. Šponer, J. Chem. Theory Comput., 2012, 8, 2506–2520 CrossRef CAS PubMed
.
- M. Zgarbová, F. J. Luque, J. Šponer, T. E. Cheatham, M. Otyepka and P. Jurečka, J. Chem. Theory Comput., 2013, 9, 2339–2354 CrossRef PubMed
.
- M. Zgarbová, J. Šponer, M. Otyepka, T. E. Cheatham, R. Galindo-Murillo and P. Jurečka, J. Chem. Theory Comput., 2015, 11, 5723–5736 CrossRef PubMed
.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS
.
- S. Izadi, R. Anandakrishnan and A. V. Onufriev, J. Phys. Chem. Lett., 2014, 5, 3863–3871 CrossRef CAS PubMed
.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed
.
-
D. Case, J. Berryman, R. Betz, D. Cerutti, T. Cheatham III, T. Darden, R. Duke, T. Giese, H. Gohlke, A. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. Lee, S. Legrand, P. Li, T. Luchko, R. Luo, B. Madej, K. Merz, G. Monard, P. Needham, H. Nguyen, H. Nguyen, I. Omelyan, A. Onufriev, D. Roe, A. Roitberg, R. Salomon-Ferrer, C. Simmerling, W. Smith, J. Swails, R. Walker, J. Wang, R. Wolf, X. Wu, D. York and P. Kollman, AMBER 14, 2015 Search PubMed
.
- P. Kührová, R. B. Best, S. Bottaro, G. Bussi, J. Šponer, M. Otyepka and P. Banáš, J. Chem. Theory Comput., 2016, 12, 4534–4548 CrossRef PubMed
.
- A. Rodriguez and A. Laio, Science, 2014, 344, 1492–1496 CrossRef CAS PubMed
.
- S. Bottaro, F. DiPalma and G. Bussi, Nucleic Acids Res., 2014, 42, 13306–13314 CrossRef CAS PubMed
.
- R. Improta, F. Santoro and L. Blancafort, Chem. Rev., 2016, 116, 3540–3593 CrossRef CAS PubMed
.
- J. J. Nogueira, F. Plasser and L. González, Chem. Sci., 2017, 8, 5682–5691 RSC
.
- A. W. Götz, M. A. Clark and R. C. Walker, J. Comput. Chem., 2014, 35, 95–108 CrossRef PubMed
.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS
.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed
.
- R. Szabla, M. Havrila, H. Kruse and J. Šponer, J. Phys. Chem. B, 2016, 120, 10635–10648 CrossRef CAS PubMed
.
-
H. Kruse, local development version, Institute of Biophysics, 2016, Brno, https://github.com/hokru/xopt Search PubMed
.
- H. Kruse and J. Šponer, Phys. Chem. Chem. Phys., 2015, 17, 1399–1410 RSC
.
- F. Eckert, P. Pulay and H.-J. Werner, J. Comput. Chem., 1997, 18, 1473–1483 CrossRef CAS
.
- C. Hättig, Advances in Quantum Chemistry, Academic Press, 2005, vol. 50, pp. 37–60 Search PubMed.
- L. Stojanović, S. Bai, J. Nagesh, A. F. Izmaylov, R. Crespo-Otero, H. Lischka and M. Barbatti, Molecules, 2016, 21, 1603 CrossRef PubMed
.
- F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106 CrossRef PubMed
.
- F. Plasser, S. A. Bäppler, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024107 CrossRef PubMed
.
- G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843 CrossRef CAS PubMed
.
- B. G. Levine, J. D. Coe and T. J. Martínez, J. Phys. Chem. B, 2008, 112, 405–413 CrossRef CAS PubMed
.
- D. Tuna, D. Lefrancois, Ł. Wolański, S. Gozem, I. Schapiro, T. Andruniów, A. Dreuw and M. Olivucci, J. Chem. Theory Comput., 2015, 11, 5758–5781 CrossRef CAS PubMed
.
- R. Szabla, R. W. Góra and J. Šponer, Phys. Chem. Chem. Phys., 2016, 18, 20208–20218 RSC
.
- C. Bergonzo, N. M. Henriksen, D. R. Roe, J. M. Swails, A. E. Roitberg and T. E. Cheatham, J. Chem. Theory Comput., 2014, 10, 492–499 CrossRef CAS PubMed
.
- J. D. Tubbs, D. E. Condon, S. D. Kennedy, M. Hauser, P. C. Bevilacqua and D. H. Turner, Biochemistry, 2013, 52, 996–1010 CrossRef CAS PubMed
.
- M. V. Schrodt, C. T. Andrews and A. H. Elcock, J. Chem. Theory Comput., 2015, 11, 5906–5917 CrossRef CAS PubMed
.
- C. Bergonzo and T. E. Cheatham, J. Chem. Theory Comput., 2015, 11, 3969–3972 CrossRef CAS PubMed
.
- N. A. Besley and J. D. Hirst, J. Am. Chem. Soc., 1999, 121, 8559–8566 CrossRef CAS
.
- R. Szabla, H. Kruse, J. Sponer and R. W. Gora, Phys. Chem. Chem. Phys., 2017, 19, 17531–17537 RSC
.
- M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallová, P. Hobza and H. Lischka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21453–21458 CrossRef CAS PubMed
.
- S. Yamazaki, W. Domcke and A. L. Sobolewski, J. Phys. Chem. A, 2008, 112, 11965–11968 CrossRef CAS PubMed
.
- R. J. Cave and M. D. Newton, J. Chem. Phys., 1997, 106, 9213–9226 CrossRef CAS
.
- J. E. Subotnik, S. Yeganeh, R. J. Cave and M. A. Ratner, J. Chem. Phys., 2008, 129, 244101 CrossRef PubMed
.
- F. Masson, T. Laino, I. Tavernelli, U. Rothlisberger and J. Hutter, J. Am. Chem. Soc., 2008, 130, 3443–3450 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details of the MD simulations, results of calculations performed for the GA-syn conformer, diabatic couplings and Cartesian coordinates of the stationary points. See DOI: 10.1039/c8sc00024g |
| This journal is © The Royal Society of Chemistry 2018 |