Open Access Article
Open Access ArticleMetal-free perovskites for non linear optical materials†
Thomas W.
Kasel‡
 a,
Zeyu
Deng‡
a,
Zeyu
Deng‡
 b,
Austin M.
Mroz‡
b,
Austin M.
Mroz‡
 a,
Christopher H.
Hendon
a,
Christopher H.
Hendon
 *a,
Keith T.
Butler
*a,
Keith T.
Butler
 *c and
Pieremanuele
Canepa
*c and
Pieremanuele
Canepa
 *b
*b
aDepartment of Chemistry and Biochemistry, University of Oregon, Eugene, OR 97403, USA. E-mail: chendon@uoregon.edu
bDepartment of Materials Science and Engineering, The National University of Singapore, 117575, Singapore. E-mail: pcanepa@nus.edu.sg
cSciML, Scientific Computing Division, Rutherford Appleton Laboratory, OX11 0QX Harwell, UK. E-mail: keith.butler@stfc.ac.uk
First published on 26th July 2019
Abstract
We identify the existence of non linear optical (NLO) activity in a number of novel ABX3-type metal-free perovskites, where A is a highly tuneable organic cation, B is a NH4 cation and X is a halide anion. Through systematic first-principles calculations, we identify important trends to chart the second-harmonic generation of this class of materials. We study three perovskites MDABCO–NH4I3, CNDABCO–NH4I3 and ODABCO–NH4I3 for use as deep-UV second-harmonic generation materials. We identify the role of the dipole moment imparted by the organic group on the A cation as an important parameter to tune the NLO properties of these materials. We apply this knowledge functionalising the organic group DABCO with the highly polar cyanide CN− group, and we demonstrate a significant improvement of the NLO response in this family of materials. These findings can accelerate the application of metalfree perovskites as inexpensive, non-toxic, earth-abundant materials for the next generation of optical communication applications.
1 Introduction
Light has been utilized as a communication device for many centuries. Recently, non-linear optics (NLO) and second harmonic generation (SHG) have been at the heart of several technological revolutions. With the advent of the internet, conveying information and data by means of fiber-optics and lasers have transformed telecommunications. The development of fiber-optic devices with increased performance has fuelled a surge of interest in the development of materials with ever-increasing data-transfer capabilities.1–10 Materials, such as LiNbO3 and LiTaO3 with NLO and SHG are at the core of high-speed electro-optic modulator devices, significantly boosting the transmission capacities of the telecommunication infrastructure (∼10 Gbit s−1).1,11 In parallel NLO materials for deep-UV lasers are being used in semiconductor manufacturing, photolithography, laser systems, and advanced instrument development.The demand for apparatus with increased performance requires the development of novel inexpensive NLO materials and every year the electronic and telecommunication industries demands the production of ∼40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tons of LiNbO3. The soaring costs of lithium and niobium,12,13 and thus LiNbO3 requires the development of the new generation of NLO materials relying on more earth-abundant elements.14–16 This is further aggravated by the fact that LiNbO3 melts incongruently and the manufacturing of congruently lithium niobate single crystals requires cooling of Li-poor nonstoichiometric melts of LiNbO3,17 adding additional production costs.
000 tons of LiNbO3. The soaring costs of lithium and niobium,12,13 and thus LiNbO3 requires the development of the new generation of NLO materials relying on more earth-abundant elements.14–16 This is further aggravated by the fact that LiNbO3 melts incongruently and the manufacturing of congruently lithium niobate single crystals requires cooling of Li-poor nonstoichiometric melts of LiNbO3,17 adding additional production costs.
Meanwhile, for deep-UV applications Tran et al.9 have shown that only a handful of materials, such as KBe2BO3F2, RbBe2BO3F2 and CsBe2BO3F2, sharing similar structural features currently fulfil the desired requirements. However, these materials contain toxic Be, whose usage is prohibited in many countries. Therefore, materials with better NLO characteristics are required to supplant deep-UV lasers.10 As identified by Halasyamani and Rondinelli,10 NLO materials for application in deep-UV lasers must fulfil a minimal number of requirements: (i) the atoms in the material should present a noncentrosymmetric arrangement, (ii) the material absorbs light in the deep-UV spectrum (i.e., absorption wavelengths ≥ 175 nm), and (iii) the material should respect the phase-matching criteria discussed in detail within the manuscript.
One promising route towards sustainable NLO materials lies in organic materials, which have shown promising SHG properties.3,18–28 However, to date organic NLO suffer from thermal instability and difficult fabrication. In contrast to typical organic-based NLO, metal-free perovskites have been shown to be structurally stable beyond 200 °C.29
In this study we present an in-depth analysis of the NLO properties of a new class of materials with ferroelectric response termed metal-free perovskites developed by Ye and co-workers.29 We use first-principles calculations, based on density functional theory (DFT) to chart the optical and NLO properties of a these novel metal-free perovskites. In contrast to typical inorganic perovskite A2+B4+O32− where A and B are metal cations (e.g., CaTiO3), in metal-free perovskites the A and B cations are replaced by organic units. The rich choice of organic units introduces the possibility of tailoring the functional properties of such metal-free perovskites, while being easy-to-synthesise, affordable and non-toxic. Note that NLO materials with inorganic perovskite structures exist (e.g., K3B6O10Cl) which are more closely related to the metal-free perovskites than organic-based NLO materials.30
We investigate such metal-free perovskites as NLO materials for SHG applications, and verify whether these perovskites are suitable as deep-UV NLO materials. Our findings reveal that metal-free perovskites, based on the organic moieties N-methyl-N-diazabicyclo[2.2.2]octonium (MDABCO2+) and N-hydroxy-N-diazabicyclo[2.2.2]octonium (ODABCO2+), posses SHG response, with magnitudes similar to some inorganic contenders, such as KBe2BO3F2, RbBe2BO3F2 and CsBe2BO3F2. We demonstrate that organic groups presenting intrinsic dipole moments can contribute positively to the ferroelectric response of the material, and provide an increased NLO response.
On the basis of our predictions, we provide guidelines to improve the SHG response of the metal-free perovskites, by tailoring the structural features of the organic cations. Following this principle, we extend the computational search to new structures. For example, we show the case where the hydroxy-group in ODABCO2+ (A-cation) is effectively replaced by a cyanide CN− group with increased polarity, which provides remarkable NLO response. While preliminary observations29 showed experimentally SHG response in MDABCO–NH4I3, we also identify ODABCO–NH4I3 and CNDABCO–NH4I3 as superior SHG materials, and their properties should be carefully verified experimentally.
2 Results
2.1 Structure of ferroelectric metal-free perovskites
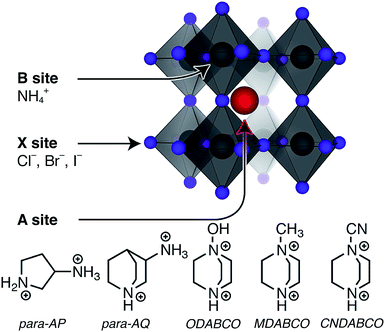
The first point when considering the suitability of a material for NLO applications is the crystal structure. All materials reported herein and shown in Fig. 1 feature the typical perovskite ABX3 structure (where A and B are cations and X are anions), with BX3 corner-sharing octahedra and charge-balancing A cations in the cavities of the framework. The structures investigated have NH4+ as B sites and halide X− sites, as seen in Fig. 1. A series of different A site divalent molecular cations are considered (i) N-methyl-N-diazabicyclo[2.2.2]octonium (MDABCO2+), (ii) M-hydroxy-N-diazabicyclo[2.2.2]octonium (ODABCO2+), (iii) R-3-ammonioquinuclidinium (R-3AQ2+), and (iv) S-3-ammoniopyrrolidinium (S-3AP2+). Starting from the ODABCO–NH4X structures, we also replaced the hydroxy group with a more polar cyanide CN− group forming a new metal-free perovskite termed CNDABCO–NH4X3. In studying the halide chemical space of these metal-free perovskites, we proposed three new structures, including MDABCO–NH4Cl3, ODABCO–NH4I3 and S-3AP–NH4I3 that were not identified by Ye et al.29 In the case of ODABCO–NH4I3 and CNDABCO–NH4X3 we assumed a R3 space group. However, we also computed the iodine-based polymorph with Pca21 space group (as in ODABCO–NH4Cl3), which converted to the R3 polymorph.To be NLO active a material must be non-centrosymmetric. As shown in Tables S1 and S2 of the ESI,† the materials considered here fall into three space groups, R3, Pca21 and P21, all of which are non-centrosymmetric. For those metal-free perovskites that have been synthesized and characterized previously the non-centrosymmetric space groups persisting up to 448 K.29
In addition, metal-free perovskites, and inorganic materials, such as LiNbO3 posses an intrinsic polarization, which is typical of ferroelectric materials. LiNbO3 charts among the most popular of NLO materials with a polarization of ∼70–75 μC cm−2.31 The presence of dipolar molecules and the off-centring of the B-site cation in the metal-free perovskites indicates the existence of an intrinsic polarization, which for MDABCO–NH4I3 has been measured to be ∼19 μC cm−2.29
2.2 Birefringence activity of metal-free perovskites
Having established the crystallographic criteria for NLO materials, we now consider the optical properties that must be satisfied for SHG. The birefringence is the maximum difference refractive indices (n) which depends on the propagation directions of light in the crystal at a fixed frequency (ω) (as in eqn (1)).| Δn = nmax(ω) − nmin(ω) | (1) |
SHG occurs efficiently whenever the refractive index n of the 2nd harmonic is equal (or close) to that of the generating wave at half-frequency, i.e., n(2ω) = n(ω); this condition is termed phase-matching. Phase-matching requires a suitable range of frequencies with refractive indexes, nmax(ω) − nmin(2ω) > 0, with nmin and nmax the lowest and the largest refractive index in the spread.32
If Δn of a material is too small the phase-matching condition for SHG will not occur. If Δn is too large the material will exhibit spatial beam walk-off, where the intensity distribution of the wave drifts away from the direction of propagation resulting in reduced SHG intensity. In general a moderate birefringence (Δn ≈ 0.07) is desired.
In uniaxial systems, such as LiNbO3 and the MDABCO–NH4X3 systems the direction of ordinary and extraordinary rays occurs along the optical axis, which lays along the highest symmetry axis.
In contrast, biaxial systems have multiple optic axes, whose directions of propagation depend on the diffraction index and measured by the 2V acute angle (see below).32 Therefore, the 2V angle provides information about the nature of the birefringence in biaxial crystals. In general, orthorhombic, monoclinic and triclinic systems are biaxial crystals.
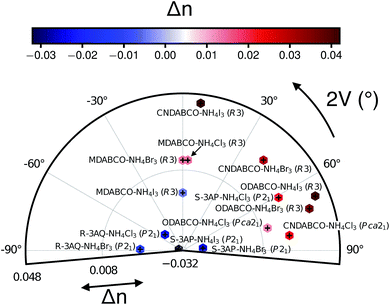
Fig. 2 plots Δn (obtained from the dielectric constants in the static regime) and the 2V acute angle. From Fig. 2, we observe that all the systems considered here have Δn ranging between values of −0.03 and +0.05, with CNDABCO, ODABCO, S-3AP and R-3AQ-based perovskites charting among the highest in magnitude. The R3 materials, which are uniaxial NLO systems, all exhibit positive birefringence. In contrast, the Pca21 and P21 systems, which are biaxial NLO materials, display both positive and negative birefringence. A closer look at Fig. 2 shows that with the exception of MDABCO-based perovskites and S-3AP–NH4I3 (whose 2V ∼ 0), the remaining materials all show a rather complex biaxial response.
 | ||
| Fig. 2 Computed birefringence Δn and 2V angle of metal-free perovskites at their experimental volume and lattice constants. Δn is plotted on the radial axis and using the colour-bar, with red indicating positive Δn. Values of n are given in Table S3 of the ESI.† The 2V angles provide information about the nature of the birefringence in biaxial crystals. | ||
2.3 NLO response in metal-free perovskites
We now discuss the NLO response of the metal-free perovskites. Among the prerequisites for SHG the materials under investigation should display a non-negligible value of the second order dielectric tensor, χ(2).χ (2) ijk = 2dijk is a third-rank tensor as defined in eqn (6), and therefore can be difficult to analyse intuitively. The i, j and k components of the d tensor identify the directions of the applied electric fields (i.e., j and k) of the incident radiation and the polarization of the generated second harmonic (i.e., i), respectively, (see eqn (6)). In SHG experiments, the directions of the electric fields of incident radiations have frequencies ω1 and ω2 (with ω1 = ω2 in SHG) and the second harmonic wave with frequency ω3 = ω1 + ω2. A complete discussion of the χ(2) and d tensors and their dependence can be found in ref. 33.
A useful proxy for presenting the ijk component of the static χ(2) tensor is the norm of the dijk components of Table 1 and eqn (2):
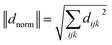 | (2) |
| X− | Spg. | d xxx | d xxy | d xxz | d xyy | d xyz | d xzz | d yyy | d yyz | d yzz | d zzz | ‖dnorm‖ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MDABCO–NH 4 X 3 | ||||||||||||
| Cl | R3 | 0.140 | −0.410 | 0.048 | −0.140 | 0.000 | 0.000 | 0.410 | 0.048 | 0.000 | −0.490 | 0.79 |
| Br | R3 | 0.230 | −0.620 | −0.058 | −0.230 | 0.000 | 0.000 | 0.620 | −0.058 | 0.000 | −0.580 | 1.10 |
| I | R3 | −0.170 | 1.200 | 0.430 | 0.170 | 0.000 | 0.000 | −1.200 | 0.430 | 0.000 | 0.021 | 1.80 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| ODABCO–NH 4 X 3 | ||||||||||||
| Cl | Pca21 | 0.000 | 0.000 | 0.230 | 0.000 | 0.000 | 0.000 | 0.000 | −0.076 | 0.000 | −0.076 | 0.25 |
| Br | R3 | 0.019 | 0.510 | −0.320 | 0.150 | −0.290 | −0.069 | 0.099 | −0.100 | −0.280 | −0.230 | 0.79 |
| I | R3 | 0.270 | 0.620 | −0.670 | −0.190 | −0.400 | 0.100 | −0.840 | −0.490 | −0.280 | 0.007 | 1.50 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| CNDABCO–NH 4 X 3 | ||||||||||||
| Cl | Pca21 | 0.000 | 0.000 | 0.650 | 0.000 | 0.000 | 0.000 | 0.000 | −0.160 | 0.000 | 0.075 | 0.68 |
| Br | R3 | −0.450 | 0.850 | 0.260 | 0.230 | 0.120 | 0.092 | −0.880 | 0.350 | 0.071 | −0.590 | 1.50 |
| I | R3 | −0.450 | 1.310 | 0.760 | 0.450 | −0.001 | 0.0006 | −1.310 | 0.760 | 0.004 | −0.014 | 2.20 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| R-3AQ–NH 4 X 3 | ||||||||||||
| Cl | P21 | 0.000 | 0.091 | 0.000 | 0.000 | 0.068 | 0.000 | 0.0121 | 0.000 | −0.160 | 0.000 | 0.19 |
| Br | P21 | 0.000 | −0.075 | 0.000 | 0.000 | 0.004 | 0.000 | −0.320 | 0.000 | 0.400 | 0.000 | 0.52 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| S-3AP–NH 4 X 3 | ||||||||||||
| Cl | P21 | 0.000 | −0.025 | 0.000 | 0.000 | −0.041 | 0.000 | −0.160 | 0.000 | −0.150 | 0.000 | 0.22 |
| Br | P21 | 0.000 | −0.029 | 0.000 | 0.000 | −0.055 | 0.000 | −0.120 | 0.000 | −0.048 | 0.000 | 0.14 |
| I | P21 | 0.000 | −0.210 | 0.000 | 0.000 | −0.075 | 0.000 | −0.140 | 0.000 | 0.029 | 0.000 | 0.26 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| LiNbO 3 | ||||||||||||
| — | R3c | 0.170 | 0.000 | 5.000 | 0.170 | 0.000 | 0.000 | 0.000 | 5.000 | 0.000 | 16.450 | 17.91 |
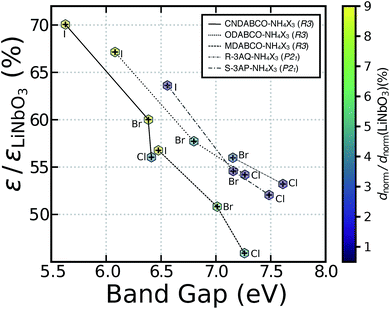
Fig. 3 presents the static dielectric constant ε (y-axis) as a function of the band gap (x-axis) for the materials studied, the data points are coloured according to the magnitude of dnorm, which are obtained at the experimental volumes at room temperature. The values of band gap, ε, χ(1), χ(2)ijk and dnorm of these materials are found in Tables S4 and S5.†
In general, volumes obtained after relaxation in hybrid systems containing a number of van der Waals interactions, such as these metal-free perovskites, tend to be highly distorted. Therefore, the main text concentrates on results obtained on structures where all the atomic coordinates are relaxed at the experimental volumes and lattice constants, whereas results on fully relaxed structures are available in the ESI.† For clarity and ease of comparison, the dielectric constant and the dnorm are scaled by that of LiNbO3, calculated at the same level of theory (Tables S4 and S5†).
The y-axis of Fig. 3 presents the average dielectric constant (in the static limit) of the metal-free perovskites rescaled to that of LiNbO3 ∼ 4.39, which compare well with experimental data (∼4.87).31 The computed dzzz values of 16.45 pm V−1 (at the experimental volume of LiNbO3) slightly underestimated the experimental value of (∼22.0 pm V−1 at λ ∼ 407.2 nm) by Magel et al.35 DFT has been known to systematically underestimate values of d in NLO materials.36 The complete dielectric and d tensors of each metal-free perovskites are reported in the ESI.†
The computed band gaps of Fig. 3 are characteristic of high-gap insulators ranging between ∼5.5 and 8 eV. The metal-free perovskites absorb light between 155 and 220 nm, i.e. the deep-UV portion of the electromagnetic spectrum, meaning that these materials fulfil another of the criteria for deep-UV SHG applications. All computed dnorm values in metal-free perovskites with the same organic A-site cation follow the order I > Br > Cl. The order of increasing dnorm moving down the halide group follows the trend in band gaps. We find that the computed dnorm of all the metal-free perovskites is a fraction (ranging between 1% and 10%) of the dnorm of LiNbO3 (Fig. 3), which is used as a reference.
From these data, we identify two iodine-based structures, MDABCO–NH4I3 and ODABCO–NH4I3 as the best NLO materials across the metal-free perovskites investigated. When the OH− group in ODABCO–NH4X3 is replaced by a polar CN− group (see Fig. 3), forming CNDABCO–NH4X3, we find improved NLO properties. In CNDABCO–NH4X3, the computed dnorm of ∼2.23 pm V−1 outperforms all other metal-free perovskites, suggesting that CN-substituted A cations offer a promising strategy to improve the optoelectronic properties of these materials.
Fig. 3 shows that both R-3AQ–NH4X3 and S-3AP–NH4X3 posses small values of dnorm, covering a narrow range between ∼0.14 and ∼0.52 pm V−1, with the highest value set by R-3AQ–NH4Br3 and the lowest by S-3AP–NH4Br3. Hence, both R-3AQ–NH4X3 and S-3AP–NH4X3 are expected to show low SHG behaviour and therefore, will not be considered further in this analysis.
3 Discussion
We have identified that MDABCO–NH4I3, ODABCO–NH4I3 and CNDABCO–NH4I3 show the largest NLO response. Our results show the largest components of the d tensor in MDABCO–NH4I3 are dxxz = dyyz ∼ 0.43 pm V−1 and dxxy ∼ 1.20 pm V−1, respectively, dyyy ∼ 0.84 pm V−1 in ODABCO–NH4I3 and dyyy ∼ 1.31 pm V−1 in CNDABCO–NH4I3, which represent three promising NLO materials with good SHG. Therefore, the discussion will only focus on the subset of metal-free perovskites showing significant SHG activity, including CNDABCO–NH4I3, ODABCO–NH4X3 and MDABCO–NH4X3.The values for SHG are similar and in most cases even larger than the prescribed minimal conditions for deep-UV applications, i.e. dxyz ∼ 0.39 pm V−1 (with λ ∼ 1.064 μm) KH2PO4.9,37 The calculated band gaps indicate that while the materials absorb in the 2ω range required for SHG, they do not absorb in the region ω, a critical consideration, as absorption at ω would lead to material damage in operation. It is important to note that in a operation scenario the light absorbed will enhance the susceptibility but will also reduce the emission, thus the calculate values of dxyz serve to demonstrate the very promising properties of these materials for NLO and SHG applications, but should be considered as guides, rather than definitive numbers of real device operation. Most importantly, the composition–structure–property relationships driving NLO response in these test systems can provide rules for designing even more SHG active materials.
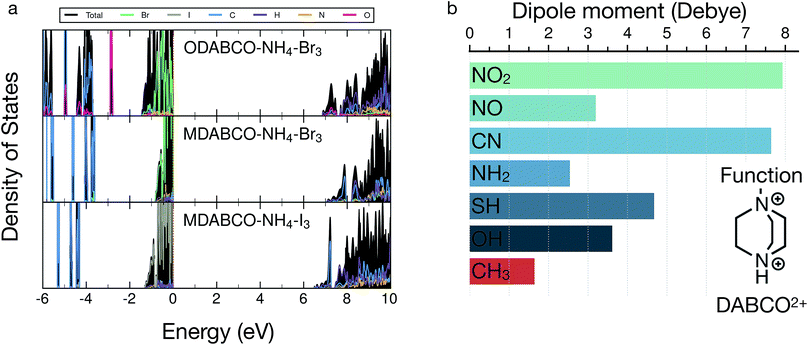
As seen in Fig. 3, the primary factor influencing the size of dnorm is the magnitude of the band gap. This is a well established trend in semiconductor materials in general and is related to lower carrier concentrations in wider gap materials at finite temperatures. A correlation between band gap and the halide species exists, we find a similar correlation in the values of the static dielectric constants vs. the anion species, following the trend ε(I−) > ε(Br−) > ε(Cl−). This observation is consistent with the density of states of Fig. 4 of ODABCO–NH4Br3 (top), MDABCO–NH4Br3 (middle) and MDABCO–NH4I3 (bottom), respectively, which shows the valence band dominated by halide species and the conduction band populated by the A organic cation, i.e., ODABCO2+ or MDABCO2+. As the frontier valence orbitals are primarily halide in character (Fig. 4), it is not surprising that the largest change in band gap is controlled by halide exchange. These findings are also supported by the DOS presented in ref. 38 and are consistent with observations in hybrid halide perovskites.39
There is a secondary contribution to the dnorm arising from the nature of the organic cation at the A-site. As seen in Fig. 3, dnorm follows the order dnorm(CNDABCO2+) ≫ dnorm(MDABCO2+) > dnorm(ODABCO2+). However, this trend becomes dnorm(CNDABCO2+) ≫ dnorm(ODABCO2+) > dnorm(MDABCO2+) when the structures are fully relaxed (see Table S5†). This is despite the fact that both CNDABCO2+ and ODABCO2+ systems have larger dielectric constants and smaller band gaps than the MDABCO2+ counterparts. As an example, while the ODABCO2+ cation is structurally very similar to the group MDABCO2+ (see Fig. 1), the apical methyl group in MDABCO2+ is substituted by a polar OH− in ODABCO2+. The presence of polar moieties in the organic cations, such as the CN− and OH− groups in CNDABCO2+ and ODABCO2+, can result in a greater intrinsic electric dipole moments, whose polarization induces an increase of the dielectric constant. The intrinsic electric dipole moment introduced by the CN− or the OH− groups increase the overall dipole of CNDABCO2+ from ∼3.61 Debye to ∼7.64 Debye, compared to MDABCO2+ ∼ 1.64 Debye, which is reflected by the values of dielectric constants of Fig. 3.
Thus, the highly modular nature of the A site cation, in particular the DABCO group, afforded by a metal-free scaffold can be exploited to fine-tune the NLO response of these perovskites. For example, the substitution of the CH3 group on MDABCO with highly polar organic groups, such as –SH (thiol), –NH2 (amine), –NO (nitroso) and –NO2 (nitro), whose computed electric dipole moments are shown in Fig. 4b, represents a viable strategy to increase the NLO response of these metal-free perovskites. Indeed, in Fig. 2 we have demonstrated that replacing the CH3 (or OH) with the CN moiety, increases substantially the values of dnorm, thus providing a clear design rule to design novel metal-free perovskites.
The properties and tunability demonstrated in metal-free perovskites are comparable to organic-based NLO materials. Organic NLOs can supersede the performance in terms of descriptors, χ(2) (see eqn (6)), even by 1–2 orders of magnitude of the inorganic NLO materials discussed so far.3,18–28 Some of these materials are even commercial.3,40,41 For example, the 4-N,N-dimethylamino-4′-N′-methyl-stilbazolium tosylate (DAST) forms organic crystals with a superior non-linear susceptibility d ∼ 580 pm V−1 (with d = 0.5χ(2)).21,25 However, organic-based NLOs display at least three major limitations curbing their use in optical devices:23,27 (i) difficult to obtain sufficiently large-size crystals, (ii) limited thermal stability above 200 °C and (iii) low mechanical strength. For example, while a good NLO organic material, such as the 3-methyl-4-methoxy-4′-nitrostilbene has a 1st hyperpolarizability β (see eqn (6)) approximately 300 times larger than the inorganic KH2PO4, it melts at 109 °C.23 Metal-free perovskites also offer the potential to overcome these challenges.
All of the above trends are also dependent on crystal structure and therefore a further understanding of how composition and structure are related is required to achieve truly targeted synthesis. In systems like these metal-free perovskites an interplay of weak forces, such as dispersion, hydrogen bonding and entropy will be important for driving structure and phase transitions, as exemplified in the hybrid halide perovskites.42,43
4 Conclusions
Using first-principles calculations, we have demonstrated the existence of NLO activity in a number of novel metal-free perovskites. In the past, density functional theory has been shown to systematically underestimate the values of χ(2)ijk. While we believe the superior quality of hybrid DFT/PBESol0-based simulations may still underestimate χ(2), our data show that MDABCO–NH4I3 and ODABCO–NH4I3 both fulfil the criteria to useful as deep-UV second-harmonic generation materials. We identify the role of the dipole moment imparted by the organic group on the A cation as an important parameter to tune the NLO properties of these materials. We apply this knowledge introducing the cyanide CN− group on the DABCO–NH4X3 structure, improving significantly the NLO properties of metal-free perovskites. Furthermore our systematic calculations allows us to extract useful trends to chart the second-harmonic generation properties of this novel class of materials. We have shown that the material band gap, and hence the dnorm can be tuned by altering the halide anion. We also show the selection of the A-site cation provides an extra degree of tuning the χ(2). By combining engineering of both the A- and X-sites we believe that these findings provide a blueprint for how to achieve high non-linear optics and second-harmonic generation activity in the desired part of the electromagnetic spectrum. We hope that these findings will help to accelerate the application of metal-free perovskites as non-toxic, earth-abundant materials for the next generation of optical communication applications.5 Linear and non-linear optic effects
Materials respond differently to incident electromagnetic waves, whose induced electric polarization P follows:33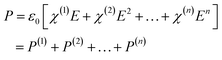 | (3) |
Here, we assess the linear and NLO properties up to χ(2) in the static regime, and accurately derived from first-principles calculations using the coupled perturbed Kohn–Sham theory (CPKS).44,45 We compute the nth-order derivatives of the total energy ETot. with respect to derivatives of the electric field components in ![[small epsilon, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e7.gif) ijk (i, j and k are the Cartesian direction of the electric field), which are cast in the form of order-n + 1 tensors. Such derivatives link to important optical descriptors, such as the electric dipole moment μi and the polarisability, αij,
ijk (i, j and k are the Cartesian direction of the electric field), which are cast in the form of order-n + 1 tensors. Such derivatives link to important optical descriptors, such as the electric dipole moment μi and the polarisability, αij,
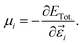 | (4) |
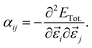 | (5) |
From αij, the components of the dielectric tensor ε are derived as 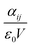 with ε0 the vacuum permittivity and V the unit-cell volume. We note that ε = n2 = 1 + χ(1), with n the refractive index. n and Δn (of eqn (1)) are computed directly from the dielectric tensor.
with ε0 the vacuum permittivity and V the unit-cell volume. We note that ε = n2 = 1 + χ(1), with n the refractive index. n and Δn (of eqn (1)) are computed directly from the dielectric tensor.
The third-order rank tensor χ(2)ijk relates to 1st hyperpolarizability βijk.
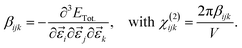 | (6) |
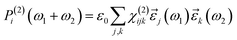 | (7) |
Typically, χ(2)ijk is reported as dijk = 0.5χ(2)ijk. Note that for hybrid functional calculations—the choice in this study—CRYSTAL17 computes only βijk, χ(2)ijk and dijk values in the static limit.
6 First-principles calculations
DFT is used to investigate the structural and optical properties of the metal-free perovskites. Structure relaxations of the experimental coordinates of the metal-free perovskites was performed using the PBESol46 functional as in VASP.47–49 The Grimme D3 (ref. 50) correction was added to capture dispersive forces. The wave functions of the valence electrons were expanded with plane-waves with a cutoff of 520 eV, and core electrons were treated with the projector augmented wave theory.51 The Brillouin-zone was integrated on a mesh with reciprocal density of 64 k-points per Å−1. The total energy was converged within 10−5 eV and forces to 10−2 eV Å−1.An accurate treatment of the electronic structure and in particular the assessment of the optical band gaps is crucial for the description of NLO properties.8,10,52 Starting from the PBEsol-D3 structures with VASP, we re-optimised the coordinates (or volume and coordinates) with the hybrid functional PBE0Sol-D3,46,53 including 25% of exact exchange as available in CRYSTAL17.54,55 We exploited the all-electron linear combination of atomic orbitals of CRYSTAL17 expanded by consistent triple-ζ plus polarization basis-sets, see ref. 56 and 57. Given the electronic configuration of I ([Kr]4d105s25p5) a fully-relativistic pseudo-potential is used.58 The total energy was converged within ∼3 × 10−9 eV and integrated over a well converged and symmetrized 4 × 4 × 4 k-point mesh (i.e., the shrinking factor is set to 4). The truncation of the (infinite) Coulomb and exchange series was set by the tolerances (TOLINTEG): 10−7, 10−7, 10−7, 10−7 and 10−30. Tables S1 and S2 of ESI† show the PBE0Sol+D3 geometries. We computed the non-linear-optical properties with these settings. The iterative solution of the CPKS equations is reached for values below 10−4. Table S6† shows a comparison of the performance of a number of DFT functionals.
The dipole moments of the DABCO units substituted by the organic groups were computed with Gaussian16 (ref. 59) using the PBE0+D3 (ref. 53) functional and the same basis-set used in the periodic calculations with CRYSTAL17.
Author contribution
P. C. and K. T. B. conceived the manuscript, performed the data analysis and wrote the first draft. T. W. K., A. M. M., C. H. H. and K. T. B. performed the initial VASP calculations. P. C., K. T. B. and Z. D. performed the CRYSTAL and Gaussian calculations. All authors contributed to the revision of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. C. acknowledges support from the Singapore Ministry of Education Academic Fund Tier 1 (R-284-000-186-133). The computational work for this article was partially performed on resources of the National Supercomputing Centre, Singapore (https://www.nscc.sg). This work benefited from access to the University of Oregon high performance computer, Talapas. P. C. acknowledges Dr Y. Wu and Prof. A. K. Cheetham for useful discussion.Notes and references
- P. A. Franken, A. E. Hill, C. W. Peters and G. Weinreich, Phys. Rev. Lett., 1961, 7, 118–119 CrossRef
.
- G. D. Stucky, M. L. F. Phillips and T. E. Gier, Chem. Mater., 1989, 1, 492–509 CrossRef CAS
.
- D. F. Eaton, Science, 1991, 253, 281–287 CrossRef CAS PubMed
.
- J. L. Brédas, C. Adant, P. Tackx, A. Persoons and B. M. Pierce, Chem. Rev., 1994, 94, 243–278 CrossRef
.
- P. S. Halasyamani and K. R. Poeppelmeier, Chem. Mater., 1998, 10, 2753–2769 CrossRef CAS
.
-
T. Schneider, Nonlinear Optics in Telecommunications, Springer, Berlin, Heidelberg, 2004 Search PubMed
.
- H. Wu, H. Yu, Z. Yang, X. Hou, X. Su, S. Pan, K. R. Poeppelmeier and J. M. Rondinelli, J. Am. Chem. Soc., 2013, 135, 4215–4218 CrossRef CAS PubMed
.
- J. M. Rondinelli and E. Kioupakis, Annu. Rev. Mater. Res., 2015, 45, 491–518 CrossRef CAS
.
- T. T. Tran, H. Yu, J. M. Rondinelli, K. R. Poeppelmeier and P. S. Halasyamani, Chem. Mater., 2016, 28, 5238–5258 CrossRef CAS
.
- P. S. Halasyamani and J. M. Rondinelli, Nat. Commun., 2018, 9, 2972 CrossRef PubMed
.
- D. Cyranoski, Nature, 2009, 457, 953–955 CrossRef CAS PubMed
.
- Niobium Price, https://www.metalary.com/niobium-price.
- E. A. Olivetti, G. Ceder, G. G. Gaustad and X. Fu, Joule, 2017, 1, 229–243 CrossRef
.
- G. B. Olson, Science, 2000, 288, 993–998 CrossRef CAS
.
- I. Chung and M. G. Kanatzidis, Chem. Mater., 2013, 26, 849–869 CrossRef
.
- N. R. Goud, X. Zhang, J.-L. Brédas, V. Coropceanu and A. J. Matzger, Chem, 2018, 4, 150–161 CAS
.
- A. P. Wilkinson, A. K. Cheetham and R. H. Jarman, J. Appl. Phys., 1993, 74, 3080–3083 CrossRef CAS
.
- J. Zyss, D. S. Chemla and J. F. Nicoud, J. Chem. Phys., 1981, 74, 4800–4811 CrossRef CAS
.
-
P. N. Prasad and D. J. Williams, Introduction to Nonlinear Optical Effects in Molecules and Polymers, John Wiley & Sons, 1st edn, 1991 Search PubMed
.
- T. Kaino and S. Tomaru, Adv. Mater., 1993, 5, 172–178 CrossRef CAS
.
- F. Pan, G. Knöpfle, C. Bosshard, S. Follonier, R. Spreiter, M. S. Wong and P. Günter, Appl. Phys. Lett., 1996, 69, 13–15 CrossRef CAS
.
- I. D. L. Albert, T. J. Marks and M. A. Ratner, J. Am. Chem. Soc., 1998, 120, 11174–11181 CrossRef CAS
.
- M.-h. Jiang and Q. Fang, Adv. Mater., 1999, 11, 1147–1151 CrossRef CAS
.
- W.-J. Kuo, G.-H. Hsiue and R.-J. Jeng, Macromolecules, 2001, 34, 2373–2384 CrossRef CAS
.
- C. Bosshard, R. Spreiter, L. Degiorgi and P. Günter, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 205107 CrossRef
.
- O. R. Evans and W. Lin, Acc. Chem. Res., 2002, 35, 511–522 CrossRef CAS PubMed
.
- S. R. Marder, Chem. Commun., 2006, 131–134 RSC
.
- C. Wang, T. Zhang and W. Lin, Chem. Rev., 2011, 112, 1084–1104 CrossRef PubMed
.
- H.-Y. Ye, Y.-Y. Tang, P.-F. Li, W.-Q. Liao, J.-X. Gao, X.-N. Hua, H. Cai, P.-P. Shi, Y.-M. You and R.-G. Xiong, Science, 2018, 361, 151–155 CrossRef CAS PubMed
.
- H. Wu, S. Pan, K. R. Poeppelmeier, H. Li, D. Jia, Z. Chen, X. Fan, Y. Yang, J. M. Rondinelli and H. Luo, J. Am. Chem. Soc., 2011, 133, 7786–7790 CrossRef CAS PubMed
.
- M. Veithen and P. Ghosez, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 214302 CrossRef
.
- W. Zhang, H. Yu, H. Wu and P. S. Halasyamani, Chem. Mater., 2017, 29, 2655–2668 CrossRef CAS
.
-
R. W. Boyd, Nonlinear Optics, Academic Press as an imprint of Elsevier, 3rd edn, 2008 Search PubMed
.
- J. Zyss and I. Ledoux, Chem. Rev., 1994, 94, 77–105 CrossRef CAS
.
- G. A. Magel, M. M. Fejer and R. L. Byer, Appl. Phys. Lett., 1990, 56, 108–110 CrossRef CAS
.
- Z. Lin, X. Jiang, L. Kang, P. Gong, S. Luo and M.-H. Lee, J. Phys. D: Appl. Phys., 2014, 47, 253001 CrossRef
.
-
D. N. Nikogosyan, Properties of Optical and Laser-Related Materials, Wiley-Blackwell, 1997 Search PubMed
.
- H. Wang, H. Liu, Z. Zhang, Z. Liu, Z. Lv, T. Li, W. Ju, H. Li, X. Cai and H. Han, npj Comput. Mater., 2019, 5, 17 CrossRef
.
- K. T. Butler, J. M. Frost and A. Walsh, Mater. Horiz., 2015, 2, 228–231 RSC
.
- T. Yamada, I. Aoki, H. Miki, C. Yamada and A. Otomo, Mater. Chem. Phys., 2013, 139, 699–705 CrossRef CAS
.
- https://www.tcichemicals.com/pdf/FF051E.pdf .
- K. T. Butler, J. Mater. Chem. C, 2018, 6, 12045–12051 RSC
.
- G. Kieslich, J. M. Skelton, J. Armstrong, Y. Wu, F. Wei, K. L. Svane, A. Walsh and K. T. Butler, Chem. Mater., 2018, 30, 8782–8788 CrossRef CAS
.
- M. Ferrero, M. Rérat, R. Orlando and R. Dovesi, J. Chem. Phys., 2008, 128, 014110 CrossRef PubMed
.
- M. Ferrero, M. Rérat, R. Orlando and R. Dovesi, J. Comput. Chem., 2008, 29, 1450–1459 CrossRef CAS PubMed
.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- V. Lacivita, M. Rérat, B. Kirtman, M. Ferrero, R. Orlando and R. Dovesi, J. Chem. Phys., 2009, 131, 204509 CrossRef PubMed
.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS
.
-
R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco, M. Llunell, M. Causà, Y. Noël, L. Maschio, A. Erba, M. Rérat and S. Casassa, CRYSTAL17 User's Manual, University of Torino, Torino, 2017 Search PubMed
.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed
.
- M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2012, 34, 451–459 CrossRef PubMed
.
- J. Laun, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2018, 39, 1285–1290 CrossRef CAS PubMed
.
- http://www.tc.uni-koeln.de/PP/clickpse.en.html .
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision B.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Structural properties, band gaps, dielectric constants, refractive indexes values of χ(1), values of χ(2) and dnorm, respectively. See DOI: 10.1039/c9sc03378e |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |