A cavity ion source for high-ionization efficiency neodymium isotope-ratio analyses in the geosciences†
Jesse R.
Reimink
 *ab,
Richard W.
Carlson
b and
Timothy D.
Mock
b
*ab,
Richard W.
Carlson
b and
Timothy D.
Mock
b
aDepartment of Geosciences, The Pennsylvania State University, University Park, PA 16803, USA. E-mail: jreimink@psu.edu
bEarth and Planets Laboratory, Carnegie Institution for Science, Washington, DC 20015, USA
First published on 22nd July 2020
Abstract
The principles governing ionization techniques used in thermal ionization mass spectrometers are relatively well understood and have remained largely unchanged for many decades. Though significant advances have been made in ion signal quantification for isotope ratio measurements, particularly for analyses of small samples by using multiple detector systems and low-noise amplifiers, the fundamental approach to sample ionization has received little focus. Modern TIMS techniques attempting to achieve parts-per-million level isotope ratios precisions are realizing limits imposed by the physics of the ionization source. A type of high-ionization efficiency thermal source employed in nuclear physics communities for decades is the so-called cavity thermal ionization source. Here, we provide a proof-of-concept study that shows cavity sources may provide a path forward to achieve a new level of precision in isotope ratio measurements from solid samples. We document our new, simple, cavity ion source design, show preliminary results from Nd isotope measurements, and discuss these new data in the context of current precision limits imposed during traditional thermal ionization methods. We show that, within the limits of our testbed mass spectrometer, mass fractionation within the cavity ion source appears similar to that from filament ion sources. We also demonstrate that oxide-versus-metal ion production plays a significant role in cavity ionization processes for Nd. Cavity ion sources may provide a viable path forward to achieving isotope ratios precisions at the sub-ppm precision level.
Introduction
Mass spectrometers used to measure isotope ratios of geologic samples have long been standard equipment in many geoscience laboratories. For the solid Earth geosciences, and geochronology in particular, the thermal ionization mass spectrometer (TIMS) has been an essential tool. Thermal ionization mass spectrometers are used to analyze the isotopic composition of a range of elements whose first ionization potential is sufficiently low such that substantial ionization can occur before complete sample evaporation from the filament (see Carlson, 2014 for a review).1 Multi-collector inductively coupled plasma mass spectrometers (MC-ICPMS), introduced to the geosciences in the 1990's, use high-temperature plasma sources that can readily ionize elements across the periodic table. At first MC-ICPMS instruments were primarily used to analyze elements that were inefficiently ionized in a TIMS instrument. Recently, ICP instruments have been used to analyze elements once thought to be securely within the domain of TIMS procedures, such as Nd2 and W3 such that the benefits of TIMS analyses become less apparent. ICP analyses are, however, not without their downsides and TIMS instruments remain on the analytical cutting edge due to their comparative simplicity of design, operation, and relatively simple mass spectrum. Both types of instruments appear to be approaching roadblocks that limit the quest for increasing precision and sensitivity in isotope ratio analyses. Overall efficiency, adopted here as the fraction of analyte atoms that end up being detected by the mass spectrometer, is a major factor limiting both functional sample size and ultimate achievable precision during isotope ratio measurements. Distinct hardware obstacles define the sensitivity limits in ICP and TIMS, limits that are unlikely to be overcome without substantial redesign of the ionization and ion transfer systems.Though TIMS instruments have been, and remain, staples of Earth science facilities, they have physical limits to their capabilities. In many cases, especially when dealing with small samples sizes or very precise measurements, total efficiency proves to be the main limitation. This is because internal precisions on isotope ratio measurements via TIMS often approach limits imposed by counting statistics uncertainty (shot noise or Poisson noise). Lowering this barrier to higher precision will require counting more ions either by increasing ionization efficiency, increasing measurement time, or both. The addition of high-ohm feedback resistor amplifiers does not improve the precision on measurements of large ion beams because ion counting statistics, not signal-to-noise ratio, is the limiting factor. Consequently, advances in low-noise detection systems do not provide a path forward for these types of measurements. Improvement is primarily needed on the front end of mass spectrometers to improve both the fraction of atoms ionized and the efficiency of transmission of generated ions to the detector systems. In modern TIMS instruments, the efficiency of ion transmission and detection can exceed 80% such that the highest fraction of analyte atoms is lost during the evaporation and ionization process. However, ion sources capable of producing a factor of 10–40 times more ions from a given amount of analyte compared to conventional flat-filament TIMS sources have been developed, so-called thermal ionization cavity (TIC) sources. Despite their obvious potential benefits, TIC ion sources have yet to achieve routine use in the geosciences (see review in ref. 4). We have taken a new approach to the TIC source and developed an ion source capable of analyzing large sample sizes at high ion beam intensities for long durations with the goal of pushing precision limits below those currently possible with the traditional flat-filament sources used in conventional TIMS.
Current precision limits in TIMS analyses
Standard TIMS instruments employ flat-filament ionizing surfaces wherein the analyte is loaded onto a thin, flat strip of refractory high-work function metal. Ionization efficiency is improved for some elements through the use of multiple filaments where one filament is kept at much higher temperature to serve as an ionization surface for neutral atoms evaporated off of one or more “sample” filaments. The flat-filament ionization assembly, though suitable for the vast array of TIMS applications, suffers from two major drawbacks when considering achievement of parts-per-million isotope ratio precision.First, in conventional TIMS flat filament sources, increasing sample size does not always translate to proportionately longer runs or higher ion beam intensities. In fact, loading more analyte can decrease the total efficiency5 such that e.g. a factor of two increase in sample size translates to less than a factor of two increase in total ions counted. More problematical is that large sample sizes often result in variable mass dependencies for the mass fractionation experienced during sample evaporation and ionization, confounding attempts to accurately correct for that fractionation. These factors combine to restrict our sample size to ∼700 ng of Nd,6,7 much less than is typically separated from an individual rock dissolution (∼2 ug of Nd). A common explanation for the fall-off in ionization efficiency for large samples suggests that large sample sizes limit the amount of analyte in direct contact with the filament, thereby favoring evaporation over ionization. While possible, making longer isotope ratio measurements, by pooling individual ∼700 ng Nd loads from a single sample dissolution, becomes increasingly time-inefficient; an analysis with 3–4 ppm internal precision already requires 9–12 hours of continuous measurement of 4 × 10−11 A signals for 142Nd+.7–9
The second major limitation in flat filament TIMS methods relates to the mass fractionation that occurs during evaporation and ionization. At a basic level, mass fractionation during thermal ionization is a straightforward and well-understood process.10–13 During evaporation and ionization, lighter isotopes are preferentially removed from the solid phase such that the isotope ratios collected early in an analysis have a lower heavy/light isotope ratio and this ratio increases with time. This bias must be removed from the analysis, and is often corrected by assuming that the fractionation is mass dependent and follows an exponential mass dependency.11,12 Although the exponential mass dependency is simply an empirical fit to the observed mass fractionation in TIMS analysis, it has been shown to be appropriate in the vast majority of TIMS analyses. However, the measured ratios can deviate from exponential law fractionation at the parts-per-million level, affecting the accuracy and precision of measurements requiring precision in this range.6,13,14 These measured deviations from exponential law are typically interpreted as reflecting an ion beam that is derived from the combination of emission from a number of variably fractionated reservoirs on a filament. This type of “mixing” imparts a linear, not exponential, overprint on the otherwise exponential mass fractionation of isotope compositions.6,11,13–15 The exact mass dependency of the fractionation present in an ion beam derived from an unknown number of reservoirs with an unknown extent of fractionation is impossible to accurately correct. The problem is compounded in runs involving larger sample sizes as they more often contain periods of complex mass fractionation during analysis. Thus, common practice involves removing sections of an analysis that show clear signs of non-exponential mass fractionation (i.e., decreasing heavy/light isotope composition with time) so as to avoid generating biases induced by inappropriate mass fractionation correction.6,7,13–15 This practice, however, may not completely account for such effects that contribute to reproducibility at the parts-per-million level.
In this work, we explore the possibility that an alternative ion source design may overcome these limiting factors and ultimately allow sub-ppm isotope ratio precisions. A suite of ion source designs has been shown to generate ions at a rate many times higher than traditional TIMS methods.4,16,17 These ion sources, which we will refer to as thermal ionization cavity sources (TIC), have gained use in the nuclear physics and on-line isotope separator communities but have never gained significant traction within the geosciences. The main limitations include the complexity of the cavity designs along with the very high temperatures involved that stress vacuum systems and exacerbate the need for ultrapure cavity materials in order to minimize background signals. In this work we present a simple TIC ion source design that shows the potential for TIC to produce very large ion beams for extended periods of time, with predicted precisions that are a necessary prerequisite to push isotope ratio precision into the sub-ppm range.
In summary, isotope ratio precisions in the ppm range are limited by two main factors: (1) the number of ions counted, and (2) variable mass fractionation behavior. As sample size increases in flat-filament TIMS, ionization efficiency decreases and non-exponential mass fractionation increases. Both can lead to less precise isotope ratios.
Previous cavity source designs
Cavity ion sources were initially proposed in the 1970's16,17 as a method to achieve isotope separation of milligram-sized samples for nuclear studies. Since that time many iterations have been developed, but to our knowledge only online isotope separators18 and one other geoscience laboratory19 currently use the technology. A recent publication4 contains a thorough review of the development history of TIC sources. Despite a wide variety of ionization geometries and mass analyzers, including magnetic sector,4,19–21 quadrupole,22,23 and time-of-flight analyzers,24 all cavity ion sources share some similarities. The essential components of TIC sources are a high-aspect-ratio cavity drilled into a high-work-function metal such as Re, Ta, or W. Sample material is loaded into the rear of this cavity, which is then electrically heated to high temperatures. Initial designs were simple and focused on generating large ion beams from large samples for isotope separator laboratories,16,17 and these forms of TIC sources remain in use among the nuclear physics community18 though they are typically used for smaller samples. However, recent TIC source developments have been driven to achieve maximum ionization efficiency from very small (picogram) sample sizes of high ionization potential elements (e.g., U, Pu, Am), usually driven by the analytical needs of the nuclear forensics community.19,25The physics of ionization in a cavity have been well-summarized.26,27 The dominant mechanism of ionization at temperatures <2700 K, in typical-sized cavities, seems to be thermal ionization from the cavity walls. This situation is similar to traditional flat-filament TIMS sources, except that confined analyte atoms do not immediately escape the hot enclosure after evaporation. Instead, any atom that evaporates, but does not ionize will likely come into contact with another hot inner surface of the cavity. Thus, the proportion of atoms that eventually get ionized is increased as each atom has many more opportunities to be ionized by thermal contact with hot cavity walls. Maden et al. (2016)27 developed modeling code that accounted for space charge within the cavity and showed that space charge along the cavity walls, dominantly derived from thermally-emitted electrons, aids in ion extraction from the cavity. At temperatures above ∼2700 K, a quasi-neutral plasma may exist inside the cavity, thus increasing ionization26 but potentially creating an environment where ion movement becomes diffusive, thus changing extraction properties.27 Independent of whether a quasi-plasma exists within a particular cavity design, TIC sources have been shown to provide higher ionization efficiencies than traditional flat filament arrangements, with ionization increases of up to a factor of 40 for elements of geologic interest. Despite decades of development by many different laboratory research groups, TIC sources have never achieved routine use in the geoscience community. Below, we highlight two recent cavity arrangements both aimed at converting modern-style TIMS mass spectrometers to TIC sources for use in isotope ratio analyses and summarize their results.
Driven by the goal of developing a mass spectrometer that could be quickly converted between a cavity and flat-filament source, the research group at Oak Ridge National Laboratory employed a TIC source first on a Finnigan MAT262,28,29 followed by installation on a Thermo-Fisher Triton TIMS instrument.20,25 This TIC geometry was created by inserting an electrically insulated barrel within the commercial Triton barrel configuration. This new inner barrel was held at the +10 kV operating voltage of the Triton instrument while the outer, conventional barrel was stepped down to +8.5 kV. Cavity rods were mounted on the inner barrel such that the conventional filaments, now held at −1.5 kV relative to the cavity rod, provided electron bombardment current upon heating. In this way 21, cavity samples could be installed on a single modified barrel yet the Triton software and data collection system remained unaffected by the presence of the cavity ion source. Using this TIC setup, the Oak Ridge group showed that small (<10 ng) loads of Nd and Sr could have total efficiencies approaching 20–30%.20,25 However, the stability and longevity of analytical runs were limited by alignment inefficiencies and arcing within the source due to the complexity of the cavity arrangement. Additionally, the dramatic total efficiency improvements found on the MAT262 instrument were apparently not seen on the Triton installation,20 perhaps due to the modification of the MAT262 ion lens system for cavity ion beams28,29 and the design constraint that the Triton ion focusing system remain unaltered for normal filament operations.
More recently, the research group at ETH Zurich has transitioned a multi-collector magnetic sector mass spectrometer (Finnigan MAT262) to a TIC machine.4,19 This design employs a dual-piece cavity assembly, a +10 kV accelerating voltage, and a cavity arrangement that utilizes a flat carbon plate to prevent electrons from impacting the ion beam while providing precise cavity location control. An additional advance is provided by a redesigned electrostatic focusing lens stack and positional drive system capable of actively moving the cavity tip location, aiding in optimizing ion transmission. Thus far, the ETH TIC has produced total efficiency data on U4,19 analyses that showed >10 times improvement in the total efficiency relative to flat-filament TIMS. The ETH TIC is distinct from the Oak Ridge design in that it can accommodate only one cavity at a time, it contains a modified lens stack, and it uses larger cavity dimensions. Nevertheless, the ETH source has produced total ionization gains relative to flat filament TIMS that were better than the Oak Ridge Triton cavity setup,20 but not substantially improved from the initial Oak Ridge cavity installed on a modified Finnigan MAT262.28,29
Though cavity ion sources have shown substantial improvements in ionization efficiency19,27,29 in isotope ratio measurements they have yet to become standard analytical tools in the geoscience community. The reasons for this are not entirely clear, but what is evident is that most recent cavity ion source developments have focused on achieving utmost efficiency from very small sample sizes. This analytical focus, though an obvious use for high-efficiency cavities, suffers from competition with design improvements that allow for quantitative measurement of small ion beam sizes30 as the signal-to-noise ratio often dominates the uncertainty budget of isotope ratio measurements of small samples using Faraday cup detectors. In the present work, we take a different approach and focus on improvements that can be made to analyses where element abundance is not the main limiting factor. Our ultimate aim is to use cavities to generate relatively large (5 × 10−10 A) ion beams from large sample sizes (>1 μg) and measure them for long periods of time (several hours) to achieve isotope ratio precisions at the level of parts-per-million or better. This approach allows us to relax design constraints aimed at peak ionization efficiency, such as operating cavities at very high temperatures, that, in part, lead to some of the issues that have kept cavity ion sources from common use, e.g. contamination of the source region by evaporated cavity material and background signals from insufficiently pure cavity metals.
Analytical background and approach
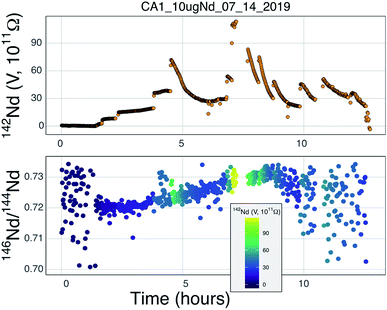
The elements samarium (Sm) and neodymium (Nd) are extremely useful for the geosciences, as well as nuclear forensic,31 applications. Particularly relevant to the geosciences are the two radioactive isotopes of Sm, 146Sm and 147Sm, that undergo alpha decay to 142Nd and 143Nd, respectively.32 Due to the slightly different chemical behavior of Sm and Nd, the long-lived 147Sm-143Nd decay system, with a half-life of ∼106 billion years, has been widely implemented in the geosciences community since the 1970's. The variations in 143Nd/144Nd induced by radioactive decay of 147Sm over geologic time are readily detectable with isotope ratio precisions of better than 100 ppm, making this system relatively easy to utilize with modern analytical systems. The other decay system, 146Sm-142Nd, has a much shorter half-life of ∼103 million years and, due to the low abundance of 146Sm at the start of the Solar System, imparted much smaller variations in the daughter isotope ratio 142Nd/144Nd. Quantification of the variability in 142Nd/144Nd allows for detection of changes in Sm/Nd during the lifetime of 146Sm, lasting for the first 500 million years of Solar System history, allowing for accurate chronology of Solar System materials,33 tracking of silicate differentiation on Earth and other rocky solar system bodies35–37 and identification of Hadean reservoirs still present on the modern Earth.8,9 These small 142Nd/144Nd variations are only detectable with isotope ratio measurements that are precise at the parts-per-million level, as the total natural variation in 142Nd/144Nd in Earth materials is only ∼50 ppm. Thus, very precise isotope ratio measurements are required to fully utilize the short-lived 146Sm-142Nd system.Modern precisions in the measurement of 142Nd/144Nd are on the order of 3–4 ppm.2,6,9 This level of precision requires measurement times on the order of a dozen hours with beams around 5 × 10−11 A (equivalent to 5 V on a 1011 Ω resistor). As shown by Garçon et al.,6 internal precision in the 142Nd/144Nd isotope ratio of multidynamic TIMS measurements is only slightly poorer than the theoretical limits imposed by shot noise (Fig. 1). This means that the internal precision is chiefly dependent on the number of ions detected during a given measurement.
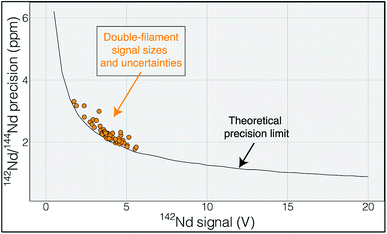 | ||
| Fig. 1 Uncertainty in 142Nd/144Nd plotted as a function of the average 142Nd signal size during a 6 hour analysis. The actual measurements are shown in orange and track the theoretical limit imposed by shot noise (Poisson noise), modeled using a multi dynamic collection routine that dramatically decreases the impact of collector efficiency variations.6 The close correlation between measured and calculated uncertainty suggests that the uncertainty budget is dominated by shot noise such that increasing signal size would be the most effective route to improving the internal precision of any given analysis. | ||
While the internal uncertainty budget is dominated by shot noise, modern measurements achieve internal precisions that push the limits of external reproducibility. In our experience, the external reproducibility on modern double-filament Nd-isotope measurements remains ∼4–5 ppm, with measurements of standards producing measured 142Nd/144Nd values that do not agree within the limits of internal uncertainties. Our interpretation of this irreproducibility relies on observations of changing mass fractionation, and deviations from exponential law, during any particular analysis (Fig. 2). Though this may seem to limit internal precision gains made by higher ion yields, cavity ion sources may provide a means to more accurately quantify, and correct for, non-exponential mass fractionation and isobaric interferences.
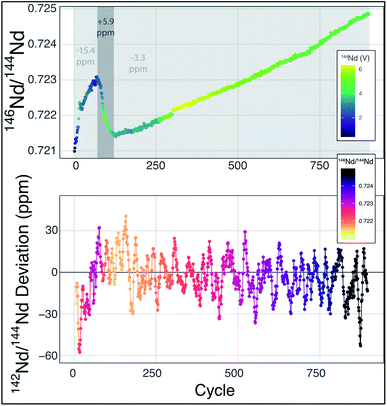 | ||
Fig. 2 Mass fractionation during a single Nd-isotope measurement using the methods described in ref. 6. The top panel shows the measured 146Nd/144Nd ratio without mass fractionation correction as a function of the cycle number (each cycle is ∼45 seconds with the total run lasting ∼13 hours) with symbol colors corresponding to the 142Nd signal size in volts across a 1011 Ω resistor. The grey fields show three sections of the run, divided by fractionation trends, with the numbers indicating the average deviation from exponentially-corrected 142Nd/144Nd over that section of the analysis (all fractionation corrected to an assumed 142Nd/144Nd = 1.141![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832). The bottom panel shows a ten-point moving average of the deviation of each fractionation-corrected 142Nd/144Nd ratio from exponential law fractionation correction. Each measured 142Nd/144Nd ratio was time- and fractionation-corrected using a multi-dynamic collection scheme,6 and then normalized to a 142Nd/144Nd = 1.141 832). The bottom panel shows a ten-point moving average of the deviation of each fractionation-corrected 142Nd/144Nd ratio from exponential law fractionation correction. Each measured 142Nd/144Nd ratio was time- and fractionation-corrected using a multi-dynamic collection scheme,6 and then normalized to a 142Nd/144Nd = 1.141![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832. The variably colored line connecting data points shows the sequence of cycles to aid interpretation. 832. The variably colored line connecting data points shows the sequence of cycles to aid interpretation. | ||
Mass fractionation during a TIMS measurement that deviates from exponential law is typically interpreted to reflect an ion beam composed of a mixture of ions derived from sample regions on the filament that have experienced different fractionation histories.6,11,13–15 This process will vary from analysis to analysis, potentially leading to significant external variability. The combination of ions originating from variably fractionated sample domains on the filament will generate isotope ratio deviations in predictable directions, calculated by considering the particular ratios used in mass fractionation corrections. For instance, while using 146Nd/144Nd to correct 142Nd/144Nd, mixing of the ions emitted from variably fractionated domains on a filament will produce positive deviations from exponential law, most easily visualized on a three-isotope plot,13,14 creating an artificial increase in 142Nd/144Nd. In fact, this type of behavior is readily observable at the ppm precision level, as shown in Fig. 2. During the analysis highlighted in Fig. 2 (a typical analysis of JNdi standard solution from ref. 7), data taken while the sample was reversely fractionating (decreasing 146Nd/144Nd with time) have a 142Nd/144Nd ratio that is ∼10 ppm higher (+5.9 versus −3.3 relative to a 142Nd/144Nd = 1.141![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832), on average, than the rest of the cycles measured during the analysis. While the analysis shown in Fig. 2 is readily filtered to remove portions of the analysis that may be affected by non-exponential mass fractionation at the >15 ppm level, other, less obvious, periods of such behavior within an analysis may not be so readily removed.
832), on average, than the rest of the cycles measured during the analysis. While the analysis shown in Fig. 2 is readily filtered to remove portions of the analysis that may be affected by non-exponential mass fractionation at the >15 ppm level, other, less obvious, periods of such behavior within an analysis may not be so readily removed.
Given the above considerations regarding precision and reproducibility during high precision Nd isotope analyses, we endeavored to implement a cavity ion source in a different manner then what has been attempted previously. Instead of optimal ionization from very small sample sizes, we aim to use the cavity ion source to generate large (>5 × 10−10 A) Nd ion beams for long periods of time (several hours). Our development and design aimed to test whether cavity ion sources can provide a path towards sub-ppm Nd-isotope ratio precisions by, (1) generating large ion beams from large samples for long periods of time, thus driving down shot noise uncertainty, and (2) providing a means to more accurately correct for mass fractionation, particularly non-exponential mass fractionation, during TIMS analyses. Our approach and implementation thus allowed us to simplify a cavity ion source design as very high temperatures are not necessarily needed for our approach. This allows us to avoid engineering issues such as deposition of evaporated metal on insulators within the source housing25 and controlling outgassing of the source components during high temperature operation that may lead to high-voltage arcs.4
The present work did not aim to produce higher total efficiencies than those achieved in modern TIMS instruments as previous publications have clearly shown that cavity ion sources have the ability to generate higher total efficiency for Nd than flat-filament TIMS.22,23,25 Thus, we did not focus our design efforts on optimizing the ionization efficiency by, for instance, testing a wide range of loading techniques or additives,19,20 or by substantially modifying the cavity dimensions; these improvements are clearly possible with cavity ionization. Instead, we focused our design on testing whether large Nd+ ion beams can be generated for long periods of time, producing total ion counting statistics that could drive down internal precisions.
Cavity design
Mass spectrometer testbed and heating design
Our cavity configurations were tested on a Carnegie-built single detector magnetic sector mass spectrometer. This instrument is a 60-degree sector, 15-inch radius, Nier geometry magnetic sector mass spectrometer with a single fixed Faraday detector that can be moved to accommodate a secondary electron multiplier. Ion beam intensities were measured by a Keithley 642 Electrometer, which was digitized using a Keithley 2001 Digital Voltmeter and later by a Solartron 7060 Systems Voltmeter. All magnet control, data collection, and data reductions were performed using a custom LabVIEW program written in-house.Our cavity ion source was heated using electron impact heating. This type of heating has been the most common design implemented in TIC sources and we chose this design to avoid the requirement for very large currents at high voltage required to resistively heat the cavity. A 0.4 mm diameter tantalum filament was used as electron source and held at ground potential. Current was passed through this filament using a Kepco JQE 0–50 V, 0–10 A power supply. Upon heating the filament provided an electron current that impacted, and heated, the cavity source. The bombardment (heating) current was monitored by the current absorbed by the cavity power supply and controlled manually. The voltage to the cavity was provided by a Spellman SL2000 power supply capable of producing +15 kV at 110 mA. The electron bombardment current was monitored by the Spellman power supply, where the current readings were equivalent to the electron bombardment current from the grounded filament to the cavity. We operated our cavity source at voltages between +5 to +7 kV. The electron bombardment currents during an analysis scaled with the cavity voltage; heating power extended up to ∼300 W, requiring 60 mA bombardment current with a +5 kV cavity and 42 mA with a +7 kV cavity.
Two different ion optical lens systems were employed during our operation. The original lens system on the 15-inch mass spectrometer is an NBS thin lens.37 This ion source consisted of several lens elements made of 0.4 mm thick stainless steel with voltages provided by a resistor chain that output voltages from +5 kV to ground. During our testing of the TIC source we determined that many of the optical elements of the original lens system were likely unnecessary as they had little impact on detected ion current across a range of voltage settings. Consequently, we simplified the lens system by removing the discriminator and draw-out plates, keeping only x-focus and z-focus (y being the ion optical axis) plates in addition to a defining plate and final collimating slits, all kept at the same dimensions as the initial configuration. Data collected using this modified NBS source is presented in Table 1. This configuration was, unfortunately, limited in its voltage range such that during many analyses the x- or z-focus plates were at their maximum voltage difference, potentially limiting ion transmission. As a potential improvement, we opted to test a second ion lens system. This second optical design was modeled after a simplified lens system designed for a triple-filament ionizing source.38 In this Loveless and Russell source focusing system, only one set of four thick plate electrodes is employed, along with a pair of grounded collimating slits as in the initial design. The four electrodes are held at a potential close to the ionization source forcing the ions to follow damped oscillatory paths that are focused at the collimating slit (Fig. 4). We employed a slightly larger version of the Loveless and Russell source design for several of our analyses where the width of the plates (in the y-direction) were 8 mm deep, the top and bottom plates were 5.5 mm wide (x-direction), and the side plates were 16 m tall (z-direction).
| Cavity no. | Source type | Cavity | Load size | AquaDAG | Re foil | Re powder | 142/144Nda | Efficiency | 142Nd volts | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Depth | Diam. | Mean | 2SEb | 2SE ppm | Nd | NdO | Nd/NdO | Equivalent | ||||||
| a Average 142Nd/144Nd ratio calculated after filtering for outliers (at the 5SE level). b Two standard errors about the mean. | ||||||||||||||
| CA1 | Simplified Shield lens | 12 | 1.54 | 10 | Y | N | Y | 1.146632 | 0.000685 | 597 | 0.650 | 0.003 | 198.2 | 55.6 |
| CA2 | Simplified Shield lens | 16 | 1.54 | 2.35 | N | Y | Y | 1.141925 | 0.000055 | 48 | 2.080 | 0.430 | 4.8 | 41.1 |
| CA2 | Simplified Shield lens | 16 | 1.54 | 2.35 | N | Y | N | 0.375 | 0.234 | 1.6 | 7.4 | |||
| CA2 | Simplified Shield lens | 16 | 1.54 | 2.35 | N | Y | N | 0.003 | 0.007 | 0.4 | 0.0 | |||
| CA2 | Simplified Shield lens | 16 | 1.54 | 2.35 | N | Y | N | 1.142222 | 0.000064 | 56 | 0.069 | 0.056 | 1.2 | 1.4 |
| CA2 | Simplified Shield lens | 16 | 1.54 | 2.35 | N | Y | N | 1.142650 | 0.000383 | 336 | 0.203 | 0.156 | 1.3 | 4.0 |
| CA2 | Simplified Shield lens | 16 | 1.54 | 2.35 | N | Y | N | 0.050 | 0.001 | 36.6 | 1.0 | |||
| CA2 | Simplified Shield lens | 16 | 1.54 | 2.35 | Y | Y | N | 0.348 | 0.005 | 70.1 | 6.8 | |||
| CA2 | Loveless and Russell | 16 | 1.54 | 2.35 | Y | Y | N | 0.045 | 0.007 | 6.7 | 0.9 | |||
| CA2 | Loveless and Russell | 16 | 1.54 | 2.35 | Y | Y | N | 0.069 | 0.011 | 6.2 | 1.4 | |||
| CB1 | Simplified Shield lens | 10 | 1.54 | 2.35 | N | Y | N | 1.141962 | 0.000064 | 56 | 0.416 | 0.624 | 0.7 | 8.2 |
| CB1 | Simplified Shield lens | 10 | 1.54 | 2.35 | N | Y | N | 1.141817 | 0.000057 | 50 | 0.930 | 0.740 | 1.3 | 18.3 |
| CB1 | Simplified Shield lens | 10 | 1.54 | 2.35 | N | Y | N | 0.170 | 0.350 | 0.5 | 3.5 | |||
| CB1 | Simplified Shield lens | 10 | 1.54 | 0.5 | Y | N | Y | 0.240 | 0.164 | 1.5 | 1.0 | |||
| CB1 | Loveless and Russell | 10 | 1.54 | 2.35 | Y | Y | N | 0.016 | 0.061 | 0.3 | 0.3 | |||
| CC1 | Simplified Shield lens | 17 | 1.54 | 2.35 | N | Y | N | 0.334 | 0.526 | 0.6 | 6.6 | |||
| CC1 | Simplified Shield lens | 17 | 1.54 | 2.35 | N | Y | N | 0.110 | 0.033 | 3.4 | 2.2 | |||
| CC1 | Loveless and Russell | 7 | 1.54 | 2.35 | Y | Y | N | 1.141163 | 0.000041 | 36 | 0.138 | 0.065 | 2.1 | 2.7 |
| CC1 | Loveless and Russell | 17 | 1.54 | 2.35 | Y | Y | N | 1.138769 | 0.000147 | 129 | 0.159 | 0.078 | 2.0 | 3.1 |
| CC2 | Simplified Shield lens | 11.5 | 1.54 | 0.5 | Y | N | Y | 0.237 | 0.434 | 0.5 | 1.0 | |||
| CC2 | Simplified Shield lens | 11.5 | 1.54 | 0.5 | Y | N | Y | 0.993 | 0.485 | 2.0 | 4.2 | |||
| CD1 | Simplified Shield lens | 40 | 1.54 | 0.5 | Y | N | Y | 0.240 | 0.164 | 1.5 | 1.0 | |||
| CD1 | Loveless and Russell | 40 | 1.54 | 2.35 | Y | Y | N | 0.181 | 0.084 | 2.2 | 3.6 | |||
The 15-inch mass spectrometer ion extraction system is mounted on four ceramic rods (Fig. 3A and B), having a ∼0.01 mm smaller bore than the lens plates, to prevent differential thermal expansion from breaking the ceramic rods. In the case of both lens stack systems, we built the cavity ion source directly out from this existing lens system such that our cavity source would be easy to position reproducibly in the center of the lens system. A large, grounded, cylindrical shielding plate surrounded most of the hot cavity to prevent cavity material from being deposited on the ceramic insulating rods. This shielding plate also surrounded the electron bombardment filament through which the filament heating leads where positioned. Finally, cavities were held by a stainless-steel block that was fixed to two of the ceramic mounting rods extending from the lens stack (Fig. 3). This block was held in place using set screws, and the entire assembly was affixed to long ceramic rods mounted to a base block mounted inside the source housing. Our cavity design left the cavity attached to the mount at its base, away from the ionization tip. The stainless steel block was held snugly against ceramic tubes cut to length to maintain a constant cavity y-position in front of the extraction lens system. Likewise, the cavity was held in the stainless steel block with a set screw, and positioned manually using a measured mounting block such that the length of cavity sticking out in front of the stainless block was reproducible. However, the cavity ionization tip was freely floating, meaning that the cavity position may have changed during an analysis through sagging during high-temperature operation, altering the focal properties. Unfortunately, this sagging was only observable through a change in the lens stack voltages that achieved optimal ion transmission and was impossible to accurately quantify. This is distinct from the ETH design which fixes the ion source location by attaching the cavity tip to a graphite plate that controls the ion extraction location in x,y,z space.4
During this work we used cavities made of Ta rod with a 3.1 mm outside diameter (supplied by H Cross company, 99.7% Ta). The cavities were made by electrical discharge machining 1.5 mm wide holes into the Ta rod, creating cavities of various depths (10–40 mm; Table 1) and 1.5 mm diameters. The diameters were chosen to match both the machining capabilities of the Carnegie machine shop and be comparable to the dimensions of cavities recently shown to produce high ionization efficiencies in other labs.4,20 Tantalum was used as the cavity material during our analyses due to the low cost and ease of machining relative to Re. Analyte Nd was loaded into cavities in a 2 M HCl solution containing 1 ppm Nd using a 10 μL syringe (Hamilton syringe 10 μL, Model 701 RN SYR, Part #7635-01). Carbon additive was loaded in the same manner using AquaDAG solution of colloidal graphite. AquaDAG was loaded on top of dried down Nd sample at the base of the cavity. During some analyses, Re powder was also added to the cavity to aid in ionization. Re powder (99.7% Re) was suspended in MilliQ water and ∼2 μL was loaded on top of the Nd HCl solution before drying. For some analyses, cavities were re-used several times. While cavities were not completely cleaned of Nd prior to loading another analysis, we are confident that only a small fraction of the total ions detected may have come from prior sample loadings. This is due to several factors. First, we typically removed and replaced the Re lining in between sample loads, which significantly reduced the amount of Nd remaining in any previously used cavity. Also, we discovered that upon cooling a cavity and reheating, the ion beam signal size would only return to significant size when it reached heating powers close to the maximum power of the previous analysis. This means that as long as subsequent analyses remained at heating power below the previous maximum, very little ionization of previous analyte occurred. We attempted to clean cavities by boiling in 8 M HNO3 overnight, and subsequent ultrasonication, but this appeared to only have a limited effect on presence of Nd in the cavity. More testing will need to be accomplished to fully clean previously used cavities.
During the latter stages of our analysis, we lined the Ta cavities with Re foil to create a higher work function surface on the inside of the cavity. The Re foil was 0.025 mm thick 99.7% pure Re foil from Thermo-Fisher (#010307-FI), which was cut to size, wrapped around a post, inserted into the cavity, and expanded to firmly contact the Ta cavity walls. After initial testing, we also inserted two Re filaments (99.7% pure from H cross) in a cross pattern into the base of the cavity before loading the cylindrical foil lining so that analyte loaded into the bottom of the cavity would be loaded onto Re instead of bare Ta. This was an attempt to further reduce NdO+ production.
Results and discussion
Signal size
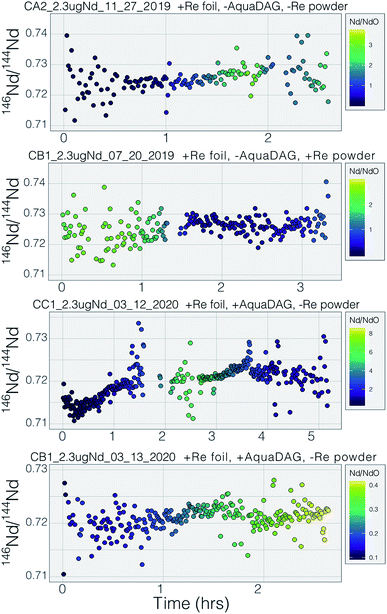
During the course of our testing and analysis we focused on generating large ion beams of Nd+ for long periods of time using cavity loads of 2 μg as we regularly separate such amounts of Nd from geological samples. A Nd+ signal was detectable on our Faraday detectors when the heating power approached ∼80 W (∼12 mA with +7 kV cavity voltage). Upon first appearance of a Nd+ beam, the signal grew rapidly during initial heating before decreasing, all at a constant heating power. Ion beam tuning was completed manually during heat up and before starting data collection. If signal sizes or isotope ratios degraded during data collection, the run was aborted and the signal refocused and tuned. After this initial signal increase, the signal size grew exponentially with increased bombardment current and eventually stabilized. Once large signals were achieved, they began to slowly decay over time and required an increase in the electron bombardment current to maintain the signal size. Overall, this behavior is similar to the behavior of Nd+ during double filament analyses, suggesting that similar processes govern the evaporation and ionization of Nd from the surface of the cavity.Several of our runs produced ion beams >5 × 10−10 A that lasted for several hours (Fig. 5 and 7). However, there was significant variability in the total efficiency of each run. The highest signal sizes were all generated using the simplified Shields lens system. However, many runs using this lens system produced low total ionization yields. These low intensity runs were conducted under sub-optimal ion focusing conditions, where the voltage difference on the x-focus or z-focus plates was at a maximum. This implies that optimum focus was not achieved, and some fraction of the ion beam was not being directed into the collimating slit, likely producing a substantial reduction in total ion yield. Our interpretation of the scatter in total ion yields using the simplified Shields source is that lower ion yields represent runs where the focusing properties of the ion source was not optimal and suffered ion transmission degradation. An added component to the variable efficiencies was the different cavity loading procedures used, as described previously. Though widely varying cavity dimensions were used, no systematic variation in ionization efficiency was observed that correlated with cavity depth. More testing is required to optimize this feature of the cavity design.
The difficulty associated with optimizing ion focusing during ionization from a cavity source has been highlighted in other work.4,20 To test a new approach, and guided by modeling using the SIMION modeling software, we implemented a modified Loveless and Russell ion optics design38 that was shown to produce significantly higher ion transmission when using a triple-filament ion source arrangement. Our design of the power supply system allowed for independent determination of the top voltage of the four steering plates in the lens system, with each plate then separately tunable using a parallel resistor chain with ∼300 V of range. Our experiments showed that the Loveless and Russell lens system had excellent ion beam steering capabilities and was insensitive to x-focus and z-focus setting; that is, the signal intensity was simple to optimize and remained relatively constant throughout each analysis. The Loveless and Russell ion source system was designed to have the steering plates held at a voltage close to the accelerating voltage (∼5 V lower than maximum), and our optimum peak shape and ion transmission occurred near the +5 kV accelerating voltage of the cavity. However, the total efficiencies were substantially decreased with this lens system compared to the modified NBS source (Table 1), indicating that overall ion transmission was suboptimal. Our interpretation for suboptimal focusing is that the ion beam was not fully collimated and focused at the defining slit such that only a small fraction of the defocused beam was transmitted through the mass spectrometer, as evidenced by the relatively insensitivity to x and z voltage settings.
Regardless of the difficulties in ion focusing, our cavity ion source has shown a promising ability to produce large ion beam sizes for long durations. When the total ion counts from our TIC source are compared to flat-filament measurements, they predict sub-ppm precisions in the 142Nd/144Nd isotope ratio (Fig. 6). These promising results were obtained in spite of several limitations in our current approach. As discussed above, our ion focusing systems suffered from suboptimal performance in both designs; the modified shield lens could not achieve optimal focusing while our modified Loveless and Russell source displayed a substantial decrease in ion transmission. We did not run the Nd loaded into our cavities to exhaustion. Though signal sizes continued to decline near the end of analyses, substantial Nd ion beams often remained upon termination of the analysis. We did not push the temperature on our cavity to the extremes that might be possible, so our ionization efficiencies (Table 1) are minimum estimates. Given the cavity ion source efficiency increase shown by other labs, substantial additional gains in total ion yields certainly appear possible with our TIC source design if ion transmission is improved with a modified focusing system and the cavities are run to higher temperature to exhaust the analyte.
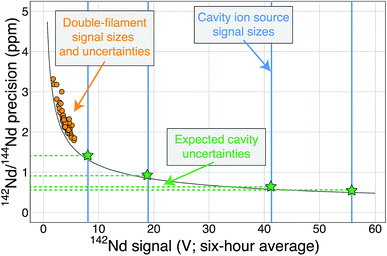 | ||
| Fig. 6 A modified version of Fig. 1 showing the cavity ion yields. The average 142Nd signal size in volts (relative to a 1011 Ω resistor) during a 6 hour multi-dynamic Triton analysis6 is plotted against the internal precision achieved during that run.7 The black curve is the precision limit imposed by shot noise while the orange circles are actual double-filament analyses from samples and standards.7 The vertical blue lines are total ion yields from the cavity ion source using 2 μg of Nd (the highest signal size line was measured using 10 μg Nd) converted to average signal size over six hours if these analyses were made on the Triton. The horizontal green dashed lines and stars are the predicted precisions of our cavity ion source analyses if mass fractionation corrections are similar, with the best analyses theoretically pushing the precision of the 142Nd/144Nd measurement below one part-per-million. | ||
Neodymium oxide production
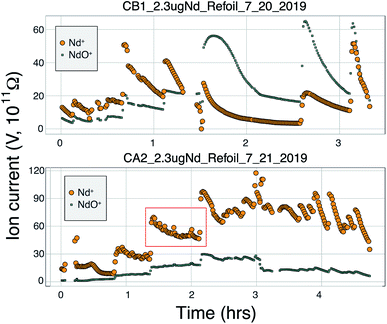
Many modern Nd isotopic analyses measure the metal ion, Nd+, though analyses of NdO+ used to be common32 and remain in use for analyses of very small analyses.39 The production of NdO+ ions occurs at a lower temperature than the metal species, so higher ionization efficiency can be achieved when analyzing NdO+ particularly when using an oxygen bleed valve or oxygen-emitter additives to the filament. Measurement of NdO+ does not, however, provide a likely path towards more precise and accurate 142Nd/144Nd measurements as multiple isobaric interferences, and potential oxygen isotope fractionation during an analysis, must be accounted for when measuring polyatomic oxide species.40To our knowledge, there has been only limited documentation of the various metal/oxide ion production abilities of Nd while using a cavity ion source, though metal/oxide production has been investigated for other elements during short analysis times (<10 min (ref. 4, 19 and 24)). Though colloidal carbon (AquaDAG) is often used during mass spectrometry as a chemical reductant on the filament, the cavity community has also used carbon (either colloidal graphite or organic resin bead loading) as an additive to increase the work function of the ionizer, in addition to a chemical reductant, where ReC has a higher work function than Re metal.4,20 To evaluate the metal/oxide ionization within cavities, we tracked Nd+/NdO+ for the vast majority of our analyses. During most of our analyses, NdO+ often had a higher signal during the initial portions of the analyses, Re and C additives or a Re foil inside of the cavity aided in production of Nd+ (Table 1), optimizing ionization of the metal ion. During some analyses, however, NdO+ was the preferred species (Fig. 5). The analysis shown in top panel of Fig. 5 is from a cavity that was lined with Re foil but did not have Re lining the base of the cavity. During the low-temperature beginning of the analysis, Nd+ is the dominant ion species, but in the middle of the analysis, NdO+ becomes the dominant species. One possible interpretation is that as temperatures increase NdO+ begins to ionize directly from the Ta base of the cavity, whereas at lower temperatures Nd evaporates as either metal or oxide and is dominantly ionized as a metal during its multiple interactions with the cavity walls after evaporation. An alternative interpretation invokes variable temperature distribution along the cavity such that ions may be extracted from the base of the cavity (as NdO+) preferentially at the beginning relative to the later, higher-temperature, portions of the analysis. The lower panel of Fig. 5 shows an analysis made with a cavity that had Re foil covering the inner walls of the cavity as well as the bottom of the cavity and had Re powder as an additive. During this analysis Nd metal ions are dominant throughout the entire duration of the run, showing that limiting the exposure of analyte to the Ta cavity walls increased the metal ionization efficiency.
In order to additionally decrease the NdO+ production in our cavity designs we loaded colloidal graphite (AquaDAG) along with Nd solution into the base of the cavities. This may have substantially decreased the NdO+ production from the cavity; average Nd+/NdO+ without AquaDAG is 4.7 and the average with AquaDAG is 24.5 (Table 1), though these values are dominated by a few analyses and other factors may play a role. This result suggests that the presence of a reductant (or Re powder) at the base of the cavity has a significant influence over the Nd+ production. Bürger et al.20 documented a dramatic increase in the ionization efficiency of Nd with either resin-bead loads or C additives from both cavity ion sources and flat filament sources. They, however, interpreted this increase to be driven by the increased work function of ReC, which aids in the ionization of all species. The impact of high-work-function ReC was also invoked by ref. 4 who interpreted an increase in U ionization over the lifetime of individual Re cavities to be due to carbon from the graphite mounting plate diffusing into the initially pure Re metal cavity. Our data show that, for Nd analyses, the competing ionization of Nd+ and NdO+ may play a dominant role over ReC as an ionizer, but this remains to be tested fully. If formation of ReC was driving the Nd+ ionization increase, metal ionization increases would be expected to match with greater production of NdO+ due to the increased work function of ReC. Instead, the data suggest that at many times Nd+ forms at the expense of NdO+ and the two signals are inversely correlated during specific periods of the analyses. However, other more complex processes such as variable temperature distributions within the cavity may have a dramatic impact.
Mass fractionation
Our testbed mass spectrometer has only a single Faraday detector so peak hopping was required to make isotope ratio measurements (typical data collection included 142Nd+, 144Nd+, 146Nd+, 148Nd+, 142Nd16O+, and 144Nd16O+, or some combination of these) therefore the isotope ratios are susceptible to ion beam intensity variations over the integration times used (between 4 and 10 seconds). Though all of our beam intensity data is time-corrected to the 144Nd integration time by linear interpolation between two consecutive measurements of the isotope of interest, non-linear ion beam behavior can substantially bias resulting isotope ratios. Additionally, significant inconsistency in the ion beam intensity was produced during analyses, caused by several different factors. First, during initial manual heat-up the electron bombardment current was often manipulated to stabilize ionization, resulting in ‘jumps’ in ion beam currents that are not readily accounted for with a linear time-correction for ion beam intensity.Second, particularly during analyses using the simplified NBS lens system at high temperature, the resistor chain experienced voltage disturbances that created oscillations in the lens voltages. These oscillations, likely due to electron currents to the front lens plate, resulted in ion beam variability on the order of several volts with a periodicity of less than a second. This instability created most of the variability in isotope ratios collected near the end of analyses using the NBS source (Fig. 7). This problem was eliminated during analyses with the Loveless and Russell ion optics system, which was powered by an independent power supply instead of a resistor-divider chain.
Prior to this study, published mass fractionation behavior from cavity ion sources is limited to short-duration (∼7 min) analyses of U4 and one of Gd isotopes24 though the latter may have been confounded by isobaric interferences. Potential shifts in mass fractionation can substantially affect high precision isotope ratio measurements.6,13,14 Similar to the Nd ion beam behavior, fractionation from a TIC source (Fig. 7 and 8), at least to the precision allowed by our single-detector configuration (Fig. 7 and 8), appears to be similar to mass fractionation from a double filament ion source (Fig. 2). The first isotope ratios collected during an analysis had compositions lighter than the 146Nd/144Nd = 0.7219 used as the standard ratio for mass fractionation correction and showed ‘normal’ fractionation behavior throughout the lifetime of an analysis, where the isotopic composition becomes heavier throughout the run. The isotopic composition near the end of analyses reached a 146Nd/144Nd value that was similar to that seen during flat filament analyses (0.725; ref. 6), at which point the ion beam began decaying substantially. Though we were not able to collect precise isotope ratios, there appeared to be no relationship between Nd+/NdO+, and 146Nd+/144Nd+ and, importantly, very little ‘reverse’ fractionation.
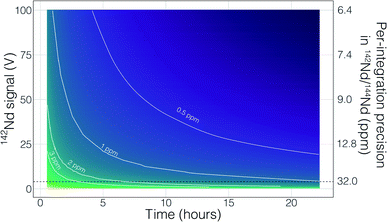
Though no ‘reverse’ fractionation is detected in our cavity ion source analyses we do not have sufficient isotope-ratio precision to completely rule this phenomenon out (142Nd/144Nd precisions were typically >40 ppm for a given run; Table 1). If cavity ion source measurements do produce periods of non-exponential mass fractionation, the higher ion beam intensities provide a path towards correcting such behavior. The secondary y-axis in Fig. 9 shows the within-integration standard deviations on the 142Nd/144Nd measurement using simple ion counting statistics and uncertainty propagation (and an 8-second integration time). The typical signal sizes achievable for our modern double-filament 142Nd analyses (∼4 V) are shown by the horizontal dashed line, which corresponds to a within-integration uncertainty of ∼32 ppm, in excellent agreement with our multi-collector TIMS observations.7 As expected, the per-integration uncertainty of any isotope ratio dramatically decreases with signal size. If measurements of ion beam currents ∼5 × 10−10 A (50 V on a 1011 Ω resistor) are made, the standard deviation on any given integration would drop to ∼9 ppm, allowing non-exponential fractionation effects to be resolved much more precisely (Fig. 9). This calculation shows that even if cavity ion sources are susceptible to mass dependency fractionation variations during an analysis, they provide a path towards more accurate data by allowing for more precise filtering of integrations that have been affected by this phenomenon.
There are also more obvious benefits to the higher beam sizes that cavity ion sources will provide over traditional flat filament sources. First, there is the clear time-savings in that higher signal sizes achieve desired precision more quickly than small beams. This is shown in Fig. 9 with a calculation that models the uncertainty of the fractionation-corrected 142Nd/144Nd as a function of analytical time and signal size. As expected, there is a decreasing precision return over time meaning that each additional hour of data collection achieves less of a relative precision increase than the last hour. The current state-of-the-art TIMS analyses for 142Nd, measuring 4 V signals for 9–12 hours, are reaching a point where quadrupling the analytical time to double the precision is inviable. Even if analyzing a 4 V beam for 25 hours was possible, the precision increase would only be on the order of a few tenths of ppm in the isotope ratio precision. However, analysis of a 50 V beam for a ∼2 hours will achieve internal precisions much lower than can be achieved currently. Thus, analyses at the same, or better, precision level could be achieved in less than half the time. Analyses of 50 V beams for this length of time with double filament assemblies have not been shown to be possible, so cavity ion sources provide a new path forward.
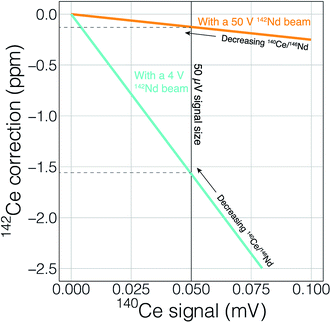
Finally, the higher ionization efficiency and signal sizes achievable with cavity ion sources will provide more accurate and readily quantifiable interference corrections. This utility can, once again, be illustrated with 142Nd measurements. The main interfering elements of concern during 142Nd measurements are Ce (with an interference of 142Ce on the Nd isotope of interest) and Sm (with several isobaric interferences on important Nd isotopes). Accurately detecting any interfering element is a major concern when dealing with isobaric interferences on isotope ratios measured at the ppm precision level. Fig. 10 shows the effect of signal size on detecting, and accurately correcting, potential interferences. To correct the isobaric 142Ce interference, 140Ce is measured and a 142Ce/140Ce ratio of 0.12565 is assumed. This correction is on the order of five ppm with a 140Ce/146Nd of 6.3 × 10−5 and falls with decreasing Ce/Nd. Fig. 10 shows two lines that calculate the 140Ce signal at a given ppm correction in 142Nd/144Nd with varying 140Ce/146Nd. When measuring Nd isotope compositions in Faraday detectors attached to amplifiers equipped with 1011 Ω resistors, a 50 μV signal is difficult to accurately quantify. If the 142Nd ion beam is 4 V, a 140Ce signal of 50 μV would relate to a correction of −1.5 ppm, meaning that interferences below ∼1.5 ppm corrections will not be accurately quantified. With a 50 V 142Nd beam, however, a 50 μV 140Ce signal will only represent a 0.1 ppm correction on 142Nd/144Nd. Thus, higher signal sizes will allow us to more accurately correct for interferences, even if such interferences are not reduced by cavity measurements. Although lower noise Faraday amplifiers are finding increasing use in the detection of small interferences, the use of such amplifiers in combination with relatively low gain amplifiers complicates multi-dynamic measurement schemes that switch ion beams between different Faradays in order to compensate for inefficient ion retention.
As well as the obvious need to accurately quantify any interfering signal, the unknown state of mass fractionation of Ce and Sm leads to uncertainty in the amount of signal correction to be applied.6 Garçon et al. (2018)6 showed that for a 142Nd analysis, the unknown fractionation state of interfering elements adds excess uncertainty at the ∼5 ppm level with 140Ce/146Nd > 1.6 × 10−3 and 147Sm/146Nd > 1.2 × 10−4. These decrease to 140Ce/146Nd > 0.3 × 10−3 and 147Sm/146Nd > 0.2 × 10−4 when considering measurements with 1 ppm precision. More precise quantification of the interfering elements, even if their relative signals compared to the analyte of interest, can lead to more accurate application of interference corrections, especially if quantification of mass fractionation of the interfering elements can be achieved by, for instance measurement of 147Sm/149Sm ratios during the analysis. Higher signals will clearly allow for more precise and accurate interference corrections, even if for instance the Nd/Sm ratio were to stay the same, leading to more accurate data.
Conclusions
We present a proof-of-concept cavity thermal ionization mass spectrometer (TIC) ion source that could be used to achieve very high isotope ratio precision for large (microgram) sample sizes. Modern Nd-isotope analyses are currently limited to precisions of ∼4–6 ppm due to counting statistics and non-exponential mass fractionation effects. We have developed a cavity ion source, heated by electron bombardment, that is capable of producing >5 × 10−10 A (50 V on a 1011 Ω resistor) Nd+ ion beam sizes for several hours. Though more development is required to make these highly productive analyses routine, the expected precision from these cavity ion source analyses, when measured using modern multi-collector instruments and based on shot-noise limitations alone can approach 0.5 ppm for the isotope ratio of interest, 142Nd/144Nd. We show that generation of large ion beams is possible from TIC sources and that the metal to oxide ratio, Nd+/NdO+, plays a major role in the total ionization of Nd+ from a TIC source. This ratio can likely be optimized using a combination of Re ionizing material and carbon additives, the latter serving as a reductant at the ionizing surface. Although our single-detector testbed mass spectrometer is not capable of making precise isotope ratio measurements, we show that mass fractionation from a TIC ion source appears to be similar to double filament sources. An improvement in precision to sub-ppm levels in Nd-isotope ratios would allow full utilization of the paired 146,147Sm-142,143Nd decay systems and produce a significant advance in the understanding of early Solar System events on Earth and other rocky bodies.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by an NSF EAR-IF grant to RWC and JRR (#1758571). The authors thank Colin Maden with help in setting up Simion models that informed earlier design decisions. Joshua Davies is thanked for enlightening comments and discussions. Mary Horan and Steve Shirey are thanked for essential assistance in various stages of mass spectrometer setup and troubleshooting.References
-
R. W. Carlson, Thermal Ionization Mass Spectrometry, Elsevier, 2014 Search PubMed
.
- N. S. Saji, D. Wielandt, C. Paton and M. Bizzarro, J. Anal. At. Spectrom., 2016, 31, 1490–1504 RSC
.
- G. J. Archer, G. A. Brennecka, P. Gleißner, A. Stracke, H. Becker and T. Kleine, Earth Planet. Sci. Lett., 2019, 528, 115841 CrossRef CAS
.
- C. Maden, A. Trinquier, A.-L. Fauré, A. Hubert, F. Pointurier, J. Rickli and B. Bourdon, Int. J. Mass Spectrom., 2018, 434, 70–80 CrossRef CAS
.
- R. L. Edwards, J. H. Chen and G. J. Wasserburg, Earth Planet. Sci. Lett., 1987, 81, 175–192 CrossRef CAS
.
- M. Garçon, M. Boyet, R. W. Carlson, M. F. Horan, D. Auclair and T. D. Mock, Chem. Geol., 2018, 476, 493–514 CrossRef
.
- J. R. Reimink, T. Chacko, R. W. Carlson, S. B. Shirey, J. Liu, R. A. Stern, A. M. Bauer, D. G. Pearson and L. M. Heaman, Earth Planet. Sci. Lett., 2018, 494, 12–22 CrossRef CAS
.
- M. F. Horan, R. W. Carlson, R. J. Walker, M. G. Jackson, M. Garçon and M. Norman, Earth Planet. Sci. Lett., 2018, 484, 184–191 CrossRef CAS
.
- B. J. Peters, R. W. Carlson, J. M. D. Day and M. F. Horan, Nature, 2018, 555, 89–93 CrossRef CAS PubMed
.
- K. Habfast, Int. J. Mass Spectrom. Ion Phys., 1983, 51, 165–189 CrossRef CAS
.
- S. R. Hart and A. Zindler, Int. J. Mass Spectrom. Ion Processes, 1989, 89, 287–301 CrossRef CAS
.
- W. A. Russell, D. A. Papanastassiou and T. A. Tombrello, Geochim. Cosmochim. Acta, 1978, 42, 1075–1090 CrossRef CAS
.
- D. Upadhyay, E. E. Scherer and K. Mezger, J. Anal. At. Spectrom., 2008, 23, 561–568 CAS
.
- R. Andreasen and M. Sharma, Int. J. Mass Spectrom., 2009, 285, 49–57 CrossRef CAS
.
- M. S. Fantle and T. D. Bullen, Chem. Geol., 2009, 258, 50–64 CrossRef CAS
.
- G. J. Beyer, E. Herrmann, A. Piotrowski, V. J. Raiko and H. Tyrroff, Nucl. Instrum. Methods, 1971, 96, 437–439 CrossRef CAS
.
- P. G. Johnson, A. Bolson and C. M. Henderson, Nucl. Instrum. Methods, 1973, 106, 83–87 CrossRef CAS
.
- T. K. Sato, M. Asai, A. Borschevsky, T. Stora, N. Sato, Y. Kaneya, K. Tsukada, C. E. Düllmann, K. Eberhardt, E. Eliav, S. Ichikawa, U. Kaldor, J. V. Kratz, S. Miyashita, Y. Nagame, K. Ooe, A. Osa, D. Renisch, J. Runke, M. Schädel, P. Thörle-Pospiech, A. Toyoshima and N. Trautmann, Nature, 2015, 520, 209–211 CrossRef CAS PubMed
.
- A. Trinquier, C. Maden, A.-L. Fauré, A. Hubert, F. Pointurier, B. Bourdon and M. Schönbächler, Anal. Chem., 2019, 91(9), 6190–6199 CrossRef CAS PubMed
.
- S. Bürger, L. R. Riciputi, D. A. Bostick, S. Turgeon, E. H. McBay and M. Lavelle, Int. J. Mass Spectrom., 2009, 286, 70–82 CrossRef
.
- Z. Li-Hua, D. Hu, W. Guan-Yi, L. Zhi-Ming, W. Chang-Hai, L. Xue-Song, Z. Guo-Qing, S. Yong-Yang and Z. Zi-Bin, Int. J. Mass Spectrom., 2011, 305, 45–49 CrossRef
.
- Y. Duan, R. E. Danen, X. Yan, R. Steiner, J. Cuadrado, D. Wayne, V. Majidi and J. A. Olivares, J. Am. Soc. Mass Spectrom., 1999, 10, 1008–1015 CrossRef CAS
.
- Y. Duan, E. P. Chamberlin and J. Olivares, Int. J. Mass Spectrom. Ion Processes, 1997, 161, 27–39 CrossRef CAS
.
- D. M. Wayne, W. Hang, D. K. McDaniel, R. E. Fields, E. Rios and V. Majidi, Spectrochim. Acta, Part B, 2001, 56, 1175–1194 CrossRef
.
- S. Bürger, L. R. Riciputi, S. Turgeon, D. Bostick, E. McBay and M. Lavelle, J. Alloys Compd., 2007, 444–445, 660–662 CrossRef
.
- R. Kirchner, Nucl. Instrum. Methods Phys. Res., Sect. A, 1981, 186, 275–293 CrossRef CAS
.
- C. Maden, H. Baur, A.-L. Fauré, A. Hubert, F. Pointurier and B. Bourdon, Int. J. Mass Spectrom., 2016, 405, 1–11 CrossRef
.
-
K. B. Ingeneri, L. R. Riciputi and P. M. L. Hedberg, Preliminary Results of Uranium and Plutonium Efficiency Measurements Using a High Efficiency Cavity Ion Source Interfaced with a Finnigan MAT 262 Mass Spectrometer, Proceedings of the Institute of Nuclear Materials Management, 43rd Annual Meeting June 24–27, Orlando, FL, USA, 2002, vol. 16 Search PubMed
.
-
K. B. Ingeneri, L. R. Riciputi and P. M. L. Hedberg, Preliminary Results of Uranium and Plutonium Efficiency Measurements Using a High Efficiency Cavity Ion Source Interfaced with a Finnigan MAT 262 Mass Spectrometer, Proceedings of the Institute of Nuclear Materials Management, 43rd Annual Meeting June 24–27, Orlando, FL, USA, 2002 Search PubMed
.
- J. M. Koornneef, I. Nikogosian, M. J. van Bergen, R. Smeets, C. Bouman and G. R. Davies, Chem. Geol., 2015, 397, 14–23 CrossRef CAS
.
- J. Krajkó, Z. Varga, E. Yalcintas, M. Wallenius and K. Mayer, Talanta, 2014, 129, 499–504 CrossRef PubMed
.
- G. W. Lugmair and K. Marti, Earth Planet. Sci. Lett., 1977, 35, 273–284 CrossRef CAS
.
- N. E. Marks, L. E. Borg, I. D. Hutcheon, I. D. Hutcheon, B. Jacobsen and R. N. Clayton, Earth Planet. Sci. Lett., 2014, 405, 15–24 CrossRef CAS
.
- M. Boyet and R. W. Carlson, Science, 2005, 309, 576–581 CrossRef CAS PubMed
.
- R. W. Carlson, L. E. Borg, A. M. Gaffney and M. Boyet, Philos. Trans. R. Soc., A, 2014, 372, 20130246 CrossRef PubMed
.
- C. L. Harper and S. B. Jacobsen, Nature, 1992, 360, 728–732 CrossRef CAS
.
-
W. R. Shields, NBS Technical Note 277: Analytical Mass Spectrometry Section: Instrumentation and Procedures for Isotopic Analysis, U.S. Department of Commerce, National Bureau of Standards, 1966, vol. 277 Search PubMed
.
- A. J. Loveless and R. D. Russell, Int. J. Mass Spectrom. Ion Phys., 1969, 3(3–4), 257–266 CrossRef CAS
.
- J. Harvey and E. F. Baxter, Chem. Geol., 2009, 258, 251–257 CrossRef CAS
.
- A. Luguet, G. M. Nowell and D. G. Pearson, Chem. Geol., 2008, 248, 342–362 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ja00228c |
| This journal is © The Royal Society of Chemistry 2020 |