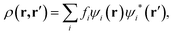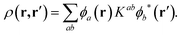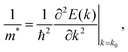Meta-analysis: the molecular organization of non-fullerene acceptors†
Pierluigi
Mondelli
a,
Gabriele
Boschetto
b,
Peter N.
Horton
c,
Priti
Tiwana
a,
Chris-Kriton
Skylaris
b,
Simon J.
Coles
 c,
Michal
Krompiec
ab and
Graham
Morse
c,
Michal
Krompiec
ab and
Graham
Morse
 *a
*a
aMerck Chemicals Ltd, Chilworth Technical Centre, University Parkway, Southampton SO16 7QD, UK. E-mail: graham.morse@merckgroup.com
bSchool of Chemistry, University of Southampton, Highfield, Southampton, SO17 1BJ, UK
cEPSRC Crystallographic Service, Department of Chemistry, University of Southampton, Highfield, SO17 1BJ, UK
First published on 18th November 2019
Abstract
The rapid development of Non-Fullerene Acceptors (NFAs) for organic solar cells has recently pushed the Power Conversion Efficiencies (PCE) over the 15% threshold, surpassing fullerene-based state-of-the-art devices. However, for the commercialization of large-scale photovoltaic modules, thick active layers films (150–300 nm) with high PCE and fill factors are required. The realization of materials with higher charge mobilities is fundamental for the roll-to-roll printing industry, and therefore understanding the factors that limit charge transport properties of NFAs becomes crucial for commercialization. The study of the molecular packing and arrangement of NFAs in the solid-state provides direct insight to the propensity of the pristine materials to crystallize and contribute efficiently to the charge transport. In this work we combine experimental techniques and molecular modelling, with the aim of analyzing the way in which NFAs interact in the solid-state and the key components of their structures for building efficient percolation pathways for charge transport. To this end, several new molecules were synthesized and crystallized by solvent vapour diffusion, which were then characterized by single crystal X-Ray Diffraction (XRD). These structures were further compared to a wide selection of literature materials. Density Functional Theory (DFT) calculations were also carried out to examine the electronic transport of these materials with respect to their molecular packing motifs.
New conceptsWe demonstrate how the unique design of non-fullerene molecules leads to their crystal structures being predominated by acceptor fragment interactions, and how this can lead to unique three-dimensionally π-conjugated crystals. These unique crystals are shown by computational calculation to produce more isotropic charge transport, which remains the most significant challenge in non-fullerene based solar cell research. Research to improve the charge transport of non-fullerenes is largely a trial and error process. Here we demonstrate ways to improve isotropic charge transport and bulk charge transport through targeting molecules which preferentially form 3-dimensional crystal packing motifs. We demonstrate that materials design of organic electronic materials should focus more energy designing molecules to preferentially favour specific motif formation. Even chemical side chains should be considered for their shape within a crystal lattice, rather than just for the solubility they impart, to ensure efficient and directed crystal packing can be ensured. In this way, unique material properties can be elucidated from existing material classes. |
Introduction
Organic Solar Cells (OSC) based on NFAs have been the focus of research since the inception of the field of Organic Photovoltaics (OPV).1–5 Recently, new designs proposed by Xiaowei Zhan6 has led to a surge in performance beyond 15% PCE,7 going far beyond the best fullerene-based OSCs.8,9 NFA molecules intrinsically possess many advantages over fullerenes, including a more efficient light absorption and tunability of the energy levels,3,10 leading to higher photocurrent and reduced voltage losses in the devices.11 Despite the advantages, NFAs are still lagging behind fullerene acceptors in terms of charge transport properties.12,13 Therefore, low electron mobilities represent a major challenge for the commercialization of solution-processed fullerene-free OPV devices, which requires high performance in the thick-film active layer regime (150–300 nm), being the most realistic window for common large-scale roll-to-roll printing techniques.14 The reason for the difference between these two classes of materials can be linked to their molecular shape, which in turn affects the molecular packing and the charge transport properties.15–18 Indeed, PC61BM possesses a unique and beneficial feature for a fast charge transport: the near-ball-shaped molecular structure allows for formation of three-dimensional charge percolation network and at the same time ensures the typical domain sizes to be within the exciton diffusion length (∼20 nm).12 On the other hand, NFAs are characterised by highly anisotropic conjugated structures, and their two-dimensional geometry makes the molecular packing, domain orientation and blend morphology19,20 crucial for the electron mobility, charge separation and charge collection at the electrodes.21–23 Therefore, it is essential to study and understand the solid-state arrangement of NFA molecules to achieve better performing systems. Despite in many fields of organic electronics the influence of molecular packing on the charge transport properties have been extensively studied both theoretically and experimentally,15,16,24–26 in OPV this topic has started to draw the attention only recently.17,26–35 In this review, we explore the way in which these molecules interact in the solid-state and how the chemical design can influence the molecular organization, focusing on a specific class of NFA materials: fused rings electron acceptors (FREA). These molecules are typically composed by linearly fused acceptor–donor–acceptor (A–D–A) aromatic backbones with the side chains located on sp3-hybridized carbon atoms near the centre of the molecule. Comparisons to related families of molecules such as small acceptor (D–A molecules) and donor molecules (D molecules) will be used to support and contrast our observations.A meta-analysis of the molecular packing and the crystallization tendencies will be carried out over a wide selection of crystal structures known in literature and newly identified ones. The discussion will identify the most common features and trends related to molecular packing; considerations about packing motifs, density of packing and π–π interaction strength will highlight the influence of the molecular organization on the charge transport. To further discuss the importance that molecular packing and topological connectivity have on the charge transport properties, DFT calculations will be performed on a few A–D–A molecules to evaluate their electron effective masses. In particular, by comparing the effective masses values calculated along different directions for several structures, it will be possible to draw conclusions about the influence of the topological connectivity at the molecular level on the charge transport anisotropy.
Experimental
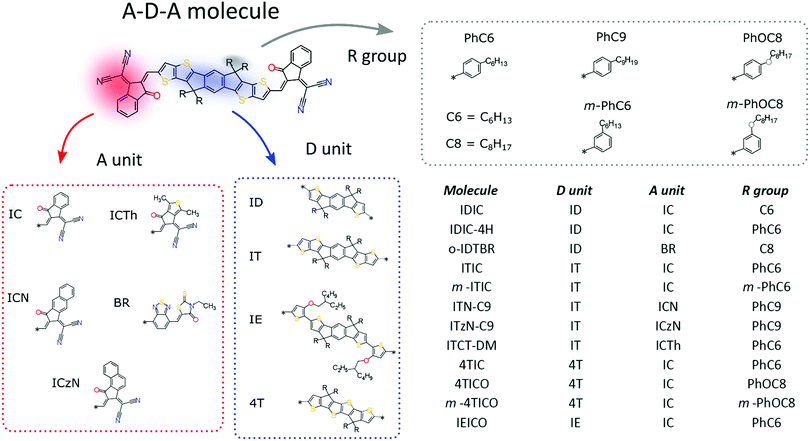
Crystal growth
Single crystals suitable for XRD analysis were grown by solvent vapour diffusion: the compound of interest was dissolved and diffused in an antisolvent vapour (Table 1). For most of the crystal structures diffracted in this work, the use of petroleum ether 40–60 (PE40–60) and chloroform have been successful with the only exception of the 4TICO molecule (chemical structure shown in Fig. 1). All the solvents were purchased from Sigma Aldrich. 4TICO and m-4TICO molecules were synthesised following the procedure described elsewhere.36,37 The chemical structures of IDT01 and ICA small molecules are shown in Fig. 2, while the ICNA small molecule acceptor is equivalent to the “ICN” acceptor unit shown in Fig. 1 with an alkyl side chain “C6”. IEICO was purchased from Solarmer Material Inc. (China) while ITIC, m-ITIC and IDIC from 1-Material (Canada). The synthetic routes for IEICO, m-ITIC, ITIC and IDIC are reported in literature.38–41| CCDC identifier | Compound name | Solvent/anti-solvent | Crystallization precipitate | Crystal system | Space group | Solvate inclusions | φ (%) | φ s (%) | Motif | π–π stackingc |
|---|---|---|---|---|---|---|---|---|---|---|
| a Void fraction of solvent-masked and/or excessively disordered structures have been omitted for consistency. b Void fraction calculated when the solvent contribution is ignored. c Only cofacial alignment between aromatic rings has been considered. d Crystal grown by slow evaporation. e Crystallites size too small to be diffracted. f Non-diffracted crystal, another sample of the same molecule was chosen as more suitable for diffraction. g Both solvent and antisolvent molecules have been found in the crystal structure. | ||||||||||
| A–D–A molecules | ||||||||||
| 1942946 | ITIC | CHCl3/PE40–60 | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
None | 35.51 | — | Herringbone | 0D |
| — | ITIC | CHCl3/C2H5OH | Amorphous solid | — | — | — | — | — | — | — |
| — | ITIC | CHCl3/CH3OH | Crystallinee | — | — | — | — | — | — | — |
| — | ITIC | C6H5Cl/C6H12 | Molecular glass | — | — | — | — | — | — | — |
| — | ITIC | CHCl3/C3H6O | Amorphous solid | — | — | — | — | — | — | — |
| KIZSUK42 | ITIC | CH2Br2/C7H16 | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
CH2Br2 | — | — | Brickwork | 2D |
| — | 4TICO | CHCl3/PE40–60 | Crystallinee | — | — | — | — | — | — | |
| — | 4TICO | CHCl3/C2H5OH | Crystallinee | — | — | — | — | — | — | — |
| — | 4TICO | CHCl3/CH3OH | Crystallinee | — | — | — | — | — | — | — |
| — | 4TICO | C6H5Cl/C6H12 | Crystallinee | — | — | — | — | — | — | — |
| 1942947 | 4TICO | CHCl3/C3H6O | Crystalline | Monoclinic | P21/c | C3H6O | 34.61 | 36.67 | Herringbone | 0D |
| 1942948 | m-4TICO | CHCl3/PE40–60 | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
CHCl3 | 33.82 | 39.25 | Brickwork | 2D |
| — | m-4TICO | CHCl3/CH3OH | Crystallinef | — | — | — | — | — | — | — |
| 1942949 | m-ITIC | CHCl3/PE40–60 | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
CHCl3 | 35.11 | 38.15 | Brickwork | 2D |
| — | m-ITIC | CHCl3/CH3OH | Molecular glass | — | — | — | — | — | — | — |
| 1942950 | IEICO | CHCl3/PE40–60 | Crystalline | Monoclinic | C2/c | CHCl3 | 37.43 | 42.1 | Reticular | 3D |
| — | IEICO | CHCl3/CH3OH | Crystallinee | — | — | — | — | — | — | — |
| 1942951 | IDIC | CHCl3/PE40–60 | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
None | 34.79 | — | Brickwork | 2D |
| — | IDIC | CHCl3/CH3OH | Crystallinef | — | — | — | — | — | — | — |
| — | IDIC | C6H5Cl/C6H12 | Crystallinef | — | — | — | — | — | — | — |
| — | IDIC | CHCl3/C3H6O | Crystallinef | — | — | — | — | — | — | — |
| YEBKEY43 | 4TIC | C7H8/CH3OH | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
Bothg | — | — | Reticular | 3D |
| 1889754 | o-IDTBR | Unknown | Crystalline | Monoclinic | P21/c | None | 36.03 | — | Reticular | 3D |
| KIQVOY28 | ITCT-DM | Unknown | Crystalline | Monoclinic | C2/c | None | 36.30 | — | Reticular | 3D |
| ZIHBAW31 | ITN-C9 | CH2Br2/C3H6O | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
CH2Br2 | 35.3 | 47.32 | Brickwork | 2D |
| ZIHBEA31 | ITzN-C9 | CH2Br2/C3H6O | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
CH2Br2 | — | — | Brickwork | 2D |
| YISJIW33 | IDIC-4H | CHCl3/C2H5OH | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
None | 35.36 | — | Brickwork | 2D |
| Small acceptor molecules – D–A molecules | ||||||||||
| 1942952 | ICA | CHCl3/PE40–60 | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
None | 31.36 | — | Slip-stacked | 1D |
| — | ICA | CHCl3/CH3OH | Crystallinee | — | — | — | — | — | — | — |
| 1942953 | ICNA | CHCl3/PE40–60 | Crystalline | Monoclinic | P21/n | None | 29.19 | — | Herringbone* | 1D |
| — | ICNA | CHCl3/CH3OH | Molecular glass | — | — | — | — | — | — | — |
| SAHZEI44 | N/A | Unknown | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
None | 33.29 | — | Slip-stacked | 1D |
| BUXYEA45 | N/A | Unknown | Crystalline | Monoclinic | P21/n | None | 31.83 | — | Herringbone* | 1D |
| HEHYAW46 | N/A | Unknown | Crystalline | Monoclinic | P21/c | None | 29.76 | — | Lamellar | 1D |
| BUXYAW45 | N/A | Unknown | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
None | 33.91 | — | Slip-stacked | 1D |
| Small donor molecules – D molecules | ||||||||||
| 1942954 | IDT01 | Unknown | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
None | 35.23 | — | Herringbone* | 1D |
| QEGHAO47 | PDT | CH2Cl2/C4H8O2 | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
None | 35.52 | — | Slip-stacked | 1D |
| SITJOW48 | N/A | CH2Cl2/CH3CN | Crystalline | Monoclinic | P21/c | None | 34.24 | — | Herringbone | 0D |
| SITJUC48 | N/A | CH2Cl2/CH3CN | Crystalline | Monoclinic | P21/c | None | 33.83 | — | Herringbone* | 1D |
| SIGMON49 | N/A | CHCl3/CH3OH | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
None | 37.22 | — | Slip-stacked | 1D |
| SERVOB50 | N/A | Unknown | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
CHCl3 | N/A | — | Slip-stacked | 1D |
| WEHNEF51 | N/A | CHCl3/C2H6OS | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
Bothg | 45.83 | 61.08 | Slip-stacked | 1D |
| SITKAJ48 | N/A | CH2Cl2/CH3CN | Crystalline | Monoclinic | P21/n | None | 35.65 | — | Herringbone | 0D |
| SITLEO48 | N/A | CD2Cl2d | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
None | 34.01 | — | Slip-stacked | 1D |
| OFUPEN52 | DMIDT | Unknown | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
None | 39.41 | — | Herringbone | 0D |
| OFUPIR52 | IDT | Unknown | Crystalline | Triclinic |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
None | 40.42 | — | Herringbone* | 1D |
DFT calculations
Computer simulations were performed within the Linear-Scaling Density Functional Theory (LS-DFT) framework, using the ONETEP code (Order-N Electronic Total Energy Package).53 In this approach, DFT can be expressed in terms of the density matrix ρ(r,r′), which in the Kohn–Sham formalism, is defined aswhere fi is the occupancy of the state ψi(r), effectively a Kohn–Sham orbital function. ONETEP relies on the density-matrix DFT formalism, however, ρ(r, r′) is expressed in terms of localized atom-centred orbital functions known as non-orthogonal generalized Wannier functions (NGWFs),54 leading to
In the above expression, φa(r) and φb(r) are the NGWFs and K is known as the density kernel. By expanding the NGWFs in a basis of periodic sinc (psinc) functions,55 the code conveniently relies on a plane-wave basis. ONETEP can achieve linear-scaling behaviour while maintaining at the same time near-complete basis set accuracy: linear-scaling computational cost is obtained by enforcing strict localization of the NGWFs and by truncation of the density kernel K via a spatial cut-off, which makes the density matrix sparse; plane-wave accuracy is achieved through the self-consistent optimization of both the density kernel and the NGWFs during calculations.
Calculation set-up
DFT calculations were performed on A–D–A like NFA crystal structures ranging from 468 to 1120 atoms. The atomic coordinates of published structures were taken from the Cambridge Crystallographic Data Centre (CCDC) database, whereas for the other structures the X-ray data was obtained in this work. X-ray data of o-IDTBR was kindly provided by Sarah Holliday.56 For each NFA crystal, a DFT geometry optimization was performed on the hydrogen atoms only, since it is well known that X-ray diffraction does not provide reliable atomic coordinates for these. The atomic positions of C, O, S, N, the lattice vectors, and the cell angles were kept fixed, in order for the simulations to be performed on experimental data only. This set of simulations was carried out using the Perdew–Burke–Ernzerhof (PBE)57 GGA exchange–correlation functional in conjunction with the projector augmented wave (PAW) method,58 and with the inclusion of the D2 correction by Grimme59 to model dispersion interactions. A psinc kinetic energy cut-off of 800 eV was used, and the NGWFs radius for each atom species was set to 9.0 Bohr. The number of NGWFs used was 4 NGWFs per C, N, O, S atom, and one NGWF per H atom. All ONETEP calculations were performed at the Γ point only.Band structure calculations were performed at the PBE-D2 level using an interpolative approach as implemented in the ONETEP code.60 For this method, it is necessary for the NGWF diameters to be less than half each lattice vector, and therefore for each structure the unit cell was doubled along the shortest vectors. Norm-conserving pseudopotentials were used to model core electrons, the kinetic energy cut-off was set to 800 eV. For reasons of computational efficiency the NGWF radii were set to 6.5 Bohr – these settings ensured minimal changes (of the order of 0.02 eV) in the DFT bandgaps, as compared to the 9.0 Bohr radii. For each crystal, the global minimum of the conduction band was located by sampling the Brillouin zone along the k-point paths suggested by Hinuma et al.61 From the aforementioned calculations, the effective masses of electrons, which at a given k point and along a specific direction can be expressed as:
X-ray diffraction
For all samples except IDT01, a suitable crystal was selected and mounted on a MITIGEN holder in oil on a Rigaku 007HF diffractometer equipped with Varimax confocal mirrors and an AFC11 goniometer and HyPix 6000 detector. The crystals were kept at T = 100 K during data collection. Data were measured using profile data from ω-scans using Cu-Kα radiation (λ = 1.54178 Å). Cell determination, data collection, data reduction, cell refinement and absorption correction were carried out using CrysalisPro.62Sample IDT01 was run on a Nonius Kappa CCD diffractometer with Mo-Kα radiation (λ = 0.71073 Å) controlled by the Collect63 software package at 120(2) K. The data were processed using Denzo64 and semi-empirical absorption corrections were applied using SADABS.65
Using Olex2,66 all the structures were solved with the ShelXT67 structure solution program and the models were refined with version 2018/3 of ShelXL67 using Least Squares minimisation. All non-hydrogen atoms were refined anisotropically. Hydrogen atom positions were calculated geometrically and refined using the riding model.
For samples 4TICO, m-ITIC and IEICO, the quality of crystals was such that they only prove gross connectivity. In general, the core of these structures solved well, but there were issues especially with included solvent and external alkyl chains for which some were highly disordered. As such various geometrical (SADI, DFIX, BUMP) and displacement (RIGU, SIMU) restraints were used.
Results and discussion
Molecular considerations
Molecular packing is, to a large extent, determined by intermolecular interactions.68,69 For this reason, a common way of identifying different packing motifs is by highlighting the dimensionality of the cofacial π–π overlap,24,25,70,71 which is commonly believed to provide efficient electronic coupling between adjacent planar organic molecules. According to literature, the most recurrent motifs in organic semiconductor crystals are:1. Herringbone packing with no extended (0D) π–π stacking (e.g. pentacene72),
2. Non-classic herringbone with reduced one-dimensional (1D) π–π stacking (e.g. rubrene73),
3. Lamellar/slip-stack packing with one-dimensional (1D) π–π overlap (e.g. 1,2,3,4-tetrafluoroanthracene74), and
4. Brickwork with two-dimensional (2D) π–π stacking (e.g. TIPS-pentacene16).
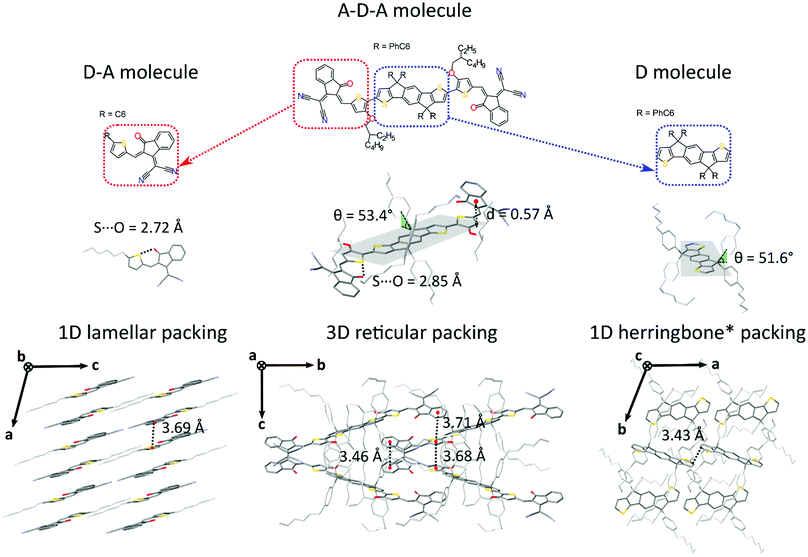
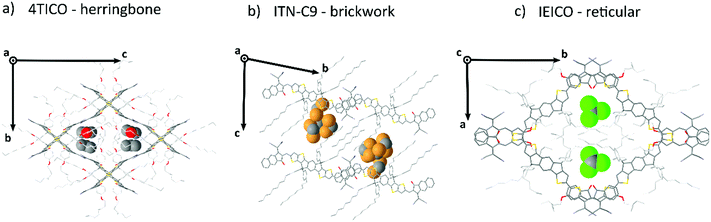
Generally speaking, flat aromatic molecules would lead to 0D herringbone or 1D lamellar structures, as a result of the electrostatic repulsion between electron rich groups or dipole–dipole attraction between polar units.71 A–D–A molecules are similarly flat aromatic molecules with a more or less pronounced dipole character (due to the simultaneous presence of electron-rich and electron-poor units), however their central core contains sidechains which protrude out-of-plane act to frustrate the 1D co-facial π-stacking. This frustration leads to the formation of more complex packing motifs: a reticular architecture with 3D π–π stacking (IEICO packing, Fig. 2 and 5) has been identified to be a common molecular arrangement amongst the ensemble of A–D–A molecules analysed in this work (Table 1, first section).
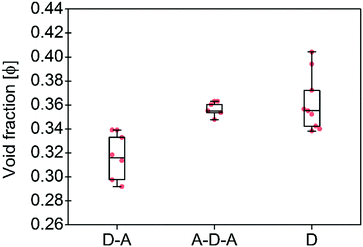 | ||
| Fig. 3 Calculated void fractions φ for the three family molecules studied in this work and listed in Table 1. The box plot denotes median (centre line), 25th quartile (bottom edge of the box), 75th quartile (top edge of the box), maximum and minimum values. Only non-solvated structures have been considered. | ||
The most prolific molecular designs for A–D–A NFAs commonly consist of two acceptor groups such as indene malononitrile (IC) or rhodanine derivatives (BR), flanking a central donor core such as indacenodithiophene (ID) and indacenodithieno[3,2-b]thiophene (IT) (Fig. 1). Researchers have been attempting to replace fullerene acceptors for over three decades, so this begs the question:
What makes recent acceptor–donor–acceptor NFAs so unique?
To support these design cues, the organization and the density of packing within the solid-state of A–D–A molecules were compared to small molecule donor (D molecules) and D–A small molecules (Table 1 and Fig. 2). An effective measure of the density of molecular packing in the unit cell is the void fraction (φ, as a percentage). This parameter has been used previously in order to compare the density of packing for different molecules, since it does not bias molecular size or weight.75 A very simple chemical design as for the D–A small molecules (composed of a few aromatic rings with small and linear sidechains) leads to the formation of molecules with high degree of planarity. All these structures have a high tendency of forming dense 1D packing motifs due to their dipolar character, as they show the lowest values of void fraction (Fig. 3) among the three families of molecules. Across a collection of crystal structures from flat aromatic donor–acceptor (D–A) molecules we observe lamellar, slip-stacked or herringbone structures with 1D co-facial π-stacking (Table 1). In comparison, the frustrated planarity of small donor molecules (D) due to the presence of out-of-plane sidechains, and their electrostatic repulsion due to their electron donating character (Fig. 2), disrupts their tendency to form highly dense packing systems in the solid-state organization. A collection of crystal structures of D molecules organizes as isolated units in 0D herringbone, or with limited co-facial π-stacking like 1D herringbone and slip-stack arrangements (Table 1). This reflects in a broad distribution of high void fraction values, indicating that D molecules form less densely packed crystals (Fig. 3).
As for A–D–A molecules, the peculiarity of their molecular shape facilitates different crystallization packing motifs with intermediate voids fractions, enabling the formation of highly interconnected systems like brickwork and reticular shapes that are not observed for D and D–A small molecules. The molecular structure is characterized by a limited flexibility of the backbone which is ensured by lock-in configurations and a high sidechain flexibility around the dihedral angle θ (Fig. 2).
Noncovalent conformational locks have been shown to be an efficient tool for increasing the electronic conjugation along the backbone.76–78 In particular, S⋯O interactions can be enabled between the acceptor groups and the central donor core of A–D–A molecules. Therefore, S⋯O close contacts ranging from 2.6 Å and 2.8 Å have been found for all the structures available (Fig. S2, ESI†), except for o-IDTBR which contains S⋯N noncovalent interaction instead, due to its unique chemical design. Similar to the S⋯O interactions, S⋯N has also been found to be responsible for a reduced torsional angle between the moieties involved, leading to a more planar configuration of the backbone.79 Nevertheless, donor and acceptor units still present a certain degree of flexibility, which plays a role for the adapting capability of the A–D–A molecules to facilitate the molecular organization in solid-state. The overall flexibility of a molecule often enables a high degree of polymorphism and conformational polymorphism.80 As a result, A–D–A molecules would be expected to have a high likelihood of polymorphism, as reported recently for ITIC.42
This flexibility reflects in a definite vertical displacement d of the acceptor units with respect to the central part of the backbone (Fig. 2). By analysing the crystal structures of the A–D–A molecules, this distance shows a value distribution ranging from 0 Å (central D unit lying in-plane with respect to the A unit) to about 1.9 Å (backbone with inflection) (Fig. S2, ESI†). Across the series of A–D–A single crystals analysed in this study, we have found that the sidechains project out-of-plane at an angle θ ranging from about 45–70° (Fig. S1, ESI†). The sidechain dihedral angle is broadly distributed around the mean value of 56°, leading to a wide variety of geometrical conformations. Their ability to change orientations indicates that these molecular fragments adapt to facilitate molecular organization. In the reticular packing geometry, for instance, sidechains volumes are protruding perpendicularly from the molecular backbones, pointing towards the central voids created by the reticular space filling (Fig. 5). This suggests for the sidechains to be relevant in the formation of this 3D motif, as they occupy the same space region in all the structure with the same arrangement. We encourage further studies to be carried out on the optimization of sidechains to guide the molecular crystallization into particular motifs, thereby ensuring more efficient space filling of void space.
Intermolecular close contacts
Besides their contribution to the overall molecular flexibility, sidechains also influence A–D–A intermolecular interactions. We analysed statistically the intermolecular close contacts for a selection of A–D–A crystal structures by looking at the centroid-to-centroid distances between aromatic rings within the conjugated donor core (D) and acceptor units (A) (Fig. 4a and b). We identified three different kinds of close contacts according to the specific molecular units involved: A⋯A, D⋯A and D⋯D. Interestingly, A units were involved in 26 out of the 27 total close contacts (i.e. their centroid-to-centroid distance d is ≤4.0 Å), while only one D⋯D contact was found. By looking at the distribution of the centroid-to-centroid distances for the contacts found in the crystal structures, it was also possible to analyse in more qualitative terms the two most common contacts configurations (A⋯A and D⋯A) by comparing the position of their centre of mass (Fig. 4d). This parameter represents the average π–π distance characteristic of a specific contact, calculated by counting its frequency in the unit volume (103 Å3). The non-negligible shift of 0.24 Å between A⋯A and D⋯A contacts demonstrates the higher propensity of the acceptor units to be involved in closer contacts. This can be explained as the bulky volume of the sidechains largely precludes co-facial π-stacking between donor cores while favouring interactions between the acceptor units, as predicted by Hou et al.1 Thus, an appropriate design of the electron deficient groups (A units) of the A–D–A molecules is crucial for the molecular organization in the solid-state.Topological connectivity and charge transport
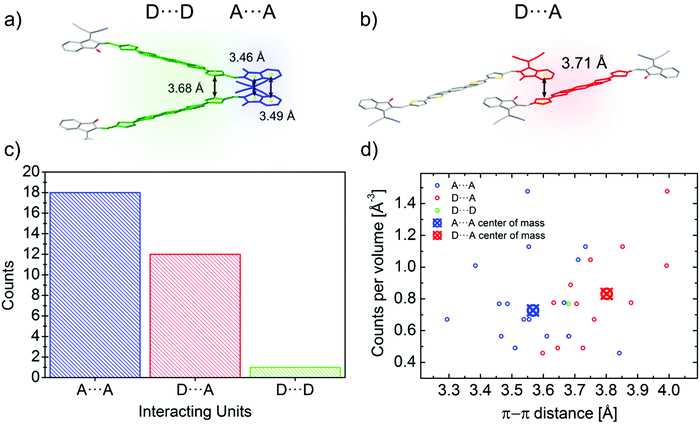
Reticular lattices result in a superior degree of geometrical connectivity, as compared to any other common packing motif within this class of materials. For example, by observing these structures in the top view (Fig. 5) it is clear how reticular lattices show a more complex texture of A–D–A conjugated backbones when compared to brickwork motifs. Theoretical studies on different systems have shown the importance of the topological connectivity towards the achievement of better performing systems in terms of charge transport.18 Moreover, resistivity measurements performed on functionalized pentacene proved how precise crystal engineering can drastically enhance the charge transport due to a more functional solid-state organization.16 One way to estimate the carrier mobility in the solid-state is by calculating the effective mass, which can be derived from the band structure of the crystal. Moreover, it is well known that this quantity can be obtained along chosen geometric directions, which makes it ideal for the evaluation of the intrinsic anisotropy of materials in terms of charge transport. A similar study has already been successfully performed on molecular crystals.81To this end, we performed DFT calculations to predict the band structure of several different A–D–A crystal structures and we explored the effect of the lattice geometry on the electron transport anisotropy. The brickwork ITIC polymorph42 was excluded from the calculations due to degenerate conduction bands (the energy difference between the first lowest conduction bands was less than 0.025 eV, which is the thermal energy at room temperature). By comparing 2D and 3D packing motifs it was possible to study how the topological connectivity of A–D–A molecules affects the anisotropy of the charge carrier transport.
By assuming the conjugated backbone (D unit) and the acceptors (A units) to be the molecular groups providing the main charge percolation pathways for the charge transport, the 2D structures can be viewed as a sequence of conducting planes extending over the d1 and d3 directions and stacking along d2 (Fig. 5a and b). Given the higher geometrical complexity of 3D lattices, we defined d1, d2 and d3 as in Fig. 5a and b. By looking at the curvature of the band structure minima calculated along those three vectors, we found that for 2D structures there is often a very high (>10) electron effective mass along the d2 direction (see Table 2), whereas the masses along both d1 and d3 are generally significantly lower: this implies that the electron mobility is favoured along those directions, but hindered along the stacking d2 direction. The very low values for the effective masses of ITzN-C9 and m-ITIC are most probably due to the smaller stacking distance along d2, as compared to the other 2D structures (Fig. S3 and S8, ESI†). This can open the possibility for the electron transport to be occurring between adjacent domains. 3D structures are generally characterized by low values along any direction (Fig. 5, Table 2 and Fig. S9–S11, ESI†). Overall, these results suggest an intrinsic anisotropy in 2D structures, whereas the transport in 3D structures seems to be more isotropic. These calculations provide theoretical justification to the intuitive expectation of charge carrier transport along π-stacking interactions and contacts.
| Structure | m 1 | m 2 | m 3 |
|---|---|---|---|
| 2D π–π stacking | |||
| IDIC | 0.30 | >10 | 0.5 |
| ITN-C9 | 0.74 | >10 | 2.88 |
| IDIC-4H | 4.98 | >10 | 2.46 |
| m-4TICO | 0.38 | >10 | 3.83 |
| ITzN-C9 | 0.37 | 3.40 | 1.45 |
| m-ITIC | 0.20 | 0.96 | 0.69 |
| 3D π–π stacking | |||
| ITCT-DM | 1.11 | 1.30 | 0.38 |
| o-IDTBR | 0.32 | 2.12 | 3.36 |
| 4TIC | 0.36 | 2.41 | 4.33 |
| IEICO | 0.63 | 1.07 | 2.38 |
Solvated structures
It is apparent from the known A–D–A crystals that solvates are commonly present in these systems, being understood that solvent inclusions occur for systems with high solvent–solute interactions (i.e. high solubility) or for systems with frustrated molecular packing.82 As a proof of concept, 4TIC and 4TICO molecules co-crystalized with antisolvent inclusions of methanol and acetone, respectively (Table 1). The presence of antisolvent inclusions cannot be explained only by solute–solvent affinity, due to the large difference in their chemical nature. In-depth analysis of our dataset shows that the solvent molecules preferentially sit in the central voids left by the sidechains away from the backbone, despite the differences in structures and molecular arrangements (Fig. 6). By calculating the short contacts involving the guest molecules, we can conclude that non-halogenated solvents do not interact with the central backbone, but rather with the sidechains. On the other hand, by increasing the solvent halogenation it becomes more common to observe close contacts which involve the molecular backbone. In the case of dibromo-methane, strong solvent–solvent interactions are observed at a Br⋯C distance of 2.52(5) Å (Br⋯C van der Waals radii sum is 3.55 Å) for the ITN-C9 structure (Fig. 6b). In this last case, the extensive solvent inclusion accounts for a non-negligible 12.02% increase in the void fraction when the solvent is ignored in the void calculation. Following this observation, the use of non-halogenated solvents can help in obtaining solvate-free crystal structures and by corollary, halogenating A–D–A molecules may be a path to encourage more intimate intermolecular interactions.Conclusions
In this work, we have presented an extensive dataset to analyse the solid-state organization of A–D–A NFAs in comparison with two families of small molecules: D and D–A molecules. We have identified how the structural design of A–D–A molecules facilitates their organizational motifs in the solid-state. These learnings can be simply categorized in terms of length-scale.From an intramolecular perspective:
• Out-of-plane sidechains disrupt this natural tendency of building dense lamellar D⋯D networks, sterically hindering the D units from being involve in π–π stacking;
• A high flexibility of the sidechain units likely facilitates their efficient packing;
• The acceptor groups should be unobstructed from interaction;
• And a similar flexibility of the attachment of the acceptor units through the conformationally locked vinylene bond likely facilitates their efficient π–π stacking of the acceptor groups;
From an intermolecular perspective:
• Strong interactions with halogenated solvents suggest that halogenation of the A–D–A molecules would likely increase intermolecular packing if used to facilitate A⋯A interactions;
• A⋯A interactions dominate the intermolecular arrangements being more frequent and with shorter on average centroid-to-centroid distances;
• Three motifs are common amongst A–D–A molecules: herringbone (0D), brickwork (2D) and reticular (3D);
• And solid-state arrangements with higher dimensional charge percolation pathways, such as the reticular motif, are most likely to provide efficient and isotropic charge transport for use in organic electronics.
A–D–A molecules offer a carefully balanced design of a strong D core, providing the donating strength to form strong visible light absorption, but with sufficient steric hinderance to ensure that the strong acceptor units dominate the charge transport. The critical role of the sidechains in these structures to prevent D⋯D interactions while simultaneous filling void space and directing the crystal packing, leads the authors to believe that future designs should meticulously adjust the sidechains to more efficiently occupy the void space of the desired crystal motif. For instance, in the case of 3D reticular crystals the sidechains occupy the central voids within the reticular frame formed by the interconnected conjugated central units. In each case we observed a clear conformational folding in the attempt of stabilizing the bulky central voids. In 2D brickwork systems fully distended alkyl units (as for ITN-C9, Fig. 6b) occupy the interstitial void between the A–D–A planes. This is further supported by the frequent observation of solvent inclusions within these voids, increasing packing density or modifying the packing motif (as for ITIC).
Additionally, the acceptor units heavily dominate the intermolecular interactions for A–D–A molecules. As a result, their design and flexibility arising from their conformationally locked vinylene bond should be further refined and optimized. Alternative acceptor designs, potentially including halogenated acceptors should further be explored to improve the formation of these charge percolation pathways.
Based on these considerations, we encourage the future research to be focusing on the development of new acceptor units and sidechain geometries (e.g. branching) with more degree of flexibility. This could help to obtain systems with a higher propensity of building strong intermolecular interactions through their A units and at the same time to stabilize more efficiently the bulky voids typical of 3D reticular crystals, with the scope of improving the charge transport isotropy of A–D–A NFAs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. M. acknowledges Merck Chemicals Ltd. and the European Union's Horizon 2020 research and innovation programme under Marie Skłodowska Curie Grant agreement no. 722651 (SEPOMO) for the support in the realization of this work. G. B. thanks both Merck and EPSRC for a PhD studentship via the Centre of Doctoral Training (CDT) in Next Generation Computational Modelling (NGCM) (grant no. EP/L015382/1). The calculations were carried out on the Iridis5 Supercomputer of the University of Southampton and on the UK national high-performance computing service, ARCHER, for which access was obtained via the UKCP consortium and funded by EPSRC grant no. EP/P022030/1.References
- J. Hou, O. Inganäs, R. H. Friend and F. Gao, Nat. Mater., 2018, 17, 119–128 CrossRef CAS PubMed
.
- P. Cheng, G. Li, X. Zhan and Y. Yang, Nat. Photonics, 2018, 12, 131–142 CrossRef CAS
.
- C. Yan, S. Barlow, Z. Wang, H. Yan, A. K. Y. Jen, S. R. Marder and X. Zhan, Nat. Rev. Mater., 2018, 3, 18003 CrossRef CAS
.
- S. Zhang, Y. Qin, J. Zhu and J. Hou, Adv. Mater., 2018, 30, 1800868 CrossRef PubMed
.
- H. Zhang, H. Yao, J. Hou, J. Zhu, J. Zhang, W. Li, R. Yu, B. Gao, S. Zhang and J. Hou, Adv. Mater., 2018, 30, 1800613 CrossRef PubMed
.
- Y. Lin, Z.-G. Zhang, H. Bai, J. Wang, Y. Yao, Y. Li, D. Zhu and X. Zhan, Energy Environ. Sci., 2015, 8, 610–616 RSC
.
- J. Yuan, Y. Zhang, L. Zhou, G. Zhang, H.-L. Yip, T.-K. Lau, X. Lu, C. Zhu, H. Peng, P. A. Johnson, M. Leclerc, Y. Cao, J. Ulanski, Y. Li and Y. Zou, Joule, 2019, 3, 1–12 CrossRef
.
- J. Zhao, Y. Li, G. Yang, K. Jiang, H. Lin, H. Ade, W. Ma and H. Yan, Nat. Energy, 2016, 1, 15027 CrossRef CAS
.
- S. Zhang, L. Ye and J. Hou, Adv. Energy Mater., 2016, 6, 1502529 CrossRef
.
- S. Li, W. Liu, C. Z. Li, M. Shi and H. Chen, Small, 2017, 13, 1701120 CrossRef PubMed
.
- D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X. K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganas, V. Coropceanu, J. L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709 CrossRef CAS PubMed
.
- J. Zhang, H. S. Tan, X. Guo, A. Facchetti and H. Yan, Nat. Energy, 2018, 3, 720–731 CrossRef CAS
.
- W. Chen and Q. Zhang, J. Mater. Chem. C, 2017, 5, 1275–1302 RSC
.
- S. Berny, N. Blouin, A. Distler, H. J. Egelhaaf, M. Krompiec, A. Lohr, O. R. Lozman, G. E. Morse, L. Nanson, A. Pron, T. Sauermann, N. Seidler, S. Tierney, P. Tiwana, M. Wagner and H. Wilson, Adv. Sci., 2016, 3, 1500342 CrossRef PubMed
.
- J.-Y. Wang, Z.-F. Yao and J. Pei, Cryst. Growth Des., 2018, 18, 7–15 CrossRef
.
- J. S. Brooks, J. E. Anthony, D. L. Eaton and S. R. Parkin, J. Am. Chem. Soc., 2001, 123, 9482–9483 CrossRef PubMed
.
- J. B. Sherman, B. Purushothaman, S. R. Parkin, C. Kim, S. Collins, J. Anthony, T.-Q. Nguyen and M. L. Chabinyc, J. Mater. Chem. A, 2015, 3, 9989–9998 RSC
.
- B. B. T. Vehoff, A. Troisi and D. Andrienko, J. Am. Chem. Soc., 2010, 132, 11702 CrossRef PubMed
.
- L. Ye, X. Jiao, M. Zhou, S. Zhang, H. Yao, W. Zhao, A. Xia, H. Ade and J. Hou, Adv. Mater., 2015, 27, 6046–6054 CrossRef CAS PubMed
.
- N. A. Ran, S. Roland, J. A. Love, V. Savikhin, C. J. Takacs, Y. T. Fu, H. Li, V. Coropceanu, X. Liu, J. L. Bredas, G. C. Bazan, M. F. Toney, D. Neher and T. Q. Nguyen, Nat. Commun., 2017, 8, 79 CrossRef PubMed
.
- H. Kang, W. Lee, J. Oh, T. Kim, C. Lee and B. J. Kim, Acc. Chem. Res., 2016, 49, 2424–2434 CrossRef CAS PubMed
.
- G. M. Su, T. V. Pho, N. D. Eisenmenger, C. Wang, F. Wudl, E. J. Kramer and M. L. Chabinyc, J. Mater. Chem. A, 2014, 2, 1781–1789 RSC
.
- S. Jinnai, Y. Ie, M. Karakawa, T. Aernouts, Y. Nakajima, S. Mori and Y. Aso, Chem. Mater., 2016, 28, 1705–1713 CrossRef CAS
.
- C. Wang, H. Dong, L. Jiang and W. Hu, Chem. Soc. Rev., 2018, 47, 422–500 RSC
.
- M. Mas-Torrent and C. Rovira, Chem. Rev., 2011, 111, 4833–4856 CrossRef CAS PubMed
.
- G. Han, Y. Guo, X. Song, Y. Wang and Y. Yi, J. Mater. Chem. C, 2017, 5, 4852–4857 RSC
.
- R. Yu, H. Yao, L. Hong, Y. Xu, B. Gao, J. Zhu, Y. Zu and J. Hou, Adv. Energy Mater., 2018, 1802131, DOI:10.1002/aenm.201802131
.
- D. Yan, W. Liu, J. Yao and C. Zhan, Adv. Energy Mater., 2018, 1800204, DOI:10.1002/aenm.201800204
.
- Q. Wu, D. Zhao, M. B. Goldey, A. S. Filatov, V. Sharapov, Y. J. Colon, Z. Cai, W. Chen, J. de Pablo, G. Galli and L. Yu, ACS Appl. Mater. Interfaces, 2018, 10, 10043–10052 CrossRef CAS PubMed
.
- M. Wu, J. Zhou, Y. Luo, N. Zheng, C. Wang, L. Liu, Z. Xie and Y. Ma, Org. Chem. Front., 2018, 5(22), 3324–3330 RSC
.
- S. M. Swick, W. Zhu, M. Matta, T. J. Aldrich, A. Harbuzaru, J. T. Lopez Navarrete, R. Ponce Ortiz, K. L. Kohlstedt, G. C. Schatz, A. Facchetti, F. S. Melkonyan and T. J. Marks, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(36), E8341–E8348 CrossRef CAS PubMed
.
- X. Shi, X. Liao, K. Gao, L. Zuo, J. Chen, J. Zhao, F. Liu, Y. Chen and A. K. Y. Jen, Adv. Funct. Mater., 2018, 1802324, DOI:10.1002/adfm.201802324,
.
- J. Qu, H. Chen, J. Zhou, H. Lai, T. Liu, P. Chao, D. Li, Z. Xie, F. He and Y. Ma, ACS Appl. Mater. Interfaces, 2018, 10, 39992–40000 CrossRef CAS PubMed
.
- Z. Liang, M. Li, X. Zhang, Q. Wang, Y. Jiang, H. Tian and Y. Geng, J. Mater. Chem. A, 2018, 6, 8059–8067 RSC
.
- S. Li, L. Ye, W. Zhao, S. Zhang, H. Ade and J. Hou, Adv. Energy Mater., 2017, 7, 1700183 CrossRef
.
-
G. Morse, L. Nanson, W. Mitchell, M. Krompiec, M. D'Lavari and A. Pron, Merck Patent GMBH, WO 2018/065350, 2018
.
- Z. Zhang, L. Feng, S. Xu, Y. Liu, H. Peng, Z. G. Zhang, Y. Li and Y. Zou, Adv. Sci., 2017, 4, 1700152 CrossRef PubMed
.
- Y. Lin, J. Wang, Z. G. Zhang, H. Bai, Y. Li, D. Zhu and X. Zhan, Adv. Mater., 2015, 27, 1170–1174 CrossRef CAS PubMed
.
- Y. Yang, Z. G. Zhang, H. Bin, S. Chen, L. Gao, L. Xue, C. Yang and Y. Li, J. Am. Chem. Soc., 2016, 138, 15011–15018 CrossRef CAS PubMed
.
- H. Yao, Y. Chen, Y. Qin, R. Yu, Y. Cui, B. Yang, S. Li, K. Zhang and J. Hou, Adv. Mater., 2016, 28, 8283–8287 CrossRef CAS PubMed
.
- Y. Lin, Q. He, F. Zhao, L. Huo, J. Mai, X. Lu, C. J. Su, T. Li, J. Wang, J. Zhu, Y. Sun, C. Wang and X. Zhan, J. Am. Chem. Soc., 2016, 138, 2973–2976 CrossRef CAS PubMed
.
- T. J. Aldrich, M. Matta, W. Zhu, S. M. Swick, C. L. Stern, G. C. Schatz, A. Facchetti, F. S. Melkonyan and T. J. Marks, J. Am. Chem. Soc., 2019, 141(7), 3274–3287 CrossRef CAS PubMed
.
- X. Shi, L. Zuo, S. B. Jo, K. Gao, F. Lin, F. Liu and A. K. Y. Jen, Chem. Mater., 2017, 29, 8369–8376 CrossRef CAS
.
- H. Burckstummer, E. V. Tulyakova, M. Deppisch, M. R. Lenze, N. M. Kronenberg, M. Gsanger, M. Stolte, K. Meerholz and F. Wurthner, Angew. Chem., Int. Ed., 2011, 50, 11628–11632 CrossRef PubMed
.
- A. Arjona-Esteban, J. Krumrain, A. Liess, M. Stolte, L. Huang, D. Schmidt, V. Stepanenko, M. Gsanger, D. Hertel, K. Meerholz and F. Wurthner, J. Am. Chem. Soc., 2015, 137, 13524–13534 CrossRef CAS PubMed
.
- M. Planells and N. Robertson, Eur. J. Org. Chem., 2012, 4947–4953 CrossRef CAS
.
- S. Wen, Y. Wu, Y. Wang, Y. Li, L. Liu, H. Jiang, Z. Liu and R. Yang, ChemSusChem, 2018, 11, 360–366 CrossRef CAS PubMed
.
- B. S. Young, D. T. Chase, J. L. Marshall, C. L. Vonnegut, L. N. Zakharov and M. M. Haley, Chem. Sci., 2014, 5, 1008–1014 RSC
.
- Z. Xiao, F. Liu, X. Geng, J. Zhang, S. Wang, Y. Xie, Z. Li, H. Yang, Y. Yuan and L. Ding, Sci. Bull., 2017, 62, 1331–1336 CrossRef CAS
.
- T.-C. Chao, K.-T. Wong, L.-C. Chi, Y.-Y. Chu, A. Balaiah, S.-F. Chiu, Y.-H. Liu and Y. Wang, Org. Lett., 2006, 8, 5033–5036 CrossRef PubMed
.
- D. Beaudoin, J. N. Blair-Pereira, S. Langis-Barsetti, T. Maris and J. D. Wuest, J. Org. Chem., 2017, 82, 8536–8547 CrossRef CAS PubMed
.
- Y. Guo, M. Li, Y. Zhou, J. Song, Z. Bo and H. Wang, Macromolecules, 2017, 50, 7984–7992 CrossRef CAS
.
- C. K. Skylaris, P. D. Haynes, A. A. Mostofi and M. C. Payne, J. Chem. Phys., 2005, 122, 84119 CrossRef PubMed
.
- C.-K. Skylaris, A. A. Mostofi, P. D. Haynes, O. Diéguez and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035119 CrossRef
.
- A. A. Mostofi, P. D. Haynes, C.-K. Skylaris and M. C. Payne, J. Chem. Phys., 2003, 119, 8842–8848 CrossRef CAS
.
- S. Holliday, R. S. Ashraf, A. Wadsworth, D. Baran, S. A. Yousaf, C. B. Nielsen, C. H. Tan, S. D. Dimitrov, Z. Shang, N. Gasparini, M. Alamoudi, F. Laquai, C. J. Brabec, A. Salleo, J. R. Durrant and I. McCulloch, Nat. Commun., 2016, 7, 11585 CrossRef CAS PubMed
.
- K. Burke, J. P. Perdew and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed
.
- N. D. Hine, J. Phys.: Condens. Matter, 2017, 29, 024001 CrossRef PubMed
.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed
.
- L. E. Ratcliff, G. J. Conduit, N. D. M. Hine and P. D. Haynes, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 125123 CrossRef CAS
.
- Y. Hinuma, G. Pizzi, Y. Kumagai, F. Oba and I. Tanaka, Comput. Mater. Sci., 2017, 128, 140–184 CrossRef CAS
.
- CrysalisPro, Oxford Diffraction, Agilent Technologies UK Ltd, Yarnton, England.
-
R. C. Hooft, Data collection software, Nonius BV, Delft, The Netherlands, 1998 Search PubMed
.
-
Z. Otwinowski and W. Minor, Methods in enzymology, Elsevier, 1997, vol. 276, pp. 307–326 Search PubMed
.
- SADABS, Version 2.10, GM Sheldrick – University of Göttingen, Germany, 2003.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS
.
- G. M. Sheldrick, Acta. Crystallogr. Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed
.
- G. R. Desiraju, Angew. Chem., Int. Ed., 2007, 46, 8342–8356 CrossRef CAS PubMed
.
- R. Li, W. Hu, Y. Liu and D. Zhu, Acc. Chem. Res., 2010, 43, 529–540 CrossRef CAS PubMed
.
- C. Wang, H. Dong, W. Hu, Y. Liu and D. Zhu, Chem. Rev., 2011, 112, 2208–2267 CrossRef PubMed
.
- C. Wang, H. Dong, H. Li, H. Zhao, Q. Meng and W. Hu, Cryst. Growth Des., 2010, 10, 4155–4160 CrossRef CAS
.
- C. C. Mattheus, G. A. de Wijs, R. A. de Groot and T. T. Palstra, J. Am. Chem. Soc., 2003, 125, 6323–6330 CrossRef CAS PubMed
.
- J. Z. Vikram, C. Sundar, V. Podzorov, E. Menard, R. L. Willett, T. Someya, M. E. Gershenson and J. A. Rogers, Sci. Rep., 2004, 303, 1644–1646 Search PubMed
.
- F. Cozzi, S. Bacchi, G. Filippini, T. Pilati and A. Gavezzotti, Chem. – Eur. J., 2007, 13, 7177–7184 CrossRef CAS PubMed
.
- G. E. Morse, I. Gong, Y. Kawar, A. J. Lough and T. P. Bender, Cryst. Growth Des., 2014, 14, 2138–2147 CrossRef CAS
.
- H. Huang, L. Yang, A. Facchetti and T. J. Marks, Chem. Rev., 2017, 117, 10291–10318 CrossRef CAS PubMed
.
- N. E. Jackson, B. M. Savoie, K. L. Kohlstedt, M. Olvera de la Cruz, G. C. Schatz, L. X. Chen and M. A. Ratner, J. Am. Chem. Soc., 2013, 135, 10475–10483 CrossRef CAS PubMed
.
- A. Mahmood, A. Tang, X. Wang and E. Zhou, Phys. Chem. Chem. Phys., 2019, 21(4), 2128–2139 RSC
.
- G. C. Welch, L. A. Perez, C. V. Hoven, Y. Zhang, X.-D. Dang, A. Sharenko, M. F. Toney, E. J. Kramer, T.-Q. Nguyen and G. C. Bazan, J. Mater. Chem., 2011, 21, 12700 RSC
.
- S. M. R.-E. L. Yu and C. A. Mitchell, Org. Process Res. Dev., 2000, 4, 396–402 CrossRef
.
- A. M. Silva, B. P. Silva, F. A. M. Sales, V. N. Freire, E. Moreira, U. L. Fulco, E. L. Albuquerque, F. F. Maia and E. W. S. Caetano, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195201 CrossRef
.
- S. Boothroyd, A. Kerridge, A. Broo, D. Buttar and J. Anwar, Cryst. Growth Des., 2018, 18, 1903–1908 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1942946–1942954. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9mh01439j |
| This journal is © The Royal Society of Chemistry 2020 |