An innovative approach to design SOFC air electrode materials: high entropy La1−xSrx(Co,Cr,Fe,Mn,Ni)O3−δ (x = 0, 0.1, 0.2, 0.3) perovskites synthesized by the sol–gel method†
Juliusz
Dąbrowa
 *a,
Anna
Olszewska
b,
Andreas
Falkenstein
*a,
Anna
Olszewska
b,
Andreas
Falkenstein
 c,
Christian
Schwab
c,
Maria
Szymczak
a,
Marek
Zajusz
a,
Maciej
Moździerz
a,
Andrzej
Mikuła
c,
Christian
Schwab
c,
Maria
Szymczak
a,
Marek
Zajusz
a,
Maciej
Moździerz
a,
Andrzej
Mikuła
 a,
Klaudia
Zielińska
a,
Katarzyna
Berent
a,
Klaudia
Zielińska
a,
Katarzyna
Berent
 d,
Tomasz
Czeppe
e,
Manfred
Martin
d,
Tomasz
Czeppe
e,
Manfred
Martin
 c and
Konrad
Świerczek
c and
Konrad
Świerczek
 bf
bf
aFaculty of Materials Science and Ceramics, AGH University of Science and Technology, al. Mickiewicza 30, 30-059 Krakow, Poland. E-mail: dabrowa@agh.edu.pl
bFaculty of Energy and Fuels, AGH University of Science and Technology, al. Mickiewicza 30, 30-059 Krakow, Poland
cInstitute of Physical Chemistry, RWTH Aachen University, Landoltweg 2, 52074 Aachen, Germany
dAcademic Centre for Materials and Nanotechnology, AGH University of Science and Technology, al. Mickiewicza 30, 30-059 Kraków, Poland
eInstitute of Metallurgy and Materials Sciences, Polish Academy of Sciences, Reymonta 25 St., 30-059, Krakow, Poland
fAGH Centre of Energy, AGH University of Science and Technology, ul. Czarnowiejska 36, 30-054 Krakow, Poland
First published on 14th September 2020
Abstract
Among the for the first time reported Cr-containing high entropy La1−xSrx(Co,Cr,Fe,Mn,Ni)O3−δ (x = 0, 0.1, 0.2, 0.3, 0.4 and 0.5) perovskite-type oxides, the selected Sr-doped La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ material is documented to possess attractive properties as a candidate air electrode material for Solid Oxide Fuel Cells (SOFCs). Nanosized powders of the considered oxides are obtained using a modified Pechini sol–gel method. In the formed solid solution with a simple perovskite structure the strontium solubility limit is found to be at least x = 0.3. Room temperature (RT) structural data indicate the presence of rhombohedral structural distortion (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c symmetry) in the materials. High-temperature structural studies for the selected La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ indicate the occurrence of a phase transition to an aristotype Pm
c symmetry) in the materials. High-temperature structural studies for the selected La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ indicate the occurrence of a phase transition to an aristotype Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure at ca. 800 °C. The linear thermal expansion coefficient in the RT-1000 °C range is found to be moderate, 16.0(3) × 10−6 K−1. The results of impedance spectroscopy measurements support the semiconducting-type behavior of the electrical conductivity for all single-phase materials, in a temperature range of RT-1000 °C. The maximum recorded conductivity for the La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ composition exceeds 16 S cm−1 in the 900–1000 °C range, being suitable for application. Furthermore, chemical stability toward the La0.8Sr0.2Ga0.8Mg0.2O3−δ (LSGM) electrolyte is proven. Considering the presence of chromium, typically deleterious to the performance, the measured value of the total cathodic polarization resistance for the La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ-based electrode, being 0.126 Ω cm−2 at 900 °C, seems to be very attractive. The results obtained for a button-type fuel cell indicate power densities at a level of 550 mW cm−2 at 900 °C. Therefore, it can be considered that the high entropy-based approach enables to propose alternative SOFC air electrode materials, with otherwise inaccessible chemical compositions.
m structure at ca. 800 °C. The linear thermal expansion coefficient in the RT-1000 °C range is found to be moderate, 16.0(3) × 10−6 K−1. The results of impedance spectroscopy measurements support the semiconducting-type behavior of the electrical conductivity for all single-phase materials, in a temperature range of RT-1000 °C. The maximum recorded conductivity for the La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ composition exceeds 16 S cm−1 in the 900–1000 °C range, being suitable for application. Furthermore, chemical stability toward the La0.8Sr0.2Ga0.8Mg0.2O3−δ (LSGM) electrolyte is proven. Considering the presence of chromium, typically deleterious to the performance, the measured value of the total cathodic polarization resistance for the La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ-based electrode, being 0.126 Ω cm−2 at 900 °C, seems to be very attractive. The results obtained for a button-type fuel cell indicate power densities at a level of 550 mW cm−2 at 900 °C. Therefore, it can be considered that the high entropy-based approach enables to propose alternative SOFC air electrode materials, with otherwise inaccessible chemical compositions.
1. Introduction
Studies on the so-called high entropy materials have become currently one of the most coveted research activities in materials science and related disciplines. Developed in analogy to previously discovered and described high entropy alloys (HEAs),1,2 high entropy oxides (HEOx) have recently emerged as a prominent and very promising group among the materials, in which the entropy-related effect is present.1–7 The first of HEOx, entropy-stabilized (Co,Cu,Mg,Ni,Zn)O solid solution, characterized by a regular Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m rock-salt structure, was synthesized in 2015 by Rost et al.3 It must be emphasized here that high entropy materials can be divided into two groups. The first of them are entropy-stabilized ones, such as the mentioned (Co,Cu,Mg,Ni,Zn)O, in which the high configurational entropy enables the formation of single-phase, solid-solution structures, which is accompanied by the occurrence of endothermic, reversible, entropy-driven phase transition into single-phase solid solution at high temperature. The second group are the materials, in which the high configurational entropy is not essential for the formation of a solid-solution structure, and such materials are also widespread among HEOx.8–10 Nevertheless, both these groups benefit from the presence of synergistic effects between the elements in the system, and both fulfill the basic definition of high entropy materials,11,12 which states that they comprise five or more components in near-equimolar proportions (in the case of ionic compounds, at least within one of the sublattices) and are characterized by a single-phase, solid solution type structure. As of today, the already known HEOx types comprise alkali-doped (Co,Cu,Mg,Ni,Zn)1−xMxO (M = Li, Na, K) monoxides,13,14 transition metal-based high entropy spinels,10,15–17 high entropy perovskites,9,18 bixbyite- and fluorite-structured high entropy oxides,19,20 high entropy lanthanide sesquioxides,21 and high entropy pyrochlores.22 Even though such materials have been developed just over the last 5 years, the already reported HEOx are recognized to exhibit a number of interesting, functional properties, such as a colossal dielectric constant,23 high ionic conductivity at low temperatures,13 and unusually low thermal conductivity.22 Regarding electrochemical activity, some of the compositions have been successfully tested with respect to their potential application as anode materials for Li-ion cells,24,25 as well as cathode materials for Na-ion batteries,26 proving the usefulness of the developed HEOx in (broadly understood) energy-related applications. With the recently increased number of reports on novel high entropy oxides, the array of their further possible applications is largely widening. It is safe to assume that HEOx also possess huge potential for usage in high-temperature energy conversion-related technologies, particularly as components for SOFCs (Solid Oxide Fuel Cells). This can be supported by the fact that the formation of solid solutions beyond a typical compositional range seems to be especially appealing regarding the development of novel cathode, anode, and electrolyte materials.
m rock-salt structure, was synthesized in 2015 by Rost et al.3 It must be emphasized here that high entropy materials can be divided into two groups. The first of them are entropy-stabilized ones, such as the mentioned (Co,Cu,Mg,Ni,Zn)O, in which the high configurational entropy enables the formation of single-phase, solid-solution structures, which is accompanied by the occurrence of endothermic, reversible, entropy-driven phase transition into single-phase solid solution at high temperature. The second group are the materials, in which the high configurational entropy is not essential for the formation of a solid-solution structure, and such materials are also widespread among HEOx.8–10 Nevertheless, both these groups benefit from the presence of synergistic effects between the elements in the system, and both fulfill the basic definition of high entropy materials,11,12 which states that they comprise five or more components in near-equimolar proportions (in the case of ionic compounds, at least within one of the sublattices) and are characterized by a single-phase, solid solution type structure. As of today, the already known HEOx types comprise alkali-doped (Co,Cu,Mg,Ni,Zn)1−xMxO (M = Li, Na, K) monoxides,13,14 transition metal-based high entropy spinels,10,15–17 high entropy perovskites,9,18 bixbyite- and fluorite-structured high entropy oxides,19,20 high entropy lanthanide sesquioxides,21 and high entropy pyrochlores.22 Even though such materials have been developed just over the last 5 years, the already reported HEOx are recognized to exhibit a number of interesting, functional properties, such as a colossal dielectric constant,23 high ionic conductivity at low temperatures,13 and unusually low thermal conductivity.22 Regarding electrochemical activity, some of the compositions have been successfully tested with respect to their potential application as anode materials for Li-ion cells,24,25 as well as cathode materials for Na-ion batteries,26 proving the usefulness of the developed HEOx in (broadly understood) energy-related applications. With the recently increased number of reports on novel high entropy oxides, the array of their further possible applications is largely widening. It is safe to assume that HEOx also possess huge potential for usage in high-temperature energy conversion-related technologies, particularly as components for SOFCs (Solid Oxide Fuel Cells). This can be supported by the fact that the formation of solid solutions beyond a typical compositional range seems to be especially appealing regarding the development of novel cathode, anode, and electrolyte materials.
Many years of systematic research activities resulted in the development of electrode and electrolyte materials for SOFC technologies exhibiting desired thermomechanical, transport and electrocatalytic properties.27–33 Among the designed state-of-the-art air electrode materials, typically Co-based oxides are listed, with some of them having a cubic (or distorted) perovskite-type crystal structure or crystallizing in related systems, e.g. exhibiting the A- and/or B-site ordered arrangement of the cations.34–37 Alternative compounds, including those from the Ruddlesden–Popper series are also of interest, but until now, their reported performance is subpar in comparison to perovskite compositions. Interestingly, excellent solid electrolytes,38,39 anode materials,40,41 and compounds effectively transporting protons,42 all having perovskite-type structures, are also designed and utilized. Until now, however, there are no studies reported regarding the possibility of usage of high entropy perovskites in SOFC technology, despite that some interesting compositions have already been synthesized.
The first study concerning the formation of high entropy perovskite structures was published in 2018 by Jiang et al.9 In this report, 13 different compositions have been examined, in which the A-site cations were selected from Ba and Sr, while the B-site was occupied by 5-element combinations from a group of Ce, Gd, Hf, Mn, Sn, Y, and Zr. Simple solid-state synthesis conducted at 1500 °C allowed obtaining six high entropy perovskite compositions, all of them characterized by the single-phase, cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure. In a similar manner to other perovskites,43 the Goldschmidt tolerance factor t was found to relate to the possibility of the formation of single-phase materials, with values of t being in the 0.97–1.03 range for all single-phase compositions. Sr(Hf,Mn,Sn,Ti,Zr)O3−δ also served as a base for further investigations conducted by Biesuz et al., who have modified this composition, obtaining the Sr(Hf,Mn,Sn,Ti,(Zr0.94Y0.06))O3−δ perovskite.44 Besides, it was found that the Spark Plasma Sintering (SPS) method provides some advantages in the preparation of such HEOx, especially regarding the phase purity and relative density of the specimens. Another study based on the compositions from previous work9 has been performed by Sharma et al.,45 who examined the possibility of growing single-crystal epitaxial films of Ba(Hf,Nb,Sn,Ti,Zr)O3−δ HEO on SrTiO3 and MgO substrates. With the use of Pulsed Laser Deposition (PLD), Pm
m structure. In a similar manner to other perovskites,43 the Goldschmidt tolerance factor t was found to relate to the possibility of the formation of single-phase materials, with values of t being in the 0.97–1.03 range for all single-phase compositions. Sr(Hf,Mn,Sn,Ti,Zr)O3−δ also served as a base for further investigations conducted by Biesuz et al., who have modified this composition, obtaining the Sr(Hf,Mn,Sn,Ti,(Zr0.94Y0.06))O3−δ perovskite.44 Besides, it was found that the Spark Plasma Sintering (SPS) method provides some advantages in the preparation of such HEOx, especially regarding the phase purity and relative density of the specimens. Another study based on the compositions from previous work9 has been performed by Sharma et al.,45 who examined the possibility of growing single-crystal epitaxial films of Ba(Hf,Nb,Sn,Ti,Zr)O3−δ HEO on SrTiO3 and MgO substrates. With the use of Pulsed Laser Deposition (PLD), Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m single-phase, uniform epitaxial films were obtained. Of importance, the thermal conductivity of the material was found to be very low, 0.58 W m−1 K−1, nearly one order of magnitude lower than those observed for conventional ABO3−δ perovskites. This indeed proves that the high entropy effect may provide a unique opportunity for the modification of the physicochemical properties of the oxides. Two further published studies focused on a different family of perovskites, namely RE(TM)O3−δ (RE: rare-earth elements; TM: transition metals). Also in 2018, Sarkar et al.18 considered the high entropy approach to modify both cationic sublattices of a perovskite-type oxide, including simultaneous doping of both A and B sites. The A-site ions were selected from the group of Gd, La, Nd, Sm, and Y elements, while the B-site ones were chosen from the following 3d metals: Co, Cr, Fe, Mn, and Ni. A systematic pattern was adapted for the studied compositions: (5A0.2)CoO3−δ, (5A0.2)CrO3−δ, Gd(5B0.2)O3−δ, La(5B0.2)O3−δ, etc., where 5A0.2 and 5B0.2 denote equimolar combinations of all listed A-site and B-site cations, respectively. After the usage of the Nebulized Spray Pyrolysis (NSP) method, followed by calcination at 1200 °C in air, out of the eleven proposed compositions, six were single-phase perovskites with orthorhombic Pbnm symmetry. This includes the complex (5A0.2) (5B0.2)O3 system, comprising ten different cations in equimolar proportions. The observed orthorhombic (rather than cubic) symmetry corresponds well with lower Goldschmidt tolerance factor values, varying from 0.900 to 0.962. Importantly, it was possible to observe the entropic stabilization in the studied compositions, with the occurrence of reversible phase transformation from the multiphase to single-phase systems upon cyclic heat treatment, which was not the case in Ba/Sr-based perovskites studied by Jiang et al.9 RE(5B0.2)O3−δ-type compositions have also been studied in the follow-up paper with the main emphasis being put on magnetic properties.46 Again, the value of the Goldschmidt tolerance factor was found to strongly correlate with the magnetic ordering temperature, showing the possibility of tailoring the properties of HEOs by careful selection of the composing ions.
m single-phase, uniform epitaxial films were obtained. Of importance, the thermal conductivity of the material was found to be very low, 0.58 W m−1 K−1, nearly one order of magnitude lower than those observed for conventional ABO3−δ perovskites. This indeed proves that the high entropy effect may provide a unique opportunity for the modification of the physicochemical properties of the oxides. Two further published studies focused on a different family of perovskites, namely RE(TM)O3−δ (RE: rare-earth elements; TM: transition metals). Also in 2018, Sarkar et al.18 considered the high entropy approach to modify both cationic sublattices of a perovskite-type oxide, including simultaneous doping of both A and B sites. The A-site ions were selected from the group of Gd, La, Nd, Sm, and Y elements, while the B-site ones were chosen from the following 3d metals: Co, Cr, Fe, Mn, and Ni. A systematic pattern was adapted for the studied compositions: (5A0.2)CoO3−δ, (5A0.2)CrO3−δ, Gd(5B0.2)O3−δ, La(5B0.2)O3−δ, etc., where 5A0.2 and 5B0.2 denote equimolar combinations of all listed A-site and B-site cations, respectively. After the usage of the Nebulized Spray Pyrolysis (NSP) method, followed by calcination at 1200 °C in air, out of the eleven proposed compositions, six were single-phase perovskites with orthorhombic Pbnm symmetry. This includes the complex (5A0.2) (5B0.2)O3 system, comprising ten different cations in equimolar proportions. The observed orthorhombic (rather than cubic) symmetry corresponds well with lower Goldschmidt tolerance factor values, varying from 0.900 to 0.962. Importantly, it was possible to observe the entropic stabilization in the studied compositions, with the occurrence of reversible phase transformation from the multiphase to single-phase systems upon cyclic heat treatment, which was not the case in Ba/Sr-based perovskites studied by Jiang et al.9 RE(5B0.2)O3−δ-type compositions have also been studied in the follow-up paper with the main emphasis being put on magnetic properties.46 Again, the value of the Goldschmidt tolerance factor was found to strongly correlate with the magnetic ordering temperature, showing the possibility of tailoring the properties of HEOs by careful selection of the composing ions.
The above-described family of RE(TM)O3−δ high entropy perovskites seems to be especially interesting from the point of view of application in SOFC technology, as they are based on practically the same elements as those used in conventional air electrode materials, such as La1−xSrxMnO3−δ (LSM),47 La1−xSrxCoO3−δ (LSC)48 or La1−xSrxCo1−yFeyO3−δ (LSCF).49 However, since the candidate material must fulfill a number of strict requirements, including good thermal and chemical stability, appropriate thermomechanical properties, high mixed ionic–electronic conductivity and good electrocatalytic activity, comprehensive studies are needed to assess the possibility of its application. Nonetheless, in the opinion of the authors of the present study, the high entropy approach should bring about a number of important advantages, such as: reduction of thermal expansion (to match the electrolyte's values), due to the limited chemical expansion; good electronic transport and catalytic activity because of the presence of multiple redox pairs; cost reduction by substantial elimination of expensive and toxic cobalt. Additionally, and what has not been elaborated so far, the formation of a Cr-resistant air electrode may be considered, assuming that the presence of chromium at the B-site can influence this property. In other words, some of the main issues related to the development of the cathode materials for SOFCs might be addressed. In view of the above, the main objective of the present study is to deliver the first data regarding the synthesis, crystal structure, and basic physicochemical properties of high entropy perovskites from the novel La1−xSrx(Co,Cr,Fe,Mn,Ni)O3−δ (LSTM HEOx) family, as well as presenting preliminary results regarding the electrochemical properties of the SOFC air electrodes manufactured using the selected La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ high entropy perovskite. For the first time doping with Sr at the A-site is considered in RE(TM)O3−δ HEOs, in order to induce the presence of the oxygen vacancies, and consequently, to enable ionic conduction, similarly as in the mentioned conventional analogs. Importantly, also for the first time, the Pechini-type sol–gel technique is applied for the synthesis of the considered materials, allowing the formation of the desired powder morphology of LSTM HEOx.
2. Methodology
The base powders of La1−xSrx(Co,Cr,Fe,Mn,Ni)O3−δ (x = 0; 0.1; 0.2; 0.3; 0.4; 0.5) materials were synthesized with the use of a modified Pechini sol–gel method, which was chosen due to its suitability for obtaining homogeneous materials comprising a high number of cations, as well as yielding a fine morphology of the resulting products.50 As starting chemicals, nitrates of all of the considered cations were used: La(NO3)3·6H2O (Chempur, 99.99%), Sr(NO3)2 (Alfa Aesar 99.9965%), Co(NO3)2·6H2O (Alfa Aesar, 98–102%), Cr(NO3)3·9H2O (Riedel-deHaën, ≥98%), Fe(NO3)3·9H2O (Sigma Aldrich ≥98%), Mn(NO3)2·4H2O (Alfa Aesar, 98%), and Ni(NO3)2·6H2O (Alfa Aesar, 99.9985%). Citric acid monohydrate (Alfa Aesar 99.5+%) and ethylene glycol (EG) were used to respectively create the chelate of the cations and ensure polycondensation. The molar ratio of all the cations, citric acid, and EG in the mixture was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. Initially, nitrates were dissolved in demineralized water, and citric acid and EG were added. The mixture was then put on a magnetic stirrer, with the heating plate set initially to 150 °C (esterification step). After obtaining a clear solution, the temperature was increased to 300 °C. The obtained gels were then calcined at 700 °C for 6 h, which was followed by a slow cooling (with a furnace), yielding fine, nanosized powders. The average rate of cooling for the whole process was within the 2–3 °C min−1 range. The powders were then used to prepare pellets of 10 mm diameter, formed under a repeatedly applied pressure of 1, 1.5 and 2 tons, using a uniaxial hydraulic press with a vacuum pump. Subsequently, the samples were free-sintered in a tube furnace for 20 hours at 1000 °C, followed by air-quenching with a use of a cooled metallic sheet for faster heat dissipation. The X-ray diffraction (XRD) measurements were performed at room temperature (RT) using a Panalytical Empyrean diffractometer with Cu Kα radiation, working in the Bragg–Brentano geometry, within the 10°–90° range. The obtained data were then analyzed with X'Pert HighScore Plus 3.0 software, using the ICDD PDF2 database. The same software was used for the Rietveld refinement. Grain sizes were determined by applying Scherrer's formula to the six most intense peaks (instrumental profile measured for the LaB6 standard). The structure at high temperatures and the corresponding thermal stability were investigated using high-temperature XRD measurements, carried out using an Anton Paar HTK 1200N oven-chamber mounted on a diffractometer. The studies were conducted in the temperature range of 25–1000 °C, with intervals of 100 °C. The morphology, chemical composition and homogeneity of the materials were studied using an FEI Versa 3D scanning electron microscope (SEM), equipped with an energy dispersive X-ray spectrometer (EDS). EDS analysis was performed at an acceleration voltage of 15 kV. Elemental EDS mapping was performed with TEAM EDS Analysis Software. Raman spectra were recorded with a WITec Alpha 300M + spectrometer, using a 633 nm diode laser and 1800 grooves per mm grating in the range of 80–1500 cm−1. The time of each measurement was 10 s, with two exposures. The depth profiling was attempted in a confocal mode; however, due to the signal's intensity deterioration, resulting from the absorption of the radiation by upper layers of ions, only the surface measurements were considered. The DTA-TG (differential thermal analysis combined with thermogravimetry) studies were conducted with the use of TA Instruments SDT-Q600 apparatus calibrated for heating conditions. The measurements were performed within the temperature range of 25 to 1000 °C in air, with a heating/cooling rate of 10 °C min−1. Due to the non-equilibrium behavior of the as-calcined powders, as indicated by other methods, two consecutive heating/cooling runs were performed. For electrochemical impedance spectroscopy (EIS) measurements of the sintered pellets, electrical connectors were prepared by applying platinum paste (ESL Electro-Science) on the surface of the samples, which were subsequently dried at 150 °C and fired at 980 °C in air, forming porous electrodes. The measurements were performed with a Zurich Instruments MFIA Impedance Analyzer, using a quasi 4-probe method, within the 1 Hz to 1 MHz frequency range and 15 measuring points per decade. The measurements were conducted within the temperature range of 25–1000 °C (steps of 50 °C). Heating and cooling runs were performed. In all cases, due to the nature of the recorded data, the considered equivalent circle was limited just to a single resistor. The selected La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ oxide was examined as a potential SOFC air electrode material. In order to adjust the optimal sintering temperature of the electrode layer from the point of view of mechanical stability and also minimization of the cathodic polarization resistance, La0.8Sr0.2Ga0.8Mg0.2O3−δ (LSGM 8282) electrolyte-supported symmetric cells with La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ|LSGM|La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ configuration were prepared and tested. Dense electrolyte pellets with a thickness of approx. 600 μm were sintered using commercial LSGM powder (fuelcellmaterials, USA), homogeneously mixed with 1 wt% of poly(vinyl butyral-co-vinyl alcohol-co-vinyl acetate). The mixture was pressed into 13 mm diameter pellets and annealed in air at 1450 °C. Screen-printing was used to manufacture electrode layers on both sides of the electrolyte. This required preparation of the electrode slurry by mixing fine (i.e. as-sintered) La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ powder, ground beforehand in an agate mortar for 1 h, with a commercial texanol-based binder (ESL ElectroScience, USA) in a 2
4. Initially, nitrates were dissolved in demineralized water, and citric acid and EG were added. The mixture was then put on a magnetic stirrer, with the heating plate set initially to 150 °C (esterification step). After obtaining a clear solution, the temperature was increased to 300 °C. The obtained gels were then calcined at 700 °C for 6 h, which was followed by a slow cooling (with a furnace), yielding fine, nanosized powders. The average rate of cooling for the whole process was within the 2–3 °C min−1 range. The powders were then used to prepare pellets of 10 mm diameter, formed under a repeatedly applied pressure of 1, 1.5 and 2 tons, using a uniaxial hydraulic press with a vacuum pump. Subsequently, the samples were free-sintered in a tube furnace for 20 hours at 1000 °C, followed by air-quenching with a use of a cooled metallic sheet for faster heat dissipation. The X-ray diffraction (XRD) measurements were performed at room temperature (RT) using a Panalytical Empyrean diffractometer with Cu Kα radiation, working in the Bragg–Brentano geometry, within the 10°–90° range. The obtained data were then analyzed with X'Pert HighScore Plus 3.0 software, using the ICDD PDF2 database. The same software was used for the Rietveld refinement. Grain sizes were determined by applying Scherrer's formula to the six most intense peaks (instrumental profile measured for the LaB6 standard). The structure at high temperatures and the corresponding thermal stability were investigated using high-temperature XRD measurements, carried out using an Anton Paar HTK 1200N oven-chamber mounted on a diffractometer. The studies were conducted in the temperature range of 25–1000 °C, with intervals of 100 °C. The morphology, chemical composition and homogeneity of the materials were studied using an FEI Versa 3D scanning electron microscope (SEM), equipped with an energy dispersive X-ray spectrometer (EDS). EDS analysis was performed at an acceleration voltage of 15 kV. Elemental EDS mapping was performed with TEAM EDS Analysis Software. Raman spectra were recorded with a WITec Alpha 300M + spectrometer, using a 633 nm diode laser and 1800 grooves per mm grating in the range of 80–1500 cm−1. The time of each measurement was 10 s, with two exposures. The depth profiling was attempted in a confocal mode; however, due to the signal's intensity deterioration, resulting from the absorption of the radiation by upper layers of ions, only the surface measurements were considered. The DTA-TG (differential thermal analysis combined with thermogravimetry) studies were conducted with the use of TA Instruments SDT-Q600 apparatus calibrated for heating conditions. The measurements were performed within the temperature range of 25 to 1000 °C in air, with a heating/cooling rate of 10 °C min−1. Due to the non-equilibrium behavior of the as-calcined powders, as indicated by other methods, two consecutive heating/cooling runs were performed. For electrochemical impedance spectroscopy (EIS) measurements of the sintered pellets, electrical connectors were prepared by applying platinum paste (ESL Electro-Science) on the surface of the samples, which were subsequently dried at 150 °C and fired at 980 °C in air, forming porous electrodes. The measurements were performed with a Zurich Instruments MFIA Impedance Analyzer, using a quasi 4-probe method, within the 1 Hz to 1 MHz frequency range and 15 measuring points per decade. The measurements were conducted within the temperature range of 25–1000 °C (steps of 50 °C). Heating and cooling runs were performed. In all cases, due to the nature of the recorded data, the considered equivalent circle was limited just to a single resistor. The selected La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ oxide was examined as a potential SOFC air electrode material. In order to adjust the optimal sintering temperature of the electrode layer from the point of view of mechanical stability and also minimization of the cathodic polarization resistance, La0.8Sr0.2Ga0.8Mg0.2O3−δ (LSGM 8282) electrolyte-supported symmetric cells with La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ|LSGM|La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ configuration were prepared and tested. Dense electrolyte pellets with a thickness of approx. 600 μm were sintered using commercial LSGM powder (fuelcellmaterials, USA), homogeneously mixed with 1 wt% of poly(vinyl butyral-co-vinyl alcohol-co-vinyl acetate). The mixture was pressed into 13 mm diameter pellets and annealed in air at 1450 °C. Screen-printing was used to manufacture electrode layers on both sides of the electrolyte. This required preparation of the electrode slurry by mixing fine (i.e. as-sintered) La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ powder, ground beforehand in an agate mortar for 1 h, with a commercial texanol-based binder (ESL ElectroScience, USA) in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 wt ratio, but also with 5 wt% addition of a pore-forming agent (starch). Sintering of the layers was performed at different temperatures: 950 °C, 1000 °C, and 1100 °C. Pt paste sintered at 900 °C was used as the current collector. The electrochemical properties of the constructed symmetrical cells were determined by EIS using a Solartron 1260 Frequency Response Analyser, combined with a 1287 Electrochemical Interface. Data were measured in the temperature range of 600–900 °C. Studies were performed in the 0.1 to 106 Hz range with a perturbation amplitude signal of 25 mV. For data fitting, an L–RO–Q1R1–Q2RL equivalent circuit was used (analyzed with ZView software). For details about the interpretation of the respective resistances (R) and meaning of the constant phase elements (Q), see previous work.51–53 In addition, an electrolyte-supported (thickness ca. 300 μm) button-type full cell with Ni–Ce0.8Gd0.2O2−δ|Ce0.8Gd0.2O2−δ|La0.8Sr0.2Ga0.8Mg0.2O3−δ|La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ configuration was prepared. Due to the known poor chemical compatibility between Ni and the LSGM electrolyte, on one side of the asymmetrical cell, a Ce0.8Gd0.2O2−δ (gadolinium-doped ceria, GDC; fuelcellmaterials, USA) buffer layer was applied with the screen-printing method, and sintered at 1300 °C for 2 h. Afterwards, the Ni-GDC cermet anode (with an initial NiO to GDC wt ratio of 60
1 wt ratio, but also with 5 wt% addition of a pore-forming agent (starch). Sintering of the layers was performed at different temperatures: 950 °C, 1000 °C, and 1100 °C. Pt paste sintered at 900 °C was used as the current collector. The electrochemical properties of the constructed symmetrical cells were determined by EIS using a Solartron 1260 Frequency Response Analyser, combined with a 1287 Electrochemical Interface. Data were measured in the temperature range of 600–900 °C. Studies were performed in the 0.1 to 106 Hz range with a perturbation amplitude signal of 25 mV. For data fitting, an L–RO–Q1R1–Q2RL equivalent circuit was used (analyzed with ZView software). For details about the interpretation of the respective resistances (R) and meaning of the constant phase elements (Q), see previous work.51–53 In addition, an electrolyte-supported (thickness ca. 300 μm) button-type full cell with Ni–Ce0.8Gd0.2O2−δ|Ce0.8Gd0.2O2−δ|La0.8Sr0.2Ga0.8Mg0.2O3−δ|La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ configuration was prepared. Due to the known poor chemical compatibility between Ni and the LSGM electrolyte, on one side of the asymmetrical cell, a Ce0.8Gd0.2O2−δ (gadolinium-doped ceria, GDC; fuelcellmaterials, USA) buffer layer was applied with the screen-printing method, and sintered at 1300 °C for 2 h. Afterwards, the Ni-GDC cermet anode (with an initial NiO to GDC wt ratio of 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40) was applied, and sintered at 1350 °C. Then, a La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ layer was screen-printed on the cathode side of the cell, and sintered at 1100 °C. During tests, humidified hydrogen with a 50 cm3 min−1 flow rate was supplied to the anode, and air with a 100 cm3 min−1 flow rate was supplied to the cathode. The Pt paste was used to prepare the current collectors.
40) was applied, and sintered at 1350 °C. Then, a La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ layer was screen-printed on the cathode side of the cell, and sintered at 1100 °C. During tests, humidified hydrogen with a 50 cm3 min−1 flow rate was supplied to the anode, and air with a 100 cm3 min−1 flow rate was supplied to the cathode. The Pt paste was used to prepare the current collectors.
3. Results and discussion
3.1. Structural properties of LSTM materials
The RT X-ray diffractograms, recorded for all the considered as-synthesized LSTM powders, revealed the presence of the desired perovskite-type structure (Fig. 1a) after the initial synthesis (i.e. without the quenching step). The basic structural data obtained by the Rietveld refinement of the X-ray diffraction patterns and application of the Scherrer equation are presented in Table 1, while more details regarding the Rietveld refinement are presented in the ESI (Tables S1 and S2).† For each composition the normalized, quasi-cubic parameters are provided (volume and lattice constant a0), calculated under the assumption that the orthorhombic unit cell is 4-times larger than the equivalent cubic one (according to the relationship 2a0 × √2a0 × √2a0), while the rhombohedral one is 6-times larger. Very broad peaks observed in the diffractograms indicate the formation of nanosized crystallites. However, in the case of La0.6Sr0.4(Co,Cr,Fe,Mn,Ni)O3−δ and La0.5Sr0.5(Co,Cr,Fe,Mn,Ni)O3−δ, additional reflections are also visible, which could not be unambiguously identified. Furthermore, some very broad features of low intensity are present in a ca. 23°–30° angular 2θ range in the data, suggesting low-level partial inhomogeneity of other powders.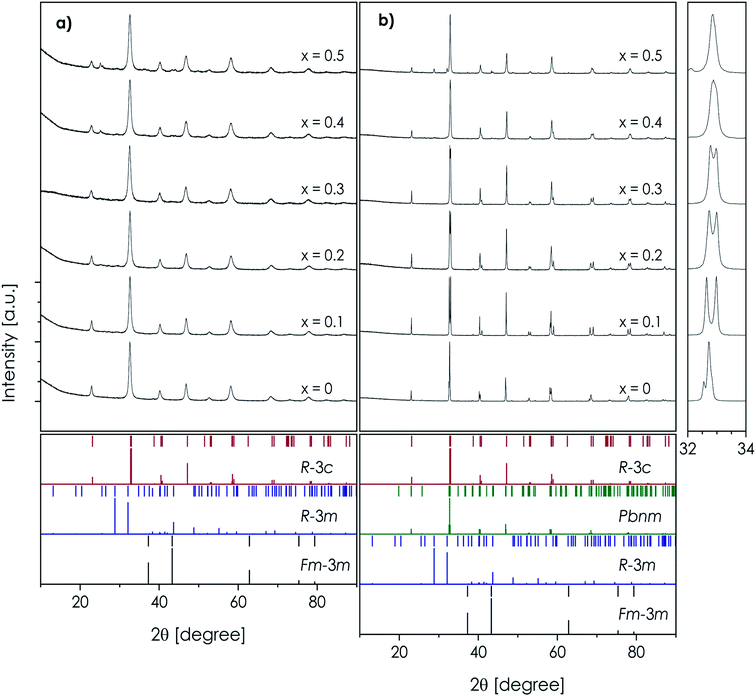 | ||
| Fig. 1 XRD diffraction patterns of the La1−xSrx(Co,Cr,Fe,Mn,Ni)O3−δ materials: (a) calcined powders and (b) sintered pellets. The magnification of the main peaks in the sintered samples is provided. | ||
| Powders | ||||||||
|---|---|---|---|---|---|---|---|---|
| Composition | Space group | Content [wt%] | a [Å] | b [Å] | c [Å] | Normalized cell volume [Å] | a 0 [Å] | Crystallite size [nm] |
| a a 0 – normalized quasi-cubic cell parameter. | ||||||||
| La(Co,Cr,Fe,Mn,Ni)O3−δ |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
100 | 5.5086(2) | 13.371(1) | 58.563(6) | 3.8834(1) | 27.4 | |
| La0.9Sr0.1(Co,Cr,Fe,Mn,Ni) O3−δ |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
100 | 5.5052(3) | 13.363(1) | 58.454(8) | 3.8809(1) | 26.4 | |
| La0.8Sr0.2(Co,Cr,Fe,Mn,Ni) O3−δ |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
100 | 5.4997(3) | 13.346(1) | 58.27(1) | 3.8768(1) | 21.4 | |
| La0.7Sr0.3(Co,Cr,Fe,Mn,Ni) O3−δ |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
100 | 5.5063(5) | 13.362(2) | 58.47(1) | 3.8814(1) | 18.2 | |
| La0.6Sr0.4(Co,Cr,Fe,Mn,Ni) O3−δ |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
— | 5.5067(6) | 13.372(3) | 58.53(2) | 3.8826(1) | ||
| La0.5Sr0.5(Co,Cr,Fe,Mn,Ni) O3−δ |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
— | 5.5049(7) | 13.380(4) | 58.53(2) | 3.8826(1) | ||
| Pellets | |||||||
|---|---|---|---|---|---|---|---|
| Composition | Space group | Content [%] | a [Å] | b [Å] | c [Å] | Normalized cell volume [Å] | a 0 [Å] |
| La(Co,Cr,Fe,Mn,Ni) O3−δ | Pbnm | 100 | 7.7472(2) | 5.5116(1) | 5.4671(1) | 58.360(2) | 3.8789(1) |
| La0.9Sr0.1(Co,Cr,Fe,Mn,Ni) O3−δ |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
100 | 5.4966(1) | 13.2676(2) | 57.858(2) | 3.8677(1) | |
| La0.8Sr0.2(Co,Cr,Fe,Mn,Ni) O3−δ |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
100 | 5.4845(1) | 13.2785(4) | 57.651(3) | 3.8631(1) | |
| La0.7Sr0.3(Co,Cr,Fe,Mn,Ni) O3−δ |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
100 | 5.4738(1) | 13.2914(4) | 57.480(3) | 3.8593(1) | |
| La0.6Sr0.4(Co,Cr,Fe,Mn,Ni) O3−δ |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
94.2 | 5.4688(2) | 13.3014(5) | 57.420(4) | 3.8579(1) | |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
4.6 | 5.542(2) | 20.252(3) | ||||
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
1.2 | 4.1825(5) | |||||
| La0.5Sr0.5(Co,Cr,Fe,Mn,Ni) O3−δ |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
87.1 | 5.4648(2) | 13.3224(8) | 57.427(5) | 3.8581(1) | |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
10.6 | 5.586(6) | 20.238(4) | ||||
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
2.3 | 4.1826(2) | |||||
Regarding the main phase, the choice of appropriate symmetry for the refinement of nanosized samples is often hindered, but in the considered case the choice of the rhombohedral R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group gave satisfactory statistics of the performed fittings (see Table S1†). It is worth noting that this also applies to the La(Co,Cr,Fe,Mn,Ni)O3−δ composition, which was previously reported by Sarkar et al. to be orthorhombic Pbnm.18 However, the mentioned broadening of the peaks, as well as possibly different oxygen content originating from a different cooling procedure, seems to explain this difference. This is further supported by the lack of a clear correlation between the strontium content and the normalized to quasi-cubic unit cell parameter data in the as-synthesized powders (Table 1). A different behavior from the above-discussed was observed for the sintered LSTM pellets, quenched directly at 1000 °C (Fig. 1b and Table 1). As expected, the undoped material can be characterized by the orthorhombic Pbnm structure. For samples with x ranging from 0.1 to 0.3, the symmetry of the crystals increases to R
c space group gave satisfactory statistics of the performed fittings (see Table S1†). It is worth noting that this also applies to the La(Co,Cr,Fe,Mn,Ni)O3−δ composition, which was previously reported by Sarkar et al. to be orthorhombic Pbnm.18 However, the mentioned broadening of the peaks, as well as possibly different oxygen content originating from a different cooling procedure, seems to explain this difference. This is further supported by the lack of a clear correlation between the strontium content and the normalized to quasi-cubic unit cell parameter data in the as-synthesized powders (Table 1). A different behavior from the above-discussed was observed for the sintered LSTM pellets, quenched directly at 1000 °C (Fig. 1b and Table 1). As expected, the undoped material can be characterized by the orthorhombic Pbnm structure. For samples with x ranging from 0.1 to 0.3, the symmetry of the crystals increases to R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c, which is in line with the bigger ionic radius of the Sr-dopant at the A-site compared to La (1.44 Å vs. 1.36 Å for 12-fold coordination). A similar phase transition upon Sr doping was observed before for other TM-based perovskites with a generally similar composition, which can be explained by an increase of the Goldschmidt factor t, becoming closer to 1.43,54 The diffractogram recorded for La0.6Sr0.4(Co,Cr,Fe,Mn,Ni)O3−δ suggests the presence of an almost cubic-like structure (indicated by the lack of main peak's multiplicity, see the inset of Fig. 1b), but some precipitation of secondary phases is visible (see the peak in the vicinity of 30°). The additional phases are more clearly visible for the x = 0.5 sample, indexed to R
c, which is in line with the bigger ionic radius of the Sr-dopant at the A-site compared to La (1.44 Å vs. 1.36 Å for 12-fold coordination). A similar phase transition upon Sr doping was observed before for other TM-based perovskites with a generally similar composition, which can be explained by an increase of the Goldschmidt factor t, becoming closer to 1.43,54 The diffractogram recorded for La0.6Sr0.4(Co,Cr,Fe,Mn,Ni)O3−δ suggests the presence of an almost cubic-like structure (indicated by the lack of main peak's multiplicity, see the inset of Fig. 1b), but some precipitation of secondary phases is visible (see the peak in the vicinity of 30°). The additional phases are more clearly visible for the x = 0.5 sample, indexed to R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and Fm
m and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, which were respectively identified as Sr3(CrO4)2 and NiO. It can be therefore stated that despite the high values of configurational entropy, the entropic stabilization mechanism is not able to overcome the Sr–Cr interaction energy for the Sr content exceeding x = 0.3.
m, which were respectively identified as Sr3(CrO4)2 and NiO. It can be therefore stated that despite the high values of configurational entropy, the entropic stabilization mechanism is not able to overcome the Sr–Cr interaction energy for the Sr content exceeding x = 0.3.
Interesting characteristics were obtained considering the normalized to quasi-cubic unit cell parameter a0 dependence as a function of Sr content in the quenched samples (Fig. S1†). As can be seen, data for oxides with x = 0 and 0.1 indicate a rather substantial a0 decrease, which can be partially associated with the change of the crystal symmetry, but mainly with the oxidation of the B-site cations upon doping. As cations with a higher charge state possess smaller radii and interact more strongly with surrounding oxygen anions, this dominates over an increase of the average A-site cation ionic radius. A very similar effect was observed before for lower Sr content LSCF perovskites.55 Within the x range of 0.1 to 0.3 the dependence of a0 on strontium doping has a linear character but deviates from this behavior for compounds with an even higher Sr concentration. Since the value of the normalized lattice parameter remains almost constant for x = 0.4 and 0.5 (which is accompanied by the precipitation of secondary phases, Table 1), it can be interpreted that the strontium solubility limit is slightly lower than 0.4 in the series, at least at a temperature of 1000 °C at which the samples were quenched. Importantly, the discussed data suggest that the charge compensation mechanism in LSTM, which occurs simultaneously with the introduction of the divalent strontium, proceeds mostly by oxidation of the B-site cations, not by the formation of a significant number of oxygen vacancies. In the latter case, not a decrease but an increase of the unit cell volume is expected to occur, as a result of the so-called chemical expansion.56 Since the chemical expansion is usually visible only for a very high Sr content LSCF (x > 0.6) and similar perovskites,57,58 the observed behavior in the high entropy La1−xSrx(Co,Cr,Fe,Mn,Ni)O3−δ is not unusual in this regard.
As shown in Table 1, the applied route of synthesis allowed for obtaining nanosized powders of the average size varying for the single-phase compositions from 18.2 to 27.4 nm, which compares favorably even with powders obtained by Sarkar et al. with the use of NSP.18 Such a small grain size should be considered as a major advantage of the proposed synthesis route, as fine powders are needed in order to manufacture high-performance cathodes for SOFCs, exhibiting desired porosity and morphology.59–61
3.2. SEM + EDS
The sintered LSTM pellets were examined with the use of SEM and EDS. The results of mappings and analyses for all materials are presented in Fig. S2–S5,† while exemplary data obtained for La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ (within the Sr solubility limit) and La0.5Sr0.5(Co,Cr,Fe,Mn,Ni)O3−δ (two-phase system) are presented in Fig. 2 and 3. The average compositions determined by EDS area analysis for all studied materials are presented in Table S3.† Based on the measured atomic concentrations, it can be said that the application of the sol–gel method allowed obtaining desired compositions with relatively high accuracy, especially considering the inherent limitations of the EDS technique. Also, the results of the SEM + EDS studies correlate very well with the XRD results. In the case of La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ, a homogeneous distribution of all elements, including Sr, is clearly visible (Fig. 2a). A similar behavior can be observed for other single-phase compositions as well (Fig. S2 and S3†). On the other hand, for La0.5Sr0.5(Co,Cr,Fe,Mn,Ni)O3−δ, clear segregation of strontium, as well as B-site elements (especially Cr), is visible (Fig. 2b). The measured stoichiometry at Sr- and Cr-enriched points (Fig. 3b) is in good agreement with the presence of the Sr3(CrO4)2 phase indicated by XRD studies. The same type of phase can be also seen for La0.6Sr0.4(Co,Cr,Fe,Mn,Ni)O3−δ although as expected, the segregation effects are less pronounced (Fig. S4†). The primary grain size visible in SEM micrographs for the materials sintered at 1000 °C is similar for all compositions, being roughly about 20–60 nm (for higher magnification see Fig. S6†). | ||
| Fig. 2 Results of EDS mapping of the air-quenched pellets sintered at 1000 °C for 20 h: (a) La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ and (b) La0.5Sr0.5(Co,Cr,Fe,Mn,Ni)O3−δ. | ||
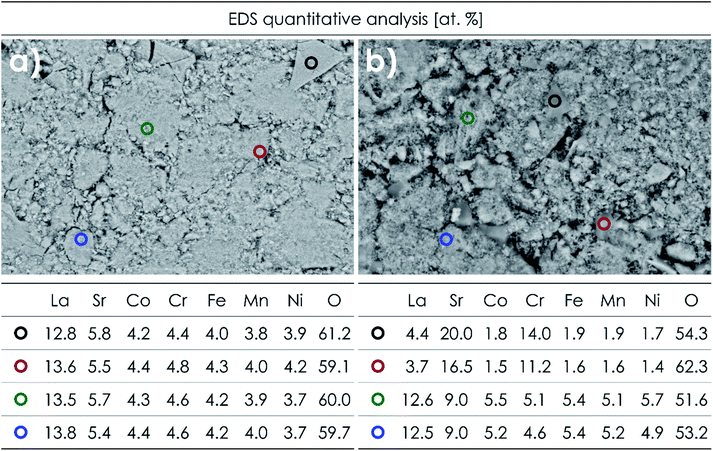 | ||
| Fig. 3 Results of EDS point analyses of the air-quenched pellets sintered at 1000 °C for 20 h: (a) La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ and (b) La0.5Sr0.5(Co,Cr,Fe,Mn,Ni)O3−δ. | ||
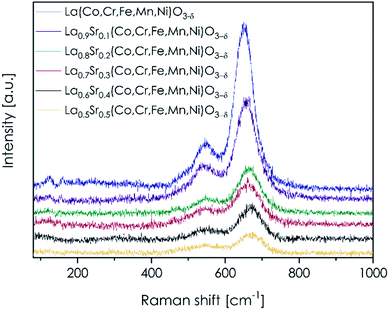
3.3. Raman spectroscopy studies of LSTM
Raman spectroscopy has been proven as a useful method to more deeply elaborate about the nature of bonding in perovskite-type materials, e.g. in LSC and LSCF oxides.62–65 Consequently, the method was also implemented in this research, with Raman spectra recorded for LSTM materials presented in Fig. 4. Exemplary fitted spectra, as well as a detailed summary on the obtained positions of the respective bands, are presented in Fig. S7 and Table S4,† respectively. It should be noted that the spectra were recorded only on the surface, as the intensity of the signal deteriorated significantly during in-depth profiling. Two main bands located at ca. 540 cm−1 and 660 cm−1 can be clearly seen, as well as a few indistinct bands with low intensity, which are present at 100–200 cm−1, making the spectra remarkably similar to the ones characteristic of LSC and LSCF materials.62–65 The latter, low-intensity bands should be attributed to the vibration of the lanthanum sublattice, mainly to the relative motion of those cations with respect to the BO6 octahedra.64 The two main apparent bands can be deconvoluted into at least three separate components, and according to Orlovskaya et al.,64 Tompsett et al.66 or Gupta et al.,67 their presence should be related to the bending (at 540 cm−1, mostly Ag vibrational mode) and stretching vibrations (660 cm−1, mostly Bg vibrational mode) of O–B–O groups. Moreover, the asymmetry of the band at 540 cm−1, resulting from the presence of a separate band at about 485 cm−1, can indicate a small amount of TM3O4 phase, which can segregate at the perovskite's surface.62 The changes in the discussed Raman spectra of LSTM perovskites induced by the introduction of strontium at lanthanum sites are of the main interest. As the strontium concentration increases, the maximum of the band at 660 cm−1 shifts toward higher wavenumbers, while the position of the band at 540 cm−1 remains practically unchanged (see Table S4†). Oxygen atoms in the BO6 cage are also bonded to A cations and the deflections of oxygen atoms during stretching vibrations of the O–B–O bonds must be related to the type of A cation and thus affect the position of the respective band. Hence, the introduction of lighter strontium at lanthanum initial sites should move the band related to stretching vibrations towards higher wavenumbers, which is indeed the case. It is also worth noting that the discussed movement of the peak occurs only if the Sr content x is varying from 0 to 0.3, being in good agreement with the strontium solubility limit discussed above.It can also be observed that as the strontium concentration increases, the intensity of the two main bands decreases, with the trend being more pronounced for the band present at 660 cm−1. Since Sr ions are bigger than La ions, their presence limits, in particular, the deflection amplitude of the stretching O–B–O vibrations, and thus, the intensity of the band at 660 cm−1 significantly decreases. During bending vibrations in BO6 octahedra, oxygen anions will tend to lean toward the center of the oxygen cage, and therefore the effect of the intensity decrease of the band at 540 cm−1 is less pronounced.
An interesting discussion can be provided regarding the possible presence of oxygen vacancies induced by the introduction of strontium cations. The lack of one oxygen in the BO6 octahedra will result in the disappearance of one of the bending vibration modes, but it should not strongly influence the intensity of the band at 540 cm−1 (degeneration of vibrational modes). On the other hand, it will cause asymmetry of the stretching vibrations, and thus, may strongly influence the intensity of the band at 660 cm−1. By comparing the integrated intensities of the bands at 540 cm−1 and 660 cm−1 in individual samples one may conclude that the oxygen vacancy concentration indeed increases as the Sr concentration rises, with the relationship between these values being almost linear for single-phase compositions (see Fig. S8†). However, the extent of this phenomenon is most likely very limited, as discussed previously, and this particular interpretation of the Raman data has a speculative character.
3.4. Transport properties of the LSTM series
The total electrical conductivity as a function of temperature for the studied, single-phase LSTM materials, measured by the EIS method and presented in Arrhenius-type coordinates, is summarized in Fig. 5. The data for multiphase compositions can be found in Fig. S9 and Table S5.† It should be noted that the sintered pellets were not fully densified, but since their relative density was comparable, on the order of 70%, the recorded data can be interpreted and related to the influence of strontium doping. Of importance, the shape of the EIS spectra (Fig. S10†), as well as relatively high recorded values of conductivity, indicates the dominance of the electronic component of conductivity, similarly as for LSCF68 and the majority of other TM-based perovskite-type oxides.69 Since the electronic conductivity is the dominant one, this further ensures that the porosity-related effect is not expected to hinder a more detailed elaboration of the results. As can be seen in Fig. 5, for all materials the electrical conductivity shows thermally activated character, with relatively low values of activation energy Ea. The determined Ea values in the respective linear regions, together with the maximum values of the conductivity, are presented in Table 2. Measured data indicate a strong decrease of the activation energy with the introduction of Sr, accompanied by a significant increase of the electrical conductivity in the whole temperature range for the single-phase (i.e. x = 0–0.3) samples. This effect corresponds well with previously reported data for LSCF oxides having a similar amount of strontium introduced.55,70,71 The improvement of the transport properties seems to relate to the oxidation state of the B-site TM elements, enabling a more efficient double exchange (Zener) mechanism of electronic charge transfer.72 It cannot be excluded that in the charge transfer small polarons are also involved,73 but further studies are needed to provide an answer for this hypothesis. For materials with x = 0.4 and 0.5, somewhat irregular behavior is visible, but this can be explained by the presence of secondary phases. Also worth mentioning is the behavior of the LSTM materials at the highest temperatures, at which a characteristic inflection of the electrical conductivity can be seen, which is more pronounced for samples having a higher amount of Sr introduced. This phenomenon was already explained in the literature as due to the influence of the oxygen vacancies, formed as a result of oxygen loss at high temperatures in e.g. LSCF materials.55,71 However, the magnitude of this effect is not so large, suggesting only a limited release of oxygen from the considered materials. As presented in the exemplary thermogravimetric studies conducted for La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ (Fig. S11†), indeed some oxygen release is visible above 900 °C. It should be emphasized that in electrochemical processes occurring at the SOFC cathode, ionic transport realized by the mobile oxygen vacancies is beneficial for the electrode's operation.74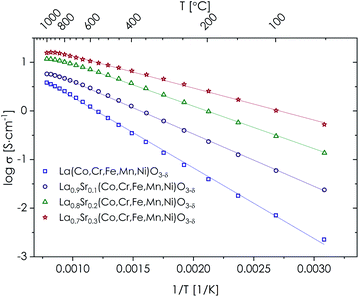 | ||
| Fig. 5 Total electrical conductivity of single-phase LSTM materials as obtained by the EIS measurements. | ||
| Composition | E a [eV] | Temperature range [°C] | σ max [S cm−1] | T max [°C] |
|---|---|---|---|---|
| La(Co,Cr,Fe,Mn,Ni)O3−δ | 0.288(3) | 25–1000 | 3.82 | 1000 |
| La0.9Sr0.1(Co,Cr,Fe,Mn,Ni)O3−δ | 0.214(2) | 25–950 | 5.76 | 1000 |
| La0.8Sr0.2(Co,Cr,Fe,Mn,Ni)O3−δ | 0.173(1) | 25–850 | 11.76 | 1000 |
| La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ | 0.131(1) | 25–850 | 16.03 | 950 |
Considering practical application in SOFC technology, the electrical conductivity of the candidate electrode material being on the order of 10 S cm−1 at the working temperatures seems suitable.27,75 Taking the phase purity, microstructure of the powder, electrical conductivity values and possible presence of oxygen nonstoichiometry at high temperatures into account, for further evaluation as a candidate air electrode material, the La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ composition was selected.
3.5. La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ as a candidate air electrode material
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c phase to cubic Pm
c phase to cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry occurring at ca. 800 °C. This is a known phenomenon, which reflects faster elongation of the A–O bonds as a function of temperature in comparison to B–O bonds.54 As a result, at high temperatures closer-to-ideal (i.e. equal 1) values of the Goldschmidt tolerance factor are attained, leading to an increase of the system's symmetry. On cooling, the cubic structure remains down to 900 °C, but at 800 °C XRD data could be refined with similar precision by both Pm
m symmetry occurring at ca. 800 °C. This is a known phenomenon, which reflects faster elongation of the A–O bonds as a function of temperature in comparison to B–O bonds.54 As a result, at high temperatures closer-to-ideal (i.e. equal 1) values of the Goldschmidt tolerance factor are attained, leading to an increase of the system's symmetry. On cooling, the cubic structure remains down to 900 °C, but at 800 °C XRD data could be refined with similar precision by both Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and R
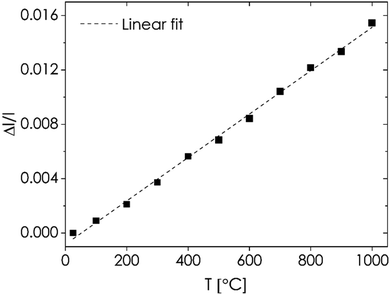
m and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space groups (see Fig. S13 and Table S6†), with the latter giving marginally better results. Additional minor reflections also appear in the diffractograms below 600 °C, which may suggest that the strontium solubility limit at high temperatures is slightly higher than at intermediate and lower temperatures. Nevertheless, the effect is present at temperatures below the considered application range. The occurrence of the mentioned high-temperature phase transition is also supported by the results of DTA-TG measurements, which indicate the occurrence of an endothermic effect at around 748 °C (Fig. S11†). Structural data obtained upon cooling also allowed evaluating the linearized thermal expansion coefficient of L7S3TM, as presented in Fig. 6. As can be seen, the dependence has a linear character in the whole temperature range. The obtained value of 16.0(3) × 10−6 K−1, while larger than those of typical solid electrolytes, e.g. Ce0.8Gd0.2O1.9 (12.4 × 10−6 K−1),76 Zr0.85Y0.15O1.925 (10.5 × 10−6 K−1),77 and La0.8Sr0.2Ga0.8Mg0.2O2.85 (11.1 × 10−6 K−1),78 is rather moderate when compared with typical cathode materials. For example, the La0.6Sr0.4Co0.2Fe0.8O3−δ composition is characterized by the TEC value of 15.3 × 10−6 K−1 in the temperature range up to 600 °C;79 however, at higher temperatures this value may exceed even 20 × 10−6 K−1, due to the prominent contribution of the chemical expansion mechanism.80 The observed low value of TEC should be considered beneficial for the mechanical stability of the fuel cell during operation. In order to investigate whether the previously mentioned formation of secondary phases may affect the long-term stability of the material at high temperatures, additional annealing of the L7S3TM pellet was performed for 100 hours at 1000 °C. The diffraction patterns obtained before and after heat treatment (see Fig. S14†) are practically identical, with the values of the lattice constant remaining practically unchanged (Table S7†), proving that the phase transitions are indeed present only in the medium-temperature range.
c space groups (see Fig. S13 and Table S6†), with the latter giving marginally better results. Additional minor reflections also appear in the diffractograms below 600 °C, which may suggest that the strontium solubility limit at high temperatures is slightly higher than at intermediate and lower temperatures. Nevertheless, the effect is present at temperatures below the considered application range. The occurrence of the mentioned high-temperature phase transition is also supported by the results of DTA-TG measurements, which indicate the occurrence of an endothermic effect at around 748 °C (Fig. S11†). Structural data obtained upon cooling also allowed evaluating the linearized thermal expansion coefficient of L7S3TM, as presented in Fig. 6. As can be seen, the dependence has a linear character in the whole temperature range. The obtained value of 16.0(3) × 10−6 K−1, while larger than those of typical solid electrolytes, e.g. Ce0.8Gd0.2O1.9 (12.4 × 10−6 K−1),76 Zr0.85Y0.15O1.925 (10.5 × 10−6 K−1),77 and La0.8Sr0.2Ga0.8Mg0.2O2.85 (11.1 × 10−6 K−1),78 is rather moderate when compared with typical cathode materials. For example, the La0.6Sr0.4Co0.2Fe0.8O3−δ composition is characterized by the TEC value of 15.3 × 10−6 K−1 in the temperature range up to 600 °C;79 however, at higher temperatures this value may exceed even 20 × 10−6 K−1, due to the prominent contribution of the chemical expansion mechanism.80 The observed low value of TEC should be considered beneficial for the mechanical stability of the fuel cell during operation. In order to investigate whether the previously mentioned formation of secondary phases may affect the long-term stability of the material at high temperatures, additional annealing of the L7S3TM pellet was performed for 100 hours at 1000 °C. The diffraction patterns obtained before and after heat treatment (see Fig. S14†) are practically identical, with the values of the lattice constant remaining practically unchanged (Table S7†), proving that the phase transitions are indeed present only in the medium-temperature range.
| Temperature [°C] | Space group | a [Å] | b [Å] | c [Å] | Normalized cell volume [Å] | a 0 [Å] |
|---|---|---|---|---|---|---|
| 1000 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
3.9208(1) | 60.274(3) | 3.9208(1) | ||
| 900 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
3.9127(1) | 59.900(3) | 3.9127(1) | ||
| 800 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
5.5313(1) | 13.5161(6) | 59.687(4) | 3.9081(1) | |
| 700 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
5.5236(1) | 13.4838(5) | 59.380(4) | 3.9013(1) | |
| 600 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
5.5146(1) | 13.4481(4) | 59.030(3) | 3.8936(1) | |
| 500 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
5.5075(1) | 13.4197(4) | 58.753(3) | 3.8876(1) | |
| 400 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
5.5023(1) | 13.3968(4) | 58.543(3) | 3.8829(1) | |
| 300 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
5.4932(1) | 13.3641(4) | 58.207(3) | 3.8755(1) | |
| 200 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
5.4859(1) | 13.3354(4) | 57.927(3) | 3.8693(1) | |
| 100 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
5.4809(1) | 13.3115(5) | 57.718(4) | 3.8646(1) | |
| 25 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
5.4770(1) | 13.2947(5) | 57.562(4) | 3.8611(1) |
As visible in Fig. S15,† only peaks corresponding to L7S3TM and LSGM oxides can be identified, with an only marginal shift of the reflections occurring, indicating high chemical stability of the materials.
| Sintering temperature of the electrodes [°C] | R p [Ω cm2] | |||
|---|---|---|---|---|
| Measurement temperature [°C] | ||||
| 900 | 850 | 800 | 750 | |
| 1100 | 0.126 | 0.272 | 0.653 | 1.751 |
| 1000 | 0.299 | 0.556 | 1.362 | 3.184 |
| 950 | 0.269 | 0.598 | 1.295 | 2.832 |
The calculated values of the electrode polarization resistance exhibit a linear dependence on temperature in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R–T−1 coordinates, as is shown in Fig. 7. Both considered contributions to resistance, namely R1 (related to processes occurring at the electrode–electrolyte interface, including charge transfer) and R2 (associated with reaction on the electrode's surface, like adsorption and dissociation of oxygen), can be seen in the plot, with the plot for the total polarization resistance being presented in Fig. S18.† The activation energies established for all the examined cells are relatively high (1.60–1.69 eV and 1.45–1.77 eV for R1 and R2, respectively; 1.48–1.71 eV for the total polarization resistance Rp), which leads to a rapid increase of the Rp value at lower temperatures, and consequently, the application of the considered material below 900 °C should be rather excluded at the current stage. On the other hand, such values of Ea, combined with further optimization of the material and morphology of the cathode layer, may allow for a substantial decrease of the operating temperature of similar electrodes in the future. The observed monotonic dependence between Ea and the sintering temperature results from the consequent microstructural changes, as higher Ea values characterize layers consisting of bigger, well-sintered grains.
R–T−1 coordinates, as is shown in Fig. 7. Both considered contributions to resistance, namely R1 (related to processes occurring at the electrode–electrolyte interface, including charge transfer) and R2 (associated with reaction on the electrode's surface, like adsorption and dissociation of oxygen), can be seen in the plot, with the plot for the total polarization resistance being presented in Fig. S18.† The activation energies established for all the examined cells are relatively high (1.60–1.69 eV and 1.45–1.77 eV for R1 and R2, respectively; 1.48–1.71 eV for the total polarization resistance Rp), which leads to a rapid increase of the Rp value at lower temperatures, and consequently, the application of the considered material below 900 °C should be rather excluded at the current stage. On the other hand, such values of Ea, combined with further optimization of the material and morphology of the cathode layer, may allow for a substantial decrease of the operating temperature of similar electrodes in the future. The observed monotonic dependence between Ea and the sintering temperature results from the consequent microstructural changes, as higher Ea values characterize layers consisting of bigger, well-sintered grains.
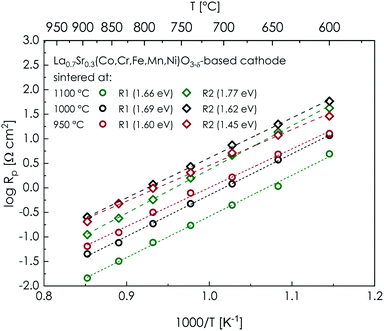 | ||
| Fig. 7 Temperature dependence of the cathodic polarization resistance for La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ-based cathodes sintered at 950 °C, 1000 °C and 1100 °C. | ||
The SEM micrograph of the cross-section of the best performing cell, studied after electrochemical measurements, together with results from EDS mapping, is presented in Fig. 8. As visible, only small inhomogeneities of Sr and Cr elements can be seen, most likely corresponding to a small amount of Sr3(CrO4)2 phase identified previously for the samples having the highest amount of strontium introduced. However, based on the results of the HT-XRD measurements and long-term stability test (Fig. S12 and S14†), it can be assumed that the inhomogeneity is rather the effect of the discussed decreasing Sr solubility on cooling and shall not have an influence on the electrode's operation at high temperatures. No additional interlayers resulting from the reactivity between the electrolyte and cathode material could be observed.
4. Conclusions
For the very first time, the possibility of applying the high-entropy approach to the design of air electrodes for SOFCs was explored, showing in the process that such a method may allow overcoming a number of current issues of electrode materials. A series of novel La1−xSrx(Co,Cr,Fe,Mn,Ni)O3−δ (x = 0, 0.1, 0.2, 0.3, 0.4 and 0.5) perovskite-type oxides were synthesized, with the use of the sol–gel method. Such a route of synthesis, previously not considered for high entropy perovskites, allowed obtaining nanosized powders of desired compositions, suitable for the preparation of SOFC electrodes. The structural studies indicate the presence of a single-phase, R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure in Sr-doped materials, with an upper solubility limit of strontium of x = 0.3. The XRD results suggest that the charge compensation, occurring as a consequence of the introduction of divalent ions into A-sites of the perovskite lattices, takes place mainly through the change of valence states of B-site, transition-metal ions. However, independent measurements with the use of Raman spectroscopy, DTA-TG, as well as the character of the conductivity temperature dependence, indicate a small degree of oxygen release at both a high Sr content and high temperatures, which should be beneficial for the transport properties of these materials. The electrical studies conducted by EIS show mostly electronic character of the charge transfer, with relatively low energies of activation, which further decrease with Sr addition. The measured maximum value of total conductivity σ = 16.03 S cm−1, observed at 950 °C for the material with x = 0.3, is within the acceptable limits for electrode materials. The selected La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ composition was further examined as a potential air electrode material. The material exhibited a high level of inertness with the commercial-grade LSGM 8282 electrolyte. The high-temperature, in situ XRD studies indicate the presence of cubic Pm
c structure in Sr-doped materials, with an upper solubility limit of strontium of x = 0.3. The XRD results suggest that the charge compensation, occurring as a consequence of the introduction of divalent ions into A-sites of the perovskite lattices, takes place mainly through the change of valence states of B-site, transition-metal ions. However, independent measurements with the use of Raman spectroscopy, DTA-TG, as well as the character of the conductivity temperature dependence, indicate a small degree of oxygen release at both a high Sr content and high temperatures, which should be beneficial for the transport properties of these materials. The electrical studies conducted by EIS show mostly electronic character of the charge transfer, with relatively low energies of activation, which further decrease with Sr addition. The measured maximum value of total conductivity σ = 16.03 S cm−1, observed at 950 °C for the material with x = 0.3, is within the acceptable limits for electrode materials. The selected La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ composition was further examined as a potential air electrode material. The material exhibited a high level of inertness with the commercial-grade LSGM 8282 electrolyte. The high-temperature, in situ XRD studies indicate the presence of cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at temperatures above 800 °C. The determined moderate value of the thermal expansion coefficient of 16.0(3) × 10−6 K−1, with no sign of chemical expansion, shows some of the advantages of the high-entropy approach. However, the full extent of the benefits coming from this approach becomes fully visible when the results of the electrode polarization resistance are considered. Despite the relatively very high content of Cr, known for its detrimental effect on the performance of cathode materials, the measurements conducted for the LSGM 8282 electrolyte-supported symmetrical cell show values of the total electrode polarization resistance of 0.126 Ω cm2 at 900 °C. Consequently, the La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ material can be considered as a suitable candidate for the air electrode material at this operational temperature. However, it remains to be seen whether the presence of chromium inside the material's structure may offer an increased resistance towards the Cr-poisoning effect, which is considered a major issue for the state-of-the-art materials. Certainly, further dedicated studies on this subject are necessary. Furthermore, the determined values of the total activation energy in the range of 1.48 to 1.71 eV, depending on the applied thermal pre-treatment, give hope for a significant decrease in working temperature in the future, thanks to the further refinement of the composition and morphology. The performance of the La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ cathode material in a button-type fuel cell was also tested, yielding a value of power density of 553 mW cm−2 at 900 °C, which can be considered promising, considering the early stage of the development and the moderate value of cathodic polarization resistance. In the light of the presented results, it can be expected that the high-entropy approach to the design of SOFC cathode materials may become a prominent trend, as it allows overcoming a number of currently unresolved issues. The current study shows the viability of the whole concept; however, we are far from exploring its full potential. Further improvement of the transport properties should be easily possible by limiting or excluding the content of Cr. The catalytic activity of the materials and, as a consequence, their operational temperature range, can be further improved by the refinement of the compositions and the selection of the composing elements, with the presence of multiple redox pairs, potentially allowing for covering wide ranges of temperatures. Certainly, further studies will be necessary to fully exploit the possibilities provided by the high-entropy approach to the design of air electrodes.
m at temperatures above 800 °C. The determined moderate value of the thermal expansion coefficient of 16.0(3) × 10−6 K−1, with no sign of chemical expansion, shows some of the advantages of the high-entropy approach. However, the full extent of the benefits coming from this approach becomes fully visible when the results of the electrode polarization resistance are considered. Despite the relatively very high content of Cr, known for its detrimental effect on the performance of cathode materials, the measurements conducted for the LSGM 8282 electrolyte-supported symmetrical cell show values of the total electrode polarization resistance of 0.126 Ω cm2 at 900 °C. Consequently, the La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ material can be considered as a suitable candidate for the air electrode material at this operational temperature. However, it remains to be seen whether the presence of chromium inside the material's structure may offer an increased resistance towards the Cr-poisoning effect, which is considered a major issue for the state-of-the-art materials. Certainly, further dedicated studies on this subject are necessary. Furthermore, the determined values of the total activation energy in the range of 1.48 to 1.71 eV, depending on the applied thermal pre-treatment, give hope for a significant decrease in working temperature in the future, thanks to the further refinement of the composition and morphology. The performance of the La0.7Sr0.3(Co,Cr,Fe,Mn,Ni)O3−δ cathode material in a button-type fuel cell was also tested, yielding a value of power density of 553 mW cm−2 at 900 °C, which can be considered promising, considering the early stage of the development and the moderate value of cathodic polarization resistance. In the light of the presented results, it can be expected that the high-entropy approach to the design of SOFC cathode materials may become a prominent trend, as it allows overcoming a number of currently unresolved issues. The current study shows the viability of the whole concept; however, we are far from exploring its full potential. Further improvement of the transport properties should be easily possible by limiting or excluding the content of Cr. The catalytic activity of the materials and, as a consequence, their operational temperature range, can be further improved by the refinement of the compositions and the selection of the composing elements, with the presence of multiple redox pairs, potentially allowing for covering wide ranges of temperatures. Certainly, further studies will be necessary to fully exploit the possibilities provided by the high-entropy approach to the design of air electrodes.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This research was supported by the Polish National Science Center (NCN) under project no. UMO-2017/25/B/ST8/02549.Notes and references
- B. Cantor, I. T. Chang, P. Knight and A. J. Vincent, Mater. Sci. Eng., A, 2004, 375–377, 213–218 CrossRef
.
- J. W. Yeh, S. K. Chen, S. J. Lin, J. Y. Gan, T. S. Chin, T. T. Shun, C. H. Tsau and S. Y. Chang, Adv. Eng. Mater., 2004, 6, 299–303 CrossRef CAS
.
- C. M. Rost, R. Schaet, T. Borman, A. Moballegh, E. C. Dickey, D. Hou, J. L. Jones, S. Curtarolo and J. P. Maria, Nat. Commun., 2015, 6, 8485 CrossRef CAS
.
- J. Zhou, J. Zhang, F. Zhang, B. Niu, L. Lei and W. Wang, Ceram. Int., 2018, 44, 22014–22018 CrossRef CAS
.
- J. Gild, Y. Zhang, T. Harrington, S. Jiang, T. Hu, M. C. Quinn, W. M. Mellor, N. Zhou, K. Vecchio and J. Luo, Sci. Rep., 2016, 6, 37946 CrossRef CAS
.
- T. K. Chen, T. T. Shun, J. W. Yeh and M. S. Wong, Surf. Coat. Technol., 2004, 188–189, 193–200 CrossRef CAS
.
- J. Gild, J. Braun, K. Kaufmann, E. Marin, T. Harrington, P. Hopkins, K. Vecchio and J. Luo, J. Materiomics, 2019, 5, 337–343 CrossRef
.
- A. Sarkar, C. Loho, L. Velasco, T. Thomas, S. S. Bhattacharya, H. Hahn and R. Djenadic, Dalton Trans., 2017, 46, 12167 RSC
.
- S. Jiang, T. Hu, J. Gild, N. Zhou, J. Nie, M. Qin, T. Harrington, K. Vecchio and J. Luo, Scr. Mater., 2018, 142, 116–120 CrossRef CAS
.
- M. Stygar, J. Dąbrowa, M. Moździerz, M. Zajusz, W. Skubida, K. Mroczka, K. Berent, K. Świerczek and M. Danielewski, J. Eur. Ceram. Soc., 2020, 40, 1644–1650 CrossRef CAS
.
- Y. Zhang, T. T. Zuo, Z. Tang, M. C. Gao, K. A. Dahmen, P. K. Liaw and C. L. Lu, Prog. Mater. Sci., 2014, 61, 1–93 CrossRef CAS
.
- D. B. Miracle and O. N. Senkov, Acta Mater., 2017, 112, 448–511 CrossRef
.
- D. Bérardan, S. Franger, A. K. Meena and D. Dragoe, J. Mater. Chem. A, 2016, 4, 9536–9541 RSC
.
- N. Osenciat, D. Bérardan, D. Dragoe, B. Leridon, S. Hole, A. K. Meena, S. Franger and N. Dragoe, J. Am. Ceram. Soc., 2019, 102, 6156–6162 CrossRef CAS
.
- J. Dąbrowa, M. Stygar, A. Mikuła, A. Knapik, K. Mroczka, W. Tejchman, M. Danielewski and M. Martin, Mater. Lett., 2018, 216, 32–36 CrossRef
.
- A. Mao, H. Z. Xiang, Z. G. Zhang, K. Koji, H. Zhang and Y. Jia, J. Magn. Magn. Mater., 2020, 497, 165884 CrossRef CAS
.
- Z. Grzesik, G. Smoła, M. Miszczak, M. Stygar, J. Dąbrowa, M. Zajusz, K. Świerczek and M. Danielewski, J. Eur. Ceram. Soc., 2020, 40, 835–839 CrossRef CAS
.
- A. Sarkar, R. Djenadic, D. Wang, C. Hein, R. Kautenburger, O. Clemens and H. Hahn, J. Eur. Ceram. Soc., 2018, 38, 2318–2327 CrossRef CAS
.
- R. Djenadic, A. Sarkar, O. Clemens, C. Loho, M. Botros, V. S. K. Chakravadhanula, C. Kübel, S. S. Bhattacharya, A. S. Gandhi and H. Hahn, Mater. Res. Lett., 2016, 5, 102–109 CrossRef
.
- J. Gild, M. Samiee, J. L. Braun, L. Braun, T. Harrington, H. Vega, P. E. Hopkins, K. Vecchio and J. Luo, J. Eur. Ceram. Soc., 2018, 38, 3578–3584 CrossRef CAS
.
- K. P. Tseng, Q. Yang, S. J. McCormack and W. M. Kriven, J. Am. Ceram. Soc., 2020, 103, 569–576 CrossRef CAS
.
- Z. Zhao, H. Xiang, Z. Peng and Y. Zhou, J. Mater. Sci. Technol., 2019, 35, 2647–2651 CrossRef
.
- D. Bérardan, S. Franger, D. Dragoe, A. K. Meena and N. Dragoe, Phys. Status Solidi RRL, 2016, 10, 328–333 CrossRef
.
- A. Sarkar, L. Velasco, D. Wang, Q. Wang, G. Talasila, L. de Basi, C. Kubel, T. Brezesisnki, S. S. Bhattacharya, H. Hahn and B. Breitung, Nat. Commun., 2018, 9, 3400 CrossRef
.
- Q. Wang, A. Sarkar, Z. Li, Y. Lu, L. Velasco, S. S. Bhattacharya, T. Brezesinski, H. Hahn and B. Breitung, Electrochem. Commun., 2019, 100, 121–125 CrossRef CAS
.
- C. Zhao, F. Ding, Y. Lu, L. Chen and Y. S. Hu, Angew. Chem., Int. Ed., 2020, 59, 264–269 CrossRef CAS
.
- C. Sun, R. Hui and J. Roller, J. Solid State Electrochem., 2010, 14, 1125–1144 CrossRef CAS
.
- P. Gao, A. Bolon, M. Taneja, Z. Xie, N. Orlovskaya and M. Radovic, Solid State Ionics, 2017, 300, 1–9 CrossRef CAS
.
- A. V. Nikonov, K. A. Kuterbekov, K. Z. Bekmyrza and N. B. Pavzderin, Eurasian Journal of Physics and Functional Materials, 2018, 2, 274–292 CrossRef
.
-
A. Hamnett, Handbook of Fuel Cells – Fundamentals, Technology and Applications, John Wiley & Sons, 2010 Search PubMed
.
- E. V. Tsipis and V. V. Kharton, J. Solid State Electrochem., 2011, 15, 1007–1040 CrossRef CAS
.
-
M. Boaro and A. S. Arico, Advances in Medium and High Temperature Solid Oxide Fuel Cell Technology, Springer, 2014 Search PubMed
.
- N. Mahato, A. Banerjee, A. Gupta, S. Omar and K. Balani, Prog. Mater. Sci., 2015, 72, 141–337 CrossRef CAS
.
- A. C. Tomkiewicz, M. Meloni and S. McIntosh, Solid State Ionics, 2014, 260, 55–59 CrossRef CAS
.
- J. H. Kim and A. Manthiram, J. Mater. Chem. A, 2015, 3, 24195 RSC
.
- R. Pelosato, G. Cordaro, D. Stucchi, C. Cristiani and G. Dotelli, J. Power Sources, 2015, 298, 46–67 CrossRef CAS
.
- S. Liu, W. Zhang, Y. Li and B. Yu, RSC Adv., 2017, 7, 16332 RSC
.
- R. L. Cook and A. F. Sammells, Solid State Ionics, 1991, 45, 311–321 CrossRef CAS
.
- N. Bonanos, K. S. Knight and B. Ellis, Solid State Ionics, 1995, 79, 161–170 CrossRef CAS
.
- B. A. Boukamp, Nat. Mater., 2003, 2, 294–296 CrossRef CAS
.
- L. Shu, J. Sunarso, S. S. Hashim, J. Mao, W. Zhou and F. Liang, Int. J. Hydrogen Energy, 2019, 44, 31275–31304 CrossRef CAS
.
- S. Hossain, M. A. Abdalla, S. N. B. Jamain, J. H. Zaini and A. K. Azad, Renewable Sustainable Energy Rev., 2017, 79, 750–764 CrossRef CAS
.
-
R. H. Mitchel, Perovskites Modern and Ancient, Almaz Press Inc., 2002 Search PubMed
.
- M. Biesuz, S. Fu, J. Dong, A. Jiang, D. Ke, Q. Xu, D. Zhu, M. Bortolott, M. J. Reece, C. Hu and S. Grasso, J. Asian Ceram. Soc., 2019, 7, 127–132 CrossRef
.
- Y. Sharma, B. L. Musico, X. Gao, C. Hua, A. F. May, A. Herklotz, A. Rastogi, D. Mandrus, J. Yan, H. N. Lee, M. F. Chisholm, V. Keppens and T. C. Ward, Phys. Rev. Mater., 2018, 2, 060404 CrossRef CAS
.
- R. Witte, A. Sarkar, R. Kruk, B. Eggert, R. A. Brand, H. Wende and H. Hahn, Phys. Rev. Mater., 2019, 3, 034406 CrossRef CAS
.
- J. Malzbender, P. Batfalsky, R. Vasen, V. Shemet and F. Tietz, J. Power Sources, 2012, 201, 196–203 CrossRef CAS
.
- T. Horita, K. Yamaji, N. Sakai, H. Yokokawa, A. Weber and E. Ibers-Tiffee, Solid State Ionics, 2000, 138, 143–152 CrossRef
.
- F. Tietz, V. A. C. Haanappel, A. Mai, J. Mertens and D. Stover, J. Power Sources, 2006, 156, 20–22 CrossRef CAS
.
-
L. Dimesso, in Handbook of Sol-Gel Science and Technology, ed. L. Klein, M. Aparicio and A. Jitanu, Springer, 2016 Search PubMed
.
- Z. Du, C. Yan, H. Zhao, Y. Zhang, C. Yang, S. Yi, Y. Lu and K. Świerczek, J. Mater. Chem. A, 2017, 5, 25641–25651 RSC
.
- Y. Zhang, H. Zhao, Z. Du, K. Świerczek and Y. Li, Chem. Mater., 2019, 31, 3784–3793 CrossRef CAS
.
- H. Zhao, Y. Zheng, C. Yang, Y. Shen, Z. Du and K. Świerczek, Int. J. Hydrogen Energy, 2013, 38, 16365–16372 CrossRef CAS
.
-
R. J. Tilley, Perovskites Structure–Property Relationships, John Wiley & Sons, 2016 Search PubMed
.
- S. P. Jiang, Int. J. Hydrogen Energy, 2019, 44, 7448–7493 CrossRef CAS
.
- D. Marrocchelli, N. H. Perry and S. R. Bishop, Phys. Chem. Chem. Phys., 2015, 17, 10028 RSC
.
- S. R. Bishop and K. L. Duncan, J. Am. Ceram. Soc., 2010, 93, 4115–4121 CrossRef CAS
.
- M. Kuhn, S. Hashimoto, K. Sato, K. Yashiro and J. Mizusaki, Solid State Ionics, 2013, 241, 12–16 CrossRef CAS
.
- V. A. C. Haanappel, J. Mertens, D. Rutenbeck, C. Tropartz, W. Herzhof, D. Sebold and F. Tietz, J. Power Sources, 2005, 141, 216–226 CrossRef CAS
.
- J. Hayd, L. Dieterle, U. Guntow, D. Gerthsen and E. Ivers-Tiffee, J. Power Sources, 2011, 196, 7263–7270 CrossRef CAS
.
- L. M. Acuna, J. Pena-Martiznez, D. Marrero-Lopez, R. O. Fuentes, P. Nunez and D. G. Lamas, J. Power Sources, 2011, 196, 9276–9283 CrossRef CAS
.
- L. Zhao, J. Zhang, T. Becker and S. P. Jiang, J. Electrochem. Soc., 2014, 161, F687–F693 CrossRef CAS
.
- Y. Chen, X. Nie, B. Wang, C. Xia, W. Dong, X. F. Wang, H. Wang and B. Zhu, Catal. Today, 2019 DOI:10.1016/j.cattod.2019.05.064
.
- N. Orlovskaya, A. Coratolo, C. Johnson and R. Gemmen, J. Am. Ceram. Soc., 2005, 87, 1981–1987 CrossRef
.
- M. Liu, D. Ding, K. Blinn, X. Li, L. Nie and M. Liu, Int. J. Hydrogen Energy, 2012, 37, 8613–8620 CrossRef CAS
.
- G. A. Tompsett and N. M. Sammes, J. Power Sources, 2004, 130, 1–7 CrossRef CAS
.
- R. K. Gupta and C. M. Whang, J. Phys.: Condens. Matter, 2007, 19, 196209 CrossRef
.
- S. Wang, M. Katsuki, M. Dokiya and T. Hashimoto, Solid State Ionics, 2003, 159, 71–78 CrossRef CAS
.
-
J. B. Goodenoug, Localized to Itinerant Electronic Transition in Perovskite Oxides, Springer-Verlag, 2001 Search PubMed
.
- L. W. Tai, M. M. Nasrallah and H. U. Anderson, J. Solid State Chem., 1995, 118, 117–124 CrossRef CAS
.
- A. Petric, P. Huang and F. Tietz, Solid State Ionics, 2000, 135, 719–725 CrossRef CAS
.
- O. Nganba Meetei, O. Erten, A. Mukherjee, M. Randeria, N. Trivedi and P. Woodward, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165104 CrossRef
.
- D. Munoz-Gil, E. Urones-Garrote, D. Perez-Coll, U. Amador and S. Garcia-Martin, J. Mater. Chem. A, 2018, 6, 5452–5460 RSC
.
- A. Barbucci, P. Carpanese, G. Cerisola and M. Viviani, Solid State Ionics, 2005, 176, 1753–1758 CrossRef CAS
.
- J. Richter, P. Holtappels, T. Graule, T. Nakamura and L. J. Gauckler, Monatsh. Chem., 2009, 140, 985–999 CrossRef CAS
.
- Y. Zhang, Q. Zhou and T. He, J. Power Sources, 2011, 196, 76–83 CrossRef CAS
.
- F. Tietz, Ionics, 1999, 5, 129–139 CrossRef CAS
.
- J. W. Stevenson, K. Hasinska, N. L. Canfield and T. R. Armstrong, J. Electrochem. Soc., 2000, 147, 3213–3218 CrossRef CAS
.
- L. W. Tai, M. M. Nasrallah, H. U. Anderson, D. M. Sparlin and S. R. Sehlin, Solid State Ionics, 1995, 76, 273–283 CrossRef CAS
.
- E. Niwa and T. Hashimoto, Solid State Ionics, 2016, 285, 187–194 CrossRef CAS
.
- A. Olszewska, Z. Du, K. Świerczek, H. Zhao and B. Dąbrowski, J. Mater. Chem. A, 2018, 6, 13271–13285 RSC
.
- N. A. Baharuddin, A. Muchtar, M. R. Somalu, S. A. Muhammed Ali and H. Rahman, Ceram.-Silik., 2016, 60, 115–121 CAS
.
- J. W. Fergus, Int. J. Hydrogen Energy, 2007, 32, 3664–3671 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta06356h |
| This journal is © The Royal Society of Chemistry 2020 |