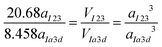Spontaneously chiral cubic liquid crystal: three interpenetrating networks with a twist†
Xiangbing
Zeng
 *a and
Goran
Ungar
*a and
Goran
Ungar
 ab
ab
aDepartment of Materials Science and Engineering, University of Sheffield, Sheffield S1 3JD, UK. E-mail: x.zeng@sheffield.ac.uk
bState Key Laboratory for Mechanical Behaviour of Materials, Shaanxi International Research Centre for Soft Matter, Xi’an Jiaotong University, Xi’an, 710049, P. R. China
First published on 26th February 2020
Abstract
A new molecular-level model is proposed for the “Smectic-D” liquid crystal whose structure has remained controversial since the 1960s. The phase has a body-centred cubic lattice, and all previous structural models assumed an Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. However, this contradicts the recent discovery that the phase is always chiral, even in non-chiral compounds. The new model has the non-centrosymmetric space group I23, and consists of three interpenetrating networks, with 3-way planar network junctions like in the double gyroid phase. Rafts of 3–4 parallel molecules stack with an 8° twist on top of each other, forming spontaneously chiral columnar network segments. Homochirality throughout the network is enforced by matching the helical sense of all confluent segments at junctions. The findings indicate that coordinated helicity, previously unrecognized, is a key driving force responsible for the formation of a number of chiral and achiral, cubic and non-cubic bicontinuous phases of rod-like molecules.
m space group. However, this contradicts the recent discovery that the phase is always chiral, even in non-chiral compounds. The new model has the non-centrosymmetric space group I23, and consists of three interpenetrating networks, with 3-way planar network junctions like in the double gyroid phase. Rafts of 3–4 parallel molecules stack with an 8° twist on top of each other, forming spontaneously chiral columnar network segments. Homochirality throughout the network is enforced by matching the helical sense of all confluent segments at junctions. The findings indicate that coordinated helicity, previously unrecognized, is a key driving force responsible for the formation of a number of chiral and achiral, cubic and non-cubic bicontinuous phases of rod-like molecules.
Introduction
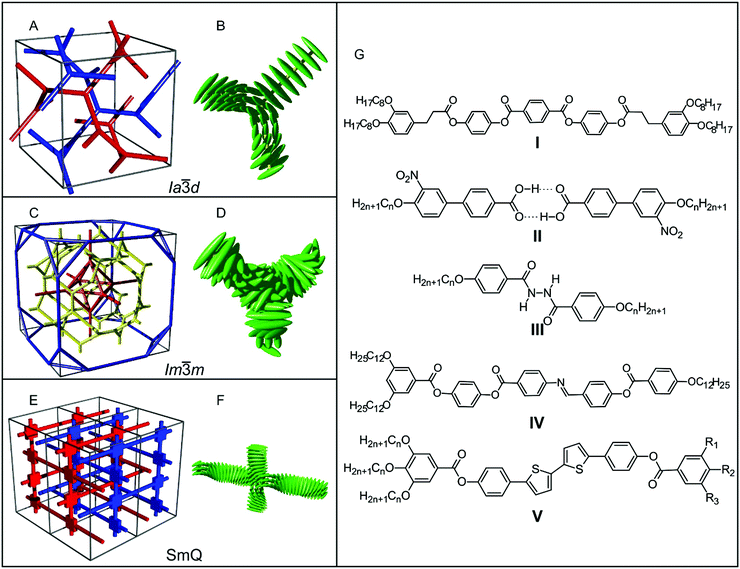
Complex liquid crystals (LCs) are typically formed by microphase separation of two or more immiscible covalently bonded moieties, such as hydrophilic–hydrophobic in lyotropic LCs or aromatic–aliphatic in thermotropics. In block polymers, a similar situation arises, with the separation of blocks on a larger scale. Such separation leads to partition of space into discrete entities such as spheres, columns or layers. In a bicontinuous phase, however, the space occupied by both moieties is continuous. The best-known examples are bicontinuous cubic (Cubbi) phases.1 The structure of one of them has never been properly clarified, although its existence has been known for over 60 years, originally termed “Smectic-D”.2,3 In light of the recently uncovered evidence of its intrinsic spontaneously developing chirality, here, we present a new model of this most complex of all liquid crystal phases, in the belief that we are close to a final solution of this longest standing enigma in the field of liquid crystal structure.Three Cubbi phases have been observed in lyotropic (water–surfactant) systems, and in all of them, one of the moieties (e.g., water or alkyl chains) forms two interpenetrating infinite periodic networks, separated by an infinite periodic surface with minimum curvature (IPMS), around which the other moiety aggregates. Lyotropic cubic phases have fancy names: “double gyroid” (DG, space group Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d, Fig. 1A), “double diamond” (DD, Pn
d, Fig. 1A), “double diamond” (DD, Pn![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and “plumber's nightmare” (PN, Im
m) and “plumber's nightmare” (PN, Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). They contain 3-, 4- and 6-way network junctions.4–6 Bicontinuous phases have also been found in block polymers.7 For a recent review on IPMS structures in biological and self-assembled systems, please refer to Han and Che.8
m). They contain 3-, 4- and 6-way network junctions.4–6 Bicontinuous phases have also been found in block polymers.7 For a recent review on IPMS structures in biological and self-assembled systems, please refer to Han and Che.8
In thermotropic LCs, the aromatic molecular cores are most commonly found in the networks, while the attached flexible chains fill the space between them.1,9,10 The DG is relatively common, while the other two double network cubics are very rare.11 This is believed to be due to the inability of the tethered chains to reach distant voids present in these structures, while in lyotropics, these are easily filled by the solvent. Another obstacle to the formation of DD and PN thermotropic phases is chain overcrowding around the 4- and 6-way junctions. The exceptions are cubics whose networks consist of coaxial bundles of rods, having side-chains but none of them attached at the junctions. In these compounds, both double11 and single diamond phases12 have recently been observed.
However, another Cubbi phase is often found in close proximity of the DG phase in rod-like thermotropic “polycatenars”, i.e., compounds with one or more end-chains; some of the examples are shown in Fig. 1G. This already mentioned phase was originally thought to be a layered phase (“Smectic-D”)3 but was subsequently recognized to have cubic symmetry.13 It has a much larger unit cell, and more complex structure, compared to the DG phase found in the same or similar compounds. Observed X-ray diffraction peaks (hkl) of the phase obey the general rule that h + k + l = 2n, indicating a body centred lattice, and the phase was assigned a space group of Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Initial structural models of the phase were built on the Schwartz P IPMS, with the two subspaces separated by the IPMS further divided forming a multi-layer structure.14–17 However, such models failed to explain the observed diffraction intensities (e.g., (321) being the strongest peak), or the strong structural relation to the DG phase. On the basis of a reconstructed electron density map of the phase, we have proposed that this phase should consist of three interpenetrating networks, instead of two as in the DG phase, as shown in Fig. 1C and Fig. S1a in the (ESI†).18,19 However, there have been some difficulties with that model, as detailed below. An alternative model of the phase has also been proposed, where it was suggested that the inner and outer “networks” should be vesicle-like instead, see Fig. S1b (ESI†).20–22 One of the key problems with that model was the unexplained coexistence of convex and concave surfaces in strongly curved layers of symmetric molecules.
m. Initial structural models of the phase were built on the Schwartz P IPMS, with the two subspaces separated by the IPMS further divided forming a multi-layer structure.14–17 However, such models failed to explain the observed diffraction intensities (e.g., (321) being the strongest peak), or the strong structural relation to the DG phase. On the basis of a reconstructed electron density map of the phase, we have proposed that this phase should consist of three interpenetrating networks, instead of two as in the DG phase, as shown in Fig. 1C and Fig. S1a in the (ESI†).18,19 However, there have been some difficulties with that model, as detailed below. An alternative model of the phase has also been proposed, where it was suggested that the inner and outer “networks” should be vesicle-like instead, see Fig. S1b (ESI†).20–22 One of the key problems with that model was the unexplained coexistence of convex and concave surfaces in strongly curved layers of symmetric molecules.
More recently, it has been discovered by optical microscopy and circular dichroism that this cubic phase is in fact chiral through spontaneous mirror symmetry breaking, even though the compounds forming it were achiral.23 At the same time, the DG phase shown by the same or similar compounds is always achiral. For this reason, we are going to call the two phases chiral and achiral bicontinuous cubic phases, respectively. In similar but intrinsically chiral compounds, an undefined body-centred cubic phase has been reported in place of the DG.24,25 It appears that this phase was in fact the same chiral cubic phase as found in achiral compounds: the diffraction patterns are virtually the same.26
Another phase found in chiral polycatenar enantiomers is the so-called smectic-Q (SmQ) phase, with a tetragonal unit cell and a chiral I4122 space group.27–30 This long-known chiral phase has recently also been discovered in achiral compounds, and its structure was finally solved.31 It turned out to be another bicontinuous phase with two inter-penetrating isochiral networks (Fig. 1E).
In order to explain the intriguing spontaneous chirality of the SmQ and chiral cubic phases, and the lack of it in DG, it has been proposed that in all three phases, each columnar network segment, formed from stacked rafts of 3–4 parallel rod-like aromatic cores, is always chiral.23 The chirality originates from slow twisting of the successive rafts about the segment helical axis in order to avoid clashes between their end-chains while still maintaining reasonable π−π stacking of the aromatic cores (Fig. 1B, E and F). Furthermore, segments joined together at a network junction should possess the same handedness for efficient packing, and consequently homochirality will propagate through such matching at junctions. While in the DG phase, the two interpenetrating networks have opposite handedness and overall chirality cancels out, in the chiral cubic phase either all three networks (in our model) are homochiral, or their chiralities do not cancel completely.
The model is most satisfactorily explained in the DG (Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d) and SmQ phases. In DG, all network segments have the same length of
d) and SmQ phases. In DG, all network segments have the same length of 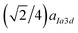 . (Fig. 1A). Three coplanar segments join at each network junction of 3-fold symmetry (Fig. 1B). At the junctions, the molecules are perpendicular to the junction plane. Rotation of molecular rafts along each segment is required as the dihedral angle between the planes of successive junctions is
. (Fig. 1A). Three coplanar segments join at each network junction of 3-fold symmetry (Fig. 1B). At the junctions, the molecules are perpendicular to the junction plane. Rotation of molecular rafts along each segment is required as the dihedral angle between the planes of successive junctions is 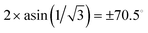 . The sign is positive or negative depending on which of the two networks the segment belongs to. From the experimentally measured lattice parameter aIa3d, and assuming that the distance between neighbouring molecular rafts is 4.5 Å, the twist angle between them is estimated as ∼8°. Note that this idea of twisted molecules in the DG phase was already proposed as early as 198732 and in a later work,33 even though both are different to our model in details, and neither of them discussed the chirality of network segments and the junctions.
. The sign is positive or negative depending on which of the two networks the segment belongs to. From the experimentally measured lattice parameter aIa3d, and assuming that the distance between neighbouring molecular rafts is 4.5 Å, the twist angle between them is estimated as ∼8°. Note that this idea of twisted molecules in the DG phase was already proposed as early as 198732 and in a later work,33 even though both are different to our model in details, and neither of them discussed the chirality of network segments and the junctions.
The SmQ phase has a tetragonal lattice, and there are two kinds of network segments, horizontal (⊥c) and vertical (‖c), with segment lengths aSmQ and cSmQ/4, respectively (Fig. 1E). The length of the vertical segments is somewhat less than twice that of the horizontal ones, as c/a is typically ∼1.75. All network junctions are 4-way coplanar, with a horizontal column and a vertical column crossing each other orthogonally (Fig. 1F). Along a vertical segment, the molecules turn by 90° between junctions, and by 180° along a horizontal segment. The twist between successive rafts is ∼9–10°, only slightly larger than that in the DG phase. In SmQ, the two interpenetrating networks have the same chirality, as they are equivalent to each other due to the body-centred symmetry.
However, when the same scheme was applied to our triple network model of the chiral cubic phase, the result was less satisfactory. The key problem is the non-chirality of the Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, a consequence being that it was impossible for molecular orientation to always match at junctions. Another problem was that in the best solution that we could find at the time, the twist between successive molecular rafts was 30–35°, much larger than the 8–10° value found for the Ia
m space group, a consequence being that it was impossible for molecular orientation to always match at junctions. Another problem was that in the best solution that we could find at the time, the twist between successive molecular rafts was 30–35°, much larger than the 8–10° value found for the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d and SmQ phases (Fig. 1D). A chiral model built in a similar way to ours, but on the basis of the vesicle/network model, also has similar problems.22 This is in contradiction to our expectation that the local arrangement of these three phases should be very similar, due to the experimental observation that the three phases are often found in compounds with very similar chemical structures, or even in the same compound but depending on temperature and thermal history.14,15,21,23
d and SmQ phases (Fig. 1D). A chiral model built in a similar way to ours, but on the basis of the vesicle/network model, also has similar problems.22 This is in contradiction to our expectation that the local arrangement of these three phases should be very similar, due to the experimental observation that the three phases are often found in compounds with very similar chemical structures, or even in the same compound but depending on temperature and thermal history.14,15,21,23
We thus undertook to re-examine this phase, with its longest standing unsolved structure in the field of liquid crystals and, probably, the most complex of all. Its structure solution has been hampered by its complexity, but initially also by its frequent coexistence with the DG phase.34–36 The chiral cubic phase is the second most common bicontinuous phase in thermotropic LCs, observed in hundreds if not thousands of compounds. The importance of understanding its structure is heightened by the fact that it sometimes appears, in achiral compounds, immediately below a recently discovered highly optically active isotropic liquid phase Iso* distinct from the normal liquid Iso.23,37 Our understanding of the fascinating Iso* phase is almost zero, but because of the similarities in optical activity and the ease of transition between Iso* and the chiral cubic phase, the solution of the cubic structure should help understand Iso*.
Results and discussion
In the current paper, we construct a new structural model of the chiral cubic phase that is compatible with all the experimental observations so far, and bears more similarity with the double network structures found in the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d (DG) and SmQ phases. In the following, we start with examining the space group of the chiral bicontinuous cubic phase and provide details on how the new structure is constructed. The new model is then evaluated by simulation of the diffraction pattern, and by reconstruction of the electron density map based on the new space group.
d (DG) and SmQ phases. In the following, we start with examining the space group of the chiral bicontinuous cubic phase and provide details on how the new structure is constructed. The new model is then evaluated by simulation of the diffraction pattern, and by reconstruction of the electron density map based on the new space group.
Initial assumptions
In order to construct a new model of the chiral bicontinuous cubic phase, it is assumed that the previous triple network model as shown in Fig. 1C, even though having the wrong space group, is related to the true, lower symmetry structure by averaging. We also assume that the structure also consists of three networks, inner, outer and middle, as in our previous model albeit with lower symmetry. This assumption is also supported by the fact that when the “Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m” and the double-network DG phases appear in the same compound, the ratio of their lattice parameters is always close to 3/2.
m” and the double-network DG phases appear in the same compound, the ratio of their lattice parameters is always close to 3/2.
The observed X-ray hkl reflections of the chiral bicontinuous cubic phase obey the h + k + l = 2n rule, indicating a body-centred lattice, with no further general extinction rules observed. There are six candidate space groups: I23, I213, Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , I432, I
, I432, I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m and Im
3m and Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The first three belong to the Laue class m
m. The first three belong to the Laue class m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and the latter three belong to m
and the latter three belong to m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, depending on whether a general (hkl) diffraction peak is equivalent to (or has the same intensity as) the corresponding (lkh) peak (m
m, depending on whether a general (hkl) diffraction peak is equivalent to (or has the same intensity as) the corresponding (lkh) peak (m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) or not (m
m) or not (m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ). Previously, the Laue class was assigned to m
). Previously, the Laue class was assigned to m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, based on a single crystal diffraction study where (321) and (123) peaks appeared to have had similar intensities.18 However, intensity measurements using single domain samples are prone to error, as they are very sensitive to the exact orientation of the single crystal, making it impossible to unequivocally rule out the m
m, based on a single crystal diffraction study where (321) and (123) peaks appeared to have had similar intensities.18 However, intensity measurements using single domain samples are prone to error, as they are very sensitive to the exact orientation of the single crystal, making it impossible to unequivocally rule out the m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) Laue class. The triple network cubic phase was previously assigned the Im
Laue class. The triple network cubic phase was previously assigned the Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group on the assumption that the structure is achiral and liquid crystals normally adopt the space group of the highest symmetry compatible with the observed extinctions. With the new experimental evidence that the phase is in fact chiral, the phase is most likely to also possess a chiral space group symmetry instead, i.e., I23, I213 or I432.
m space group on the assumption that the structure is achiral and liquid crystals normally adopt the space group of the highest symmetry compatible with the observed extinctions. With the new experimental evidence that the phase is in fact chiral, the phase is most likely to also possess a chiral space group symmetry instead, i.e., I23, I213 or I432.
Inner and outer networks
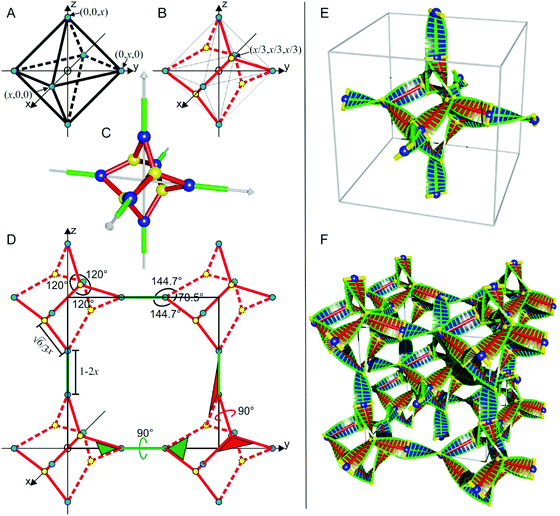
We will discuss the inner and outer networks first, which should be exactly the same apart from a translation by (1/2, 1/2, 1/2) between them.In the outer network of the previous model, there are 6 junction points around the origin of the lattice, at (±x, 0, 0), (0, ±x, 0) and (0, 0, ±x), respectively, forming an octahedron (Fig. 2A). Neighbouring octahedra are connected between their closest corners, e.g., (x, 0, 0) and (1 − x, 0, 0), with a segment along x, y or z edges of the unit cell. The main problem with such a network is that the junctions (junction points coloured blue, Fig. 2A) are 5-ways,22 and the segments connected are not coplanar, meaning that there is no common direction of molecules at the point of merger of all confluent segments.
The modification of the inner and outer networks that we have now adopted is to change the 5-way junctions to 3-way ones. To achieve this, we have added extra 3-way planar junctions at the centre of every other triangular face of the octahedron, i.e., at (x/3, x/3, x/3) (yellow in Fig. 2B and C). These are now connected to the blue junctions at the apices of the triangle, i.e., at (x, 0, 0), (0, x, 0) and (0, 0, x). These connections replace the previous direct links between the apices of the octahedron, making now the blue apex junctions also 3-way planar, instead of 5-way non-planar. The rotational symmetry along the x-axis must now be reduced from 4-fold to 2-fold. This rules out the space group I432. This is also in line with the fact that a segment with twisting molecular rafts possesses 2-fold, not 4-fold symmetry. The coordinates of the four face-centre (yellow) junctions on the outer network are thus (x/3, x/3, x/3), (x/3, −x/3, −x/3), (−x/3, x/3, −x/3), and (−x/3, −x/3, x/3), respectively. The inner network is obtained from the outer one by simple translation by (1/2, 1/2, 1/2). A 3D interactive model of the new inner network is available at https://materials.dept.shef.ac.uk/inner.html. The new inner/outer networks are compatible only with the space group symmetry I23, and hereafter we will refer to the chiral bicontinuous cubic phase as the I23 cubic phase.
In the new inner/outer networks, the yellow junctions (Fig. 2B, C and E) have 3-fold symmetry, as stated above, and the angles between the segments are all 120°. The blue junctions at the apices have a lower symmetry, with the angles between segments of 144.7°, 70.5° and 144.7° (Fig. 2D). There are also two kinds of segments, those from an apex to a face centre of the octahedron (coloured red in Fig. 2E), and those from an apex to an apex of a neighbouring octahedron (coloured green). The dihedral angle between the junction planes at the ends of segments of both kinds turns out to be the same, 90° (Fig. 2D). Assuming the dihedral angle is proportional to segment length, the lengths of the two segments, (1 − 2x) and 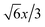 , should be the same too. Consequently,
, should be the same too. Consequently, 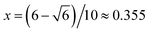 and the segment length ≈0.290aI23. Using the previous lattice parameters of the chiral cubic phase, the length of the segment ranges from 4.5–5.2 nm, consisting of 10–12 molecular rafts, assuming the distance between successive rafts is 0.45 nm, as found experimentally in most polycatenar cubic and columnar phases. This gives a twist angle between neighbouring rafts of 7.5–9°, very similar to that observed in the achiral DG Ia
and the segment length ≈0.290aI23. Using the previous lattice parameters of the chiral cubic phase, the length of the segment ranges from 4.5–5.2 nm, consisting of 10–12 molecular rafts, assuming the distance between successive rafts is 0.45 nm, as found experimentally in most polycatenar cubic and columnar phases. This gives a twist angle between neighbouring rafts of 7.5–9°, very similar to that observed in the achiral DG Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase (∼8°) and SmQ phase (9–10°). In Fig. 2D, a twisting ribbon is placed on each segment of the network showing the changing direction of molecules along it. The interactive 3D model can be viewed at https://materials.dept.shef.ac.uk/inner%20with%20ribbons.html. If we try to keep the twist angle between neighbouring rafts the same, we can in fact derive that the ratio between the lattice parameters of the two phases should be aI23/aIa
d phase (∼8°) and SmQ phase (9–10°). In Fig. 2D, a twisting ribbon is placed on each segment of the network showing the changing direction of molecules along it. The interactive 3D model can be viewed at https://materials.dept.shef.ac.uk/inner%20with%20ribbons.html. If we try to keep the twist angle between neighbouring rafts the same, we can in fact derive that the ratio between the lattice parameters of the two phases should be aI23/aIa![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d = 1.56, while experimentally, when one compound shows both phases, the ratio has been measured as ∼1.53 at the transition temperature.14,15,36,38
d = 1.56, while experimentally, when one compound shows both phases, the ratio has been measured as ∼1.53 at the transition temperature.14,15,36,38
Therefore, we have a new model of inner and outer networks, where all junctions are 3-way planar, all segments have the same length, with the same end-to-end twist angle of 90°, and with the twist angle between successive rafts being similar to that observed in other bicontinuous phases. The inner/outer networks are compatible with the space group symmetry I23, but not with the other two candidate space groups, I213 or I432. Different views of the inner and outer networks are shown in Fig. S2 and S3 (ESI†).
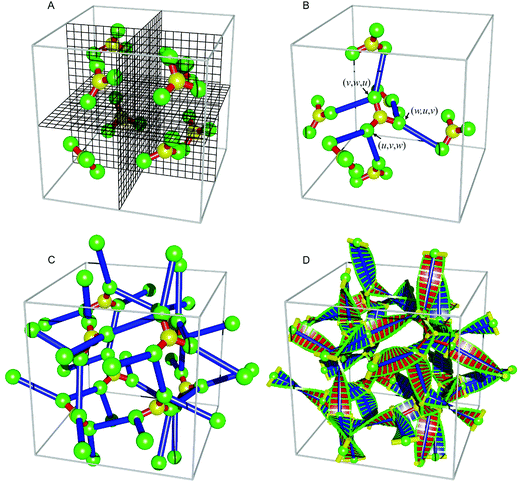
Middle network
Next, we attempt to construct a new middle network, under the assumption that it should have the same I23 space group symmetry. Unfortunately, previous models of the middle network22,23 are incompatible with the I23 symmetry, if the chirality of the segments is considered. As the previous middle network has only 3-way coplanar junctions, it is assumed the new lower symmetry network would also contain only 3-way planar junctions. Starting with a junction point at a general position (u,v,w) (Wyckoff position f), there are 24 equivalent points in the unit cell and all of them should be on the middle network. The cubic unit cell can be divided into 8 sub-cubes by three planes normal to x-, y- and z-axes through its body centre (Fig. 3A). Assuming 0.5 > u > v > w > 0.0, there are three equivalent junction points, at (u,v,w), (w,u,v), and (v,w,u), in the sub-cube bounded by (0,0,0) and (0.5,0.5,0.5) – coloured green in Fig. 3. The three junction points are related by a 3-fold axis along the body diagonal, and so are their equivalents in other sub-cubes. Direct connection between the three junction points within each sub-cube is not an option as that would not make all three segments joined at each junction coplanar.In view of the above, we take the natural step to connect the nearest two junction points in neighbouring sub-cubes (blue segments, Fig. 3B). It turns out, due to the I23 symmetry of the phase, that each junction point has two nearest neighbours. For example, the nearest neighbours of the junction point at (u, v, w) are at (1/2 + w, 1/2 − u, 1/2 − v) and (1/2 − v, 1/2 − w, −1/2 + u). This leaves one more segment to be added to each junction point, to comply with the principle that all network junctions are 3-way coplanar. This can be achieved by adding another eight junction points to the network, placed on the body diagonal of the unit cell, at ((u + v + w)/3, (u + v + w)/3, (u + v + w)/3) (Wyckoff positions c) and the symmetrical equivalents (yellow junctions in Fig. 3). Thus, in each sub-cube, there is a 3-way coplanar junction on the body diagonal connected to the other three, with 3-fold symmetry, i.e., with the same segment length and 120° angle between segments (red segments in Fig. 3B). Each of the three green junctions in the sub-cube has one (red) segment joining it to the yellow junction on the body diagonal, and the other two (blue) segments connecting it to the nearest junctions in neighbouring sub-cubes.
The requirement that the segments at junction points must be co-planar puts limitations on the values that coordinates u, v and w can take. Once this condition is satisfied, a network is obtained with two different segment lengths. We have then added an additional condition that the dihedral angle between junction planes is proportional to the length of the segment joining them. Numerical calculations show that all such conditions can be satisfied with (u, v, w) = (0.410, 0.233, 0.233). The new middle network is shown in Fig. 3C, along with its “ribbon” view, which shows how molecular orientation changes along each segment and in the network as a whole (Fig. 3D) – see also the 3D models at https://materials.dept.shef.ac.uk/middle%20network.html and https://materials.dept.shef.ac.uk/middle%20network%20ribbon.html. Different views of the middle network are shown in Fig. S4 (ESI†).
The new middle network therefore contains 8 yellow and 24 green junctions in a unit cell. The former can be generated through symmetry operations of the I23 space group, starting with (0.292, 0.292, 0.292) (Wyckoff position c). Each connects three coplanar segments of length 0.145aI23. The 24 green junctions are at (0.410, 0.233, 0.233) and its symmetrical equivalent (Wyckoff position f). Each junction joins together one shorter segment (0.145aI23) with two longer segments (0.355aI23). In total, there are 24 shorter (red) segments and 24 longer (blue) segments. The cumulative twist angle of the shorter segments is 44.6°, and that of the longer segments is 109.3°; these correspond to a twist of 308.2° per unit cell length aI23. In comparison, for the inner and outer networks, the twist is 310.5° per aI23, i.e., there is less than 1% difference between the two. Using the experimental unit cell dimension, we can put 5–6 and 12–14 molecular rafts on the shorter and longer segments, respectively; again, this converts to ∼7.5–9° twist between successive molecular rafts.
Properties of triple networks
The total length of the network segments in the new model of the chiral bicontinuous cubic phase is calculated as 20.68aI23. For comparison, for the double gyroid Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase, the total length of the network is 8.485aIa3d. As in both cases, the length of the network should be proportional to the number of molecules in the unit cell and hence its volume, thus we have
d phase, the total length of the network is 8.485aIa3d. As in both cases, the length of the network should be proportional to the number of molecules in the unit cell and hence its volume, thus we haveConsequently the ratio aI23/aIa3d is expected to be 1.56. This is extremely satisfactory as exactly the same ratio was derived in the previous section by assuming the same twist per unit length in the two structures, and very close to the experimentally determined values of ∼1.53.
The complete new model of all three networks is shown in Fig. 4, with the segments represented both as simple bars and as ribbons describing the molecular twist (different views of the complete model are shown in Fig. S5, ESI†). A close inspection of the model shows that the three networks fit nicely around each other, and the space in between is compatible with the size of the molecules.
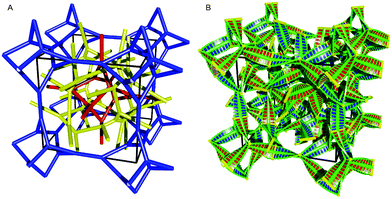 | ||
| Fig. 4 (A) New network model of the triple network cubic phase. (B) All network segments are represented by twisted ribbons showing changing molecular orientation. | ||
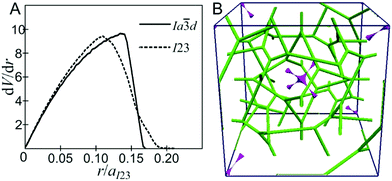
In the self-assembly of thermotropic LCs, space filling plays a much greater role than in lyotropics, as the presence of solvent in lyotropics makes it easier to fill interstices furthest away from, e.g., the aromatic/aliphatic interface. This is believed to be one of the reasons behind the prevalence of the DG Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d over other Cubbi phases in thermotropic LCs. We have previously used dV/dr curves to quantify such space filling properties of LC compounds in different phases. Here, V(r) is that part of the unit cell volume that is within a distance r of the closest network segment.11,12 For infinite unbranched parallel and equidistant cylinders, as in the hexagonal columnar (Colh) phase, dV/dr ∝ r, i.e., an ascending linear function, until the widening cylinders of radius r touch; dV/dr then starts dropping steeply to zero at which point all space is filled and V = Vcell. For branched cylinders, the slope of the initial ascent slows down as r increases. We calculated the dV/dr curve for the I23 phase based on the above model and the plot is shown in Fig. 5A along with those for the DG (Ia
d over other Cubbi phases in thermotropic LCs. We have previously used dV/dr curves to quantify such space filling properties of LC compounds in different phases. Here, V(r) is that part of the unit cell volume that is within a distance r of the closest network segment.11,12 For infinite unbranched parallel and equidistant cylinders, as in the hexagonal columnar (Colh) phase, dV/dr ∝ r, i.e., an ascending linear function, until the widening cylinders of radius r touch; dV/dr then starts dropping steeply to zero at which point all space is filled and V = Vcell. For branched cylinders, the slope of the initial ascent slows down as r increases. We calculated the dV/dr curve for the I23 phase based on the above model and the plot is shown in Fig. 5A along with those for the DG (Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d) phase. Unlike dV/dr of the Ia
d) phase. Unlike dV/dr of the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase, the I23 curve has an extended tail at large r. The longest distance from the network in the I23 phase is 0.205aI23, which is significantly larger than the longest distance of ∼0.167aI23 in the Ia
d phase, the I23 curve has an extended tail at large r. The longest distance from the network in the I23 phase is 0.205aI23, which is significantly larger than the longest distance of ∼0.167aI23 in the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase (0.167aI23 = 0.255aIa3d taking aI23/aIa3d = 1.53). In Fig. 5B, the regions furthest from the networks (green) are shown in purple; they are found in the centres of the octahedra of the inner and outer networks. A slight distortion of the network(s) may be needed to improve the space filling of the I23 structure; e.g., the above dV/dr calculations do not consider the non-cylindrical nature of the network segments. However, the dV/dr curve comparison in Fig. 5A already helps explain certain experimental observations. Thus, in both ANBC-n and BABH-n series of compounds,39 it was found that the compounds with the shortest alkyl tails (smallest n) exhibit the Ia
d phase (0.167aI23 = 0.255aIa3d taking aI23/aIa3d = 1.53). In Fig. 5B, the regions furthest from the networks (green) are shown in purple; they are found in the centres of the octahedra of the inner and outer networks. A slight distortion of the network(s) may be needed to improve the space filling of the I23 structure; e.g., the above dV/dr calculations do not consider the non-cylindrical nature of the network segments. However, the dV/dr curve comparison in Fig. 5A already helps explain certain experimental observations. Thus, in both ANBC-n and BABH-n series of compounds,39 it was found that the compounds with the shortest alkyl tails (smallest n) exhibit the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase, while those with longer chains show “Im
d phase, while those with longer chains show “Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m” (now I23). Keeping in mind that r = 0 at the centre of the rod-like molecules and that it is largest at the chain ends, this observation is consistent with short chains being unable to reach the octahedral centre voids in the I23 lattice. Furthermore, where both phases are seen in the same compound, it is Ia
m” (now I23). Keeping in mind that r = 0 at the centre of the rod-like molecules and that it is largest at the chain ends, this observation is consistent with short chains being unable to reach the octahedral centre voids in the I23 lattice. Furthermore, where both phases are seen in the same compound, it is Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d that is most often found at higher temperatures, even though examples of a reverse phase sequence are also known.18,36 This is again consistent with the chains adopting shorter and wider conformations at high T, better suited to the high-peak-short-tail dV/dr curve of Ia
d that is most often found at higher temperatures, even though examples of a reverse phase sequence are also known.18,36 This is again consistent with the chains adopting shorter and wider conformations at high T, better suited to the high-peak-short-tail dV/dr curve of Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d. However, explaining the re-emergence of Ia
d. However, explaining the re-emergence of Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d for very long chains may not be so straightforward, but again the preference for more coiled conformations of these long chains is likely to favour dV/dr of Ia
d for very long chains may not be so straightforward, but again the preference for more coiled conformations of these long chains is likely to favour dV/dr of Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d. We recognize that the dV/dr model will not be sufficient to explain all experimental observations.
d. We recognize that the dV/dr model will not be sufficient to explain all experimental observations.
Electron density map and chirality of the networks
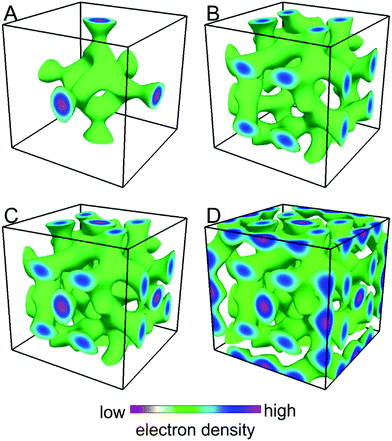
While mathematically, the new model of the I23 phase is very satisfactory on many counts, it also has to be tested for compatibility with the observed X-ray intensities. For centrosymmetric LC structures, an electron density map is usually constructed using diffraction amplitudes and the phase angle choices of only 0 or π being decided by trial and error. However, I23 is a non-centrosymmetric space group, meaning that the phase of a diffraction peak can be of any value between 0 and 2π. Another difficulty is that for I23, a general (hkl) peak with h ≠ k ≠ l is only cyclically permutable: it is equivalent to (klh) and (lhk) but not to (hlk), (lkh) and (khl) peaks. Consequently, even though the (hkl) and (lkh) peaks coincide in a powder diffractogram, their intensities and corresponding structure factor phases are different. In order to circumvent these two problems, we have calculated the diffraction intensities and phases for each observed peak from the Fourier transform of the model, where the electron density of a point in the unit cell is chosen to be a higher constant value if it is within a certain distance of the network segments, and a lower constant value if it is not (ESI†). The distance is chosen so that the volume ratio of the high electron density regions in the unit cell matches that of the rigid aromatic core in the molecule. After that, we have simply taken from the simulation the intensity ratio of (hkl) and (lkh) peaks, and the phase angle of each peak, combining them with experimentally observed diffraction intensities (data previously published)23 to reconstruct the electron density map shown in Fig. 6. The three networks can be easily identified, and they are almost exactly as predicted by the mathematical model. This is extremely satisfactory as no additional optimization steps were used to “beautify” the map. The largest discrepancy is that there is a certain waviness of the columnar segments connecting the “octahedra” in the inner and outer networks. This feature could be attributed to some variation in the number of molecules in the rafts along the segment, or simply to imperfect estimates of hkl/lkh intensity ratios or of the phase angles. Further optimization of the phases and hkl/lkh intensity ratios for a better reconstructed electron density map is still ongoing. The diffraction peak intensities used and their phases are listed in Table 1.| (hkl) | Intensity | Multiplicity | Phase |
|---|---|---|---|
| a The simulated (310) peak is much weaker than (301) so no (310) peak is used in the reconstruction; similarly, the (402) peak is omitted. b (321) and (312) are overlapping in the powder diffraction pattern but not equivalent to each other. The intensity ratio between the two is taken to be the same as from the simulation. | |||
| (211) | 0.1 | 24 | −0.97π |
| (301)a | 1.2 | 12 | 0 |
| (222) | 7.7 | 8 | −0.24π |
| (321)b | 27.9 | 24 | −0.91π |
| (312)b | 61.7 | 24 | −0.59π |
| (400) | 100 | 6 | 0 |
| (411) | 2.1 | 24 | −0.81π |
| (330) | 2.3 | 12 | 0 |
| (420)a | 21.2 | 12 | 0 |
| (422) | 0.9 | 24 | −0.66π |
While the chirality of the middle network described above is left-handed, a right-handed version of the network can be generated by the application of a mirror symmetry operation, e.g., by switching the y- and z-coordinates of all junction points. In fact, as the y and z components of the starting point (0.410, 0.233, 0.233) are equal, a simple change of connections between the junctions is all that is needed. Regarding the inner and outer networks, since the dihedral angles around all junctions are 90° (and +90° is equivalent to −90°), their chirality can be changed from left- to right-handed by merely changing the twist sense of molecular rafts in each segment, while the network itself is kept intact. However, the body centred cubic symmetry of the phase requires that the inner and outer networks must be identical in all respects, including chirality.
As the chirality of the inner and outer networks is not predetermined by the networks themselves, their preferred chirality must be decided by their interaction with the intercalated chiral middle network. There are indications that all three networks have the same hand. For example, it can be shown that the combined length of the inner and outer networks in a unit cell is 8.697a, while that of the middle network alone is 11.985a. So, the difference between the middle and inner + outer networks is 3.288a, or 15.9% of the total length of all network segments. Thus, while it is the middle network that will determine the sign of the overall optical activity, the magnitude of the effect would be very different, i.e., more than 6 times stronger, in the case of homochiral, compared to the antichiral case. While we have no theoretical values of optical activity with which to compare those observed, qualitatively, we have noted that in similar dithiophene-based polycatenar compounds, optical rotation in the I23 phase is comparable to that in the fully isochiral Sm-Q phase.31 This makes a case for the isochirality of all three networks in the I23 phase. However, a scenario where the middle network has chirality opposite to that of the other two networks cannot be ruled out completely at this stage. Further work is needed to obtain fully conclusive proof of isochirality.
Previously, it has been observed that on transition from chiral isotropic (Iso*) phase to the triple network cubic phase, no obvious change in material optical rotation power is observed.23 If, as suggested by our model, in the I23 phase, all the networks in each chiral domain are enantiopure, i.e., not a mixture of left- and right, then this should be true for the Iso* phase as well.
The proposed I23 space group, as mentioned above, belongs to Laue class m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) instead of the previously assigned m
instead of the previously assigned m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. In order to confirm or disprove this, a single crystal (single LC domain) diffraction experiment will be needed to check whether or not a general (hkl) diffraction peak is equivalent to, i.e., has the same intensity as, its (lkh) counterpart. The quality of the single crystal has to be high and it is probably best grown from an enantiomer of an intrinsically chiral compound, so that the possible coexistence of twins/domains of different chiralities can be avoided.
m. In order to confirm or disprove this, a single crystal (single LC domain) diffraction experiment will be needed to check whether or not a general (hkl) diffraction peak is equivalent to, i.e., has the same intensity as, its (lkh) counterpart. The quality of the single crystal has to be high and it is probably best grown from an enantiomer of an intrinsically chiral compound, so that the possible coexistence of twins/domains of different chiralities can be avoided.
Conclusions
A new model for the chiral bicontinuous cubic phase formed by rod-like polycatenar LC molecules has been proposed. It consists of three interpenetrating networks with a chiral space group I23. Like in all other bicontinuous phases of such compounds, cubic or non-cubic, the columnar network segments are helical, formed by stacking of transverse-lying rafts of 3–4 mutually parallel rods, twisted along the segment axis. All junctions in the three networks of this phase are 3-way and coplanar, as in the double gyroid Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase. Smooth confluence at the junctions necessitates chirality matching of all three adjoining segments, thus propagating homochirality throughout the infinite network. The twist angle between successive molecular rafts is found to be very similar to that in Ia
d phase. Smooth confluence at the junctions necessitates chirality matching of all three adjoining segments, thus propagating homochirality throughout the infinite network. The twist angle between successive molecular rafts is found to be very similar to that in Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d and SmQ phases. The model can easily explain the ratio between the unit cell parameters of the triple and double network Cubbi phases, and is supported by reconstructed electron density maps on the basis of the I23 space group. All three networks in the I23 phase appear to be homochiral.
d and SmQ phases. The model can easily explain the ratio between the unit cell parameters of the triple and double network Cubbi phases, and is supported by reconstructed electron density maps on the basis of the I23 space group. All three networks in the I23 phase appear to be homochiral.
The results provide a better understanding of the formation of bicontinuous phases from chiral and achiral LC compounds, and of chirality synchronization and amplification in general. Due to the close relation between I23 and the recently discovered spontaneously chiral isotropic liquid phase Iso*, the current results bring us a step closer to understanding this intriguing new state of matter with long-range chirality but without positional or orientational order. The results also suggest that similar spontaneous chirality formation behaviour may exist for other network-based mesophases, and further work in this direction is currently being explored.
The fact that the three networks of the I23 structure are likely to be homochiral makes this phase a good candidate for circularly polarized luminescence materials. The addition of a small amount of chiral dopant will be able to ensure the homochirality of the entire film, without the need for stereospecific synthesis. Moreover, no alignment procedure will be required, and problems with light scattering will be avoided, as the material is isotropic and non-birefringent due to its cubic symmetry. The phase could also be used as a template for chiral porous ceramics.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by EPSRC (EP-T003294, EP-P002250), the 111 Project 2.0 of China (BP2018008), and the National Natural Science Foundation of China (No. 21674099).References
-
G. Ungar, F. Liu and X. B. Zeng, in Handbook of Liquid Crystals, ed. J. W. Goodby, P. J. Collings, T. Kato, C. Tschierske, H. Gleeson and P. Raynes, Wiley-VCH, Weinheim, Germany, 2nd edn, 2014, ch. 7, vol. 5 Search PubMed
.
- G. W. Gray, B. Jones and F. Marson, Mesomorphism and Chemical Constitution. Part VIII. The Effect of 3′-Substituents on the Mesomorphism of the 4′-n-Alkoxydiphenyl-4-Carboxylic Acids and Their Alkyl Esters, J. Chem. Soc., 1957, 393–401 RSC
.
- D. Demus, G. Kunicke, J. Neelsen and H. Sachmann, Die Polymorphie der Kristallin-Fluessigen Modifikationen in der Homogoen Reihe der 4′n-Alkoxy-3′-Nitrodiphenyl-4-Carbonsaeuren, Z. Naturforsch., 1968, 23a, 84–90 Search PubMed
.
- J. Seddon, Lyotropic Phase Behaviour of Biological Amphiphiles, Ber. Bunsen-Ges., 1996, 100, 380–393 CrossRef CAS
.
- S. T. Hyde, Bicontinuous Structures in Lyotropic Liquid Crystals and Crystalline Hyperbolic Surfaces, Curr. Opin. Solid State Mater. Sci., 1996, 1, 653–662 CrossRef CAS
.
- S. T. Hyde and G. E. Schroder, Novel Surfactant Mesostructural Topologies: Between Lamellae and Columnar (Hexagonal) Forms, Curr. Opin. Colloid Interface Sci., 2003, 8, 5–14 CrossRef CAS
.
- A. J. Meuler, M. A. Hillmyer and F. S. Bates, Ordered Network Mesostructures in Block Polymer Materials, Macromolecules, 2009, 42(19), 7221–7250 CrossRef CAS
.
- L. Han and S. Che, An Overview of Materials with Triply Periodic Minimal Surfaces and Related Geometry: From Biological Structures to Self-Assembled Systems, Adv. Mater., 2018, 30, 1705708 CrossRef PubMed
.
- S. Diele, On Thermotropic Cubic Mesophases, Curr. Opin. Colloid Interface Sci., 2002, 7, 333–342 CrossRef CAS
.
- M. Clerc and E. Dubois-Violette, X-ray-Scattering by Bicontinuous Cubic Phases, J. Phys. II, 1994, 4, 275–286 CrossRef
.
- X. B. Zeng, M. Prehm, G. Ungar, C. Tschierske and F. Liu, Formation of a Double Diamond Cubic Phase by Thermotropic Liquid Crystalline Self-Assembly of Bundled Bolaamphiphiles, Angew. Chem., Int. Ed., 2016, 55, 8324–8327 CrossRef CAS PubMed
.
- X. B. Zeng, S. Poppe, A. Lehmann, M. Prehm, C. L. Chen, F. Liu, H. J. Lu, G. Ungar and C. Tschierske, A Self-Assembled Bicontinuous Cubic Phase with Single Diamond Network, Angew. Chem., Int. Ed., 2019, 58, 7375–7379 CrossRef CAS PubMed
.
- A. M. Levelut and Y. Fang, Structural Study of the Lamellar to Columnar Transition in Thermotropic Liquid Crystals: The Thermotropic Cubic Phase of Some Phasmidic Molecules, J. Phys., Colloq., 1990, 51, 229–236 CrossRef
.
- A. M. Levelut and M. Clerc, Structural investigations on ‘Smectic D’ and Related Mesophases. Liquid Crystals, Liq. Cryst., 1998, 24, 105–115 CrossRef CAS
.
- S. Kutsumizu, K. Morita, S. Yano and S. Nojima, Cubic Phases of Binary Systems of 4′-N-Tetradecyloxy-3′-Nitrobiphenyl-4-Carboxylic Acid (ANBC-14)-N-Alkane. Liquid Crystals, Liq. Cryst., 2002, 29, 1459–1468 CrossRef CAS
.
- K. Saito and M. Sorai, Quasi-binary picture of thermotropic liquid crystals and its application to cubic mesophases, Chem. Phys. Lett., 2002, 366, 56–61 CrossRef CAS
.
- M. Impéror-Clerc, Thermotropic Cubic Mesophases, Curr. Opin. Colloid Interface Sci., 2005, 9, 370–376 CrossRef
.
- X. B. Zeng, G. Ungar and M. Imperor-Clerc, A Triple-Network Tricontinuous Cubic Liquid Crystal, Nat. Mater., 2005, 4, 562–567 CrossRef CAS PubMed
.
- X. B. Zeng, L. Cseh, G. H. Mehl and G. Ungar, Testing the Triple Network Structure of The Cubic Im
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) mI Phase by Isomorphous Replacement and Model Refinement, J. Mater. Chem., 2008, 18, 2953–2961 RSC
mI Phase by Isomorphous Replacement and Model Refinement, J. Mater. Chem., 2008, 18, 2953–2961 RSC .
- K. Saito, Y. Yamamura and S. Kutsumizu, Possible Formation of Multicontinuous Structures by Rodlike Particles, J. Phys. Soc. Jpn., 2008, 77, 093601 CrossRef
.
- K. Ozawa, Y. Yamamura, S. Yasuzuka, H. Mori, S. Kutsumizu and K. Saito, Coexistence of Two Aggregation
Modes in Exotic Liquid-Crystalline Superstructure: Systematic Maximum Entropy Analysis for Cubic Mesogen, 1,2-Bis(4′-n-alkoxybenzoyl)hydrazine [BABH(n)], J. Phys. Chem. B, 2008, 112, 12179–12181 CrossRef CAS PubMed
.
- K. Saito, Y. Yamamura, Y. Miwa and S. Kutsumizu, A Structural Model of The Chiral “Im3m” Cubic Phase, Phys. Chem. Chem. Phys., 2016, 18, 3280–3284 RSC
.
- C. Dressel, F. Liu, M. Prehm, X. B. Zeng, G. Ungar and C. Tschierske, Dynamic Mirror-Symmetry Breaking in Bicontinuous Cubic Phases, Angew. Chem., Int. Ed., 2014, 126, 13331–13336 CrossRef
.
- P. Goering, S. Diele, S. Fischer, A. Wiegeleben, G. Pelzl, H. Stegemeyer and W. Thyen,, The Cubic Mesophase of Analogous Chiral and Achiral Hydrazine Derivatives, Liq. Cryst., 1998, 25, 467–474 CrossRef
.
- Y. Takanishi, T. Ogasawara, A. Yoshizawa, J. Umezawa, T. Kusumoto, T. Hiyama, K. Ishikawa and H. Takezoe, Structures in Optically Isotropic and Bluish Colored Cubic Phases Formed by Enantiomeric Association in an (R,S) Dichiral Compound and a Stereoisomeric (R,R) and (S,S) Mixture, J. Mater. Chem., 2002, 12, 1325–1330 RSC
.
- M. Vogrin, N. Vaupotic, M. M. Wojcik, J. Mieczkowski, K. Madrak, D. Pociecha and E. Gorecka, Thermotropic Cubic and Tetragonal Phases Made of Rod-Like Molecules, Phys. Chem. Chem. Phys., 2014, 16, 16067–16074 RSC
.
- A. M. Levelut, C. Germain, P. Keller, L. Liebert and J. Billard, Two New Mesophases in a Chiral Compound, J. Phys., 1983, 44, 623–629 CrossRef CAS
.
- A. M. Levelut, E. Hallouin, D. Bennemann, G. Heppke and D. Loetzsch, The Smectic Q phase, a Crystal of Twist Grain Boundaries with Smectic Order, J. Phys. II, 1997, 7, 981–1000 CrossRef CAS
.
- B. Pansu, Y. Nastishin, M. Imperor-Clerc, M. Veber and H. T. Nguyen, New Investigation on the Tetragonal Liquid-Crystalline Phase or SmQ, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 15, 225–230 CrossRef CAS PubMed
.
- M. Yoneya, Toward Rational Design of Complex Nanostructured Liquid Crystals, Chem. Rec., 2011, 11, 66–76 CrossRef CAS PubMed
.
- H. J. Lu, X. B. Zeng, G. Ungar, C. Dressel and C. Tschierske, The Solution of the Puzzle of Smectic-Q: The Phase Structure and the Origin of Spontaneous Chirality, Angew. Chem., Int. Ed., 2018, 57, 2835–2840 CrossRef CAS PubMed
.
- D. Gillon and A. Skoulios,, Molecular Model for the “Smectic-D” Mesophase, Europhys. Lett., 1987, 3, 79–85 CrossRef
.
- Y. Nakazawa, Y. Yammura, S. Kutsumizu and K. Saito, Molecular Mechanism Responsible for Reentrance to Ia
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d Gyroid Phase in Cubic Mesogen BABH(n), J. Phys. Soc. Jpn., 2012, 81, 094601 CrossRef
d Gyroid Phase in Cubic Mesogen BABH(n), J. Phys. Soc. Jpn., 2012, 81, 094601 CrossRef .
- S. Diele, H. Sackmann and P. Brand,, X-ray Diffraction and Polymorphism of Smectic Liquid-Crystals. II. D and E Modifications, Mol. Cryst. Liq. Cryst., 1972, 17(2), 163–169 CrossRef CAS
.
- G. Etherington, A. J. Leadbetter, X. J. Wang, G. W. Gray and A. Tajbakhsh, Structure of the Smectic D-Phase, Liq. Cryst., 1986, 1(3), 209–214 CrossRef CAS
.
- S. Kutsumizu, H. Mori, M. Fukatami, S. Naito, K. Sakajiri and K. Saito, Cubic Phase Formation and Interplay between Alkyl Chains and Hydrogen Bonds in 1,2-Bis(4′-n-alkoxybenzoyl)hydrazines (BABH-n), Chem. Mater., 2008, 20, 3675–3687 CrossRef CAS
.
- C. Dressel, T. Reppe, M. Prehm, M. Brautzsch and C. Tschierske, Isotropic Liquids of Achiral Molecules, Nat. Chem., 2014, 6, 971–977 CrossRef CAS PubMed
.
- S. Kutsumizu, K. Morita, T. Ichikawa, S. Yano, S. Nojima and T. Yamaguchi, Cubic phases of 4′-n-alkoxy-3′-nitrobiphenyl-4-carboxylic acids (ANBC-n), Liq. Cryst., 2010, 29, 1447–1458 CrossRef
.
- S. Kutsumizu, H. Mori, M. Fukatami and K. Saito, X-ray Studies of the Self-Organized Structure Formed by 1,2-bis(4′-n-Alkoxybenzoyl)Hydrazine (BABH-n) Homologues. 1. Ia
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d-Gyroid Structure, J. Appl. Crystallogr., 2007, 40, S279–S282 CrossRef CAS
d-Gyroid Structure, J. Appl. Crystallogr., 2007, 40, S279–S282 CrossRef CAS .
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0tc00447b |
| This journal is © The Royal Society of Chemistry 2020 |