The role of intermolecular forces in ionic reactions: the solvent effect, ion-pairing, aggregates and structured environment
Josefredo R.
Pliego
Jr.

Departamento de Ciências Naturais, Universidade Federal de São João del-Rei, 36301-160, São João del-Rei, MG, Brazil. E-mail: pliego@ufsj.edu.br
First published on 20th January 2021
Abstract
The environment enclosing an ionic species has a critical effect on its reactivity. In a more general sense, medium effects are not limited to the solvent, but involve the counter ion effect (ion pairing), formation of larger aggregates and structured environment as provided by the host in the case of host–guest complexes. In this review, a general view of the medium effect on anion-molecule reactions is presented. Nucleophilic substitution reactions of aliphatic (SN2) and aromatic (SNAr) systems, as well as elimination reactions (E2), are the focus of the discussion. In particular, nucleophilic fluorination with KF, CsF and tetraalkylammonium fluoride was used as the main model, because of the importance of this kind of reaction and the recent advances in the study of these systems. The solvent effect, ion pairing, formation of aggregates and formation of complexes with crown ethers, cryptands and calixarenes are discussed. For a deeper insight into the medium effect, many results of reliable theoretical calculations in close agreement with experiments were chosen as examples.
1. Introduction
The ability to control chemical reactions has been a long-standing goal in chemistry. The solvent effect is a very important aspect of chemical reactivity and has been widely used by chemists for controlling reaction rate and selectivity.1 The important role of solvents in chemical reactions was first described in the XIX century and we can single out the work of Menschutkin on the reaction of trialkyl amines with alkyl halides. In his study, a considerable solvent effect was observed on the reaction rate, implicating that chemical reactivity cannot be dissociated from the reaction medium.1In the sixties, a set of studies by Parker and co-workers established that solvents with a high dielectric constant and dipole moment can produce a wide range of reactivities on anion-molecule SN2 and SNAr reactions.2 Indeed, a high rate acceleration effect is observed when going from protic solvents such as methanol to dipolar aprotic solvents (or non-hydrogen-bond donor solvents) such as dimethyl sulfoxide (DMSO). This effect results from the ability of protic solvents to solvate anions more efficiently than dipolar aprotic ones. Consequently, protic solvents lead to higher solvent-induced free energy barriers.3–5
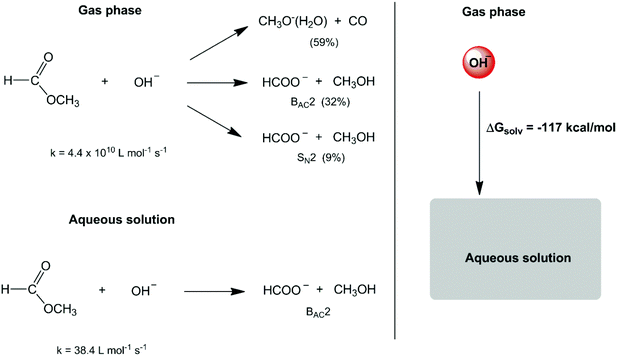
In the second half of the XX century, the development of gas-phase ion chemistry has provided important information on intrinsic (or non-solvated) ion reactivity.6 At the same time, the evolution of computational theoretical chemistry has allowed detailed analysis of the transition state structure and energetics in the gas phase and in the solution phase.7–10 These studies have emphasized a much more substantial role of solvents in chemical reactions. A dramatic example is the reactivity of small anions such as the hydroxide ion. The reaction of this anion with methyl formate in the gas phase leads to three reaction pathways (Scheme 1),11,12 with an overall rate constant of 4.4 × 1010 L mol−1 s−1. In water solvent, the high solvation (hydration free energy of −117.4 kcal mol−1)13 and stabilization of this intrinsically reactive hydroxide ion makes the respective rate constant decrease to 38.4 L mol−1 s−1 (a factor of 109) and only one reaction mechanism is observed.14,15
It is worth observing that the high absolute value of the hydration free energy of the hydroxide ion, dominated by electrostatic interactions, is as large as the energy of a strong chemical bond. For example, the bond dissociation energy of the C–O bond of dimethyl ether is 80 kcal mol−1.16 This fact explains why the medium surrounding an ionic species can produce a substantial effect on the reactions.
For understanding the ability of the solvent to interact with the solute, different parameters have been used, such as the dielectric constant, the dipole moment, the solvent donor number17 and the solvent acceptor number,18 to name the most important.1 Nevertheless, it is the solvation free energy that determines the overall solute–solvent interaction19,20 and determines the influence of the solvent on the thermodynamics and kinetics of chemical reactions.21,22 Thus, this property is emphasized in this review. At this point, it is important to distinguish between the solvation phenomenon, which is a microscopic interaction of the solute with the medium, and the solvent effect, which is a macroscopically observed effect.
In many situations, the surrounding medium is not limited to the solvent. For example, with the decrease of the dielectric constant of a solvent, formation of ion pairs can become substantial.23 Even larger aggregates such as dimers, trimers and tetramers can be formed. The interaction with the counter-ion can produce an important effect on the reactivity. For example, the competition between C and O-alkylation of the phenoxide ion by allyl chloride has an important counter-ion influence, which participate in the transition state assisting the leaving chloride ion.24 In addition, if an aprotic solvent has solute molecules with hydroxyl groups, an aggregation of these molecules can take place around any anionic species dissolved and change the reactivity. Some interesting examples are the aggregates formed by the fluoride ion with bulky alcohols and ureas in an aprotic solvent.25–28 Protic solvents can be more effective in dissolving inorganic salts. At the same time, high solvation can lead to small reactivity. We can think about creating a nano-structured environment for tailor-made intermolecular interactions, aimed to control the chemical reactivity. Thus, Jadhav et al. have designed a new structure based on a combination of calix[4]arene with crown ether and bulk diol able to solubilize and activate CsF for nucleophilic fluorination.29 The idea behind this review is to conduct the reader from the key concepts of the solvent effect (mainly electrostatic interactions) to the design of supramolecular structures working as transition state receptors. The author hopes that this discussion on how intermolecular forces work for modulating chemical reactivity can inspire more development in this area. Further, it is important to say that this is not a comprehensive review. Selected examples have been chosen, focusing on ionic reactions. Where possible, a quantitative comparison between theory and experiment was performed. The use of examples separating intrinsic reactivity, the solvent effect and intermolecular interactions allows better understanding of ionic reactivity. The review covers since the year 2000, although some previous key articles have also been cited.
2. Intermolecular forces and solvent effect on anion-molecule reactions
Reactions in the condensed phase are ubiquitous in organic chemistry and biochemistry. In the case of ions, the electrostatic interaction between the solute and solvent is the main contribution to the solvation free energy. The dipole moment and dielectric constant of the solvent are widely used parameters for understanding ion–solvent interactions. Thus, the dipole moment of the solvent determines the direct solute–solvent interaction in the first solvation shell, whereas dielectric constant is more related to the bulk solvation and the ability of the solvent to separate the pair of ions. However, dipole moment alone cannot differentiate the solvation ability of polar solvents such as methanol and DMSO. Molecular details are important for understanding the different solvation ability of these solvents. Thus, another set of parameters that can be useful for understanding solute–solvent electrostatic interactions are the atomic charges of the solvent. These atomic charges represent how specific parts of the solvent interact with anions or cations. In this way, it is interesting to take a brief look at atomic charges in some representative solvents to better understand these interactions. These properties are presented in Scheme 2. We should observe that there are different definitions of atomic charges and some interesting definitions are based on charges able to reproduce the electrostatic potential of the molecule.30,31 In this review, the atomic charges used in the computer simulations of liquids (OPLS force-field) were taken from ref. 32.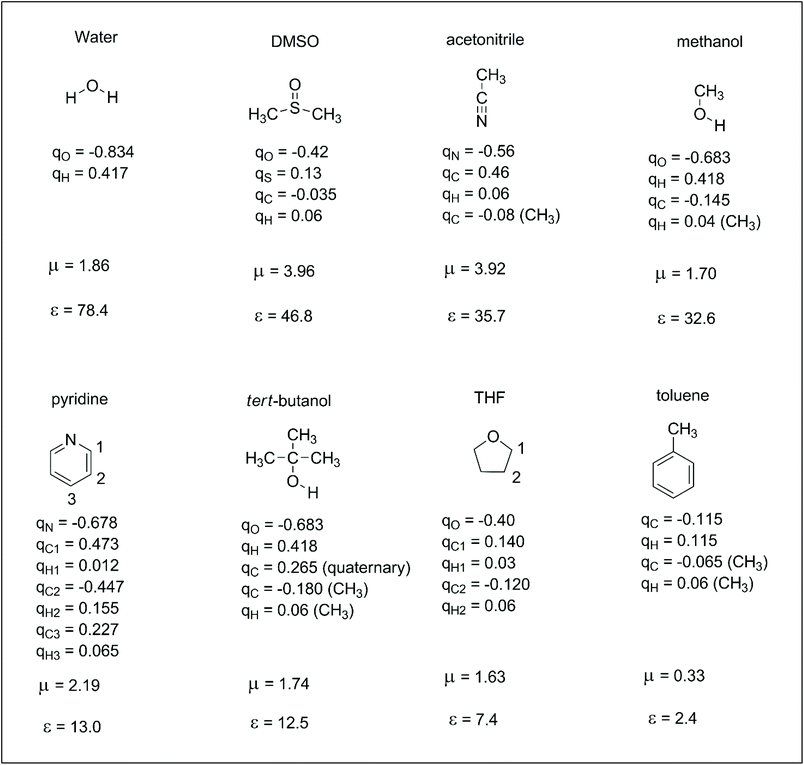 | ||
| Scheme 2 Some representative solvents with their respective atomic charges (q, in units of electron charge),32,33 dipole moment (μ, in Debye) and dielectric constant (ε).34 | ||
For comparing the relationship between the ion solvation and molecular properties of the solvent, the solvation free energies of some selected ions in four solvents are presented in Table 1. Thus, anions are much more solvated in water, although the dipole moment of DMSO is twice that of water. The explanation is based on the high positive charge in the hydrogen of water because water is a small molecule. Consequently, more water molecules are in the first solvation shell of an anion. In the same way, methanol is less able to solvate anions than water, although it also has hydroxyl groups. Acetonitrile is the least effective solvent among those presented in Table 1. Another point to observe is that small and charge centered anions are more solvated. In addition, the difference in the ΔGsolv for anions with high charge dispersion is smaller when two solvents are compared. For example, the variation of the ΔGsolv for the fluoride ion in water and DMSO is 20.6 kcal mol−1 and becomes 11.5 kcal mol−1 for the PhS− ion. Thus, a smaller variation in the solvent effect is expected for reactions involving anions with larger charge dispersion.
| ΔGsolv | ||||
|---|---|---|---|---|
| Ion | Water | Methanol | DMSO | Acetonitrile |
| a Units in kcal mol−1, 298.15 K. Data taken from ref. 13 and 35. | ||||
| F− | −116.7 | −109.2 | −96.1 | −88.4 |
| Cl− | −87.0 | −81.1 | −74.3 | −65.6 |
| Br− | −80.5 | −75.1 | −71.2 | −61.7 |
| OH− | −117.4 | −111.5 | −88.4 | — |
| CH3O− | 107.6 | −104.5 | −81.5 | — |
| CN− | −82.8 | — | −70.0 | — |
| CH3COO− | −89.8 | −81.6 | −72.1 | −64.2 |
| CH2NO2− | −88.4 | — | −71.3 | — |
| PhS− | −75.8 | — | −64.3 | — |
In the case of solvents with a lower dielectric constant, such as pyridine, tert-butanol, THF and toluene, there is considerable ion pairing and formation of larger aggregates.23 Thus, the solvation free energy of single ions is less available and the solvent effect occurs for the ion pair reaction, or even reactions involving larger aggregates. These cases will be discussed in the next section.
The kinetics of chemical reactions in the liquid phase is determined by the activation free energy in the solution phase,21 given by ΔG‡sol, which is related to the rate constant by transition state theory through the Eyring equation:
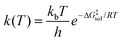 | (1) |
The ΔG‡sol term has two contributions: the activation free energy in the gas phase (ΔG‡g), which is the intrinsic free energy barrier, and the solvent induced barrier (ΔΔG‡solv), created by the solvent:
| ΔG‡sol = ΔG‡g + ΔΔG‡solv | (2) |
The ΔΔG‡solv term is usually positive in anion-molecule reactions, which corresponds to a solvent induced barrier. It is also worth observing that the ΔG‡g term, as well as the ΔG‡sol term, must both adopt the standard state of 1 mol L−1 to provide a consistent rate constant.
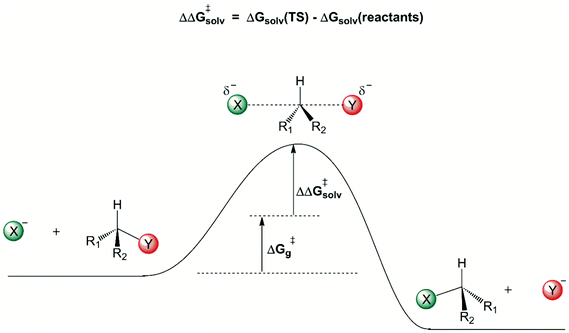
A general view of how the solvent induces a free energy barrier for anion-molecule nucleophilic substitution reactions is shown in Fig. 1. The charged ionic nucleophile is more solvated than the transition state, because there is considerable charge dispersion in the transition state, weakening the intermolecular solute–solvent interaction. Once the solvation free energy becomes more positive, there is formation of a solvent-induced free energy barrier, given by ΔΔG‡solv. The first solvation shell, in close contact with the solute, makes the more important contribution to this solvent induced barrier. Some reliable theoretically estimated ΔG‡g and ΔΔG‡solv contributions for several reactions are depicted in Table 2.
| Entry | Reaction | Reaction type | Solvent | ΔG‡g | ΔΔG‡solv | ΔG‡sol | Ref. |
|---|---|---|---|---|---|---|---|
| a Units in kcal mol−1, 298 K, 1 mol L−1 standard state. | |||||||
| 1 | CN− + CH3CH2Cl → Cl− + CH3CH2–CN | SN2 | DMSO | 10.2 | 13.9 | 24.1 | 36 |
| 2 | CN− + CH3CH2Cl → Cl− + CH2CH2 + HCN | E2 | DMSO | 18.6 | 17.8 | 36.4 | 36 |
| 3 | CN− + PhBr → Br− + Ph–CN | SNAr | DMSO | 27.2 | 16.4 | 43.6 | 37 |
| 4 | CN− + PhBr → Br− + Ph–CN | SNAr | CH3OH | 27.2 | 19.9 | 47.0 | 37 |
| 5 | F− + CH3CHClCH2CH3 → Cl− + CH3CHFCH2CH3 | SN2 | DMSO | −7.8 | 28.2 | 20.3 | 38 |
| 6 | F− + CH3CHClCH2CH3 → Cl− + HF + trans-CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH3 CHCH3 |
E2 | DMSO | −11.4 | 30.6 | 19.2 | 38 |
| 7 | F− + p-NC-Ph-Cl → Cl− + p-NC-Ph-F | SNAr | DMSO | −18.7 | 39.1 | 20.3 | 39 |
| 8 | F− + o-NC-Ph-Br → Br− + p-NC-Ph-F | SNAr | CH3OH | −16.0 | 49.1 | 33.1 | 40 |
| 9 | PhS− + CH3CHBrCH3 → Br− + CH3CH(PhS)CH3 | SN2 | DMSO | 12.4 | 9.8 | 22.2 | 41 |
| 10 | PhS− + CH3CHBrCH3 → Br− + CH3CH(PhS)CH3 | SN2 | CH3OH | 12.4 | 11.7 | 24.1 | 42 |
| 11 | NO2− + CH3CH2Br → Br− + CH3CH2–NO2 | SN2 | DMSO | 6.10 | 17.0 | 23.3 | 43 |
| 12 | NO2− + CH3CH2Br → Br− + CH3CH2–ONO | SN2 | DMSO | 6.9 | 17.2 | 24.1 | 43 |
| 13 | CH3O− + PhBr → Br− + Ph–OCH3 | SNAr | DMSO | 5.1 | 22.0 | 27.1 | 37 |
| 14 | CH3O− + PhBr → Br− + Ph–OCH3 | SNAr | CH3OH | 5.1 | 31.0 | 36.1 | 37 |
Observing the nucleophile and the type of reaction (SN2, E2 or SNAr) provides a general view of the gas phase ΔG‡g and solvent induced ΔΔG‡solv values. Thus, ions with charge dispersion like CN−, NO−2 and PhS− have positive values of ΔG‡g, whereas small or charge centered ions have lower barriers. For example, the charge centered ion CH3O− has a ΔG‡g of only 5.1 kcal mol−1 for an SNAr reaction, whereas the charge dispersed CN− ion has a barrier of 27.2 kcal mol−1 (entries 3 and 13). In the latter case, the final barrier in the solution phase (ΔG‡sol) becomes so high that makes this reaction very difficult. In the case of the small negative F− ion it is possible to observe a very high intrinsic reactivity, because the ΔG‡g barriers for SN2, E2 and SNAr reactions are negative (entries 5 to 8). In the same way, the solvent induced barrier (ΔΔG‡solv) is smaller for charge dispersed ions and higher for the small charge centered fluoride and methoxide ions. For example, the ΔΔG‡solv for the SNAr reaction of CN− with phenyl bromide in DMSO solvent (entry 3) is 16.4 kcal mol−1 and becomes 39.1 kcal mol−1 for the SNAr reaction of F− with p-chlorobenzonitrile in the same solvent (entry 7). It is worth observing that these SNAr reactions proceed via a single step, without involvement of a Meisenheimer intermediate. This single step mechanism supported by theoretical calculations has been recently recognized as very usual.44,45
Another interesting observation is the competition between the SN2 and E2 (entries 1, 2 and 5, 6). The solvent induced barrier is higher for E2 than for SN2. This effect is important for controlling the selectivity, in particular in fluorination reactions. We can also observe an important difference in SN2 and SNAr for F− reaction (entries 5 and 7). The latter has a much more pronounced solvent effect and partially explains why anion-molecule SNAr reactions are difficult. On the other hand, in the case of the CN− nucleophile (entries 1 and 3) this difference in the solvent effect is much smaller. Recently, Rablen et al. have reported an extensive theoretical study on the structural effects on the barriers of competing SN2 and E2 reactions in the liquid phase.46
3. Ion pairing effects
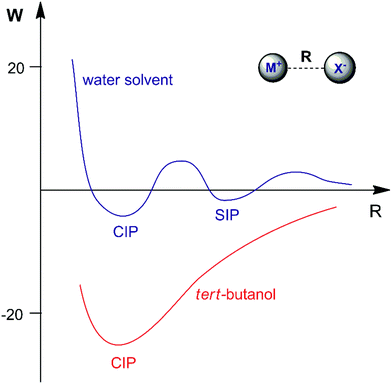
The association of a pair of ions is a common phenomenon in solutions and can take place even in highly polar and solvating media such as aqueous solution.23,47,48 However, ion-pairing becomes more important in lower dielectric constant solvents, because the energy between a pair of ions in a dielectric medium (named the potential of mean force, W) is given by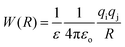 | (3) |
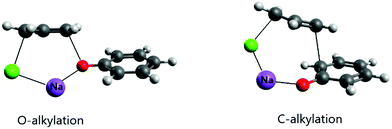
An important effect of the counter-ion on the alkylation of the phenolate ion was recently elucidated using theoretical calculations.24 It is known that alkylation of the phenolate anion occurs selectively on the oxygen atom in dipolar aprotic solvents and even alcohols.52–54 However, in aqueous solution, the reaction of this ion with allyl chloride proceeds via both O- and C-alkylation. Kornblum et al. explained this effect as resulting from selective solvation of the phenoxide ion by water molecules through strong hydrogen bonds.54 In the light of recent theoretical studies, this explanation does not have support. The theoretical study of the reaction of the phenolate ion with allyl chloride has indicated that water solvent, even including explicit water molecules in the modeling, was not able to revert the selective O-alkylation.24 On the other hand, when the counter ion was included in the modeling via ion pairing, both O- and C-alkylation (in the ortho position) were competitive, with close free energy barriers. Further, the barrier was 6 kcal mol−1 lower than the single phenolate reaction in aqueous solution. The ion pairing transition states are presented in Fig. 3. It is worth observing that when the alkylation of the phenolate ion takes place via phase-transfer catalysis, involving the CIP in the organic phase with a large counter cation, only O-alkylation is observed.55
Another interesting example of a CIP reaction was reported by Kim and co-workers: nucleophilic fluorination with cesium fluoride salt in tert-butanol solvent.56,57 Based on the discussion in Section 2, dipolar aprotic solvents are the ideal solvents for anion-molecule SN2 reactions. At first sign, the report of Kim et al. is a break of paradigm because tert-butanol is superior to acetonitrile and dimethyl formamide solvents. However, the superior performance of dipolar aprotic solvents occurs for free, solubilized ions. When the anion has strong ion pairing with the counter cation or the salt has low solubility, this rule is not valid anymore. In addition, in many cases the solubility of ionic salts does not indicate the presence of free ions. Large and unreactive aggregates can be present as observed in organolithium compounds.58,59 Thus, cesium fluoride and potassium fluoride salts are not fully soluble in organic solvents and form stable contact ion pairs. In this case, solubilization and reaction of the CIP determines the reactivity.51,60 Density functional theory, the cluster-continuum solvation approach and molecular dynamics calculations were used for the reaction of the cesium and potassium fluorides with ethyl bromide in tert-butanol solution.51 The mechanism of the reaction is presented in Fig. 4. The free energy for solubilization of the CsF salt, forming the CIP, was calculated to be 6.6 kcal mol−1. The transition state takes place via separation of the Cs+ and F− ions, with explicit tert-butanol molecules solvating both the ions. Further, the cesium ion assists the leaving of bromide ions and the calculated activation free energy of the reaction involving the solubilized CIP is calculated to be 21.8 kcal mol−1. Considering both the solubilization and activation steps, the final observed activation free energy is 28.4 kcal mol−1, in close agreement with the experimental value of 28.9 kcal mol−1. A similar calculation was performed for the KF reaction. However, the solubilization step has a free energy of 7.9 kcal mol−1 and the activation step has an activation free energy of 24.8 kcal mol−1, resulting in the final observed free energy barrier of 32.7 kcal mol−1. This result is in agreement with the fact that no reaction is observed with KF reagent using bulky alcohol as the reaction medium at 100 °C, while with CsF the reaction takes place.
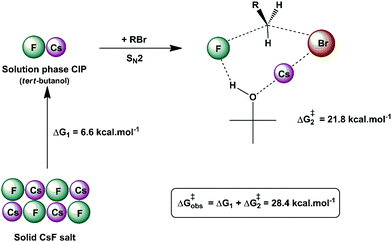 | ||
| Fig. 4 Example of the CIP reaction, involving cesium fluoride in tert-butanol solution. Values are obtained from theoretical calculations. | ||
Another interesting experimental study by Kim and co-workers reported the use of a mixture of acetonitrile and ionic liquids, in particular 1-butyl-3-methylimidazolium tetrafluoroborate.61,62 This mixture was effective even for KF reagent in the fluorination of alkyl mesylate. Very recently, a theoretical study using umbrella sampling and molecular dynamics calculations of this reaction in ionic liquids has been reported. These calculations have also indicated that the ion pair participates in the transition state.63
An interesting example of dramatic solvent and ion pairing effects is the fluorination of aromatic rings. Fluorination of unactivated aromatic rings is so difficult that a palladium catalyzed process has been only recently achieved.64 Nevertheless, Riveros and co-workers have reported a very fast fluorination of nitrobenzene in the gas phase, indicating the high intrinsic reactivity of the fluoride ion for the SNAr reaction.65 After this interesting finding, Sun and di Magno were able to obtain true anhydrous tetrabutylammonium fluoride (TBAF), which was shown to be effective in the fluorination of aromatic rings in DMSO solvent with only one activating group.66,67 For example, the fluorination of p-chlorobenzonitrile leads to 95% yield in 18 h reaction time at room temperature. Posterior 1H–19F HOESY NMR spectroscopy studies have indicated that several tetraalkylammonium fluoride salts, including TBAF, form the CIP in the solution phase (DMSO solvent).68 However, theoretical calculations have suggested that in the case of TBAF, there is dissociation of the CIP before the reaction proceeds, whereas in the case of more associated tetramethylammonium fluoride (TMAF), the reaction proceeds by the CIP participating in the transition state.39 The calculations have also pointed out that TBAF is more reactive than TMAF, which is attributed to less association of the ion pair. This lower reactivity of the TMAF can be verified from the experimental studies by Sanford and co-workers on the reactivity of several aryl halides in DMF solvent.69 For comparison, the activation free energies of these reactions were estimated based on the reaction time, yield, concentration of the reagents and temperature. The obtained data are presented in Table 3, which compares the reactivity of TBAF, TMAF and CsF, all of them involving an ion pair in the reaction. In the case of CsF, the solubilization of the salt also plays a role, as shown in Fig. 4. Based on this analysis, we can see that TBAF is 1 to 2 kcal mol−1 more reactive than TMAF in SNAr reactions. In the case of CsF, the reaction is much more difficult, requiring more extreme conditions.
| Substrate | TBAFb | TMAFc | CsFd |
|---|---|---|---|
| a Units in kcal mol−1, standard state of 1 mol L−1. Experimental data from ref. 66 and 69. b DMSO solvent, 20 °C. c DMF solvent, 25 °C. d DMF solvent, 140 °C. e DMF solvent, 80 °C. | |||
| o-Chlorobenzonitrile | 22.3 | 24.2 | 34.0 |
| o-Bromobenzonitrile | — | 23.8 | 34.1 |
| p-Chlorobenzonitrile | 23.3 | — | — |
| 2-Chloropyridine | 25.2 | 26.5e | 35.7 |
| 2-Bromopyridine | — | 25.7e | 35.2 |
A question that arises in these theoretical studies is the role of formation of larger aggregates and how the formation of these complexes determines the reactivity. This point is discussed in the next section.
4. Formation of larger aggregates
When the solvation of the solute by the solvent decreases, the interaction between solute molecules increases (see Fig. 2), leading to the formation of aggregates. Ion pairing is an example which has an important effect on the reactivity. With a further decrease of the dielectric constant or in absence of groups in the solvent molecules able to interact strongly with the ion pair, formation of dimers, trimers, tetramers and large aggregates can occur. The equilibria involving these species explain why despite the fact that less polar solvents lead to a smaller solvent effect (lower solvent induced barrier in anion-molecule reactions), the ionic reaction rate can become slower in these solvents. This kind of problem has been recently investigated by theoretical calculations using the TMAF reaction with o-bromobenzonitrile in 5 solvents: methanol, DMF, THF, pyridine and benzene.40 In that study, molecular dynamics calculations were used to show that the CIP is stable in DMF and dissociates in methanol.40 Thus, the reaction in methanol takes place via a single fluoride ion, while in DMF it occurs via an ion pair. The study also investigated the formation of dimers and tetramers of TMAF, which are presented in Scheme 3. For each solvent, the concentration of the species changes and each aggregate has its respective reactivity.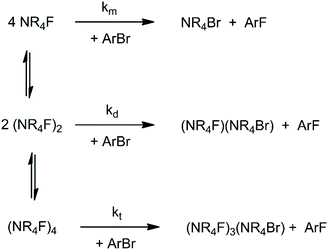 | ||
| Scheme 3 Equilibria involving TMAF, forming dimers and tetramers. The reaction steps are bimolecular SNAr reactions involving the monomer (km), dimer (kd) and tetramer (kt). | ||
The resolution of the equilibria and kinetic equations related to Scheme 3 led to the reaction rate for simulated total concentrations of TMAF and ArBr, which are 0.40 and 0.20 mol L−1, respectively.40 Based on these calculations, we can estimate an observed free energy barrier for each solvent, using the relation
| Rate = kobsCTMAFCArBr | (4) |
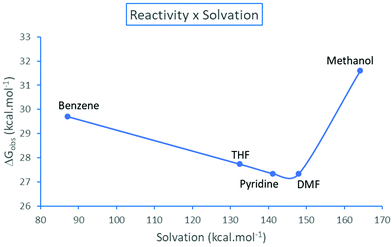 | ||
| Fig. 5 Observed effective free energy barrier for the TMAF + ArBr reaction as a function of the solvation free energy (absolute values) of the pair of ions N(CH3)4+ + F−. Theoretical values.40 | ||
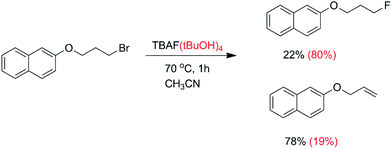
Another kind of aggregate that has an important effect on the reactivity and selectivity involves the interaction of anions with hydrogen bond donor molecules such as alcohols and ureas in aprotic solvents. Thus, Kim and co-workers have reported that when the anhydrous TBAF reacts with a primary alkyl bromide (Scheme 4), there is formation of only 22% fluorination product and 78% elimination.25 However, in the case of the use of the TBAF(tBuOH)4 complex, the fluorinated product increases to 80% with only 19% elimination. In a more recent and comprehensive study by Gouverneur and co-workers, this same reaction was studied, along with reactions involving several complexes of TBAF with different bulky alcohols.26 The rate constant for the reaction with TBAF(tBuOH)4 was determined to be 0.013 L mol−1 s−1, corresponding to ΔG‡ = 23.1 kcal mol−1. Following this study, the Gouverneur group has reported a similar analysis using ureas as hydrogen bonding donors.27 The TBAF(urea)n complexes reacted considerably slower than the TBAF(tBuOH)4, although the proportion of the SN2/E2 product was increased. In the analysis reported by the authors, they considered that there is dissociation of the ion pair and the fluoride ion forms clusters with the bulky alcohols or ureas in the solution phase. These clusters are considered as the reactive species. Another very recent study makes use of polysaccharide supported-TBAF for fluorination.71
In line with these experimental reports, a theoretical study of the symmetric Cl− + CH3Cl reaction in chloroform solution, with additional water molecules in solution forming Cl−(H2O)n clusters, predicts the participation of these water molecules in the transition state and a substantial increases in the activation barrier.72 Nelson and Benjamin have calculated that for n = 5, the free energy barrier is 10 kcal mol−1 above the barrier in pure chloroform and only 3 kcal mol−1 below the barrier in pure aqueous solution.
5. Structured environment
The effect of water, alcohol and urea molecules solvating an anion in an aprotic solvent has consequences of the increase of the free energy barrier and improvement of the selectivity of SN2 versus E2. This is an effect of the first solvation shell, which makes the most important contribution to the reactivity. Thus, we could wonder about designing a molecule with hydrogen bond donor groups able to interact more selectively with the transition state than with the nucleophilic anion. Such species could lead to a lower ΔG‡ and more selectivity towards SN2 reactions. 1,4-Benzenedimethanol (Fig. 6) was envisioned to be able to produce such an effect.38,70,73,74 Theoretical calculations have predicted that this molecule is able to decrease the ΔG‡ for SN2 reactions and to increase the selectivity of SN2 in relation to E2 for fluoride38 and acetate74 nucleophiles in DMSO solvent.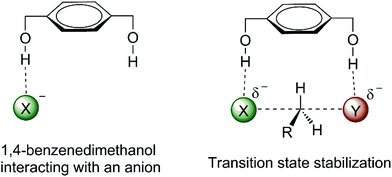 | ||
| Fig. 6 Envisioned catalytic effect in SN2 reactions by hydrogen bonds to the incoming and leaving groups. | ||
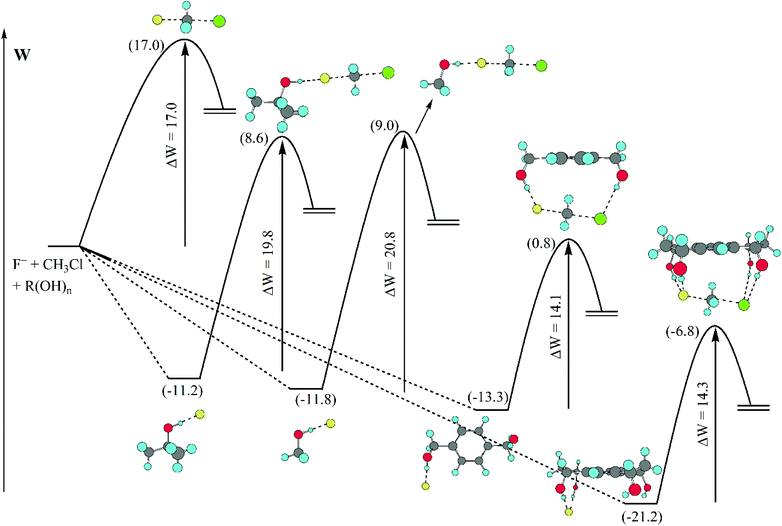
A detailed analysis of the effect of hydrogen bonds provided by different alcohols in DMSO solvent is presented in Fig. 7.70 The barrier (potential of mean force) for the model SN2 reaction is predicted by theoretical calculations to be 17.0 kcal mol−1 in DMSO. The presence of methanol or tert-butanol in this solvent increases the barrier to 20.8 and 19.8 kcal mol−1, respectively. However, the 1,4-benzenedimethanol has the inverse effect, decreasing the barrier to 14.1 kcal mol−1. A tetraol was also investigated and the effect was similar to that of the diol, decreasing the barrier to 14.3 kcal mol−1. Thus, controlling the number of hydrogen bonds, with less hydrogen bonds to the nucleophile and more hydrogen bonds to the transition state can be useful to produce a rate acceleration effect.
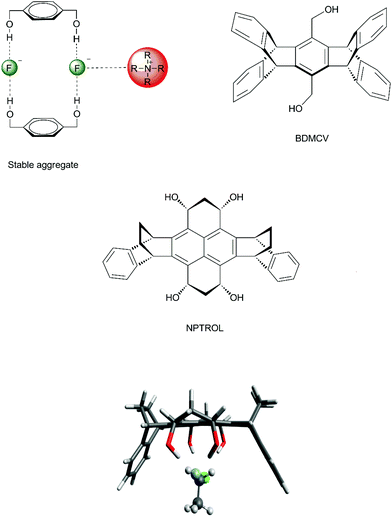
In order to improve the control of the number of hydrogen bonds in a real system, it is important to avoid any possible formation of aggregates involving the diol and tetraol. Otherwise, no catalytic effect would be observed. In the case of 1,4-benzenedimethanol, there is formation of stable aggregates involving 2 molecules of 1,4-benzenedimethanol, 2 fluoride ions and tetrabutylammonium counter ions (Fig. 8), inhibiting any catalytic effect.70 Thus, to overcome this problem, molecular cavities able to avoid dimerization were proposed, such as the diol BDMCV and the tetraol NPTROL (Fig. 8).70,75 In particular, it was predicted that the NPTROL is effective in accelerating the SN2 reaction of the fluoride ion with alkyl chloride in DMSO solvent (calculated ΔG‡ = 18.0 kcal mol−1), leading to very high selectivity towards the SN2 product and minimal formation of the E2 product.75
In 1984, Dolling and co-workers reported a very important study on the asymmetric phase transfer catalyzed alkylation of indanone, using the cinchoninium ion.76 They obtained 92% enantiomeric excess and 95% yield (Scheme 5). The explanation for the enantiomeric excess was based on a model that considers the close contact ion pair between the cinchoninium catalyst and the indanone anion. This ion pair would block the electrophilic attack of the methyl chloride on the indanone side closer to the cinchoninium, leading to the selectivity.
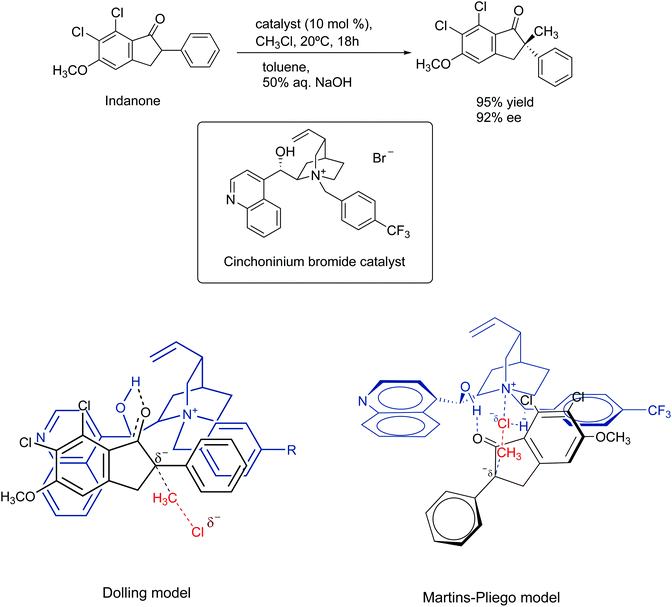 | ||
| Scheme 5 Mechanism of asymmetric phase transfer catalyzed alkylation of indanone. The Martins–Pliego model was based on DFT calculations. | ||
The model of Dolling and co-workers has lasted up to 2013, when Martins and Pliego have reported the first theoretical study of this reaction.76,77 They found that the reaction mechanism takes place via transition state stabilization, similar to the concept presented in Fig. 6. In the cinchoninium ion catalysis, the enolate group of indanone makes a hydrogen bond with the hydroxyl group of the cinchoninium, whereas the hydrogens close to the ammonium group interact with the leaving chloride ion, as shown in Scheme 5. Following this study, a more complete theoretical analysis of the mechanism, including the phase transfer process, was able to reproduce the kinetics of this system.78 Houk and co-workers have more explored this mechanism.79
6. Structured environment: solubilization and activation
In some situations, the source of the nucleophile in nucleophilic substitution reactions can be an insoluble salt. An example is the nucleophilic fluorination with KF or CsF. In these cases, the structured environment needs to have both properties: solubilizing the salt and activating the nucleophile for the reaction. Macrocycles are a good scaffold for building a structured environment able to interact with both cations and anions. The early report by Liotta and Harris in 1974 showed that the 18-crown-6 is able to solubilize and activate KF for fluorination of alkyl halides.80 Under this condition, the fluoride ion was named “naked ion”, because it was thought that the strong interaction between the crown ether and the potassium ion would make the fluoride ion free to react. However, this view is not correct. Theoretical studies of the interaction of the KF with crown ether and the catalytic process pointed out that the reaction takes place via ion pairs and the ring of the ether plays an important role in the selectivity of SN2 versus E2.28,81Fig. 9 presents these solubilization and activation steps using the 18-crown-6 as the catalyst. The free energy barrier of 32.0 kcal mol−1 obtained from theoretical calculations for a model reaction can be compared to the experimentally estimated value of 30.1 kcal mol−1.28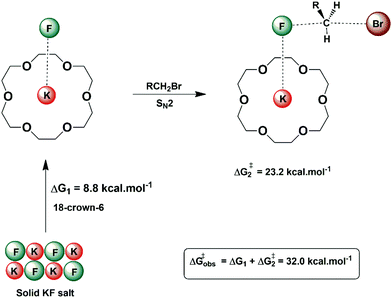 | ||
| Fig. 9 Solubilization and activation of the KF using 18-crown-6 in acetonitrile solvent. The free energy for each step was obtained from theoretical calculations. | ||
In the past decade, efforts have been made for developing macrocycle-based catalysts for fluorination with CsF and KF salts. These several structures are presented in Scheme 6 and the respective reactivity and selectivity are shown in Table 4. The determination of the ΔG‡ from experiments was described in ref. 82. The theoretical barriers were based on reliable calculations of a process similar to that described in Fig. 9. Two examples of computational modeling of the reaction taking place inside these environments are presented in Fig. 10. Thus, Jadhav et al. have reported the use of pentaethylene glycol (pentaEG) for fluorination of alkyl mesylates and halides with CsF.83 The reaction was very effective, with experimental ΔG‡ = 27.2 kcal mol−1 (alkyl mesylate, entry 8, Table 4) and very high selectivity, only forming traces of the E2 product. The detailed and high level calculations,84 including the solubilization step, have ΔG‡ = 27.9 kcal mol−1, in an excellent agreement. The selectivity was also predicted to be very high, with ΔG‡E2 − ΔG‡SN2 = 6.3 kcal mol−1. On the other side, in the case of KF salt, the reactivity decreases considerably and the theoretical calculations (entry 2, Table 4) predict ΔG‡ = 29.2 kcal mol−1, with reactivity close to that observed for 18-crown-6. However, pentaEG is much more selective. An important aspect of the pentaEG catalysis, which makes this species less efficient than it could be, is the dimerization of the MF(pentaEG) complex, as shown by theoretical calculations.84
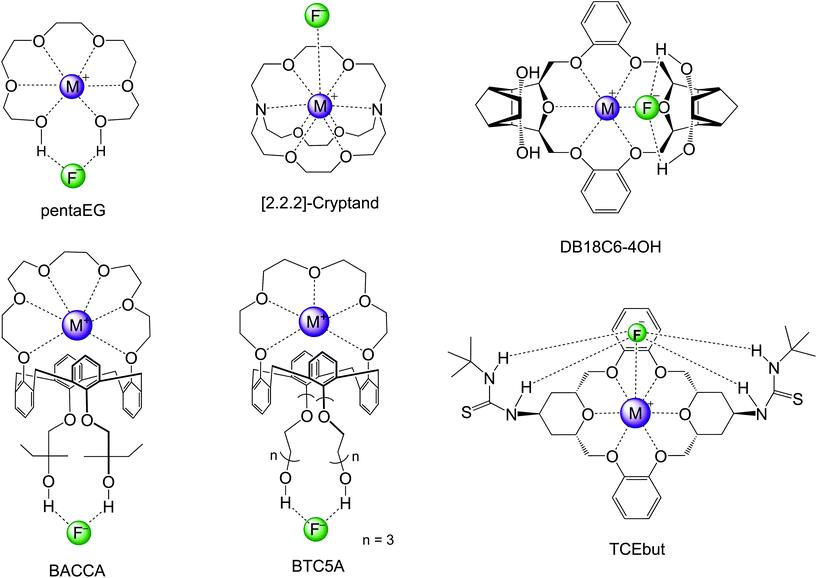 | ||
| Scheme 6 Macrocycles investigated for nucleophilic fluorination of alkyl halides and mesylates with CsF and KF. DB18C6-4OH and TCEbut only have theoretical studies. | ||
| Entry | Catalyst | R–X | Reaction conditions | ΔG‡obs | ΔG‡E2 − ΔG‡SN2 | Ref. |
|---|---|---|---|---|---|---|
| a Theoretical values in parentheses. Units in kcal mol−1. Standard state of 1 mol L−1. | ||||||
| 1 | 18-Crown-6 | R–Br | KF, 82 °C, acetonitrile | 30.1 (32.0) | (−0.2) | 28 |
| 2 | PentaEG | R–OMs | (KF, 25 °C, acetonitrile) | (29.9) | (6.2) | 84 |
| 3 | 18-Crown-6 + tert-butanol | R–Br | KF, 82 °C, acetonitrile | 28.6 (28.4) | 1.7 (3.1) | 28 |
| 4 | 18-Crown-6 + BDMb | R–Br | KF, 82 °C, acetonitrile | 28.1 (24.3) | 1.9 (5.0) | 90 |
| 5 | BACCA | R–OMs | CsF, 100 °C, acetonitrile | 27.6 | >3 | 29 |
| 6 | BTC5A | R–OMs | KF, 100 °C, acetonitrile | 27.5 | 2.6 | 85 |
| 7 | [2.2.2]-Cryptand | R–OMs | KF, 100 °C, acetonitrile | 27.3 | 1.5 | 85 |
| 8 | PentaEG | R–OMs | CsF, 100 °C, acetonitrile | 27.2 (27.9) | >3 (6.3) | 83 and 84 |
| 9 | DB18C6-4OH | R–Br | (KF, 25 °C, toluene) | (27.0) | (2.2) | 88 and 91 |
| 10 | BACCA | R–OMs | CsF, 100 °C, tert-amyl alcohol | 26.2 (27.3) | >3 | 29 and 82 |
| 11 | [2.2.2]-Cryptand | R–OMs | (KF, 25 °C, toluene) | (26.1) | — | 84 |
| 12 | TCEbut | R–OMs | (KF, 25 °C, toluene) | (24.5) | (3.9) | 84 |
[2.2.2]-Cryptand has been reported to be one of the most effective phase transfer catalysts for activating KF.84–88 An early report on the use of this catalyst for fluorination with K[18F] and 30 min of reaction aimed to obtain 2-[18F]-Fluoro-2-deoxy-D-glucose has shown that this macrocycle is very useful for fast fluorination.87 Schwesinger et al. have also reported that [2.2.2]-cryptand promotes a very fast fluorination of 1-iodoundecane.86 However, the E2 product was the majority. More recently, Kim and co-workers have used [2.2.2]-cryptand for fluorination of a primary alkyl mesylate with KF.85 Although the reaction was fast, about 11% E2 product was generated. The estimated experimental ΔG‡ is 27.3 kcal mol−1, and ΔG‡E2 − ΔG‡SN2 = 1.5 kcal mol−1 (entry 7, Table 4). Theoretical calculations have shown that the main contribution for the catalytic effect of the [2.2.2]-cryptand in relation to 18-crown-6 is the solubilization step.84,88
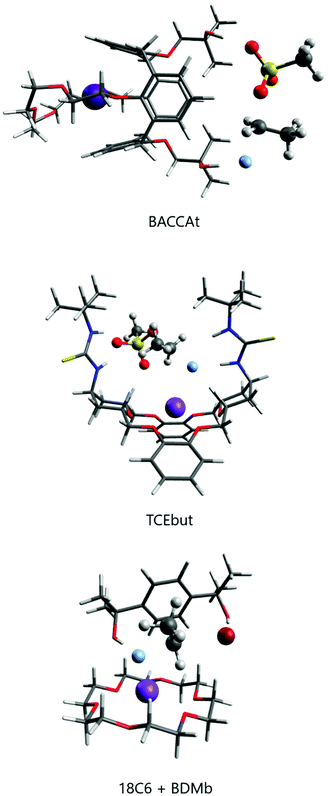
The group of Kim has made recent efforts to develop a new class of catalysts involving macrocycles combined with calix[4]arenes and hydroxyl groups, as the structures BACCA and BTC5A in Scheme 6.29,85,89 The BACCA structure is very selective towards SN2, although it only works for CsF salt.29 The respective experimental ΔG‡ values for fluorination of acetonitrile (entry 5) and tert-amyl alcohol (entry 10) are 27.6 kcal mol−1 and 26.2 kcal mol−1. Theoretical calculations have elucidated the mechanism and found that the two hydroxyls work by interacting with the incoming and leaving groups, as shown in Fig. 10 for a slightly modified BACCA, named BACCAt.82 These calculations have determined that ΔG‡ = 27.3 kcal mol−1, in very good agreement with the experimental value of 26.2 kcal mol−1.
Aimed to improve the catalysis of fluorination using the more challenging KF salt, Kim and co-workers have proposed a new structure, BTC5A, with 5 ether groups instead of 6 in BACCA, and longer carbon chain bonds to the hydroxyls.85 The new species was much more effective, with a catalytic effect similar to that of the [2.2.2]-cryptand, but substantial better selectivity toward SN2 reaction (entry 6). It is also interesting to observe that the authors have reported that the use of apolar solvents such as toluene is more effective than the polar aprotic acetonitrile solvent.
Our group has also recently designed new macrocycles for activating KF salt.88,91 The new designed structure was the DB18C6-4OH (Scheme 6), based on the idea of combining the crown ether ability to complex the cation, with hydroxyl groups in distant positions able to interact with the incoming and leaving groups in the SN2 transition state, as shown for the NPTROL in Fig. 8. The calculations have indicated that this basic scaffold is effective in catalyzing the reaction, leading to ΔG‡ = 27.0 kcal mol−1 (entry 9). Nevertheless, this species can form dimers and a true functional structure requires the addition of bulk groups close to the hydroxyls to inhibit dimerization.88
Recent theoretical design studies have been reported, aimed to create more effective catalysts. As a result, a new structure named TCEbut was found to be a very efficient phase-transfer catalyst for fluorination. This species has two thiourea groups able to interact with the fluoride ion via four hydrogen bonds, whereas the crown ether group interacts with the potassium ion. This very strong interaction leads to easy solubilization of the KF salt. In the transition state, the thiourea groups interact with the incoming and leaving groups (Fig. 10), leading to the final ΔG‡ = 24.5 kcal mol−1 (entry 12). Thus, the calculations suggest that this species is a highly effective phase-transfer catalyst, overcoming the [2.2.2]-cryptand.
Although structures such as BTC5A are very effective for activating KF, and calculations have suggested that TECbut could be even more efficient, these species have some complexity and the use of simpler species with a similar effect would be an interesting alternative. In line with this thinking, crown ethers could be combined with bulky alcohols or bulky diols. Thus, it was theoretically predicted and experimentally found that stoichiometric addition of tert-butanol to 18-crown-6 improves the catalysis.28 The effect is even better with the addition of bulky diol 1,4-bis(2-hydroxy-2-propyl)benzene (named BDMb), which is able to stabilize the transition state via two hydrogen bonds (see Fig. 10).90 For comparison, see entries 1, 3 and 4 in Table 4. In a study by Jadhav et al. the KF(18-crown-6) complex was used as a reagent for fluorination in tert-amyl alcohol solvent.92
The use of chiral bis-urea able to provide hydrogen bonds for asymmetric fluorination and involving the solubilization of KF or CsF was recently reported by Gouverneur and co-workers.93–95 It is worth observing that the substrate undergoing the SN2 reaction is an ammonium or sulfonium ion, which is ion paired to the hydrogen bonded fluoride ion. The development of an asymmetric fluorination of general alkyl halides or mesylates with KF is an important step ahead.
7. Conclusion
Ionic species, mainly small and charge centered ions, are very reactive species in the gas phase and solvation attenuates the rate of ion-molecule reactions. A more solvating medium leads to less reactivity. The role of counter-ions also needs be considered for understanding ionic reactivity in the condensed phase. In fact, ion pairing can lead to the participation of the counter-ion in the transition state and can change the ionic reactivity. In a less solvating medium, larger aggregates can be formed and the effect on the reactivity can be even higher. It is important to take into account these multiple equilibria in the solution phase for rationalizing the best solvent able to promote the reaction.The first solvation shell of an ion plays an important role in determining the reactivity and selectivity. Thus, with adequate design of the solvation shell with a large structure able to interact with the ion and with the transition state, ionic reactivity can be modulated. In a sense, the interaction of the solute with the medium can be seen as a continuum, going from the solvent, made of small molecules that fit to the solute, to a highly structured medium, where the solute fits to the surrounding. This is an important concept for taking control of chemical reactivity by intermolecular forces.
In the case of insoluble ionic salts, the structured environment must be able to solubilize the salt. The interaction with both the cation and the anion is advantageous in relation to cation interactions only, provided by macrocycles. Modification of the macrocycles, with the addition of groups able to provide multiple hydrogen bonds with the anion, can lead to better solubilization of the salt. Further, multiple hydrogen bonds interacting with the incoming and leaving groups in the SN2 transition state can lead to more efficient catalysis. This combination of macrocycles with alcohols can also involve separated species, as the catalysis promoted by 18-crown-6 combined with a bulky diol. More studies involving design of new species with a structured environment, also including a chiral backbone, can lead to even better reactivity and selectivity of SN2 reactions, mainly nucleophilic fluorination.
Conflicts of interest
Patent applications were filled.Acknowledgements
The author thanks the agency CNPq for support.References
- C. Reichardt and T. Welton, Solvents and Solvent Effects in Organic Chemistry, WILEY-VCH, Weinheim, Germany, Fourth edn, 2011 Search PubMed.
- A. J. Parker, Chem. Rev., 1969, 69, 1 CrossRef CAS.
- W. L. Jorgensen, Acc. Chem. Res., 1989, 22, 184 CrossRef CAS.
- O. Acevedo and W. L. Jorgensen, Org. Lett., 2004, 6, 2881 CrossRef CAS.
- D. W. Tondo and J. R. Pliego Jr., J. Phys. Chem. A, 2005, 109, 507 CrossRef CAS.
- S. Gronert, Chem. Rev., 2001, 101, 329 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, Chem. Rev., 1999, 99, 2161 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS.
- O. Acevedo and W. L. Jorgensen, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 422 CAS.
- J. R. Pliego Jr. and J. M. Riveros, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1440 Search PubMed.
- K. Takashima and J. M. Riveros, J. Am. Chem. Soc., 1978, 100, 6128 CrossRef CAS.
- J. R. Pliego Jr. and J. M. Riveros, Chem. – Eur. J., 2001, 7, 169 CrossRef CAS.
- N. F. Carvalho and J. R. Pliego, Phys. Chem. Chem. Phys., 2015, 17, 26745 RSC.
- H. M. Humphreys and L. P. Hammett, J. Am. Chem. Soc., 1956, 78, 521 CrossRef CAS.
- J. R. Pliego Jr. and J. M. Riveros, Chem. – Eur. J., 2002, 8, 1945 CrossRef.
- J. A. Kerr, Chem. Rev., 1966, 66, 465 CrossRef CAS.
- V. Gutmann and E. Wychera, Inorg. Nucl. Chem. Lett., 1966, 2, 257 CrossRef CAS.
- U. Mayer, V. Gutmann and W. Gerger, Monatsh. Chem., 1975, 106, 1235 CrossRef CAS.
- A. Ben-Naim and Y. Marcus, J. Chem. Phys., 1984, 81, 2016 CrossRef CAS.
- A. Ben-Naim, J. Phys. Chem., 1978, 82, 792 CrossRef CAS.
- D. G. Truhlar and J. R. Pliego Jr., in Continuum Solvation Models in Chemical Physics: From Theory to Applications, ed. B. Mennucci and R. Cammi, John Wiley & Sons, Chippenham, Wiltshire, Great Britain, 2007, pp. 338 Search PubMed.
- I. Soteras, D. Blanco, O. Huertas, A. Bidon-Chanal and F. J. Luque, in Continuum Solvation Models in Chemical Physics: From Theory to Applications, ed. B. Mennucci and R. Cammi, John Wiley & Sons, Chippenham, Wiltshire, 2007, pp. 323 Search PubMed.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585 CrossRef CAS.
- I. C. Nogueira and J. R. Pliego Jr., J. Phys. Org. Chem., 2019, 32, e3947 CrossRef.
- D. W. Kim, H.-J. Jeong, S. T. Lim and M.-H. Sohn, Angew. Chem., Int. Ed., 2008, 47, 8404 CrossRef CAS.
- K. M. Engle, L. Pfeifer, G. W. Pidgeon, G. T. Giuffredi, A. L. Thompson, R. S. Paton, J. M. Brown and V. Gouverneur, Chem. Sci., 2015, 6, 5293 RSC.
- L. Pfeifer, K. M. Engle, G. W. Pidgeon, H. A. Sparkes, A. L. Thompson, J. M. Brown and V. Gouverneur, J. Am. Chem. Soc., 2016, 138, 13314 CrossRef CAS.
- S. L. Silva, M. S. Valle and J. R. Pliego, J. Mol. Liq., 2020, 319, 114211 CrossRef CAS.
- V. H. Jadhav, W. Choi, S.-S. Lee, S. Lee and D. W. Kim, Chem. – Eur. J., 2016, 22, 4515 CrossRef CAS.
- M. A. Spackman, J. Comput. Chem., 1996, 17, 1 CrossRef CAS.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225 CrossRef CAS.
- C. Caleman, P. J. van Maaren, M. Hong, J. S. Hub, L. T. Costa and D. van der Spoel, J. Chem. Theory Comput., 2012, 8, 61 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS.
- J. R. Pliego and E. L. M. Miguel, J. Phys. Chem. B, 2013, 117, 5129 CrossRef CAS.
- G. I. Almerindo and J. R. Pliego Jr., Org. Lett., 2005, 7, 1821 CrossRef CAS.
- D. R. Silva and J. R. Pliego, Struct. Chem., 2019, 30, 75 CrossRef CAS.
- J. R. Pliego Jr. and D. Piló-Veloso, J. Phys. Chem. B, 2007, 111, 1752 CrossRef.
- J. R. Pliego Jr. and D. Pilo-Veloso, Phys. Chem. Chem. Phys., 2008, 10, 1118 RSC.
- E. V. Dalessandro and J. R. Pliego, Theor. Chem. Acc., 2020, 139, 27 Search PubMed.
- E. L. M. Miguel, C. I. L. Santos, C. M. Silva and J. R. Pliego Jr., J. Braz. Chem. Soc., 2016, 27, 2055 CAS.
- N. M. Silva, P. Deglmann and J. R. Pliego, J. Phys. Chem. B, 2016, 120, 12660 CrossRef CAS.
- E. Westphal and J. R. Pliego Jr., J. Phys. Chem. A, 2007, 111, 10068 CrossRef CAS.
- E. E. Kwan, Y. Zeng, H. A. Besser and E. N. Jacobsen, Nat. Chem., 2018, 10, 917 CrossRef CAS.
- J. Murphy, S. Rohrbach, A. J. Smith, J. H. Pang, D. L. Poole, T. Tuttle and S. Chiba, Angew. Chem., Int. Ed., 2019, 58, 16368 CrossRef.
- P. R. Rablen, B. D. McLarney, B. J. Karlow and J. E. Schneider, J. Org. Chem., 2014, 79, 867 CrossRef CAS.
- N. F. A. van der Vegt, K. Haldrup, S. Roke, J. Zheng, M. Lund and H. J. Bakker, Chem. Rev., 2016, 116, 7626 CrossRef CAS.
- M. Kohagen, E. Pluhařová, P. E. Mason and P. Jungwirth, J. Phys. Chem. Lett., 2015, 6, 1563 CrossRef CAS.
- C. Houriez, V. Vallet, F. Real, M. Meot-Ner (Mautner) and M. Masella, J. Chem. Phys., 2017, 147, 161720 CrossRef.
- Y. Yao and Y. Kanai, J. Chem. Theory Comput., 2018, 14, 884 CrossRef CAS.
- J. R. Pliego Jr., J. Mol. Liq., 2017, 237, 157 CrossRef.
- I. C. Nogueira and J. R. Pliego, Comput. Theor. Chem., 2018, 1138, 117 CrossRef CAS.
- R. J. Mayer, M. Breugst, N. Hampel, A. R. Ofial and H. Mayr, J. Org. Chem., 2019, 84, 8837 CrossRef CAS.
- N. Kornblum, P. J. Berrigan and W. J. Le Noble, J. Am. Chem. Soc., 1963, 85, 1141 CrossRef CAS.
- S. E. Denmark, R. C. Weintraub and N. D. Gould, J. Am. Chem. Soc., 2012, 134, 13415 CrossRef CAS.
- D. W. Kim, H. J. Jeong, S. T. Lim, M. H. Sohn, J. A. Katzenellenbogen and D. Y. Chi, J. Org. Chem., 2008, 73, 957 CrossRef CAS.
- D. W. Kim, D. S. Ahn, Y. H. Oh, S. Lee, H. S. Kil, S. J. Oh, S. J. Lee, J. S. Kim, J. S. Ryu, D. H. Moon and D. Y. Chi, J. Am. Chem. Soc., 2006, 128, 16394 CrossRef CAS.
- H. J. Reich, Chem. Rev., 2013, 113, 7130 CrossRef CAS.
- L. M. Pratt, S. C. Nguyen and B. T. Thanh, J. Org. Chem., 2008, 73, 6086 CrossRef CAS.
- Y. H. Oh, D. S. Ahn, S. Y. Chung, J. H. Jeon, S. W. Park, S. J. Oh, D. W. Kim, H. S. Kil, D. Y. Chi and S. Lee, J. Phys. Chem. A, 2007, 111, 10152 CrossRef CAS.
- D. W. Kim, C. E. Song and D. Y. Chi, J. Org. Chem., 2003, 68, 4281 CrossRef CAS.
- D. W. Kim, C. E. Song and D. Y. Chi, J. Am. Chem. Soc., 2002, 124, 10278 CrossRef CAS.
- J. Sánchez-Badillo, M. Gallo, R. A. Guirado-López and R. González-García, J. Phys. Chem. B, 2020, 124, 4338 CrossRef.
- A. C. Sather and S. L. Buchwald, Acc. Chem. Res., 2016, 49, 2146 CrossRef CAS.
- T. Giroldo, L. A. Xavier and J. M. Riveros, Angew. Chem., Int. Ed., 2004, 43, 3588 CrossRef CAS.
- H. Sun and S. G. DiMagno, Angew. Chem., Int. Ed., 2006, 45, 2720 CrossRef CAS.
- H. Sun and S. G. DiMagno, J. Am. Chem. Soc., 2005, 127, 2050 CrossRef CAS.
- H. R. Su, B. Wang and S. G. DiMagno, Chim. Oggi, 2008, 26, 4 Search PubMed.
- S. D. Schimler, S. J. Ryan, D. C. Bland, J. E. Anderson and M. S. Sanford, J. Org. Chem., 2015, 80, 12137 CrossRef CAS.
- J. R. Pliego Jr., J. Phys. Chem. B, 2009, 113, 505 CrossRef.
- M. S. Said, N. S. Khonde, M. N. Thorat, R. S. Atapalkar, A. A. Kulkarni, J. Gajbhiye and S. G. Dastager, Asian J. Org. Chem., 2020, 9, 1022 CrossRef CAS.
- K. V. Nelson and I. Benjamin, J. Chem. Phys., 2009, 130, 194502 CrossRef.
- J. R. Pliego Jr., Org. Biomol. Chem., 2006, 4, 1667 RSC.
- J. R. Pliego Jr., J. Mol. Catal. A: Chem., 2005, 239, 228 CrossRef.
- J. R. Pliego Jr., Phys. Chem. Chem. Phys., 2011, 13, 779 RSC.
- U. H. Dolling, P. Davis and E. J. J. Grabowski, J. Am. Chem. Soc., 1984, 106, 446 CrossRef CAS.
- E. F. Martins and J. R. Pliego, ACS Catal., 2013, 3, 613 CrossRef.
- E. F. Martins and J. R. Pliego Jr., J. Mol. Catal. A: Chem., 2016, 417, 192 CrossRef CAS.
- C. Q. He, A. Simon, Y.-H. Lam, A. P. J. Brunskill, N. Yasuda, J. Tan, A. M. Hyde, E. C. Sherer and K. N. Houk, J. Org. Chem., 2017, 82, 8645 CrossRef CAS.
- C. L. Liotta and H. P. Harris, J. Am. Chem. Soc., 1974, 96, 2250 CrossRef CAS.
- J. R. Pliego Jr. and J. M. Riveros, J. Mol. Catal. A: Chem., 2012, 363–364, 489 CrossRef.
- J. R. Pliego, Int. J. Quantum Chem., 2018, 118, e25648 CrossRef.
- V. H. Jadhav, S. H. Jang, H.-J. Jeong, S. T. Lim, M.-H. Sohn, J.-Y. Kim, S. Lee, J. W. Lee, C. E. Song and D. W. Kim, Chem. – Eur. J., 2012, 18, 3918 CrossRef CAS.
- E. V. Dalessandro and J. R. Pliego, Mol. Syst. Des. Eng., 2020, 5, 1513 RSC.
- S. M. Kang, C. H. Kim, K. C. Lee and D. W. Kim, Org. Lett., 2019, 21, 3062 CrossRef CAS.
- R. Schwesinger, R. Link, P. Wenzl and S. Kossek, Chem. – Eur. J., 2006, 12, 438 CrossRef.
- K. Hamacher, H. H. Coenen and G. Stöcklin, J. Nucl. Med., 1986, 27, 235 CAS.
- J. R. Pliego, Org. Biomol. Chem., 2018, 16, 3127 RSC.
- H. J. Han, S.-S. Lee, S. M. Kang, Y. Kim, C. Park, S. Yoo, C. H. Kim, Y.-H. Oh, S. Lee and D. W. Kim, Eur. J. Org. Chem., 2020, 728 CrossRef CAS.
- S. L. Silva, M. S. Valle and J. R. Pliego, J. Org. Chem., 2020, 85, 15457 CrossRef CAS.
- N. F. Carvalho and J. R. Pliego, J. Org. Chem., 2016, 81, 8455 CrossRef CAS.
- V. H. Jadhav, H. J. Jeong, W. Choi and D. W. Kim, Chem. Eng. J., 2015, 270, 36 CrossRef CAS.
- G. Roagna, D. M. H. Ascough, F. Ibba, A. C. Vicini, A. Fontana, K. E. Christensen, A. Peschiulli, D. Oehlrich, A. Misale, A. A. Trabanco, R. S. Paton, G. Pupo and V. Gouverneur, J. Am. Chem. Soc., 2020, 142, 14045 CrossRef CAS.
- G. Pupo, A. C. Vicini, D. M. H. Ascough, F. Ibba, K. E. Christensen, A. L. Thompson, J. M. Brown, R. S. Paton and V. Gouverneur, J. Am. Chem. Soc., 2019, 141, 2878 CrossRef CAS.
- G. Pupo, F. Ibba, D. M. H. Ascough, A. C. Vicini, P. Ricci, K. E. Christensen, L. Pfeifer, J. R. Morphy, J. M. Brown, R. S. Paton and V. Gouverneur, Science, 2018, 360, 638 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |