Open Access Article
Open Access ArticleLithium nickel borides: evolution of [NiB] layers driven by Li pressure†
Volodymyr
Gvozdetskyi
a,
Yang
Sun
 d,
Xin
Zhao
d,
Xin
Zhao
 b,
Gourab
Bhaskar
b,
Gourab
Bhaskar
 a,
Scott L.
Carnahan
ab,
Colin P.
Harmer
a,
Scott L.
Carnahan
ab,
Colin P.
Harmer
 ab,
Feng
Zhang
b,
Raquel A.
Ribeiro
c,
Paul C.
Canfield
bc,
Aaron J.
Rossini
ab,
Feng
Zhang
b,
Raquel A.
Ribeiro
c,
Paul C.
Canfield
bc,
Aaron J.
Rossini
 ab,
Cai-Zhuang
Wang
ab,
Cai-Zhuang
Wang
 bc,
Kai-Ming
Ho
c and
Julia V.
Zaikina
bc,
Kai-Ming
Ho
c and
Julia V.
Zaikina
 *a
*a
aDepartment of Chemistry, Iowa State University, Ames, Iowa 50011, USA. E-mail: yzaikina@iastate.edu
bAmes Laboratory, US DOE, Iowa State University, Ames, Iowa 50011, USA
cDepartment of Physics and Astronomy, Iowa State University, Ames, Iowa 50011, USA
dDepartment of Applied Physics and Applied Mathematics, Columbia University, New York, NY, 10027, USA
First published on 25th November 2020
Abstract
Here we show the effect of Li chemical pressure on the structure of layered polymorphs with LiNiB composition: RT-LiNiB (room temperature polymorph) and HT-LiNiB (high temperature polymorph), resulting in stabilization of the novel RT-Li1+xNiB (x ∼ 0.17) and HT-Li1+yNiB (y ∼ 0.06) phases. Depending on the synthesis temperature and initial Li content, precisely controlled via hydride route synthesis, [NiB] layers undergo structural deformations, allowing for extra Li atoms to be accommodated between the layers. In situ variable temperature synchrotron and time-dependent laboratory powder X-ray diffraction studies suggest Li step-wise deintercalation processes: RT-Li1+xNiB → RT-LiNiB (high temp.) → LiNi3B1.8 → binary Ni borides and HT-Li1+yNiB → HT-LiNiB (high temp.) → LiNi3B1.8 → binary Ni borides. Quantum chemistry calculations and solid state 7Li and 11B NMR spectroscopy shed light on the complexity of real superstructures of these compounds determined from high resolution synchrotron powder diffraction data.
Introduction
The story of lithium nickel borides began in 1976 when four ternary phases were identified in the Li–Ni–B system.1–3 Crystal structures were reported for three of these compounds, LiNi3B1.8 (MgNi3B2 structure type, P6222 space group), Li3Ni20B6 (Cr23C6, Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), and Li2.8Ni16B8 (Li3Ni16B8, P4/mbm). Only a tentative composition of 1
m), and Li2.8Ni16B8 (Li3Ni16B8, P4/mbm). Only a tentative composition of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was assigned for the fourth compound, a phase with the richest Li content. To the best of our knowledge, no other ternary compounds in all A–T–B systems (A = alkali metal, T = Ti–Zn) have been reported. The lack of the ternary A–T–B compounds can be due to the drastically different reactivity of refractory boron (melting point 2348 K) and alkali metals (boiling point 944–1615 K) making traditional synthesis methods (e.g. arc melting) non-applicable.
1 was assigned for the fourth compound, a phase with the richest Li content. To the best of our knowledge, no other ternary compounds in all A–T–B systems (A = alkali metal, T = Ti–Zn) have been reported. The lack of the ternary A–T–B compounds can be due to the drastically different reactivity of refractory boron (melting point 2348 K) and alkali metals (boiling point 944–1615 K) making traditional synthesis methods (e.g. arc melting) non-applicable.
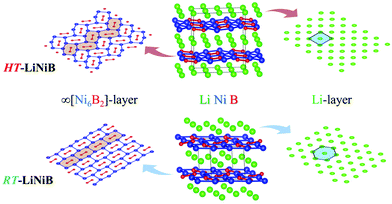
The hydride synthesis route, where salt-like alkali metal hydrides are used as a source of alkali metals, has been successfully utilized for the preparation of alkali/alkali-earth antimonides, arsenides, germanides, and silicides.4–10 Application of this method for the Li–Ni–B system significantly shortened the synthesis time of ternary phases. For instance, LiNi3B1.8 can be synthesized in a span of ∼24 hours compared with the previously reported 3-month annealing for the reaction of elements.9 The hydride route also permitted the compositional control and comprehensive screening of unknown compounds. This way, two lithium nickel boride polymorphs RT-LiNiB (room temperature polymorph) and HT-LiNiB (high temperature polymorph), with unique layered crystal structures, were discovered.11 In these polymorphic compounds, Li layers, featuring hexagonal-like or squared motif, alternate with nearly planar [NiB] layers, whose structure differs depending on the polymorph (Fig. 1). A structural relationship between the RT-LiNiB and HT-LiNiB polymorphs, Li-depleted phase LiNi3B1.8, Ni2B, and Li has been found,11 indicating on the ∞[NiB] framework evolves with the changing of Li content and/or temperature variation (Fig. S1†).
Layered lithium nickel borides are of interest from the functional materials perspective. Firstly, ∼33 at% of Li is stored between [NiB] layers in RT- and HT-LiNiB (9.1 wt% of Li as compared to 8.8 wt% of Li in LiC6 anode material) gives these compounds potential for applications in Li-ion batteries. Secondly, due to the unique arrangement of Li and [NiB] layers in their structures, exfoliation of these materials can open a pathway to novel two-dimensional (2D) nickel borides.11,12 The search for 2D borides or MBene has been accelerated after successful preparation of the 2D transition metal carbides or MXene.13,14 MXenes are extensively studied due to their attractive thermal, magnetic, mechanical and electric properties.15–20 MBenes were predicted to have similarly fascinating properties21–24 but have not yet been obtained experimentally, despite several prominent attempts.24–28
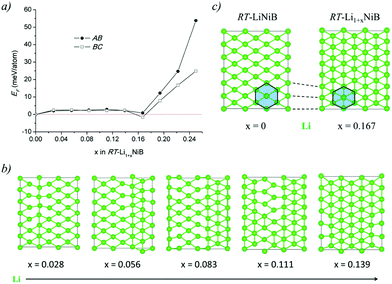
Recent theoretical investigation of the Li–Ni–B system29 revealed a new Li-rich layered compound Li2NiB, whose structure is derived from RT-LiNiB. According to the calculations, only a little extra energy is needed to accommodate an additional Li layer in the structure of the LiNiB parent phase. Here, we have experimentally explored the Li-rich compositions of the Li–Ni–B phase diagram and discovered two compounds that are Li-enriched versions of RT-LiNiB and HT-LiNiB polymorphs. Both RT-Li1+xNiB (x ∼ 0.17) and HT-Li1+yNiB (y ∼ 0.06) phases feature layered crystal structures with the original topology of the [NiB] layers modified due to the incorporation of extra Li between the layers. We use in situ synchrotron and laboratory powder X-ray diffraction, solid state NMR spectroscopy, and quantum chemical calculations to study structural relationships, reactivity, and phase transformations upon heating or exposure to air of these lithium-rich layered nickel borides.
Results and discussion
Synthesis and composition
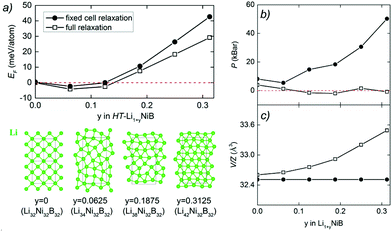
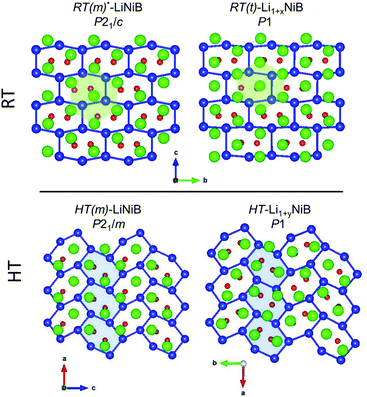
In our recent study,11 the Li–Ni–B ternary system was evaluated using an adaptive genetic algorithm (AGA) search for potentially stable ternary phases. As a result, a RT-LiNiB compound with a unique layered structure was computationally predicted and further synthesized experimentally using the hydride route. The structure of RT-LiNiB can be represented as almost planar [NiB] layers alternating with Li layers (Fig. 1).However, as evident from high-resolution synchrotron data, the real structure is more complex and includes intergrowth of two polytypes (Table 1). Above 1173 K RT-LiNiB transforms to its high-temperature polymorph HT-LiNiB featuring different topology of [NiB] and Li layers (Fig. 1).
| Phase (space group) | a, Å | b, Å | c, Å | α, ° | β, ° | γ, ° | V, Å3 | V/Z,e Å3 | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| a Different polytypes of RT-LiNiB compound. b Superstructure of two polytypes of RT-LiNiB. c Idealized structure of RT-Li1+xNiB compound. d Idealized structure of HT-Li1+yNiB compound. e Volume normalized per formula units. | |||||||||
| RT(m)-LiNiB (P21/c)a | 4.6114 | 4.8333 | 6.156 | 90 | 109.607 | 90 | 129.26 | 32.32 | 11 |
| RT*(m)-LiNiB (P21/c)b | 18.451 | 4.8336 | 6.1573 | 90 | 109.636 | 90 | 517.21 | 32.33 | 11 |
| RT(o)-LiNiB (Cmc21)a | 4.8341 | 6.1573 | 8.6888 | 90 | 90 | 90 | 258.62 | 32.33 | 11 |
| RT(m)-Li1+xNiB (P21/c)c | 18.277(1) | 4.86606(5) | 6.1818(2) | 90 | 107.623(1) | 90 | 524.00(2) | 32.75 | This work |
| RT(t)-Li1+xNiB (P1) | 18.2763(4) | 4.86589(3) | 18.5447(5) | 89.9810(6) | 107.6202(9) | 90.056(2) | 1571.82(3) | 32.75 | This work |
| HT-LiNiB (P21/m) | 3.9095 | 8.8087 | 7.5234 | 90 | 90.070 | 90 | 259.08 | 32.39 | 11 |
| HT(m)-Li1+yNiB (P21/c)d | 3.92591(7) | 7.5593(1) | 8.8181(2) | 90 | 92.6245(7) | 90 | 261.42(1) | 32.68 | This work |
| HT(t)-Li1+yNiB (P1) | 7.85184(9) | 15.1183(2) | 8.8179(1) | 89.9079(7) | 92.6271(5) | 90.0008(5) | 1045.63(3) | 32.68 | This work |
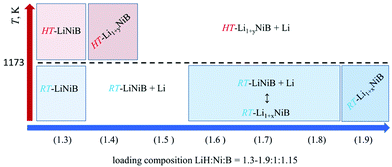
Previously we showed10,11 the hydride route is feasible for preparation of ternary lithium nickel borides providing fast reactions and accurate compositional control. The experimentally determined, LiH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni
Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B = 1.3
B = 1.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.15, molar ratio results in phase-pure samples of LiNiB phases with minimal excess of LiH and B needed.11 A further increase of the LiH ratio to values of 1.4 to 1.9 leads to stabilization of two new phases RT-Li1+xNiB and HT-Li1+yNiB (Table 1, Fig. 2). A slight excess of lithium hydride (LiH
1.15, molar ratio results in phase-pure samples of LiNiB phases with minimal excess of LiH and B needed.11 A further increase of the LiH ratio to values of 1.4 to 1.9 leads to stabilization of two new phases RT-Li1+xNiB and HT-Li1+yNiB (Table 1, Fig. 2). A slight excess of lithium hydride (LiH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni
Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B = 1.4
B = 1.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.15) is necessary for the synthesis of the HT-Li1+yNiB compound. For stabilization of the RT-Li1+xNiB phase, a considerable excess of LiH must be used (LiH
1.15) is necessary for the synthesis of the HT-Li1+yNiB compound. For stabilization of the RT-Li1+xNiB phase, a considerable excess of LiH must be used (LiH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni
Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B = 1.9
B = 1.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.15). Moreover, we found that synthesis of RT-Li1+xNiB compound requires that the sample be ground and annealed following the initial heating of precursors. After the first annealing, samples always comprise the RT-LiNiB phase. RT-LiNiB was the major phase and only a small amount of RT-Li1+xNiB compound was detected experimentally in the sample synthesized with loading composition LiH
1.15). Moreover, we found that synthesis of RT-Li1+xNiB compound requires that the sample be ground and annealed following the initial heating of precursors. After the first annealing, samples always comprise the RT-LiNiB phase. RT-LiNiB was the major phase and only a small amount of RT-Li1+xNiB compound was detected experimentally in the sample synthesized with loading composition LiH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni
Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B = 1.6
B = 1.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.15. With a further increase in Li content, the fraction of RT-Li1+xNiB increases accordingly (Fig. S2†), while loading composition LiH
1.15. With a further increase in Li content, the fraction of RT-Li1+xNiB increases accordingly (Fig. S2†), while loading composition LiH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni
Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B = 1.9
B = 1.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.15 gives phase pure RT-Li1+xNiB samples.
1.15 gives phase pure RT-Li1+xNiB samples.
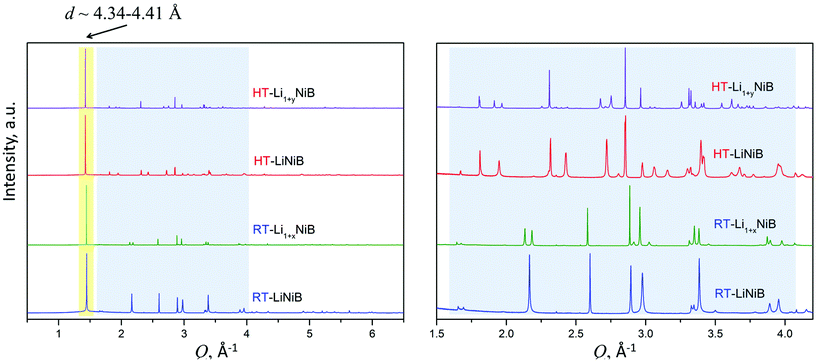
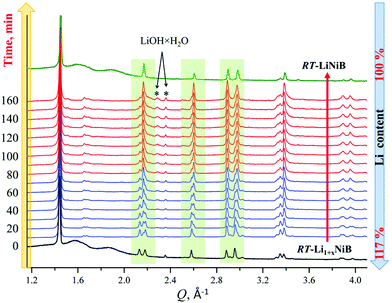
As evident from the high-resolution synchrotron powder X-ray diffraction (PXRD) data (Fig. 3), experimental PXRD patterns of RT-Li1+xNiB and HT-Li1+yNiB compounds are similar. Both feature an intensive peak corresponding to the interlayer distance of d ∼ 4.34–4.41 Å between the [NiB] layers (yellow-shaded, Fig. 3). In contrast, the structure of [NiB] layers in two phases is different, resulting in the difference in PXRD patterns (blue-shaded, Fig. 3).
Crystal structures
Determination of RT-Li1+xNiB and HT-Li1+yNiB crystal structures is challenging for several reasons: (1) extreme air-sensitivity (vide infra), (2) hydride synthesis did not yield large enough crystals suitable for laboratory single crystal X-ray diffraction; (3) the presence of light elements, Li and B, which makes X-ray data less informative, since heavier Ni atoms dominate X-ray scattering. Therefore, we used a synergistic combination of PXRD data refinement and theoretical calculations to elucidate crystal structures of RT-Li1+xNiB and HT-Li1+yNiB. Solving structures from PXRD data yields the positions of Ni atoms, thus the [NiB] layers (Tables S1–S6†). The structure of Li layers, including the atomic coordinates of extra-Li atoms in RT-Li1+xNiB and HT-Li1+yNiB, was determined using theoretical calculations.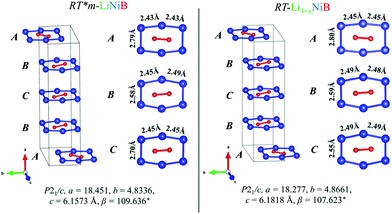 | ||
| Fig. 4 Comparison between [NiB] layers (ABCB stacking sequence) of RT-LiNiB and RT-Li1+xNiB compounds. Bond distances between Ni atoms in the [Ni6B2] units are highlighted. | ||
The unit cell volume of RT-Li1+xNiB is larger than that of RT*(m)-LiNiB, consistent with the incorporation of extra Li atoms (Table 1). This increased volume is due to the longer Ni–Ni distances within the Ni6B2 units leading to the slightly longer b and c parameters in the structure of RT-Li1+xNiB compared to RT*(m)-LiNiB.
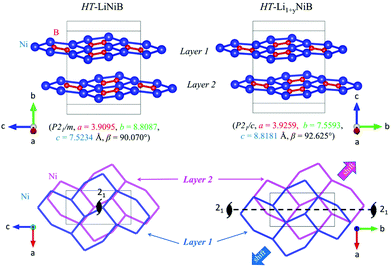
The topology of the [NiB] layers in HT-LiNiB and HT-Li1+yNiB compounds is similar. Here the fused Ni6B2 units form zig-zag chains within the layers. However, the stacking of [NiB] layers differs between the two compounds, resulting in the respective change of the space group from P21/m to P21/c, as well as in a swap of the b- and c-axes (Fig. 5 and Tables 1, S4–S6†). The [NiB] planar layers in HT-LiNiB are stacked along the two-fold screw axis 21, e.g. b axis is a stacking direction. On the contrary, for the HT-Li1+xNiB phase the c axis is a stacking direction, thus perpendicular to the axis 21. The change in the space group arises from the more pronounced relative shift between the two adjacent [NiB] layers in structure of HT-Li1+yNiB as compared to the HT-LiNiB structure (Fig. 5).
The Li layer configuration with x = 0.167 is stable in both AB-type and BC stacking types since they have the same formation energy as RT-LiNiB. Incorporation of extra Li atoms into the Li layer is accomplished by shortening of Li–Li distances to 2.6–2.8 Å, resulting in the denser hexagonal lattice (Fig. 6c) compared to RT-LiNiB (Li–Li distances ∼2.8–3.1 Å). The configurations with intermediate Li excess 0 < x < 0.167 form combinations of loose (x = 0) and dense (x = 0.167) hexagonal lattices, resulting in a locally disordered packing motif and have an excess in the formation energy in a range of 3 meV (Fig. 6a).
Temperature stability, reactivity and phase transformations
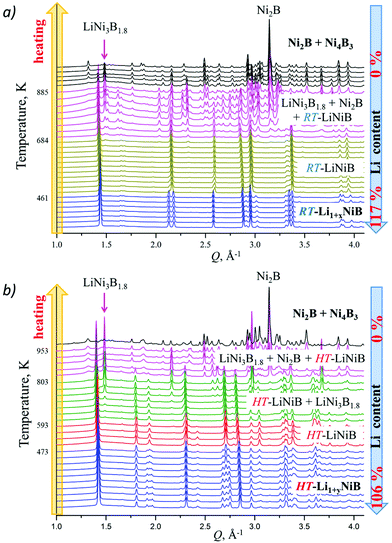
High-temperature synchrotron powder X-ray diffraction (HT-PXRD) was used to study the thermal stability of RT-Li1+xNiB and HT-Li1+yNiB. Samples were vacuum-sealed into silica capillaries for high temperature PXRD experiments. Upon heating Li is gradually “leached” from the structure, presumably reacting with silica. This leads to RT-Li1+xNiB and HT-Li1+yNiB transformation into RT-LiNiB and HT-LiNiB at 461 and 473 K, respectively (Fig. 9a and b). This again confirms the presence of extra Li atoms in RT-Li1+xNiB and HT-Li1+yNiB compared to their parent compounds. With a further increase in temperature above 684 K, RT-LiNiB transforms to Li-depleted LiNi3B1.8 phase10 and binary Ni2B. Between 684 K and 885 K, all three phases, RT-LiNiB, LiNi3B1.8 and binary Ni2B, are present. Above ∼885 K, binary nickel borides Ni2B, Ni4B3, Ni3B are the major products.Interestingly, HT-PXRD data of the HT-LiNiB polymorph (Fig. S13b†) shows considerable structural distortion, which was refined in the same structure type (same space group P21/m and Wyckoff sequence) (Table S7†). The distorted structure features substantially deformed Ni6B2 units within [NiB] layers and the relative shift of [NiB] layers (Fig. S13c and d†). This distorted structure was only observed in in situ PXRD experiments, while attempts to quench it from ∼620 K were not successful. With further increase in temperature, the HT-LiNiB phase decomposes into Li-depleted LiNi3B1.8, and finally, binary Ni borides similarly to RT-LiNiB polymorph (Fig. S13†).
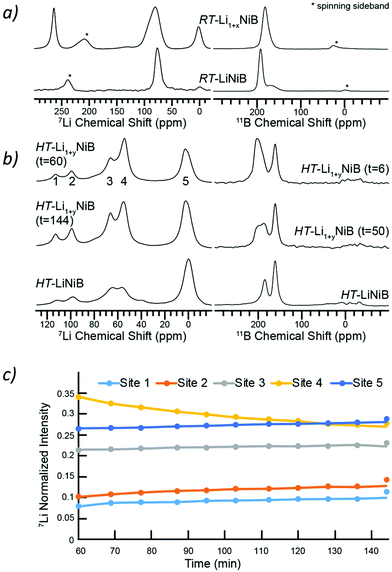
Solid-state NMR spectroscopy
To further shed light on the evolution of Li and B coordination environment upon incorporation of extra-Li in the structures of RT-Li1+xNiB and HT-Li1+yNiB compounds, 7Li and 11B solid-state magic angle spinning (MAS) NMR spectra were collected (Fig. 11a). The 7Li MAS NMR spectra of RT-Li1+xNiB compound have two major peaks at ∼265 and ∼80 ppm and a minor one at ∼0 ppm. The peak at 0 ppm originates from diamagnetic impurity phases, such as Li2O (2.8 ppm), LiOH·H2O (0.4 ppm), or LiOH (1.3 ppm), and is also present in 7Li MAS NMR spectrum of RT-LiNiB phase.11 The peak at 265 ppm is most likely due to a Li metal impurity,33 as a result of the significant excess of LiH required for synthesis and its further decomposition upon heating. The peak at ∼80 ppm is attributed to the RT-Li1+xNiB phase and is consistent with a single type of Li site expected in the structure. It is slightly positively shifted compared to the peak at ∼75 ppm for RT-LiNiB phase but within the range of 7Li chemical shifts in other Li-containing intermetallics.9,11 The slight increase in the 7Li chemical shift for RT-Li1+xNiB as compared to RT-LiNiB can likely be attributed to the subtle differences in the Li coordination environment in the two compounds. The increased width of the 7Li peak may be a result of the increased complexity of RT-Li1+xNiB structure, where extra Li atoms are incorporated between the [NiB] layers, leading to a variety of local 7Li environments and distribution of shifts. The peak at ∼80 pm is shifted to higher frequencies compared to the diamagnetic signal, indicative of Knight shift from conduction electrons, and thus metallic behavior is expected for RT-Li1+xNiB phase. The 7Li MAS NMR spectra of HT-Li1+yNiB is akin to HT-LiNiB and is distinctive from that of RT-Li1+xNiB and RT-LiNiB. There are two intense peaks at ∼55–65 ppm and two peaks with lower intensity at ∼95 and 110 ppm, in addition to the peak at ∼0 ppm (diamagnetic impurity, e.g. Li2O). Multiple peaks with positive chemical shifts are expected for HT-Li1+xNiB, since it would be consistent with its metallic nature and a structure model with three Li sites (2a, 2c, 4e, P21/c).The NMR spectroscopy data also confirms the high reactivity of HT-Li1+yNiB compound, which rapidly transforms in the air to HT-LiNiB compound (Fig. S14†). Fig. 11b shows the evolution of NMR spectra of a HT-Li1+xNiB sample with time while the sample is undergoing magic angle spinning in a 2.5 mm rotor. The nitrogen gas used for spinning is approximately 99.9% pure and the 2.5 mm rotors are not gas-tight. Hence the reaction is likely driven by the slow diffusion of residual oxygen and water in the MAS gas into the sample. There are clear variations in intensities of five observed 7Li peaks, likely because of the changes in Li local environment between the layers. Li is also partly deintercalated and forms Li2O, explaining the increased intensity of the 5th peak. During the course of MAS experiments, the 11B solid-state NMR spectra of HT-Li1+yNiB become more similar in appearance to HT-LiNiB.
The 11B solid-state NMR spectrum for RT-Li1+xNiB and HT-Li1+yNiB is consistent with their metallic behavior. The 150–220 ppm range of 11B chemical shifts is similar to the chemical shift observed for RT-LiNiB and HT-LiNiB compounds11 and other metallic borides and borocarbides.9,34,35 Boron atoms in all RT-Li1+xNiB, RT-LiNiB, HT-LiNiB, HT-Li1+yNiB layered phases form B–B pairs, which are further surrounded by 6 Ni atoms (Fig. 1, 4 and 5). However, the different topology of the layers, as well as differences in boron coordination by Li, likely explains the observed differences in the 11B solid-state NMR spectra.
Magnetic properties
Temperature dependence of the molar magnetic susceptibility in the range 5–300 K of RT-Li1+xNiB and HT-Li1+yNiB (Fig. S15†) is consistent with both phases being temperature-independent Pauli paramagnets. No magnetic ordering was observed down to 5 K. The field dependence of the magnetization in the same temperature range (Fig. S15†) at high magnetic field (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe–50
000 Oe–50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe) is linear with no tendency for saturation, which is again consistent with temperature independent paramagnetism. Small deviation from linearity of the field dependence of the magnetization at low magnetic field (0–10
000 Oe) is linear with no tendency for saturation, which is again consistent with temperature independent paramagnetism. Small deviation from linearity of the field dependence of the magnetization at low magnetic field (0–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe, see Fig. S15†) could be attributed to some magnetic moment bearing impurity, concentration of which is under the detection limit of X-ray analysis (below 1%). The intrinsic susceptibility values were estimated to be in the range of 0.7–1.2 × 10−4 emu mol−1 (Fig. S15†). The parent compounds RT-LiNiB and HT-LiNiB also exhibit temperature-independent paramagnetism.11 Thus, incorporation of additional Li atoms does not affect the magnetic properties. This is in stark contrast to the partial deintercalation of Li from paramagnetic LiNiB, inducing magnetic ordering in Li1−δNiB.12
000 Oe, see Fig. S15†) could be attributed to some magnetic moment bearing impurity, concentration of which is under the detection limit of X-ray analysis (below 1%). The intrinsic susceptibility values were estimated to be in the range of 0.7–1.2 × 10−4 emu mol−1 (Fig. S15†). The parent compounds RT-LiNiB and HT-LiNiB also exhibit temperature-independent paramagnetism.11 Thus, incorporation of additional Li atoms does not affect the magnetic properties. This is in stark contrast to the partial deintercalation of Li from paramagnetic LiNiB, inducing magnetic ordering in Li1−δNiB.12
Experimental
Synthesis
Starting materials for the synthesis were powders of lithium hydride (AlfaAesar, 99.4%), nickel (AlfaAesar, 99.996%), and boron (AlfaAesar, amorphous & crystalline, 98%). All manipulations of the starting materials and samples were performed in an argon-filled glovebox with p(O2) < 1 ppm. Powders of the starting materials (total mass = 0.3 g) were weighted in LiH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni
Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B = 1.9
B = 1.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.15 (RT-Li1+xNiB) and 1.4
1.15 (RT-Li1+xNiB) and 1.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.15 (HT-Li1+yNiB) molar ratios and loaded into polystyrene grinding vial set with slip-on cap. These loading compositions were determined empirically to get the highest yield of the target phases. The vials were then sealed into double-sided polypropylene bag under argon atmosphere and brought out for the powder mixing/milling using ball-mill (8000M MIXER/MILL) for 18 min (vials were enclosed in poly-bags during the process to ensure O2-free environment). Afterward, freshly prepared fine powders were loaded in Ta tubes inside argon-filled glovebox. The metal containers were sealed by arc-melting and placed into silica reactors equipped with Swagelok safety check valves to prevent over-pressurization of the reactors due to the release of hydrogen gas during the heat treatment. The silica reactors were evacuated down to 4 × 10−5 Bar and slowly (1.25 K min−1) heated from room temperature to 1173 K, held at that temperature for 12 hours and quenched into cold water for the preparation of HT-Li1+yNiB phase or cooled to room temperature by switching off furnace in the case of RT-Li1+xNiB phase. The second annealing of the manually ground sample loaded to the Ta tube using the same temperature profile was necessary to obtain RT-Li1+xNiB, otherwise RT-LiNiB compound forms. The synthesized compounds are air and moisture sensitive.
1.15 (HT-Li1+yNiB) molar ratios and loaded into polystyrene grinding vial set with slip-on cap. These loading compositions were determined empirically to get the highest yield of the target phases. The vials were then sealed into double-sided polypropylene bag under argon atmosphere and brought out for the powder mixing/milling using ball-mill (8000M MIXER/MILL) for 18 min (vials were enclosed in poly-bags during the process to ensure O2-free environment). Afterward, freshly prepared fine powders were loaded in Ta tubes inside argon-filled glovebox. The metal containers were sealed by arc-melting and placed into silica reactors equipped with Swagelok safety check valves to prevent over-pressurization of the reactors due to the release of hydrogen gas during the heat treatment. The silica reactors were evacuated down to 4 × 10−5 Bar and slowly (1.25 K min−1) heated from room temperature to 1173 K, held at that temperature for 12 hours and quenched into cold water for the preparation of HT-Li1+yNiB phase or cooled to room temperature by switching off furnace in the case of RT-Li1+xNiB phase. The second annealing of the manually ground sample loaded to the Ta tube using the same temperature profile was necessary to obtain RT-Li1+xNiB, otherwise RT-LiNiB compound forms. The synthesized compounds are air and moisture sensitive.
Powder X-ray diffraction
The purity of polycrystalline samples was checked using Rigaku MiniFlex600 powder diffractometer with Cu Kα radiation (λ = 1.54051 Å) and Ni-Kβ filter. Data were collected in zero-background plate holder for air-sensitive samples at room temperature. Phase analysis was performed using the PDF-2 database incorporated into PDXL2 program software.36 Powder diffractograms during controlled samples oxidation in the air were collected using open zero-background plate holder with ∼10 min time intervals.Crystal structure determination from synchrotron powder X-ray diffraction data
High-resolution synchrotron powder diffraction data were collected at beamline 11-BM-B Advanced Photon Source (APS), Argonne National Laboratory at 295 K and 100 K and λ = 0.412815 Å for a sample of RT-Li1+xNiB and λ = 0.412818 Å for a sample of HT-Li1+yNiB. Data were collected at ambient pressure.The unit cell symmetry, metrics, and atomic arrangement in the structures of RT-Li1+xNiB and HT-Li1+yNiB were obtained using program FOX for the ab initio structure determination from powder diffraction.37 After indexing, positions of heavy Ni atoms were determined and further refined in the triclinic space group P1. After the atomic coordinates of heavy Ni atoms were found, the structure was analyzed with the program Platon,38 and the correct space group was determined. The residual electron density peaks were assigned to tentative B and Li atomic positions based on the analysis of interatomic distances.
Rietveld refinement with the GSAS II software package39 was further performed using the derived structural models. The profile parameters, background parameters, zero shift, and cell parameters were refined first. The background was fitted using a shifted 24-points linear interpolation function, a pseudo-Voigt function was applied to generate the profile shape. Atomic coordinates of Ni atoms were refined, while atomic coordinates of light B and Li atoms were fixed to the values obtained computationally. Experimental details and crystallographic data are compiled in Tables S1–S3, Fig. S4–S7† (RT-Li1+xNiB), and Tables S4–S6, Fig. S8–S11† (HT-Li1+yNiB). The final refinements of the structures were performed with isotropic displacement parameters for all atoms. Crystal structures were visualized using the program VESTA 3.40
First-principles calculations were carried out using the density functional theory (DFT) within a generalized gradient approximation (GGA) of the exchange–correlation functional as implemented in the VASP code.42,43 The projector augmented-wave method44 was used to describe the valence configuration: 1s22s1 for Li, 3d84s2 for Ni, and 2s22p1 for B. The GGA exchange–correlation energy functional parametrized by Perdew, Burke, and Ernzerhof was used.45 A plane-wave basis was used with a kinetic energy cutoff of 650 eV. The Monkhorst–Pack's scheme46 was adopted for Brillouin zone sampling using a k-point grid with a spacing of 2π × 0.033 Å−1, and the ionic relaxations stopped when the forces on every atom became smaller than 0.01 eV Å−1.
Conclusions
Li chemical pressure is a driving force for the formation of RT-Li1+xNiB and HT-Li1+yNiB, which accommodate up to 16.7% and 12.5% excess Li into their structure compared to their parent compounds RT-LiNiB and HT-LiNiB. The crystal structures of RT-Li1+xNiB and HT-Li1+yNiB compounds are similar to that of RT-LiNiB and HT-LiNiB, built up from alternating Li layers with hexagonal or squared motif respectively, and [NiB] layers. The complex Li environments in layers of these two new compounds were determined using DFT methods, while subtle variations in the [NiB] layers were elucidated from synchrotron powder X-ray diffraction. Deintercalation of Li from the [NiB] layers was observed at elevated temperatures resulting in the gradual “leaching” of Li from the layers of these Li-enriched compounds and their subsequent transformation into their parent phases: RT-Li1+xNiB → RT-LiNiB at 461 K and HT-Li1+yNiB → HT-LiNiB at 473 K. Upon further heating decomposition into LiNi3B1.8 and finally, into binary nickel borides (∼900 K) takes place. Upon oxidation in air at room temperature, both RT-Li1+xNiB and HT-Li1+yNiB phases slowly release Li and transform to RT-LiNiB and HT-LiNiB compounds, respectively. Controlled oxidation and deintercalation as a route of further modification of layered LiNiB structures is a subject of future investigation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the National Science Foundation (DMR-1944551) CAREER award is gratefully acknowledged. A. J. R. and S. L. C. (NMR spectroscopy) and P. C. C. were supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Science and Engineering Division. The Ames Laboratory is operated for the U.S. Department of Energy by Iowa State University under contract #DE-AC02-07CH11358. X. Z., F. Z., and C. Z. W. were supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Science and Engineering Division including a grant of computer time at the National Energy Research Scientific Computing Centre (NERSC) in Berkeley, CA. Y. S. was supported by NSF Awards No. EAR-1918134 and No. EAR-1918126. K. M. H. was supported by NSF Awards No. EAR-1918134. R. A. R was supported by the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant GBMF4411. Use of the Advanced Photon Source at Argonne National Laboratory was supported by the U. S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under contract no. DE-AC02-06CH11357.References
- W. Jung, Ternäre Phasen im System Lithium-Nickel-Bor, Naturwissenschaften, 1976, 63, 246 CrossRef CAS
.
- W. Jung, Die Kristallstrukturen von Li3Ni20B6 und Li∼3Ni16B∼8, Z. Kristallogr., 1980, 151, 113–120 CAS
.
- W. Jung, Darstellung und Kristallstruktur von MgNi2.5B2 und Li1.2Ni2.5B2, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1977, 32, 1371–1374 Search PubMed
.
- T. Yi, S. Chen, S. Li, H. Yang, S. Bux, Z. Bian, N. A. Katcho, A. Shakouri, N. Mingo, J. P. Fleurial, N. D. Browning and S. M. Kauzlarich, Synthesis and characterization of Mg2Si/Si nanocomposites prepared from MgH2 and silicon, and their thermoelectric properties, J. Mater. Chem., 2012, 22, 24805–24813 RSC
.
- X. Ma, F. Xu, T. M. Atkins, A. M. Goforth, D. Neiner, A. Navrotsky and S. M. Kauzlarich, A versatile low temperature synthetic route to Zintl phase precursors: Na4Si4, Na4Ge4 and K4Ge4 as examples, Dalton Trans., 2009, 10250–10255 RSC
.
- J. V. Zaikina, M. Batuk, A. M. Abakumov, A. Navrotsky and S. M. Kauzlarich, Facile synthesis of Ba1−xKxFe2As2 superconductors via hydride route, J. Am. Chem. Soc., 2014, 136, 16932–16939 CrossRef CAS
.
- T. Cox, V. Gvozdetskyi, B. Owens-Baird and J. Zaikina, Rapid phase screening via hydride route: A discovery of K8−x,Zn18+3xSb16, Chem. Mater., 2018, 30, 8707–8715 CrossRef CAS
.
- V. Gvozdetskyi, B. Owens-Baird, S. Hong and J. Zaikina, Materials, 2019, 30, 2–14 Search PubMed
.
- V. Gvozdetskyi, M. P. Hanrahan, R. A. Ribeiro, T. Kim, L. Zhou, A. J. Rossini, P. C. Canfield and J. V. Zaikina, A hydride route to ternary alkali metal borides: a case study of lithium nickel borides, Chem. – Eur. J., 2019, 25, 4123–4135 CrossRef CAS
.
- V. Gvozdetskyi, B. Owens-Baird, S. Hong, T. Cox, G. Bhaskar, C. Harmer, Y. Sun, F. Zhang, C. Zh. Wang, K.-M. Ho and J. V. Zaikina, From NaZn4Sb3 to HT-Na1−xZn4−ySb3: Panoramic hydride synthesis, structural diversity, and thermoelectric properties, Chem. Mater., 2019, 31, 8695–8707 CrossRef CAS
.
- V. Gvozdetskyi, G. Bhaskar, M. Batuk, X. Zhao, R. Wang, S. Carnahan, M. Hanrahan, R. Ribeiro, P. Canfield, A. Rossini, C.-Z. Wang, K.-M. Ho, J. Hadermann and J. V. Zaikina, Computationally driven discovery of a family of layered LiNiB polymorphs, Angew. Chem., Int. Ed., 2019, 58, 15855–15862 CrossRef CAS
.
- G. Bhaskar, V. Gvozdetskyi, M. Batuk, K. Wiaderek, Y. Sun, R. Wang, C. Zhang, S. L. Carnahan, X. Wu, R. A. Ribeiro, S. L. Bud'ko, P. C. Canfield, W. Huang, A. J. Rossini, C.-Zh. Wang, K.-M. Ho, J. Hadermann and J. V. Zaikina, Topochemical deintercalation of Li from layered LiNiB: towards 2D MBene, manuscriptunder review, 2020.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Two–Dimensional Nanocrystals Produced by Exfoliation of Ti3AlC2, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS
.
- M. Alhabeb, K. Maleski, B. Anasori, P. Lelyukh, L. Clark, S. Sin and Y. Gogotsi, Guidelines for synthesis and processing of two-dimensional titanium carbide (Ti3C2Tx MXene), Chem. Mater., 2017, 29, 7633–7644 CrossRef CAS
.
- Y. Zhang, W. Tang, R. Zhan, H. Liu, H. Chen, J. Yang and M. Xu, An N-doped porous carbon/MXene composite as a sulfur host for lithium–sulfur batteries, Inorg. Chem. Front., 2019, 6, 2894–2899 RSC
.
- J. L. Hart, K. Hantanasirisakul, A. C. Lang, B. Anasori, D. Pinto, Y. Pivak, J. T. van Omme, S. J. May, Y. Gogotsi and M. L. Taheri, Control of MXenes electronic properties through termination and intercalation, Nat. Commun., 2019, 10, 522 CrossRef CAS
.
- M. Zhang, X. Chen, J. Sui, B. S. Abraha, Y. Li, W. Peng, G. L. Zhang, F. Zhang and X. Fan, Improving the performance of a titanium carbide MXene in supercapacitors by partial oxidation treatment, Inorg. Chem. Front., 2020, 7, 1205–1211 RSC
.
- J. Pang, R. G. Mendes, A. Bachmatiuk, L. Zhao, H. Q. Ta, T. Gemming, H. Liu, Z. Liu and M. Rummeli, 3D flexible, conductive, and recyclable Ti3C2Tx MXene-Melamine foam for high-areal-capacity and long-lifetime alkali-metal anode, Chem. Soc., 2019, 48/1, 1–408 Search PubMed
.
- G. Du, M. Tao, W. Gao, Y. Zhang, R. Zhan, S. Bao and M. Xugg, TiS2 nanosheets for efficient electrocatalytic N2 fixation to NH3 under ambient conditions, Inorg. Chem. Front., 2019, 6, 1986–1989 RSC
.
- S. Chen, Y. Xiang, W. Xu and C. Peng, A novel MnO2/MXene composite prepared by electrostatic self-assembly and its use as an electrode for enhanced supercapacitive performance, Inorg. Chem. Front., 2019, 6, 199–208 RSC
.
- M. Khazaei, J. Wang, M. Estili, A. Ranjbar, S. Suehara, S. Arai, K. Esfarjani and S. Yunoki, Novel MAB phases and insights into their exfoliation into 2D MBenes, Nanoscale, 2019, 11, 11305–11314 RSC
.
- Z. Jiang, P. Wang, X. Jiang and J. Zhao, MBene (MnB): a new type of 2D metallic ferromagnet with high Curie temperature, Nanoscale Horiz., 2018, 3, 335–341 RSC
.
- Z. Guo, J. Zhou and Z. Sun, New two-dimensional transition metal borides for Li ion batteries and electrocatalysis, J. Mater. Chem. A, 2017, 5, 23530–23535 RSC
.
- T. Bo, P. F. Liu, J. Zhang, F. Wang and B. T. Wang, Tetragonal and trigonal Mo2B2 monolayers: two new low-dimensional materials for Li-ion and Na-ion batteries, Phys. Chem. Chem. Phys., 2019, 21, 5178–5188 RSC
.
- H. Nishino, T. Fujita, N. Cuong, S. Tominaka, M. Miyauchi, S. Limura, A. Hirata, N. Umezawa, S. Okada, E. Nishibori, A. Fujino, T. Fujimori, S. Ito, J. Nakamura, H. Hosono and T. Kondo, Formation and Characterization of Hydrogen Boride Sheets Derived from MgB2 by Cation Exchange, J. Am. Chem. Soc., 2017, 139, 13761–13769 CrossRef CAS
.
- L. T. Alameda, P. Moradifar, Z. P. Metzger, N. Alem and R. E. Schaak, Topochemical deintercalation of Al from MoAlB: stepwise etching pathway, layered intergrowth structures, and two-dimensional MBene, J. Am. Chem. Soc., 2018, 140, 8833–8840 CrossRef CAS
.
- L. T. Alameda, R. W. Lord, J. A. Barr, P. Moradifar, Z. P. Metzger, B. C. Steimle, C. F. Holder, N. Alem, S. B. Sinnott and R. E. Schaak, Multi-Step Topochemical pathway to metastable Mo2AlB2 and related two-dimensional nanosheet heterostructures, J. Am. Chem. Soc., 2019, 141, 10852–10861 CrossRef CAS
.
- J. Wang, T. N. Ye, Y. Gong, J. Wu, N. Miao, T. Tada and H. Hosono, Discovery of hexagonal ternary phase Ti2InB2 and its evolution to layered boride TiB, Nat. Commun., 2019, 10, 2284 CrossRef
.
- R. Wang, Y. Sun, V. Gvozdetskyi, X. Zhao, F. Zhang, L.-H. Xu, J. V. Zaikina, Z. Lin, C.-Z. Wang and K.-M. Ho, Theoretical search for possible Li–Ni–B crystal structures using an adaptive genetic algorithm, J. Appl. Phys., 2020, 127, 094902 CrossRef CAS
.
- S. Q. Wu, M. Ji, C. Z. Wang, M. C. Nguyen, X. Zhao, K. Umemoto, R. M. Wentzcovitch and K. M. Ho, An adaptive genetic algorithm for crystal structure prediction, J. Phys.: Condens. Matter, 2014, 26, 035402 CrossRef CAS
.
- X. Zhao, M. C. Nguyen, W. Y. Zhang, C. Z. Wang, M. J. Kramer, D. J. Sellmyer, X. Z. Li, F. Zhang, L. Q. Ke, V. P. Antropov and K. M. Ho, Exploring the Structural Complexity of Intermetallic Compounds by an Adaptive Genetic Algorithm, Phys. Rev. Lett., 2014, 112, 045502 CrossRef CAS
.
- M. S. Daw and M. I. Baskes, Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals, Phys. Rev. Lett., 1983, 50, 1285–1288 CrossRef CAS
.
- R. Bhattacharyya, B. Key, H. Chen, A. S. Best, A. F. Hollenkamp and C. P. Grey, In situ NMR observation of the formation of metallic lithium microstructures in lithium batteries, Nat. Mater., 2010, 9, 504–510 CrossRef CAS
.
- D. Koumoulis, J. P. Scheifers, R. S. Touzani, B. P. T. Fokwa and L. S. Bouchard, Pseudogap formation and vacancy ordering in the new perovskite boride Zr2Ir6B, Acta Mater., 2016, 120, 32–39 CrossRef CAS
.
- R. E. J. Sears,
11B chemical shifts and quadrupole coupling constants in the alkaline–earth hexaborides, J. Chem. Phys., 1982, 76, 5651–5652 CrossRef CAS
.
-
PDXL: Integrated X-ray powder diffraction software, Version 2.8.1.1, Rigaku, 2018 Search PubMed
.
- V. Favre-Nicolin and R. Cerny, FOX, “free objects for crystallography”: a modular approach to ab initio structure determination from powder diffraction, J. Appl. Crystallogr., 2002, 35, 734–743 CrossRef CAS
.
- A. L. Spek, Structure validation in chemical crystallography, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS
.
- B. H. Toby and R. B. Von Dreele, GSAS-II: the genesis of a modern open-source all purpose crystallography software package, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS
.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS
.
- P. J. Chupas, K. W. Chapman, C. Kurtz, J. C. Hanson, P. L. Lee and C. P. Grey, A versatile sample-environment cell for non-ambient X-ray scattering experiments, J. Appl. Crystallogr., 2008, 41, 822–824 CrossRef CAS
.
- G. Kresse and J. Furthmuller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS
.
- P. E. Bloechl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef CAS
.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available: Tables with crystallographic information, figures with PXRD patterns, Rietveld refinements plots, magnetic susceptibility plots. CCDC 2031377, 2031379, 2031381, 2031382, 2031386, 2031387, 2031389, 2031390. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0qi01150a |
| This journal is © the Partner Organisations 2021 |