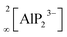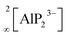Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Supertetrahedral polyanionic network in the first lithium phosphidoindate Li3InP2 – structural similarity to Li2SiP2 and Li2GeP2 and dissimilarity to Li3AlP2 and Li3GaP2†
Tassilo M. F.
Restle
a,
Volker L.
Deringer
 b,
Jan
Meyer
a,
Gabriele
Raudaschl-Sieber
a and
Thomas F.
Fässler
b,
Jan
Meyer
a,
Gabriele
Raudaschl-Sieber
a and
Thomas F.
Fässler
 *a
*a
aDepartment of Chemistry, Technische Universität München, Lichtenbergstraße 4, D-85747 Garching, Germany. E-mail: Thomas.Faessler@lrz.tum.de
bDepartment of Chemistry, University of Oxford, South Parks Road, Oxford OX1 3QR, UK
First published on 27th November 2020
Abstract
Phosphide-based materials have been investigated as promising candidates for solid electrolytes, among which the recently reported Li9AlP4 displays an ionic conductivity of 3 mS cm−1. While the phases Li–Al–P and Li–Ga–P have already been investigated, no ternary indium-based phosphide has been reported up to now. Here, we describe the synthesis and characterization of the first lithium phosphidoindate Li3InP2, which is easily accessible via ball milling of the elements and subsequent annealing. Li3InP2 crystallizes in the tetragonal space group I41/acd with lattice parameters of a = 12.0007(2) and c = 23.917(5) Å, featuring a supertetrahedral polyanionic framework of interconnected InP4 tetrahedra. All lithium atoms occupy tetrahedral voids with no partial occupation. Remarkably, Li3InP2 is not isotypic to the previously reported homologues Li3AlP2 and Li3GaP2, which both crystallize in the space group Cmce and feature 2D layers of connected tetrahedra but no supertetrahedral framework. DFT computations support the observed stability of Li3InP2. A detailed geometrical analysis leads to a more general insight into the structural factors governing lithium ion mobility in phosphide-based materials: in the non-ionic conducting Li3InP2 the Li ions exclusively occupy tetrahedral voids in the distorted close packing of P atoms, whereas partially filled octahedral voids are present in the moderate ionic conductors Li2SiP2 and Li2GeP2.
Introduction
All-solid-state batteries (ASSB) have recently become the focus of research as an attractive alternative to state-of-the-art liquid-based batteries due to their enhanced safety combined with high energy/power density and mechanical stability.1–7 One of the main obstacles for the commercialization of ASSBs is the difficulty to develop superionic solid conductors, which are crucial for fast ionic diffusion in ASSBs. Recently, our group investigated new classes of lithium ion conductors based on phosphides. Starting with Li8SiP4 in 2016, we introduced phosphidosilicates with an ionic conductivity of 4.5 × 10−5 S cm−1.8 Lately, in the Li-richer compound Li14SiP6 the conductivity was even higher with up to 1 × 10−3 S cm−1.9 Furthermore, we extended the system to the heavier tetrel (group-14) homologues, phosphidogermanates, with two Li-ion conducting modifications of Li8GeP4 that show ionic conductivities of up to 8.6 × 10−5 S cm−1 and with Li14GeP6, which achieves an ionic conductivity of 1.7 × 10−3 S cm−1.10,11 The structural building units in these phosphides are [TtP4]8− tetrahedra surrounded by lithium atoms (Tt = Si, Ge). They exhibit a huge structural variety, and by decreasing the amount of lithium, condensed and covalently connected tetrahedra are formed, thereby offering different polyanionic networks: Li10Si2P6 features pairs of edge-sharing SiP4 tetrahedra,12 in Li2SiP2/Li2GeP2 and LiSi2P3, respectively, SiP4 and GeP4 tetrahedra are condensed to networks of supertetrahedra.8,13,14 Layered structures have been reported as well: in Li3Si3P7, vertex-sharing SiP4 tetrahedra form double layers,12 and LiGe3P3 is built up by a two dimensionally extended polyanion comprising GeP4 and Ge(P3Ge) tetrahedra.13Phosphide-based materials as lithium ionic conductors originated from the aliovalent substitution of [TtS4]4− tetrahedra, which are the main building block in sulfide-based conductors. This leads to analogous structures with more negatively charged [TtP4]8− tetrahedra, which can therefore accommodate more lithium than the well-known sulfur-based analogues. In recent investigations we expanded this class of compound further to phosphidoaluminates, which contain tetrahedral AlP4 building units, and we discovered the fast lithium ion conductor Li9AlP4, which shows ionic conductivities of 3 × 10−3 S cm−1.15 In addition, we also obtained Li3AlP2, which is built up by 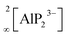 layers of corner- and edge-sharing AlP4 tetrahedra,16 and we then also introduced the isotypic gallium compound Li3GaP2 as the first phosphidogallate.16 Both trielate (Tr = Al, Ga) compounds do not show moderate lithium ion conductivity but unexpectedly turned out to be direct band gap semiconductors with optical band gaps of 3.1 and 2.8 eV, respectively.
layers of corner- and edge-sharing AlP4 tetrahedra,16 and we then also introduced the isotypic gallium compound Li3GaP2 as the first phosphidogallate.16 Both trielate (Tr = Al, Ga) compounds do not show moderate lithium ion conductivity but unexpectedly turned out to be direct band gap semiconductors with optical band gaps of 3.1 and 2.8 eV, respectively.
Prior to the present work, no ternary Li–In–P phase has been described in the literature, and only one ternary Na–In–P phase was mentioned: Na3InP2 is built up by a distorted hcp of P atoms with all octahedral voids filled by Na, whereas the tetrahedral voids are occupied by Na and In, giving rise to a polyanionic network of corner-sharing InP4 tetrahedra.17
In the present work, we report the first lithium phosphidoindate, Li3InP2, synthesized via ball milling of the elements and subsequent annealing. The compound retains the principal structural building unit of TrP4 tetrahedra, but their arrangement is notably different from that of Li3AlP2 and Li3GaP2. In Li3InP2, the InP4 tetrahedra are condensed to supertetrahedra in a three-dimensional framework. The structure is determined by single crystal X-ray diffraction and analyzed by complementary solid-state NMR experiments and first-principles computations. The knowledge of the lithium ion mobilities of the now-completed series of phosphidotrielates allows us to suggest a structural design rule linked to ionic conductivity, namely, the presence (or absence) of partially occupied Li-containing octahedral sites between which the ions can move rapidly.
Results and discussion
Synthesis and structure of Li3InP2
Li3InP2 was synthesized from the elements via a two-step procedure. At first, stoichiometric amounts of lithium, indium and phosphorus were ball milled resulting in a reactive mixture. Besides small amounts of the desired phase, Li3InP2, the polycrystalline powder contains considerable amounts of InP and Li0.3In1.7 (see Fig. S4†). Subsequently, pellets of the mixture were annealed in sealed niobium ampules at 1023 K for 22 h. Afterwards, the ampoules were rapidly cooled to room temperature by quenching in an ice-water mixture yielding almost phase-pure Li3InP2 with 3.3(1) % Li0.3In1.7 as an impurity according to Rietveld analysis (Fig. S3†). Annealing at lower temperatures such as 673 K or slow cooling rates led to impurities such as InP. Powdered Li3InP2 is brick-red. Complete data of the Rietveld refinement are given in the ESI; Tables S5 and S6.†Red single crystals of Li3InP2 were obtained after reacting the elements with the formal stoichiometry “Li3In2P3” at 1073 K in tantalum ampoules. Besides Li3InP2, the resulting product contains InP and at least one more, so far unknown phase according to unassigned reflections in the powder X-ray diffractogram (see Fig. S5†). Details of the structure refinement of the single crystal X-ray diffraction data of Li3InP2 are listed in the ESI in Tables S1–S4.†
According to the single crystal structure determination, Li3InP2 crystallizes in the tetragonal space group I41/acd (no. 142) with seven independent crystallographic positions (one for In, three each for Li and P; Table S2†). Considering that the crystal structure is based on a tetragonally distorted cubic close packing of phosphorus atoms, the multiplicity of the phosphorus Wyckoff positions (32g + 16e + 16e) leads to a total of 128 tetrahedral voids and 64 octahedral voids. One quarter of these tetrahedral voids is filled by the indium atoms (Wyckoff position 32g). The remaining 96 tetrahedral voids are occupied by lithium (3 × 32g). Hence, the tetrahedral voids are fully occupied, whereas all octahedral voids are empty. The unit cell determined by single crystal X-ray diffraction is displayed in Fig. 1a.
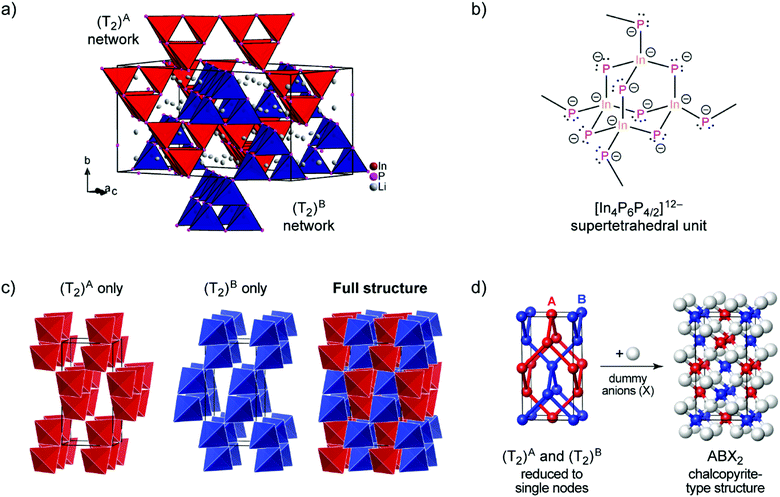 | ||
| Fig. 1 (a) The crystal structure of Li3InP2. The T2-supertetrahedra consist of four InP4 tetrahedra and form two independent adamantane-like networks (the two networks, denoted as (T2)A and (T2)B, are shown in red and blue color, respectively). Li+ ions are located in tetrahedral voids of the distorted ccp of P atoms. Li, In and P atoms are depicted in grey, brown and purple color, respectively (displacement ellipsoids set at 90% at 150 K). Crystal data and structure refinement are shown in Tables S1–S4 in the ESI.† CSD 2026514 contains the ESI crystallographic data for this paper.† (b) Lewis structure with formal charges of the atoms. (c) The two independent adamantane-like supertetrahedral networks (T2)A and (T2)B and the penetration of the two networks (each T2 unit is represented by a tetrahedron). (d) A simplified view of the structure, in which the center of gravity of each T2 unit is represented by a colored sphere (“node”), inspired by ref. 18 Notice: the ABX2 chalcopyrite structure type is formed by the formal insertion of X atoms shown as grey spheres. Structural drawings in panels (c and d) were created using VESTA.19 | ||
Indium and phosphorus form InP4 tetrahedra, and four corner-sharing InP4 tetrahedra build a T2-supertetrahedron. These T2-supertetrahedra are interconnected via corners, yielding two independent adamantane-like networks, which are shown in red and blue colors in Fig. 1a and c.
The In and P atoms are covalently connected to four and two atoms, respectively, resulting in a formal negative charge for both In and P of (−1). Since the P atoms at the corner of the supertetrahedron are shared with the next supertetrahedron, one such unit can be written as [In4P6P4/2]12− (Fig. 1b), which leads to an electronically balanced formula Li3InP2 (≡(Li+)12[In4P6P4/2]12− or Li12In4P8).
The InP4 units slightly deviate from an ideal tetrahedron with P–In–P angles ranging from 107.20(1) to 111.55(1)°. The bond lengths within the InP4 tetrahedra are in the narrow range between 2.5676(5) and 2.5899(5) Å and are very similar to those in compounds with strong In–P interactions like InP (2.5412(1) Å)20 and Na3InP2 (2.592(3)–2.682(3) Å)17 and in excellent agreement with DFT computations after full structural optimization (2.57–2.58 Å). The Li–P bonds in Li3InP2 range from 2.526(2) to 2.673(2) Å and are in good agreement with those in other binary or ternary phases containing Li and P.8–10,12,13,15 DFT optimization yields 2.51–2.67 Å, again practically superimposable with the experimental results.
Considering each center of gravity of the supertetrahedra, the arrangement of the independent networks of the T2-supertetrahedra corresponds in a hierarchical relationship to the arrangement of the Cu and Fe cations in the chalcopyrite structure, which is highlighted in Fig. 1d. The concept of supertetrahedra is already known in the literature, including supertetrahedral sulfides,21,22 which show structures with huge cavities, and also phosphidosilicates.8,23
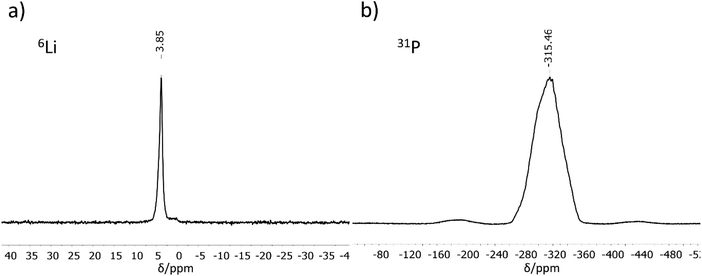
MAS-NMR spectroscopy
6Li and 31P MAS-NMR measurements (Fig. 2) support the results of the crystal structure determination. The 6Li NMR spectrum shows only one signal with a chemical shift of 3.85 ppm. As expected, the NMR experiment cannot distinguish between the three crystallographically different lithium atoms, all of which are tetrahedrally coordinated by phosphorus in a very similar chemical environment. The chemical shift of the Li atoms is in the same range as those for related compounds like Li9AlP4 (4.2 ppm), Li3AlP2 (4.0 and 3.0 ppm), Li3GaP2 (4.1 and 3.4 ppm), Li2SiP2 (2.1 ppm from 7Li MAS-NMR spectroscopy), and Li2GeP2 (3.6 and 2.4 ppm).8,13,15,16 Compared to the above-mentioned compounds with two signals in the 6Li NMR spectrum, the difference in local coordination, which is expressed by the P–Li–P angles, is the lowest for Li3InP2 (Li3InP2: 104.99(8)–113.25(8)°, Li3AlP2: 100.0(3)–116.647(1)°, Li3GaP2: 102.258(1)–115.2(3)°, Li2GeP2: 84.68(1)–158.89(2)°). The 31P NMR spectrum displays a very broad, asymmetric signal in the range of −260 to −360 ppm. This range is typical for chemical shifts of two-fold connected P1− atoms such as in Li3AlP2 (−300 and −308.7 ppm) or Li3GaP2 (−234.8 and −280.5 ppm).16 However, the signals of two-fold connected P1− atoms in the related phosphidotetrelates are much more downfield shifted (Li2SiP2: −129.1 and −241.5 ppm and Li2GeP2: −59.9, −164.8 and −178.4 ppm) due to the deshielding of the more electronegative tetrel elements compared to indium.8,13Interestingly, only one 31P NMR signal is observed for Li3InP2, whereas two signals are obtained for all other related compounds. This correlates with the fact that the smallest distortion of the E–P–E bond angles is observed for Li3InP2 [106.411(9)–111.41(1)°] if compared to the others with E = Al, Ga, In, Si, Ge such as Li3AlP2 [78.298(1)–111.709(1)°], Li3GaP2 [79.943(1)–110.253(1)°], Li2SiP2 [102.669(9)–114.937(9)°], and Li2GeP2 [101.726(7)–112.609(7)°].
Comparison of Li3InP2 with the lighter homologues Li3AlP2 and Li3GaP2
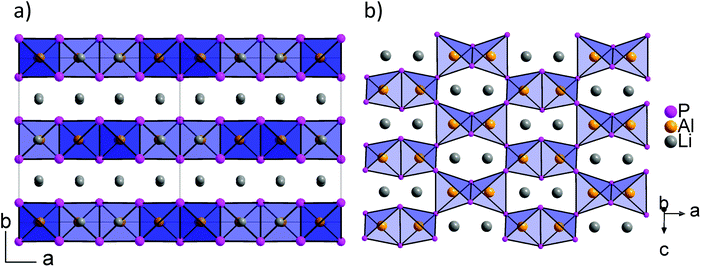
Recently, we described the two isotypic phases Li3AlP2 and Li3GaP2,16 which crystallize in a distorted orthorhombic packing of phosphorus atoms in the space group Cmce (no. 64) with lattice parameters a = 11.5138(2), b = 11.7634(2), c = 5.8202(1) Å and a = 11.5839(2), b = 11.7809(2), c = 5.8129(2) Å, respectively, both determined by Rietveld refinement at room temperature. The crystal structures are built up by corner- and edge-sharing TrP4 (Tr = Al, Ga) tetrahedra in two-dimensional layers. Based on a close packing of P atoms, the lithium atoms are located in all tetrahedral voids (Fig. 3). By contrast, Li3InP2 crystallizes in a tetragonal distorted phosphorus lattice in the space group I41/acd (no. 142) with lattice parameters of a = 12.03049(8) and c = 23.9641(3) Å, determined by Rietveld refinement at room temperature, and as mentioned above, the single crystal structure determination reveals a three-dimensional structure with exclusively corner-sharing InP4 tetrahedra for t-Li3InP2 (Fig. 1).
layers. Based on a close packing of P atoms, the lithium atoms are located in all tetrahedral voids (Fig. 3). By contrast, Li3InP2 crystallizes in a tetragonal distorted phosphorus lattice in the space group I41/acd (no. 142) with lattice parameters of a = 12.03049(8) and c = 23.9641(3) Å, determined by Rietveld refinement at room temperature, and as mentioned above, the single crystal structure determination reveals a three-dimensional structure with exclusively corner-sharing InP4 tetrahedra for t-Li3InP2 (Fig. 1).
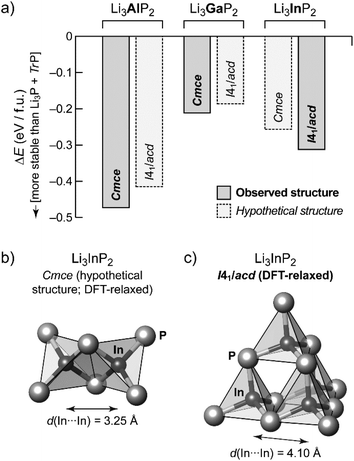
In order to gain additional insight into the experimentally observed structure types, we performed DFT-based structural optimizations for the Al, Ga and In compounds using the PBEsol functional24 as implemented in CASTEP25 (computational details are given in the ESI†). In addition to the experimentally determined unit cells we performed a substitutional “cross-check”: both modifications, orthorhombic o-Li3TrP2 and tetragonal t-Li3TrP2, were used for Tr = Al, Ga and In, starting either from the experimentally determined structure or from a hypothetical one obtained by substituting the Tr species. The DFT-optimized cell parameters are in excellent agreement with the experiment for the title compound (we obtained aDFT = 11.96 Å and cDFT = 23.74 Å); full results are listed in Table S7.†Fig. 4a shows the resulting energies, relative to the respective binary phosphides similar in spirit to our recent work on Li9AlP4.15 We compute the DFT electronic energy, E, for the relaxed ternary structure as well as for Li3P and the respective zinc blende-type phase of AlP, GaP or InP; the difference (in the sense of a “reaction energy”) then allows us to estimate the stability of the ternary phase:
| ΔE = E(Li3TrP2) − [E(Li3P) + E(TrP)] |
Negative values of ΔE therefore indicate that the ternary phase is stable with respect to the binaries (Fig. 4a).
The compounds Li3TrP2 are energetically favored over their respective binary components Li3P and AlP, GaP and InP. The latter all adapt the cubic zinc blende type. The energy gain is significant considering the known stability of the zinc blende type that is most frequent among III–V semiconductors. More importantly, the difference in pairs of ΔE values allows us to compare the tendency for assuming either the Cmce or the I41/acd structure for all of the Li3TrP2 phases. For the Al and Ga compounds, the Cmce structure is favored by about 0.06 and 0.03 eV per formula unit (f.u.), respectively; by contrast, the I41/acd structure is preferred for Li3InP2 (by about 0.06 eV f.u.−1), all in agreement with experiments. The stabilization of the title compound compared to the constituent binary phosphides is computed to be 0.31 eV f.u.−1 (indicated by a negative sign in the convention of Fig. 4a), which represents a significant gain in stability and explains the synthetic accessibility of the ternary compound. Whilst there will always remain a certain error due to the DFT approximation and the neglect of thermal effects, we do trust that the computed trends shown in Fig. 4a are robust, and we note that they are fully consistent with the experimental observations.
As expected, the unit cell volume for the heavier homologues increases, however the In compound shows a much stronger increase: 788.30 Å3 for Al and 793.28 Å3 for Ga if compared to 867.10 Å3 (=3468.39 Å3:4) for In. This correlates with a larger increase of the size of the InP4 tetrahedron (8.8857 Å3) compared to AlP4 (7.0897 Å3) and GaP4 (7.1334 Å3).
The trends of the interatomic Tr–Tr (Tr = Al, Ga, In) distances in Li3AlP2, Li3GaP2 and Li3InP2 are listed in Table 1. Regarding the different orthorhombic (Li3AlP2, Li3GaP2) and tetragonal structures (Li3InP2), the interatomic distances of the metal atoms are shorter in the orthorhombic structures, where edge-sharing tetrahedra occur compared to the tetragonal structure, where only corner-sharing tetrahedra are present. One may ask for the origin of the preference of one structure type over the other when comparing all three phosphidotrielates side-by-side. Interestingly, the results of the calculations are in agreement with Pauling's third rule. At least qualitatively and within the limits of such empirical concepts,26 edge-sharing tetrahedra are disfavored on account of the repulsion of positively charged central atoms (Fig. 4b and c). This effect might be expected to be strongest in the In compound, where not only the ionic radius is the largest of the three, but the computed Mulliken charges for the series of Cmce structures (Al: +0.42e, Ga: +0.57e, hypothetical In structure: +0.65e) appear to be consistent with an increasing repulsion of Tr atoms in the case of edge-sharing tetrahedra. Note that the Mulliken charges, derived from quantum-mechanical computation, are not to the same as the formal negative charge of the Tr atom using the Lewis valence model (Fig. 1b). Accordingly, a structure containing edge-sharing tetrahedra is observed for Li3AlP2 and Li3GaP2, but not for Li3InP2 (Fig. 4c). This trend of the differences of the different metal to metal distances by DFT calculation is confirmed by the experimental interatomic Tr–Tr (Tr = Al, Ga, In) distances (Table 1). The experimental In–In distance is significantly longer than the Al–Al or Ga–Ga distances (4.116(3) Å (In) vs. 3.028(5) Å (Al) and 3.089(2) Å (Ga)).
| o-Li3AlP2 | o-Li3GaP2 | t-Li3InP2 | |
|---|---|---|---|
| Cell volume/Å3 | 788.29(2) | 793.28(2) | 3468.39(6) (3468.39:4 = 867.10) |
| Volume per formula unit/Å3 | 98.54 | 99.16 | 108.38 |
| Tetrahedron volume/Å3 | 7.0897 | 7.1334 | 8.8857 |
| Tr–Tr distances/Å | 3.028(5) | 3.089(2) | 4.116(3) |
Comparison of Li3InP2 with the phosphidotetrelates Li2SiP2 and Li2GeP2
The crystal structure of Li3InP2 is related to the structure of Li2SiP2 and Li2GeP2.8,13 The two latter isotypic phases also crystallize in the space group I41/acd (no. 142), with lattice parameters of a = 12.1111(1) and c = 18.6299(4) Å for Li2SiP2 and a = 12.3070(1) and c = 19.0307(4) Å for Li2GeP2 and a slightly longer a, but much shorter c parameter as compared to Li3InP2. A full comparison of the lattice parameters and the tetrahedral volumes in Li3InP2, Li2SiP2 and Li2GeP2 is given in Table 2.| Li3InP2 | Li2SiP2 | Li2GeP2 | |
|---|---|---|---|
| a/Å | 12.0007(2) | 12.1111(1) | 12.3070(1) |
| c/Å | 23.917(5) | 18.6299(4) | 19.0307(4) |
| V/Å3 | 3447.7(1) | 2732.61(7) | 2882.42(9) |
| V (Tr/Tt)P4 tetrahedra/Å3 | 8.7944 | 5.8042 | 6.4083 |
| Distances (Å) between the centers of the T2-supertetrahedra | 8.4729(1), 8.4899(9) | 7.6395(1), 8.5638(1) | 7.7782(1), 8.7023(1) |
Assuming an average volume of 18 Å3 per heavy atom, the increase in cell volume corresponds approximately to the volume of 32 additional lithium atoms in the unit cell of Li2SiP2. Besides the change in the number of Li atoms, also the larger volume of the InP4 tetrahedra compared to SiP4/GeP4 (see Table 2) contributes to an overall increase of the volume. However, this increase is highly anisotropic, since in Li3InP2 the lattice parameter c increases strongly, whereas the lattice parameter a is even slightly shorter compared to the one in Li2SiP2 and Li2GeP2.
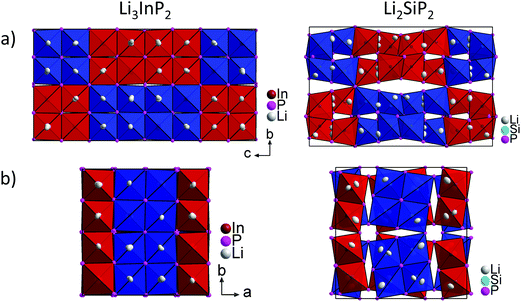
Fig. 5 shows a comparison of the structures of Li3InP2 and Li2SiP2 viewed along the a and c direction. In Li3InP2 the InP4 tetrahedra respectively the T2-supertetrahedra are aligned in an almost parallel fashion, whereas in Li2SiP2 the T2-supertetrahedra are rotated along the tetragonal axes. Interestingly, the parallel alignment in Li3InP2 leads to a slight decrease of the a and b axes despite the higher lithium content, but to a significant increase of the c axes.
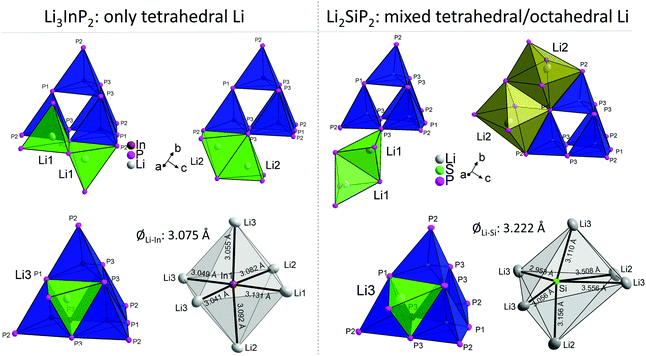
In Table 3 the Wyckoff positions in Li3InP2 and Li2SiP2 are compared (Li2GeP2 is omitted since it is isotypic to Li2SiP2). The higher Li content of the In compound arises from the occupation of two 32g Wyckoff sites instead of two 16f sites in the tetrelates. As a consequence, the coordination environments of the lithium atoms in the structures are different. The coordination of the lithium atoms in Li3InP2 and Li2SiP2 by phosphorus is illustrated in Fig. S2 and S8,† respectively. The positions Li1 and Li3 are similarly coordinated by four phosphorus atoms forming a distorted tetrahedron. By contrast, Li2 fills a strongly distorted octahedral void of phosphorus atoms with significant longer Li–P distances compared to Li1 and Li3. Here, the lithium atom Li2 is not located in the center of gravity of the octahedron but shows two much longer distances to neighboring P atoms of the distorted octahedron, resulting in a butterfly-type coordination of four P atoms. Interestingly, despite the smaller amount of Li atoms in Li2SiP2, not all the tetrahedral voids are occupied. In both compounds 25% of the tetrahedral voids are occupied by In or Si. Whereas all of the remaining 75% tetrahedral voids in Li3InP2 are filled with Li, only 37.5% are occupied by Li in Li2SiP2. In the latter, however, Li atoms occupy 25% of the distorted octahedral voids.
| Atom | Li3InP2 | Li2SiP2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Wyck. | x | y | z | Wyck. | x | y | z | |
| In1/Si | 32g | 0.11730(2) | 0.12523(2) | 0.31365(2) | 32g | 0.08345(2) | 0.12967(2) | 0.30710(1) |
| P1 | 16d | 0 | 1/4 | 0.00065(2) | 16d | 0 | 1/4 | 0.23093(2) |
| P2 | 16e | 0.23884(3) | 0 | 1/4 | 16e | 0.18335(3) | 0 | 1/4 |
| P3 | 32g | 0.25031(2) | 0.25604(2) | 0.12516(2) | 32g | 0.21330(2) | 0.21711(2) | 0.37222(2) |
| Li1 | 32g | 0.1279(2) | 0.3720(2) | 0.0615(1) | 16f | 0.0946(2) | 0.3446(2) | 1/8 |
| Li2 | 32g | 0.1179(2) | 0.1250(2) | 0.0651(1) | 16f | 0.1506(2) | 0.0995(2) | 1/8 |
| Li3 | 32g | 0.3635(2) | 0.1212(2) | 0.19053(9) | 32g | 0.3426(2) | 0.1271(2) | 0.2173(1) |
The different occupation of voids in Li3InP2 and Li2SiP2 also results in a different coordination of the supertetrahedra by lithium, which is shown in Fig. 6.
The different Li coordination arises from the different charges of the supertetrahedra Si4P88−/Ge4P88− and In4P812− (Fig. 1b). In Li3InP2 the lithium atoms form an almost regular octahedron around the indium atom with In–Li distances in the narrow range of 3.041 to 3.131 Å with an average of 3.075 Å, whereas in Li2SiP2 the octahedron formed by lithium atoms around silicon is strongly distorted with longer average distances of 3.222 Å and values between 2.958 and 3.556 Å. As a consequence, also octahedral voids of P atoms are filled with Li ions in Li2SiP2.
Impedance spectroscopy
For Li3InP2 two impedance measurements were performed to determine the ionic conductivity. The results are shown in Fig. S10.† The semi-circle can be described as parallel circuit element of a resistor and a constant phase element (R/Q). For the constant phase element the fit of the data acquired at 298 K resulted in α values of ≈0.99 and Q parameters of ≈2 × 10−8 F s(α − 1); the conductivity was determined to σ(Li3InP2) = 2.8(2) × 10−9 S cm−1 at 298 K (obtained from two independently measured cells). DC polarization measurements in the range from 50 to 150 mV reveal an electronic conductivity of 2.7(3) × 10−9 S cm−1 at 298 K (based on the standard deviation of two cells). The conductivity value obtained by DC polarization measurements is in the same range as the value obtained by PEIS measurements. Hence, the Nyquist plot shows only the semi-circle of the electronic conductivity, and no semi-circle for the ionic conductivity appears.Conclusions
Li3InP2 is the first lithium phosphidoindate and can be described as a tetragonally distorted fcc lattice of P atoms (space group I41/acd), in which the In atoms occupy tetrahedral voids, thus forming a polyanionic framework of InP4 supertetrahedra. The lithium atoms occupy the remaining tetrahedral voids. The structure of the compound is not isotypic to the previously reported ones of the lighter homologues, the orthorhombic compounds Li3AlP2 and Li3GaP2 (space group Cmce), which feature 2D layers of connected tetrahedra. First-principles DFT computations confirm the trend for the Al and Ga (In) compounds to crystallize in the orthorhombic (tetragonal) structure, respectively, which might originate in the different repulsive cation⋯cation interactions in both structures. Impedance spectroscopy reveals a very low electronic, but no ionic conductivity, whereas Li2SiP2 and Li2GeP2 show a moderate ionic mobility (2.2(3) × 10−7 S cm−1 at 293 K and 1.5(3) × 10−7 S cm−1 at 300 K, respectively).8,13 The geometrical analysis of the Li positions shows that in Li3InP2 all tetrahedral voids are fully occupied by lithium, whereas in Li2SiP2 and Li2GeP2 tetrahedral voids remain empty, and especially strongly distorted octahedral voids are filled. In accordance with the observations in fcc phosphide-based lithium ion conductors such as Li9AlP4,15 lithium diffusion preferably appears on pathways via partially occupied octahedral sites.Overall, these results demonstrate that even though crystal structures of phosphide compounds can contain complex polyanionic networks, a relatively simple description in terms of distorted close-packed arrangements of phosphorus atoms gives better insight for the description of lithium ion mobility. The title compound Li3InP2 provides a missing link in two respects: (i) it shows the structure changes in the series Li3TrP2 for Tr = Al, Ga, In, and (ii) it shows changes in lithium ion mobility in the series Li3InP2, Li2SiP2 and Li2GeP2.
Author contributions
TMFR carried out the crystal structure determination by single crystal and powder X-ray diffraction, performed the impedance spectroscopy measurements and wrote the manuscript draft. VLD carried out the DFT computations and provided discussion. JM contributed to the synthesis and data evaluation. GRS performed NMR experiments. TF designed research, provided guidance, and critically reviewed the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The work was carried out as part of the research project ASSB coordinated by ZAE Bayern. The project is funded by the Bavarian Ministry of Economic Affairs, Regional Development and Energy. V. L. D. acknowledges a Leverhulme Early Career Fellowship. The authors would like to acknowledge the use of the University of Oxford Advanced Research Computing (ARC) facility in carrying out this work (see DOI: 10.5281/zenodo.22558).References
- P. Knauth, Solid State Ionics, 2009, 180, 911–916 CrossRef CAS
.
- Y.-S. Hu, Nat. Energy, 2016, 1, 16042 CrossRef CAS
.
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 16141 CrossRef
.
- Z. Gao, H. Sun, L. Fu, F. Ye, Y. Zhang, W. Luo and Y. Huang, Adv. Mater., 2018, 30, 1705702 CrossRef
.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS
.
- Y. Meesala, A. Jena, H. Chang and R.-S. Liu, ACS Energy Lett., 2017, 2, 2734–2751 CrossRef CAS
.
- Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier, M. Armand and L. Chen, Energy Environ. Sci., 2018, 11, 1945–1976 RSC
.
- L. Toffoletti, H. Kirchhain, J. Landesfeind, W. Klein, L. van Wüllen, H. A. Gasteiger and T. F. Fässler, Chem.–Eur. J., 2016, 22, 17635–17645 CrossRef CAS
.
- S. Strangmüller, H. Eickhoff, D. Müller, W. Klein, G. Raudaschl-Sieber, H. Kirchhain, C. Sedlmeier, V. Baran, A. Senyshyn, V. L. Deringer, L. van Wüllen, H. A. Gasteiger and T. F. Fässler, J. Am. Chem. Soc., 2019, 141, 14200–14209 CrossRef
.
- H. Eickhoff, S. Strangmüller, W. Klein, H. Kirchhain, C. Dietrich, W. G. Zeier, L. van Wüllen and T. F. Fässler, Chem. Mater., 2018, 30, 6440–6448 CrossRef CAS
.
- S. Strangmüller, H. Eickhoff, G. Raudaschl-Sieber, H. Kirchhain, C. Sedlmeier, L. van Wüllen, H. A. Gasteiger and T. F. Fässler, Chem. Mater., 2020, 32, 6925–6934 CrossRef
.
- H. Eickhoff, L. Toffoletti, W. Klein, G. Raudaschl-Sieber and T. F. Fässler, Inorg. Chem., 2017, 56, 6688–6694 CrossRef CAS
.
- H. Eickhoff, C. Sedlmeier, W. Klein, G. Raudaschl-Sieber, H. A. Gasteiger and T. F. Fässler, Z. Anorg. Allg. Chem., 2020, 646, 95–102 CrossRef CAS
.
- A. Haffner, T. Bräuniger and D. Johrendt, Angew. Chem., 2016, 128, 13783–13786 CrossRef
.
- T. M. F. Restle, C. Sedlmeier, H. Kirchhain, W. Klein, G. Raudaschl-Sieber, V. L. Deringer, L. v. Wüllen, H. A. Gasteiger and T. F. Fässler, Angew. Chem., Int. Ed., 2020, 59, 5665–5674 CrossRef CAS
.
- T. M. F. Restle, J. V. Dums, G. Raudaschl-Sieber and T. F. Fässler, Chem.–Eur. J., 2020, 26, 6812–6819 CrossRef CAS
.
- W. Blase, G. Cordier and M. Somer, Z. Kristallogr., 1991, 195, 119–120 CrossRef CAS
.
- V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576–3586 CrossRef CAS
.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS
.
- A. Addamiano, J. Am. Chem. Soc., 1960, 82, 1537–1540 CrossRef CAS
.
- H. Li, A. Laine, M. O'Keeffe and O. M. Yaghi, Science, 1999, 283, 1145–1147 CrossRef CAS
.
- N. Zheng, X. Bu, B. Wang and P. Feng, Science, 2002, 298, 2366–2369 CrossRef CAS
.
- A. Haffner, A.-K. Hatz, I. Moudrakovski, B. V. Lotsch and D. Johrendt, Angew. Chem., Int. Ed., 2018, 57, 6155–6160 CrossRef CAS
.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef
.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. Cryst. Mater., 2005, 220, 567–570 CAS
.
- J. George, D. Waroquiers, D. Di Stefano, G. Petretto, G.-M. Rignanese and G. Hautier, Angew. Chem., Int. Ed., 2020, 59, 7569 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, details of the crystal structure determination, experimental powder X-ray diffraction pattern, coordination polyhedra, differential scanning calorimetry thermogram, Nyquist plot. CSD 2026514. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc05851c |
| This journal is © The Royal Society of Chemistry 2021 |