Bypassed ion-selective electrodes – self-powered polarization for tailoring of sensor performance
Anna
Kisiel
 ,
Agata
Michalska
,
Agata
Michalska
 and
Krzysztof
Maksymiuk
and
Krzysztof
Maksymiuk
 *
*
Faculty of Chemistry, University of Warsaw, Pasteura 1, 02-093 Warsaw, Poland. E-mail: kmaks@chem.uw.edu.pl
First published on 23rd April 2022
Abstract
Potentiometric ion-selective sensors are attractive analytical tools as they have simple apparatus and facile use; however their analytical parameters cannot be easily tuned. To tailor the performance of these sensors, application of instrumental control – electrochemical trigger – is usually required. The proposed approach offers a self-powered instrument-free alternative. It benefits from a spontaneous redox process for the ion-selective electrode bypassed by a zinc wire and a resistor connected in series. Spontaneous oxidation of zinc induces charge flow and the accompanying reduction of the solid contact material of the sensor, magnitude of the current and finally the potential of the electrode can be controlled by adjusting the bypass resistance. The ultimate result of the proposed approach is qualitatively equivalent to recording sensor response under polarized electrode potentiometry conditions, however, it does not require application of a galvanostat. The change in the magnitude of the resistance connected can be used to tailor analytical parameters such as detection limit, linear response range, and selectivity of the sensor. As a model example, potassium-selective all-solid-state sensors with a polypyrrole solid contact were used.
Introduction
Ion-selective electrodes (ISEs) represent one of the oldest and most popular groups of electrochemical sensors. Their practical advantages relate to high selectivity and signal stability as well as simple experimental setup. The recent two decades have brought impressive progress concerning both analytical parameters and construction improvement resulting in robust all-solid-state sensors that are intended also for disposable use.1–3Another ISE development possibility studied in recent years has been the application of electrochemical trigger control,4 mainly chronopotentiometry5–14 and recently also coulometric15–18 and voltammetric methods.19–24 These methods offer significant advantages related to adjustable analytical parameters: linear response range, in particular low detection limit, selectivity, high sensitivity, and the possibility of multi-analyte assessment. Although electrochemical control has become a standard in sensor diagnostic approach,25 it can also affect processes occurring during sensor pretreatment.26,27 The latter issue was helpful in achieving, especially for all-solid-state sensors, lower detection limit. For classical internal solution arrangement, a tremendous decrease of the detection limit to the picomolar level due to internal solution buffering has been obtained.28 The other option to achieve this effect is galvanostatic polarization affecting ion fluxes across the ISE membrane/solution interface, compensating spontaneous leakage of primary ions to the adjacent solution layer.5–10
Successful applicability of instrumental electrochemical non-zero current techniques for ISEs is, however, biased by the need for electrochemical apparatus. This can significantly limit applications of sensors, especially outside specialized laboratories. From this point of view it is highly desirable to find simplified systems allowing electrochemical control of ISEs and resulting in sensors of better performance, but not requiring electrochemical instrumentation.29,30 This benefit can be offered by self-powered ion-selective sensors. In recent years this idea has reached a significant attention leading to a concept of self-powered bipolar electrode system with ion-selective electrode.29 In the proposed model arrangement comprising potassium-selective electrode with polypyrrole solid contact and zinc, spontaneous charge transfer was induced. Zinc as active metal undergoes oxidation coupled with the reduction of the solid contact material. In this way, the presence of analyte (potassium) ions in the solution stimulates reduction of the solid contact and oxidation of zinc, while released zinc ions can be determined fluorimetrically. Ultimately, the potentiometric signal of ISE can be transformed to a fluorimetric readout.
In this work, we explore another original concept of self-powered bipolar electrode system, a fully electrochemical one, requiring just a classical potentiometric setup. In this work we propose an approach to allow effective application of galvanostatic polarization to tune potentiometric sensor performance (recorded open-circuit potentials), advantageously requiring only a classical potentiometric setup, i.e. not needing any additional electrochemical instrumentation. The resulting benefits, similar as for instrumental control, are related to tuning the detection limit and observed selectivity.
In the studied arrangement we introduced galvanostatic cathodic electrochemical trigger by applying a bypass using (reactive) zinc wire. Zinc spontaneously undergoes oxidation and therefore, while it is connected to ISE, it stimulates a spontaneous process of charge flow related to the reduction of the solid contact material of ISE and thus cathodic polarization of the sensor. Connecting a resistor in series into the circuit can be used to fine tune the spontaneously induced current flowing in the system and ultimately the ISE performance. This idea was studied on a model example of an all-solid-state potassium selective electrode with a polypyrrole solid contact.
Experimental
Apparatus and reagents
In the open circuit potentiometric experiments a multichannel data acquisition setup and software (Lawson Labs. Inc., 3217 Phoenixville Pike, Malvern, PA 19355, USA) was used, and stable (within ± 0.2 mV) potential readings were recorded. Pump systems 700 Dosino and 711 Liquino (Metrohm, Herisau, Switzerland) were used to obtain sequential dilutions of calibrating solutions. In other electrochemical measurements, the galvanostat–potentiostat CH-Instruments model 760A (Austin, TX, USA) and conventional three electrode cell were used.Tetrahydrofuran (THF), poly(vinyl chloride) (PVC), bis(2-ethylhexyl) sebacate (DOS), sodium tetrakis[3,5-bis(trifluoromethyl)phenyl]borate (NaTFPB), ionophore valinomycin, monomer pyrrole and inorganic salts were obtained from Merck (Germany).
Pyrrole prior to use was purified by passing through an alumina gel mini-column. Freshly deionized and distilled water (resistance 18.2 MΩ cm, MilliQ plus, Millipore, Austria) was used throughout this work.
Potassium-selective membranes
The potassium-selective membrane contained (% by weight): 1.3% of NaTFPB, 2.8% of valinomycin, 31.0% of PVC and 64.9% of plasticizer – DOS. Total 100 mg of membrane components was dissolved in 1 ml of THF and applied as described below.Electrodes
Glassy carbon disc electrodes of area 0.07 cm2 (Mineral, Poland) were used as the working/indicator electrodes. They were polished with Al2O3, 0.3 mm, and a mirror smooth polishing was avoided to prevent peeling off the relatively thick polymer film. A double junction silver/silver chloride reference electrode with 1 M lithium acetate in the outer sleeve (Möller Glasbläserei, Zürich, Switzerland) for the open circuit potentiometric experiments was used. A platinum counter electrode of surface area around 0.42 cm2 (Foton Institute, Poland) and a silver/silver chloride with 3 M KCl as the reference electrode (Mineral, Poland) for other electrochemical measurements were used.Glassy carbon electrodes were covered by polypyrrole films, doped by chloride ions, under conditions of constant potential 900 mV, from solution containing 0.1 M KCl and 0.5 M pyrrole, and polymerization charge was 200 mC.
Electrodes with polypyrrole films obtained as described above were placed in a position with the polymer film facing up. The top of the electrode was covered with pipetted 5 μl of THF solution of membrane components, resulting in approximately a 30 μm thick membrane.
After THF evaporation the obtained electrodes were conditioned overnight in 1 mM KCl solution.
Zinc wire (surface area 0.628 cm2) of purity 99.999% from Merck was used as additional electrode bypassed to a potassium-selective electrode.
During measurements resistors with resistance within the range from 100 kΩ to 20 MΩ were used. Resistors were connected in series with the zinc wire and with the potassium ion selective electrode (K-ISE). Zinc wire, K-ISE and the reference electrode were immersed in the potassium chloride solution during the open circuit potentiometric experiments. All experiments were repeated at least 3 times using various electrode exemplars, at ambient temperature (23 °C).
The concept of the instrumental free tuning of ISE performance
Under typical conditions, for electrochemically polarized ISE, ion transfer from the solution to the membrane is obtained in the presence of cathodic current, and the rate of this process is dependent on the magnitude of the flowing current resulting from the reduction of the material of the internal reference electrode or the reduction of the solid contact.The idea explored in this work is based on inducing self-powered polarization by spontaneous charge flow across the ion-selective membrane of ISE, accompanied by cation incorporation from the solution to the membrane. As shown in our previous work, connecting an ion-selective electrode with zinc wire,29 can result in a spontaneous process, with the reduction of the solid contact material and oxidation of metallic zinc. This process occurs spontaneously in neutral solutions, e.g. KCl. This idea can be further exploited to result in instrument-free electrochemical tuning of ISE performance, as shown in Fig. 1. As is clear from Fig. 1, the potassium-selective ISE (K-ISE) is applied as an indicator electrode, and it is connected to a potentiometer (together with the reference electrode). At the same time, the K-ISE is bypassed by a zinc wire, immersed in the sample solution, to induce the spontaneous process of solid contact reduction, resulting (to preserve the electroneutrality of the contact) in potassium cation flow to the membrane. However, for direct connection of the zinc wire to the ISE, the potentiometer would measure the redox potential of the zinc electrode, characterized by much lower impedance compared to K-ISE. This unwanted effect can be minimized by introducing a high resistance in series with zinc wire. If the applied bypass resistance, Rb, is significantly higher than that of ISE, the potential of the ion-selective electrode will not be biased by bypassing zinc. On the other hand, changing the resistance applied can be used to tailor the magnitude of the apparent current, flowing spontaneously between ISE and zinc. Ultimately change of the applied resistance, has the same effect as changing of the applied current (in galvanostatic mode) and results in fine tuning of the performance of ISE. It should be stressed that the application of this approach does not require any modification of the sample composition.
 | ||
| Fig. 1 Scheme of the cell with bypassed ion-selective electrode (no modification of the sample solution is required). | ||
Results and discussion
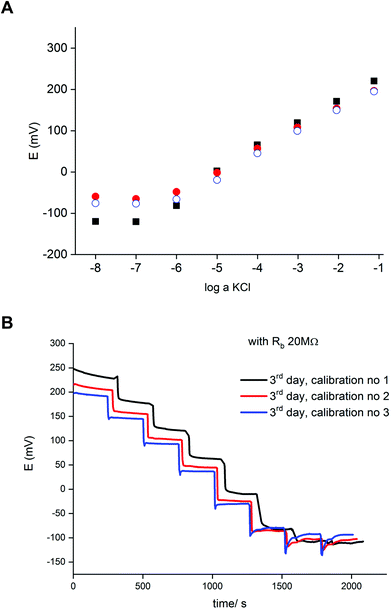
Fig. 2 presents an example of a typical potentiometric calibration plot for the studied K-ISE recorded in the absence of the bypass applied. As expected, the dependence is linear within the concentration range from 0.1 M to 10−5 M, with near Nernstian slope equal to 55.0 ± 0.9 mV dec−1 (R2 = 0.999). Fig. 3A presents the EIS spectrum for this sensor, recorded at the potential 0.4 V, within a frequency range from 105 Hz to 0.1 Hz and amplitude 10 mV. A semicircle in the range of higher frequencies was obtained, and the diameter of the semicircle points to the membrane resistance over 30 kΩ. For frequencies lower than 1 Hz, a linear part with slope close to 45 degrees was obtained, pointing to the influence of Warburg impedance. Based on these results the diffusion coefficients of ionic forms in the membrane could be estimated as close to 10−8 cm2 s−1, i.e. the obtained value is typical for the diffusion coefficient of monovalent ions in PVC-based membranes.31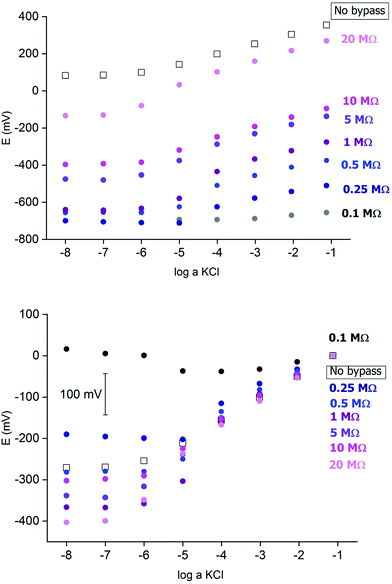 | ||
Fig. 2 Potentiometric calibration plots for K+-selective ISEs, non-bypassed or bypassed by zinc wire and resistor Rb. Bottom panel: experimental points were shifted to common value for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a KCl = −1. a KCl = −1. | ||
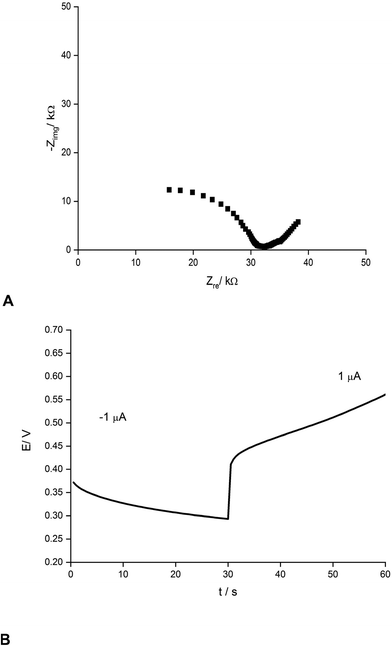 | ||
| Fig. 3 (A) Nyquist plot and (B) chronopotentiometric cathodic/anodic curve (±1 μA) for potassium-selective ISEs. | ||
The chronopotentiometric experiment, as shown in Fig. 3B, resulted in an almost linear dependence of potential on time, both for anodic and cathodic currents. Using the method of Bobacka,25 from the potential jump accompanying the current direction change, the resistance of the sensor was estimated to be close to 50 kΩ, i.e. slightly higher than that determined from EIS measurement. The higher resistance value in the latter case may result from concentration polarization effects in the membrane due to the unidirectional current flow in the case of chronopotentiometry.32
From the slope of the linear part of dependence potential vs. time, the low frequency capacitance was estimated, characterizing the polypyrrole solid contact. It was equal to 0.48 mF and 0.24 mF for cathodic and anodic polarization, respectively. The observed difference in capacitance value for opposite current directions results from the effects of concentration polarization in the membrane, as discussed earlier.32
Potentiometric characteristics of bypassed ISEs
In the next step the potentiometric measurement setup was modified, according to Fig. 1, by connecting a zinc wire immersed in the same solution and additionally connecting a (bypass) resistor between the K-ISE and zinc wire. A series of potentiometric measurements was carried out for potassium-selective ISE for increasing bypass resistance value. Fig. 2 shows potentiometric characteristics recorded for various resistance values for the resistor incorporated into the circuit (within the range covering over two orders of magnitude, from 100 kΩ to 20 MΩ). The error of potential readings was in the range of single mV, reaching 2–3 mV for concentrations lower than 10−4 M or 10 mV in the range, where the super-Nernstian effect was observed. The difference in potentials (outside the super-Nernstian range) of various exemplars of the same ISE was in the range of 3 mV, resulting from possible tiny differences in membrane properties.As shown in Fig. 2, connecting the zinc wire results in a significant shift of recorded potentials towards lower values. The highest shift was recorded in the presence of the lowest resistance (100 kΩ), in this case the potential was only slightly dependent on KCl concentration in solution and the dependence was not Nernstian. Moreover, the measured potential was close to the redox potential of the zinc wire. This effect results, as expected, from low bypass resistance and thus much lower resistance of the bypassing branch compared to K-ISE.
However, in the presence of an added resistor of higher resistance, the recorded potentials are shifted to higher values, and the higher the bypass resistance the higher potentials that were obtained. The recorded potentials, for a given bypass resistance, are dependent on the KCl concentration in solution. The potential is linearly dependent on the logarithm of KCl concentration in the range of higher concentrations for lower bypass resistance (250 kΩ), the slopes for higher concentration range are slightly smaller than for ISE in the absence of zinc wire, as shown in Table 1. Nevertheless, even for Rb = 250 kΩ for the concentration change from 10−4 to 10−5 M the recorded potential change is higher than Nernstian (a super-Nernstian effect is observed). Moreover, for the highest resistance values the super-Nernstian effect is less exposed, and the magnitude of the super-Nernstian effects for various Rb values is clearly visible on the bottom panel of Fig. 2. The concentration range corresponding to the super-Nernstian effect is shifted to lower values with increasing bypass resistance (Fig. 2, bottom panel).
| Bypass resistance | Slope ± SD (mV dec−1) | R 2 | Current, A (determined by method A) | Current, A (determined by method B) |
|---|---|---|---|---|
| a The value was determined for the range from 0.1 to 10−5 M. | ||||
| No bypass | 55.0 ± 0.9a | 0.999 | ||
| 250 kΩ | 39.5 ± 2.2 | 0.994 | 9 × 10−8 | |
| 500 kΩ | 46.9 ± 2.2 | 0.996 | 6 × 10−8 | |
| 1 MΩ | 54.5 ± 3.4 | 0.992 | 2.5 × 10−8 | 3 × 10−8 |
| 5 MΩ | 52.0 ± 1.5 | 0.998 | 2 × 10−8 | |
| 10 MΩ | 52.9 ± 0.9 | 0.999 | 1 × 10−8 | |
| 20 MΩ | 57.9 ± 0.02 | 1.000 | 2.5 × 10−9 | 3 × 10−9 |
The origin of the super-Nernstian effect can be explained by the spontaneous process of zinc oxidation coupled with solid contact reduction, stimulating the forced flow of potassium ions from the solution to the membrane, resulting in the depletion of KCl close to the membrane surface, observed for dilute KCl solutions. The results presented in Fig. 2 (top panel) show also that increasing the bypass resistance shifts the potentiometric calibration curve to higher values. This effect may be explained by the ohmic drop – for small Rb the potential of ISE is closer to the potential of the zinc wire, while for higher resistance, due to more significant ohmic drop, the ISE potential will be closer to the potential in the absence of the bypassing circuit.
The results presented in Fig. 2 suggest that higher resistance applied in the circuit should be more useful from the analytical point of view, due to less pronounced super-Nernstian effect and extended linear response range to cover the range from 0.1 to 10−6 M, as observed e.g. for 10 MΩ. Therefore, in the subsequent experiments we focused on bypassed ISE with added highest applied resistance: 20 MΩ. For this system the bypass resistance is significantly higher than the resistance of ISE (membrane), therefore the recorded potential of ISE is not significantly affected by the potential of zinc wire presence.
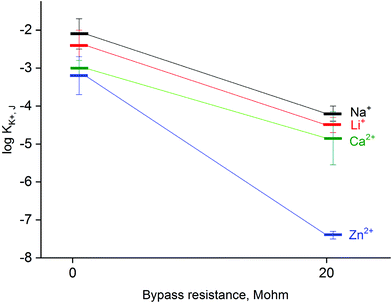
Fig. 4A shows a series of calibration plots, obtained consecutively for successive days, and always the third calibration of the day is shown. For this electrode the potentials were always lower than for typical ISE (without zinc and resistor, cf. plots in Fig. 2). For the first day calibration a small super-Nernstian effect for KCl concentration smaller than 10−5 M was observed, and this effect disappeared for the subsequent calibrations. At the same time, a slight shift of the plot to lower potential values was recorded. Both effects observed are the results of flowing charge between zinc and ISE, resulting in gradual reduction of the polypyrrole solid contact (lower potential) and diminishing driving force for potassium ion incorporation (disappearance of super-Nernstian effect). On the other hand, the extension of the linear part of the potentiometric characteristics results also in lowering of the detection limit to 10−6.5 M, i.e. 3 times lower than in the absence of a bypassing circuit, as shown in Fig. 4.
Fig. 4B shows time traces recorded for following calibrations of the third day. The plot representing the first calibration shows less stable values, resulting from the abovementioned slight super-Nernstian effect. For the longer times (following calibrations) the recorded potentials were stable in time. The difference between traces for the second and third calibration, resulting from the spontaneous process of polypyrrole reduction, is in the range of a few mV. However, the time span between following measurements for the same concentration is quite long. Under typical analytical conditions (routine analysis), due to the much shorter measurement time, the potential change resulting from spontaneous process is of minor significance and the accuracy is practically the same as for typical potentiometric measurement.
The above presented results confirm that the herein proposed, novel simple approach – self-powered method of ISEs polarization offers flexibility in affecting analytical parameters of ion-selective electrodes. By tailoring the applied bypass resistance advantageous effects are revealed as e.g. lowering of detection limit (observed for Rb = 20 MΩ).
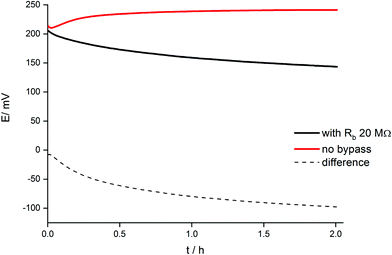
The applied method of tailoring fluxes through the ion-selective membrane also affects the selectivity,33 as shown in Fig. 5. When the system is bypassed by 20 MΩ resistance, the obtained values of selectivity coefficients were significantly lower compared to non-bypassed system, and the difference was found to be significant (statistical significance: 0.05, Student's test). The decrease in obtained values of the logarithm of the selectivity coefficient was almost 2 for sodium, lithium or calcium ions tested as model interferents. The decrease of selectivity coefficients can be explained by limitations in primary ion leakage from the membrane, biasing these coefficients under typical potentiometric conditions. As a part of proof of concept also zinc ion selectivity of a potassium-selective membrane was tested. It was found that in the absence of applied bypassing resistance the potassium-selective sensor is characterized with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KK+, Zn2+ value equal to −3.2, while under applied Rb = 20 MΩ significantly lower value equal to −7.4 was obtained, as shown in Fig. 5. Clearly, the presence of zinc ions generated from the zinc metal wire does not affect the recorded potential values.
KK+, Zn2+ value equal to −3.2, while under applied Rb = 20 MΩ significantly lower value equal to −7.4 was obtained, as shown in Fig. 5. Clearly, the presence of zinc ions generated from the zinc metal wire does not affect the recorded potential values.
Quantitative description of dynamic phenomena in the bypassed ISEs
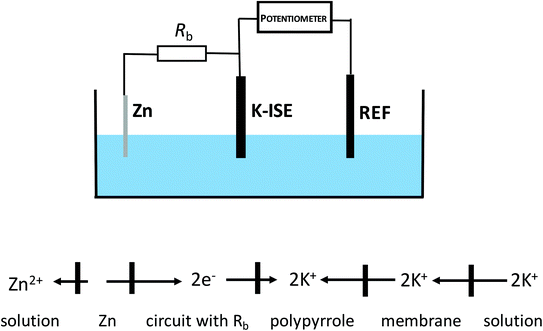
The dynamic phenomena occurring in this system can be now analyzed in a more quantitative manner. Fig. 6 shows the comparison of potential transients during conditioning in 1 mM KCl solution for a classical arrangement and the systems bypassed by zinc wire and resistor 20 MΩ. The reproducibility is (within the range of experimental error) the same as the reproducibility of potential reading for the selected concentration of potassium ions. In the case of 1 mM KCl solution it is in the range of 2–3 mV. For two various ISEs the potential difference may be equal to 3–4 mV, however the slope of the potential vs. time dependence is almost the same.A significant difference in potential vs. time dependence is observed: for the classical arrangement (no bypass) a small potential increase was observed followed by an almost constant value, whereas for the electrode with Zn wire and resistor the potential slowly decreased. The observed decrease in potential in time results from the gradual reduction of the polypyrrole solid contact of ISE. Because the ion-selective membrane and its initial state in both cases (in the absence and in the presence of Zn) was the same, the difference in potentials recorded in the presence and absence of bypass (dashed line, Fig. 6) can be ascribed to the presence of zinc and ongoing spontaneous process of zinc oxidation and polypyrrole solid contact reduction. The potential difference shown in Fig. 6 decreases significantly at the beginning of the conditioning process and then decreases almost linearly, in contrast to the non-bypassed electrode, where the potential is almost constant. The difference between values of potential recorded for the two systems, (ΔE), can be used to calculate the charge flowing due to the spontaneous process of zinc oxidation and polypyrrole reduction, assuming capacitive properties of polypyrrole films used as the solid contact.29 In this case eqn (1) can be used, expressing the relation between potential change and charge for a purely capacitive element:
| Q = C ΔE | (1) |
The value of the current flowing in this system can be also estimated in another way, based on the magnitude of the super-Nernstian effect, and the procedure was proposed by us previously.34 In this approach it is assumed that for KCl concentration, where the potential decrease due to super-Nernstian effect exceeds 0.1 V (e.g. for 10−5.8 M KCl and Rb = 20 MΩ), the surface concentration of K+ ions (in solution) is close to zero.
In this case the equation describing the concentration polarization under conditions of constant flux (current) may be applied:35
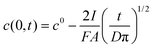 | (2) |
Assuming c(0,t) = 0 for the super-Nernstian effect exceeding 0.1 V, taking into account the diffusion coefficient for potassium ions in aqueous solution D = 2 × 10−5 cm2 s−1,36A = 0.07 cm2, and t = 180 s (potentiometric measurement time for a single solution), after rearrangement of eqn (2), the current, I, can be estimated. The current calculated using this method, for Rb = 20 MΩ, is 3 × 10−9 A, i.e. very close to the value obtained basing on data from Fig. 6 (Table 1).
Similar results were obtained while analyzing the system using the bypass resistance 1 MΩ. In this case, based on potential vs. time dependence during conditioning in 1 mM KCl solution (results not shown), the current representing the spontaneous process is close to 2.5 × 10−8 A. On the other hand, the value determined from the super-Nernstian effect (eqn (2)) for this bypass resistance is similar, equal to 3 × 10−8 A. Both values are in good agreement within the range of experimental error.
Basing on the super-Nernstian effect for electrodes bypassed with different resistors, the flowing current in each case can be estimated. The obtained data are listed in Table 1. These results show, as expected, that for lower bypass resistance higher currents are observed.
The current related to the spontaneous oxidation of zinc and reduction of polypyrrole solid contact can affect the ionophore concentration in the membrane at close to the interface. Due to the incorporation of potassium ions to the membrane, the ionophore concentration can decrease. Assuming the current of 2.5 × 10−8 A (as recorded for the resistance 1 MΩ), the change of ionophore concentration can be estimated, based on eqn (2). Assuming the ionophore concentration in the membrane bulk, c0 = 0.02 M, taking into account the diffusion coefficient of ionophore in the membrane D = 2 × 10−8 cm2 s−137 and A = 0.07 cm2, t = 180 s, the change of ionophore concentration due to depletion is close to 2% of the bulk concentration. Due to ion exchange equilibrium on the membrane/solution interface, the lower concentration of free ionophore (0.98c0) will result in potential decrease (according to Nernst equation) of close to 0.5 mV (for t = 180 s). This potential decrease corresponds to a change of 3 × 10−3 mV s−1. Because the experimentally recorded potential change in time is over 0.05 mV s−1, the influence of ionophore depletion would be around 6% contribution to the observed potential change.
The low value of the flowing current results also in negligible polarization of the ion-selective membrane. Assuming the membrane resistance equal to 30 kΩ and using the Ohm's law for estimated currents (Table 1), the potential drop in the membrane would be close to 0.1 mV or 0.8 mV in the presence of bypass resistance of 20 MΩ and 1 MΩ, respectively.
On the other hand, the change of the oxidation state of polypyrrole under applied experimental conditions could be estimated. Assuming the highest calculated current as 9 × 10−8 A (Table 1) and measurement time as 2 h, the flowing charge is 0.65 mC, being around 3% of the oxidation charge of polypyrrole (around 20 mC). In other cases, the amount is smaller, e.g. in the presence of bypass resistance of 20 MΩ (determined current: 3 × 10−9 A), and the flowing charge is only 0.1% of the oxidation charge of polypyrrole.
It should be noted that although the bypass resistance used was changed by two orders of magnitude, the determined current changes are smaller – the range of the obtained values is limited to over one order of magnitude (from 9 × 10−8 A for resistance of 250 kΩ to 3 × 10−9 A for 20 MΩ). This result means that the formally calculated ohmic effect alone does not explain the observed changes. For instance, based only on the potential difference (ISE and zinc) around 1 V and total resistance slightly exceeding 20 MΩ (for the highest bypass resistance + membrane resistance), the current expected from Ohm's law (1 V/20 MΩ) would be around 5 × 10−8 A, considerably higher than observed experimentally.
The relatively low difference between currents determined for various resistors, being generally lower than expected based on Ohm's law, may result from the influence of additional effects. One of the factors affecting the magnitude of flowing current can be some concentration polarization effects in the membrane. However, as described above, the ionophore concentration polarization in the membrane is of minor influence.
The other factors potentially affecting the observed low variability of currents in dependence on Rb may be (i) lower potential of ISE compared to ISE in the absence of zinc and (ii) higher potential of ISE for higher bypass resistance (cf.Fig. 2), resulting in an increase of potential difference between ISE and zinc with increasing resistance. The higher potential difference for higher Rb would result in some compensation of current decrease due to higher resistance. This assumption was checked by dividing the actual potential difference of ISE and zinc wire by the applied resistance. It was found that variation of currents in the studied resistance range is slightly over one order of magnitude. This result is consistent with current variation shown in Table 1, although the currents calculated from Ohm's law were still a few times higher than those reported in Table 1.
An additional significant effect may be the actual potential difference between the polypyrrole solid contact and zinc wire, as a trigger for the current flow. The potential of the polypyrrole layer is lower than the recorded potential of K-ISE due to additional contribution from the membrane potential and potential drop on the membrane/polypyrrole layer interface in the case of K-ISE.
A different effect occurring in the studied system, which should be taken into account is the spontaneous release of Zn2+ ions into the sample solution (due to redox process occurring). However, assuming even the highest current (for low bypass resistance) equal to 10−7 A, for a measurement time of 3 min, the amount of released zinc ions is below 10−10 moles, i.e. beyond the detection range of the applied potentiometric sensor, as can be expected based on the determined value of the selectivity coefficient for zinc ions (Fig. 5).
It should be underlined however, that the above discussed deviation of current flowing in the system from the value expected taking into account Ohm's law, or the related effects, does not compromise the usefulness of the above proposed approach for a simple, apparatus-free control of ion gradients in the membrane phase. Due to intrinsic simplicity, the herein proposed approach can be a useful alternative for existing instrumental approaches, allowing (due to a change of the resistance applied) fine tuning of sensor performance.
Conclusions
In this work a novel self-powered method of galvanostatic polarization of ion-selective electrode was proposed, allowing instrument-free tailoring of fluxes through the ion-selective membrane and ultimately the performance of the sensor. In the proposed arrangement the current flow is triggered by bypassing the (potassium) ion-selective electrode with zinc wire and a resistor (with resistance higher than that of the ion-selective membrane) connected in series. The spontaneous oxidation of zinc and reduction of polypyrrole solid contact induces charge flow across the sensor, and the magnitude of the current and potential of the electrode can be controlled by adjusting the bypass resistance. However, the magnitude of the flowing current (due to spontaneous process) is dependent not only on the bypass resistance but also on the contact time with solution (in longer time scale) and effective potential difference between the polypyrrole solid contact and zinc wire.It was demonstrated that by tailoring the applied bypass resistance advantageous effects can be observed such as the lowering of detection limit, selectivity increase or the super-Nernstian effect, offering higher sensitivity in the selected concentration range of the analyte. Therefore, the proposed simple, self-powered method of ISE polarization offers flexibility in affecting the analytical parameters of ion-selective electrodes. The proposed idea was checked on a model example of potassium-selective ISE, however, it may be used also for other electrodes, as basically the concept will be the same.
The above described studies were carried out on the example of zinc; however, other active metals, characterized by low redox potential and resistivity to corrosion or dissolution processes (if not connected to ISE) may be taken into consideration for such applications.
Author contributions
Anna Kisiel: investigation, resources, data curation, validation. Agata Michalska: conceptualization, methodology, formal analysis, writing – review and editing. Krzysztof Maksymiuk: conceptualization, writing – original draft, writing – review and editing, supervision, funding acquisition, project administration.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Financial support from the National Science Centre (NCN, Poland), project 2018/31/B/ST5/02687, in the years 2019–2023, is gratefully acknowledged.References
- Y. Shao, Y. Ying and J. Ping, Chem. Soc. Rev., 2020, 49, 4405–4465 RSC
.
- E. Bakker, Trends Anal. Chem., 2014, 53, 98–105 CrossRef CAS
.
- J. Bobacka, A. Ivaska and A. Lewenstam, Chem. Rev., 2008, 108, 329–351 CrossRef CAS PubMed
.
- E. Bakker, Anal. Chem., 2016, 88, 395–413 CrossRef CAS PubMed
.
- E. Pergel, R. E. Gyurcsanyi, K. Toth and E. Lindner, Anal. Chem., 2001, 73, 4249–4253 CrossRef CAS PubMed
.
- A. Michalska, J. Dumanska and K. Maksymiuk, Anal. Chem., 2003, 75, 4964–4974 CrossRef CAS
.
- I. Bedlechowicz, T. Sokalski, A. Lewenstam and M. Maj-Żurawska, Sens. Actuators, B, 2005, 108, 836–839 CrossRef CAS
.
- G. Lisak, F. Ciepiela, J. Bobacka, T. Sokalski, L. Harju and A. Lewenstam, Electroanalysis, 2013, 25, 123–131 CrossRef CAS
.
- A. Michalska, M. Wojciechowski, E. Bulska and K. Maksymiuk, Electrochem. Commun., 2008, 10, 61–65 CrossRef CAS
.
- M. A. Peshkova, T. Sokalski, K. N. Mikhelson and A. Lewenstam, Anal. Chem., 2008, 80, 9181–9187 CrossRef CAS PubMed
.
- A. Shvarev and E. Bakker, J. Am. Chem. Soc., 2003, 125, 11192–11193 CrossRef CAS PubMed
.
- A. K. Bell-Vlasov, J. Zajda, A. Eldourghamy, E. Malinowska and M. E. Meyerhoff, Anal. Chem., 2014, 86, 4041–4046 CrossRef CAS PubMed
.
- S. Makarychev-Mikhailov, A. Shvarev and E. Bakker, Anal. Chem., 2006, 78, 2744–2751 CrossRef CAS PubMed
.
- K. L. Gemene and E. Bakker, Anal. Chem., 2008, 80, 3743–3750 CrossRef CAS PubMed
.
- E. Hupa, U. Vanamo and J. Bobacka, Electroanalysis, 2015, 27, 591–594 CrossRef CAS
.
- U. Vanamo, E. Hupa, V. Yrjana and J. Bobacka, Anal. Chem., 2016, 88, 4369–4374 CrossRef CAS PubMed
.
- E. Grygolowicz-Pawlak and E. Bakker, Anal. Chem., 2010, 82, 4537–4542 CrossRef CAS PubMed
.
- Z. Jarolimova, T. Han, U. Mattinen, J. Bobacka and E. Bakker, Anal. Chem., 2018, 90, 8700–8707 CrossRef CAS PubMed
.
- J. Zhang, A. R. Harris, R. W. Cattrall and A. M. Bond, Anal. Chem., 2010, 82, 1624–1633 CrossRef CAS PubMed
.
- Z. Kim and S. Amemiya, Anal. Chem., 2008, 80, 6056–6065 CrossRef PubMed
.
- Z. Kim, P. J. Rodgers and S. Amemiya, Anal. Chem., 2009, 81, 7262–7270 CrossRef PubMed
.
- M. Cuartero, G. A. Crespo and E. Bakker, Anal. Chem., 2016, 88, 1654–1660 CrossRef CAS PubMed
.
- D. Yuan, M. Cuartero, G. A. Crespo and E. Bakker, Anal. Chem., 2017, 89, 586–594 CrossRef CAS PubMed
.
- D. Kaluza, A. Michalska and K. Maksymiuk, Electroanalysis, 2019, 31, 2379–2386 CrossRef CAS
.
- J. Bobacka, Anal. Chem., 1999, 71, 4932–4937 CrossRef CAS PubMed
.
- A. Michalska, Electroanalysis, 2005, 17, 400–407 CrossRef CAS
.
- P. Pawlowski, A. Kisiel, A. Michalska and K. Maksymiuk, Talanta, 2011, 84, 814–819 CrossRef CAS PubMed
.
- T. Sokalski, A. Ceresa, T. Zwickl and E. Pretsch, J. Am. Chem. Soc., 1997, 119, 11347–11348 CrossRef CAS
.
- E. Jaworska, A. Michalska and K. Maksymiuk, Electrochim. Acta, 2018, 284, 321–327 CrossRef CAS
.
- S. Jansod and E. Bakker, Anal. Chem., 2021, 93, 4263–4269 CrossRef CAS PubMed
.
- E. Bakker, P. Bühlmann and E. Pretsch, Chem. Rev., 1997, 97, 3083–3132 CrossRef CAS PubMed
.
- A. Kisiel, A. Michalska and K. Maksymiuk, Synth. Met., 2018, 246, 246–253 CrossRef CAS
.
- T. Sokalski, A. Ceresa, M. Fibbioli, T. Zwickl, E. Bakker and E. Pretsch, Anal. Chem., 1999, 71, 1210–1214 CrossRef CAS
.
- A. Michalska, M. Ocypa and K. Maksymiuk, Anal. Bioanal. Chem., 2006, 385, 203–207 CrossRef CAS PubMed
.
-
Z. Galus, Fundamentals of Electrochemical Analysis, Ellis Horwood Ltd., Chichester, 1994 Search PubMed
.
-
R. A. Robinson and R. H. Stokes, Electrolyte Solutions, Butterworth, London, 1959 Search PubMed
.
- J. M. Zook, R. P. Buck, R. E. Gyurcsanyi and E. Lindner, Electroanalysis, 2008, 20, 259–269 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2022 |