Open Access Article
Open Access ArticleInvestigating charge-up and fragmentation dynamics of oxygen molecules after interaction with strong X-ray free-electron laser pulses†
G.
Kastirke
a,
F.
Ota
b,
D. V.
Rezvan
c,
M. S.
Schöffler
 a,
M.
Weller
a,
J.
Rist
a,
M.
Weller
a,
J.
Rist
 a,
R.
Boll
a,
R.
Boll
 d,
N.
Anders
a,
T. M.
Baumann
d,
S.
Eckart
d,
N.
Anders
a,
T. M.
Baumann
d,
S.
Eckart
 a,
B.
Erk
a,
B.
Erk
 e,
A.
De Fanis
d,
K.
Fehre
a,
A.
Gatton
f,
S.
Grundmann
e,
A.
De Fanis
d,
K.
Fehre
a,
A.
Gatton
f,
S.
Grundmann
 a,
P.
Grychtol
a,
P.
Grychtol
 d,
A.
Hartung
a,
M.
Hofmann
a,
M.
Ilchen
cd,
C.
Janke
a,
M.
Kircher
a,
M.
Kunitski
a,
X.
Li
g,
T.
Mazza
d,
N.
Melzer
d,
A.
Hartung
a,
M.
Hofmann
a,
M.
Ilchen
cd,
C.
Janke
a,
M.
Kircher
a,
M.
Kunitski
a,
X.
Li
g,
T.
Mazza
d,
N.
Melzer
 a,
J.
Montano
d,
V.
Music
cd,
G.
Nalin
a,
J.
Montano
d,
V.
Music
cd,
G.
Nalin
 a,
Y.
Ovcharenko
d,
A.
Pier
a,
N.
Rennhack
d,
D. E.
Rivas
d,
R.
Dörner
a,
D.
Rolles
a,
Y.
Ovcharenko
d,
A.
Pier
a,
N.
Rennhack
d,
D. E.
Rivas
d,
R.
Dörner
a,
D.
Rolles
 g,
A.
Rudenko
g,
Ph.
Schmidt
g,
A.
Rudenko
g,
Ph.
Schmidt
 cd,
J.
Siebert
a,
N.
Strenger
a,
D.
Trabert
a,
I.
Vela-Perez
a,
R.
Wagner
d,
Th.
Weber
cd,
J.
Siebert
a,
N.
Strenger
a,
D.
Trabert
a,
I.
Vela-Perez
a,
R.
Wagner
d,
Th.
Weber
 h,
J. B.
Williams
i,
P.
Ziolkowski
d,
L. Ph. H.
Schmidt
a,
A.
Czasch
a,
Y.
Tamura
b,
N.
Hara
b,
K.
Yamazaki
h,
J. B.
Williams
i,
P.
Ziolkowski
d,
L. Ph. H.
Schmidt
a,
A.
Czasch
a,
Y.
Tamura
b,
N.
Hara
b,
K.
Yamazaki
 j,
K.
Hatada
b,
F.
Trinter
j,
K.
Hatada
b,
F.
Trinter
 ek,
M.
Meyer
d,
K.
Ueda
lm,
Ph. V.
Demekhin
ek,
M.
Meyer
d,
K.
Ueda
lm,
Ph. V.
Demekhin
 c and
T.
Jahnke
c and
T.
Jahnke
 *d
*d
aInstitut für Kernphysik, Goethe-Universität, Max-von-Laue-Straße 1, 60438 Frankfurt am Main, Germany
bDepartment of Physics, University of Toyama, Gofuku 3190, Toyama 930-8555, Japan
cInstitut für Physik und CINSaT, Universität Kassel, Heinrich-Plett-Straße 40, 34132 Kassel, Germany. E-mail: demekhin@physik.uni-kassel.de
dEuropean XFEL, Holzkoppel 4, 22869 Schenefeld, Germany. E-mail: till.jahnke@xfel.eu
eDeutsches Elektronen-Synchrotron DESY, Notkestraße 85, 22607 Hamburg, Germany
fSLAC National Accelerator Laboratory, Menlo Park, California 94025, USA
gJ.R. Macdonald Laboratory, Department of Physics, Kansas State University, Manhattan, Kansas 66506, USA
hLawrence Berkeley National Laboratory, Chemical Sciences Division, Berkeley, California 94720, USA
iDepartment of Physics, University of Nevada, Reno, Nevada 89557, USA
jRIKEN Center for Advanced Photonics, RIKEN, 2-1 Hirosawa, Wako, Saitama, 351-0198, Japan
kMolecular Physics, Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany
lInstitute of Multidisciplinary Research for Advanced Materials, Tohoku University, Katahira 2-1-1, Aoba-ku, Sendai 980-8577, Japan
mDepartment of Chemistry, Tohoku University, 6-3 Aramaki Aza-Aoba, Aoba-ku, Sendai, 980-8578, Japan. E-mail: kiyoshi.ueda@tohoku.ac.jp
First published on 7th November 2022
Abstract
During the last decade, X-ray free-electron lasers (XFELs) have enabled the study of light–matter interaction under extreme conditions. Atoms which are subject to XFEL radiation are charged by a complex interplay of (several subsequent) photoionization events and electronic decay processes within a few femtoseconds. The interaction with molecules is even more intriguing, since intricate nuclear dynamics occur as the molecules start to dissociate during the charge-up process. Here, we demonstrate that by analyzing photoelectron angular emission distributions and kinetic energy release of charge states of ionic molecular fragments, we can obtain a detailed understanding of the charge-up and fragmentation dynamics. Our novel approach allows for gathering such information without the need of complex ab initio modeling. As an example, we provide a detailed view on the processes happening on a femtosecond time scale in oxygen molecules exposed to intense XFEL pulses.
1 Introduction
Accessing atomic and molecular length and time scales is a key necessity of many disciplines in physics, chemistry, and biology. Accordingly, several experimental approaches have been developed during the last decades, targeting different aspects of this challenge. For example, the geometrical structure even of very large molecules nowadays can be retrieved routinely by means of X-ray diffraction in cases, where nano-crystals of the examined molecules can be created.1 Studying single molecules in the gas phase2,3 poses even more challenges than X-ray diffraction methods, because they suffer from the weak scattering properties of light elements as, e.g., hydrogen atoms. Accordingly, several alternative approaches employing electron waves as molecular structure probes (thus, compensating this deficiency) have emerged.4–9A particular variant of electron diffraction imaging uses molecular photoelectrons to sample the structure of molecules. Studies of so-called molecular-frame photoelectron angular distributions (MFPADs) record the emission pattern of photoelectrons in a molecular frame of reference.10 This angular distribution is a result of the photoelectron wave being scattered by the molecular potential as it propagates through the molecule. It is therefore not only sensitive to the molecular geometry but also for instance to the electron's wavelength, the initial state of the electron, the emission site inside the molecule (in case of core-electron emission), and the polarization properties of the ionizing light. Since the 90s of the last century, many experiments using synchrotron radiation investigated different aspects of such MFPADs,11 as their sensitivity to molecular vibrations12 and molecular shape resonances,13 to the bound-state momentum-space wave function of the emitted electron,14 and even the temporal response of an electronic orbital to ionizing radiation.15 With respect to extracting geometrical structure information, so-called polarization-averaged MFPADs (PA-MFPADs) are favorable: Williams et al. demonstrated that in special cases the MFPAD of carbon K-shell electrons emitted from methane molecules directly resembles the three-dimensional molecular geometry,16 and Fukuzawa et al. showed in general that the full information on molecular bond lengths is encoded in such PA-MFPADs.17
With the advent of X-ray free-electron lasers (XFELs), a further intriguing aspect emerged. XFELs are capable of producing ultra-bright pulses of X-rays with shortest duration in the regime of a few tens of femtoseconds. This opened the route to time-resolved studies, where MFPADs record snapshots of nuclear motion occurring inside a molecule.18
Recently, Kastirke et al. demonstrated a first step towards obtaining such molecular movies using an XFEL.19 They triggered the dissociation of an oxygen molecule by absorption of an X-ray photon. The PA-MFPAD of a secondary photoelectron (which was emitted during the fragmentation process) depicted a fingerprint of the increasing internuclear distance during the fragmentation. In the present paper, we depict results that go one step further. By applying a novel analysis approach of extracting information from the PA-MFPADs, we were able to trace the femtosecond charge-up and fragmentation dynamics of the oxygen molecule occurring during the illumination with an ultra-short free-electron X-ray pulse.
In pioneering work, Young et al. demonstrated that the interaction of X-ray free-electron laser light with atoms gives rise to a complex interplay of multiple photoionization and Auger decay events20 which was then further studied, revealing the role of resonances in such charge-up processes in atoms21 and recently also in molecules.22,23 In case of molecules, a further dimension of complexity is added to this charge-up process, as typically additional nuclear dynamics are triggered as soon as the first charges are generated and the molecules start to dissociate.24 If, for instance, during a XFEL pulse an oxygen molecule absorbs two X-ray photons of a sufficient energy, it ends up typically in a total charge state of four, as both inner-shell photoionization events (P) trigger a subsequent Auger decay (A). However, the exact sequence may differ from case to case: If the two ionization events occur prior to Auger decay, the photo-process is termed double core-hole creation and labelled as a ‘PPAA’ sequence. This can also be triggered by single-photon absorption at sufficiently high photon energies (see, e.g., ref. 25) which however precludes access to the evolving system. The double core-hole can be either located at a single atom of the molecule (single-site double core-hole), or the two electrons may emerge from different atoms (two-site double core-hole).26 If the second ionization happens after a first Auger decay, this process is labelled as a ‘PAPA’ sequence of consecutive photoionization and Auger decay events. In addition, the absorption of two photons may even yield a total molecular charge of five, if an additional electron is shaken off during one of the photoionization or Auger decay events. In all above-mentioned cases, the molecule starts to fragment as soon as two vacancies have been created. Adding further complexity, charge-transfer processes may occur during the fragmentation as long as the internuclear distances are not yet too large.22 Such charge transfer is an important aspect of chemical reactions as it changes their path and outcome. It occurs on ultrafast time scales and is at the heart of investigations of fundamental processes of modern ultrafast science. The aim of this paper is to demonstrate how these processes can be examined in an experiment in large detail by employing coincident imaging of emitted electrons and molecular ionic fragments.
For our study, we employed the SQS-REMI end-station located at the European X-ray free-electron laser facility.27 The COLTRIMS reaction microscope28,29 was used to measure in coincidence the ionic fragments and at least one of the emitted photoelectrons occurring during the interaction of the XFEL light with single oxygen molecules in the gas phase. The X-ray pulses had an initial pulse energy of 2.4 mJ and were attenuated to (30 ± 5) μJ using a nitrogen-containing gas absorber. Taking into account the beamline transmission,30 this resulted in pulse energies of (14 ± 2) μJ on target in a focus of a size of approximately 1 × 2 μm2. The pulse duration is estimated to be approximately 25 fs, based on the electron-bunch charge of 250 pC. More details on the experimental setup are provided in ref. 19 and 31. Accordingly, from our experiment we obtain the following information for each photoreaction event: The kinetic energy of the photoelectron, its emission direction with respect to the molecular axis, the kinetic energy of the fragment ions, their charge state, and their emission directions. As will be demonstrated below, this information can be employed to follow the route of the charge-up and fragmentation dynamics of O2.
2 Results and discussion
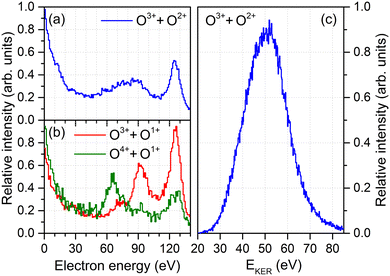
As a starting point, we analyze the electron energy spectra (obtained after irradiating the molecules with XFEL pulses of an energy of hν = 665 eV) for different fragmentation channels shown in Fig. 1(a) and (b). The spectrum for the O3+ + O2+ channel, which is of primary interest of this work, is shown in Fig. 1(a). It gives us the ability to distinguish between the first and second emitted photoelectron: The main line of the first photoelectron occurs at a kinetic energy of approximately 130 eV and a feature of multiple photoionization, which can be attributed to the second photoelectron in the PAPA sequence, is seen in a range of 55 eV to 110 eV.19 This feature is, however, much broader than expected for the PAPA process.In order to understand its origin, we examine other fragmentation channels in Fig. 1(b). There, the red curve depicts the energy spectrum of the O3+ + O1+ final state. A clear peak belonging to the PAPA process is visible at an energy of about 90 eV. The most probable pathway to generate these electrons (and this molecular charge state) is a photoionization with subsequent Auger decay (generating the O1+ + O1+ intermediate state) followed by a second photoionization and Auger decay during the fragmentation of the molecule (resulting in the final O3+ + O1+ state). The green curve in Fig. 1(b) shows the corresponding electron energy spectrum if the O4+ + O1+ final state is created. In this case, the PAPA peak moves to lower energies of about 65 eV. This suggests that the O4+ + O1+ state is created, to large extent, by an additional shake-off event in the second photoionization step. This diminishes the energy of that second photoelectron by the energy needed to release an additional electron. Thus, after the first photoionization and Auger decay event, the molecule is further photoionized, emits a shake-off electron and an Auger electron, adding in total three more charges: O1+ + O1+ → O4+ + O1+. These shake-off electrons are visible in the increase of the respective contribution below 20 eV, as compared to the other channel [cf., green and red curves in Fig. 1(b)].
These observations imply that the broad feature observable in the electron energy spectrum obtained for the O3+ + O2+ channel in Fig. 1(a) may consist of a mixture of both charge-up schemes. Electrons generated by a regular second photoionization event are responsible for the high-energy part of that feature, whereas the other ionization pathway, in which the second photoionization was accompanied by shake-off, contributes to the low-energy part. However, since the molecule is five-fold charged in the final state, in the former case an additional shake-off event occurred during the first photoionization step, and the second ionization step of this route reads: O1+ + O2+ → O3+ + O2+. This line of arguments would suggest that if the shake-off took place during the second photoionization event, the final charge state of the molecule should be O4+ + O1+. However, we barely observe the O4+ + O1+ charge state in our experiment, which indicates that this channel is either not as probable as the O3+ + O2+ channel, or that this transient charge state relaxes further into O3+ + O2+via charge transfer as long as the internuclear separation is not too large. Under the given experimental conditions, such short internuclear distances are present for a large part of the pulse duration. The classical ‘over-the-barrier’ charge-transfer model of ref. 32 suggests that this happens efficiently at internuclear distances of up to R ≤ 3Req ≈ 6.85 a.u., where Req is the equilibrium internuclear distance. Here, the total energy of O4+ + O1+ is still larger than the potential energy of O3+ + O2+. In what follows, we refer to the different routes yielding O3+ + O2+ by indicating whether in the second photoionization step only the photoelectron was emitted or two electrons were emitted by shake-off photoionization. Accordingly, we label the photoionization route O1+ + O2+ → O3+ + O2+ as the main pathway and the O1+ + O1+ → O3+ + O2+ case as the satellite channel.
The nuclear dynamics during the charge-up are dominated by the fragmentation of the molecule. Information on the internuclear separation R of the two ionic fragments at the instant of the secondary O 1s photoionization is imprinted on the ions’ kinetic energy release EKER. In order to interconnect R and EKER, a very simple classical Coulomb-explosion model19 can be applied. It assumes a sequence of the following steps: At first, the primary O 1s photoionization and subsequent Auger decay take place at the equilibrium separation Req which form the Ozl+ + Ozr+ charge state (with zl and zr denoting the possible charge states at the left and right side of the molecule). Thereafter, the O–O bond elongates on the repulsive potential zlzr/r (with r being the distance between the two charges) until the internuclear separation R is reached, where the secondary O 1s photoionization and an immediate Auger decay take place forming the final 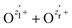 charge state. Finally, the resulting-state fragments on the repulsive potential
charge state. Finally, the resulting-state fragments on the repulsive potential 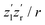 of the two ions are detected. The resulting kinetic energy release EKER and internuclear distance R are, thus, related as:
of the two ions are detected. The resulting kinetic energy release EKER and internuclear distance R are, thus, related as:
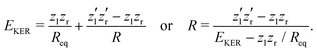 | (1) |
To this end, however, it is not clear to what extent this simplistic model is capable of capturing the complex charge-up dynamics. For example, synchrotron work on O2 molecules on low-final-charge states depicts very complex (i.e., feature-rich) kinetic energy release distributions which can be attributed to a multitude of accessible intermediate states.33 As depicted in Fig. 1(c), we observe a kinetic energy release of the O3+ + O2+ fragments in a range of about 30 eV < EKER < 75 eV in the experiment, which exhibits mainly a single peak. From the solitary KER distribution the ionization pathways and different intermediate states, thus, cannot be disentangled.
PA-MFPADS do allow to unravel the full charge-up and bond-breaking dynamics as we will show in the following. Fig. 2 depicts examples of such distributions for different distances between the oxygen atoms as obtained from a full theoretical modeling employing the single-center method.34,35 The calculations were performed as described in detail in our previous works on this molecule.19,31 The modeled angular distributions have been normalized to the forward peak pointing towards the doubly charged oxygen ion. While the details of the PA-MFPAD depend strongly on the internuclear distance R, a closer inspection of the photoelectron flux towards the singly charged oxygen ion, which after the photoionization and Auger decay becomes triply charged, shows an oscillatory trend with respect to R. In particular, starting from a minimum at the largest distance of 6 a.u., several minima and maxima in the emission pattern emerge in the direction labeled as ‘Backward’ in Fig. 2 for smaller internuclear separations (i.e., from yellow- to blue-colored MFPADs).
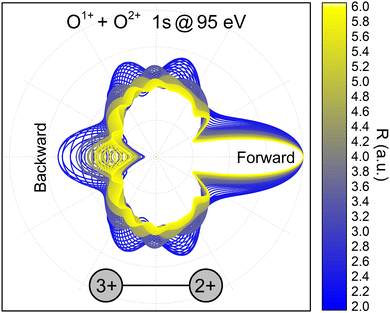 | ||
| Fig. 2 Polarization-averaged MFPADs of the second 1s photoelectron, computed in the relaxed-core Hartree–Fock approximation at different internuclear separations for the O1+ + O2+ → O3+ + O2+ channel. After the second photoionization and Auger decay, the left singly charged oxygen ion becomes triply charged. An electron energy of 95 eV was used in the calculations, as these electrons represent the high-energy part of the broad feature in Fig. 1(a). The PA-MFPADs are normalized to the forward peak. The color encodes the internuclear separation between the two oxygen ions at the instant of the photoionization. | ||
This behavior of the backward peak of the PA-MFPAD can be explained already within a simplified theoretical model.36,37 It employs the single-channel, single-scattering, plane-wave, and muffin-tin approximations. It also includes a superposition of a direct electron wave with momentum k emitted from the left oxygen ion in Fig. 2 with an electron wave which occurs due to scattering at the second oxygen ion at the right. Using the site T-matrix expansion,38,39 we obtain the following analytic expression for the polarization-averaged differential probability of the 1s photoionization of the left oxygen atom Ol of a fixed-in-space oxygen molecule (see ref. 36 and 37 on details of the derivation):
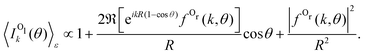 | (2) |
Substituting θ = 0 in eqn (2) removes the phase factor exp[ikR (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)] from the forward intensity, while for θ = π, the backward intensity oscillates as a function of 2kR.40
θ)] from the forward intensity, while for θ = π, the backward intensity oscillates as a function of 2kR.40
It is straightforward to obtain the following parametrization of the ratio of the backward to forward intensities:
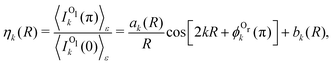 | (3) |
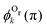 . One can see that this ratio oscillates with cos(2kR), i.e., with the phase accumulated by the scattered wave on its way 2R from the Ol to Or atoms and back.
. One can see that this ratio oscillates with cos(2kR), i.e., with the phase accumulated by the scattered wave on its way 2R from the Ol to Or atoms and back.
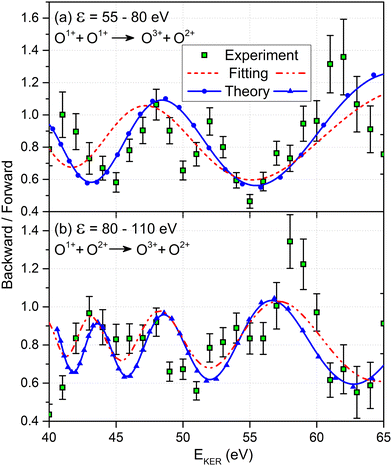
We now analyze the backward–forward ratio of the PA-MFPADs given by eqn (3) of the secondary photoelectron as a function of EKER for two regions with low ε = 55–80 eV and high ε = 80–110 eV electron energies, which we attributed previously to the satellite and main pathways. The corresponding results are shown in Fig. 3(a) and (b), respectively, as symbols with error bars for the experiment. The measured ratios possess clear oscillations in a wide range of the measured kinetic energy release EKER. The internuclear separation R at the instant of the second photoionization event is linked with EKERviaeqn (1). In order to support our assumption that photoelectrons with higher kinetic energies are mainly produced by the main pathway (O1+ + O2+ → O3+ + O2+) and those with lower energy by the satellite channel (O1+ + O1+ → O3+ + O2+), we apply our simplified analytical model and perform a fitting of the ratios determined by the experiment using eqn (3). We assume the coefficients ak(R), bk(R), and the back-scattering phase 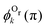 to be constant parameters for each photoionization channel. Furthermore, we use average photoelectron kinetic energies of ε = 95 eV and ε = 67.5 eV for the main and satellite channels. In order to interrelate the internuclear distance R with EKERviaeqn (1), we used
to be constant parameters for each photoionization channel. Furthermore, we use average photoelectron kinetic energies of ε = 95 eV and ε = 67.5 eV for the main and satellite channels. In order to interrelate the internuclear distance R with EKERviaeqn (1), we used 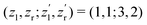 for the satellite channel O1+ + O1+ → O3+ + O2+ in Fig. 3(a) and
for the satellite channel O1+ + O1+ → O3+ + O2+ in Fig. 3(a) and 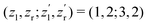 for the main channel O1+ + O2+ → O3+ + O2+ in Fig. 3(b). The results are depicted in Fig. 3 by the dashed (red) curves (see legend). Details on the fitting procedure are summarized in the ESI.†
for the main channel O1+ + O2+ → O3+ + O2+ in Fig. 3(b). The results are depicted in Fig. 3 by the dashed (red) curves (see legend). Details on the fitting procedure are summarized in the ESI.†
Our findings are furthermore confirmed as we extract the corresponding ratios from our full ab initio calculations (solid blue curves with symbols in Fig. 3). The same assumption for the transformation of R to EKERviaeqn (1) and the same mean photoelectron kinetic energies were used in our calculations. Both the ab initio theoretical results and the results employing our analytical model reproduce the experimentally observed backward–forward emission ratios. This supports that our assumption on the decay path generating low- and high-energy photoelectrons in producing the O3+ + O2+ charge state as being correct. We attribute the deviation of our simple scattering model and the ab initio calculations to remaining contributions from a multiple scattering of the outgoing photoelectron wave.
After having substantiated our interpretation of the two charge-up routes leading to O3+ + O2+ and determined the connection between EKER and internuclear distance R, we will now provide information on the time-domain properties of the charge-up process as a final step of our analysis. We use the same simple Coulomb-explosion model to examine the temporal evolution of the internuclear distances in the intermediate states O1+ + O1+ and O1+ + O2+ during the XFEL pulse. The Newtonian equation of motion for the O–O separation along the bond in the Ozl+ + Ozr+ intermediate state reads
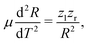 | (4) |
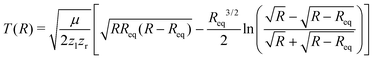 | (5) |
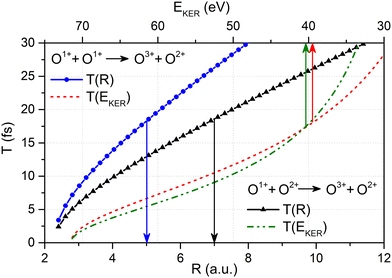 | ||
| Fig. 4 The relation between the O–O bond length R and the time delay T between first and second ionization event given by eqn (5) (solid curves with symbols, refer to the lower horizontal scale) together with the relation between EKER and the time delay T between first and second ionization event obtained viaeqn (5) with the O–O bond length R given as a function of EKERviaeqn (1) (broken curves, refer to the upper horizontal scale) for the O1+ + O2+ → O3+ + O2+ main and the O1+ + O1+ → O3+ + O2+ satellite channel, respectively (see legends). | ||
3 Conclusions
In conclusion, we have demonstrated that the charge-up and fragmentation dynamics of a small molecule interacting with intense ultra-short X-ray pulses can be examined in intriguing detail by employing COLTRIMS reaction microscopy. The information content of our electron-ion coincidence measurement reveals the charge-up during the photo-dissociation process and its time evolution, while applying very modest assumptions and simplified scattering models. Our ab initio treatment of the emitted photoelectrons confirms this assessment. Our work suggests that charge-up and fragmentation dynamics of even larger molecules should be addressable with similar analysis concepts. In addition, future time-resolved studies using X-ray pump/X-ray probe schemes for the two photoionization events could directly investigate the process described in this article and confirm that PA-MFPADs in connection with additional observables measured in coincidence are a suitable tool for obtaining a detailed understanding of molecular charge-up processes.Author contributions
All authors except for P. V. D., D. V. R., F. O., Y. T., N. H., K. Y., and K. H. have participated in the experiment. D. V. R. and P. V. D. performed the theoretical calculations. T. J., A. C., and G. K.: Data analysis. F. O., K. Y., K. H., K. U., T. J., and P. V. D.: Interpretation of the data. F. O., Y. T., N. H., K. Y., K. H., and K. U. conceived the simplified model. F. O., Y. T., N. H., K. Y., and K. H. performed the simulations based on the simplified model. P. V. D., T. J., F. O., K. Y., K. H., and K. U. drafted the manuscript. All authors discussed the results and revised/contributed to the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge European XFEL in Schenefeld, Germany, for provision of X-ray free-electron laser beam time at the SQS instrument and would like to thank the staff for their assistance. We are indebted to A. Bräuning-Demian for timely support during the beamtime preparations. This work has been supported by the Bundesministerium für Bildung und Forschung (BMBF) grants 05K13RF4 and 05K16RF1. M. S. S., S. G., K. F., and R. D. acknowledge support from Deutsche Forschungsgemeinschaft (DFG) – Project No. 328961117 – SFB 1319 ELCH (Extreme light for sensing and driving molecular chirality). D. V. R. and P. V. D. acknowledge support from DFG Project No. 492619011 (DE 2366/6-1). M. I., Ph. S., and V. M. acknowledge funding by the Volkswagen foundation within a Peter Paul Ewald-Fellowship. F. O., K. H., and K. U. acknowledge the Cooperative Research Program of “Network Joint Research Center for Materials and Devices”. K. H. also acknowledges funding by JSPS KAKENHI under Grant No. 18K05027 and 19KK0139, while K. U. acknowledges the X-ray Free Electron Laser Utilization Research Project and the X-ray Free Electron Laser Priority Strategy Program of the Ministry of Education, Culture, Sports, Science, and Technology of Japan (MEXT) and the IMRAM program of Tohoku University. K. Y. is grateful to the financial support from JSPS KAKENHI Grant Number 19H05628. Th. W. was supported by the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 and by the U.S. Department of Energy Office of Basic Energy Sciences, Division of Chemical Sciences, Biosciences and Geosciences. X. L. was supported by the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Sciences, Office of Science, US Department of Energy, Grant No. DE-SC0019451; D. R. and A. R. acknowledge support by grant no. DE-FG02-86ER13491 from the same funding agency. J. B. W. acknowledges funding by National Science Foundation Grant No. NSF-PHY-1807017. M. M. acknowledges support by the DFG, German Research Foundation – SFB-925 – project 170620586 and by the Cluster of Excellence Advanced Imaging of Matter of the DFG, EXC 2056, Project ID 390715994. Data recorded for the experiment at the European XFEL are available at https://doi.org/110.22003/XFEL.EU-DATA-002412-00.Notes and references
- H. N. Chapman,
et al.
, Nature, 2011, 470, 73–77 CrossRef CAS PubMed
.
- J. Küpper,
et al.
, Phys. Rev. Lett., 2014, 112, 083002 CrossRef
.
- M. P. Minitti,
et al.
, Phys. Rev. Lett., 2015, 114, 255501 CrossRef CAS PubMed
.
- T. Gruene,
et al.
, Angew. Chem., Int. Ed., 2018, 57, 16313–16317 CrossRef CAS PubMed
.
- C. J. Hensley, J. Yang and M. Centurion, Phys. Rev. Lett., 2012, 109, 133202 CrossRef PubMed
.
- B. Wolter,
et al.
, Science, 2016, 354, 308–312 CrossRef CAS PubMed
.
- J. Yang,
et al.
, Science, 2018, 361, 64–67 CrossRef CAS PubMed
.
- T. J. A. Wolf,
et al.
, Nat. Chem., 2019, 11, 504–509 CrossRef CAS PubMed
.
- E. G. Champenois,
et al.
, Science, 2021, 374, 178–182 CrossRef CAS PubMed
.
- A. Landers,
et al.
, Phys. Rev. Lett., 2001, 87, 013002 CrossRef CAS PubMed
.
- A. V. Golovin, N. A. Cherepkov and V. V. Kuznetsov, Z. Phys. D: At., Mol. Clusters, 1992, 24, 371–375 CrossRef CAS
.
- J. Adachi, K. Hosaka, S. Furuya, K. Soejima, M. Takahashi, A. Yagishita, S. K. Semenov and N. A. Cherepkov, Phys. Rev. Lett., 2003, 91, 163001 CrossRef CAS PubMed
.
- E. Shigemasa, J. Adachi, K. Soejima, N. Watanabe, A. Yagishita and N. A. Cherepkov, Phys. Rev. Lett., 1998, 80, 1622 CrossRef CAS
.
- M. Waitz,
et al.
, Nat. Commun., 2017, 8, 2266 CrossRef CAS PubMed
.
- S. Grundmann,
et al.
, Science, 2020, 370, 339–341 CrossRef CAS PubMed
.
- J. B. Williams,
et al.
, Phys. Rev. Lett., 2012, 108, 233002 CrossRef CAS PubMed
.
- H. Fukuzawa,
et al.
, J. Chem. Phys., 2019, 150, 174306 CrossRef PubMed
.
- R. Boll,
et al.
, Phys. Rev. A, 2013, 88, 061402(R) CrossRef
.
- G. Kastirke,
et al.
, Phys. Rev. X, 2020, 10, 021052 CAS
.
- L. Young,
et al.
, Nature, 2010, 466, 56–61 CrossRef CAS PubMed
.
- B. Rudek,
et al.
, Nat. Photonics, 2012, 6, 858–865 CrossRef CAS
.
- A. Rudenko,
et al.
, Nature, 2017, 546, 129–132 CrossRef CAS PubMed
.
- X. Li,
et al.
, Phys. Rev. A, 2022, 105, 053102 CrossRef CAS
.
- X. Li,
et al.
, Sci. Rep., 2021, 11, 505 CrossRef CAS PubMed
.
- G. Goldsztejn,
et al.
, Phys. Rev. A, 2017, 96, 012513 CrossRef
.
- N. Berrah,
et al.
, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16912–16915 CrossRef CAS PubMed
.
- T. Tschentscher, C. Bressler, J. Grünert, A. Madsen, A. P. Mancuso, M. Meyer, A. Scherz, H. Sinn and U. Zastrau, Appl. Sci., 2017, 7, 592 CrossRef
.
- J. Ullrich, R. Moshammer, A. Dorn, R. Dörner, L. Ph. H. Schmidt and H. Schmidt-Böcking, Rep. Prog. Phys., 2003, 66, 1463 CrossRef CAS
.
- T. Jahnke, Th. Weber, T. Osipov, A. L. Landers, O. Jagutzki, L. Ph. H. Schmidt, C. L. Cocke, M. H. Prior, H. Schmidt-Böcking and R. Dörner, J. Electron Spectrosc. Relat. Phenom., 2004, 141, 229–238 CrossRef CAS
.
- T. Mazza, T. M. Baumann, R. Boll, A. De Fanis, P. Grychtol, M. Ilchen, J. Montano, V. Music, Y. Ovcharenko, N. Rennhack, D. E. Rivas, A. Rörig, P. Schmidt, S. Usenko, P. Ziolkowski, D. La Civita, M. Vannoni, H. Sinn, B. Keitel, E. Plönjes, K. Mann, B. Schäfer, S.-K. Son and M. Meyer, J. Synchrotron Radiat., 2022 Search PubMed
, to be submitted.
- G. Kastirke,
et al.
, Phys. Rev. Lett., 2020, 125, 163201 CrossRef CAS PubMed
.
- H. Ryufuku, K. Sasaki and T. Watanabe, Phys. Rev. A, 1980, 21, 745 CrossRef CAS
.
- Z. Bao, R. F. Fink, O. Travnikova, D. Céolin, S. Svensson and M. N. Piancastelli, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 125101 CrossRef
.
- Ph. V. Demekhin, A. Ehresmann and V. L. Sukhorukov, J. Chem. Phys., 2011, 134, 024113 CrossRef PubMed
.
- S. A. Galitskiy, A. N. Artemyev, K. Jänkälä, B. M. Lagutin and Ph. V. Demekhin, J. Chem. Phys., 2015, 142, 034306 CrossRef CAS PubMed
.
- F. Ota, K. Yamazaki, D. Sébilleau, K. Ueda and K. Hatada, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 024003 CrossRef CAS
.
- F. Ota, K. Hatada, D. Sébilleau, K. Ueda and K. Yamazaki, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 084001 CrossRef CAS
.
- J. S. Faulkner and G. M. Stocks, Phys. Rev. B, 1980, 21, 3222 CrossRef CAS
.
- K. Hatada, K. Hayakawa, M. Benfatto and C. R. Natoli, J. Phys.: Condens. Matter, 2010, 22, 185501 CrossRef PubMed
.
- B. Zimmermann,
et al.
, Nat. Phys., 2008, 4, 649–655 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02408j |
| This journal is © the Owner Societies 2022 |