Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Can the isonitrile biosynthesis enzyme ScoE assist with the biosynthesis of isonitrile groups in drug molecules? A computational study†
Henrik P. H.
Wong
 ab,
Thirakorn
Mokkawes
ab,
Thirakorn
Mokkawes
 ab and
Sam P.
de Visser
ab and
Sam P.
de Visser
 *ab
*ab
aManchester Institute of Biotechnology, 131 Princess Street, Manchester M1 7DN, UK. E-mail: sam.devisser@manchester.ac.uk
bDepartment of Chemical Engineering, Oxford Road, Manchester M13 9PL, UK
First published on 14th October 2022
Abstract
Many drug molecules contain isonitrile substituents; however, synthesizing these compounds remains challenging in organic chemistry. The isonitrile synthesizing enzyme ScoE utilizes a substrate with the γ-Gly substituent, and using two molecules of dioxygen and α-ketoglutarate converts it to an isonitrile group through an oxidative decarboxylation reaction. To explore its substrate scope and whether this process could be used for the biosynthesis of isonitrile-containing drug molecules, we performed a predictive computational study. We started with the recent crystal structure coordinates of ScoE, removed the substrate and inserted two potential precursor molecules of the drug molecules axisonitrile-1 and xanthocillin into the structure, whereby both molecules have their isonitrile groups replaced by γ-Gly. Both substrates fit into the substrate binding pocket of the enzyme well and position them in the correct orientation for catalysis on the iron center. Based on a molecular dynamics simulation, we created a quantum chemical cluster model of the enzyme active site with γ-Gly-substituted axisonitrile-1 and studied the oxidative decarboxylation reaction to form axisonitrile-1 products. The calculations give similar barriers to wildtype substrate for either the initial C–H or N–H hydrogen atom abstraction, which leads to a radical intermediate and form desaturated reactants. We then took the desaturated substrate and created another iron(IV)–oxo model complex to study the subsequent hydrogen atom abstraction and decarboxylation and found this to be feasible as well although we predict to see by-products for hydroxylation in the second cycle. Nevertheless, we believe that the ScoE enzyme can be utilized for the biosynthesis of isonitrile substituents in substrates with γ-Gly components as an environmentally benign alternative to organic chemistry approaches for the synthesis of isonitrile groups. We hope that experimental studies will be able to confirm our hypothesis.
Introduction
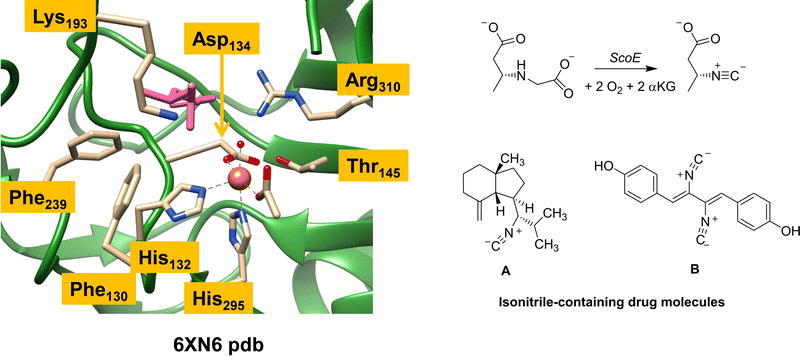
Isonitrile is an important chemical compound in organic chemistry and can react as a nucleophile or electrophile.1,2 It is isoelectronic to CO and as a result coordinates to metal complexes really well. Over the years, hundreds of natural products containing isonitrile groups have been discovered and as a consequence, isonitrile-containing compounds have become popular as drug targets.3,4 Some of these compounds have interesting medicinal properties and act as antifungal, antimalarial and antibacterial entities.5–7 Understanding how nature synthesizes these natural products, therefore, is important. However, since most of these reaction processes happen fast, a computational analysis is needed to establish details of the reaction mechanism and the oxidants involved in the process.There are several enzymes in nature responsible for the biosynthesis of isonitrile groups in natural compounds.1–17 One of those is a nonheme iron enzyme called ScoE, which uses dioxygen and α-ketoglutarate (αKG) as the co-substrate on an iron centre and converts a γ-glycine subunit in a peptide chain to isonitrile through initial desaturation followed by decarboxylation.14 Several crystal structures of ScoE have been reported and the active site structure of the most recent one as reported in the 6XN6 protein databank (pdb) file is shown in Fig. 1.16,18
 | ||
| Fig. 1 Extract of the active site of ScoE as taken from the 6XN6 pdb file and the overall reaction catalysed by the enzyme. Also shown are two typical drug molecules A and B with isonitrile substituents. | ||
ScoE has a nonheme iron(II) active site that has the metal connected to the protein through interactions with the side chains of His132, Asp134 and His295 (see Fig. 1). In octahedral symmetry that leaves three metal binding sites open for the co-substrate (αKG binds as a bidentate ligand) and dioxygen. Substrate CABA ((R)-3-carboxyaminobutanoic acid) was used in the work of Ref 16 to characterize a structure of ScoE. It is highlighted in pink in Fig. 1 and bound in the active site near the side chain of Arg310, which forms a salt bridge with the carboxylate group of the substrate. Several aromatic amino acids, e.g. Phe130 and Phe239, line the substrate binding pocket and position the substrate and the oxidant in a specific orientation. The substrate binding is further stabilized by an active site Lys residue (Lys193), which pointed to the surface in an earlier crystal structure13 but is directed to the active site in the structure shown in Fig. 1. It has been implicated that Lys193 has a role related to substrate positioning and catalysis but details remain unknown.
Several computational studies investigated the mechanism of isonitrile formation by ScoE enzymes.17,19,20 The modelling predicted the enzyme to operate in two consecutive catalytic cycles that use both one molecule of O2 and αKG and on the iron centre react to form an iron(IV)–oxo species, succinate and CO2. In nonheme iron/αKG-dependent dioxygenases, the iron(II) centre binds αKG and subsequently dioxygen to form an iron(III)–superoxo species.21–31 The superoxo is expected to attack the α-keto position of αKG and form an iron-persuccinate and CO2 prior to heterolytic cleavage of the O–O bond to give an iron(IV)–oxo species and succinate. The iron(IV)–oxo species in nonheme iron dioxygenases typically reacts through aliphatic hydroxylation of a C–H bond of the substrate although there are also examples, e.g. in the flavonol biosynthesis enzyme, of desaturation reactions to form a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond.32–34 The iron(IV)–oxo species in ScoE, however, is predicted to be involved in the subsequent oxidative decarboxylation of the substrate to give the isonitrile product through two cycles that use one molecule of O2 and αKG each. The various computational studies, however, had conflicting results on whether a rate-determining C–H or N–H abstraction from the substrate takes place initially. A second hydrogen atom abstraction from the substrate then gives an iron(II)–water complex and a desaturated substrate with N
C bond.32–34 The iron(IV)–oxo species in ScoE, however, is predicted to be involved in the subsequent oxidative decarboxylation of the substrate to give the isonitrile product through two cycles that use one molecule of O2 and αKG each. The various computational studies, however, had conflicting results on whether a rate-determining C–H or N–H abstraction from the substrate takes place initially. A second hydrogen atom abstraction from the substrate then gives an iron(II)–water complex and a desaturated substrate with N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds. All computational studies agree that the second cycle with another dioxygen molecule and αKG gives another iron(IV)–oxo species that then reacts with the desaturated substrate and abstracts the final hydrogen atom from the N
C double bonds. All computational studies agree that the second cycle with another dioxygen molecule and αKG gives another iron(IV)–oxo species that then reacts with the desaturated substrate and abstracts the final hydrogen atom from the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond of the substrate followed by decarboxylation to give isonitrile products and CO2.
C bond of the substrate followed by decarboxylation to give isonitrile products and CO2.
As ScoE appears to convert substrates with γ-glycine substituents to isonitrile efficiently, we were wondering whether the ScoE template could be used for drug synthesis reactions instead. In particular, there are many drug molecules with isonitrile substituents and two of those are shown in Fig. 1, namely axisonitrile-1 (designated A) and xanthocillin (designated B). In this work, we explored the isonitrile biosynthesis of axisonitrile-1 and xanthocyllin by using a precursor complex with a γ-Gly group in the position of the isonitrile group, designated as γ-Gly-A and γ-Gly-B. To this end, we docked γ-Gly-A and γ-Gly-B into the crystal structure coordinates of ScoE and created a QM cluster model, whereby we attempted to follow a similar reaction mechanism as previously described for the wildtype system. The work shows that γ-Gly-A fits neatly into the substrate binding pocket and in a position for oxidative decarboxylation to form isonitrile, whereas γ-Gly-B due to its longer shape binds weaker and may not reside in the substrate binding pocket long enough to be activated on the γ-Gly group. As such, ScoE may have potential in biotechnology for the synthesis of isonitrile groups in compounds.
Computational methods
Docking and molecular dynamics simulations
We started the work with a detailed docking and molecular dynamics study on the ScoE enzymatic structure with γ-Gly-A and γ-Gly-B bound. To this end, we took the 6XN6 pdb file,16,18 which is an enzyme monomer with iron(II), acetate and CABA substrate bound. We replaced the iron(II)–water group with iron(IV)–oxo with the atoms at a distance of 1.61 Å and manually inserted bound succinate to iron in the position of acetate. Substrate CABA, acetate and Cl− ions were removed from the pdb. Hydrogen atoms were added in Chimera under pH 7 conditions,35 whereby all basic amino acids (Glu/Asp) were in their deprotonated state, while the Lys/Arg residues were all protonated. The active sites His132 and His295 were in the singly protonated form, while all other His residues are surface bound and hence were taken as doubly protonated.After a UB3LYP/6-31+G*36–38 geometry optimization in Gaussian-0939 of γ-Gly-A and γ-Gly-B, the two substrates were docked into the ScoE protein using the Autodock Vina software as implemented in Chimera (see the ESI† for details).35,40 The best substrate-bound conformations were then selected and the system was prepared for a molecular dynamics simulation. First, the system was solvated by TIP3P-based water molecules in a box with a minimum distance of 10 Å to the side of the box.41 Thereafter, a molecular dynamics (MD) simulation was run on the lowest energy conformers in the Amber software package42 using the ff14SB4 force field.43 After an initial equilibration and heating stage, an MD simulation was run using the system minimized by 2000 steps of steepest descent with all heavy atoms fixed. In the second stage, the system was heated to 310 K in 100 ps intervals under NPT conditions. A production MD run for 100 ns was performed in the Amber 16 software package for the structures with γ-Gly-A and γ-Gly-B bound.42
After analysing the structures from the MD runs, we used umbrella sampling approaches to investigate the tightness of binding of the substrate in the binding pocket by adding a potential to the distance separating the centre-of-mass of the substrate with the oxo group of the iron–oxo complex.44,45
Model set-up
Our previous work on the ScoE enzyme utilized a density functional theory (DFT) cluster model of the first- and second-coordination sphere of the enzyme with the substrate and αKG bound.20 Details on the procedures of the set-up and validation of cluster models can be found in review papers of our group and others.46–49 In particular, a recent comparison of experimentally obtained rates and selectivities compared to DFT cluster models gave correct regioselectivity prediction using cluster models of >200 atoms and a free energy of activation within 2 kcal mol−1 from the experiment.50 For the best comparison with the wildtype structure, we included the same protein residues in our model here as those that were used in calculations were reported in ref. 20 but here we use substrate γ-Gly-A instead of CABA. The optimized geometry of the γ-Gly-A bound iron(IV)–oxo model of ScoE (ReI) is similar to the one obtained after the MD simulation and has a structure that can be compared well with the original pdb and the wild-type optimized reactant geometry. Details of the residues and atoms included in the model are shown in Scheme 1.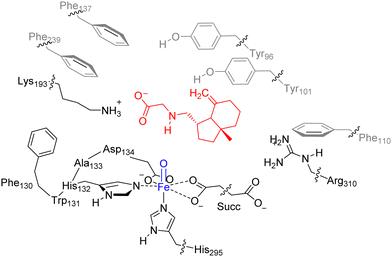 | ||
| Scheme 1 Cluster model of ScoE with substrate γ-Gly-A as investigated in this work. The wiggly lines identify where the protein chain was cut and a hydrogen link-atom was added. | ||
In order to keep the size and shape of the substrate and oxidant binding models closest to the actual enzyme system, we kept a number of protein chains and residues in the model that determine the second-coordination sphere. In particular, our model includes a short protein chain Phe130–Trp131–His132–Ala133–Asp134, whereby Trp131 and Ala133 were abbreviated to Gly, and several amino acid side chains truncated at the α-carbon atom of the protein: residues Tyr96, Tyr101, Phe110, Phe137, Lys193, Phe239, His295 and Arg310. The new ScoE model with substrate I bound is therefore 231 atoms in size and was calculated with +1 charge. No geometric constraints were put on the system and consequently the geometry optimizations of local minima had real frequencies only. An overlay of our optimized geometry with the last point of the MD simulation shows minor structural differences, which implies that the model is a good representation of the real system.
Procedures
The calculations utilized the Gaussian-09 software package39 using density functional theory (DFT) methods and the unrestricted B3LYP density functional theory method.36,37 Geometry optimizations were followed by analytical frequency calculations to confirm the nature of the local minima, whereby all transition states were characterized with a single imaginary mode for the correct transition. The geometry optimizations and analysis of frequencies for local minima and transition states were performed using the LANL2DZ basis set on iron that includes an electron core potential, while 6-31G* was applied on the rest of the atoms: basis set BS1.38,51 Geometry scans were performed to explore the potential energy surface and to obtain starting structures for the transition state optimizations. These calculations were done using a more modest basis set that had LANL2DZ on iron (with core potential) and 6-31G on the rest of the atoms: basis set BS0.Energies of the optimized geometries of the local minima and transition states were corrected for solvent effects through single point calculations using the continuum polarized conductor model (CPCM)52 included with a dielectric constant mimicking chlorobenzene. In addition, these single points incorporated an enlarged basis set on all atoms, namely LANL2DZ (with electron core potential) on iron and 6-311+G* on the rest of the atoms (basis set BS2). A second set of single point calculations was performed, whereby the basis set was further enlarged to cc-pVTZ on iron and 6-311+G* on the rest of the atoms (basis set BS3).53 The methods employed here have been extensively benchmarked and validated previously and generally reproduce experimental structures, spectroscopic parameters and free energies of activation of oxygen atom transfer reactions well.54–56 Free energies are reported at a temperature of 298 K and a pressure of 1 bar and use unscaled vibrational frequencies.
Results and discussion
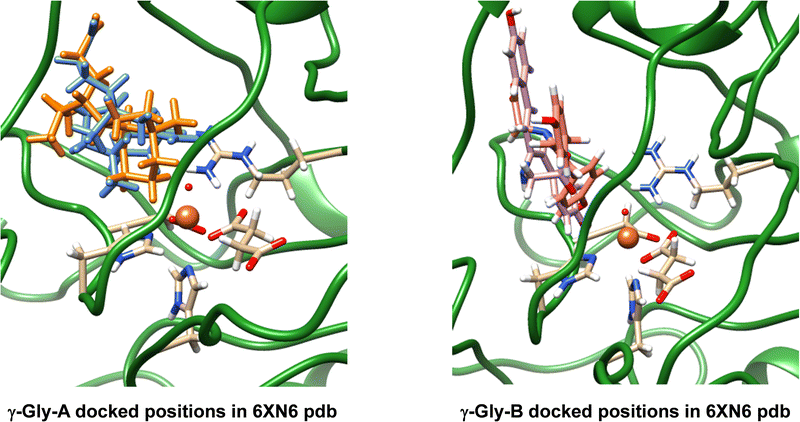
The work reported in this article focuses on the 6XN6 pdb file,16,18 where we converted iron(II)–water(acetate) in the active site to iron(IV)–oxo(succinate). Hydrogen atoms were added to all protein residues in Chimera.35 Thereafter, we manually moved the succinate position in the structure, so that it formed a bidentate ligand bound to iron trans to the His132 and Asp134 residues. Next, we created structures of the drug-synthesis substrates γ-Gly-A and γ-Gly-B (Fig. 1), which are the drug molecules A and B with their isonitrile substituents replaced by a γ-glycine group. The geometries of γ-Gly-A and γ-Gly-B were minimized at the UB3LYP/6-31+G* level of theory and converted to pdb structures. In ScoE, a peptide chain with a γ-glycine branch is activated and with two molecules of O2 and αKG on an iron(II) centre is reduced to isonitrile. Because of their chemical structure, we reasoned that γ-Gly-A and γ-Gly-B may be suitable substrates for ScoE as well and attempted to insert them into the protein structure and investigate the oxidative decarboxylation reaction on the iron centre using DFT methods.After a geometry optimization of γ-Gly-A and γ-Gly-B in Gaussian,39 we docked both substrates into our wildtype ScoE structure with iron(IV)–oxo succinate as the active site and the original substrate removed. The docking revealed several possible active site binding poses for the substrates as shown in Fig. 2. Particularly, substrate γ-Gly-A appears to fit the substrate-binding pocket nicely and several low-energy orientations (shown in blue and amber colours) were located with the substrate in close contact with the iron active site centre. Substrate γ-Gly-B has a longer shape and consequently cannot form good interactions with its carboxylate group with active site Arg residues, such as Arg310. As such, the substrate binding pocket is more open, but two low-energy binding poses of γ-Gly-B close to the iron centre are shown in purple and pink in Fig. 2.
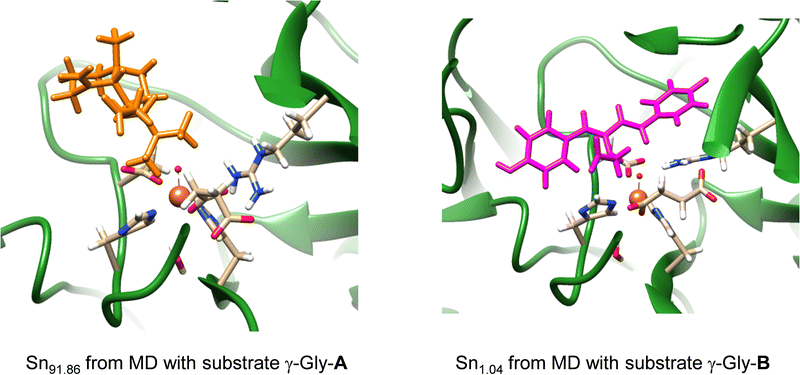
Subsequently, we took the most favourable binding poses of ScoE with γ-Gly-A and γ-Gly-B bound as shown in Fig. 2 and ran a 100 ns MD simulation for each of them. In both 100 ns MD runs, the root-mean-square-deviation of the protein, oxidant and substrate geometric features converges well within the time frame of the simulation (Fig. S3, ESI†). With both substrates, the MD simulations reproduce the results on the wildtype structure with a highly rigid substrate binding conformation and little flexibility in the protein chains. In particular, the MD simulation with substrate γ-Gly-A gives a very rigid system where the substrate is locked in position by interactions with protein residues and remains close to the iron centre throughout. A representative snapshot after 91.86 ns (Sn91.86) of the MD simulation for γ-Gly-A is shown in Fig. 3, which has the γ-Gly-A substrate in a similar position as CABA in the original crystal structure coordinates and held in position with a hydrogen bonding interaction with Arg310. The MD simulation with γ-Gly-B present gives the substrate close to the iron centre at the beginning of the MD simulation, while it moved to a larger distance toward the end of the MD simulation. As such an early snapshot from the MD simulation on γ-Gly-B binding to ScoE is taken after 1.04 ns (Sn1.04) and is shown in Fig. 3. The structure has the γ-Gly group of substrate pointing towards the iron(IV)–oxo group at a relatively close distance that could trigger its desaturation.
To find out how strongly the substrate is bound inside the protein structure, we took the last snapshot from the MD simulations with substrate γ-Gly-A and γ-Gly-B bound and used umbrella sampling methods with various force constant values for the substrate–oxo interaction and ran another 100 ns simulation in Amber. Details are given in Fig. S4 (ESI†). Umbrella sampling keeps γ-Gly-A into the substrate binding pocket during the second 100 ns simulation in roughly the same orientation and position as in the original MD simulation. Therefore, the substrate is tightly bound in a closed substrate-binding pocket with strong interactions with the protein. On the other hand, umbrella sampling on the last snapshot of the MD simulation for the protein with γ-Gly-B bound results in major differences. In particular, a subsequent second 100 ns simulation of this system results in the expulsion of γ-Gly-B from the substrate binding pocket when umbrella sampling is applied. As such our work does not establish a strongly-bound γ-Gly-B binding in the substrate-binding pocket and the MD simulations show that its binding and release back into solution may be in equilibrium because of a weak-binding interaction. This is probably due to the long and large size of the substrate that does not fit the active site well. As a result, γ-Gly-B will be highly mobile in the protein and it may be difficult to obtain isonitrile products from the reaction of γ-Gly-B in ScoE. Consequently, the MD simulations with γ-Gly-A and γ-Gly-B bound inside the ScoE structure implicate that the γ-Gly-A substrate has its γ-Gly residue close to the iron centre and appears tightly bound in the substrate-binding pocket, and hence we anticipate that it may be a viable substrate of ScoE. By contrast, γ-Gly-B appears much less tightly bound and more mobile and may not reach sufficiently close to the iron centre so that it can be activated. Therefore, we decided to proceed with substrate γ-Gly-A activation by ScoE and set up a quantum chemical cluster model.
We created a cluster model of the ScoE active site with γ-Gly-A bound as based on the Sn91.86 snapshot taken from the MD simulation. In order to compare the results with those reported previously for the wildtype system, we included the same protein residues in the model as those described in ref. 20. In particular, the model includes the iron(IV)–oxo succinate active site (with succinate truncated to acetate) with the direct ligands to iron and six active site aromatic amino acid side chains (Tyr96, Tyr101, Phe110, Phe130, Phe137 and Phe239). In addition, the positively charged chains of Lys193 and Arg310 were included in the model (see Scheme 1 above). We started the DFT calculations with a geometry optimization in the quintet and triplet spin states of the iron(IV)–oxo species with γ-Gly-A bound (5,3ReI) and the optimized geometries are shown in Fig. 4. The substrate binds in an orientation where it forms hydrogen-bonding interactions of its carboxylate group with the side chains of Lys193 and Arg310. This substrate-bound orientation positions the hydrogen atom from the N–H group of the substrate at a distance of 5.251 Å from the oxo atom of the FeO group, while the nearest C–H distance to the oxo is 6.858 Å for 5ReI. These distances are relatively long and hence may affect enzymatic turnover and barrier heights for the abstraction of hydrogen atoms from the substrate. As CABA is substantially smaller in size than γ-Gly-A, it fits better into the substrate-binding pocket and can move closer to the iron(IV)–oxo species. Nevertheless, we calculate a binding energy for γ-Gly-A from the difference in energy (calculated at the UB3LYP/BS2 level of theory) between 5ReI and an isolated γ-Gly-A group and 5ReI with the substrate removed. The obtained binding energy is thus 183 kcal mol−1 and consequently, the substrate is strongly bound in the pocket particularly, thanks to a salt bridge between the carboxylate group of the substrate and the side chain of Arg310 and several hydrogen-bonding interactions.
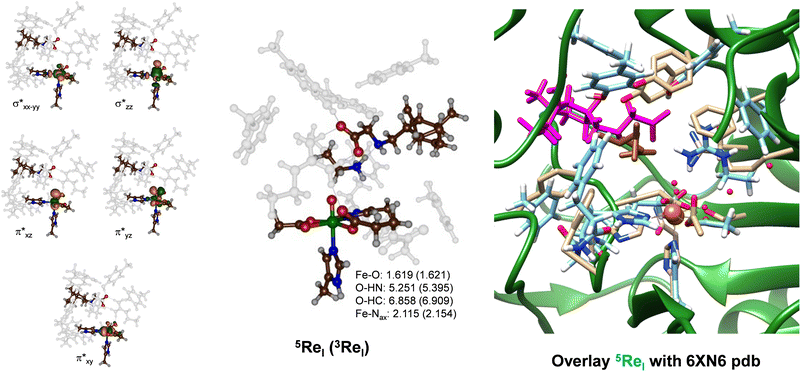 | ||
| Fig. 4 Optimized geometry of 5ReI and 3ReI as obtained in Gaussian at the UB3LYP/BS1 level of theory with bond lengths in Å. Left-hand side: Singly occupied and virtually low-lying orbitals of 5ReI. Right-hand side: Overlay of 5ReI with the 6XN6 pdb file. In the overlay protein chains of the pdb file are in green with atoms in grey and the substrate in brown, while the DFT optimized structure of the γ-Gly-A bound ScoE model is in light-blue with the substrate in purple. | ||
The iron–oxo bond is short, i.e. 1.619 Å, which is typical for iron(IV)–oxo complexes in enzymes and biomimetic model complexes as observed experimentally and computationally.57–83 The structure in the triplet spin state is very similar to the one in the quintet spin state and most covalent distances are within 0.1 Å. Our optimized geometry also has a three-dimensional structure that is not too far off from the original crystal structure coordinates. Thus, on the right-hand side of Fig. 4, we display an overlay of the 6XN6 pdb file with the 5ReI optimized structure, where we aligned the iron(IV)–oxo and its first coordination sphere atoms. As can be seen from Fig. 4, most residues are in approximately similar positions in the overlay of the cluster models with the crystal structure coordinates, including Arg310 and the amino acid residues Tyr96, Tyr101 and Phe110. Therefore, the γ-Gly-A substrate fits in the substrate-binding pocket neatly and little geometric changes have occurred from the crystal structure coordinates.
The metal-based molecular orbitals of 5ReI are shown on the left-hand side of Fig. 4. The lowest three of those are the π*xy, π*xz and π*yz molecular orbitals that are built up from the interactions of the atomic 3dxy, 3dxz and 3dyz orbitals on iron with first-coordination sphere ligands. In particular, the π*xz and π*yz orbitals are the antibonding interactions along the Fe–O bond, while the π*xy orbital represents antibonding interactions in the equatorial plane with the carboxylates of succinate and Asp134. The top two orbitals shown in Fig. 4 are the σ* antibonding orbitals along the Fe–O axis (σ*z2) and in the equatorial plane with His132, Asp134 and succinate (σ*x2−y2). The electronic ground state of 5ReI is the quintet spin state with orbital occupation π*xy1π*xz1π*yz1 σ*x2−y21, while the σ*z2 orbital is virtual. The triplet spin state (3ReI) with π*xy2π*xz1π*yz1 configuration is higher in energy by 4.5 kcal mol−1 than the quintet spin state. Generally, calculations on nonheme iron enzymes and model complexes have shown that the triplet spin iron(IV)–oxo species reacts usually with higher barriers than the corresponding quintet spin state and hence we do not expect 3ReI to play an important role here.64–66 Indeed our calculated triplet spin transition states are >10 kcal mol−1 above those found at the quintet spin state surface (see the ESI,† Table S2). Therefore, the reaction mechanism for the iron(IV)–oxo with the substrate will start from 5ReI and take place on a quintet spin surface only leading to products through single-spin-state-reactivity. This contrasts heme systems that typically react on close-lying spin state surfaces through multistate reactivity patterns.84,85 Nevertheless, the quintet spin ground state matches previous calculations on enzymatic nonheme iron(IV)–oxo complexes as well as electron paramagnetic resonance and Mössbauer spectroscopic results on nonheme iron enzymes.19,20,57–83
Subsequently, we investigated the reaction mechanism for isonitrile biosynthesis in γ-Gly-A in ScoE enzymes using the pathway as described in Scheme 2. Starting from 5ReI, we considered hydrogen atom abstraction from the N–H group of the substrate (pathway 1) to form the iron(III)-hydroxo intermediate 5IM1Ivia transition state 5TS1I. This local minima abstracts another hydrogen atom but from the C–H group via transition state 5TS2I to form the desaturated intermediate 5IM2I. The latter can also be formed when the hydrogen atom abstractions happen in reverse order via pathway 2 via5TS3I, 5IM3I and 5TS4I. After the optimized geometry of 5IM2I was obtained, we replaced the iron(II)–water group by iron(IV)–oxo to start the second cycle with 5Re2I. The iron(IV)–oxo species in the 2nd cycle abstracts the remaining hydrogen atom from the C–H group to form an iron(III)-hydroxo complex 5IM5I, which through decarboxylation via transition state 5TS6I gives the isonitrile products 5Prod. A proton transfer will then return the catalytic cycle to the resting state and an iron(II)–water complex. The alternative pathway where OH rebound occurs in 5IM5I was also tested via5TS7I to give the hydroxylated product 5Prod2I.
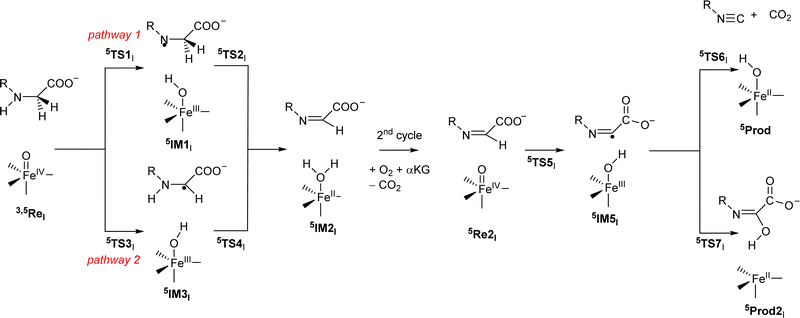 | ||
| Scheme 2 Reaction mechanism investigated in this work by labelling of the local minima and transition states. | ||
The DFT calculated the potential energy landscape for pathway 1, where an initial hydrogen atom is abstracted from the N–H group and is followed by C–H abstraction for γ-Gly-A by ScoE as compared to the wildtype results20 (calculated using the same methods and similar model) as shown in Fig. 5. For wildtype, negligible N–H abstraction led to exothermic formation of a radical intermediate 5IM1ScoE with exothermicity of ΔE + ZPE = −14.5 kcal mol−1 (ZPE stands for zero-point energy). A substantial hydrogen atom abstraction from the C–H position (ΔE + ZPE = 9.2 kcal mol−1 above the reactants’ complex) leads to a desaturated substrate. With γ-Gly-A as a substrate, the initial N–H hydrogen atom abstraction is substantially higher in energy (ΔE + ZPE = 8.2 kcal mol−1 above 5ReI) and hence the reaction will be much slower. Nevertheless, the barrier is sufficiently low in energy under room temperature conditions. Similar to the wildtype system, the hydrogen atom abstraction is overall exothermic and followed by a large barrier for the second hydrogen atom abstraction of 10.7 kcal mol−1 (via5TS2I). Therefore, replacing the wildtype substrate with γ-Gly-A does not appear to dramatically alter the first desaturation mechanism, although this process may be faster for γ-Gly-A than wildtype due to a smaller rate-determining step via5TS2I. These barriers are relatively modest and imply that the reaction will be feasible under room temperature conditions.
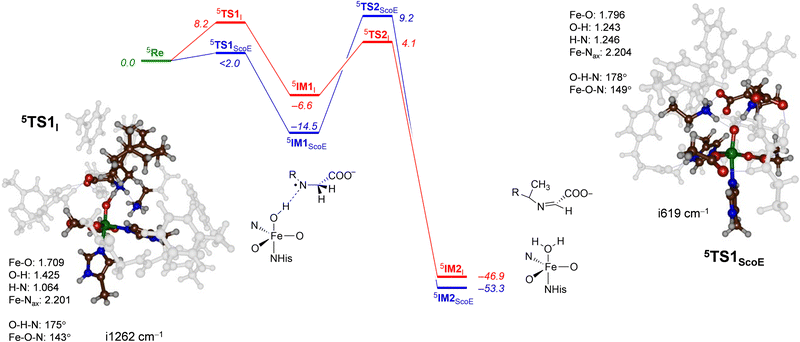 | ||
| Fig. 5 Potential energy landscape for γ-Gly-A desaturation via pathway 1 with initial N–H abstraction followed by C–H abstraction in red, while the wildtype landscape is in blue. Energies are UB3LYP/BS2//UB3LYP/BS1 with zero-point energy and solvent corrections in kcal mol−1. The optimized geometries of the transition states give bond lengths in Å, bond angles in degrees and the imaginary frequency in cm−1. The data of wildtype are taken from ref. 20. | ||
The transition state for abstraction of a hydrogen atom from the N–H bond (5TS1I) is shown in Fig. 5. It is early on the potential energy landscape with a short N–H distance of 1.064 Å, while the O–H distance to the oxo group is still long (1.425 Å). Nevertheless, the transition state represents a hydrogen atom transfer and has an imaginary frequency of i1262 cm−1 for the O–H–N stretch mode. The O–H–N angle is almost linear at 175°, while the Fe–O–N angle is bent at 143°. This large angle for the substrate versus iron–oxo orientation is often seen in nonheme iron dioxygenases33,86 and implicates an electron transfer from the substrate into the σ*z2 orbital to give a radical intermediate with configuration π*xy1π*xz1π*yz1σ*x2−y21σ*z21ϕSub1 with the substrate radical in orbital ϕSub as down-spin, while all metal-type unpaired electrons are up-spin. Indeed, the group spin densities for 5TS1I give a value of −0.22 on the substrate and 4.22 on the FeO group. The spin on the substrate increases to −0.96 when the structure relaxes to the iron(III)-hydroxo radical intermediate 5IM1I.
Geometrically, the 5TS1I structure is very different from the one reported in ref. 20 for the wildtype system. Thus, 5TS1ScoE has the transferring hydrogen atom almost midway between donor and acceptor groups at distances of 1.246 and 1.243 Å. Generally, early transition states, such as 5TS1I, correspond to relatively high reaction barriers, while central transition states have lower barriers.87,88 The difference in geometry between 5TS1I and 5TS1ScoE explains the rise in barrier height along the reaction mechanism. The transition state has a large imaginary frequency of i1262 cm−1 for the N–H–O stretch vibration, characteristic for hydrogen atom abstraction transition states.89,90
To understand the structural differences between wildtype and γ-Gly-A-bound models and particularly related to the second hydrogen atom abstraction step, we display in Fig. 6 the two 5TS2 barriers. Both structures have a large imaginary frequency for the C–H–O stretch vibration with a magnitude of i666 cm−1 for 5TS2I and i1182 cm−1 for 5TS2ScoE. Structurally, the two transition states are very similar to C–H, O–H and Fe–O distances 0.04 Å. The main difference, however, is the large angle Fe–O–C for the wildtype system of 164°, while it is 141° in the γ-Gly-A-bound structure. As the second electron transfer from the substrate to the metal complex leads to filling of a π* molecular orbital, this will benefit substrate approach from the side and give smaller angles as shown on the right-hand side of Fig. 6. In the wildtype system, the substrate is positioned in such a way that good first electron-transfer, but lesser good second electron transfer takes place, whereas the situation is reversed when γ-Gly-A binds where the first electron transfer is more difficult leading to higher barrier 5TS1I as compared to 5TS1ScoE. On the other hand, γ-Gly-A is positioned better for the second electron transfer and consequently has a lower barrier for TS2 than that for the wildtype system.
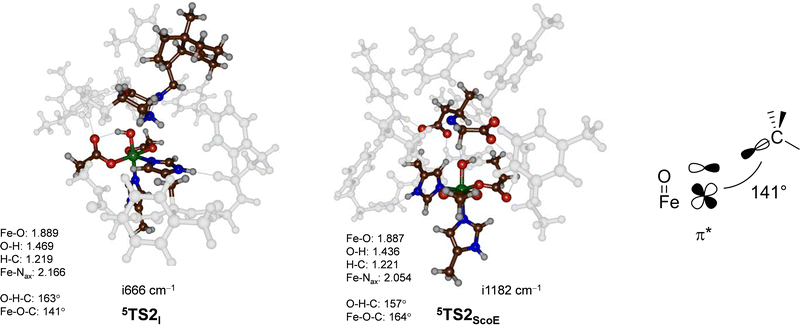 | ||
| Fig. 6 UB3LYP/BS2//UB3LYP/BS1 optimized geometries of the second hydrogen atom abstraction transition states 5TS2I and 5TS2ScoE. The optimized geometries of the transition states give bond lengths in Å, bond angles in degrees and the imaginary frequency in cm−1. The data of wildtype are taken from ref. 20. The right-hand side shows the orbital interactions during the transition state and the Fe–O–C angle. | ||
Next, we explored the alternative hydrogen atom abstraction mechanism where first the C–H bond is cleaved followed by abstraction from the N–H group (pathway 2) and the comparison of wildtype and γ-Gly-A results is given in Fig. 7. With the wildtype system, this reaction happens through a hydride-transfer and the formation of an N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond with a cation on the substrate. No unpaired spin density was observed in the intermediate 5IM3ScoE. By contrast, to the wildtype results, our intermediate 5IM3I is a radical with spin −0.98 located on the substrate and with the spin density of 4.48 on the FeO group. Consequently, structure 5IM3I has the same electronic configuration as 5IM1I with orbital occupation: π*xy1π*xz1π*yz1σ*x2−y21σ*z21ϕSub1. We attempted to swap molecular orbitals for 5IM3I but the electronic state converged back to the configuration with a radical on the substrate, hence this state is not feasible for the system with the γ-Gly-A substrate bound. A comparison of the 5IM3ScoE and 5IM3I structures shows that the protonated Lys group in the active site forms a hydrogen bond to the nitrogen atom of the substrate of γ-Gly-A in 5IM3I, thereby destabilizing a potential cation on the substrate. With wildtype, by contrast, the protonated Lys residue hydrogen bonds with the carboxylate group of the substrate and hence enables a cation on the terminal group of the substrate.
C double bond with a cation on the substrate. No unpaired spin density was observed in the intermediate 5IM3ScoE. By contrast, to the wildtype results, our intermediate 5IM3I is a radical with spin −0.98 located on the substrate and with the spin density of 4.48 on the FeO group. Consequently, structure 5IM3I has the same electronic configuration as 5IM1I with orbital occupation: π*xy1π*xz1π*yz1σ*x2−y21σ*z21ϕSub1. We attempted to swap molecular orbitals for 5IM3I but the electronic state converged back to the configuration with a radical on the substrate, hence this state is not feasible for the system with the γ-Gly-A substrate bound. A comparison of the 5IM3ScoE and 5IM3I structures shows that the protonated Lys group in the active site forms a hydrogen bond to the nitrogen atom of the substrate of γ-Gly-A in 5IM3I, thereby destabilizing a potential cation on the substrate. With wildtype, by contrast, the protonated Lys residue hydrogen bonds with the carboxylate group of the substrate and hence enables a cation on the terminal group of the substrate.
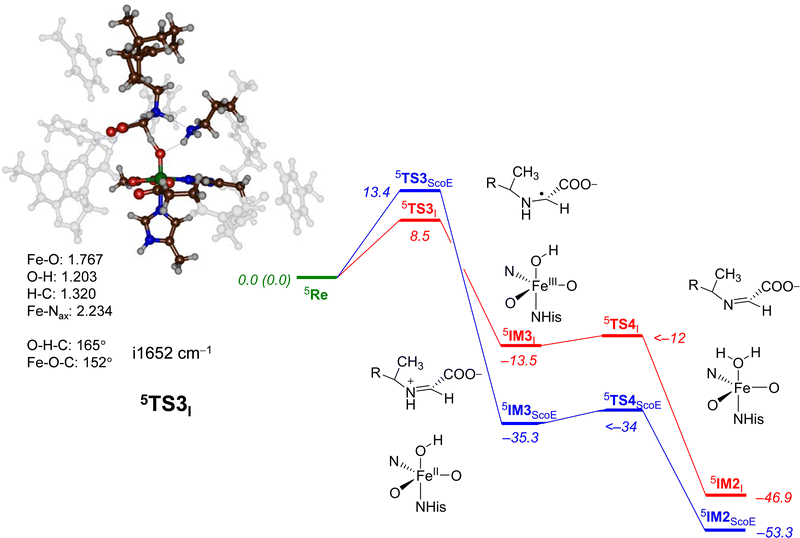 | ||
| Fig. 7 Potential energy landscape for γ-Gly-A desaturation via pathway 2 with initial C–H abstraction followed by N–H abstraction in red, while the wildtype landscape is in blue. Energies are UB3LYP/BS2//UB3LYP/BS1 with zero-point energy and solvent corrections in kcal mol−1. The optimized geometries of the transition states give bond lengths in Å, bond angles in degrees and the imaginary frequency in cm−1. The data of wildtype are taken from ref. 20. | ||
The C–H hydrogen atom abstraction of γ-Gly-A is ΔE + ZPE = 8.5 kcal mol−1 in energy and is somewhat lower than the analogous barrier for the wildtype structure with CABA bound: 5TS3ScoE has ΔE + ZPE = 13.4 kcal mol−1. It appears, therefore, that hydrogen atom abstraction from γ-Gly-A happens relatively fast with competing hydrogen atom abstraction barriers for the N–H and C–H bonds of the substrate with similar energies. This contrasts the mechanism found for the WT system with a negligible N−H hydrogen atom abstraction and much higher energy C–H abstraction. Nevertheless, both pathways after the second hydrogen atom abstraction lead to the same desaturated product 5IM2I. Both 5TS1I and 5TS3I lead to a radical intermediate with considerable exothermicity with respect to the reactants’ complex. Therefore, the hydrogen atom abstraction will be irreversible.
For the pathway starting in 5IM3I, we were unable to locate the second hydrogen atom abstraction barrier via5TS4I but a constraint geometry scan reveals it to be low in energy (less than 1.5 kcal mol−1 above 5IM3I). It is clear that the basic N–H bond of the substrate in 5IM3I will rapidly release its proton to the iron-hydroxo species as a conjugated π-system is created that stabilizes the product considerably.
The optimized geometry of 5TS3I is shown in Fig. 7. The transition state has a large imaginary frequency of i1652 cm−1 with a mode describing the O–H–C stretch vibration. This implies that the reaction will happen with a large kinetic isotope effect when the substrate C–H bonds are replaced by C–D.69 The transition state is relatively central with C–H and O–H distances of 1.320 and 1.203 Å, respectively. In contrast to the structure of 5TS1I, the angle C–H–O versus N–H–O is more bent, namely 165° versus 175°. This is probably due to the orientation of the substrate in the substrate-binding pocket that has stereochemical constraints due to hydrogen bonding interactions with protein residues. The change in structure does not appear to have affected the electronic configuration dramatically and the spin densities are similar for 5TS1I and 5TS3I. Similar to wildtype, after the formation of the intermediate 5IM3, a fast second hydrogen atom abstraction with a negligible barrier leads to the saturated substrate 5IM2. For neither system, we were able to characterize the transition state but the constraint geometry scans show it to be less than 1–2 kcal mol−1 above 5IM3.
Next, the second oxygen activation cycle was studied, whereby we took the optimized geometry of 5IM3I and replaced the iron(II)–water(succinate) with iron(IV)–oxo(succinate) and assumed that water and succinate would be expelled from the active site and replaced by α-KG and dioxygen to initiate a second catalytic cycle that forms another iron(IV)–oxo(succinate) species. This structure, designated as 5Re2I, was optimized with DFT, and the decarboxylation of the substrate to form product A was studied. Fig. 8 shows the obtained potential energy surface starting from 5Re2I. As can be seen, a modest barrier of ΔE + ZPE = 9.4 kcal mol−1 for hydrogen atom abstraction from the C–H bond of the substrate leads to 5IM5I efficiently. Interestingly, the exothermicity of this hydrogen atom abstraction is similar for γ-Gly-A and the wildtype substrate (ΔE + ZPE = −6.8 versus −6.6 kcal mol−1) and so is the formation of isonitrile products (ΔE + ZPE = −43.2 versus −42.5 kcal mol−1).
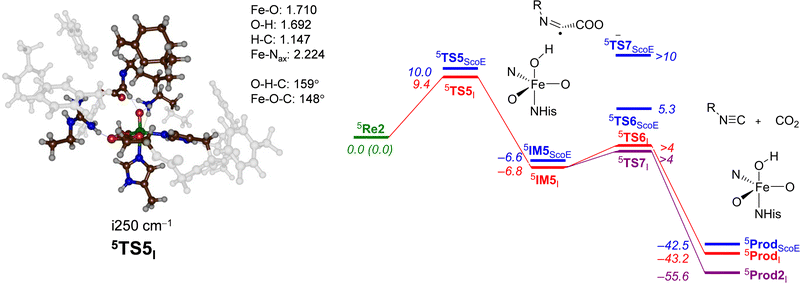 | ||
| Fig. 8 Potential energy landscape for desaturated γ-Gly-A activation by an iron(IV)–oxo species of the ScoE model for the second cycle leading to isonitrile products. The wildtype energy landscape is given in blue. Energies are UB3LYP/BS2//UB3LYP/BS1 with the zero-point energy and solvent corrections in kcal mol−1. The optimized geometries of the transition states give bond lengths in Å, bond angles in degrees and the imaginary frequency in cm−1. The data of wildtype are taken from ref. 20. | ||
The optimized geometry of the hydrogen atom abstraction transition state for cycle 2 is shown in Fig. 8. The transition state (5TS5I) has a relatively small imaginary frequency of i250 cm−1 and an animation of the mode shows hydrogen transfer from the donor group to the oxo group. However, due to constraints on substrate approach as a result of the protein residues, the hydrogen atom abstraction does not takes place under an ideal angle and orientation. In particular, the O–H–C angle was close to 180° in structure 5TS1I (see Fig. 4 above), while it is considerably bent at 159° in 5TS5I. As a consequence, this hydrogen transfer structure experiences geometric strain. Nevertheless, energetically, it is only slightly higher in energy than the corresponding barrier for the wildtype system. From 5IM5I, we ran extensive constraint geometry scans for both the decarboxylation pathway to form isonitrile products 5ProdI as well as OH rebound to form the alcohol product complex 5Prod2I. In contrast to the wildtype results that showed a high-energy OH rebound step and negligible decarboxylation, for the γ-Gly-A substrate, bound pathways are low in energy. Consequently, the calculations predict a mixture of OH rebound and decarboxylation of the substrate.
Conclusions
In this work, a series of computational studies are presented on the formation of isonitrile substituents in several target substrates as catalysed by ScoE. The results show that the ScoE enzyme can accommodate various substrates with different size and shape and specifically those with γ-Gly substituents. Particularly, we attempted to bind γ-Gly-A and γ-Gly-B to ScoE as precursors for the isonitrile-containing drug molecules axisonitrile-1 and xanthocillin. Initial molecular mechanics and molecular dynamics studies show that both substrates bind to ScoE enzymes and fit the substrate-binding pocket well. However, γ-Gly-B has the target group located far from the iron centre, while it is closer in the γ-Gly-A bound structure. Thereafter, we created a QM cluster model of the active site of ScoE with γ-Gly-A bound and studied the oxidative desaturation and decarboxylation pathways. In general, the structure and energetics for ScoE with γ-Gly-A give low energy barriers and an overall low-energy mechanism for isonitrile biosynthesis with energetics at par with those found previously for the wildtype system. The studies imply that ScoE should be able to synthesize axisonitrile-1 from γ-Gly-A efficiently although the calculations predict by-products for substrate hydroxylation. Interestingly, replacement of the substrate by a substrate analogue as done here does not shift all individual barriers in the same way and in this particular system, the TS1 barrier is raised, while the TS2 barrier reduced due to better positioning of γ-Gly-A than the native substrate.Conflicts of interest
There are no conflicts to declare.Acknowledgements
HW thanks Learning-Through-Research for a Summer Internship.Notes and references
- A. Massarotti, F. Brunelli, S. Aprile, M. Giustiniano and G. C. Tron, Chem. Rev., 2021, 121, 10742 CrossRef CAS PubMed.
- Y. Zhu, J.-Y. Liao and L. Qian, Front. Chem., 2021, 9, 670751 CrossRef CAS PubMed.
- J. Emsermann, U. Kauhl and T. Opatz, Mar. Drugs, 2016, 14, 16 CrossRef PubMed.
- T.-Y. Chen, J. Chen, Y. Tang, J. Zhou, Y. Guo and W.-c Chang, Chin. J. Chem., 2021, 39, 463 CrossRef CAS PubMed.
- G. Ernouf, I. K. Wilt, S. Zahim and W. M. Wuest, ChemBioChem, 2018, 19, 2448 CrossRef CAS PubMed.
- K. Kyei-Baffour, D. C. Davis, Z. Boskovic, N. Kato and M. Dai, Bioorg. Med. Chem., 2020, 28, 115678 CrossRef CAS PubMed.
- B. Dose, S. P. Niehs, K. Scherlach, S. Shahda, L. V. Flórez, M. Kaltenpoth and C. Hertweck, ChemBioChem, 2021, 22, 1920 CrossRef CAS PubMed.
- M. F. Clarke-Pearson and S. F. Brady, J. Bacteriol., 2008, 190, 6927 CrossRef CAS PubMed.
- M. L. Micallef, D. Sharma, B. M. Bunn, L. Gerwick, R. Viswanathan and M. C. Moffitt, BMC Microbiol., 2014, 14, 213 CrossRef PubMed.
- X. Zhang, L. Evanno and E. Poupon, Eur. J. Org. Chem., 2020, 1919 CrossRef CAS.
- R. J. B. Schäfer, M. R. Monaco, M. Li, A. Tirla, P. Rivera-Fuentes and H. Wennemers, J. Am. Chem. Soc., 2019, 141, 18644 CrossRef PubMed.
- Y. Chen, K.-L. Wu, J. Tang, A. Loredo, J. Clements, J. Pei, Z. Peng, R. Gupta, X. Fang and H. Xiao, ACS Chem. Biol., 2019, 14, 2793 CrossRef CAS PubMed.
- N. C. Harris, M. Sato, N. A. Herman, F. Twigg, W. Cai, J. Liu, X. Zhu, J. Downey, R. Khalaf, J. Martin, H. Koshino and W. Zhang, Proc. Natl. Acad. Sci. U.S.A., 2017, 114, 7025 Search PubMed.
- N. C. Harris, D. A. Born, W. Cai, Y. Huang, J. Martin, R. Khalaf, C. L. Drennan and W. Zhang, Angew. Chem., Int. Ed., 2018, 57, 9707 CrossRef CAS PubMed.
- T.-Y. Chen, J. Chen, Y. Tang, J. Zhou, Y. Guo and W.-c Chang, Angew. Chem., Int. Ed., 2020, 59, 7367 CrossRef CAS PubMed.
- R. Jonnalagadda, A. Del Rio Flores, W. Cai, R. Mehmood, M. Narayanamoorthy, C. Ren, J. P. T. Zaragoza, H. J. Kulik, W. Zhang and C. L. Drennan, J. Biol. Chem., 2021, 296, 100231 CrossRef CAS PubMed.
- A. Del Rio Flores, D. W. Kastner, Y. Du, M. Narayanamoorthy, Y. Shen, W. Cai, V. Vennelakanti, N. A. Zill, L. B. Dell, R. Zhai, H. J. Kulik and W. Zhang, J. Am. Chem. Soc., 2022, 144, 5893 CrossRef CAS PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucl. Acids Res., 2000, 28, 235 CrossRef CAS PubMed.
- H. Li and Y. Liu, ACS Catal., 2020, 10, 2942 CrossRef CAS.
- H. S. Ali, S. Ghafoor and S. P. de Visser, Top. Catal., 2022, 65, 528 CrossRef CAS.
- E. I. Solomon, T. C. Brunold, M. I. Davis, J. N. Kemsley, S. K. Lee, N. Lehnert, F. Neese, A. J. Skulan, Y. S. Yang and J. Zhou, Chem. Rev., 2000, 100, 235 CrossRef CAS PubMed.
- T. D. H. Bugg, Curr. Opin. Chem. Biol., 2001, 5, 550 CrossRef CAS PubMed.
- M. J. Ryle and R. P. Hausinger, Curr. Opin. Chem. Biol., 2002, 6, 193 CrossRef CAS PubMed.
- M. Costas, M. P. Mehn, M. P. Jensen and L. Que Jr, Chem. Rev., 2004, 104, 939 CrossRef CAS PubMed.
- M. M. Abu-Omar, A. Loaiza and N. Hontzeas, Chem. Rev., 2005, 105, 2227 CrossRef CAS PubMed.
- C. Krebs, D. G. Fujimori, C. T. Walsh and J. M. Bollinger Jr, Acc. Chem. Res., 2007, 40, 484 CrossRef CAS PubMed.
- Iron-containing enzymes: Versatile catalysts of hydroxylation reactions in nature, ed. S. P. de Visser and D. Kumar, Royal Society of Chemistry Publishing, Cambridge, UK, 2011 Search PubMed.
- A. R. McDonald and L. Que Jr, Coord. Chem. Rev., 2013, 257, 414 CrossRef CAS.
- M. R. A. Blomberg, T. Borowski, F. Himo, R.-Z. Liao and P. E. M. Siegbahn, Chem. Rev., 2014, 114, 3601 CrossRef CAS PubMed.
- G. Mukherjee, J. K. Satpathy, U. K. Bagha, M. Q. E. Mubarak, C. V. Sastri and S. P. de Visser, ACS Catal., 2021, 11, 9761 CrossRef CAS.
- S. P. de Visser, G. Mukherjee, H. S. Ali and C. V. Sastri, Acc. Chem. Res., 2022, 55, 65 CrossRef CAS PubMed.
- D. Kumar, S. P. de Visser and S. Shaik, J. Am. Chem. Soc., 2004, 126, 5072 CrossRef CAS PubMed.
- S. Ghafoor, A. Mansha and S. P. de Visser, J. Am. Chem. Soc., 2019, 141, 20278 CrossRef CAS PubMed.
- S. P. de Visser, Y.-T. Lin, H. S. Ali, U. K. Bagha, G. Mukherjee and C. V. Sastri, Coord. Chem. Rev., 2021, 439, 213914 CrossRef CAS.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455 CAS.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 43, 9954 CrossRef.
- D. A. Case, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, D. Ghoreishi, M. K. Gilson, H. Gohlke, A. W. Goetz, D. Greene, R. Harris, N. Homeyer, Y. Huang, S. Izadi, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, D. J. Mermelstein, K. M. Merz, Y. Miao, G. Monard, C. Nguyen, H. Nguyen, I. Omelyan, A. Onufriev, F. Pan, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, J. Smith, R. Salomon-Ferrer, J. Swails, R. C. Walker, J. Wang, H. Wei, R. M. Wolf, X. Wu, L. Xiao, D. M. York and P. A. Kollman, AMBER-2018, University of California, San Francisco, 2018 Search PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696 CrossRef CAS PubMed.
- C. Domene and S. Furini, Methods Enzymol., 2009, 466, 155 CAS.
- Q. Liao, Prog. Mol. Biol. Transl. Sci., 2020, 170, 177 CAS.
- M. G. Quesne, T. Borowski and S. P. de Visser, Chem. – Eur. J., 2016, 22, 2562 CrossRef CAS PubMed.
- H. S. Ali, R. H. Henchman and S. P. de Visser, Chem. – Eur. J., 2020, 26, 13093 CrossRef CAS PubMed.
- S. P. de Visser, Chem. – Eur. J., 2020, 26, 5308 CrossRef CAS PubMed.
- F. Himo and S. P. de Visser, Commun. Chem., 2022, 5, 29 CrossRef.
- H. S. Ali and S. P. de Visser, Chem. – Eur. J., 2022, 28, e202104167 CrossRef CAS PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS PubMed.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef.
- F. G. Cantú Reinhard, M. A. Sainna, P. Upadhyay, G. A. Balan, D. Kumar, S. Fornarini, M. E. Crestoni and S. P. de Visser, Chem. – Eur. J., 2016, 22, 18608 CrossRef PubMed.
- F. G. Cantú Reinhard, A. S. Faponle and S. P. de Visser, J. Phys. Chem. A, 2016, 120, 9805 CrossRef PubMed.
- T. Yang, M. G. Quesne, H. M. Neu, F. G. Cantú Reinhard, D. P. Goldberg and S. P. de Visser, J. Am. Chem. Soc., 2016, 138, 12375 CrossRef CAS PubMed.
- P. J. Riggs-Gelasco, J. C. Price, R. B. Guyer, J. H. Brehm, E. W. Barr, J. M. Bollinger Jr and C. Krebs, J. Am. Chem. Soc., 2004, 126, 8108 CrossRef CAS PubMed.
- V. F. Oswald, J. L. Lee, S. Biswas, A. C. Weitz, K. Mittra, R. Fan, J. Li, J. Zhao, M. Y. Hu, E. E. Alp, E. L. Bominaar, Y. Guo, M. T. Green, M. P. Hendrich and A. S. Borovik, J. Am. Chem. Soc., 2020, 142, 11804 CrossRef CAS PubMed.
- F. Tiago de Oliveira, A. Chanda, D. Banerjee, X. Shan, S. Mondal, L. Que Jr, E. L. Bominaar, E. Münck and T. J. Collins, Science, 2007, 315, 835 CrossRef CAS PubMed.
- W. Nam, Y.-M. Lee and S. Fukuzumi, Acc. Chem. Res., 2018, 51, 2014 CrossRef CAS PubMed.
- F. Banse, J.-J. Girerd and V. Robert, Eur. J. Inorg. Chem., 2008, 4786 CrossRef CAS.
- T. Borowski, A. Bassan and P. E. M. Siegbahn, Chem. – Eur. J., 2004, 10, 1031 CrossRef CAS PubMed.
- S. Sinnecker, N. Svensen, E. W. Barr, S. Ye, J. M. Bollinger Jr, F. Neese and C. Krebs, J. Am. Chem. Soc., 2007, 129, 6168 CrossRef CAS PubMed.
- E. Godfrey, C. S. Porro and S. P. de Visser, J. Phys. Chem. A, 2008, 112, 2464 CrossRef CAS PubMed.
- H. Chen, W. Lai, J. Yao and S. Shaik, J. Chem. Theory Comput., 2011, 7, 3049 CrossRef CAS PubMed.
- E. A. C. Bushnell, G. B. Fortowsky and J. W. Gauld, Inorg. Chem., 2012, 51, 13351 CrossRef CAS PubMed.
- H. J. Kulik and C. L. Drennan, J. Biol. Chem., 2012, 288, 11233 CrossRef PubMed.
- K. M. Light, J. A. Hangasky, M. J. Knapp and E. I. Solomon, J. Am. Chem. Soc., 2013, 135, 9665 CrossRef CAS PubMed.
- H. S. Ali, R. H. Henchman, J. Warwicker and S. P. de Visser, J. Phys. Chem. A, 2021, 125, 1720 CrossRef CAS PubMed.
- A. Wójcik, M. Radoń and T. Borowski, J. Phys. Chem. A, 2016, 120, 1261 CrossRef PubMed.
- S. Álvarez-Barcia and J. Kästner, J. Phys. Chem. B, 2017, 121, 5347 CrossRef PubMed.
- A. Timmins, M. Saint-André and S. P. de Visser, J. Am. Chem. Soc., 2017, 139, 9855 CrossRef CAS PubMed.
- R. N. Manna, T. Malakar, B. Jana and A. Paul, ACS Catal., 2018, 8, 10043 CrossRef CAS.
- S. R. Iyer, V. D. Chaplin, M. J. Knapp and E. I. Solomon, J. Am. Chem. Soc., 2018, 140, 11777 CrossRef CAS PubMed.
- J. Xue, J. Lu and W. Lai, Phys. Chem. Chem. Phys., 2019, 21, 9957 RSC.
- S. S. Chaturvedi, R. Ramanan, N. Lehnert, C. J. Schofield, T. G. Karabencheva-Christova and C. Z. Christov, ACS Catal., 2020, 10, 1195 CrossRef CAS PubMed.
- H. Hirao, F. Li, L. Que Jr and K. Morokuma, Inorg. Chem., 2011, 50, 6637 CrossRef CAS PubMed.
- F. Wang, W. Sun, C. Xia and Y. Wang, J. Biol. Inorg. Chem., 2017, 22, 987 CrossRef CAS PubMed.
- S. Stepanović, D. Angelone, M. Gruden and M. Swart, Org. Biomol. Chem., 2017, 15, 7860 RSC.
- I. Prat, A. Company, V. Postils, X. Ribas, L. Que Jr, J. M. Luis and M. Costas, Chem. – Eur. J., 2013, 19, 6724 CrossRef CAS PubMed.
- H. S. Ali, R. H. Henchman and S. P. de Visser, ChemCatChem, 2021, 13, 3054 CrossRef CAS.
- H. S. Ali, R. H. Henchman and S. P. de Visser, Chem. – Eur. J., 2021, 27, 1795 CrossRef CAS PubMed.
- Y.-T. Lin, H. S. Ali and S. P. de Visser, Chem. – Eur. J., 2022, 28, e202103982 CAS.
- H. Hirao, D. Kumar, L. Que Jr and S. Shaik, J. Am. Chem. Soc., 2006, 128, 8590 CrossRef CAS PubMed.
- S. P. de Visser, Angew. Chem., Int. Ed., 2006, 45, 1790 CrossRef CAS PubMed.
- C.-C. G. Yeh, S. Ghafoor, J. K. Satpathy, T. Mokkawes, C. V. Sastri and S. P. de Visser, ACS Catal., 2022, 12, 3923 CrossRef CAS.
- D. Kumar, R. Latifi, S. Kumar, E. V. Rybak-Akimova, M. A. Sainna and S. P. de Visser, Inorg. Chem., 2013, 52, 7968 CrossRef CAS PubMed.
- Y.-T. Lin, H. S. Ali and S. P. de Visser, Chem. – Eur. J., 2021, 27, 8851 CrossRef CAS PubMed.
- P. Barman, P. Upadhyay, A. S. Faponle, J. Kumar, S. S. Nag, D. Kumar, C. V. Sastri and S. P. de Visser, Angew. Chem., Int. Ed., 2016, 55, 11091 CrossRef CAS PubMed.
- P. Barman, F. G. Cantú Reinhard, U. K. Bagha, D. Kumar, C. V. Sastri and S. P. de Visser, Angew. Chem., Int. Ed., 2019, 58, 10639 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Energies, spin densities, charges and Cartesian coordinates of optimized geometries discussed in this work. See DOI: https://doi.org/10.1039/d2cp03409c |
| This journal is © the Owner Societies 2022 |