Open Access Article
Open Access ArticleSingle-molecule conductance of double-stranded RNA oligonucleotides†
Subrata
Chandra
,
Keshani G.
Gunasinghe Pattiya Arachchillage
,
Evgenii
Kliuchnikov
,
Farkhad
Maksudov
,
Steven
Ayoub
,
Valeri
Barsegov
and
Juan M.
Artés Vivancos
 *
*
Department of Chemistry, University of Massachusetts, Lowell, 01854 MA, USA. E-mail: juan_artesvivancos@uml.edu; Tel: (+1)9789344337
First published on 2nd February 2022
Abstract
RNA oligonucleotides are crucial for a range of biological functions and in many biotechnological applications. Herein, we measured, for the first time, the conductance of individual double-stranded (ds)RNA molecules and compared it with the conductance of single DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrids. The average conductance values are similar for both biomolecules, but the distribution of conductance values shows an order of magnitude higher variability for dsRNA, indicating higher molecular flexibility of dsRNA. Microsecond Molecular Dynamics simulations explain this difference and provide structural insights into the higher stability of DNA
RNA hybrids. The average conductance values are similar for both biomolecules, but the distribution of conductance values shows an order of magnitude higher variability for dsRNA, indicating higher molecular flexibility of dsRNA. Microsecond Molecular Dynamics simulations explain this difference and provide structural insights into the higher stability of DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA duplex with atomic level of detail. The rotations of 2′-OH groups of the ribose rings and the bases in RNA strands destabilize the duplex structure by weakening base stacking interactions, affecting charge transport, and making single-molecule conductance of dsRNA more variable (dynamic disorder). The results demonstrate that a powerful combination of state-of-the-art biomolecular electronics techniques and computational approaches can provide valuable insights into biomolecules’ biophysics with unprecedented spatial resolution.
RNA duplex with atomic level of detail. The rotations of 2′-OH groups of the ribose rings and the bases in RNA strands destabilize the duplex structure by weakening base stacking interactions, affecting charge transport, and making single-molecule conductance of dsRNA more variable (dynamic disorder). The results demonstrate that a powerful combination of state-of-the-art biomolecular electronics techniques and computational approaches can provide valuable insights into biomolecules’ biophysics with unprecedented spatial resolution.
Oligonucleotides play essential roles in cell functions1,2 and several biotechnological applications.3,4 In particular, RNA has recently gained importance in the research focus for several reasons. Not only do several pathogens (e.g., SARS-CoV2) have RNA genomes, but many therapeutic, biotechnological, and modern molecular technologies (e.g., gene editing5) also use RNA and its biophysics. Additionally, nucleic acids have interesting electronic and self-assembly properties that make them promising candidates as building blocks for nanotechnological6,7 and sensory applications.8,9 For these reasons, it is crucial to characterize the biophysical properties of RNA, particularly at the single-molecule level.
In the last decades, single-molecule techniques have allowed biological and biophysical studies with unprecedented resolution.10–12 On the biomolecular electronics side, the electronic and charge-transport (CT) properties of short oligonucleotides have been reported.13,14 They have resulted in proposing proof-of-concept sensors based on individual biomolecule detection.8
Short double-stranded (ds)DNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrids have been extensively characterized, including the length,13–15 sequence,13–16 and conformational dependence17 of the conductance of individual molecules. Although some controversy remains regarding the role of the nucleic acid backbone in mediating the CT,18 there is a consensus that the CT process is mainly mediated by base stacking in the double helix and deeply affected by the delocalization length through the bases.14,17,19 Consequently, changes in conformation17 or base mismatches that disrupt the base stacking pattern; or the delocalization length8,16 can modify the conductance value measured in experiments. Also, despite its biophysical and biological importance, the single-molecule electronic properties of dsRNA have not yet been reported.
RNA hybrids have been extensively characterized, including the length,13–15 sequence,13–16 and conformational dependence17 of the conductance of individual molecules. Although some controversy remains regarding the role of the nucleic acid backbone in mediating the CT,18 there is a consensus that the CT process is mainly mediated by base stacking in the double helix and deeply affected by the delocalization length through the bases.14,17,19 Consequently, changes in conformation17 or base mismatches that disrupt the base stacking pattern; or the delocalization length8,16 can modify the conductance value measured in experiments. Also, despite its biophysical and biological importance, the single-molecule electronic properties of dsRNA have not yet been reported.
Here, we use a combination of single-molecule conductance experiments and computer simulations to explore the conductance of individual dsRNA molecules. The conductance histograms show that dsRNA has a conductance within experimental error of DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrids of the same nucleotide sequence, in agreement with the notion that both biomolecules are in the A-form.15,17 However, our results show differences in the distribution of molecular conductance values for dsRNA vs. DNA
RNA hybrids of the same nucleotide sequence, in agreement with the notion that both biomolecules are in the A-form.15,17 However, our results show differences in the distribution of molecular conductance values for dsRNA vs. DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA. The electrical conductance histogram for dsRNA is an order of magnitude broader than the histogram for DNA
RNA. The electrical conductance histogram for dsRNA is an order of magnitude broader than the histogram for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA, suggesting higher molecular flexibility and lower stability for dsRNA. To help provide dynamic structural insights into the biophysics of these molecules, we employed Molecular Dynamics (MD) simulations of dsRNA and DNA
RNA, suggesting higher molecular flexibility and lower stability for dsRNA. To help provide dynamic structural insights into the biophysics of these molecules, we employed Molecular Dynamics (MD) simulations of dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA duplexes, which show that conformational transitions in the ribose rings and bases in RNA strands destabilize base stacking, affecting the CT process.
RNA duplexes, which show that conformational transitions in the ribose rings and bases in RNA strands destabilize base stacking, affecting the CT process.
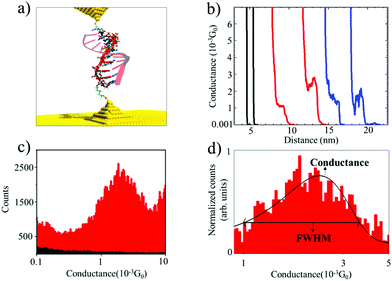
We used the Scanning Tunneling Microscope-assisted Break Junction (STM-BJ)20 method to measure individual biomolecule conductance (see the ESI† for detailed materials and methods). Briefly, the electrodes of a Scanning Tunneling Microscope (STM) are repeatedly brought into contact and retracted in the presence of a buffer solution containing the oligonucleotides modified with thiol binding groups at 5′ and 3′ ends so that they can bind to the electrodes (Fig. 1a). At the same time, the current (I) in the molecular junction is measured by applying a moderate bias voltage (V). The molecular conductance (G) can be obtained from G = I/V by recording thousands of conductance vs. distance traces and combining them into conductance histograms (using an automatic selection algorithm21). After saving 5000–1000 traces per experiment, selectivity (defined as the number of curves containing significant “steps”) ranged from less than 1% in blank and control experiments to 5 to 10% in experiments with nucleic acids. This assists in obtaining the most probable molecular conductance and in accessing subpopulations of molecular conformations.17,22 These characteristics provide valuable information about the biophysical properties of oligonucleotide molecules12,17 and the molecular-electrode contacts they form.22,23 These experiments were performed by applying a 100 mV bias voltage between the tip and the substrate in a phosphate buffer media. For this reason, it is necessary to cover the STM tips with Apiezon wax to isolate them from any leakage currents.
Fig. 1a shows an idealized schematic of the experimental setup for the 11 base pairs (bp) DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrid oligonucleotide bridging between two gold electrodes. Fig. 1b shows raw data of conductance-distance measurements for dsRNA (blue traces), DNA
RNA hybrid oligonucleotide bridging between two gold electrodes. Fig. 1b shows raw data of conductance-distance measurements for dsRNA (blue traces), DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrids (red curves), and control measurements (clean Au substrate in phosphate buffer, in black); see ESI Fig. S1–S3† for more results from control experiments. The blank phosphate buffer shows no detectable conductance events or “steps”, whereas dsRNA and DNA
RNA hybrids (red curves), and control measurements (clean Au substrate in phosphate buffer, in black); see ESI Fig. S1–S3† for more results from control experiments. The blank phosphate buffer shows no detectable conductance events or “steps”, whereas dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA duplexes show similar features in the 0.001G0 range (G0 is 2e2/h, where e is the electron charge and h is the Planck constant), indicating the formation of biomolecular junctions. By analyzing thousands of individual conductance-distance curves, we obtained the histogram-based estimates of the conductance distributions. These can be used to calculate the most probable conductance (peak conductance) and conductance variability quantified by the full width at half maximum (FWHM). Fig. 1c and d show the conductance histograms for an 11 bp DNA
RNA duplexes show similar features in the 0.001G0 range (G0 is 2e2/h, where e is the electron charge and h is the Planck constant), indicating the formation of biomolecular junctions. By analyzing thousands of individual conductance-distance curves, we obtained the histogram-based estimates of the conductance distributions. These can be used to calculate the most probable conductance (peak conductance) and conductance variability quantified by the full width at half maximum (FWHM). Fig. 1c and d show the conductance histograms for an 11 bp DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrid (CCCGCGCGCCC) constructed with raw data with and without baseline subtraction and normalization (to the highest number of counts in the histogram), respectively. Fig. 1d also includes a Gaussian curve fit centered at 1.7 × 10−3G0, in agreement with previously reported values for this DNA
RNA hybrid (CCCGCGCGCCC) constructed with raw data with and without baseline subtraction and normalization (to the highest number of counts in the histogram), respectively. Fig. 1d also includes a Gaussian curve fit centered at 1.7 × 10−3G0, in agreement with previously reported values for this DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrid15 and other A-form oligonucleotides.17 This single-molecule conductance value is remarkably high for a biomolecule around 2.5 nm long, but not surprising considering this is an A-form GC-rich oligonucleotide sustaining a hopping charge transport process with a high coherence length.15,17
RNA hybrid15 and other A-form oligonucleotides.17 This single-molecule conductance value is remarkably high for a biomolecule around 2.5 nm long, but not surprising considering this is an A-form GC-rich oligonucleotide sustaining a hopping charge transport process with a high coherence length.15,17
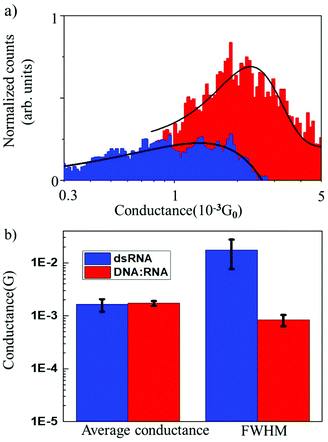
The results of conductance measurements for an 11 bp dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrid with the same sequence (CCCGCGCGCCC) are compared in Fig. 2, which shows the normalized conductance histograms (Fig. 2a), as well as conductance statistics (Fig. 2b) from the Gaussian curve fitting, i.e., the most probable conductance and standard deviations estimated as the FWHM.
RNA hybrid with the same sequence (CCCGCGCGCCC) are compared in Fig. 2, which shows the normalized conductance histograms (Fig. 2a), as well as conductance statistics (Fig. 2b) from the Gaussian curve fitting, i.e., the most probable conductance and standard deviations estimated as the FWHM.
The single-molecule conductance for dsRNA is 1.6 × 10−3G0vs. 1.7 × 10−3G0 for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA, without statistically significant differences. This is not surprising since dsRNA is an A-form oligonucleotide with a similar structure to DNA
RNA, without statistically significant differences. This is not surprising since dsRNA is an A-form oligonucleotide with a similar structure to DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA and is consistent with the notion that the conformation of the oligonucleotide plays a crucial role in defining the electronic and CT properties.17 However, the distribution of conductance values is broader for dsRNA than for DNA
RNA and is consistent with the notion that the conformation of the oligonucleotide plays a crucial role in defining the electronic and CT properties.17 However, the distribution of conductance values is broader for dsRNA than for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA by one order of magnitude (Fig. 2a; see also Table 1). Higher standard deviations for dsRNA indicate a larger dispersion in the molecular conductance values for dsRNA. Since single-molecule conductance is mainly influenced by the base stacking, which depends on the oligonucleotides’ molecular conformation, these results point to a more considerable extent of conformational fluctuations for dsRNA (larger dynamic disorder) and increased molecular flexibility. This is remarkable because a subtle difference in the oligonucleotide composition (RNA vs. DNA) translates into a noticeable change in measured single-molecule conductance. Notably, the results obtained demonstrate that STM-BJ is a sensitive technique capable of detecting small changes in the conformation-dependent biophysical properties of individual biomolecules.12
RNA by one order of magnitude (Fig. 2a; see also Table 1). Higher standard deviations for dsRNA indicate a larger dispersion in the molecular conductance values for dsRNA. Since single-molecule conductance is mainly influenced by the base stacking, which depends on the oligonucleotides’ molecular conformation, these results point to a more considerable extent of conformational fluctuations for dsRNA (larger dynamic disorder) and increased molecular flexibility. This is remarkable because a subtle difference in the oligonucleotide composition (RNA vs. DNA) translates into a noticeable change in measured single-molecule conductance. Notably, the results obtained demonstrate that STM-BJ is a sensitive technique capable of detecting small changes in the conformation-dependent biophysical properties of individual biomolecules.12
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrids: average and standard deviations for conductance and FWHM values
RNA hybrids: average and standard deviations for conductance and FWHM values
| Molecule | Average conductance (×10−3G0) | FWHM (×10−2G0) |
|---|---|---|
| dsRNA | 1.63 ± 0.43 | 1.75 ± 0.98 |
DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrid RNA hybrid |
1.72 ± 0.18 | 0.083 ± 0.02 |
To provide a structure-based interpretation for the single biomolecular conductance experiments, we turned to computational molecular modeling. Molecular Dynamics (MD) simulations play an increasingly important role not only in complementing experimental techniques but also in helping to understand the physical properties of single biomolecules at an atomic level of detail.24–28 Here, we employed MD simulations, accelerated on Graphics Processing Units (GPUs),29 to explore and directly compare the conformational dynamics of dsRNA vs. DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrids in a long timescale spanning a few microseconds to explain the difference in their electrical conductance characteristics.
RNA hybrids in a long timescale spanning a few microseconds to explain the difference in their electrical conductance characteristics.
Molecular modeling of dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrids, including the sequence reconstruction, MD simulation protocol, and analyses of the output from MD simulations, are described in detail in ESI.† Briefly, SimRNA software30 was utilized to model RNA and DNA sequences. The MD simulations for dsRNA and DNA
RNA hybrids, including the sequence reconstruction, MD simulation protocol, and analyses of the output from MD simulations, are described in detail in ESI.† Briefly, SimRNA software30 was utilized to model RNA and DNA sequences. The MD simulations for dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA were performed for 1 μs using the CUDA version of pmemd31 and GPU accelerated version32 of AMBER 20 software package.33 The force fields bsc0χOL334 and bsc035 used for RNA and DNA strands are a part of ff14SB.36 The TIP3P model was used to describe water molecules explicitly.37 A total of 3730 water molecules were included in the solvation box with volume 143.4 Å. The phosphate groups in the backbone of RNA and DNA strands were neutralized using 20 Na+ ions, and excess ions (0.1 M) were added to mimic the experimental conditions (9 Na+ ions and 9 Cl− ions). We carried out two independent sets of MD simulations of dsRNA and DNA
RNA were performed for 1 μs using the CUDA version of pmemd31 and GPU accelerated version32 of AMBER 20 software package.33 The force fields bsc0χOL334 and bsc035 used for RNA and DNA strands are a part of ff14SB.36 The TIP3P model was used to describe water molecules explicitly.37 A total of 3730 water molecules were included in the solvation box with volume 143.4 Å. The phosphate groups in the backbone of RNA and DNA strands were neutralized using 20 Na+ ions, and excess ions (0.1 M) were added to mimic the experimental conditions (9 Na+ ions and 9 Cl− ions). We carried out two independent sets of MD simulations of dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA molecules. In the first set, the ends of the molecules were not constrained. To mimic the effect of experimental constraints on the molecular flexibility of dsRNA and DNA
RNA molecules. In the first set, the ends of the molecules were not constrained. To mimic the effect of experimental constraints on the molecular flexibility of dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrid due to coupling to junctions, in the second set, we “clamped” (harmonically constrained) the 5′-end and the 3′-end phosphorus atoms in dsDNA and DNA
RNA hybrid due to coupling to junctions, in the second set, we “clamped” (harmonically constrained) the 5′-end and the 3′-end phosphorus atoms in dsDNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA molecules. The two strands forming the dsRNA and DNA
RNA molecules. The two strands forming the dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA duplexes were found to be stable during 1 μs MD simulations.
RNA duplexes were found to be stable during 1 μs MD simulations.
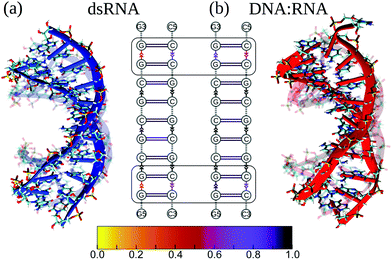
First, we compared the conformational variability in dsRNA vs. DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA structures (see S4 and S5†). Fig. 3 shows both structures undergoing large-amplitude conformational fluctuations while preserving the duplex arrangement of RNA and DNA helical structure. Because the intra-strand interactions (base stacking) and inter-strand interactions (base pairing) are known to reinforce the duplex structure of RNA and DNA molecules, we, first, qualitatively described the strength of base stacking and base pairing in dsRNA and DNA
RNA structures (see S4 and S5†). Fig. 3 shows both structures undergoing large-amplitude conformational fluctuations while preserving the duplex arrangement of RNA and DNA helical structure. Because the intra-strand interactions (base stacking) and inter-strand interactions (base pairing) are known to reinforce the duplex structure of RNA and DNA molecules, we, first, qualitatively described the strength of base stacking and base pairing in dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrid (see ESI†). We found that the most robust base stacking bonds, i.e., the most persistent (longer-lasting) base stacks, form in DNA and RNA strands in the center of dsRNA and DNA
RNA hybrid (see ESI†). We found that the most robust base stacking bonds, i.e., the most persistent (longer-lasting) base stacks, form in DNA and RNA strands in the center of dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA molecules (Fig. 3b). The weakest (or short-lasting) base stacking bonds are formed at the 3′- and 5′-ends (Fig. 3b). This agrees well with the results of previous experimental studies on other sequences.38
RNA molecules (Fig. 3b). The weakest (or short-lasting) base stacking bonds are formed at the 3′- and 5′-ends (Fig. 3b). This agrees well with the results of previous experimental studies on other sequences.38
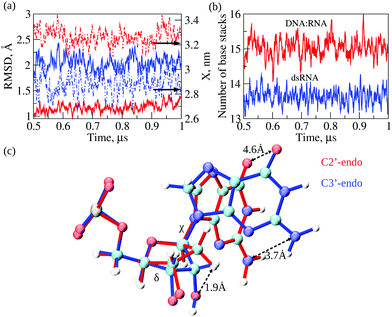
Next, we compared conformational fluctuations in dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA by analyzing the root-mean-square deviations (RMSD) and end-to-end distance X. These metrics of molecular flexibility can be accessed using the simulation output (see ESI†). The RMSD was calculated for the backbone heavy atoms of the RNA or DNA strands. The end-to-end distance X was calculated as the distance between the first (at the 5′-end) and the last (at the 3′-end) P-atoms in the complementary strand in dsRNA or DNA strand in DNA
RNA by analyzing the root-mean-square deviations (RMSD) and end-to-end distance X. These metrics of molecular flexibility can be accessed using the simulation output (see ESI†). The RMSD was calculated for the backbone heavy atoms of the RNA or DNA strands. The end-to-end distance X was calculated as the distance between the first (at the 5′-end) and the last (at the 3′-end) P-atoms in the complementary strand in dsRNA or DNA strand in DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA (ESI†). The time-dependent profiles of RMSD and X are compared in Fig. 4a. The RMSD profile for dsRNA lies above the RMSD profile for DNA
RNA (ESI†). The time-dependent profiles of RMSD and X are compared in Fig. 4a. The RMSD profile for dsRNA lies above the RMSD profile for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA by ≈1 Å, which shows that dsRNA is characterized by a more considerable molecular flexibility than DNA
RNA by ≈1 Å, which shows that dsRNA is characterized by a more considerable molecular flexibility than DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA. Interestingly, the profile of X for dsRNA is lower than that for DNA
RNA. Interestingly, the profile of X for dsRNA is lower than that for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA by ≈0.5 nm, which means that dsRNA is on average a shorter duplex than DNA
RNA by ≈0.5 nm, which means that dsRNA is on average a shorter duplex than DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA. We also analyzed the statistics of RMSDs and X (averages and standard deviations; see Table 2). The average RMSDs with standard deviations comes to 2.0 ± 0.2 Å for dsRNA vs. 1.2 ± 0.1 Å for DNA
RNA. We also analyzed the statistics of RMSDs and X (averages and standard deviations; see Table 2). The average RMSDs with standard deviations comes to 2.0 ± 0.2 Å for dsRNA vs. 1.2 ± 0.1 Å for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA. The average X is 2.9 ± 0.1 nm for dsRNA vs. 3.3 ± 0.1 nm for DNA
RNA. The average X is 2.9 ± 0.1 nm for dsRNA vs. 3.3 ± 0.1 nm for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA (Table 2). The statistics of RMSD and X did not change upon constraining the 5′-end and the 3′-end phosphorus atoms in dsRNA and DNA
RNA (Table 2). The statistics of RMSD and X did not change upon constraining the 5′-end and the 3′-end phosphorus atoms in dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA. Therefore, these numbers show that our conclusions about the differences in molecular flexibility for dsRNA vs. DNA
RNA. Therefore, these numbers show that our conclusions about the differences in molecular flexibility for dsRNA vs. DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA are statistically significant.
RNA are statistically significant.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA. Shown are the root-mean-square deviations (RMSD) of atomic positions, end-to-end distance (X), number of base pairs (Nbp) and base stacks (Nbs), dihedral angles δ and χ, and van der Waals energy EvdW
RNA. Shown are the root-mean-square deviations (RMSD) of atomic positions, end-to-end distance (X), number of base pairs (Nbp) and base stacks (Nbs), dihedral angles δ and χ, and van der Waals energy EvdW
| Molecule | dsRNA | DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrid RNA hybrid |
|---|---|---|
| RMSD, Å | 2.0 ± 0.2 | 1.2 ± 0.1 |
| X, nm | 2.9 ± 0.1 | 3.3 ± 0.1 |
| N bp | 11.3 ± 0.3 | 10.7 ± 0.8 |
| N bs | 13.6 ± 0.6 | 15.0 ± 0.8 |
| δ, deg | 78 ± 7 | 116 ± 23 |
| χ, deg | 197 ± 8 | 236 ± 24 |
| E vdW, kcal mol−1 | −179 ± 4 | −162 ± 4 |
The results of MD simulations demonstrate a larger extent of conformational fluctuations in dsRNA compared to DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA. These findings correlate well with more significant standard deviations observed for the experimental values of molecular conductance (see Table 1 and Fig. 2b). Because the base-stacking interactions influence the conductance of oligonucleotides, we next analyzed the dynamics of base-stacking interactions in dsRNA and DNA
RNA. These findings correlate well with more significant standard deviations observed for the experimental values of molecular conductance (see Table 1 and Fig. 2b). Because the base-stacking interactions influence the conductance of oligonucleotides, we next analyzed the dynamics of base-stacking interactions in dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrids. The time profiles of the number of base-stacking bonds are compared for dsRNA and DNA
RNA hybrids. The time profiles of the number of base-stacking bonds are compared for dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA in Fig. 4b, which shows that fewer base-stacking bonds reinforce the duplex structure in dsRNA duplex than in DNA
RNA in Fig. 4b, which shows that fewer base-stacking bonds reinforce the duplex structure in dsRNA duplex than in DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA duplex. The average number of base stacks Nbs comes to 13.6 ± 0.6 for dsRNA vs. 15.0 ± 0.8 for DNA
RNA duplex. The average number of base stacks Nbs comes to 13.6 ± 0.6 for dsRNA vs. 15.0 ± 0.8 for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA (Table 2). Interestingly, the average number of base pairs Nbp is 11.3 ± 0.3 for dsRNA vs. 10.7 ± 0.8 for DNA
RNA (Table 2). Interestingly, the average number of base pairs Nbp is 11.3 ± 0.3 for dsRNA vs. 10.7 ± 0.8 for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA (Table 2), which are not statistically different. These results show that the weaker base-stacking bonds do not imply the weaker base-pairing bonds in the dsRNA duplex. The statistics of Nbp and Nbs did not change upon constraining the 5′-end and 3′-end of dsRNA and DNA
RNA (Table 2), which are not statistically different. These results show that the weaker base-stacking bonds do not imply the weaker base-pairing bonds in the dsRNA duplex. The statistics of Nbp and Nbs did not change upon constraining the 5′-end and 3′-end of dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA duplexes.
RNA duplexes.
That shorter dsRNA is more flexible and has fewer base-stacking bonds than DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrids prompted us to explore the structural origin underlying these differences. We carried out a detailed analysis of transient structures of dsRNA and DNA
RNA hybrids prompted us to explore the structural origin underlying these differences. We carried out a detailed analysis of transient structures of dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA as observed in the course of 1 μs MD simulations. We analyzed and compared the statistics of dihedral angles, namely the torsion angle δ formed by a quartet of heavy atoms C5′–C4′–C3′–O3′ and the glycosidic angle χ formed by heavy atoms O4′–C1′–N9–C4 in purine bases and atoms O4′–C1′–N1–C2 in pyrimidine bases (see Fig. 4c). The torsion angle δ quantifies rotation of the ribose ring with respect to the backbone, whereas glycosidic angle χ quantifies rotation of the base with respect to the ribose ring (Fig. 4c). The statistics of δ and χ are compared for dsRNA vs. DNA
RNA as observed in the course of 1 μs MD simulations. We analyzed and compared the statistics of dihedral angles, namely the torsion angle δ formed by a quartet of heavy atoms C5′–C4′–C3′–O3′ and the glycosidic angle χ formed by heavy atoms O4′–C1′–N9–C4 in purine bases and atoms O4′–C1′–N1–C2 in pyrimidine bases (see Fig. 4c). The torsion angle δ quantifies rotation of the ribose ring with respect to the backbone, whereas glycosidic angle χ quantifies rotation of the base with respect to the ribose ring (Fig. 4c). The statistics of δ and χ are compared for dsRNA vs. DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA in Table 2, which shows large statistically significant differences: δ is 116 ± 23° for DNA
RNA in Table 2, which shows large statistically significant differences: δ is 116 ± 23° for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA vs. 78 ± 7° for dsRNA; and χ is 236 ± 24° for DNA
RNA vs. 78 ± 7° for dsRNA; and χ is 236 ± 24° for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA vs. 197 ± 8° for dsRNA. The statistics of dihedral angles δ and χ did not change upon constraining the 5′- and 3′-ends of dsRNA and DNA
RNA vs. 197 ± 8° for dsRNA. The statistics of dihedral angles δ and χ did not change upon constraining the 5′- and 3′-ends of dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA duplexes.
RNA duplexes.
Structural analysis of RNA and DNA strands in dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrid revealed essential differences in the packing of nucleobases in dsRNA vs. DNA
RNA hybrid revealed essential differences in the packing of nucleobases in dsRNA vs. DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA duplexes. Due to the C3′-endo arrangement of ribose rings in the RNA strand; the ribose ring is rotated Δδ ≈116–78 = 38° with respect to the phosphate backbone as compared to C2′-endo arrangement of ribose ring in the DNA strand, and the base is rotated Δχ ≈236–197 = 39° with respect to the ribose ring (Fig. 4c). These rotations result in the 1.9 Å shift in the C3′-atom position, 3.7 Å shift in the position of NH2-group, and 4.6 Å shift in the position of CO-group (Fig. 4c). We hypothesize that a driving force for these large-amplitude structural rearrangements is the propensity of dsRNA to minimize steric clashes in RNA strands. Therefore, we calculated the values of van der Waals energy EvdW, which quantifies the excluded volume interactions, for an RNA strand in the dsRNA duplex and in DNA
RNA duplexes. Due to the C3′-endo arrangement of ribose rings in the RNA strand; the ribose ring is rotated Δδ ≈116–78 = 38° with respect to the phosphate backbone as compared to C2′-endo arrangement of ribose ring in the DNA strand, and the base is rotated Δχ ≈236–197 = 39° with respect to the ribose ring (Fig. 4c). These rotations result in the 1.9 Å shift in the C3′-atom position, 3.7 Å shift in the position of NH2-group, and 4.6 Å shift in the position of CO-group (Fig. 4c). We hypothesize that a driving force for these large-amplitude structural rearrangements is the propensity of dsRNA to minimize steric clashes in RNA strands. Therefore, we calculated the values of van der Waals energy EvdW, which quantifies the excluded volume interactions, for an RNA strand in the dsRNA duplex and in DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA duplex (ESI†). The more negative value of EvdW implies smaller steric clashes and weaker excluded volume interactions. EvdW came to −179 ± 4 kcal mol−1 for dsRNA vs. −162 ± 4 kcal mol−1 for DNA
RNA duplex (ESI†). The more negative value of EvdW implies smaller steric clashes and weaker excluded volume interactions. EvdW came to −179 ± 4 kcal mol−1 for dsRNA vs. −162 ± 4 kcal mol−1 for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrid (see Table 2). Hence, the structural rearrangements in dsRNA, i.e., rotations of ribose rings and bases described above result in lowering the energy associated with excluded volume interactions in dsRNA duplex by ΔEvdW = 179–162 = 17 kcal mol−1. This conclusion did not change when we analyzed the results of MD simulations for dsRNA and DNA
RNA hybrid (see Table 2). Hence, the structural rearrangements in dsRNA, i.e., rotations of ribose rings and bases described above result in lowering the energy associated with excluded volume interactions in dsRNA duplex by ΔEvdW = 179–162 = 17 kcal mol−1. This conclusion did not change when we analyzed the results of MD simulations for dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA with constrained ends. This agrees with the notion that the presence of OH-groups in RNA results in lower chemical stability of RNA compared to DNA, thus, making DNA more tailored for the long-term storage of genetic information39 and making RNA more capable of carrying out various regulatory functions.40
RNA with constrained ends. This agrees with the notion that the presence of OH-groups in RNA results in lower chemical stability of RNA compared to DNA, thus, making DNA more tailored for the long-term storage of genetic information39 and making RNA more capable of carrying out various regulatory functions.40
In summary, for the first time, we explored the single-molecule electrical conductance of dsRNA and compared the dsRNA conductance with that for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrids formed by identical sequences. The average conductance values were similar for both biomolecules, but the dsRNA conductance was more variable. The conductance distribution for dsRNA is one order of magnitude broader than that for DNA
RNA hybrids formed by identical sequences. The average conductance values were similar for both biomolecules, but the dsRNA conductance was more variable. The conductance distribution for dsRNA is one order of magnitude broader than that for DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA hybrids, which indicates that dsRNA is a more flexible duplex. We employed computational molecular modeling to uncover the structural underpinnings of the experimental results. The MD simulations of dsRNA and DNA
RNA hybrids, which indicates that dsRNA is a more flexible duplex. We employed computational molecular modeling to uncover the structural underpinnings of the experimental results. The MD simulations of dsRNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RNA both without and with constrained ends confirmed higher flexibility of dsRNA and illuminated, in atomic detail, the molecular mechanism of this effect. The results obtained demonstrate that the CT process in oligonucleotides is mainly mediated by base stacking. Our experiments also show that single-molecule conductance is a sensitive parameter and that STM-BJ is a powerful method capable of detecting even slight differences in the dynamic structural properties of biomolecules. Our results are a good starting point to motivate future biophysical characterization of single biomolecules of larger complexity.
RNA both without and with constrained ends confirmed higher flexibility of dsRNA and illuminated, in atomic detail, the molecular mechanism of this effect. The results obtained demonstrate that the CT process in oligonucleotides is mainly mediated by base stacking. Our experiments also show that single-molecule conductance is a sensitive parameter and that STM-BJ is a powerful method capable of detecting even slight differences in the dynamic structural properties of biomolecules. Our results are a good starting point to motivate future biophysical characterization of single biomolecules of larger complexity.
Author contributions
JMAV and SC conceptualized and designed the research. SC, KGGPA, SA, and JMAV performed experimental work and data analyses. EK, FM, and VB carried out the computational work and data analyses. All the authors discussed the results and contributed to manuscript writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support from the NSF (Award Number 2027530) and from UMass Lowell (the Immersive Scholars program, the Wong research award 2020, and the Kennedy College of Sciences Giants fund 2021).References
- A. L. Lehninger, D. L. Nelson, M. M. Cox and M. M. Cox, et al., Lehninger principles of biochemistry, Macmillan, 2005 Search PubMed.
- C. F. Bennett and E. E. Swayze, Annu. Rev. Pharmacol. Toxicol., 2010, 50, 259–293 CrossRef CAS PubMed.
- J. A. Doudna and E. Charpentier, Science, 2014, 346, 6213 CrossRef PubMed.
- C. A. Batt, Science, 2007, 316, 1579–1580 CrossRef CAS PubMed.
- D. B. T. Cox, R. J. Platt and F. Zhang, Nat. Med., 2015, 21, 121–131 CrossRef CAS PubMed.
- A. V. Pinheiro, D. Han, W. M. Shih and H. Yan, Nat. Nanotechnol., 2011, 6, 763–772 CrossRef CAS PubMed.
- N. C. Seeman and H. F. Sleiman, Nat. Rev. Mater., 2017, 3, 1–23 Search PubMed.
- Y. Li, J. M. Artés, B. Demir, S. Gokce, H. M. Mohammad, M. Alangari, M. P. Anantram, E. E. Oren and J. Hihath, Nat. Nanotechnol., 2018, 13, 1167–1173 CrossRef CAS PubMed.
- J. Veselinovic, M. Alangari, Y. Li, Z. Matharu, J. M. Artés, E. Seker and J. Hihath, Electrochim. Acta, 2019, 313, 116–121 CrossRef CAS.
- H. Miller, Z. Zhou, J. Shepherd, A. J. Wollman and M. C. Leake, Rep. Prog. Phys., 2017, 81, 024601 CrossRef PubMed.
- Y. M. Sigal, R. Zhou and X. Zhuang, Science, 2018, 361, 880–887 CrossRef CAS PubMed.
- K. G. G. P. Arachchillage, S. Chandra, A. Piso, T. Qattan and J. M. A. Vivancos, J. Mater. Chem. B, 2021, 9(35), 6994–7006 RSC.
- B. Xu, P. Zhang, X. Li and N. Tao, Nano Lett., 2004, 4, 1105–1108 CrossRef CAS.
- Y. Li, J. M. Artés and J. Hihath, Small, 2016, 12, 432–437 CrossRef CAS PubMed.
- Y. Li, J. M. Artés, J. Qi, I. A. Morelan, P. Feldstein, M. P. Anantram and J. Hihath, J. Phys. Chem. Lett., 2016, 7, 1888–1894 CrossRef CAS PubMed.
- J. Hihath, B. Xu, P. Zhang and N. Tao, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 16979–16983 CrossRef CAS PubMed.
- J. M. Artés, Y. Li, J. Qi, M. Anantram and J. Hihath, Nat. Commun., 2015, 6, 1–8 Search PubMed.
- R. Zhuravel, H. Huang, G. Polycarpou, S. Polydorides, P. Motamarri, L. Katrivas, D. Rotem, J. Sperling, L. A. Zotti and A. B. Kotlyar, et al. , Nat. Nanotechnol., 2020, 15, 836–840 CrossRef CAS PubMed.
- L. Xiang, J. L. Palma, C. Bruot, V. Mujica, M. A. Ratner and N. Tao, Nat. Chem., 2015, 7, 221–226 CrossRef CAS PubMed.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- J. Hihath and N. Tao, Nanotechnology, 2008, 19, 265204 CrossRef PubMed.
- L. Venkataraman, J. E. Klare, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nature, 2006, 442, 904–907 CrossRef CAS PubMed.
- H. Rascón-Ramos, J. M. Artés, Y. Li and J. Hihath, Nat. Mater., 2015, 14, 517–522 CrossRef PubMed.
- R. I. Litvinov, O. Kononova, A. Zhmurov, K. A. Marx, V. Barsegov, D. Thirumalai and J. W. Weisel, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8575–8580 CrossRef CAS PubMed.
- K. A. Minin, A. Zhmurov, K. A. Marx, P. K. Purohit and V. Barsegov, J. Am. Chem. Soc., 2017, 139, 16168–16177 CrossRef CAS PubMed.
- A. Zhmurov, O. Kononova, R. I. Litvinov, R. I. Dima, V. Barsegov and J. W. Weisel, J. Am. Chem. Soc., 2012, 134, 20396–20402 CrossRef CAS PubMed.
- Y. Matsunaga and Y. Sugita, Curr. Opin. Struct. Biol., 2020, 61, 153–159 CrossRef CAS PubMed.
- H. Geng, F. Chen, J. Ye and F. Jiang, Comput. Struct. Biotechnol. J., 2019, 17, 1162–1170 CrossRef CAS PubMed.
- A. Zhmurov, R. Dima, Y. Kholodov and V. Barsegov, Proteins: Struct., Funct., Bioinf., 2010, 78, 2984–2999 CrossRef CAS PubMed.
- M. J. Boniecki, G. Lach, W. K. Dawson, K. Tomala, P. Lukasz, T. Soltysinski, K. M. Rother and J. M. Bujnicki, Nucleic Acids Res., 2016, 44, e63 CrossRef PubMed.
- T.-S. Lee, D. S. Cerutti, D. Mermelstein, C. Lin, S. LeGrand, T. J. Giese, A. Roitberg, D. A. Case, R. C. Walker and D. M. York, J. Chem. Inf. Model., 2018, 58, 2043–2050 CrossRef CAS PubMed.
- A. Zhmurov, K. Rybnikov, Y. Kholodov and V. Barsegov, J. Phys. Chem. B, 2011, 115, 5278–5288 CrossRef CAS PubMed.
- D. A. Case, K. Belfon, I. Ben-Shalom, S. R. Brozell, D. Cerutti, T. Cheatham, V. W. D. Cruzeiro, T. Darden, R. E. Duke, G. Giambasu, et al., AMBER 2020, University of California, San Francisco, 2020.
- M. Zgarbová, M. Otyepka, J. Sponer, A. Mladek, P. Banas, T. E. Cheatham III and P. Jurecka, J. Chem. Theory Comput., 2011, 7, 2886–2902 CrossRef PubMed.
- A. Pérez, I. Marchán, D. Svozil, J. Sponer, T. E. Cheatham III, C. A. Laughton and M. Orozco, Biophys. J., 2007, 92, 3817–3829 CrossRef PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- C. Bruot, L. Xiang, J. L. Palma and N. Tao, ACS Nano, 2015, 9, 88–94 CrossRef CAS PubMed.
- J. Sponer, G. Bussi, M. Krepl, P. Banas, S. Bottaro, R. A. Cunha, A. Gil-Ley, G. Pinamonti, S. Poblete and P. Jurecka, et al. , Chem. Rev., 2018, 118, 4177–4338 CrossRef CAS PubMed.
- I. Barbieri and T. Kouzarides, Nat. Rev. Cancer, 2020, 20, 303–322 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr06925j |
| This journal is © The Royal Society of Chemistry 2022 |