From droplets to ions: a comprehensive and consecutive ion formation modelling in atmosphere pressure interface of electrospray ionization mass spectrometry†
He
Xingliang
 ,
Guo
Xing
,
Wu
Mengfan
,
Guo
Xing
,
Wu
Mengfan
 ,
Deng
Fulong
,
Zeng
Pengyu
,
Zhao
Zhongjun
,
Deng
Fulong
,
Zeng
Pengyu
,
Zhao
Zhongjun
 * and
Duan
Yixiang
*
* and
Duan
Yixiang
*
Research Center of Analytical Instrumentation, School of Mechanical Engineering, Sichuan University, China. E-mail: zhaozj@scu.edu.cn
First published on 6th June 2023
Abstract
In this study, we propose a novel ion formation simulation method for electrospray ionization (ESI) and atmosphere pressure interface (API). In this method, not the sheer particle trajectory, but the evolution of droplets and the offspring of gaseous ions are introduced instead. For the first time, the dynamic droplet-to-ion transformation process in the API of ESI-MS is visualized. The results suggest that this model provides a better understanding of the ion evolution mechanism and we propose a way for mass spectrometer structure optimization and ion source parameter adjustment in new aspects.
One of the remarkable progresses in mass spectrometry achieved in the past decades is its coupling with liquid chromatography (LC-MS).1 Most of the attractions of LC-MS instruments are attributed to their unique ionization mechanism, typically, electrospray ionization (ESI). The ESI is the leading one among the group of atmospheric pressure ionization methods, also known as the “soft” ionization methods. These methods are distinguished by their capability of operating under atmosphere pressure, which can preserve the structural integrity of the target analyte.2 A tricky problem for ESI mass spectrometry (ESI-MS) is the huge pressure drop between the ion source (ambient pressure) and the vacuum required for mass analysis (pressure lower than 10−5 torr). This indicates that, for a standard ESI ion source, despite multi-stage pumping is used, only a small fraction of analytes can enter the narrow inlet necessary to preserve the vacuum.3 In addition, the ESI process is accompanied by rapid solvent evaporation and the production of residue droplets that are hard to be ionized (for the ion evaporation mechanism3), which will certainly disrupt the analysis of the target analytes.3–5
In view of these problems, an elaborately designed ion source and API in ESI-MS that simultaneously attends to both the transmission and the anti-contamination is of vital importance. Since numerical methods have become a standard procedure in the R&D of MS instruments,6,7 the accurate numerical modelling of ions in the API of ESI-MS can be very important but rather challenging, which is distinct by its intricate multi-physical nature.8 In current studies, the Lagrange model that treats the particles (droplets or ions) as a discrete phase in the fluid is often adopted.9–13 Specifically, the choice of fluid-particle interaction model in these studies is decided by the particle Knudsen number (Kn), which is defined as the ratio of the mean free path and the particle diameter.10 For example, for droplets in dense air, the Stokes drag force model is adopted.9,10 For the ions in a vacuum, only the ion optics model that involves the ion-neutral collision can be applied.13 In these studies, without an ion formation mechanism, the droplets and ions cannot be studied synchronously. In addition, the droplets or ions are simply treated as particles with constant mass and charge that are released at some arbitrarily given coordinates, which clearly deviates from the very basic principle of ESI.
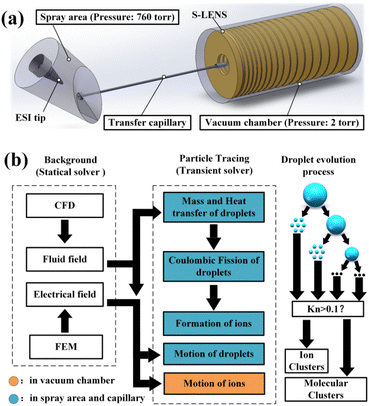
For the purpose of modelling the ionization mechanism of ESI comprehensively, a multi-physical coupling strategy that combines the gas dynamics and electrodynamics is taken in our simulation based on the ANSY Fluent (ver. 2022 R1, Cecil Township, PA) and COMSOL Multiphysics (ver.6.0, COMSOL AB, Stockholm, Sweden). Actually, when an ESI ion source is running in cone-jet mode14 (the mode of greatest interest due to its application), uniformly sized droplets that can be estimated using the scaling law15 will be released.14 With the knowledge of evaporation and the coulombic fission principle (the ion evaporation mechanism for small molecules is applied in our work),16 it is feasible for us to model the entire ion formation procedure numerically with some critical simplifications. The computation was conducted on a basic desktop computer (CPU: AMD Ryzen9 5950X, 3.4 GHz, RAM: 32 GB) and the whole process took about 96 h. The geometrical model used in our simulation is shown in Fig. 1(a), which is established according to our experimental setup. The model is composed of three parts: spray area (pressure at 760 torr), transfer capillary (length: 60.27 mm, heated to 573 K), and vacuum chamber (pressure at 2 torr). In the spray area, a simplified model of the H-ESI ion source (Thermo Fisher Scientific, Waltham, MA, USA) is established. There are three gas (N2) inlets in the ion source: sheath gas, auxiliary gas, and curtain gas. The initially charged droplets are released near the ESI tip in the spray area. After rapid evaporation and coulombic fissions, a massive amount of progeny droplets and gaseous ions are formed in the spray area and transfer capillary. Traveling through the capillary, the ions and droplets enter the vacuum chamber, where the ions of specified mass-to-charge ratio can be captured by an S-LENS type RF ion guide.17
The schematic diagram of the simulation process is shown in Fig. 1(b). Generally, the simulation can be divided into two parts: 1. Background field simulation. 2. Particle tracing simulation. The background fluid field and the electrical field of the whole system are calculated using the ANSYS Fluent based on the finite volume method (FVM) and the COMSOL Multiphysics based on the finite element method (FEM), separately. The background data is then input into a particle tracing module (modified from the standard particle tracing module of COMSOL Multiphysics), and in this module, the motion, mass, temperature, and charge of each droplet are evaluated at every time step using a transient solver. The evolution of droplets is carried in the spray area and capillary (both filled with dense air, coloured in blue in Fig. 1(b)), and the ion optics proceed in the vacuum chamber (coloured in orange in Fig. 1(b)). As also shown in Fig. 1(b), an initial droplet will undergo several fission events and be transferred into residue (primary) droplets and highly charged progeny droplets.
Since the ESI process is rather complex, some simplification is needed to be performed to make the calculation implementable for a common computer. The particle tracing modelling is established based on the assumptions listed below:
1. The ESI ion source is in cone-jet mode, and the initial size of the droplets is uniform in our simulation.
2. The effect of the droplet morphology on the evolution is not considered, and they are all shaped in spheres in our simulation.
3. The gas dynamic effect on the Rayleigh limit is not considered.
4. The secondary rupture of progeny droplets is not under consideration.
5. When Kn > 0.1, the droplet evaporation stops.
Particularly, assumption 5 needs to be clarified. According to the value of Kn, the mass and heat transfer model of particles in the fluid can be categorized into 3 regimes:18 the continuum regime (Kn ≪ 1), the transition regime (Kn![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (1)), and the free molecular regime (Kn ≫ 1). In our simulation, only the evaporation model in the continuum regime is adopted (Stefan-Fuchs model19). As the droplets become finer (after coulombic fission events) and the air becomes thinner (Kn > 0.1, near the transition regime), the evaporation rate rises dramatically18 and the droplets may turn into vapor utterly in an extremely short time (the evaporation stops). In this case, to reduce the computational burden, it is unwise to continually estimate the evaporation using the models in the transition regime, since only the statistically significant results are of our interest. These droplets are regarded as solvent clusters (evolved from residue droplets) or ion clusters (evolved from progeny droplets) with constant mass and charge. When these clusters reached the outlet of the transfer capillary, they will be counted statistically as ion current or solvent current (contamination). In this way, the transformation and anticontamination efficiency of the API can be properly evaluated. Besides, according to the calculated ion current, the ions will be reemitted in the vacuum chamber, where their trajectories are decided by ion optics (collision model) rather than the drag force model applied for the droplets and clusters. The theoretical and technical details about the simulation are shown in the ESI.†
O (1)), and the free molecular regime (Kn ≫ 1). In our simulation, only the evaporation model in the continuum regime is adopted (Stefan-Fuchs model19). As the droplets become finer (after coulombic fission events) and the air becomes thinner (Kn > 0.1, near the transition regime), the evaporation rate rises dramatically18 and the droplets may turn into vapor utterly in an extremely short time (the evaporation stops). In this case, to reduce the computational burden, it is unwise to continually estimate the evaporation using the models in the transition regime, since only the statistically significant results are of our interest. These droplets are regarded as solvent clusters (evolved from residue droplets) or ion clusters (evolved from progeny droplets) with constant mass and charge. When these clusters reached the outlet of the transfer capillary, they will be counted statistically as ion current or solvent current (contamination). In this way, the transformation and anticontamination efficiency of the API can be properly evaluated. Besides, according to the calculated ion current, the ions will be reemitted in the vacuum chamber, where their trajectories are decided by ion optics (collision model) rather than the drag force model applied for the droplets and clusters. The theoretical and technical details about the simulation are shown in the ESI.†
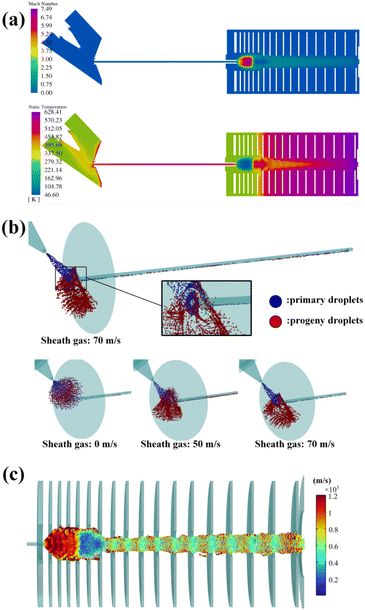
To verify the proposed model, the effect of sheath gas velocity on the ion formation was studied both numerically and experimentally. The sheath gas velocity was set in the range of 0–70 m s−1 and the other boundary conditions can be found in the ESI.† The simulated background results are shown in Fig. 2(a) (sheath gas speed = 70 m s−1). According to Fig. 2(a), in the spray area, the sheath gas flow is entrained in the hot auxiliary gas flow and quickly heated to around 370 K, which benefits evaporation. The gas is then accelerated rapidly around the transfer capillary entrance due to the sub-atmosphere pressure inside the capillary. As the gas speed inside the capillary reaches 1 Mach, the choke flow is established.20 At the same time, attributed to the continuous heat transfer from the inner wall, the stagnation temperature of the flow in the capillary increases up to 470 K. Entering the vacuum chamber, the gas speed rapidly exceeds 1 Mach and forms a supersonic expansion (maximum speed: 7.49 Mach) with a sharp Mach disk and barrel shock.21
The solvent used in the particle tracing is set as a mixture of water and methanol (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50). The thermal parameters of the solvent are illustrated in the ESI.† The flow rate of the ESI tip is set as 10 μL min−1 and correspondingly, the initial diameter of the drops was estimated to be 4.17 μm.15 The initial temperature of the droplet was set as 297 K and the atmospheric temperature was set as 300 K. The charge of the initial droplet was set as 80% of the Rayleigh limit,16 which is approximately 9.5 × 10−15 C. During each coulombic fission, each primary droplet losses 2% of its mass and 15% of its charge, and releases 8 progeny droplets of even charge and mass.16 The initial droplets are released at the position 0.5 mm (the typical length of Taylor cone jet) away from the ESI tip.15 The time interval of the offspring events was set as 2.27 × 10−7 s (see S4 in the ESI†), and the corresponding ion current was around 50 nA. Fig. 2(b) shows the trajectory of the primary (blue) and progeny droplets (red) at different sheath gas speeds (0 m s−1, 50 m s−1, and 70 m s−1). According to the results, the plume structure is related to the sheath gas speed. Attributed to the space charge effect (mainly formed by the primary droplets with higher net charge), the plume is diffused radially and the offspring droplets are repulsed outward (consistent with the reported results14). For the 0 m s−1 case, most droplets are ruined on the skimmer surface. For the cases of 50 m s−1 and 70 m s−1, the droplets are accelerated axially, the radial diffusion is restrained accordingly and more droplets are inhaled into the capillary inlet. Besides, in these cases, more primary droplets that bring in contamination are also transmitted. Fortunately, thanks to the off-axis configuration of the H-ESI, some of these droplets are lost immediately on the inner wall of the capillary due to their excessive inertia (magnified in Fig. 2(b)), and this off-axis structure is actually functioned as a filter of the droplet mass, which removes the heavy droplets that are hard to be ionized. But for the 70 m s−1 case, too many droplets that could have been ionized were filtered and lost. Then, those survival droplets in the capillary were heated by the inner wall of the capillary, which quickened the unleash of ions. Afterwards, the ion current and solvent current were calculated (for sheath gas speed = 70 m s−1, the values are 9.95 nA and 0.11 nA) and the ions are reemitted in the vacuum chamber. To be consistent with the experiment, the analyte was set as the protonated reserpine (C33H40N2O9) with m/z 609.28 and collision cross section22 253.28 Å2. The initial speed of these ions is set as equal to the flow speed, which is approximately 500 m s−1. The trajectory and the velocity of the ions of the 70 m s−1 case are shown in Fig. 2(c). The final transmitted ion current was 5.54 nA, which means the efficiency was 55.67%. In fact, almost all the ions are well trapped by the RF field and the ion expiration essentially happens on the aperture due to the space charge effect. Finally, the total transmission efficiency under these configurations can be calculated, which is 11.30%. The above discussion suggests that the sheath gas speed is critical in balancing the transmission and anti-contamination.
50). The thermal parameters of the solvent are illustrated in the ESI.† The flow rate of the ESI tip is set as 10 μL min−1 and correspondingly, the initial diameter of the drops was estimated to be 4.17 μm.15 The initial temperature of the droplet was set as 297 K and the atmospheric temperature was set as 300 K. The charge of the initial droplet was set as 80% of the Rayleigh limit,16 which is approximately 9.5 × 10−15 C. During each coulombic fission, each primary droplet losses 2% of its mass and 15% of its charge, and releases 8 progeny droplets of even charge and mass.16 The initial droplets are released at the position 0.5 mm (the typical length of Taylor cone jet) away from the ESI tip.15 The time interval of the offspring events was set as 2.27 × 10−7 s (see S4 in the ESI†), and the corresponding ion current was around 50 nA. Fig. 2(b) shows the trajectory of the primary (blue) and progeny droplets (red) at different sheath gas speeds (0 m s−1, 50 m s−1, and 70 m s−1). According to the results, the plume structure is related to the sheath gas speed. Attributed to the space charge effect (mainly formed by the primary droplets with higher net charge), the plume is diffused radially and the offspring droplets are repulsed outward (consistent with the reported results14). For the 0 m s−1 case, most droplets are ruined on the skimmer surface. For the cases of 50 m s−1 and 70 m s−1, the droplets are accelerated axially, the radial diffusion is restrained accordingly and more droplets are inhaled into the capillary inlet. Besides, in these cases, more primary droplets that bring in contamination are also transmitted. Fortunately, thanks to the off-axis configuration of the H-ESI, some of these droplets are lost immediately on the inner wall of the capillary due to their excessive inertia (magnified in Fig. 2(b)), and this off-axis structure is actually functioned as a filter of the droplet mass, which removes the heavy droplets that are hard to be ionized. But for the 70 m s−1 case, too many droplets that could have been ionized were filtered and lost. Then, those survival droplets in the capillary were heated by the inner wall of the capillary, which quickened the unleash of ions. Afterwards, the ion current and solvent current were calculated (for sheath gas speed = 70 m s−1, the values are 9.95 nA and 0.11 nA) and the ions are reemitted in the vacuum chamber. To be consistent with the experiment, the analyte was set as the protonated reserpine (C33H40N2O9) with m/z 609.28 and collision cross section22 253.28 Å2. The initial speed of these ions is set as equal to the flow speed, which is approximately 500 m s−1. The trajectory and the velocity of the ions of the 70 m s−1 case are shown in Fig. 2(c). The final transmitted ion current was 5.54 nA, which means the efficiency was 55.67%. In fact, almost all the ions are well trapped by the RF field and the ion expiration essentially happens on the aperture due to the space charge effect. Finally, the total transmission efficiency under these configurations can be calculated, which is 11.30%. The above discussion suggests that the sheath gas speed is critical in balancing the transmission and anti-contamination.
To validate the simulation, a homemade ESI-TOFMS platform was established. The API of this platform is similar to that described before in numerical modelling. A methanol solution (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
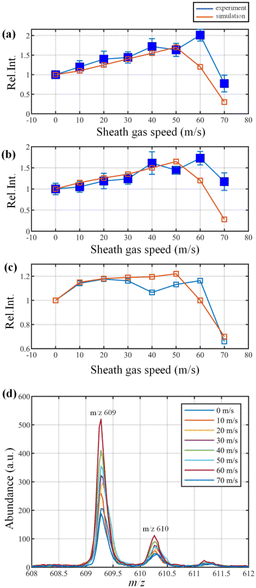
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50) containing 10 ng mL−1 reserpine and 1 ng mL−1 ammonium acetate was utilized in the experiment. All the solutions and analytes were purchased from Sigma (Sigma-Aldrich, St Louis, MO, USA). The solutions were injected into the ion source at 10 μL min−1 using a syringe pump. In this experiment, the HESI was operated at 760 torr and the first pumping stage pressure was maintained at 2 torr. Besides, the sprayer voltage was set as 3200 V, the voltage of the transfer capillary was 50 V, the aperture voltage was set as 25 V and the RF voltage (peak-to-peak value) of the ion guide was 140 V (RF frequency: 1 MHz, offset voltage: 35 V). The stainless transfer capillary (inner diameter: 0.35 mm, outer diameter: 1.56 mm, length: 60.27 mm) is embedded in a copper block and heated to 573 K. The sheath gas speed varies from 0 m s−1 to 70 m s−1. While adjusting the sheath gas speed, the intensity of protonated reserpine (m/z 609.27) and chemical noise were monitored,23 in which the mass spectra are shown in Fig. 3(d). The curves of the relative ion intensity of reserpine and noise at a sheath gas speed 0–70 m s−1 are shown in Fig. 3(a) and (b), in which the blue curves are the data obtained in the experiment and the red curves are those obtained from the simulation. First of all, these curves indicate that the changing trend of the intensity of reserpine and noise are similar at different gas speeds, both in the experiments and simulations. As the sheath gas speed increases from 0 m s−1 to about 50 m s−1, the intensity of both curves is rising steadily. This is due to the radial focusing effect of the sheath gas, as introduced before. When the gas speed reaches 60–70 m s−1, the ion intensities dropped dramatically to about half of the initial status (0 m s−1). As predicted before, in the spray area, the excessive sheath gas speed will reduce the dwelling time of droplets and increase their velocity. Thus, the droplets with higher kinetic energy will hit the inner wall of the transfer capillary straight and the signal intensities will be diminished correspondingly. Fig. 3(c) is the relative signal-to-noise ratio (SNR) of reserpine. With the increase of gas speed, the SNR is rising concurrently, which indicates that the chemical noise is inhibited by the sheath gas. Similarly, as the speed approaches 60 m s−1, the SNR declines suddenly. This can be explained by the fact that, when the sheath gas speed is too high, the droplets entering the capillary may encounter fewer fission events and thus fewer gas phase ions will be released. It should be noticed that the simulated curves are not reversed at exactly the same sheath gas speed as observed in the experiments. This discrepancy can be aroused by: 1. Errors in evaluating the size of initial droplets. 2. Errors in calculating the thermal dynamic properties of droplets. 3. The introduction of the Reynolds average Navier-Stokes turbulence model. 4. The calculation errors introduced by the meshing process, choice of discretization scheme, and boundary conditions. 5. The geometric discrepancies between the computation model and the real device in the experiment. Although the model is simplified and slightly different from the real situation, the discussions above suggest that the numerical modelling agrees well with the experiments.
50) containing 10 ng mL−1 reserpine and 1 ng mL−1 ammonium acetate was utilized in the experiment. All the solutions and analytes were purchased from Sigma (Sigma-Aldrich, St Louis, MO, USA). The solutions were injected into the ion source at 10 μL min−1 using a syringe pump. In this experiment, the HESI was operated at 760 torr and the first pumping stage pressure was maintained at 2 torr. Besides, the sprayer voltage was set as 3200 V, the voltage of the transfer capillary was 50 V, the aperture voltage was set as 25 V and the RF voltage (peak-to-peak value) of the ion guide was 140 V (RF frequency: 1 MHz, offset voltage: 35 V). The stainless transfer capillary (inner diameter: 0.35 mm, outer diameter: 1.56 mm, length: 60.27 mm) is embedded in a copper block and heated to 573 K. The sheath gas speed varies from 0 m s−1 to 70 m s−1. While adjusting the sheath gas speed, the intensity of protonated reserpine (m/z 609.27) and chemical noise were monitored,23 in which the mass spectra are shown in Fig. 3(d). The curves of the relative ion intensity of reserpine and noise at a sheath gas speed 0–70 m s−1 are shown in Fig. 3(a) and (b), in which the blue curves are the data obtained in the experiment and the red curves are those obtained from the simulation. First of all, these curves indicate that the changing trend of the intensity of reserpine and noise are similar at different gas speeds, both in the experiments and simulations. As the sheath gas speed increases from 0 m s−1 to about 50 m s−1, the intensity of both curves is rising steadily. This is due to the radial focusing effect of the sheath gas, as introduced before. When the gas speed reaches 60–70 m s−1, the ion intensities dropped dramatically to about half of the initial status (0 m s−1). As predicted before, in the spray area, the excessive sheath gas speed will reduce the dwelling time of droplets and increase their velocity. Thus, the droplets with higher kinetic energy will hit the inner wall of the transfer capillary straight and the signal intensities will be diminished correspondingly. Fig. 3(c) is the relative signal-to-noise ratio (SNR) of reserpine. With the increase of gas speed, the SNR is rising concurrently, which indicates that the chemical noise is inhibited by the sheath gas. Similarly, as the speed approaches 60 m s−1, the SNR declines suddenly. This can be explained by the fact that, when the sheath gas speed is too high, the droplets entering the capillary may encounter fewer fission events and thus fewer gas phase ions will be released. It should be noticed that the simulated curves are not reversed at exactly the same sheath gas speed as observed in the experiments. This discrepancy can be aroused by: 1. Errors in evaluating the size of initial droplets. 2. Errors in calculating the thermal dynamic properties of droplets. 3. The introduction of the Reynolds average Navier-Stokes turbulence model. 4. The calculation errors introduced by the meshing process, choice of discretization scheme, and boundary conditions. 5. The geometric discrepancies between the computation model and the real device in the experiment. Although the model is simplified and slightly different from the real situation, the discussions above suggest that the numerical modelling agrees well with the experiments.
In this research, for the first time, a droplet-to-ion transformation in the API of ESI-MS is simulated and visualized. In particular, the evaporation-driven coulombic fission of charged droplets is solved in accordance with the particle motion. Combining the droplet tracing and ion optics model, a comprehensive and consecutive numerical modelling of the droplet evolution is enabled and validated experimentally. This model provides a more insightful and systematic explanation of the behaviour of the droplets as well as the ions within a specified API and is more promising in evaluating the performance of ion source and API designs than the tools that existed.
Conflicts of interest
There are no conflicts to declare.References
- M. S. Lee and E. H. Kerns, Mass Spectrom. Rev., 1999, 18, 187–279 CrossRef CAS.
- D. B. Robb, T. R. Covey and A. P. Bruins, Anal. Chem., 2000, 72, 3653–3659 CrossRef CAS PubMed.
- J. H. Gross, Mass spectrometry: a textbook, Springer Science & Business Media, 2006 Search PubMed.
- R. Juraschek, T. Dülcks and M. Karas, J. Am. Soc. Mass Spectrom., 1999, 10, 300–308 CrossRef CAS.
- J. S. Page, R. T. Kelly, K. Tang and R. D. Smith, J. Am. Soc. Mass Spectrom., 2007, 18, 1582–1590 CrossRef CAS PubMed.
- B. B. Schneider, E. G. Nazarov, F. Londry, P. Vouros and T. R. Covey, Mass Spectrom. Rev., 2016, 35, 687–737 CrossRef CAS PubMed.
- A. V. Tolmachev, T. Kim, H. R. Udseth, R. D. Smith, T. H. Bailey and J. H. Futrell, Int. J. Mass Spectrom., 2000, 203, 31–47 CrossRef CAS.
- S. Garimella, X. Zhou and Z. Ouyang, J. Am. Soc. Mass Spectrom., 2013, 24, 1890–1899 CrossRef CAS PubMed.
- N. Gimelshein, S. Gimelshein, T. Lilly and E. Moskovets, J. Am. Soc. Mass Spectrom., 2014, 25, 820–831 CrossRef CAS PubMed.
- W. Wang, S. Bajic, B. John and D. R. Emerson, J. Am. Soc. Mass Spectrom., 2018, 29, 600–612 CrossRef CAS PubMed.
- A. D. Appelhans and D. A. Dahl, Int. J. Mass Spectrom., 2005, 244, 1–14 CrossRef CAS.
- A. Zacharos, A. Lekkas, M. Sudakov, D. Papanastasiou, D. Kounadis, I. Nikolos and E. Raptakis, Proceedings of the 61st ASMS Conference on Mass Spectrometry and Allied Topics, Minneapolis, MN, 2013.
- X. Zhou and Z. Ouyang, Anal. Chem., 2016, 88, 7033–7040 CrossRef CAS PubMed.
- J. Rosell-Llompart, J. Grifoll and I. G. Loscertales, J. Aerosol Sci., 2018, 125, 2–31 CrossRef CAS.
- J. F. De La Mora and I. G. Loscertales, J. Fluid Mech., 1994, 260, 155–184 CrossRef.
- C. J. Hogan Jr. and P. Biswas, J. Am. Soc. Mass Spectrom., 2008, 19, 1098–1107 CrossRef PubMed.
- R. T. Kelly, A. V. Tolmachev, J. S. Page, K. Tang and R. D. Smith, Mass Spectrom. Rev., 2010, 29, 294–312 Search PubMed.
- W. Li and E. J. Davis, Aerosol Sci. Technol., 1996, 25, 11–21 CrossRef CAS.
- S. Basu, A. K. Agarwal, A. Mukhopadhyay and C. Patel, Droplets and sprays: applications for combustion and propulsion, Springer, 2017 Search PubMed.
- R. D. Zucker and O. Biblarz, Fundamentals of gas dynamics, John Wiley & Sons, 2019 Search PubMed.
- P. B. Farnsworth and R. L. Spencer, Spectrochim. Acta, Part B, 2017, 134, 105–122 CrossRef CAS.
- D. H. Ross, J. H. Cho and L. Xu, Anal. Chem., 2020, 92, 4548–4557 CrossRef CAS PubMed.
- P. A. Kottke, J. Y. Lee, A. P. Jonke, C. A. Seneviratne, E. S. Hecht, D. C. Muddiman, M. P. Torres and A. G. Fedorov, Anal. Chem., 2017, 89, 8981–8987 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3an00607g |
| This journal is © The Royal Society of Chemistry 2023 |