Sub 20 cm−1 computational prediction of the CH bond energy – a case of systematic error in computational thermochemistry†
James H.
Thorpe
 a,
David
Feller
a,
David
Feller
 bc,
David H.
Bross
bc,
David H.
Bross
 d,
Branko
Ruscic
d,
Branko
Ruscic
 *d and
John F.
Stanton
*d and
John F.
Stanton
 *a
*a
aThe Quantum Theory Project, Department of Chemistry, University of Florida, Gainesville, Florida 32611, USA. E-mail: johnstanton@chem.ufl.edu
bWashington State University, Pullman, Washington 99164-4630, USA
cUniversity of Alabama, Tuscaloosa, Alabama 35487-0336, USA
dChemical Sciences and Engineering Division, Argonne National Laboratory, Argonne, Illinois 60439, USA. E-mail: ruscic@anl.gov
First published on 3rd October 2022
Abstract
The bond dissociation energy of methylidyne, D0(CH), is studied using an improved version of the High-Accuracy Extrapolated ab initio Thermochemistry (HEAT) approach as well as the Feller–Peterson–Dixon (FPD) model chemistry. These calculations, which include basis sets up to nonuple (aug-cc-pCV9Z) quality, are expected to be capable of providing results substantially more accurate than the ca. 1 kJ mol−1 level that is characteristic of standard high-accuracy protocols for computational thermochemistry. The calculated 0 K CH bond energy (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 954 ± 15 cm−1 for HEAT and 27
954 ± 15 cm−1 for HEAT and 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 956 ± 15 cm−1 for FPD), along with equivalent treatments of the CH ionization energy and the CH+ dissociation energy (85
956 ± 15 cm−1 for FPD), along with equivalent treatments of the CH ionization energy and the CH+ dissociation energy (85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 829 ± 15 cm−1 and 32
829 ± 15 cm−1 and 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946 ± 15 cm−1, respectively), were compared to the existing benchmarks from Active Thermochemical Tables (ATcT), uncovering an unexpected difference for D0(CH). This has prompted a detailed reexamination of the provenance of the corresponding ATcT benchmark, allowing the discovery and subsequent correction of a systematic error present in several published high-level calculations, ultimately yielding an amended ATcT benchmark for D0(CH). Finally, the current theoretical results were added to the ATcT Thermochemical Network, producing refined ATcT estimates of 27
946 ± 15 cm−1, respectively), were compared to the existing benchmarks from Active Thermochemical Tables (ATcT), uncovering an unexpected difference for D0(CH). This has prompted a detailed reexamination of the provenance of the corresponding ATcT benchmark, allowing the discovery and subsequent correction of a systematic error present in several published high-level calculations, ultimately yielding an amended ATcT benchmark for D0(CH). Finally, the current theoretical results were added to the ATcT Thermochemical Network, producing refined ATcT estimates of 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 957.3 ± 6.0 cm−1 for D0(CH), 32
957.3 ± 6.0 cm−1 for D0(CH), 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946.7 ± 0.6 cm−1 for D0(CH+), and 85
946.7 ± 0.6 cm−1 for D0(CH+), and 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831.0 ± 6.0 cm−1 for IE(CH).
831.0 ± 6.0 cm−1 for IE(CH).
Introduction
The prediction of molecular bond energies and associated enthalpies of formation represents perhaps the most fundamental area of application for the field of quantum chemistry. While such properties are, in and of themselves, quite important for our understanding of chemical processes, the pursuit of increasingly accurate methods to calculate these quantities has historically driven development of theories for electron correlation,1–19 construction of basis sets,20–30 and advanced our understanding of the fundamental nature of, and various contributions to, molecular energies.31–40The usual approaches for calculating relative molecular energies to an accuracy of ca. 1 kJ mol−1 (“subchemical accuracy”) have typically been based on so-called “composite model chemistries”, a concept inspired by the work of Pople and collaborators.41–46 Originally, the aim of the pursuit was to achieve “chemical accuracy”, conventionally taken as ±1 kcal mol−1, or about ±4 kJ mol−1 (in terms of 95% confidence intervals for the calculated property, which is, by accepted convention, the measure of uncertainties in thermochemistry47,48). In order to achieve subchemical accuracy, the exact relativistic energy in a complete basis set is usually estimated by state-of-the-art composite approaches as the sum of contributions for the non-relativistic electronic energy, an incorporation of relativistic effects (scalar relativity and those associated with the spin–orbit interaction), and nuclear motion terms such as the vibrational zero-point energy (ZPE) and the diagonal Born–Oppenheimer correction (DBOC). Broadly speaking, a specific composite model chemistry falls into one of two categories. “Fixed” recipes such as High-Accuracy ab initio Extrapolated Thermochemistry (HEAT),30,49–52 Weizmann-n (W n),53–57 and Argonne National Laboratory-n (ANL-n)58 are founded upon a particular and precisely-defined treatment of the above energy contributions. By benchmarking calculations against sufficiently accurate thermochemistry for a suitable test suite of species, fixed recipes can be calibrated to establish generic associated statistical uncertainties (known as “Type A” or statistically-based uncertainties47), and can be carefully designed to facilitate error cancellation. In contrast, “free” recipes, such as Focal Point Analysis (FPA)59–63 and Feller–Peterson–Dixon (FPD),29,38,64–67 are adapted to each species in question. By observing the convergence of each energy contribution with respect to level of theory and size of basis set, and estimating its uncertainty (known as “Type B” or experience-based uncertainties47), it is possible to control the error of these recipes for a specific species to achieve a fixed objective of accuracy (provided the calculations are computationally feasible).
As time passes and computational capabilities (software and hardware) improve, new model chemistries (or modifications to extant recipes) are developed to either increase the chemical space spanned by an old recipe or to improve upon its accuracy. The Active Thermochemical Tables (ATcT) approach, which is based on a unique paradigm that enables the derivation of accurate, reliable, robust, and internally consistent thermochemistry,68–70 has played a key role in the development and benchmarking of a number of sub-kJ mol−1 theoretical approaches.29,30,49–52,55,56,58,71–74 The ATcT approach is based on constructing, statistically analyzing, and solving a Thermochemical Network (TN), which contains all available high-quality information from both experiments and high-level theoretical treatments. For many small molecular species, there is sufficient high-quality experimental data that allows the ATcT approach to provide uncertainties far tighter than the accuracy of quantum-chemical computations, and thus is the measure against which these methods can be calibrated. However, there are exceptions where computed values provide most of the foundation for an ATcT enthalpy of formation, an example being the title molecule of this work. This is not necessarily a cause for concern, provided that the stated uncertainties of the theoretical predictions incorporated in the TN are an accurate reflection of the 95% confidence interval for the calculated property. However, particularly in computational thermochemistry, there is always an underlying danger that unknown systematic errors may be present. Such is the case for methylidyne (CH).
In the course of ongoing work intended to extend the HEAT protocol30 to target ca. 20 cm−1 accuracy (provisionally termed “semi-spectroscopic”), the computed bond dissociation energy of methylidyne, D0(CH), was benchmarked against the most recent ATcT values of 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 970.5 ± 7.3 cm−1
970.5 ± 7.3 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 or 27
75 or 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 971.0 ± 7.3 cm−1.70 It was found that the new, very high-level theoretical value was lower than the ATcT estimate by ca. 16–17 cm−1, and by an additional ca. 4 cm−1 from the even earlier ATcT value of 27
971.0 ± 7.3 cm−1.70 It was found that the new, very high-level theoretical value was lower than the ATcT estimate by ca. 16–17 cm−1, and by an additional ca. 4 cm−1 from the even earlier ATcT value of 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 974.6 ± 8.4 cm−1.76 While technically still within the combined uncertainties of the quoted ATcT values and the stated accuracy objective of the protocol, the CH system is sufficiently small so that essentially full CI accuracy in the valence space is readily achieved. Indeed, close examination of the computed bond energy contributions suggested that the procedure was likely within 10 cm−1 of convergence, nearly a factor of two better than the apparent overall error in the calculations.
974.6 ± 8.4 cm−1.76 While technically still within the combined uncertainties of the quoted ATcT values and the stated accuracy objective of the protocol, the CH system is sufficiently small so that essentially full CI accuracy in the valence space is readily achieved. Indeed, close examination of the computed bond energy contributions suggested that the procedure was likely within 10 cm−1 of convergence, nearly a factor of two better than the apparent overall error in the calculations.
Significantly, the six largest contributors to the provenance of the CH thermochemistry in ATcT TN 1.122r70 are computational, rather than experimental, studies. As will be discussed in this report, much of the initial discrepancy between the extended HEAT and the available ATcT values for D0(CH) can be traced to a systematic error arising from improper treatment of rotational-electronic coupling in some of the earlier high-level theoretical values that are incorporated in the ATcT TN.
Namely, the spin–orbit (SO) correction to the computed D0(CH) has two components: one relates to the dissociation limit and involves the correction for the splitting between the 3P0,1,2 states of carbon atom, the other to the molecular spin–orbit interaction in the 2Π1/2,3/2 ground state of methylidyne. There are no particular issues with the former component, which corresponds to the weighted average of the 3P0,1,2 states of carbon atom of 29.59 cm−177–79 and lowers the C + H dissociation asymptote by the same amount. However, as pointed out in some of the previous literature,48,58 the correct molecular spin–orbit contribution to the energy – which must include coupling to the rotational angular momentum, a.k.a. rotational zero-point effect – nearly vanishes for the 2Π electronic state of CH (vide infra). The common approximation of using half the molecular spin–orbit constant (Ae), which has been apparently used in several of the published theoretical values that contribute to the ATcT value, produces a theoretical D0(CH) that is systematically too large by ca. 14 cm−1. This suggests that a detailed scrutiny of prior theoretical results for D0(CH) that are incorporated in the ATcT TN is in order, with the hope that incorporating a proper treatment of the molecular spin–orbit effect in calculations that have used the simplified spin–orbit correction might narrow the gap between the provisional semi-spectroscopic HEAT result and ATcT. The purpose of this work is to explore this issue, as well as to provide new computational benchmarks for the ionization energy of CH and the bond energy of the resulting CH+ ion.
Computational
Extended HEAT calculations
The calculations employed in the extended HEAT treatment are more fully described in ref. 52, but are summarized here and in Table 1. Briefly, the non-relativistic electronic energy is approximated from a series of CCSD(T), CCSDT(Q)Λ, and CCSDTQ(P)Λ calculations employing the aug-cc-pCV{8,9}Z, aug-cc-pCV{Q,5}Z, and pVTZ basis sets, respectively, where the {X,Y} notation indicates an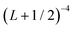 extrapolation.80–84 The very large 9-ζ basis sets for C and H were constructed during the process of this work, and facilitate a very good approximation to the complete basis set limit for the important (non-relativistic) CCSD(T) contribution to the properties studied here. Scalar relativistic effects are accounted for by inspecting the difference between spin-free Dirac Coulomb85,86 and non-relativistic CCSD(T)/unc-aug-cc-pCVQZ (unc indicating an uncontracted basis) energies.
extrapolation.80–84 The very large 9-ζ basis sets for C and H were constructed during the process of this work, and facilitate a very good approximation to the complete basis set limit for the important (non-relativistic) CCSD(T) contribution to the properties studied here. Scalar relativistic effects are accounted for by inspecting the difference between spin-free Dirac Coulomb85,86 and non-relativistic CCSD(T)/unc-aug-cc-pCVQZ (unc indicating an uncontracted basis) energies.
| Component | Extended HEAT | ΔD0(CH) | ΔIE(CH) | ΔD0(CH+) | FPD | ΔD0(CH) |
|---|---|---|---|---|---|---|
| SCF | aCV9Z | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 916.1 916.1 |
82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 199.2 199.2 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 825.3 825.3 |
None | |
| CCSD(T) | aCV{8,9}Z | 9481.6 | 3606.5 | 9588.6 | [fc] aV{8,9}Z | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 354.2 354.2 |
| [cv] awCV{Q,5}Z | 48.6 | |||||
| Post-(T) | (Q)Λ–(T)/aCV{Q,5}Z | 51.8 | 49.2 | 43.7 | [fc] T–(T)/aV5Z | 31.5 |
| [fc] (P)Λ–(Q)Λ/VTZ | 1.8 | −4.6 | 8.4 | [fc] Q–T/aVQZ | 12.6 | |
| [fc] FCI/VQZ | 0.3 | |||||
| [cv] T–(T)/wCVTZ | 5.2 | |||||
| [cv] Q–T/wCVDZ | −0.3 | |||||
| Total NREE | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 451.2 451.2 |
85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850.2 850.2 |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 465.9 465.9 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 452.2 452.2 |
||
| Scalar rel. | SFDC CCSD(T)/unc-aCVQZ | −13.9 | −25.9 | −20.1 | [fc] CCSD(T)-DK/V5Z-DK | −14.0 |
| Rot-spin–orbit | Hill–Van Vleck/atomic exp. | −29.8 | −0.2 | −42.2 | Hill–Van Vleck/atomic exp. | −29.8 |
| DBOC | CCSD/aCVQZ | −36.7 | 4.9 | −41.7 | [fc] CCSD/aVTZ | −36.7 |
| [fc] Q–D/VTZ | −0.8 | −0.6 | −0.4 | |||
| ZPE | Dunham | −1416.1 | 0.0 | −1416.1 | Dunham | −1416.1 |
| Total | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 954.0 954.0 |
85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 828.7 828.7 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 945.5 945.5 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 955.6 955.6 |
||
The goal of an ab initio composite chemistry is to determine the electronic energy as accurately as possible for a given degree of computational cost. For molecules, this electronic energy corresponds to the bottom of a potential energy well, which, of course, is not an observable. Instead, 0 K thermochemistry refers to the lowest actually existing rovibrational energy level.48 For many polyatomic species, it is entirely sufficient to simply calculate the vibrational zero-point energy (ZPE) by performing a geometry optimization and frequency analysis and, depending on the desired accuracy, further improve the ZPE by explicitly including anharmonic contributions. However, for some species the nominal vibrational ground state does not correspond to the lowest actually existing rovibrational level. There are several potential reasons that can lead to this situation, some of which have been explained in detail elsewhere.48 For example, the putative lowest rotational level is simply wiped out in some species by nuclear spin statistics, such as in O251,68,87 or CH3+.88 A different type of situation, of particular relevance here, occurs in open-shell chemical species that have a degenerate ground state and undergo a molecular spin–orbit interaction. In a typical computational approach for such cases, the ZPE correction would be augmented by a contribution from molecular spin–orbit coupling, the magnitude of which is frequently taken simply as half the experimentally determined spin–orbit constant Ae. However, this procedure tacitly assumes that the contribution comes entirely from the coupling of the electronic angular momentum to the spin, and that the coupling to the rotational angular momentum is negligible. The latter generally does not hold for small hydrides, which require additional care.
In particular, the detailed coupling of rotational, spin, and electronic angular momenta in diatomics is normally described either via pure or intermediate Hund's cases.89 Bearing some analogy with the cause célèbre of the (inverted) 2Πi ground state of OH,51,64,65 the coupling pertinent to the regular 2Πr ground electronic state of CH presents a case of spin uncoupling corresponding to the transition from Hund's case (a) to (b), quantitatively described by the 2Π Hamiltonian elaborated by Hill and Van Vleck.89,90 The zero of the energy scale of this Hamiltonian is the hypothetical vibrationless ground level before any coupling of spin and angular momenta is considered, which computationally corresponds to the non-relativistic (i.e. spin–orbit averaged) electronic energy corrected for the purely vibrational ZPE. Using the available spectroscopic constants for the 2Π state of CH, including Ae = 28.05 cm−1,91–93 the Hill–Van Vleck Hamiltonian indicates that the lowest rotational level, R = 0, N = 1, J = 1/2, is 0.16 cm−1above the vibrationless level of the 2Π state, rather than Ae/2 = 14.02 cm−1below it. Ironically, one would be better off by committing the error of altogether “forgetting” to consider the molecular spin–orbit of methylidyne, than by including it via the simplistic Ae/2 approach. Thus, the extended HEAT calculations reported here use the typical weighted-average treatment of the atomic spin–orbit corrections and the Hill–Van Vleck treatment of the CH spin–orbit correction. As the ground state of the CH+ cation is 1Σ+, its first-order spin–orbit coupling is zero.
In addition to the ZPE and spin–orbit corrections (where second-order spin–orbit corrections have been ignored but are expected to be negligible94), the computed values also include the diagonal Born–Oppenheimer correction, which is determined using a sequence of CCSD and CCSDTQ wavefunctions with aug-cc-pCVQZ (for the former) and cc-pVTZ (for both) basis sets. The CH vibrational zero-point energy (ZPE) is 1416.07 cm−1, as obtained from the best available spectroscopic parameters91–93 of the Dunham expansion95 (including the small Y00 term96 of 1.76 cm−1), while the CH+ ZPE of 1416.1 cm−1 was taken from the work of Cho and Le Roy.97
Calculations for CH+ used the geometry from Cho and LeRoy97 (1.12846 Å). The CH calculations reported below were performed at 1.11810 Å, a geometry determined via fit of extended HEAT energies calculated at four points around the region of the minimum. This geometry is far away from the value (1.1199 Å) reported by Huber and Herzberg,93 which is ultimately an interesting consequence of the electronic contribution to the moment of inertia, a point that will be elaborated in a forthcoming publication. However, the difference in D0(CH) between the Huber and Herzberg and the fit geometries is less than a wavenumber, and thus is not critical to this work.
The CCSDTQ(P)Λ correlation energies and the post-CCSD DBOC contributions were calculated with the MRCC program of Kallay.98,99 All other calculations employed the CFOUR program suite.100,101 UHF references were used for all species, with no symmetry equivalencing performed (calculations enforced only D2h symmetry).
Extended FPD calculations
As mentioned previously, the FPD66,67 approach to thermochemical and spectroscopic properties is a flexible composite model chemistry that seeks to include all physically significant effects judged on a molecule-specific criterion. For example, in the case of a heavy atom diatomic, like HI (1Σ+), the FPD approach would include a second order molecular spin–orbit correction even though for lighter molecules that contribution might prove to be negligible.94 For even heavier elements relativistic effects are incorporated with a full 4-component treatment.102 Chemical systems that involve a notable degree of multi-configurational character could require the use of multi-reference singles and doubles configuration interaction (MRSD-CI), as opposed to single reference coupled cluster theory, as the primary level of theory. The FPD approach has been under development for almost 20 years, and, while FPD and HEAT involve some of the same components, details of the former procedure varies from molecule to molecule.When applied to light main group chemical systems, such as CH, the first step in the FPD approach is a series of valence CCSD(T)(FC) geometry optimizations with the diffuse function augmented correlation consistent basis sets, aug-cc-pVnZ, n = D,T,Q…9.20,21,23,24,82,103 Note that, in general, all FPD components are evaluated at the respective optimal geometries for each basis set/method combination. Exceptions occur when individual energy evaluations require multiple days or weeks of computer time to complete. In such cases geometries are taken from the next closest level of theory. The use of optimal geometries yields accurate equilibrium structures and their associated harmonic vibrational frequencies that have been shown to agree well with experimental (or semi-experimental104) re structures and ωi. As will be discussed, the availability of results from multiple basis sets and the resulting uniform convergence pattern makes possible a simple extrapolation to the complete basis set (CBS) limit.
Open shell systems are described with the R/UCCSD(T) method available in the MOLPRO105–107 program package, which begins with restricted open-shell Hartree–Fock (ROHF) orbitals, but allows a small amount of spin contamination in the solution of the CCSD equations.108–110 Because MOLPRO only supports up to Lmax = 6 (i-functions), it was necessary to approximate R/U energies for Lmax > 6 by assuming that the difference between UCCSD(T)(FC) energies, obtained with Gaussian 09, and R/UCCSD(T) energies was constant to 10−6Eh. Atomic calculations imposed an orbital symmetry equivalencing restriction, i.e. px = py = pz.
In order to approximately account for the residual 1-particle basis set incompleteness, a CBS extrapolation formula, 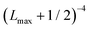 , was applied to the raw energies. There are multiple such formulas in the literature. Examination of the performance of four widely used formulas involving nearly 500 comparisons with reliable estimates of the CBS limit revealed that none of them proved to be superior across all basis sets and molecules studied.83 Therefore, we take half the spread among four different extrapolation formulas as a crude, conservative estimate of the uncertainty in the CBS dissociation energies. These include both two term (Lmax−3,
, was applied to the raw energies. There are multiple such formulas in the literature. Examination of the performance of four widely used formulas involving nearly 500 comparisons with reliable estimates of the CBS limit revealed that none of them proved to be superior across all basis sets and molecules studied.83 Therefore, we take half the spread among four different extrapolation formulas as a crude, conservative estimate of the uncertainty in the CBS dissociation energies. These include both two term (Lmax−3, 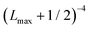 ) and three term formulas (Aexp(−bLmax), Aexp(−(Lmax−1)) + Bexp(−(Lmax−1)2)).
) and three term formulas (Aexp(−bLmax), Aexp(−(Lmax−1)) + Bexp(−(Lmax−1)2)).
While the valence CCSD(T) contribution clearly dominates the FPD calculation of thermodynamic properties, a number of smaller corrections are required in order to achieve uniform accuracy at the highest level. The most important of these is typically the outer-core/valence (CV) correlation correction. CV correlation is determined with R/UCCSD(T) calculations using the aug-cc-pwCVnZ, n = 3,4,5 basis sets25 and incorporates the 1s pair of electrons in first row atoms in the correlation treatment. For elements further down the Periodic Table, only the outermost core electrons are included, for example 2s2 2p6 in sulfur. The CV component is also extrapolated to the CBS limit. A simplistic definition of the valence electron space obtained from a casual examination of the Periodic Table can be inadequate for practical use. For example, in order to achieve quantitative accuracy in CV corrections to binding energies, it has been found necessary to include the first set of “core” electrons in the valence space. This is the case for compounds containing transition metals and heavier elements. The motivation for decomposing the CCSD(T) correlation energy into valence and CV pieces is the desire to avoid costly CV calculations with large basis sets. This savings comes at the cost of assuming additivity in the valence and CV components.
Higher order correlation recovery beyond CCSD(T) was achieved with CCSDT and CCSDTQ using awCV5Z and awCVQZ basis sets, respectively. In the case of a small diatomic like CH, which possesses only five valence electrons, it was also possible to carry out full configuration interaction (FCI) calculations with the VQZ basis set.
Scalar relativistic (SR) contributions to the binding energy were obtained with second-order Douglas–Kroll–Hess (DKH) R/UCCSD(T)(FC)-DK calculations with the aV5Z-DK basis set111 which was recontracted specifically for DKH.111–113 The SR correction is insensitive to the quality of the 1-particle and n-particle expansions.
Hydrogen-containing molecules can display a significant (>0.1 kcal mol−1 for atomization energies) diagonal corrections to the Born–Oppenheimer (DBOC) approximation. In the FPD approach as applied to CH we describe this effect with UCCSD-DBOC(FC)/aVTZ calculations. Even triple zeta basis sets have been found to yield nearly converged results.
The FPD and extended HEAT results reported in this work use an identical treatment of the spin–orbit coupling and vibrational zero-point energy effects; this approach results in essentially exact treatments of these contributions to the CH bond energy.
Results and discussion
New computational benchmarks for CH and CH+
Table 1 summarizes the new FPD and HEAT benchmarks for the bond dissociation energy of methylidyne, D0(CH), and additionally details the extended HEAT values for the adiabatic ionization energy of methylidyne, IE(CH), and the dissociation energy of methyliumylidene, D0(CH+).One striking feature of Table 1 is the ca. 2 cm−1 agreement between the FPD and extended HEAT predictions of D0(CH), particularly in the sum of the non-relativistic electronic-energy (NREE) components. The details of the FPD and extended HEAT calculations differ in a few ways: FPD utilizes core-valence separation where extended HEAT does not, FPD evaluates each component at the equilibrium geometry for that level of theory and basis set where HEAT performs all calculations at a single geometry, FPD employs an ROHF reference where HEAT employs UHF, etc. At the end of the day, however, both of these methods are designed to closely approximate (or converge towards) a nearly exact treatment of molecular bond energies, provided that enough computational effort can be expended. In the case of CH, where the NREE components of the electronic energy are relatively well-behaved and the valence full-CI limit is well within reach of modern algorithms and hardware, the current FPD and extended HEAT approaches agree for the bond energy of CH to a remarkable degree. Of note, however, is that both calculations disagree with previous ATcT determinations for the CH bond energy, a point discussed further below.
A detailed breakdown of the various contributions to the extended HEAT calculations is provided in Tables 2–5. As was observed in ref. 30 for HF, CO, N2, and H2O, the spin-free relativistic (Table 2) and DBOC (Table 3) components of the calculated properties seem very well converged. Despite the fact that spin-free relativistic contributions to the total energies converge slowly with respect to single-particle basis set size, the increment between the uncontracted aug-cc-pCVTZ and aug-cc-pCVQZ basis sets is less than 0.2 cm−1 for all three energy differences. The vibrational ZPE and the combined spin–orbit and rotational contributions (vide supra), which come from experimental values or empirical potential energy surfaces, are also essentially exact.
| Component | Calculation | ΔD0(CH) | ΔIE(CH) | ΔD0(CH+) |
|---|---|---|---|---|
| Spin-free | SCF/unc-aCVTZ | −15.6 | −30.9 | −22.8 |
| SCF/unc-aCVQZ | −15.6 | −30.7 | −22.8 | |
| CCSD/unc-aCVTZ | 1.7 | 4.5 | 3.0 | |
| CCSD/unc-aCVQZ | 1.6 | 4.4 | 2.8 | |
| (T)–D/unc-aCVTZ | 0.1 | 0.4 | −0.1 | |
| (T)–D/unc-aCVQZ | 0.1 | 0.5 | −0.1 | |
| Total | −13.9 (±0.2) | −25.9 (±0.2) | −20.1 (±0.1) | |
| Rot-spin–orbit | Exp. & Hill–Van Vleck | −29.8 (±0.0) | −0.2 (±0.0) | −42.2 (±0.0) |
| Component | Calculation | CH ΔD0 | CH ΔIE | CH+ ΔD0 |
|---|---|---|---|---|
| DBOC | SCF/aCVTZ | −29.2 | 1.3 | −29.1 |
| SCF/aCVQZ | −29.3 | 1.2 | −29.2 | |
| CCSD/aCVTZ | −7.8 | 3.6 | −12.8 | |
| CCSD/aCVQZ | −7.4 | 3.7 | −12.5 | |
| [fc] T–D/VDZ | −0.7 | −0.8 | −0.2 | |
| [fc] T–D/VTZ | −0.8 | −0.7 | −0.2 | |
| [fc] Q–T/VDZ | −0.1 | 0.1 | −0.2 | |
| [fc] Q–T/VTZ | −0.1 | 0.1 | −0.2 | |
| Total | −37.5 (±0.5) | 4.4 (±0.3) | −42.0 (±0.3) | |
| ZPE | Dunham/empirical | −1416.1 (±1.0) | 0.0 (±1.0) | −1416.1 (±1.0) |
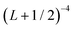 extrapolation formula. Estimated uncertainties are reported in parenthesis. All values are in cm−1
extrapolation formula. Estimated uncertainties are reported in parenthesis. All values are in cm−1
| Component | Calculation | ΔD0(CH) | ΔIE(CH) | ΔD0(CH+) |
|---|---|---|---|---|
| SCF | aCVTZ | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880.7 880.7 |
82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166.2 166.2 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 799.8 799.8 |
| aCVQZ | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 909.7 909.7 |
82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.9 192.9 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 816.4 816.4 |
|
| aCV5Z | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915.0 915.0 |
82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198.8 198.8 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 825.5 825.5 |
|
| aCV6Z | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915.8 915.8 |
82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 199.3 199.3 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 825.3 825.3 |
|
| aCV7Z | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 916.0 916.0 |
82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 199.2 199.2 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 825.3 825.3 |
|
| aCV8Z | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 916.1 916.1 |
82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 199.2 199.2 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 825.3 825.3 |
|
| aCV9Z | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 916.1 (±0.0) 916.1 (±0.0) |
82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 199.2 (±0.0) 199.2 (±0.0) |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 825.3 (±0.1) 825.3 (±0.1) |
|
| CCSD | aCVTZ | 8643.3 | 2945.8 | 8776.1 |
| aCVQZ | 8972.8 | 3186.9 | 9117.3 | |
| aCV5Z | 9069.5 | 3262.4 | 9217.8 | |
| aCV6Z | 9108.5 | 3292.7 | 9258.4 | |
| aCV7Z | 9128.4 | 3307.1 | 9279.3 | |
| aCV8Z | 9138.9 | 3314.8 | 9290.0 | |
| aCV9Z | 9145.1 | 3319.4 | 9296.6 | |
| aCV{T,Q}Z | 9163.0 | 3326.0 | 9314.2 | |
| aCV{Q,5}Z | 9148.0 | 3323.7 | 9299.5 | |
| aCV{5,6}Z | 9149.5 | 3324.7 | 9301.1 | |
| aCV{6,7}Z | 9154.1 | 3325.6 | 9306.3 | |
| aCV{7,8}Z | 9155.0 | 3326.7 | 9306.6 | |
| aCV{8,9}Z | 9156.1 (±2.2) | 3327.6 (±1.8) | 9308.3 (±3.3) | |
| (T)–D | aCVTZ | 305.1 | 253.5 | 257.5 |
| aCVQZ | 319.0 | 270.4 | 272.7 | |
| aCV5Z | 322.8 | 275.0 | 277.1 | |
| aCV6Z | 324.1 | 276.8 | 278.7 | |
| aCV7Z | 324.7 | 277.7 | 279.4 | |
| aCV8Z | 325.0 | 278.1 | 279.7 | |
| aCV9Z | 325.2 | 278.4 | 279.9 | |
| aCV{T,Q}Z | 327.0 | 280.1 | 281.4 | |
| aCV{Q,5}Z | 325.9 | 278.8 | 280.6 | |
| aCV{5,6}Z | 325.4 | 278.7 | 280.3 | |
| aCV{6,7}Z | 325.5 | 278.9 | 280.3 | |
| aCV{7,8}Z | 325.5 | 278.8 | 280.3 | |
| aCV{8,9}Z | 325.5 (±0.1) | 278.9 (±0.3) | 280.3 (±0.1) | |
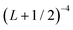 extrapolation formula. Estimated uncertainties are reported in parenthesis. All values are in cm−1
extrapolation formula. Estimated uncertainties are reported in parenthesis. All values are in cm−1
| Component | Calculation | ΔD0(CH) | ΔIE(CH) | ΔD0(CH+) |
|---|---|---|---|---|
| T–(T) | aCVTZ | 40.9 | 56.3 | 25.1 |
| aCVQZ | 41.1 | 51.7 | 25.2 | |
| aCV5Z | 40.6 | 49.2 | 24.6 | |
| aCV{T,Q}Z | 41.2 | 49.0 | 25.3 | |
| aCV{Q,5}Z | 40.2 (±2.0) | 47.1 (±3.8) | 24.0 (±2.6) | |
| (Q)Λ–T | aCVTZ | 10.2 | 0.3 | 18.6 |
| aCVQZ | 11.1 | 1.5 | 19.4 | |
| aCV5Z | 11.3 | 1.8 | 19.5 | |
| aCV{T,Q}Z | 11.6 | 2.3 | 19.8 | |
| aCV{Q,5}Z | 11.5 (±0.2) | 2.0 (±0.3) | 19.7 (±0.2) | |
| [fc] (P)Λ–(Q)Λ | VDZ | 1.9 | −4.5 | 8.2 |
| VTZ | 1.8 (±0.2) | −4.6 (±0.2) | 8.4 (±0.2) | |
From the above, it can be expected that the overwhelming majority of error in the calculations will come from the non-relativistic electronic energy, the contributions to which are listed in Tables 4 and 5. These certainly appear to be converged to better than 5 cm−1. Even the CCSD correlation energy contribution to the bond energy of CH – known to be the most difficult to converge with respect to single-particle basis set – differs by at most 1 cm−1 between extrapolations with the aug-cc-pCV6Z, -7Z, -8Z, and -9Z basis sets. The IE(CH) and D0(CH+) are slightly less well behaved, but all extrapolations beyond aug-cc-pCV5,6Z differ by less than 3 cm−1, indicating these values are quite close to the basis set limit. The post-CCSD(T) contributions are also apparently tightly converged, with the basis-set dependence of the T–(T) contribution being the only term with an uncertainty larger than 1 cm−1. Given the small magnitude of the (P)Λ–(Q)Λ valence-correlation increment, it is unlikely that correlation beyond CCSDTQ(P)Λ needs to be considered. In this context, it should be noted that the species considered here have at most seven electrons, so CCSDTQ(P)Λ is essentially equivalent to full configuration interaction in the valence space.
With all the composite contributions totalled, the extended HEAT bond dissociation energy of methylidyne is D0(CH) = 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 954 cm−1, the adiabatic ionization energy of methylidyne is IE(CH) = 85
954 cm−1, the adiabatic ionization energy of methylidyne is IE(CH) = 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 829 cm−1, and the bond dissociation energy of the corresponding cation, methyliumylidene, is D0(CH+) is 32
829 cm−1, and the bond dissociation energy of the corresponding cation, methyliumylidene, is D0(CH+) is 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 945 cm−1. We assign these values a rather conservative confidence interval of ±15 cm−1. The agreement of the CH cation bond energy with the value obtained from Cho and Le Roy97 (32
945 cm−1. We assign these values a rather conservative confidence interval of ±15 cm−1. The agreement of the CH cation bond energy with the value obtained from Cho and Le Roy97 (32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 945 cm−1vs. 32
945 cm−1vs. 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946 cm−1) is outstanding, although neglect of contributions such as second-order spin–orbit coupling suggests that asserting any fundamental meaning to agreement within 2 cm−1 is likely not well-founded.
946 cm−1) is outstanding, although neglect of contributions such as second-order spin–orbit coupling suggests that asserting any fundamental meaning to agreement within 2 cm−1 is likely not well-founded.
Benchmarking the benchmark and updating the ATcT thermochemical network
As mentioned above, the best ATcT value available prior to the commencement of this study and considered as the initial benchmark was D0(CH) = 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 971.0 ± 7.3 cm−1.70 In contrast, as detailed in the previous section, the extended HEAT protocol produced D0(CH) = 27
971.0 ± 7.3 cm−1.70 In contrast, as detailed in the previous section, the extended HEAT protocol produced D0(CH) = 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 954 ± 15 cm−1, or 17 cm−1 less.
954 ± 15 cm−1, or 17 cm−1 less.
The discrepancy surrounding D0(CH) was a bit of a surprise and prompted additional four-pronged action, carried out in parallel: (1) a careful reanalysis of the enhanced HEAT procedure and of all the components of the final theoretical value, (2) an entirely independent recalculation of D0(CH) using the FPD approach, (3) additional enhanced HEAT computations of the components of the positive ion thermodynamic cycle that can lead to D0(CH) via IE(CH) and D0(CH+), and (4) a careful analysis of the provenance of the ATcT value.
Additional scrutiny of all the components of the final theoretical value obtained by the enhanced HEAT procedure (which are detailed above) did not turn up any obvious suspects. Furthermore, the independently computed FPD bond dissociation energy of CH was essentially the same as the extended HEAT value (vide supra), differing from the cited ATcT value by 15 cm−1. At the same time, the extended HEAT value for D0(CH+) = 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 945 cm−1 was essentially identical to the ATcT value from the same version,70D0(CH+) = 32
945 cm−1 was essentially identical to the ATcT value from the same version,70D0(CH+) = 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946.6 ± 2.2 cm−1, with the determination by Hechtfischer et al.114 of D0(CH+) = 32
946.6 ± 2.2 cm−1, with the determination by Hechtfischer et al.114 of D0(CH+) = 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946.7 ± 2.2 cm−1 as the leading contributor, further confirmed by the even more accurate subsequent determination by Cho and Le Roy97 of D0(CH+) = 32
946.7 ± 2.2 cm−1 as the leading contributor, further confirmed by the even more accurate subsequent determination by Cho and Le Roy97 of D0(CH+) = 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946.7 ± 0.6 cm−1. (Note that the latter determination was included in the subsequent ATcT TN ver. 1.130,115 further tightening the uncertainty of the ATcT value to ±0.6 cm−1, without changing the value itself.)
946.7 ± 0.6 cm−1. (Note that the latter determination was included in the subsequent ATcT TN ver. 1.130,115 further tightening the uncertainty of the ATcT value to ±0.6 cm−1, without changing the value itself.)
In view of the fact that there are no direct high-accuracy experimental determinations of IE(CH) (the most recent direct determination being 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 817 ± 65 cm−1,116 preceded by 85
817 ± 65 cm−1,116 preceded by 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850 ± 100 cm−1
850 ± 100 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117), and that the ATcT value for IE(CH) is consequently heavily influenced by the difference between the ATcT values for D0(CH+), D0(CH), and IE(C) = 90
117), and that the ATcT value for IE(CH) is consequently heavily influenced by the difference between the ATcT values for D0(CH+), D0(CH), and IE(C) = 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820.36 ± 0.06 cm−1
820.36 ± 0.06 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 – obeying the thermodynamic identity IE(CH) + D0(CH+) = IE(C) + D0(CH) – it is not surprising that the ATcT value70 for IE(CH) = 85
70 – obeying the thermodynamic identity IE(CH) + D0(CH+) = IE(C) + D0(CH) – it is not surprising that the ATcT value70 for IE(CH) = 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 844.6 ± 7.6 cm−1 and the corresponding extended HEAT value differ by 16 cm−1, essentially the same as the difference observed for D0(CH) itself, and with a consistent sign.
844.6 ± 7.6 cm−1 and the corresponding extended HEAT value differ by 16 cm−1, essentially the same as the difference observed for D0(CH) itself, and with a consistent sign.
The above findings cast suspicion on the thermochemical determinations that are responsible for the provenance of the ATcT bond dissociation energy of CH (and indirectly for the adiabatic ionization energy of CH) and strongly advised their careful inspection. In this respect, the first important observation is that although the ATcT TN contains several experimental measurements of D0(CH),117–123 these are of rather limited accuracy, and thus the most influential contributors to the ATcT value (as obtained through the variance decomposition analysis87) are high-level theoretical calculations extracted from the literature29,36,39,49,51,54,55,58,71,82,124–134 and inserted in the ATcT TN. The second relevant observation is that the difference between the enhanced HEAT computation and the quoted ATcT value appears to suspiciously correspond both in sign and (approximately) in size to the systematic error that would be introduced in a theoretical treatment that would use Ae/2 as a spin–orbit correction for D0(CH).
A detailed scrutiny of the individual components of each of the composite calculations extant in the ATcT TN and related to CH was rendered somewhat challenging by the fact that in some of the original theoretical reports not all of the computational components were given explicitly, thus requiring that these be inferred by reverse engineering and/or consulting other studies from the same research group. Nevertheless, the analysis demonstrated that only a small minority of calculations29,58,133 employed the correct approach to the molecular spin–orbit correction for D0(CH) (or simply reported De(CH) rather than D0(CH)131,132). However, the majority of ATcT TN entries related to CH that are based on high-level calculations36,39,49,51,54,55,71,82,124–130 required a replacement of the original Ae/2 spin–orbit component in the reported calculated value. Admittedly, the size of this post-factum correction is in most cases significantly smaller than the individual uncertainties of these calculations, the only exception being the leading FPA calculation124 (reporting 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 982+11−28 cm−1), in which the systematic error and declared uncertainty are of comparable size. However, the use of Ae/2 does represent a recurring systematic error, which will have a strong tendency to influence the resulting ATcT value through a cumulative effect.
982+11−28 cm−1), in which the systematic error and declared uncertainty are of comparable size. However, the use of Ae/2 does represent a recurring systematic error, which will have a strong tendency to influence the resulting ATcT value through a cumulative effect.
Indeed, after modifying the most recent developmental version of the TN, ATcT TN ver. 1.130,115 to create an updated version 1.130a of the ATcT TN, the resulting ATcT value for the bond dissociation energy of CH became D0(CH) = 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 961.0 ± 8.0 cm−1, a shift downwards by about 10 cm−1. Noting that this shift is still contained within the combined uncertainties of the original ATcT benchmark (27
961.0 ± 8.0 cm−1, a shift downwards by about 10 cm−1. Noting that this shift is still contained within the combined uncertainties of the original ATcT benchmark (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 971.0 ± 7.3 cm−1
971.0 ± 7.3 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70) and the amended ATcT value, the correction of the systematic error in previous computations reduces the difference between the extended HEAT value and the amended ATcT value to 7 cm−1, which is well within the desired target accuracy of the extended HEAT result.
70) and the amended ATcT value, the correction of the systematic error in previous computations reduces the difference between the extended HEAT value and the amended ATcT value to 7 cm−1, which is well within the desired target accuracy of the extended HEAT result.
Generally speaking, developing and benchmarking a new high-accuracy computational protocol using ATcT thermochemical quantities is essentially a two-way road.48 Namely, the ATcT values are at first used to obtain an estimate of the expected accuracy of the new protocol. Under ordinary circumstances, once the expected accuracy of the new theoretical approach is understood, the computational results obtained using the new protocol can be used to expand and significantly enrich the ATcT TN, further improving both the ATcT results and the original computational values, primarily because the ATcT TN is capable of incorporating thermochemically relevant determinations irrespective of whether they were generated by actual (experimental) or virtual (computational) measurements – as long as the latter can be qualified by realistic uncertainty intervals. Indeed, after generating a new version of ATcT TN (ver. 1.140) by adding the current computational results for D0(CH) (from both the extended HEAT and FPD approaches), D0(CH+), and IE(CH), the final ATcT values are: D0(CH) = 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 957.3 ± 6.0 cm−1 (a further reduction by 3.7 cm−1, accompanied by an improvement in the uncertainty), D0(CH+) = 32
957.3 ± 6.0 cm−1 (a further reduction by 3.7 cm−1, accompanied by an improvement in the uncertainty), D0(CH+) = 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946.7 ± 0.6 cm−1, and IE(CH) = 85
946.7 ± 0.6 cm−1, and IE(CH) = 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831.0 ± 6.0 cm−1. These correspond to the following standard enthalpies of formation at 0 K (298.15 K): ΔfH° (CH) = 592.979 (596.314) ± 0.081 kJ mol−1, ΔfH° (CH+) = 1619.746 (1623.090) ± 0.041 kJ mol−1. These, as well as related enthalpies of formation at 0 K and 298.15 K obtained from ATcT TN ver. 1.140 relevant to the broader CHn, n = 4–0, group of chemical species, are given in Table 6, while the corresponding adiabatic ionization energies, adiabatic electron affinities, and relevant 0 K bond dissociation energies are given in Table 7.
831.0 ± 6.0 cm−1. These correspond to the following standard enthalpies of formation at 0 K (298.15 K): ΔfH° (CH) = 592.979 (596.314) ± 0.081 kJ mol−1, ΔfH° (CH+) = 1619.746 (1623.090) ± 0.041 kJ mol−1. These, as well as related enthalpies of formation at 0 K and 298.15 K obtained from ATcT TN ver. 1.140 relevant to the broader CHn, n = 4–0, group of chemical species, are given in Table 6, while the corresponding adiabatic ionization energies, adiabatic electron affinities, and relevant 0 K bond dissociation energies are given in Table 7.
| Quantity | 0 K | 298.15 K | Uncert. |
|---|---|---|---|
| ΔfH° (CH4) | −66.550 | −74.519 | ±0.044 |
| ΔfH° (CH4+) | 1150.679 | 1144.296 | ±0.057 |
| ΔfH° (CH3) | 149.872 | 146.472 | ±0.050 |
| ΔfH° (CH3+) | 1099.346 | 1095.402 | ±0.045 |
| ΔfH° (CH3−) | 141.15 | 137.71 | ±0.24 |
| ΔfH° (3CH2) | 391.063 | 391.609 | ±0.094 |
| ΔfH° (1CH2) | 428.72 | 429.13 | ±0.11 |
| ΔfH° (CH2+) | 1393.20 | 1394.06 | ±0.10 |
| ΔfH° (CH2−) | 328.17 | 328.60 | ±0.18 |
| ΔfH° (2CH) | 592.979 | 596.314 | ±0.081 |
| ΔfH° (4CH) | 664.70 | 668.04 | ±0.52 |
| ΔfH° (CH+) | 1619.746 | 1623.090 | ±0.041 |
| ΔfH° (CH−) | 475.77 | 479.09 | ±0.21 |
| ΔfH° (C) | 711.389 | 716.874 | ±0.040 |
| ΔfH° (C+) | 1797.842 | 1803.440 | ±0.040 |
| ΔfH° (C−) | 589.613 | 594.759 | ±0.041 |
| ΔfH° (H) | 216.034 | 217.998 | ±0.000 |
| ΔfH° (H+) | 1528.084 | 1530.047 | ±0.000 |
| ΔfH° (H−) | 143.264 | 145.228 | ±0.000 |
| Quantity | Value | Uncert. |
|---|---|---|
| IE(CH4) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1752.4 1752.4 |
±3.0 |
| IE(CH3) | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 369.7 369.7 |
±2.0 |
| IE(3CH2) | 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 771.9 771.9 |
±3.0 |
| IE(1CH2) | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 623.8 623.8 |
±5.3 |
| IE(2CH) | 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831.0 831.0 |
±6.0 |
| IE(4CH) | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 835 835 |
±43 |
| IE(C) | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820.38 820.38 |
±0.06 |
| EA(CH3) | 729 | ±20 |
| EA(3CH2) | 5257 | ±14 |
| EA(1CH2) | 8405 | ±15 |
| EA(2CH) | 9798 | ±18 |
| EA(4CH) | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 794 794 |
±46 |
| EA(C) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 179.68 179.68 |
±0.30 |
| D 0(CH4) | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150.6 150.6 |
±2.2 |
| D 0(CH4+) | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 767.8 767.8 |
±3.2 |
| D 0(CH3 to 3CH2 + H) | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 221.0 221.0 |
±7.9 |
| D 0(CH3 to 1CH2 + H) | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 369.1 369.1 |
±8.6 |
| D 0(CH3+) | 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 623.1 623.1 |
±8.3 |
| D 0(CH3− to 3CH2 + H−) | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 867 867 |
±21 |
| D 0(CH3− to CH2− + H) | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 692 692 |
±24 |
| D 0(CH3− to 1CH2 + H−) | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015 015 |
±22 |
| D 0(3CH2 to 2CH + H) | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 937.9 937.9 |
±8.5 |
| D 0(3CH2 to 4CH + H) | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 934 934 |
±44 |
| D 0(1CH2 to 2CH + H) | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 789.8 789.8 |
±9.1 |
| D 0(1CH2 to 4CH + H) | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 786 786 |
±44 |
| D 0(CH2+) | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 997.0 997.0 |
±8.4 |
| D 0(CH2− to 3CH− + H) | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 397 397 |
±22 |
| D 0(CH2− to 2CH + H−) | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 112 112 |
±16 |
| D 0(2CH) | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 957.3 957.3 |
±6.0 |
| D 0(4CH) | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 962 962 |
±43 |
| D 0(CH+) | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946.7 946.7 |
±0.6 |
| D 0(CH−) | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 576 576 |
±18 |
Rarely, the benchmarking procedure itself may already provide some useful feedback to ATcT even before the just described expansion of the ATcT TN with new computational results, as was demonstrated in the present study. Namely, if one of the ATcT benchmark values differs from the corresponding computed values by more than the expected amount and thus effectively represents an outlier, baring the possibility that the particular chemical species in question happens to be a pathological case within the framework of the benchmarked procedure, such an occurrence may well imply that one or more determinations governing the provenance of the corresponding ATcT values may be in error. Earlier, there were at least three cases where highly accurate FPD-type computations helped demonstrate that the accepted thermochemical value, based on apparently accurate experimental data, is in error (spectroscopic D0(OH) and the resulting D0(H–OH), with new experimental data using photoionization mass spectrometry augmented with high-level theory;64,65 the enthalpy of formation of gas-phase hydrazine135 and the enthalpy of formation of gas-phase oxalic acid,136 both of which were originally based on experimental combustion calorimetry of the condensed phase combined with the corresponding vaporization enthalpy). However, the present study is the first case where we were able to demonstrate that a substantial number of ostensibly highly accurate theoretical results had, in common, a hidden systematic error.
Conclusions
This work establishes new computational benchmarks for the bond dissociation energy of methylidyne. Extended versions of the HEAT and FPD composite model chemistries, which feature large CCSD(T) calculations with up to 9-ζ basis sets predict the bond dissociation energy of methylidyne, D0(CH), to be 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 954 ± 15 cm−1 and 27
954 ± 15 cm−1 and 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 956 ± 15 cm−1, respectively. An important aspect of these estimates is the correct treatment of the coupling of spin, electronic, and rotational angular momenta in the ground 2Π state of CH. Additionally, the CH adiabatic ionization energy, IE(CH), is determined via extended HEAT to be 85
956 ± 15 cm−1, respectively. An important aspect of these estimates is the correct treatment of the coupling of spin, electronic, and rotational angular momenta in the ground 2Π state of CH. Additionally, the CH adiabatic ionization energy, IE(CH), is determined via extended HEAT to be 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 829 ± 15 cm−1, and the bond dissociation energy of methyliumylidene, D0(CH+), as 32
829 ± 15 cm−1, and the bond dissociation energy of methyliumylidene, D0(CH+), as 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946 ± 15 cm−1. In terms of direct experimental determinations, only D0(CH+) has a sufficiently accurate empirical value97 (32
946 ± 15 cm−1. In terms of direct experimental determinations, only D0(CH+) has a sufficiently accurate empirical value97 (32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946.7 ± 0.6 cm−1), and the extended HEAT calculations reproduce this value to within 2 cm−1. For the bond dissociation energy and the adiabatic ionization energy of methylidyne, the theoretical values reported here may be taken as the newest and most accurate computational benchmarks.
946.7 ± 0.6 cm−1), and the extended HEAT calculations reproduce this value to within 2 cm−1. For the bond dissociation energy and the adiabatic ionization energy of methylidyne, the theoretical values reported here may be taken as the newest and most accurate computational benchmarks.
The ATcT thermochemical network has been updated by adjusting the description of coupling of the spin to electronic and rotational angular momenta and vibrational zero-point energies, as appropriate, in previously reported high-level theoretical values. The effect of these changes is to move the ATcT D0(CH) that was based on unadjusted calculated values from the literature by 10 cm−1. The ATcT TN was subsequently expanded by incorporating the present FPD and extended HEAT computational results, providing the final values D0(CH) = 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 957.3 ± 6.0 cm−1, D0(CH+) = 32
957.3 ± 6.0 cm−1, D0(CH+) = 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946.7 ± 0.6 cm−1, and IE(CH) = 85
946.7 ± 0.6 cm−1, and IE(CH) = 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831.0 ± 6.0 cm−1. It is hoped that this work will inspire future experimental determinations of D0(CH) and IE(CH), as the ATcT paradigm works best when both experimental and theoretical data are available.
831.0 ± 6.0 cm−1. It is hoped that this work will inspire future experimental determinations of D0(CH) and IE(CH), as the ATcT paradigm works best when both experimental and theoretical data are available.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The calculations in this work would not have been possible without the general coupled cluster code, MRCC, of Kallay,98,99 and the extremely efficient NCC module of CFOUR written by Devin Matthews (SMU). J. H. T. and J. F. S. were supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division, under Contract No. DE-SC0018164, and by the NSF under Award No. CHE-1664325. The work at Argonne National Laboratory was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division, under Contract No. DE-AC02-06CH11357, through the Gas-Phase Chemical Physics Program (BR) and the Computational Chemical Sciences Program (DHB). Most of the authors are members of ATcT Task Force One.Notes and references
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS.
- J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041–7050 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- Y. J. Bomble, J. F. Stanton, M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 054101 CrossRef.
- M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 214105 CrossRef.
- J. Noga, S. Kedžuch, J. Šimunek and S. Ten-no, J. Chem. Phys., 2008, 128, 174103 CrossRef PubMed.
- J. Noga, S. Kedžuch, J. Šimunek and S. Ten-no, J. Chem. Phys., 2009, 130, 029901 CrossRef.
- A. Köhn, J. Chem. Phys., 2009, 130, 131101 CrossRef.
- W. L. McMillan, Phys. Rev., 1965, 138, A442–A451 CrossRef.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- G. H. Booth, A. J. W. Thom and A. Alavi, J. Chem. Phys., 2009, 131, 054106 CrossRef PubMed.
- F. R. Petruzielo, A. A. Holmes, H. J. Changlani, M. P. Nightingale and C. J. Umrigar, Phys. Rev. Lett., 2012, 109, 230201 CrossRef CAS.
- N. M. Tubman, J. Lee, T. Y. Takeshita, M. Head-Gordon and K. B. Whaley, J. Chem. Phys., 2016, 145, 044112 CrossRef.
- S. R. White, Phys. Rev. Lett., 1992, 69, 2863–2866 CrossRef.
- U. Schollwöck, Rev. Mod. Phys., 2005, 77, 259–315 CrossRef CAS.
- J. J. Eriksen, F. Lipparini and J. Gauss, J. Phys. Chem. Lett., 2017, 8, 4633–4639 CrossRef CAS.
- E. Xu, M. Uejima and S. L. Ten-no, Phys. Rev. Lett., 2018, 121, 113001 CrossRef.
- J. E. Deustua, I. Magoulas, J. Shen and P. Piecuch, J. Chem. Phys., 2018, 149, 151101 CrossRef PubMed.
- J. J. Eriksen, T. A. Anderson, J. E. Deustua, K. Ghanem, D. Hait, M. R. Hoffmann, S. Lee, D. S. Levine, I. Magoulas, J. Shen, N. M. Tubman, K. B. Whaley, E. Xu, Y. Yao, N. Zhang, A. Alavi, G. K.-L. Chan, M. Head-Gordon, W. Liu, P. Piecuch, S. Sharma, S. L. Ten-no, C. J. Umrigar and J. Gauss, J. Phys. Chem. Lett., 2020, 11, 8922–8929 CrossRef CAS PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS.
- A. K. Wilson, T. van Mourik and T. H. Dunning, THEOCHEM, 1996, 388, 339–349 CrossRef CAS.
- T. V. Mourik, A. K. Wilson and T. H. Dunning, Mol. Phys., 1999, 96, 529–547 CrossRef.
- K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- D. H. Bross and K. A. Peterson, Theor. Chem. Acc., 2013, 133, 1434 Search PubMed.
- L. McCaslin and J. Stanton, Mol. Phys., 2013, 111, 1492–1496 CrossRef CAS.
- D. Feller, K. A. Peterson and B. Ruscic, Theor. Chem. Acc., 2014, 133, 1407 Search PubMed.
- J. H. Thorpe, J. L. Kilburn, D. Feller, P. B. Changala, D. H. Bross, B. Ruscic and J. F. Stanton, J. Chem. Phys., 2021, 155, 184109 CrossRef CAS PubMed.
- H. Sellers and P. Pulay, Chem. Phys. Lett., 1984, 103, 463–465 CrossRef CAS.
- R. J. Bartlett and J. F. Stanton, Applications of Post-Hartree–Fock Methods: A Tutorial, John Wiley & Sons, Ltd, 1994, pp. 65–169 Search PubMed.
- G. Tarczay, A. G. Császár, W. Klopper and H. M. Quiney, Mol. Phys., 2001, 99, 1769–1794 CrossRef CAS.
- W. Klopper, F. R. Manby, S. Ten-No and E. F. Valeev, Int. Rev. Phys. Chem., 2006, 25, 427–468 Search PubMed.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- A. Karton, B. Ruscic and J. M. L. Martin, THEOCHEM, 2007, 811, 345–353 CrossRef CAS.
- B. Galabov, V. Nikolova, J. J. Wilke, H. F. Schaefer and W. D. Allen, J. Am. Chem. Soc., 2008, 130, 9887–9896 CrossRef CAS.
- D. A. Dixon, D. Feller and K. A. Peterson, in Annual Reports in Computational Chemistry, ed. R. A. Wheeler, Elsevier, 2012, ch. 1, vol. 8, pp. 1–28 Search PubMed.
- D. Feller, J. Chem. Phys., 2016, 144, 014105 CrossRef PubMed.
- A. Karton, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 292–310 CAS.
- J. A. Pople, M. Head-Gordon, D. J. Fox, K. Raghavachari and L. A. Curtiss, J. Chem. Phys., 1989, 90, 5622–5629 CrossRef CAS.
- L. A. Curtiss, C. Jones, G. W. Trucks, K. Raghavachari and J. A. Pople, J. Chem. Phys., 1990, 93, 2537–2545 CrossRef CAS.
- L. A. Curtiss, K. Raghavachari, G. W. Trucks and J. A. Pople, J. Chem. Phys., 1991, 94, 7221–7230 CrossRef CAS.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern, V. Rassolov and J. A. Pople, J. Chem. Phys., 1998, 109, 7764–7776 CrossRef CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108 CrossRef.
- J. A. Pople, Rev. Mod. Phys., 1999, 71, 1267–1274 CrossRef CAS.
- B. Ruscic, Int. J. Quantum Chem., 2014, 114, 1097–1101 CrossRef CAS.
- B. Ruscic and D. H. Bross, Comput.-Aided Chem. Eng., 2019, 45, 3–114 CAS.
- A. Tajti, P. G. Szalay, A. G. Császár, M. Kállay, J. Gauss, E. F. Valeev, B. A. Flowers, J. Vázquez and J. F. Stanton, J. Chem. Phys., 2004, 121, 11599–11613 CrossRef CAS PubMed.
- Y. J. Bomble, J. Vázquez, M. Kállay, C. Michauk, P. G. Szalay, A. G. Császár, J. Gauss and J. F. Stanton, J. Chem. Phys., 2006, 125, 064108 CrossRef PubMed.
- M. E. Harding, J. Vázquez, B. Ruscic, A. K. Wilson, J. Gauss and J. F. Stanton, J. Chem. Phys., 2008, 128, 114111 CrossRef PubMed.
- J. H. Thorpe, C. A. Lopez, T. L. Nguyen, J. H. Baraban, D. H. Bross, B. Ruscic and J. F. Stanton, J. Chem. Phys., 2019, 150, 224102 CrossRef.
- J. M. L. Martin and G. de Oliveira, J. Chem. Phys., 1999, 111, 1843–1856 CrossRef CAS.
- A. D. Boese, M. Oren, O. Atasoylu, J. M. L. Martin, M. Kállay and J. Gauss, J. Chem. Phys., 2004, 120, 4129–4141 CrossRef CAS.
- A. Karton, E. Rabinovich, J. M. L. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 144108 CrossRef.
- A. Karton and J. M. L. Martin, J. Chem. Phys., 2012, 136, 124114 CrossRef.
- N. Sylvetsky, K. A. Peterson, A. Karton and J. M. L. Martin, J. Chem. Phys., 2016, 144, 214101 CrossRef.
- S. J. Klippenstein, L. B. Harding and B. Ruscic, J. Phys. Chem. A, 2017, 121, 6580–6602 CrossRef CAS PubMed.
- A. G. Császár, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 1998, 108, 9751–9764 CrossRef.
- J. P. Kenny, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 2003, 118, 7353–7365 CrossRef CAS.
- A. L. L. East and W. D. Allen, J. Chem. Phys., 1993, 99, 4638–4650 CrossRef CAS.
- M. S. Schuurman, S. R. Muir, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 2004, 120, 11586–11599 CrossRef CAS PubMed.
- H. M. Jaeger, H. F. Schaefer, J. Demaison, A. G. Császár and W. D. Allen, J. Chem. Theory Comput., 2010, 6, 3066–3078 CrossRef CAS.
- B. Ruscic, D. Feller, D. A. Dixon, K. A. Peterson, L. B. Harding, R. L. Asher and A. F. Wagner, J. Phys. Chem. A, 2000, 105, 1–4 CrossRef.
- B. Ruscic, A. F. Wagner, L. B. Harding, R. L. Asher, D. Feller, D. A. Dixon, K. A. Peterson, Y. Song, X. Qian, C.-Y. Ng, J. Liu, W. Chen and D. W. Schwenke, J. Phys. Chem. A, 2002, 106, 2727–2747 CrossRef CAS.
- K. A. Peterson, D. Feller and D. A. Dixon, Theor. Chem. Acc., 2012, 131, 1079 Search PubMed.
- D. Feller, K. A. Peterson and D. A. Dixon, Mol. Phys., 2012, 110, 2381–2399 CrossRef CAS.
- B. Ruscic, R. E. Pinzon, M. L. Morton, G. von Laszewski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 108, 9979–9997 CrossRef CAS.
- B. Ruscic, R. E. Pinzon, G. von Laszewski, D. Kodeboyina, A. Burcat, D. Leahy, D. Montoya and A. F. Wagner, J. Phys. Conf. Ser., 2005, 16, 561–570 CrossRef CAS.
- B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) Values Based on Ver. 1.122r of the Thermochemical Network, 2021, available at https://ATcT.anl.gov; accessed: 2022-08-10.
- A. Karton, S. Daon and J. M. L. Martin, Chem. Phys. Lett., 2011, 510, 165–178 CrossRef CAS.
- A. Karton, Chem. Phys. Lett., 2019, 737, 136810 CrossRef CAS.
- W. Klopper, B. Ruscic, D. P. Tew, F. A. Bischoff and S. Wolfsegger, Chem. Phys., 2009, 356, 14–24 CrossRef CAS.
- W. Klopper, R. A. Bachorz, C. Hättig and D. P. Tew, Theor. Chem. Acc., 2010, 126, 289–304 Search PubMed.
- B. Ruscic and D. H. Bross, Mol. Phys., 2021, 119, e1969046 CrossRef.
- B. Ruscic, J. Phys. Chem. A, 2015, 119, 7810–7837 CrossRef CAS.
- K. Haris and A. Kramida, Astrophys. J., Suppl. Ser., 2017, 233, 16 CrossRef.
- S. Yamamoto and S. Saito, Astrophys. J., 1991, 370, L103–L105 CrossRef CAS.
- A. Beckmann, K. D. Böklen, G. Bremer and D. Elke, Z. Phys. A, 1975, 272, 143–145 CrossRef CAS.
- J. M. Martin, Chem. Phys. Lett., 1996, 259, 669–678 CrossRef CAS.
- J. M. L. Martin, AIP Conf. Proc., 2018, 2040, 020008 CrossRef.
- D. Feller, K. A. Peterson and D. A. Dixon, J. Chem. Phys., 2008, 129, 204105 CrossRef.
- D. Feller, K. A. Peterson and J. Grant Hill, J. Chem. Phys., 2011, 135, 044102 CrossRef PubMed.
- D. Feller, J. Chem. Phys., 2013, 138, 074103 CrossRef.
- K. G. Dyall, J. Chem. Phys., 1994, 100, 2118–2127 CrossRef CAS.
- L. Cheng and J. Gauss, J. Chem. Phys., 2011, 134, 244112 CrossRef PubMed.
- B. Ruscic, D. Feller and K. A. Peterson, Theor. Chem. Acc., 2014, 133, 1415 Search PubMed.
- Y.-C. Chang, B. Xiong, D. H. Bross, B. Ruscic and C. Y. Ng, Phys. Chem. Chem. Phys., 2017, 19, 9592–9605 RSC.
- G. Herzberg, Molecular Spectra and Molecular Structure. I. Spectra of Diatomic Molecules, Van Nostrand, Princeton, 2nd edn, 1950 Search PubMed.
- E. Hill and J. H. Van Vleck, Phys. Rev., 1928, 32, 250–272 CrossRef CAS.
- M. Zachwieja, J. Mol. Spectrosc., 1995, 170, 285–309 CrossRef CAS.
- P. F. Bernath, C. R. Brazier, T. Olsen, R. Hailey, W. T. M. L. Fernando, C. Woods and J. L. Hardwick, J. Mol. Spectrosc., 1991, 147, 16–26 CrossRef CAS.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules, Van Nostrand Reinhold, New York, 1979 Search PubMed.
- D. Feller, K. A. Peterson, W. A. de Jong and D. A. Dixon, J. Chem. Phys., 2003, 118, 3510–3522 CrossRef CAS.
- J. L. Dunham, Phys. Rev., 1932, 41, 721–731 CrossRef CAS.
- K. K. Irikura, J. Phys. Chem. Ref. Data, 2007, 36, 389–397 CrossRef CAS.
- Y.-S. Cho and R. J. L. Roy, J. Chem. Phys., 2016, 144, 024311 CrossRef.
- M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy, B. Hégely, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and A. Ganyecz, J. Chem. Phys., 2020, 152, 074107 CrossRef PubMed.
- Mrcc, a quantum chemical program suite written by M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy, B. Hégely, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei, and Á. Ganyecz. See http://www.mrcc.hu.
- D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108 CrossRef CAS PubMed.
- J. F. Stanton, J. Gauss, L. Cheng, M. E. Harding, D. A. Matthews and P. G. Szalay, CFOUR, Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package, With contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, S. Blaschke, Y. J. Bomble, S. Burger, O. Christiansen, D. Datta, F. Engel, R. Faber, J. Greiner, M. Heckert, O. Heun, M. Hilgenberg, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, T. Kirsch, K. Klein, G. M. Kopper, W. J. Lauderdale, F. Lipparini, T. Metzroth, L. A. Mück, D. P. O'Neill, T. Nottoli, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the current version, see https://www.cfour.de.
- P. B. Armentrout and K. A. Peterson, Inorg. Chem., 2020, 59, 3118–3131 CrossRef CAS.
- D. Feller and K. A. Peterson, J. Chem. Phys., 1999, 110, 8384–8396 CrossRef CAS.
- D. Feller and N. C. Craig, J. Phys. Chem. A, 2009, 113, 1601–1607 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and M. Welborn, MOLPRO, a package of ab initio programs, see https://www.molpro.net Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS.
- P. J. Knowles, C. Hampel and H. Werner, J. Chem. Phys., 1993, 99, 5219–5227 CrossRef CAS.
- P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 2000, 112, 3106–3107 CrossRef CAS.
- M. J. Deegan and P. J. Knowles, Chem. Phys. Lett., 1994, 227, 321–326 CrossRef CAS.
- W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48–53 CrossRef CAS.
- M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155 CAS.
- G. Jansen and B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 6016–6017 CrossRef PubMed.
- U. Hechtfischer, C. J. Williams, M. Lange, J. Linkemann, D. Schwalm, R. Wester, A. Wolf and D. Zajfman, J. Chem. Phys., 2002, 117, 8754–8777 CrossRef CAS.
- N. Genossar, P. B. Changala, B. Gans, J.-C. Loison, S. Hartweg, M.-A. Martin-Drumel, G. A. Garcia, J. F. Stanton, B. Ruscic and J. H. Baraban, J. Am. Chem. Soc., 2022 DOI:10.1021/jacs.2c07740.
- B. Gans, F. Holzmeier, J. Krüger, C. Falvo, A. Röder, A. Lopes, G. A. Garcia, C. Fittschen, J.-C. Loison and C. Alcaraz, J. Chem. Phys., 2016, 144, 204307 CrossRef CAS PubMed.
- G. Herzberg and J. W. C. Johns, Astrophys. J., 1969, 158, 399–418 CrossRef CAS.
- R. G. Brewer and F. L. Kester, J. Chem. Phys., 1964, 40, 812–817 CrossRef CAS.
- M. J. Linevsky, J. Chem. Phys., 1967, 47, 3485–3490 CrossRef.
- N. H. Brooks and W. H. Smith, Astrophys. J., 1974, 194, 513–517 CrossRef CAS.
- J. Brzozowski, P. Bunker, N. Elander and P. Erman, Astrophys. J., 1976, 207, 414–424 CrossRef CAS.
- M. Danielsson, P. Erman, A. Hishikawa, M. Larsson, E. Rachlew-Kallne and G. Sundstrom, J. Chem. Phys., 1993, 98, 9405–9409 CrossRef CAS.
- R. A. Jesinger and R. R. Squires, Int. J. Mass Spectrom., 1999, 187, 745–757 CrossRef.
- A. G. Császár, P. G. Szalay and M. L. Leininger, Mol. Phys., 2002, 100, 3879–3883 CrossRef.
- A. G. Császár, M. L. Leininger and V. Szalay, J. Chem. Phys., 2003, 118, 10631–10642 CrossRef.
- A. Karton, P. R. Taylor and J. M. L. Martin, J. Chem. Phys., 2007, 127, 064104 CrossRef PubMed.
- D. Feller and D. A. Dixon, J. Phys. Chem. A, 2000, 104, 3048–3056 CAS.
- A. Karton, A. Tarnopolsky, J.-F. Lamère, G. C. Schatz and J. M. L. Martin, J. Phys. Chem. A, 2008, 112, 12868–12886 CrossRef CAS PubMed.
- A. Karton and J. M. L. Martin, J. Phys. Chem. A, 2007, 111, 5936–5944 CrossRef CAS PubMed.
- D. A. Dixon and D. Feller, J. Phys. Chem. A, 1998, 102, 8209–8216 CrossRef CAS.
- A. Kalemos, A. Mavridis and A. Metropoulos, J. Chem. Phys., 1999, 111, 9536–9548 CrossRef CAS.
- K. A. Peterson, R. A. Kendall and T. H. Dunning Jr, J. Chem. Phys., 1993, 99, 1930–1944 CrossRef CAS.
- J. Aguilera-Iparraguirre, A. D. Boese, W. Klopper and B. Ruscic, Chem. Phys., 2008, 346, 56–68 CrossRef CAS.
- N. L. Doltsinis and P. J. Knowles, J. Chem. Soc., Faraday Trans., 1997, 93, 2025–2027 RSC.
- D. Feller, D. H. Bross and B. Ruscic, J. Phys. Chem. A, 2017, 121, 6187–6198 CrossRef CAS PubMed.
- D. Feller, D. H. Bross and B. Ruscic, J. Phys. Chem. A, 2019, 123, 3481–3496 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the aug-cc-pCV9Z basis sets. See DOI: https://doi.org/10.1039/d2cp03964h |
| This journal is © the Owner Societies 2023 |
