Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Universal ion-transport descriptors and classes of inorganic solid-state electrolytes†
Cibrán
López
abc,
Agustí
Emperador
a,
Edgardo
Saucedo
bd,
Riccardo
Rurali
c and
Claudio
Cazorla
 *ab
*ab
aDepartament de Física, Universitat Politècnica de Catalunya, 08034 Barcelona, Spain. E-mail: claudio.cazorla@upc.edu
bBarcelona Research Center in Multiscale Science and Egineering, Universitat Politècnica de Catalunya, 08019 Barcelona, Spain
cInstitut de Ciència de Materials de Barcelona, ICMAB-CSIC, Campus UAB, 08193 Bellaterra, Spain
dDepartment of Electronic Engineering, Universitat Politècnica de Catalunya, 08034 Barcelona, Spain
First published on 9th February 2023
Abstract
Solid-state electrolytes (SSEs) with high ion conductivity are pivotal for the development and large-scale adoption of green-energy conversion and storage technologies such as fuel cells, electrocatalysts and solid-state batteries. Yet, SSEs are extremely complex materials for which general rational design principles remain indeterminate. Here, we combine first-principles materials modelling, computational power and modern data analysis techniques to advance towards the solution of such a fundamental and technologically pressing problem. Our data-driven survey reveals that the correlations between ion diffusivity and other materials descriptors in general are monotonic, although not necessarily linear, and largest when the latter are of vibrational nature and explicitly incorporate anharmonic effects. Surprisingly, principal component and k-means clustering analyses show that elastic and vibrational descriptors, rather than the usual ones related to chemical composition and ion mobility, are best suited for reducing the high complexity of SSEs and classifying them into universal classes. Our findings highlight the need for considering databases that incorporate temperature effects to improve our understanding of SSEs and point towards a generalized approach to the design of energy materials.
New conceptsWe present a data-driven analysis of solid-state electrolytes (SSEs) that covers aspects generally unaddressed by previous computational studies and the existing density functional theory (DFT) materials databases. A comprehensive first-principles database was created for prototypical families of inorganic SSEs containing both sets of zero-temperature DFT and finite-temperature ab initio molecular dynamics (AIMD) results. The generated SSE DFT-AIMD database has been made publicly available at the url https://superionic.upc.edu/. By applying modern data analysis (e.g., principal component and k-means clustering analyses) and machine learning techniques on the created SSE DFT-AIMD database, it is demonstrated that the diffusion of ions in SSEs strongly and monotonically correlates with vibrational descriptors that explicitly incorporate anharmonic effects (i.e., those obtained from AIMD simulations). Also, the bulk of the variance in SSEs is encoded in the elastic and vibrational properties of the materials, not in their ion mobility or in their chemical composition (thus, SSEs that rigorously can be considered as overall highly similar in practice may exhibit very different ion diffusion and chemical features). Our work highlights the necessity to consider finite-temperature effects in a high-throughput fashion to better understand SSEs and improve the predictions of machine learning models in them. In addition, it provides new theoretical guidelines for analyzing materials that in analogy to SSEs are complex, highly anharmonic and technologically relevant (e.g., thermoelectrics and superconductors). |
Social networks use modern data analysis techniques to improve their customer experience and increase advertising revenues.1 Each mouse click and finger action on the touchscreen reveal information on the user preferences that can be employed to classify individuals into similarity groups and thus better select the contents they are exposed to. Materials, in analogy to humans, conform to highly diverse and complex collectives and as such advanced data analysis techniques are being increasingly applied on them to improve their design and recommend possible uses.2,3 A necessary condition for the meaningful development and application of data-driven materials design strategies is the existence of comprehensive and reliable databases.
Solid-state electrolytes (SSEs) are a class of energy materials in which specific groups of ions may start to diffuse throughout the crystalline matrix driven by thermal excitations.4 SSEs are the pillars of green-energy conversion and storage technologies like fuel cells, electrocatalysts and solid-state batteries; hence tuning of their ion-transport properties turns out to be critical in the fields of energy and sustainability. SSEs, however, are highly complex materials that present disparate compositions, structures, thermal behaviors and ion mobilities; thus, it is difficult to ascribe them to general and rational design principles. These difficulties have motivated researchers to seek for easy to measure (or calculate) quantities that may serve as good descriptors of the ion conductivity; examples of such descriptors include structural parameters, defect formation energies, atomic polarizabilities and lattice dynamics.5–9 In recent years, pinpointing the role of phonon dynamics in ion transport has attracted special and increasing attention. Actually, for some specific SSEs, it has been demonstrated that lattice anharmonicity is one of the most influential factors affecting their ion mobility.9–14
Quantum mechanics-based density functional theory (DFT)15 has proven to be tremendously successful in the field of computational materials science and currently several databases of automated DFT calculations are being widely employed for materials design applications.16–19 Nevertheless, despite their great success, the existing DFT databases might not be entirely adequate for progressing in the design and understanding of SSEs because they mostly contain information generated at zero temperature (e.g., structural parameters and formation energies) and thus completely disregard anharmonicity and T-induced effects.20 In addition, modern high-throughput and machine learning studies relying on such DFT databases mainly have targeted Li- and Na-based SSE families due to their predominance in electrochemical storage applications.8,21,22 To holistically better understand the phenomena of ion transport, however, it might be necessary to analyse in equal measure other classes of SSEs, like those involving mobile O, Cu, Ag and halide ions, which are technologically relevant as well.23–25
Here, we present a data-driven analysis of SSEs that covers aspects generally unaddressed by previous computational studies and the existing DFT materials databases. First, a comprehensive first-principles database was created for prototypical families of inorganic SSEs containing both sets of zero-temperature DFT and finite-temperature ab initio molecular dynamics (AIMD) results. Subsequently, a thorough correlation study of the ion diffusion coefficient (D) and other materials features was performed to determine universal ion-transport descriptors (as well as those specific to Li-based SSEs). By relying on this new knowledge and the introduced DFT-AIMD database, several machine learning models were trained for the prediction of D and other T-dependent quantities. Finally, principal component and k-means clustering analyses and data techniques customarily employed in the social sciences were applied to reduce the high complexity of the SSE landscape and determine universal classes of fast-ion conductors.
Curated first-principles SSE database
The generated SSE DFT-AIMD database26 comprises a total of 61 materials, of which 46% contain Li, 23% halides (i.e., F, Cl, Br and I), 15% Na, 8% O and 8% Ag/Cu atoms as the mobile ions. These percentages were selected in order to roughly reproduce the relative abundances of fast-ion conductors reported in the literature.27 The generated SSE DFT-AIMD database contains materials with both stoichiometric and non-stoichiometric compositions and the AIMD results were obtained over a broad range of temperatures (ESI,† Tables S1–S3 and ref. 26).
To analyze the degree of similarity between all the surveyed SSEs, a great variety of descriptors were estimated for each material adding up to a total of 54 (the complete list of descriptors is detailed in the Methods section). Some of these descriptors had already been proposed in the literature (e.g., band gap and vacancy formation energy) while some others were totally new (e.g., harmonic phonon energy and Pugh's modulus ratio). The descriptors were classified into three general categories: “mechanical–elastic”, “diffusive–vibrational” and “structural–compositional”. The values of some descriptors were obtained from zero-temperature DFT calculations (“mechanical–elastic” and “structural–compositional”) while the rest (“diffusive–vibrational”) were deduced from AIMD simulations performed at temperatures above ambient conditions (Methods section and ESI,† Tables S1–S3).
It is worth noting that the results obtained from the extensive AIMD simulations explicitly account for anharmonic effects, which constitutes one of the most important novelties and technical advances of the present work and the introduced SSE database. Moreover, most vibrational descriptors were estimated considering the following cases: (1) all the ions, (2) only non-diffusive ions and (3) only diffusive ions, in order to better substantiate the role of the vibrating crystalline matrix in ion transport (Methods section). The approximate computational cost of the generated SSE DFT-AIMD database was 50 Million CPU hours.
Correlations between pairs of SSE descriptors
The correlation for a couple of materials descriptors, x and y, can be quantified in several non-unique ways.28 In this work, we considered the Pearson (cP) and Spearman (cS) correlation coefficients which are defined as
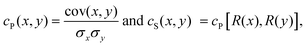 | (1) |
| cov(x,y) = 〈xy〉 − 〈x〉〈y〉, | (2) |
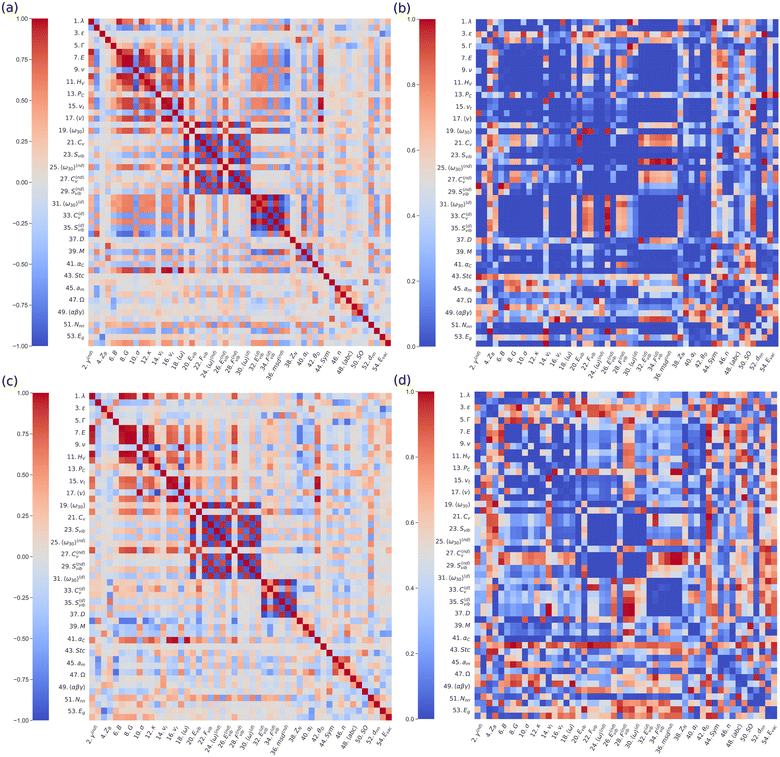
Fig. 1(a) shows the Spearman correlation coefficients estimated for all pairs of materials descriptors considering all the materials in the DFT-AIMD database and T-dependent properties calculated at T = 500 ± 100 K. We note that for this type of analysis the temperature conditions should be equivalent for all the compounds; otherwise some correlation coefficients may be significantly biased (e.g., those involving D). An analogous Pearson correlogram is found in the ESI,† Fig. S1. In view of the preeminence of Li-based SSEs in electrochemical applications, the same correlation analysis was performed for this family of materials alone (Fig. 1(c)). To assess the statistical significance of the estimated cS correlograms, we computed the corresponding p-value matrices (Fig. 1(b) and (d)). The p-value represents the probability for a particular correlation result to arise if the null hypothesis (i.e., no correlation at all) were true, thus the smaller the calculated p-value the more statistically significant cS is.
From a bird's eye view, the two correlograms obtained for all SSEs and only those containing Li ions look quite similar. Nevertheless, the p-value matrix estimated for all SSEs displays a noticeably higher number of statistically significant cases (arbitrarily defined here as p < 0.2), probably due to the larger amount of samples. Reassuringly, a number of already expected high correlation coefficients, like those estimated for couples of vibrational and elastic quantities that are physically related (e.g., Fvib and Svib), emerge from the calculated cS maps. For the sake of focus, hereafter, we will concentrate on the correlations involving the ion diffusion coefficient (D).
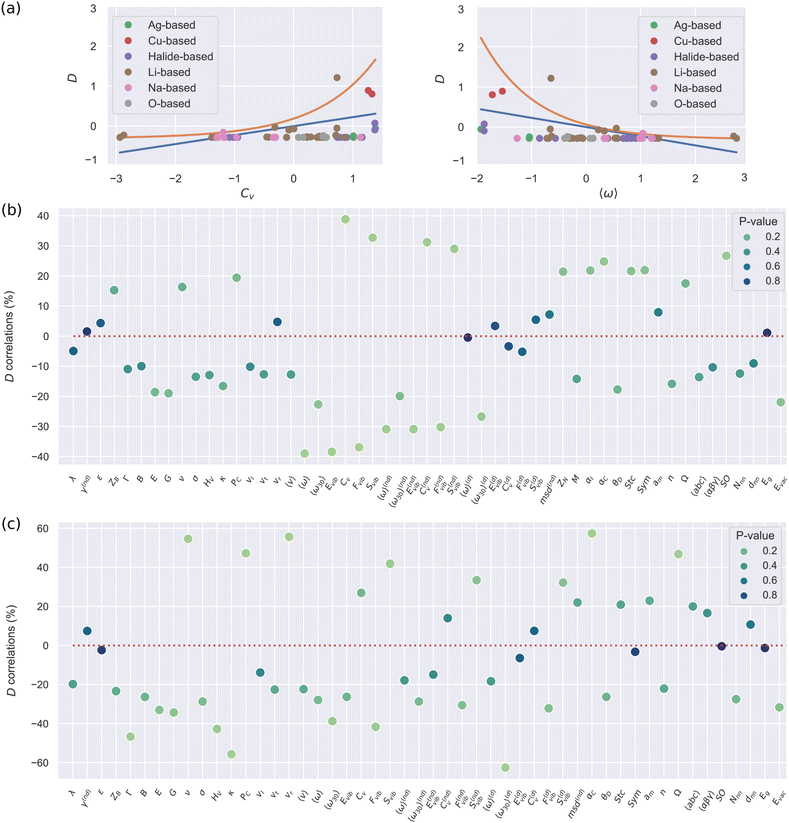
Fig. 2(a) shows a standardized representation [that is, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ≡ (x − 〈x〉)/σx] of the pairs of descriptors D–Cv and D–〈ω〉, where Cv stands for the lattice heat capacity and 〈ω〉 stands for the average vibrational frequency (Methods). In these two cases, as well as in others not shown here, it is clearly appreciated that the dependency between D and other quantities is far from linear although roughly monotonic (ESI,† Fig. S2). This outcome confirms that for determining reliable relationships between SSE features the Spearman correlation analysis is certainly more suitable than the usual Pearson approach. Actually, there are significant discrepancies between the calculated Spearman and Pearson correlation maps; for instance, cS amounts to −39% for the pair of descriptors D–〈ω〉 (Fig. 1(a)), whereas cP renders a significantly smaller value of −23% (ESI,† Fig. S3).
≡ (x − 〈x〉)/σx] of the pairs of descriptors D–Cv and D–〈ω〉, where Cv stands for the lattice heat capacity and 〈ω〉 stands for the average vibrational frequency (Methods). In these two cases, as well as in others not shown here, it is clearly appreciated that the dependency between D and other quantities is far from linear although roughly monotonic (ESI,† Fig. S2). This outcome confirms that for determining reliable relationships between SSE features the Spearman correlation analysis is certainly more suitable than the usual Pearson approach. Actually, there are significant discrepancies between the calculated Spearman and Pearson correlation maps; for instance, cS amounts to −39% for the pair of descriptors D–〈ω〉 (Fig. 1(a)), whereas cP renders a significantly smaller value of −23% (ESI,† Fig. S3).
Universal ion diffusion descriptors
Fig. 2(b) shows the Spearman correlation coefficients estimated for all pairs of descriptors involving D and considering all the materials in the DFT-AIMD database. All the AIMD-based vibrational and diffusive descriptors were estimated at T = 500 ± 100 K. First, we note that larger |cS| values are associated with statistically more significant correlation results (i.e., smaller p-values). And secondly, the estimated correlation coefficients in general are not very high: only 19 out of the 53 pairs of materials descriptors present |cS| values larger than 20% while the maximum correlation value only amounts to 39% (obviously, the D–D pair was excluded here). Thus, none of the many proposed features alone is particularly correlated to D. This general outcome is consistent with the usual difficulties encountered in the identification of robust ion transport descriptors.6
Interestingly, the largest D correlations are found for AIMD-based vibrational descriptors (Methods section) like the phonon band center (or an average lattice frequency), 〈ω〉 (−39%), lattice heat capacity, CV (+39%), vibrational free energy, Fvib (−37%), and vibrational entropy, Svib (+33%). These results indicate that insulator materials with small average phonon frequencies, large heat capacities and large vibrational entropies should be good ion conductors (ESI,† Fig. S2). It is worth noticing that strongly anharmonic materials perfectly fit into this description; thus our data-driven results generalize the conclusions of recent experimental SSE studies revealing that low-energy phonon modes can actively influence ion diffusion in some specific materials.9–14
Our correlation analysis provides further valuable insights. First, when the vibrational descriptors were estimated considering either non-diffusive or diffusive ions alone (superscripts “nd” and “d” in Fig. 2(b), respectively), the value of the D correlation coefficients slightly decreased in the first case (|cS| = 30%) and practically vanished in the second (except that corresponding to 〈ω30〉(d)). This outcome highlights the existence of a strong and general interplay between the vibrating crystalline matrix and mobile ions. And secondly, when considering vibrational descriptors that do not explicitly take into account anharmonic effects, like the lowest-energy optical phonon mode calculated at T = 0 K (Γ in Fig. 2(b)), the resulting D correlation coefficient (−11%) significantly decreases in comparison to those obtained for anharmonic quantities (besides, the corresponding p-value increases). Thus, scrutiny of anharmonicity appears to be indispensable for the evaluation of reliable and statistically meaningful D correlation coefficients.
Few descriptors belonging to the “structural–compositional” category also correlate appreciably high with D. Of special mention are the vacancy formation energy of the mobile ions (Evac, −22%), the crystal polarizability (αC, +25% –calculated with the Clausius–Mossotti relation –) and the symmetry of the perfect lattice (SO, +27%).29 On the other hand, intrinsically electronic properties like the energy band gap (Eg) and dielectric constant (ε) have virtually no correlation with the ion diffusivity (|cS| ≤ 5%). As a word of caution, we note that when the correlations between D and other materials descriptors are assumed to be linear (i.e., Pearson's approach), the resulting conclusions significantly differ from those just explained (ESI,† Fig. S3). In particular, most D correlation coefficients turn out to be smaller than the corresponding Spearman values and the materials descriptors belonging to the “mechanical–elastic” category (e.g., the Young and shear moduli – E and G – ) become similarly as relevant as the vibrational features.
Fig. 2(c) shows the Spearman D correlation coefficients estimated exclusively for Li-based SSEs. Intriguingly, the resulting cS chart differs appreciably from that estimated considering all the SSEs in the DFT-AIMD database (Fig. 2(b)). First, the D correlation coefficients in general present larger values with a total of 11 pairs of materials descriptors scoring above 40%. Some of the largest |cS| values correspond to the AIMD-based vibrational descriptors Fvib (−42%), Svib (+42%) and 〈ω30〉(d) (−63%). However, in contrast to the all-SSE case, now Γ, which is estimated at T = 0 K and does not explicitly account for anharmonicity, is strongly correlated with D as well (− 47%). Moreover, several descriptors belonging to the “mechanical–elastic” category that, to the best of our knowledge, have not been previously proposed in the literature like Vickers’ hardness, HV (−43%), Pugh's modulus ratio, κ (−56%), Poisson's ratio, ν (+55%), Cauchy's pressure, PC (+48%), and velocity ratio, vr (+56%), now also render very high |cS| values. Therefore, in terms of key D descriptors, Li-based compounds are plainly different from the average SSEs, a finding that fundamentally justifies the large number of studies focusing on the ion transport properties of this family of materials.
Machine learning models for the prediction of T-dependent properties
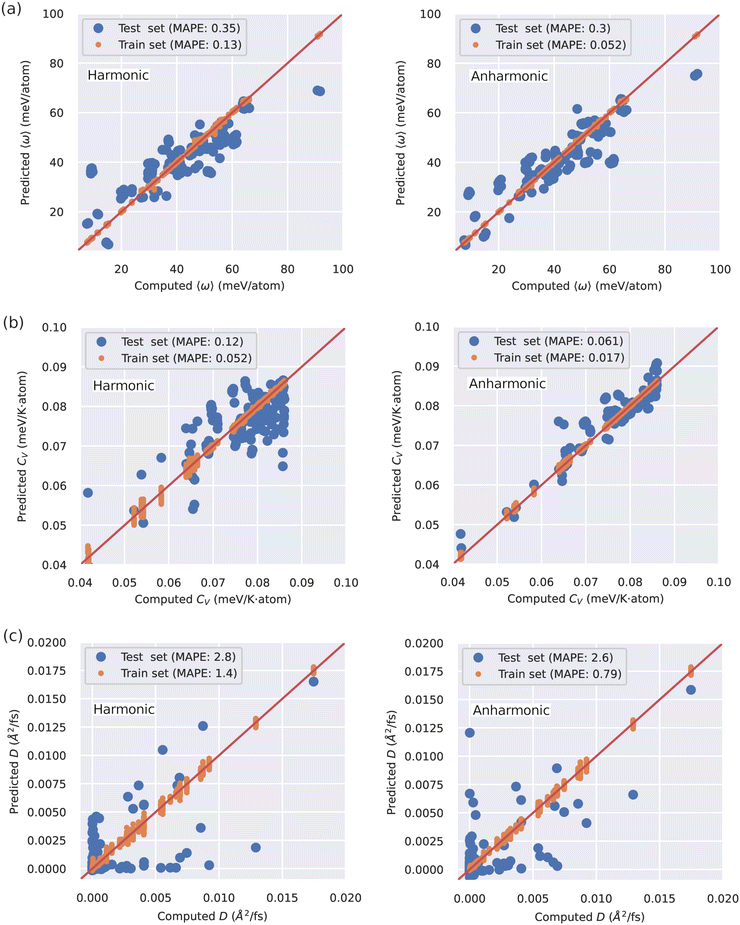
In view of the complex relationships between D and other materials descriptors (Fig. 2(a)), several machine learning (ML) models based on artificial neural networks were trained on the SSE DFT-AIMD database with the aim of predicting the ion diffusion coefficient and other relevant T-dependent properties such as 〈ω〉 and CV (Methods section). To this end, we considered all the simulated temperatures listed in the ESI,† Tables S1–S3 and.26 Two different ML training schemes were contemplated: (1) considering all the materials descriptors (denoted as “anharmonic”) and (2) excluding the AIMD-based vibrational descriptors (“harmonic”). The predictions of our trained ML models, quantified with a K-fold validation strategy (Methods section), are shown in Fig. 3. Therein, it is appreciated that the trained ML models can predict the finite-temperature values of 〈ω〉 and CV with relatively high accuracy. In particular, the mean absolute percentage error (MAPE, Methods) of the “anharmonic” (“harmonic”) ML model for the “test set” amounts to 30% (35%) for 〈ω〉 and only to 6% (12%) for CV. In stark contrast, the ML predictions for the ion diffusion coefficient are much less accurate, for both the “anharmonic” (MAPE of 260%) and the “harmonic” (280%) cases, and a precise evaluation of how good these ML models are is challenging.
Several conclusions follow from the ML results shown in Fig. 3. First, the SSE DFT-AIMD database introduced in this work appears to be comprehensive enough to ensure appropriate training of ML models able to make accurate predictions for certain T-dependent materials properties. And secondly, the ML-based prediction of the ion diffusivity appears to be a particularly difficult task. In this latter case, however, a non-negligible improvement is achieved when AIMD-based anharmonic vibrational descriptors are explicitly incorporated into the ML model (also in the 〈ω〉 and CV cases). This outcome indirectly corroborates our previous finding that anharmonicity is a key general factor influencing ion transport. Nonetheless, to improve the “anharmonic” ML predictions of D probably it is necessary to increase the number of SSE materials and descriptors in our DFT-AIMD database and/or resort to alternative and more advanced ML approaches (e.g., graph neural networks30).
Complexity reduction in the SSE landscape
Principal component analysis (PCA) is a statistical technique widely employed for analyzing large data sets containing a high number of features. PCA increases the interpretability of a data set by reducing its dimensionality and simultaneously preserving the maximum amount of information. Complexity reduction is accomplished by linearly transforming the data into a new coordinate system where most of its variation can be described with fewer dimensions. The principal components are the eigenvectors of the data set correlation matrix, which are expressed as linear combinations of the initial descriptors. The first principal component, the one with the largest eigenvalue, maximizes the variance of the projected data. The i-th principal component corresponds to a direction that is orthogonal to the previous i − 1 principal components and along which the variance of the projected data is maximized as well.
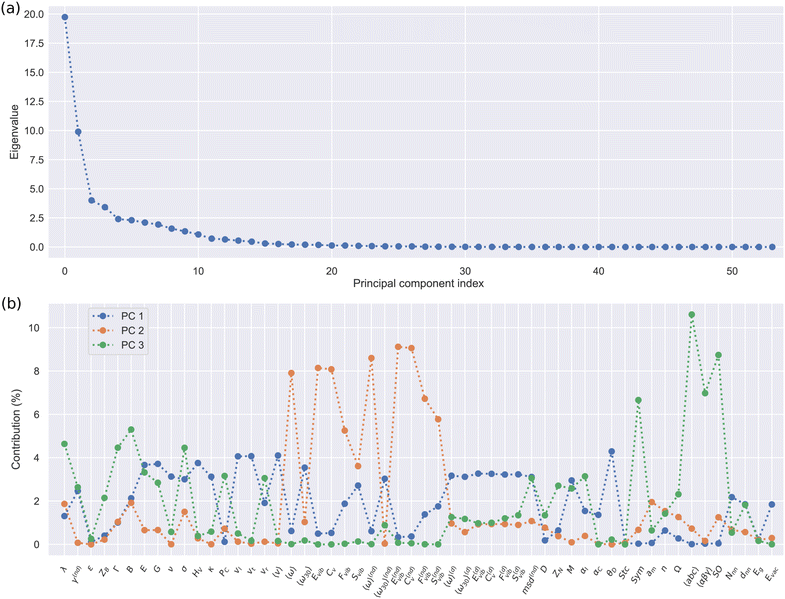
Fig. 4 shows the results of diagonalizing the Spearman correlation matrix obtained for all the materials in the SSE DFT-AIMD database at T = 500 ± 100 K (Fig. 1(a)). The first three principal components (PC) account for about two thirds of the total variance in the original 54-dimensional data set (as quantified by the sum of their normalized eigenvalues, ≈62%); hence, its complexity can be greatly reduced by considering data projections on the orthogonal three-dimensional space PC1–PC2–PC3 (which also fulfill the marginal variance increase criterion, Fig. 4(a)). PC1 presents mixed “elastic” and “vibrational” character while PC2 and PC3 are predominantly “vibrational” and “structural” (Fig. 4(b)). Intriguingly, the contribution of the ion diffusivity to each of these PC's is practically zero, namely, 0.2% to PC1, 0.8% to PC2 and 1.3% to PC3. This data-driven outcome indicates that when it comes to characterize the great disparity of SSEs, with the aim of fundamentally better understanding them and to establish general SSE categories, the ubiquitous D descriptor is actually irrelevant. Likewise, the compound stoichiometry (Stc) and dielectric constant (ε) hardly contribute to the first three PC's; hence, they neither can be regarded as universally distinctive SSE features. By contrast, elastic and vibrational descriptors like E, HV, 〈ω〉 and CV become most pertinent for the evaluation of SSE similarities and general classification purposes.
k-Means clustering analysis
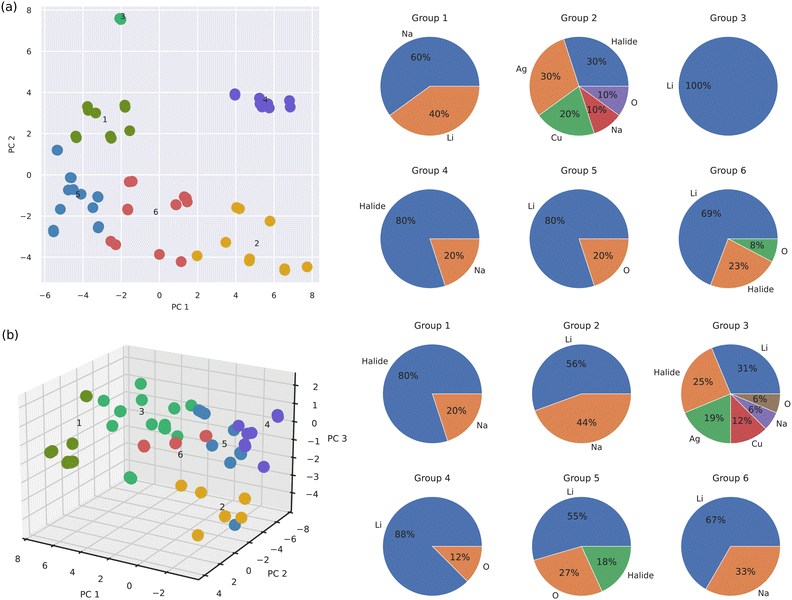
Fig. 5 shows the results of our k-means clustering analysis performed for all the materials in the SSE DFT-AIMD database at T = 500 ± 100 K. k-Means clustering is an unsupervised learning algorithm that classifies sets of objects in such a way that objects within the same group, called “cluster”, are more similar to each other in a broad sense than to the objects in other clusters. We selected a subminimal number of 6 clusters to account for the SSE database variance based on the outcomes of the elbow and silhouette methods (ESI,† Fig. S4 and S5). (By increasing the number of clusters up to 7, the final conclusions presented next did not change appreciably, ESI,† Fig. S6.) This number of clusters is equal to the number of A-based SSE families considered in this study (i.e., A = Li, Na, halide, Ag, Cu and O). Thus, in principle, if each SSE family appeared in one single k-means cluster, the ion mobile species, which we typically use for naming and classifying the SSE, would be a fine descriptor of SSE diversity.
Fig. 5(a) shows the results of our k-means clustering analysis performed in the simplified PC1–PC2 space. It is noted that Li-based SSEs are present in 4 out of the 6 total clusters. From these 4 clusters, Li-based SSEs are the most abundant in 75% of the cases and overall, they share similarities with other Na-, halide- and O-based SSEs (although not necessarily in terms of ion conductivity). In clusters number 5 and 3, which are respectively characterized by dominant PC1 (“elastic–vibrational”) and PC2 (“vibrational”) components, Li-based SSEs actually conform to the 80% and 100% of the entire population. From these outcomes, we may readily infer that (1) Li-based SSEs are intrinsically different from Ag- and Cu-based SSEs since these species are never found together in the same cluster (on the other hand, Ag- and Cu-based SSEs are highly similar because they inhabit the same cluster), and (2) Li-based SSEs can be partitioned into several similarity subgroups attending to their elastic and vibrational properties. Likewise, halide-, Na- and O-based SSEs appear in 3 out of the 6 total clusters. Thus, overall it can be concluded that the ion mobile species is not a good proxy for grouping SSEs into similarity categories.
Fig. 5(b) shows the k-means clustering results obtained in the expanded PC1–PC2–PC3 space. In this case, the main findings are very similar to those just explained for the reduced P1–P2 space; namely, Li-based SSEs are present in 5 out of the total 6 clusters and they are particularly numerous in the majority of these groups (e.g., 88% in cluster number 4 and 67% in cluster number 6). Likewise, halide-, Na- and O-based SSEs spread over 3 different clusters while Cu- and Ag-based SSEs appear only in one. Interestingly, now in the three-dimensional PC space, Li-based SSEs share similarities with all the rest of the SSE families, including Cu- and Ag-based SSEs (cluster number 3). It is worth noting that most subgroup differences (i.e., relative distances between clusters centroids located at the numbered positions in Fig. 5) are contained within the P1–P2 plane, with the exception of cluster number 2. Thus, the PC3 (“structural”) dimension does not appear to add sensible information on SSE diversity and for grouping purposes is practically expendable (in accordance with its relatively small eigenvalue of ≈4%, Fig. 4(a)).
The presented k-means clustering analysis highlights the difficulties encountered in the rational design of SSEs with specific ion mobility. The bulk of the variation in the SSE family is encoded in the elastic and vibrational properties of the materials, not in the ion mobility or their ion mobile species. This finding implies that materials which can be rigorously considered as overall highly similar (because they belong to a same k-means cluster) in practice may exhibit very different ion diffusion and chemical features (e.g., Li-based and halide-based SSEs). Conversely, materials which render very similar ion mobilities and chemical compositions (e.g., Li-based SSEs inhabiting groups 2 and 3 in Fig. 5(b)) may behave radically different in terms of other measurable quantities. These conclusions are consistent with the D correlation results shown in Fig. 2, which showed that Li-based SSEs can significantly depart from the general trends averaged over all SSEs.
In summary, we have presented an original and comprehensive SSE data-driven study on the correlations of ion diffusion with other materials descriptors as well as a rigorous examination of universal SSE categories based on a new and thorough DFT-AIMD database comprising both zero-temperature and finite-T first-principles results. It has been demonstrated that ion diffusion correlates most noticeably with vibrational descriptors that explicitly incorporate anharmonic effects (i.e., those estimated from AIMD simulations). In the particular case of Li-based SSEs, the ion mobility also correlates significantly with elastic quantities like Vickers’ hardness, Pugh's modulus ratio, Poisson's ratio and Cauchy's pressure, all relevant ion-diffusion descriptors that previously were overlooked in the literature. Furthermore, most of the variation in the generated SSE 54-fold dimensional space can be resolved in terms of elastic and vibrational descriptors; ion mobility and chemical composition are very much irrelevant when it comes to quantifying the SSE diversity, a fact that complicates the rational design of SSEs with targeted ion conductivities. The present data-driven study highlights the necessity to consider finite-temperature effects in a high-throughput fashion to better understand SSEs and improve the predictions of related machine learning models; it also provides new theoretical guidelines for analyzing materials that in analogy to SSEs are highly anharmonic and technologically relevant (e.g., thermoelectrics and superconductors).
Methods
First-principles calculation outline
Ab initio calculations based on density functional theory (DFT) were performed to analyse the physico-chemical properties of the bulk SSEs. We performed these calculations with the VASP code31 by following the generalized gradient approximation to the exchange-correlation energy due to Perdew et al.32 (For some halide compounds, possible dispersion interactions were captured with the D3 correction scheme developed by Grimme and co-workers.33) The projector augmented-wave method was used to represent the ionic cores34 and for each element the maximum possible number of valence electronic states was considered. Wave functions were represented in a plane-wave basis typically truncated at 750 eV. By using these parameters and dense k-point grids for Brillouin zone integration, the resulting zero-temperature energies were converged to within 1 meV per formula unit. In the geometry relaxations, a tolerance of 0.005 eV Å−1 was imposed in the atomic forces.First-principles molecular dynamics simulations
Ab initio molecular dynamics (AIMD) simulations based on DFT were performed in the canonical (N,V,T) ensemble (i.e., constant number of particles, volume, and temperature) for all the considered bulk materials.35 The selected volumes were those determined at zero temperature and hence thermal expansion effects were neglected; nevertheless, based on previously reported molecular dynamics tests,12 thermal expansion effects are not expected to significantly affect the estimation of the ion-transport properties of SSEs at moderate temperatures (i.e., T = 500 ± 100 K). The concentration of ion vacancies in the non-stoichiometric compounds was also considered independent of the temperature and equal to ∼1–2%. The temperature in the AIMD simulations was kept fluctuating around a set-point value by using Nose–Hoover thermostats. Large simulation boxes containing Nion ∼ 200–300 atoms were employed in all the cases and periodic boundary conditions were applied along the three Cartesian directions. Newton's equations of motion were integrated by using the customary Verlet's algorithm and a time-step length of δt = 1.5 × 10−3 ps. Γ-Point sampling for integration within the first Brillouin zone was employed in all the AIMD simulations. The finite-temperature simulations typically comprised long simulation times of ttotal ∼ 100–200 ps. For each material, we typically ran an average of 3 AIMD simulations at different temperatures within the range 400 ≤ T ≤ 1600 K, considering both stoichiometric and non-stoichiometric compositions (ESI,† Tables S1–S3 and26). Previous tests performed on the numerical bias stemming from the finite size of the simulation cell and the duration of the molecular dynamics runs reported in previous work12 indicate that the adopted Nion and ttotal values should provide reasonably well converged results for the ion diffusivity and vibrational density of states of SSEs.Estimation of key diffusive and vibrational properties
The mean-squared displacement (MSD) was estimated as
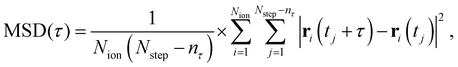 | (3) |
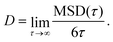 | (4) |
In practice, we performed linear fits over the averaged MSD(τ) values calculated within the lag time interval τmax/2 ≤ τ ≤ τmax.
To estimate the vibrational density of states (VDOS) of the bulk SSE considering anharmonic effects, g(ω), we calculated the Fourier transform of the corresponding velocity–velocity autocorrelation function as obtained directly from the AIMD simulations, namely
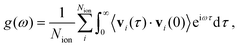 | (5) |
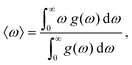 | (6) |
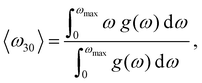 | (7) |
Machine learning models
The Scikit-learn package in Python37 was used to encode the non-numeric descriptors as well as to implement the Artificial Neural Network (ANN) conforming our machine learning model. For the generation of the input data, the simulations involving all compounds, compositions and temperatures in our SSE DFT-AIMD database were taken into consideration (i.e., a total of 174 samples, ESI,† Tables S1–S3 and ref. 26). The non-numeric descriptors (i.e., the diffusive chemical element, stoichiometry, the chemical composition of the compound and the symmetry of the relaxed structure) were encoded using the one-hot encoding approach, and all input data were normalized using a standard scaler. Specifically, a Multi-Layer Perceptron Regressor (MLPR) was implemented, consisting of input, hidden and output layers. As the output layer, the algorithm was defined in such a way that any of the considered descriptors could be used as the dependent variable. Consequently, the input layer was constructed as the set of all the other descriptors. Optionally, anharmonic descriptors could be removed from the input layer if desired. Finally, 6 hidden layers of 200, 500, 50, 150, 70 and 100 neurons showed the best performance.
Attending to the extraction of metrics, a K-fold validation was implemented: for each iteration, the model was required to predict the output for one element using the rest as the training set. Therefore, given that each element consists of a different number of simulations (the original data set presents a variable number of simulated temperatures and stoichiometries for each element), the computed metrics were weighted with the number of predicted outputs and then divided by the total amount of simulations. The optimization of the model was monitored by using the mean absolute percentage error (MAPE) defined as
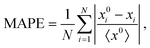 | (8) |
Furthermore, we also tested a kernel-ridge regression algorithm for the construction of ML models. Concretely, a linear kernel with α = 1 regularization strength provided the best performance. However, in this case, the resulting models did not capture the complexity of the analyzed SSEs and the MLPR models since the corresponding MAPE values were appreaciably higher (ESI,† Fig. S7).
SSE descriptor abbreviations
To analyze the similarities and dissimilarities between fast-ion conductors, a great variety of different physical descriptors were estimated for each SSE, which are summarized in Table 1. The descriptors are generally classified according to the quality they refer to, in particular: “mechanical–elastic” (M–E), “diffusive–vibrational” (D–V) and “structural–compositional” (S–C). It may be noted that most D–V descriptors, like the mean phonon frequency (both with and without cut-off), harmonic phonon energy, constant-volume heat capacity, Helmholtz free energy and entropy, were calculated for the materials as a whole (i.e., considering both diffusive and non-diffusive ions) and also exclusively considering either the non-diffusive (denoted as “nd” in the figures) or the diffusive atoms (denoted as “d” in the figures). The total number of descriptors considered in this work is equal to 54. For the presented descriptor correlations, PC and k-means clustering analyses, the quantities obtained from AIMD (DFT) simulations were calculated at T = 500 ± 100 K (T = 0 K).| Symbol | Descriptor (M–E) | Estimation approach |
|---|---|---|
| λ | 1st Lamé parameter | DFT |
| B | Bulk modulus | DFT |
| E | Young modulus | DFT |
| G | Shear modulus | DFT |
| v | Poisson's ratio | DFT |
| σ | P-wave modulus | DFT |
| H V | Vickers’ hardness | DFT |
| κ | Pugh's modulus ratio | DFT |
| P c | Cauchy's pressure | DFT |
| v l | Longitudinal wave velocity | DFT |
| v t | Transverse wave velocity | DFT |
| v r | Velocity ratio | DFT |
| 〈v〉 | Average wave velocity | DFT |
| Symbol | Descriptor (D–V) | Estimation approach |
|---|---|---|
| γ | Lindemann ratio | AIMD |
| Γ | Lowest-energy optical phonon mode | DFT |
| 〈ω〉 | Mean frequency | AIMD |
| 〈ω30〉 | Mean frequency (cut-off at 30 meV) | AIMD |
| E vib | Vibrational phonon energy | AIMD |
| C v | Constant volume heat capacity | AIMD |
| θ d | Debye temperature | AIMD |
| F vib | Vibrational Helmholtz free energy | AIMD |
| S vib | Vibrational entropy | AIMD |
| D | Diffusion coefficient | AIMD |
| msd | Mean-squared displacement | AIMD |
| Symbol | Descriptor (S–C) | Estimation approach |
|---|---|---|
| Z N | Nominal charge | Formula |
| Z B | Born effective charge | DFT |
| ε | Ion-clamped macroscopic dielectric constant | DFT |
| M | Mobile ion atomic mass | Formula |
| α I | Mobile ion polarizability | DFT |
| α C | Crystal polarizability | DFT |
| Stc | Stoichiometry | Formula |
| Sym | Crystal symmetry | DFT |
| a m | Minimal lattice constant | DFT |
| n | Number of formula units | DFT |
| Ω | Volume per formula unit | DFT |
| 〈abc〉 | Standard deviation of lattice constants | DFT |
| 〈αβγ〉 | Standard deviation of lattice angles | DFT |
| SO | Number of crystal symmetry operations | DFT |
| N nn | Number of nearest neighbors | DFT |
| d nn | Nearest neighbors distance | DFT |
| E g | Band gap | DFT |
| E vac | Vacancy energy of the mobile ion | DFT |
Data availability
The data that support the findings of this study are available upon reasonable request from the authors C. L. and C. C., and all the simulation files comprising the SSE DFT-AIMD database introduced in this work can be downloaded from the URL https://superionic.upc.edu/.Author contributions
C. C. conceived the study and planned the research, which was discussed in-depth with the rest of the co-authors. C. C. and R. R. performed and analyzed the first-principles calculations. C. L. carried out the data analysis of the generated DFT-AIMD database as well as the training of the SSE machine learning models. A. E. created the website that gives access to the DFT-AIMD database. The manuscript was written by C. C. with substantial input from the rest of the co-authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from the MCIN/AEI/10.13039/501100011033 under Grant no. PID2020-119777GB-I00, the “Ramón y Cajal” fellowship RYC2018-024947-I, the Severo Ochoa Centres of Excellence Program (CEX2019-000917-S), the Generalitat de Catalunya under Grant no. 2017SGR1506, and the CSIC under the “JAE Intro SOMdM 2021” grant program. The authors acknowledge computational support from the Red Española de Supercomputación (RES) under the grants FI-2022-1-0006, FI-2022-2-0003 and FI-2022-3-0014.References
-
D. Sumpter, Outnumbered: Exploring the Algorithms that Control Our Lives, Bloomsbury Sigma, 2018 Search PubMed
.
- S. V. Kalinin, B. G. Sumpter and R. K. Archibald, Big-deep-smart data in imaging for guiding materials design, Nat. Mater., 2015, 14, 973 CrossRef CAS PubMed
.
- V. Tshitoyan, J. Dagdelen, L. Weston, A. Dunn, Z. Rong, O. Kononova, K. A. Persson, G. Ceder and A. Jain, Unsupervised word embeddings capture latent knowledge from materials science literature, Nature, 2019, 571, 95 CrossRef CAS PubMed
.
- S. Hull, Superionics: Crystal structures and conduction processes, Rep. Prog. Phys., 2004, 67, 1233 CrossRef CAS
.
- M. Guin and F. Tietz, Survey of the transport properties of sodium superionic conductor materials for use in sodium batteries, J. Power Sources, 2015, 273, 1056 CrossRef CAS
.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Inorganic solid-state electrolytes for lithium batteries: Mechanisms and properties governing ion conduction, Chem. Rev., 2016, 116, 140 CrossRef CAS
.
- S. Muy, J. C. Bachman, L. Giordano, H.-H. Chang, D. L. Abernathy, D. Bansal, O. Delaire, S. Hori, R. Kanno, F. Magglia, S. Lupart, P. Lamp and Y. Shao-Horn, Tuning mobility and stability of lithium ion conductors based on lattice dynamics, Energy Environ. Sci., 2018, 11, 850 RSC
.
- N. A. Katcho, J. Carrete, M. Reynaud, G. Rouse, M. Casas-Cabanas, N. Mingo, J. Rodríguez-Carvajal and J. Carrasco, An investigation of the structural properties of Li and Na fast ion conductors using high-throughput bond-valence calculations and machine learning, J. Appl. Crystallogr., 2019, 52, 148 CrossRef CAS
.
- S. Muy, R. Schlem, Y. Shao-Horn and W. G. Zeier, Phonon-ion interactions: Designing ion mobility based on lattice dynamics, Adv. Energy Mater., 2021, 11, 2002787 CrossRef CAS
.
- J. L. Niedziela, D. Bansal and A. F. May,
et al., Selective breakdown of phonon quasiparticles across superionic transition in CuCrSe2, Nat. Phys., 2019, 15, 73 Search PubMed
.
- M. K. Gupta, J. Ding, D. Bansal, D. L. Abernathy, G. Ehlers, N. C. Osti, W. G. Zeier and O. Delaire, Strongly anharmonic phonons and their role in superionic diffusion and ultralow thermal conductivity of Cu7PSe6, Adv. Energy Mater., 2022, 12, 2200596 Search PubMed
.
- A. Sagotra, D. Chu and C. Cazorla, Influence of lattice dynamics on lithium-ion conductivity: A first-principles study, Phys. Rev. Mater., 2019, 3, 035405 Search PubMed
.
- M. K. Gupta, J. Ding, N. C. Osti, D. L. Abernathy, W. Arnold, H. Wang, Z. Hood and O. Delaire, Fast Na diffusion and anharmonic phonon dynamics in superionic Na3PS4, Energy Environ. Sci., 2021, 14, 6554 RSC
.
- J. Ding, J. L. Niedziela, D. Bansal, J. Wang, X. He, A. F. May, G. Ehlers, D. L. Abernathy, A. Said, A. Alatas, Y. Ren, G. Arya and O. Delaire, Anharmonic lattice dynamics and superionic transition in AgCrSe2, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 3930 CrossRef CAS PubMed
.
- C. Cazorla and J. Boronat, Simulation and understanding of atomic and molecular quantum crystals, Rev. Mod. Phys., 2017, 89, 035003 CrossRef
.
- S. Curtarolo, W. Setyawan and S. Wang,
et al., AFLOWLIB.ORG: A distributed materials properties repository from high-throughput ab initio calculations, Comput.
Mater. Sci., 2012, 58, 227 CrossRef CAS
.
- A. Jain, S. P. Ong and G. Hautier,
et al., Commentary: The materials project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef
.
- S. Kirklin, J. E. Saal and B. Meredig,
et al., The Open Quantum Materials Database (OQMD): Assessing the accuracy of DFT formation energies, npj Comput. Mater, 2015, 1, 15010 CrossRef CAS
.
- G. Pizzi, A. Cepellotti, R. Sabatini, N. Marzari and B. Kozinsky, AiiDA: Automated interactive infrastructure and database for computational science, Comput. Mater. Sci., 2016, 111, 218 CrossRef
.
- L. Kahle, A. Marcolongo and N. Marzari, High-throughput computational screening for solid-state Li-ion conductors, Energy Environ. Sci., 2020, 13, 928 RSC
.
- Y. Zhang, X. He, Z. Chen, Q. Bai, A. M. Nolan, C. A. Roberts, D. Banerjee, T. Matsunaga, Y. Mo and C. Ling, Unsupervised discovery of solid-state lithium ion conductors, Nat. Commun., 2019, 10, 5260 CrossRef PubMed
.
- X. He, Q. Bai, Y. Liu, A. M. Nolan, C. Ling and Y. Mo, Crystal structural framework of lithium super-ionic conductors, Adv. Energy Mater., 2019, 9, 1902078 CrossRef CAS
.
- S. Hu, Y. Zhu and W. Han,
et al., High-conductive protonated layered oxides from H2 O vapor-annealed brownmillerites, Adv. Mater., 2021, 33, 2104623 CrossRef CAS PubMed
.
- A. Aznar, P. Lloveras and M. Romanini,
et al., Giant barocaloric effects over a wide temperature range in superionic conductor AgI, Nat. Commun., 2017, 8, 1851 CrossRef PubMed
.
- S. M. K. N. Islam, P. Mayank and Y. Ouyang,
et al., Copper diffusion rates and hopping pathways in superionic Cu2 Se, Acta Mater., 2021, 215, 117026 CrossRef
.
- The files conforming the DFT-AIMD database presented in this work can be found at the URL: https://superionic.upc.edu/.
- Searches in the “Web of Science” of the type “Ion name fast-ion conductor” rendered materials relative abundances of 51% containing Li, 12% halide (i.e., F, Cl, Br and I), 14% Na, 12% O and 11% Ag/Cu atoms as the mobile ions.
- P. Schober, C. Boer and L. A. Schwarte, Correlation coefficients: Appropriate use and interpretation, Anesth. Analg., 2018, 126, 1763 CrossRef
.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Design principles for solid-state lithium superionic conductors, Nat. Mater., 2015, 14, 1026 CrossRef CAS PubMed
.
- V. Fung, J. Zhang, E. Juarez and B. G. Sumpter, Benchmarking graph neural networks for materials chemistry, npj Comput. Mater., 2021, 7, 84 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS
.
- S. Grimme, J. Antony, S. Ehrlich and S. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed
.
-
Z. Zhu, Z. Deng, I. H. Chu, B. Radhakrishnan and S. Ping Ong, Ab Initio Molecular Dynamics Studies of Fast Ion Conductors in Computational Materials System Design, ed. D. Shin, and J. Saal, Springer, Cham, 2018 DOI:10.1007/978-3-319-68280-8-7
.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1 CrossRef CAS
.
- F. Pedregosa, G. Varoquaux and A. Gramfort,
et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2mh01516a |
| This journal is © The Royal Society of Chemistry 2023 |