Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular engineering on a MoS2 interlayer for high-capacity and rapid-charging aqueous ion batteries†
Xuefei
Han
abc,
Jing
Yang
 a,
Yong-Wei
Zhang
a,
Yong-Wei
Zhang
 *ab and
Zhi Gen
Yu
*ab and
Zhi Gen
Yu
 *ab
*ab
aInstitute of High Performance Computing (IHPC), Agency for Science, Technology and Research (A*STAR), 1 Fusionopolis Way, #16-16 Connexis, Singapore 138632, Republic of Singapore. E-mail: zhangyw@ihpc.a-star.edu.sg; yuzg@ihpc.a-star.edu.sg
bDepartment of Materials Science and Engineering, National University of Singapore, Singapore 117575, Singapore
cAVIC Xi'an Flight Automatic Control Research Institute, 710065, China
First published on 4th April 2023
Abstract
Rechargeable aqueous ion batteries (AIBs) play essential roles in the increasing demand for high-performance energy storage systems, and yet they are hampered by the lack of suitable cathode materials because of the sluggish intercalation kinetics. In this work, we develop an effective and feasible strategy to enhance the performance of AIBs by broadening the interlayer spacing by using intercalated CO2 molecules to promote the intercalation kinetics by using first principles simulations. Compared with pristine MoS2, the intercalation of CO2 molecules with a 3/4 ML coverage significantly increases the interlayer spacing to 9.383 Å from 6.369 Å and the diffusivity is boosted by 12 orders of magnitude for Zn ions, 13 orders for Mg ions and one order for Li ions. Moreover, the concentrations of intercalating Zn, Mg and Li ions are enhanced by 7, 1 and 5 orders of magnitude, respectively. The significantly increased diffusivity and intercalation concentration of metal ions signify that intercalating CO2 bilayer MoS2 is a promising cathode material to realize metal ion batteries with a rapid charging capability and high storage capacity. The strategy developed in this work can be generally applied to increase the metal ion storage capacity in transition metal dichalcogenide (TMD)- and other layered material-based cathodes and make them promising for next-generation rapidly rechargeable batteries.
Introduction
Renewable and clean energy generation is a promising solution to counter the carbon dioxide emission mainly originating from burning fossil fuels. Several renewable energy harvesting technologies have been well developed.1–5 The rapid development and high demands of renewable and clean energy sources, portable electronic devices, and electric vehicles have triggered great ambition for low cost, large-scale, and high energy density battery systems for energy storage. Due to the high cost and safety hazards and the scarce source of metal Li, it is desirable to find alternative energy storage systems to replace Li-ion batteries (LIBs). In this regard, aqueous multivalent metal ion batteries (AMMIBs) are attracting tremendous attention and are considered promising substitutes for LIBS.6–13 Due to high safety, low cost, eco-friendliness, and high ionic conductivity (1000 times higher than organic electrolytes), rechargeable AMMIBs are promising batteries for grid-scale electrochemical energy storage. Among rechargeable AMMIBs, aqueous zinc-ion batteries (ZIBs)14–17 and aqueous magnesium-ion batteries (MIBs)18–20 have attracted remarkable attention worldwide because they exhibit a high volumetric energy density of 5851 mA h mL−1 for ZIBs21,22 and 3833 mA h mL−1 for MIBs.23–25 However, the main challenge lies in developing suitable cathode materials for AMMIBs.Several materials have been developed as promising cathode materials for AMMIBs. Vanadium oxides with a tunnel structure as cathode materials show high Zn-ion storage properties,26–31 but the dissolution of vanadium in water-based electrolytes remains a significant challenge.32 A composite of manganese dioxide and carbon molecular sieves (δ-MnO2@CMS) with a core–shell structure and Chevrel phase Mo6S8 were reported as cathode materials for MIBs.33–35 The practicality of MIBs is hampered by the absence of suitable high-performance cathode materials with rapid Mg ion diffusion.36 Transition metal dichalcogenides (TMDs) have attracted extensive attention due to their potential applications in cathode materials for rechargeable AMMIBs. The layer structure of TMDs and their weak interlayer interaction via van der Waals (vdW) force are appealing properties for multivalent metal ion diffusion and intercalation,37–41 especially for large metal ion-based AMMIBs. Among TMDs, MoS2 is considered one of the most promising cathode materials for AMMIBs,42,43 which suggests the feasibility of employing MoS2 as a functional AMMIB cathode material. This scarcity in the report suggests the heightened challenges in observing reversible metal ion storage in pristine MoS2. The high intercalation energy barrier of metal ions leads to the low specific capacities recorded for the MoS2 systems (for Zn 1–40 mA h g−1).44–46 For example, it was found that Zn2+ diffusion across the MoS2 framework was further hampered by its low electrochemical activity and low conductivity.45 Hence, it is essential to explore effective modification methods to “activate” MoS2 towards reversible metal ion storage for leveraging the advantages of MoS2. Phase engineering was a highly appealing strategy for modulating the chemical and electrical properties. 1T-MoS2, with a tetragonal symmetry, in which each Mo atom has an octahedral coordination with S atoms, has metallic conductivity, resulting in a lower metal ion diffusion barrier than in 2H-MoS2. However, 1T MoS2 is a metastable phase, and producing 1T MoS2 on a large scale remains a big challenge. An alternative strategy is to tune the intercalation energy by changing the interlayer spacing. It was demonstrated that intercalation oxygen could increase their interlay spacing (9.5 Å) and tune hydrophilicity, resulting in boosting the Zn ion diffusion kinetics by 3 orders of magnitude in MoS2.44 Sandwiched structures consisting of monolayer MoS2 and carbon (MoS2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C)47 and MoS2/graphene48 were reported to realize high-performance sodium ion and Zn ion batteries thanks to the expanded interlayer spacing (11.6 Å). Although many efforts have been made to study layered MoS2, the high capacity and long life-cycle times of MoS2-based cathodes have not yet been coexisting for practical utilization. More work needs to be conducted to expand the interlayer spacing further and enhance the hydrophilicity of MoS2 to realize high reversible capacity and superb durability, which remains a big challenge.
C)47 and MoS2/graphene48 were reported to realize high-performance sodium ion and Zn ion batteries thanks to the expanded interlayer spacing (11.6 Å). Although many efforts have been made to study layered MoS2, the high capacity and long life-cycle times of MoS2-based cathodes have not yet been coexisting for practical utilization. More work needs to be conducted to expand the interlayer spacing further and enhance the hydrophilicity of MoS2 to realize high reversible capacity and superb durability, which remains a big challenge.
In this study, we demonstrate a feasible and effective strategy to reduce metal ion diffusion barrier by using intercalation of CO2 molecules to expand the MoS2 interlayer spacing through density functional theory (DFT) simulations. Our comprehensive DFT results reveal that the intercalated MoS2 by CO2 is a promising cathode material for realizing rapidly chargeable metal ion batteries.
Results and discussion
AA′ stacking bilayer MoS2 was chosen to investigate the metal ion diffusion in this study since it has the lowest relative formation energy among five possible stacking configurations.49 The optimized unit cell of AA′ stacking bilayer MoS2 is shown in Fig. S1a.† The optimized lattice constants are a = b = 3.204 Å and the layer spacing is 6.37 Å, which is quite close to the reported value of 6.21 Å.49 The stacking formation ES of bilayer MoS2 was calculated based on the definition of the total energy difference per atom between the bilayer and two individual monolayers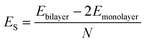 , where N is the total number of atoms in bilayer MoS2 unit cell (4 S and 2 Mo atoms). The calculated AA′ stacking formation energy is −34.33 meV per atom, well agreeing with the reported value of −25.13 meV.49 The tiny difference may originate from the van der Waals (vdW) correction methods.50 The optimized unit cell was expanded to build 5 × 5 × 1 supercells containing 50 Mo and 100 S atoms shown in Fig. S1b,† and rectangle supercells (a = 22.201 Å and b = 19.224 Å) with 96 Mo and 192 S atoms shown in Fig. S1b.†
, where N is the total number of atoms in bilayer MoS2 unit cell (4 S and 2 Mo atoms). The calculated AA′ stacking formation energy is −34.33 meV per atom, well agreeing with the reported value of −25.13 meV.49 The tiny difference may originate from the van der Waals (vdW) correction methods.50 The optimized unit cell was expanded to build 5 × 5 × 1 supercells containing 50 Mo and 100 S atoms shown in Fig. S1b,† and rectangle supercells (a = 22.201 Å and b = 19.224 Å) with 96 Mo and 192 S atoms shown in Fig. S1b.†
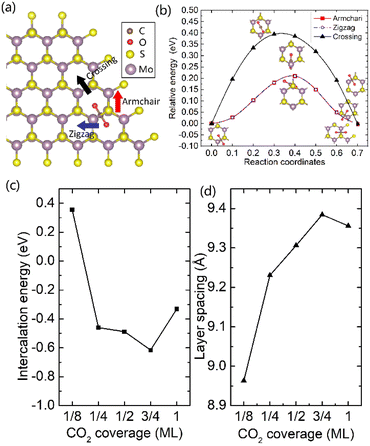
It was well explored that the interlayer spacing and coupling have a strong effect on the intercalation energy of metal ions.44,47,48 In this study, the intercalating CO2 molecules were used to expand the interlayer spacing of bilayer MoS2. First, the possible embedding configurations of the intercalating CO2 molecules were investigated, and the optimized configurations and the calculated relative energies are shown in Fig. S2.† In which, the CO2 molecule has two possible embedding sites, and the computed relative energies reveal that CO2 prefers to stay at the bridge site rather than the hollow site. The intercalation energy of an intercalating CO2 molecule EIn was calculated based on EIn = E(MoS2+CO2) − (EMoS2 + ECO2), where, E(MoS2+CO2), EMoS2 and ECO2 are the total energies of bilayer MoS2 with one embedding CO2 molecule, pristine bilayer MoS2 and an isolated CO2 molecule. For an isolated CO2 molecule energy calculation, we put one CO2 molecule in a cube model (a = b = c = 15 Å), and the calculated ground state energy is considered the energy of an isolated CO2 molecule. The calculated intercalation energy of one embedding CO2 molecule is 2.98 eV at the bridge site. With one intercalating CO2 molecule, the interlayer spacing slightly increases to 7.61 Å from 6.37 Å (pristine bilayer MoS2). The relatively high intercalation energy of the CO2 molecule may originate from the strong interlayer coupling. Therefore, more CO2 molecules may need to be intercalated to expand the interlayer spacing and reduce the interlayer coupling further. Meanwhile, we also investigate the intercalating CO2 molecule diffusion in bilayer MoS2. According to the symmetry of the 2H MoS2 structure, the intercalating CO2 has three possible diffusion pathways: armchair, zigzag and crossing, as shown in Fig. 1a. The calculated diffusion barriers are 0.209, 0.209 and 0.394 eV as shown in Fig. 1b. The computed results reveal that the CO2 diffusion barriers along the zigzag and armchair directions are identical, revealing an isotropic diffusivity of the intercalating CO2 in the bilayer MoS2. Also, the direct crossing diffusion is more difficult due to its higher diffusion barrier than zigzag and armchair directions originating from the high relative energy at the hollow site. The calculated diffusion barriers of 0.209 and 0.394 eV also show that the intercalation CO2 would be kinetically stable in the bilayer MoS2 since the room temperature is about 0.0256 eV. Temperature and pressure contributions are not included in the results obtained from DFT simulations, which only are valid at T = 0 K and P = 0 atm. The results from DFT simulations can be used as an input to thermodynamics considerations to describe a situation of finite temperature and pressure. To investigate the thermodynamic stability of the CO2 intercalated MoS2, we performed DFT simulations considering appropriate thermodynamic functions, and the CO2 intercalated stacking Gibbs free energy as a function of the temperature and pressure can be calculated
| ΔG(T, P) = ES + ΔEZPE − TΔSvib + PV | (1) |
| ES = (E(MoS2+nCO2) − (E(MoS2) + nECO2))/n | (2) |
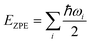 , and Svib can be calculated using
, and Svib can be calculated using 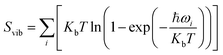 , where ℏ is the reduced Planck's constant and ωi is the i-th vibrational frequency of the diffusing ion. As a benchmark, we computed the entropy CO2 molecule and the calculated entropy is 214.419 J (mol−1 K−1), which is comparable with the standard molar entropy of 213.79 J (mol−1 K−1). In this study, we proposed two pathways to intercalate CO2 into MoS2, directly intercalating CO2 molecules into one bilayer MoS2 (P1) or two monolayers (P2) one by one as shown in Fig. S6a.† Under the condition of P = 0 atm, we calculated the CO2 intercalated stacking Gibbs free energies, and the results are shown in Fig. S6b.† In comparison, using two monolayers (P2) may easily realize the CO2 intercalated MoS2. As shown in Fig. S6b,† the stacking Gibbs free energy of one CO2 intercalated MoS2 is 3.48 eV using the P1 pathway and dramatically decreases to −3.50 eV. When the CO2 coverage increases to 3/4 and 1 ML, the stacking Gibbs free energies of the CO2 intercalated MoS2 are 0.36 and 0.26 eV using the P1 pathway, much higher than those of −0.16 eV and −0.13 eV using the P2 pathway, respectively. Based on the definition of the stacking Gibbs free energy, the negative value denotes that the final product of the CO2 intercalated MoS2 is thermodynamically stable, and the reaction is exothermic. It should be noted that the calculated stacking Gibbs free energies of the CO2 intercalated MoS2 are based on P = 0 atm. Based on eqn (1), we may estimate the pressure needed to realize 3/4 ML CO2 intercalation when the Gibbs free energy is zero using the P1 process. The estimated pressure is 107 atm (0.0108 GPa) to stabilize CO2 molecule (3/4 ML) intercalating in bilayer MoS2. Furthermore, intercalating one CO2 molecule may require higher pressure (P = 961 atm). Based on the results shown in Fig. S6b,† it can be seen that the intercalated structure appears unstable at a low coverage and becomes more stable at a high coverage, which reveals a substantial kinetic barrier in realizing the CO2 molecules intercalated structure. Not surprisingly, the calculated CO2 diffusion barriers of 0.209 and 0.394 eV shown in Fig. 1b can be considered the kinetic barrier for realizing a stable structure at a high coverage. The diffusion barriers also reveal that the intercalating CO2 would be kinetically stable in the bilayer MoS2 since the diffusion barriers are much higher than 0.0256 eV (room temperature). Also, we performed ab initio molecular dynamics (AIMD) for one CO2 molecule intercalated MoS2 and bilayer MoS2 with a CO2 coverage of 1 ML at 300 K within 1000 fs. Fig. S7† shows intercalated CO2 molecules stabilized in the bilayer MoS2, maintaining the 2H structural symmetry. The optimized models obtained from AIMD simulations also confirm the thermodynamical stability. Therefore, the CO2 intercalated MoS2 is thermodynamically stable and feasible. The diffusion barrier also indicates that intercalating CO2 molecules can easily form a uniform distribution in bilayer MoS2. The relative energy results also reveal that intercalating CO2 molecules prefer to separate rather than cluster in the bilayer MoS2.
, where ℏ is the reduced Planck's constant and ωi is the i-th vibrational frequency of the diffusing ion. As a benchmark, we computed the entropy CO2 molecule and the calculated entropy is 214.419 J (mol−1 K−1), which is comparable with the standard molar entropy of 213.79 J (mol−1 K−1). In this study, we proposed two pathways to intercalate CO2 into MoS2, directly intercalating CO2 molecules into one bilayer MoS2 (P1) or two monolayers (P2) one by one as shown in Fig. S6a.† Under the condition of P = 0 atm, we calculated the CO2 intercalated stacking Gibbs free energies, and the results are shown in Fig. S6b.† In comparison, using two monolayers (P2) may easily realize the CO2 intercalated MoS2. As shown in Fig. S6b,† the stacking Gibbs free energy of one CO2 intercalated MoS2 is 3.48 eV using the P1 pathway and dramatically decreases to −3.50 eV. When the CO2 coverage increases to 3/4 and 1 ML, the stacking Gibbs free energies of the CO2 intercalated MoS2 are 0.36 and 0.26 eV using the P1 pathway, much higher than those of −0.16 eV and −0.13 eV using the P2 pathway, respectively. Based on the definition of the stacking Gibbs free energy, the negative value denotes that the final product of the CO2 intercalated MoS2 is thermodynamically stable, and the reaction is exothermic. It should be noted that the calculated stacking Gibbs free energies of the CO2 intercalated MoS2 are based on P = 0 atm. Based on eqn (1), we may estimate the pressure needed to realize 3/4 ML CO2 intercalation when the Gibbs free energy is zero using the P1 process. The estimated pressure is 107 atm (0.0108 GPa) to stabilize CO2 molecule (3/4 ML) intercalating in bilayer MoS2. Furthermore, intercalating one CO2 molecule may require higher pressure (P = 961 atm). Based on the results shown in Fig. S6b,† it can be seen that the intercalated structure appears unstable at a low coverage and becomes more stable at a high coverage, which reveals a substantial kinetic barrier in realizing the CO2 molecules intercalated structure. Not surprisingly, the calculated CO2 diffusion barriers of 0.209 and 0.394 eV shown in Fig. 1b can be considered the kinetic barrier for realizing a stable structure at a high coverage. The diffusion barriers also reveal that the intercalating CO2 would be kinetically stable in the bilayer MoS2 since the diffusion barriers are much higher than 0.0256 eV (room temperature). Also, we performed ab initio molecular dynamics (AIMD) for one CO2 molecule intercalated MoS2 and bilayer MoS2 with a CO2 coverage of 1 ML at 300 K within 1000 fs. Fig. S7† shows intercalated CO2 molecules stabilized in the bilayer MoS2, maintaining the 2H structural symmetry. The optimized models obtained from AIMD simulations also confirm the thermodynamical stability. Therefore, the CO2 intercalated MoS2 is thermodynamically stable and feasible. The diffusion barrier also indicates that intercalating CO2 molecules can easily form a uniform distribution in bilayer MoS2. The relative energy results also reveal that intercalating CO2 molecules prefer to separate rather than cluster in the bilayer MoS2.
To expand the interlayer spacing and reduce the interlayer coupling further, more CO2 molecules were intercalated into the bilayer MoS2. The CO2 coverage-dependent intercalation energy Ef was computed based on the definition of Ef = E(MoS2+nCO2) − E(MoS2+(n−1)CO2) − ECO2, where E(MoS2+nCO2), E(MoS2+(n−1)CO2) and ECO2 are the energies of nCO2 intercalating into MoS2, (n − 1)CO2 intercalating into MoS2 and an isolated CO2 molecule. In this study, we only consider the CO2 coverage of 1/8 ML, 1/4 ML, 1/2 ML, 3/4 ML and 1 ML (24 CO2 molecules) using big rectangle supercells composed of 96 Mo and 192 S atoms, and the optimized models are shown in Fig. S5.† The calculated CO2 molecule coverage-dependent intercalation energies and the corresponding layer spacings are shown in Fig. 1c and d. The simulation results show that the intercalation energy decreases with the increase in coverage, and the 3/4 ML coverage of the CO2 molecules results in the lowest intercalation energy of −0.615 eV, and the intercalation energy is increased when the CO2 coverage further increases. Not surprisingly, the interlayer spacing increases with the increase in coverage, resulting in the largest layer spacing of 9.384 Å among five considered coverages. A further increase in coverage (1 ML) makes the interlayer spacing decrease when the CO2 coverage is higher than 3/4 ML. Based on the results shown in Fig. S5,† the CO2 intercalated MoS2 keeps the structural stability with increased coverage even at the coverage of 1 ML. The calculated AA′ stacking formation energy of bilayer MoS2 with a CO2 molecule coverage of 3/4 ML increases to −28.01 meV per atom, which is higher than that in pristine MoS2 of −34.33 meV per atom. A comparison of these results reveals that the intercalation of CO2 weakens the layer coupling. The calculated interlay spacing of the bilayer MoS2 with 3/4 ML coverage is 9.384 Å, slightly higher than that with a 1 ML coverage of 9.356 Å. It should be noted that the interlay spacing is the average distance between two Mo atoms in the different layers. Based on the results shown in Fig. 1d, we may consider that the expanded interlayer spacing is converged when the CO2 coverage is more than 3/4 ML. Therefore, we adopted the optimized bilayer MoS2 models with a CO2 coverage of 3/4 ML to investigate the diffusion of metal ions.
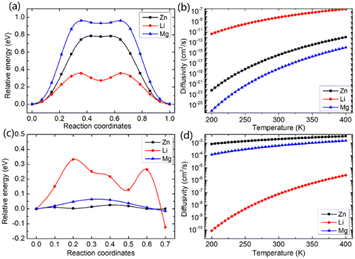
In this study, we investigated the diffusion barriers of three metal ions (Zn, Mg, and Li) in bilayer MoS2. Based on the structure and 2H symmetry of the bilayer MoS2, we proposed two possible embedding sites (tetrahedral Th and octahedral Oh), as shown in Fig. S3† Considering the Zn ion as a representative, we calculated the relative energies of two possible embedding sites, and the results are shown in Fig. S4† and proposed the possible diffusion pathway of metal ions as (b) → (c) → (d), as shown in Fig. S4.† The diffusion barriers of Zn, Mg and Li ions in the pristine bilayer MoS2 were calculated, and the results are shown in Fig. 2a. The calculated diffusion barriers of Zn, Mg and Li ions in the pristine bilayer MoS2 are 0.785, 0.942 and 0.356 eV, respectively. The temperature-dependent ion diffusivity of the three metal ions was predicted based on the computed diffusion barriers considering thermal corrections (ESI†), and the results are shown in Fig. 2b. The calculated ion diffusivities are 4.18 × 10−16 cm2 s−1, 1.01 × 10−16 cm2 s−1 and 6.90 × 10−9 cm2 s−1 at room temperature, corresponding to the Zn, Mg, and Li ions, respectively. These calculation results indicate that the pristine bilayer MoS2 is a cathode material with limited performance for metal ion batteries. Clearly, new strategies are highly demanded to reduce the ion diffusion barrier for high-performance batteries.
We further demonstrated a feasible and effective strategy to reduce the ion diffusion barrier by using intercalating CO2 molecules to expand the MoS2 interlayer spacing. With a high coverage of 3/4 ML CO2, the interlayer spacing of MoS2 is expanded to 9.383 Å. Compared with the interlay spacing of 6.369 Å obtained from the pristine bilayer MoS2, a bigger interlayer spacing results in a weak interaction between layers and lower diffusion barriers of metal Li, Zn and Mg ions. With the intercalating CO2 molecules, the results shown in Fig. 2c and d reveal that the diffusion barriers of Zn and Mg were dramatically reduced to 0.026 and 0.064 eV, significantly boosting the Zn and Mg ion diffusion by 12 and 14 orders of magnitude at room temperature, while only by one order of magnitude for Li ions. Our comprehensive DFT results reveal that the CO2 intercalated MoS2 is a promising cathode material for realizing rapidly chargeable Zn and Mg metal ion batteries. Compared with previously reported results shown in Table 1, the calculated diffusivity of Zn in the bilayer MoS2 is much smaller than the experimental one in the bulk MoS2,51 and Mg has a higher diffusivity in the bilayer MoS2 than in the bulk MoS2. As for Li ions, they have nearly the same diffusivity in the bilayer MoS2 as in the bulk MoS2. It should be noted that the diffusivities of three ions are very low, showing that the pristine bilayer and bulk MoS2 are not suitable for metal ion batteries. Comparing the experimental values shown in Table 1 and our theoretical values reveal that the CO2 intercalated MoS2 has significant potential for metal ion batteries. However, Zn and Mg ions have much higher diffusivity in the CO2 intercalated MoS2 than in O-modified51 and MoS2/graphene heterojunctions.52 Not surprisingly, no significant improvement in Li ion diffusivity was found in our study compared with W and Mo alloyed MoS2.53
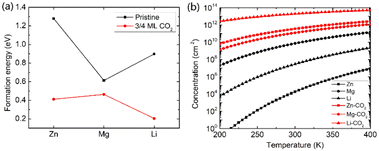
Beyond the metal ion diffusion barrier and diffusivity, another challenge is to improve the storage capacity of AMMIBs, mainly determined by the embedding concentration of ions. Meanwhile the ion concentration or solubility in cathode materials is governed by the intercalation energy of metal ions.49 Consequently, we calculated the intercalation energy of embedded metal ions in the pristine and the intercalating CO2 bilayer MoS2 (ESI†). The results are shown in Fig. 3a reveal that the intercalation energy of Zn ion significantly decreases to 0.411 eV from 1.279 eV in the pristine bilayer MoS2, and the intercalation energy of Li dramatically decreases to 0.204 eV from 0.898 eV. However, the intercalation energy of Mg slightly decreases to 0.463 eV from 0.613 eV. Based on the calculated intercalation energies of metal ions in the pristine and CO2 embedded bilayer MoS2, we computed the temperature-dependent intercalation ion concentration (ESI†), and the results are shown in Fig. 3b. The Zn ion embedding concentration is enhanced by 7 orders of magnitude to 3.63 × 1011 cm−2, and the Li ion embedding concentration is enhanced by 5 orders of magnitude to 1.98 × 1013 cm−2 at 300 K. However, the Mg ion embedding concentration is slightly boosted by just one order of magnitude to 1.25 × 1011 cm−2. In contrast, the intercalating CO2 molecules have significant contributions to the enhancement of the embedding concentration of Zn and Li ions but have a feeble effect on Mg ions. Hence, we consider that the intercalation of CO2 molecules significantly promotes bilayer MoS2 to be a promising cathode material for high-capacity Zn and Li ion batteries, but only slightly for Mg ion batteries.
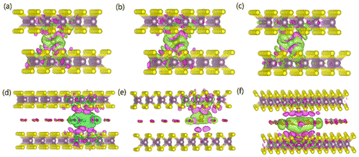
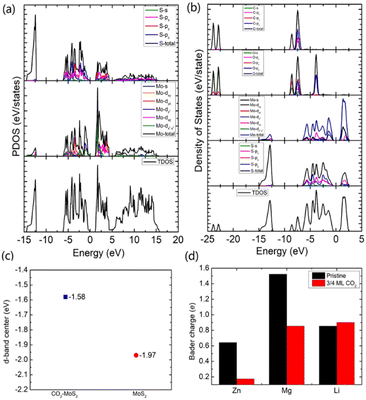
To gain an in-depth understanding of the diffusion barrier decrease originating from the intercalating CO2 and the possible chemical reaction between CO2 and embedding metal ions, we analyzed the charge difference between embedding metal ions and bilayer MoS2. As a benchmark, the charge differences of metal ions in the pristine bilayer MoS2 were evaluated as well. We calculate the charge density difference between the embedding ions and CO2 molecule intercalated bilayer MoS2 systems by using the formula of Δρ = ρ(host+M) − (ρhost+ρM), where ρ(host+M), ρhost and ρM represent the charge density of the ion embedded MoS2, the pristine MoS2 and the isolated metal ion, respectively. The simulation results are shown in Fig. 4, in which the purple color corresponds to the charge accumulation forming bonding states, and the green color represents the charge depletion forming anti-bonding states. Fewer bonding states and more anti-bonding states make the interaction stronger between embedded ions and their host systems. For the Zn ion embedding system as shown in Fig. 4a and d, the intercalating CO2 molecules result in more charge depletion than in the pristine MoS2, resulting in a decrease of the Zn ion intercalation energy. A similar tendency is also found in the Li ion embedding system shown in Fig. 4c and f. However, no significant change can be seen in the Mg ion embedding system shown in Fig. 4b and e. The results shown in Fig. 4 indicate that the intercalation of CO2 molecules has a great contribution to the intercalation energy of Zn and Li ions only, consistent with the calculated intercalation energies of metal ions as shown in Fig. 3a. Also, we found no electron transfer and bond formation between intercalating CO2 and embedded Zn and Mg ions, except for the Li-ion system. We also calculated the projected density of states (PDOS) of the pristine and intercalated CO2 (3/4 ML) MoS2 as shown in Fig. 5a and b, respectively. It can be seen that O-p orbitals have strong interaction with Mo-d orbitals. The results reveal that CO2 can be stabilized in the bilayer MoS2. We also computed d-band centers of Mo from the intercalated CO2 (3/4 ML) and pristine MoS2, and the results are shown in Fig. 5c. Intercalated CO2 molecules push the d-band of Mo to a higher energy state and result in a lower d-band center than in the pristine MoS2, and further enhance the metal ion solubility in intercalating CO2 bilayer MoS2. Bader charge54 provides the definition of the chemical bond for charge analysis, which is based on the electronic charge density. In Fig. 5d, the Bader charges for Zn and Mg are significantly decreased but there is a little increase for Li ions with CO2 embedding. The result reveal that intercalating CO2 molecules weaken the ion interaction of Zn and Mg with host elements, while the slightly increased Bader charge of Li ions reveals that Li ions have strong chemical interaction with CO2 as shown in Fig. 4f, which well explains the multi-saddle points in Li NEB results shown in Fig. 2c. We consider that those embedding CO2 molecules would not react with Zn and Mg and may form chemical bonds with Li ions. Therefore, we believe that it is feasible to use CO2 intercalation for improving the performance of MoS2-based Zn and Mg ion batteries.
To gain an in-depth understanding of the location of CO2 insertion at active sites, we computed the work function of pristine and CO2 with/without metal ion intercalation bilayer MoS2. The work function Φ is defined as the vacuum energy respective to the Fermi level (Φ = Evac − Ef). The work function of bilayer MoS2 highly depends on the crystal orientation, the presence of impurities, defects, and doping. The calculated local potentials along the z-direction are shown in Fig. S8a.† It should be noted that the results shown in Fig. S8a† are simply plotted in one figure without considering the common alignment reference. Based on the calculated local potential along the z-direction shown in Fig. S8a,† we computed the work functions of selected five cases and the results are shown in Fig. S8b.† It can be seen that the calculated work function of the pristine bilayer MoS2 is 6.02 eV, and the same as that of 3/4 ML CO2 embedded MoS2. The results reveal that intercalated CO2 molecules do not affect the work function. Therefore, we considered that CO2 is a promising material to expand the interlay spacing of layered MoS2. With metallic ion (Zn, Mg and Li) insertion, the work function decreases to 5.65 eV in Zn intercalated 3/4 ML CO2 embedded MoS2, further decreases to 4.78 eV in Mg intercalated 3/4 ML CO2 embedded MoS2, and further decreases to 4.53 eV in Li intercalated 3/4 ML CO2 embedded MoS2.
Conclusions
In conclusion, we developed a simple and effective strategy by tuning the interlayer spacing of MoS2 and the intercalation energy of Zn, Mg and Li ions for cathode materials of rapidly chargeable batteries. Employing DFT simulations, we demonstrate that the intercalation of CO2 molecules with a 3/4 ML coverage effectively expands the interlayer spacing, reduces layer coupling of bilayer MoS2, and significantly reduces the diffusion barrier and intercalation energies of metal ions, achieving high performance metal ion batteries. As a result, the diffusivities of Zn and Li increase by 12 and 13 orders of magnitude, and the intercalating ion concentration or the storage capacities of Zn and Li ion batteries are boosted by 7 and 5 orders of magnitude. Our simulation result demonstrated that intercalated CO2 molecules significantly contribute to both diffusivity and embedding concentration of Zn ions but they contribute to only the diffusivity of Mg and the embedding concentration of Li ions. Therefore, we demonstrate that CO2 molecule intercalated bilayer MoS2 is a promising cathode material for high-capacity and rapid-charging ZIBs. The strategy of expanding interlay spacing and reducing intercalation energy developed in this study can be generally applied to increase the ion storage capability in layered structure-based electrode materials and sheds light on the development of advanced materials for next-generation high-performance energy storage.Author contributions
Xuefei Han: methodology, investigation, writing – original draft, and writing – review & editing. Jing Yang: writing – review & editing. Yong-Wei Zhang: conceptualization and writing – review & editing. Zhi Gen Yu: conceptualization, methodology, writing – review & editing, and supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was sponsored by the Agency for Science, Technology and Research (A*STAR), and the Department of Materials Science and Engineering (MSE), the National University of Singapore (NUS). The computational resource was provided by the A*STAR Computational Resource Centre, Singapore (A*CRC) and the National Supercomputing Centre, Singapore (https://www.nscc.sg/). Y.-W. Z acknowledges the support from A*STAR-SERC-CRF Award.Notes and references
- P. K. Santra and P. V. Kamat, J. Am. Chem. Soc., 2012, 134, 2508–2511 CrossRef CAS PubMed
.
- B. C. H. Steele and A. Heinzel, Nature, 2001, 414, 345–352 CrossRef CAS PubMed
.
- Y. Yang, K. C. Pradel, Q. Jing, J. M. Wu, F. Zhang, Y. Zhou, Y. Zhang and Z. L. Wang, ACS Nano, 2012, 6, 6984–6989 CrossRef CAS PubMed
.
- S. Xu, Y. Wei, J. Liu, R. Yang and Z. L. Wang, Nano Lett., 2008, 8, 4027–4032 CrossRef CAS PubMed
.
- Z. L. Wang, ACS Nano, 2013, 7, 9533–9557 CrossRef CAS PubMed
.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS
.
- V. Etachri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243–3262 RSC
.
- Y. Zhang, P. Wang, T. Zheng, D. Li, G. Li and Y. Yue, Nano Energy, 2018, 49, 596–602 CrossRef CAS
.
- H. M. A. Hamid and Z. Çelik-Butler, Nano Energy, 2018, 50, 159–168 CrossRef CAS
.
- Y. Liang, H. D. Yoo, Y. Li, J. Shuai, H. A. Calderon, F. C. R. Hernandez, L. C. Grabow and Y. Yao, Nano Lett., 2015, 15, 2194–2202 CrossRef CAS PubMed
.
- W. Ye, F. F. Wu, N. X. Shi, H. Zhou, Q. Q. Chi, W. H. Chen, S. Y. Du, P. Gao, H. B. Li and S. L. Xiong, Small, 2020, 16, 1906607 CrossRef CAS PubMed
.
- Z. Hu, L. Wang, K. Zhang, J. Wang, F. Cheng, Z. Tao and J. Chen, Angew. Chem., Int. Ed., 2014, 53, 12794–12798 CrossRef CAS PubMed
.
- Y. Xu, F. Bahmani, M. Zhou, Y. Li, C. Zhang, F. Liang, S. Habib Kazemi, U. Kaiser, G. Meng and Y. Le, Nanoscale Horiz., 2019, 4, 202–207 RSC
.
- T. Xiong, Z. G. Yu, H. Wu, Y. Du, Q. Xie, J. Chen, Y.-W. Zhang, S. J. Pennycook, W. S. V. Lee and J. Xue, Adv. Energy Mater., 2019, 9, 1803815 CrossRef
.
- M. Liu, Q. Zhao, H. Liu, J. Yang, X. Chen, L. Yang, Y. Cui, W. Huang, W. Zhao, A. Song, Y. Wang, S. Ding, Y. Song, G. Qian, H. Chen and F. Pan, Nano Energy, 2019, 64, 103942 CrossRef CAS
.
- P. He, M. Yan, G. Zhang, R. Sun, L. Chen, Q. An and L. Mai, Adv. Energy Mater., 2017, 7, 1601920 CrossRef
.
- M. Song, H. Tan, D. Chao and H. J. Fan, Adv. Funct. Mater., 2018, 28, 1802564 CrossRef
.
- J. Yang, J. Wang, X. Dong, L. Zhu, D. Hou, W. Zeng and J. Wang, Appl. Surf. Sci., 2021, 544, 148775 CrossRef CAS
.
- L. Zhou, F. Xiong, S. Tan, Q. An, Z. Wang, W. Yang, Z. Tao, Y. Yao, J. Chen and L. Mai, Nano Energy, 2018, 54, 360–366 CrossRef CAS
.
- N. Wu, Y. Lyu, R. Xiao, X. Yu, Y.-X. Yin, X.-Q. Yang, H. Li, L. Gu and Y.-G. Gu, NPG Asia Mater., 2014, 6, e120 CrossRef CAS
.
- X. Jia, C. Liu, Z. G. Neale, J. Yang and G. Cao, Chem. Rev., 2020, 120, 7795–7866 CrossRef CAS PubMed
.
- F. Wan and Z. Niu, Angew. Chem., Int. Ed., 2019, 58, 16358–16367 CrossRef CAS PubMed
.
- D. Aurbach, D. Aurbach, Z. Lu, A. Schechter, Y. Gofer, H. Gizbar, R. Turgeman, Y. Cohen, M. Moshkovich and E. Levi, Nature, 2000, 407, 724–727 CrossRef CAS PubMed
.
- J. Muldoon, C. B. Bucur and T. Gregory, Chem. Rev., 2014, 114, 11683–11720 CrossRef CAS PubMed
.
- H. D. Yoo, I. Shterenberg, Y. Gofer, G. Gershinsky, N. Poura and D. Aurbach, Energy Environ. Sci., 2013, 6, 2265–2279 RSC
.
- Q. Wang, T. Sun, S. Zheng, L. Li, T. Ma and J. Liang, Inorg. Chem. Front., 2021, 8, 4497–4506 RSC
.
- F. Ming, H. Liang, Y. Lei, S. Kandambeth, M. Eddaoudi and H. N. Alshareef, ACS Energy Lett., 2018, 3, 2602–2609 CrossRef CAS
.
- D. Kundu, B. D. Adams, V. Duffort, S. H. Vajargah and L. F. Nazar, Nat. Energy, 2016, 1, 16119 CrossRef CAS
.
- C. Xia, J. Guo, Y. Lei, H. Liang, C. Zhao and H. N. Alshareef, Adv. Mater., 2018, 30, 1705580 CrossRef PubMed
.
- D. Chao, C. Zhu, M. Song, P. Liang, X. Zhang, N. H. Tiep, H. Zhao, J. Wang, R. Wang, H. Zhang and H. J. Fan, Adv. Mater., 2018, 30, 1803181 CrossRef PubMed
.
- W. Shi, B. Yin, Y. Yang, M. B. Sullivan, J. Wang, Y.-W. Zhang, Z. G. Yu, W. Si, V. Lee and J. Xue, ACS Nano, 2021, 15, 1273–1281 CrossRef CAS PubMed
.
- F. Wan, L. Zhang, X. Dai, X. Wang, Z. Niu and J. Chen, Nat. Commun., 2018, 9, 1656 CrossRef PubMed
.
- H. Zhang, D. Cao and X. Bai, J. Power Sources, 2019, 444, 227299 CrossRef CAS
.
- E. Levi, Y. Gofer and D. Aurbach, Chem. Mater., 2010, 22, 860–868 CrossRef CAS
.
- R. Zhang, T. S. Arthur, C. Ling and F. Mizuno, J. Power Sources, 2015, 282, 630–638 CrossRef CAS
.
- I. Shterenberg, M. Salama, Y. Gofer, E. Levi and D. Aurbach, MRS Bull., 2014, 39, 453–460 CrossRef CAS
.
- M. Chhowalla, H. S. Shin, G. Eda, L.-J. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263–275 CrossRef PubMed
.
- X. Huang, Z. Zeng and H. Zhang, Chem. Soc. Rev., 2013, 42, 1934–1946 RSC
.
- J. Xu, J. Zhang, W. Zhang and C.-S. Lee, Adv. Energy Mater., 2017, 7, 1700571 CrossRef
.
- Y. Liu, S. Liu, X. Xie, Z. Li, P. Wang, B. Lu, S. Liang, Y. Tang and J. Zhou, InfoMat, 2023, 5, e12374 CAS
.
- X. Chen, P. Ruan, X. Wu, S. Liang and J. Zhou, Acta Phys.-Chim. Sin., 2022, 38, 2111003 Search PubMed
.
- V. P. Hoang Huy, Y. N. Ahn and J. Hur, Nanomaterials, 2021, 11, 1517 CrossRef PubMed
.
- H. Li, L. Ma, C. Han, Z. Wang, Z. Liu, Z. Tang and C. Zhi, Nano Energy, 2019, 62, 550–587 CrossRef CAS
.
- H. Liang, Z. Cao, F. Ming, W. Zhang, D. H. Anjum, Y. Cui, L. Cavallo and H. N. Alshareef, Nano Lett., 2019, 19, 3199–3206 CrossRef CAS PubMed
.
- H. Li, Q. Yang, F. Mo, G. Liang, Z. Liu, Z. Tang, L. Ma, J. Liu, Z. Shi and C. Zhi, Energy Storage Mater., 2019, 19, 94–101 CrossRef
.
- W. Xu, C. Sun, K. Zhao, X. Cheng, S. Rawal, Y. Xu and Y. Wang, Energy Storage Mater., 2019, 16, 527–534 CrossRef
.
- Z.-T. Shi, W. Kang, J. Xu, Y.-W. Sun, M. Jiang, T.-W. Ng, H.-T. Xue, D. Y. W. Yu, W. Zhang and C.-S. Lee, Nano Energy, 2016, 22, 27–37 CrossRef CAS
.
- S. Li, Y. Liu, X. Zhao, Q. Shen, W. Zhao, Q. Tan, N. Zhang, P. Li, L. Jiao and X. Qu, Adv. Mater., 2021, 33, 2007480 CrossRef CAS PubMed
.
- P. Tao, H.-H. Guo, T. Yang and Z.-D. Zhang, Chin. Phys. B, 2014, 10, 106801 CrossRef
.
- J. He, K. Hummer and C. Franchini, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 075409 CrossRef
.
- H. Liang, Z. Cao, F. Ming, W. Zhang, D. H. Anjum, Y. Cui, L. Cavallo and H. N. Alshareef, Nano Lett., 2019, 19, 3199–3206 CrossRef CAS PubMed
.
- C. Wu, G. Zhao, X. Yu, C. Liu, P. Lyu, G. Maurin, S. Le, K. Sun and N. Zhang, Chem. Eng. J., 2021, 412, 128736 CrossRef CAS
.
- S. Bhoyate, J. Kim, E. Lee, B. Park, E. Lee, J. Park, S. H. Oh, J. Kim and W. Choi, J. Mater. Chem. A, 2020, 8, 12436–12445 RSC
.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 254–360 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00068k |
| This journal is © The Royal Society of Chemistry 2023 |