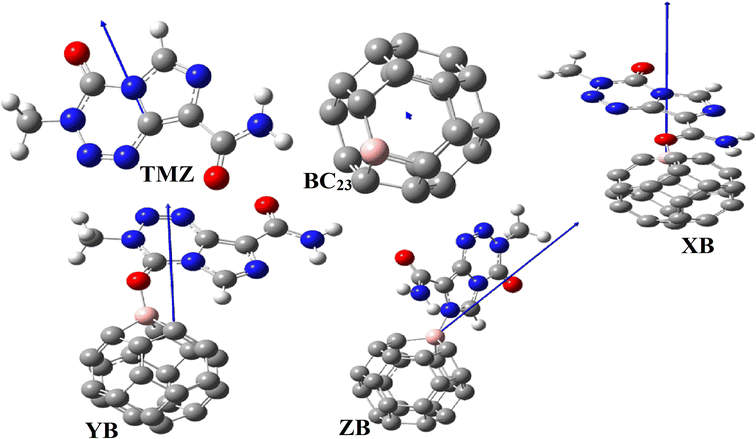
Open Access Article
Open Access ArticleDFT investigation of temozolomide drug delivery by pure and boron doped C24 fullerene-like nanocages
Aymard Didier
Tamafo Fouegue
 *a,
Vincent
de Paul Zoua
b,
Gervais Ndongo
Kounou
c,
Brice Laure
Ndjopme Wandji
b,
Julius Numbonui
Ghogomu
d and
Rahman Abdoul
Ntieche
*a
*a,
Vincent
de Paul Zoua
b,
Gervais Ndongo
Kounou
c,
Brice Laure
Ndjopme Wandji
b,
Julius Numbonui
Ghogomu
d and
Rahman Abdoul
Ntieche
*a
aDepartment of Chemistry, Higher Teacher Training College, The University of Bertoua, P.O. Box 652, Bertoua, Cameroon. E-mail: Didier_tamafo@yahoo.fr; rahmino@gmail.com
bDepartment of Chemistry, Faculty of Science, The University of Maroua, P.O. Box 814, Maroua, Cameroon
cUniversity Institute of Wood Technology of Mbalmayo, University of Yaoundé I, P.O. Box 306, Mbalmayo, Cameroon
dDepartment of Chemistry, Faculty of Science, The University of Bamenda, P.O. Box 39, Bambili-Bamenda, Cameroon
First published on 8th September 2023
Abstract
In this paper, the DFT/M05-2X-D3/6-31+G(d,p) theoretical chemistry method is used to probe the adsorption ability of pure and boron doped C24 toward the temozolomide (TMZ) anticancer drug. The study is conducted in both gas and aqueous phases. The positive values of the Gibbs free energy of formation (12.03, 9.14 and 2.51 kcal mol−1) show that the adsorption of TMZ on C24 is not allowed. However, the boron-doped C24 (BC23) forms a very stable molecular complex with TMZ in the gas phase, characterized by the adsorption energy and Gibbs free energy values of −32.07 and −21.27 kcal mol−1 respectively. Analysis of Hirshfeld's atomic charge revealed the transfer of 0.6395e from TMZ to BC23, which is confirmed by the value of the dipole moment of the complex (13.42 D in the gas phase) as well as its molecular electrostatic potential map. The change in the frontier molecular orbital energy difference of BC23 is found to be 21.67% proving the good sensitivity of the cage toward the drug. The TMZ–BC23 molecular complex is very stable in water though the sensitivity of the cage is hugely reduced in that solvent. The reliability of these results was confirmed by checking the outcomes at both wB97XD/6-31+G(d,p) and B3LYP-D3/6-31+G(d,p) levels. This work shows that pristine BC23 is a better adsorbent of TMZ than some reported nanomaterials from the theoretical chemistry point of view.
1 Introduction
Cancer is one of the main reasons for mortality in the whole world. However, the administration of an efficient cancer drug is still substantially difficult, since the common use of a single therapy strategy in several cases does not represent the optimal way to provide a complete and effective cure.1 The combination of chemotherapeutic agents has also been used to prevent drug resistance, but the ability of cancer cells to adapt and develop new resistance pathways has led to unsatisfactory results. In recent studies, many researchers have employed targeted Drug Delivery Systems (DDSs) for obliterating cancer tissues.2–4 In that purpose, nanomaterials (NMs) have emerged in recent decades as very interesting candidates not only for the delivery of anticancer drugs but also to improve the antioxidant capacity of phenolic compounds.5–7 Therefore, theoretical chemistry methods are being extensively employed to evaluate the ability of NMs toward the adsorption of toxic wastes and gases,8–13 heavy metal ions,14 the catalysis of chemical reactions,15 and the delivery of drugs of different types,16–20 just to mention a few. Among these NMs, carbon based NMs (like graphene, nanotubes, nanocones, nanodiamonds and fullerenes) being applied in all the above mentioned fields are of great interest.21,22 Indeed, carbon-based nanomaterials (CBNMs) have significantly attracted the interest of researchers in various areas because of their remarkable structural dimensions and physicochemical properties.22 With excellent optical activity and a considerable multifunctional surface area, these materials have demonstrated higher drug-loading capacity, improved biocompatibility, and lower immunogenicity.23 C24 is one of the fullerene like nanocages recently largely investigated in adsorption and drug delivery systems because of its low toxicity and minimal side effects. Indeed, theoretical chemistry methods have been used to report pure and/or doped C24 as good adsorbents and sensors of nitrosamine conformers,24 juglone,25 5-fluorouracil,3 melphalan,26 ephedrine27 and chlormethine,17 just to mention a few.Temozolomide (TMZ) is an imidazotetrazine that is 3,4-dihydro-3-methyl-4-oxoimidazole, which is substituted at the positions 3, 4 and 8 by methyl, oxo and carboxamide groups respectively. TMZ was first synthesized at Aston University in the early 1980s as one of the series of novel imidazotetrazinones. It is a 3-methyl derivative of mitozolomide (a prodrug that decomposes spontaneously to a highly reactive DNA-cross linking metabolite), which is also an imidazotetrazinone. It is an alkylating agent and is used to treat brain tumors such as glioblastoma and anaplastic astrocytoma.28 Temozolomide is a chemotherapeutic cytotoxic prodrug (inactive form designated to breakdown inside the body to form the active drug) that inhibits DNA replication by methylating nucleotide bases when hydrolyzed, and has shown a broad spectrum of antineoplastic activity.29 The methylation of DNA seems to be the principal mechanism responsible for the cytotoxicity of temozolomide to malignant cells. This methylation occurs at the N7 and O6 positions of guanine and the O3 position of adenine, and damages the DNA and triggers the death of tumor cells.28 The drug is rapidly absorbed after oral administration and undergoes spontaneous hydrolysis at physiological pH to the active metabolite, 3-methyl-(triazen-1-yl)imidazole-4-carboxamide likely the active methylating agent. The main advantages of TMZ are its lipophilic properties, its high oral bioavailability (almost 100% although the concentration found in the cerebrospinal fluid was approximately 20% of the plasma concentration), and its small size that endow it with the ability to cross the blood–brain barrier.30 Compared to other drugs like lomustine and carmustine, TMZ has a high survival benefit in patients.30 The most common side effects of temozolomide are fatigue, vomiting, fever, constipation, loss of appetite, anorexia, alopecia, head ache, tiredness, convulsions, rash, anemia, neutropenia or lymphopenia (low white blood cell count), and thrombocytopenia (low blood platelet count). The numerous side effects of the anti-cancer drug motivate the development of new particles called nano-carriers that can facilitate the transport of the anticancer drug directly to damaged organs thus limiting their side effects. It is in that vein that iron-oxide Fe3O4,31 pure and doped B12/Al12N12 FLNs2 as well as boron carbide nanotubes BC3NT32 have recently been reported as good delivery systems for TMZ.
The results from these papers as well as those on pure and doped C24 have motivated the probing of the sensing ability of pure and boron-doped C24 toward temozolomide anticancer drug as the main objective of the present research endeavor, via DFT methods. More precisely, the effects of TMZ on the geometric parameters, electronic properties, and energetic and thermochemical properties of pristine C24 and BC23 have been studied. The outcomes from this work can lead to new efficient materials for the delivery of TMZ, which to the best of our knowledge, have not yet been reported.
2 Computational methodology
All calculations in this paper have been performed using DFT methods,33 combined with the M05-2X functional.34 Indeed, this functional is very reliable for the study of structural (since it captures medium range electron correlation) and thermodynamic parameters and have been widely applied in similar studies.5,25 This functional is complemented by Grimme's type dispersion forces (GD3)35 that take into account the long range electron correlation for a deep description of adsorbent–adsorbate interactions. The Pople's type 6-31+G(d,p)36,37 basis set is used to simulate molecular orbitals. Indeed, split-valence basis sets allow the modification of the size of orbitals but not their shape. Therefore, the polarization of the basis sets is used to overcome this limitation by including orbitals with an angular momentum greater than what is needed for the ground state to describe each atom. For that purpose, p-orbitals are added to H-atoms whereas d-orbitals are added to all other atoms in the systems studied herein. Moreover, diffuse functions represented by the + sign are added to all atoms other than H atoms, to accurately represent electrons which are far from the nuclei. Accordingly, the 6-31+G(d,p) basis set is large enough and well suited to describe molecular orbitals in this work. In order to best evaluate the reliability of our theoretical results, B3LYP-D3 (ref. 38) and wB97XD39 functionals were applied to some relevant parameters best describing the adsorption of TMZ on BC23 in both gas and water phases. These functionals are all associated with the 6-31+G(d,p) basis sets. Bader's approach to topological analysis40 was complemented by the reduced density gradient (RDG)41 to identify all types of interactions between the cages and TMZ. No symmetry constraint was applied for calculations, and all geometry relaxation was followed by harmonic frequency calculation, which revealed that all structures correspond to the real minima of the potential energy surface. The close shell systems (TMZ, C24 and their molecular complexes) were relaxed in the neutral states and singlet multiplicities, whereas the open shell structures (BC23 cluster as well as its molecular complexes) were simulated in the neutral state with doublet multiplicities. The stability of the molecular complexes formed between the cages and the drug was probed via the calculations of adsorption energy and Gibbs free energy as shown in eqn (1) and (2). EX in eqn (1) stands for the electronic energy of the species X, corrected with zero point energy, whereas GX represents the free energy for the formation of X. Negative values of Eads account for stable complexes, while negative values of ΔG mean that the adsorption process is spontaneous under standard conditions. BSSE (Basis Set Superposition Error) was calculated using the counterpoise correction method to get more reliable values of Eads. The sensing ability of the cages was studied via the change in the frontier molecular orbital (FMO) energy gap (Eg) of the cage, the change in its dipole moment as well as the isosurface of the FMOs and the molecular electrostatic potential (MEP) map.41 The degree of charge transfer was also evaluated via the calculation of Hirshfeld's atomic charges through natural bond orbital (NBO) analysis. The software packages used are summarized in Table 1.| Eads = Ecomp − Ecage − ETMZ | (1) |
| ΔG = Gcomp − Gcage − GTMZ | (2) |
| Program | Use | Reference |
|---|---|---|
| Gaussian 09 | All geometry optimization, frequency calculations and NBO | 42 |
| Gaussview 06 | Introduction of data and visualization of results | 43 |
| Multiwfn | Topological analysis and identification of non-covalent interactions (NCIs) | 44 |
| VMD | Identification of NCIs concomitantly with multiwfn | 45 |
3 Results and discussion
3.1 Geometric analysis of TMZ and C24
The relaxed structure of TMZ obtained at the M05-2X-D3/6-31+G(d,p) level of theory is depicted in Fig. 1 along with some geometric parameters which agree with those previously published by Ndjopme and coworkers2 at the DFT/M06-2X-D3/6-311G(d,p) level. Its calculated Eg value is 161.62 kcal mol−1 and is in good agreement with that found in the literature at the DFT/M06-2X-D3/6-311G(d,p) level.2 These values of Eg are however far from those reported by Zhu et al. at the B3LYP-D/6-31G* level (Eg = 91.53 eV) because of the strong dependence of this parameter on the quantum chemical method used.32 It turns out from NBO analysis performed on TMZ at the M05-2X-D3/6-31+G(d,p) that O12, O16, N10 and N13 with respective Hirshfeld's charges of −0.32, −0.28, −0.17 and 0.14e are the most prominent atoms to interact with the adsorbent during the adsorption process. These observations in good agreement with previous findings of Ndjopme and coworkers.2 Moreover, in previous reports on TMZ adsorption by nanomaterials via theoretical chemistry means, only O12 and O16 are considered because of the high electronegative character of the O-atom compared to nitrogen.31,32 However, TMZ was found to preferably link to pure and doped B12N12 and Al12N12via O12 and N10.2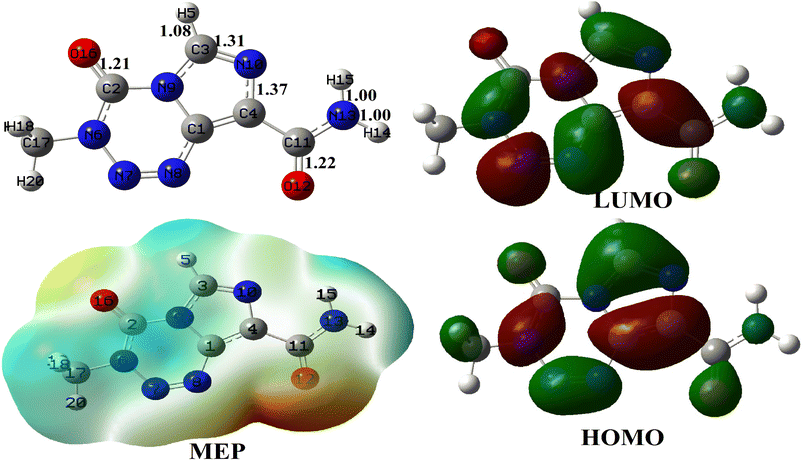 | ||
| Fig. 1 Relaxed structure of TMZ, along with some relevant bond lengths (Å), its MEP map and its FMO distribution. | ||
Geometry optimization of C24 was also performed at the M05-2X-D3/6-31+G(d,p) level (Fig. 2). This pristine compound has six 4-membered rings (4-MR) and eight 6-membered rings (6-MR). The C–C bond length (BL) in the 4-MRs and 6-MRs are 1.49 and 1.37 Å respectively in the gas phase. Moreover, their  bond angles have respective values of about 90.00° and 120.00°. These values of the geometric parameters are in agreement with those obtained in the literature.25,46 Its HOMO–LUMO energy difference (Eg) is found to be 160.53 kcal mol−1, a value which differs from that obtained by other research groups13,17 because of the high sensitivity of that parameter to the theoretical chemistry method used.2,25 NBO analysis reveals that the natural charges of the C-atoms are in the range |0.00| − |0.04|e, showing their almost neutral character.
bond angles have respective values of about 90.00° and 120.00°. These values of the geometric parameters are in agreement with those obtained in the literature.25,46 Its HOMO–LUMO energy difference (Eg) is found to be 160.53 kcal mol−1, a value which differs from that obtained by other research groups13,17 because of the high sensitivity of that parameter to the theoretical chemistry method used.2,25 NBO analysis reveals that the natural charges of the C-atoms are in the range |0.00| − |0.04|e, showing their almost neutral character.
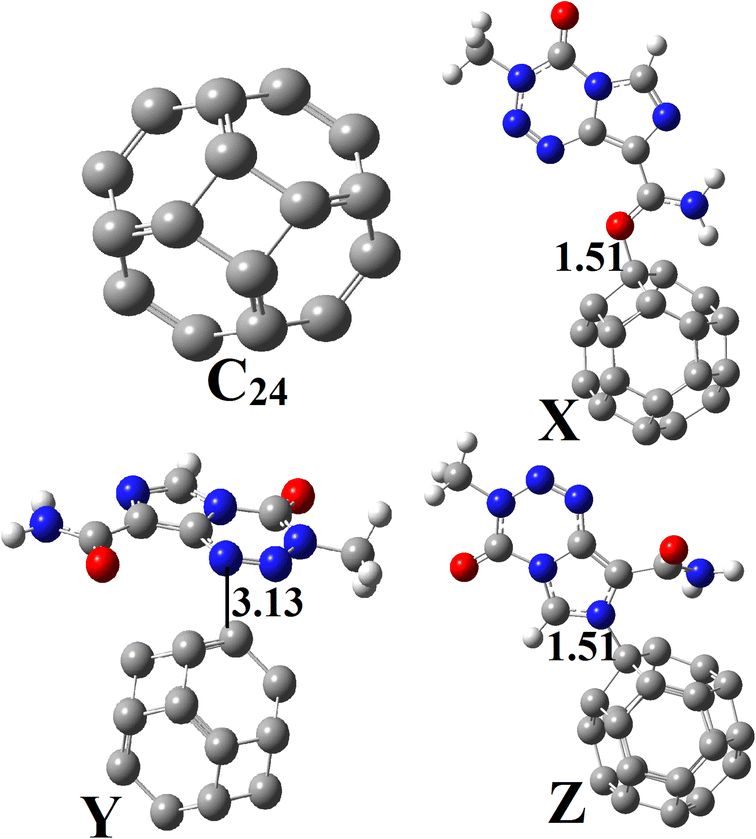 | ||
| Fig. 2 Optimized structures of C24, X, Y and Z obtained at the DFT/M05-2X-D3/6-31+G(d,p) level in the gas phase. | ||
3.2 Interaction between TMZ and C24
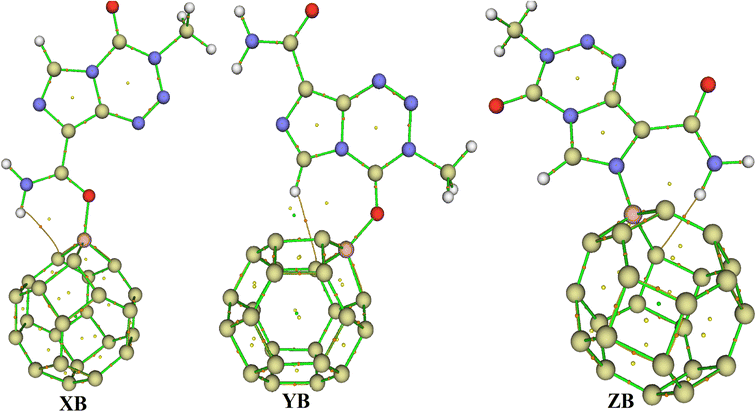
Based on the aforementioned observations, the ability of C24 to adsorb TMZ was probed through the simulation of the direct interaction between the two moieties via O12, O16 and N10 and the most acidic C-atom of C24. Three molecular states respectively called X, Y and Z were thus allowed to relax at the M05-2X-D3/6-31+G(d,p) level. The resulting optimized structures are presented in Fig. 2, whereas the values of adsorption energy and the Gibbs's free energy of adsorption are summarized in Table 2. It turns out from the analysis of Fig. 2 that the smallest interatomic distance between the adsorbent and the adsorbate is 1.51, 3.13 and 1.51 Å respectively in X, Y and Z. In X, the C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O12 BL is 1.28 Å, meaning that the said parameter is elongated upon the adsorption process. In the case of Z, the N10–C3 and N10–C4 BLs are slightly changed (≈0.01 Å) after adsorption of TMZ on C24via N10. The average values of the C–C BL of the cage are between 1.50 and 1.55 Å after the fixation of TMZ, which indicates a slight elongation. These observations show changes in the structures of both C24 and TMZ due the interaction between them. It is found from Table 2 that though all simulated molecular complexes seem stable with negative values of ΔE, their formation is not thermodynamically allowed under standard conditions since ΔG values are all positive. Furthermore, the values of Eads are −1.08, −7.89 and −4.93 kcal mol−1 respectively for X, Y and Z, which indicate a weak adsorption. Therefore, this nanocage (NC) is not suitable for the delivery of TMZ. Similar results were published by Zoua and coworkers in their study of the ability of the same cage to adsorb juglone in the gas phase, pentyl ethanoate and water.25 The adsorption of two TMZ molecules was also probed using the most stable configuration Y as the basis and was still found to be endergonic (ΔG = 2.02 kcal mol−1) under standard conditions. The adsorption process was also simulated in water via Y, and still shows a weak Eads value (−3.65 kcal mol−1) and a non-spontaneous character (ΔG = 1.89 kcal mol−1). In order to overcome this problem, the C24 NC has been doped by substituting the most acidic (with the smallest value of Hirshfeld's atomic charge) of its carbon atoms by a boron atom.
O12 BL is 1.28 Å, meaning that the said parameter is elongated upon the adsorption process. In the case of Z, the N10–C3 and N10–C4 BLs are slightly changed (≈0.01 Å) after adsorption of TMZ on C24via N10. The average values of the C–C BL of the cage are between 1.50 and 1.55 Å after the fixation of TMZ, which indicates a slight elongation. These observations show changes in the structures of both C24 and TMZ due the interaction between them. It is found from Table 2 that though all simulated molecular complexes seem stable with negative values of ΔE, their formation is not thermodynamically allowed under standard conditions since ΔG values are all positive. Furthermore, the values of Eads are −1.08, −7.89 and −4.93 kcal mol−1 respectively for X, Y and Z, which indicate a weak adsorption. Therefore, this nanocage (NC) is not suitable for the delivery of TMZ. Similar results were published by Zoua and coworkers in their study of the ability of the same cage to adsorb juglone in the gas phase, pentyl ethanoate and water.25 The adsorption of two TMZ molecules was also probed using the most stable configuration Y as the basis and was still found to be endergonic (ΔG = 2.02 kcal mol−1) under standard conditions. The adsorption process was also simulated in water via Y, and still shows a weak Eads value (−3.65 kcal mol−1) and a non-spontaneous character (ΔG = 1.89 kcal mol−1). In order to overcome this problem, the C24 NC has been doped by substituting the most acidic (with the smallest value of Hirshfeld's atomic charge) of its carbon atoms by a boron atom.
| Gas | Water | Gas | Water | ||||||
|---|---|---|---|---|---|---|---|---|---|
| E ads | ΔG | E ads | ΔG | E ads | ΔG | E ads | ΔG | ||
| X | −1.08 | 12.03 | — | — | XB | −32.07 | −21.17 | −36.50 | −23.14 |
| Y | −7.89 | 2.51 | −3.65 | 1.89 | YB | −16.45 | −5.44 | — | — |
| Z | −4.93 | 9.14 | — | — | ZB | −30.61 | −19.08 | — | — |
3.3 Interaction between TMZ and BC23
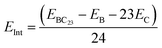 | (3) |
The relaxed structure of BC23 (Fig. 3) reveals that the B–C bond lengths of the 4-MRs and the 6-MRs are 1.57 and 1.55 Å. The value of the 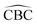 bond angle remains close to 90.0° and 120.0° respectively in the 4-MRs and the 6-MRs, whereas the
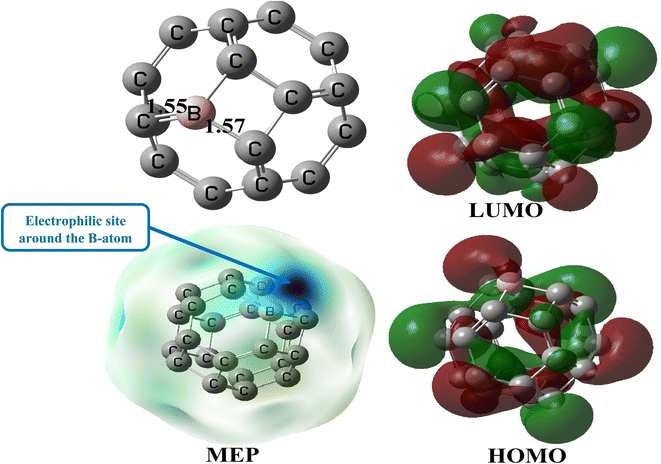
bond angle remains close to 90.0° and 120.0° respectively in the 4-MRs and the 6-MRs, whereas the 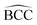 bond angle is found to be 87.3 and 116.3° in these respective rings. These parameters show a significant change in the structure of C24 after the doping with a B-atom. Its gas phase HOMO–LUMO energy difference is found to be 4.66 eV, a value somehow close to that obtained for C24 (4.60 eV). It is evident from the MEP map of BC23 (Fig. 3) that the region near the vicinity of the B-atom (with a blue colored isosurface) has the greatest electron deficiency (or the highest electrophile character), making this atom the most prone to nucleophile attacks since all other atoms have almost neutral charges. This observation is corroborated by the values of Hirshfeld's atomic charges, the boron site having the most positive value (0.19e). The aforementioned results are in good agreement with theoretically available data on pristine BC23.25,47 Finally, the change in the above geometric and electronic parameters of BC23 in water is found to be meaningless.
bond angle is found to be 87.3 and 116.3° in these respective rings. These parameters show a significant change in the structure of C24 after the doping with a B-atom. Its gas phase HOMO–LUMO energy difference is found to be 4.66 eV, a value somehow close to that obtained for C24 (4.60 eV). It is evident from the MEP map of BC23 (Fig. 3) that the region near the vicinity of the B-atom (with a blue colored isosurface) has the greatest electron deficiency (or the highest electrophile character), making this atom the most prone to nucleophile attacks since all other atoms have almost neutral charges. This observation is corroborated by the values of Hirshfeld's atomic charges, the boron site having the most positive value (0.19e). The aforementioned results are in good agreement with theoretically available data on pristine BC23.25,47 Finally, the change in the above geometric and electronic parameters of BC23 in water is found to be meaningless.
3.3.2.1 Geometric structures of the molecular complexes. In order to mimic the adsorption of TMZ on the external surface of BC23, three molecular complexes involving O12, O16 and N10 (giving respectively XB, YB and ZB) interacting directly with the NC via dative covalent bonds were simulated at the DFT/M05-2X-D3/6-31+G(d,p) level. Geometry optimization in the gas phase, followed by frequency calculation at the same level, reveals no imaginary frequency. The relaxed structures of the TMZ–BC23 molecular complexes are depicted in Fig. 4 along with some geometry parameters around the adsorption site. It is observed from Fig. 3 that the shortest adsorbent–adsorbate (B–O/N) interatomic interactions are 1.53, 1.58 and 1.58 Å respectively in XB, YB and ZB. Accordingly, XB with the smallest B–O bond length might be the most stable molecular state. Comparatively, the B–O interatomic distance between TMZ and the B12N12 pristine was found to be ≈1.55 Å in the gas phase at the M06-2X/6-311G(d,p) level,2 whereas Zhu and coworkers published a value of 1.82 Å for the smallest interatomic distance (B–O) between TMZ and the BC3NT at the B3LYP-D/6-31G(d) level.32 The difference observed in the values of the B–O bond length obtained by different authors is certainly due to the type of nanomaterial used. Furthermore, the adsorption of TMZ leads to increments in the B–C bond lengths of the pristine compound, whose values in the 6-MRs pass from 1.55 to 1.62 Å and from 1.57 to 1.63–1.66 Å in the 4-MRs of XB for instance. In the same way, the C11
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O12 and C2
O12 and C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O16 bond lengths of TMZ increase respectively from 1.21 to 1.27 and 1.20–1.25 Å after adsorption.
O16 bond lengths of TMZ increase respectively from 1.21 to 1.27 and 1.20–1.25 Å after adsorption.
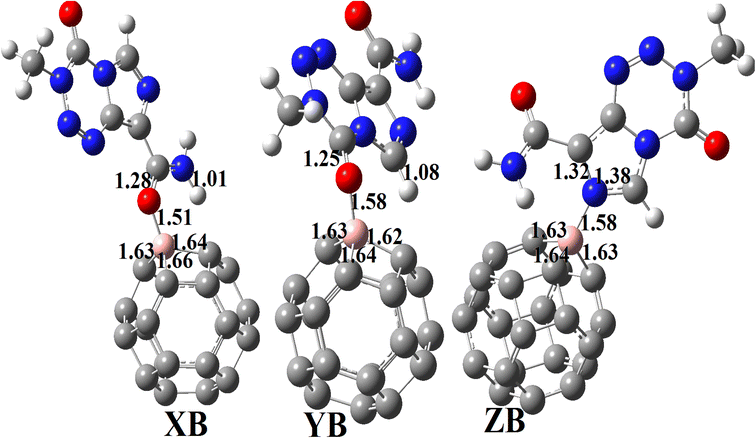 | ||
| Fig. 4 Optimized structures of XB, YB and ZB obtained at the DFT/M05-2X/6-31+G(d,p) level in the gas phase. | ||
3.3.2.2 Energetic parameters. The adsorption energy (Eads) and Gibbs free energy of adsorption ΔG have been calculated to evaluate the affinity between BC23 and TMZ. The negative values of Eint, corrected with BSSE and summarized in Table 2, clearly show that the formation of XB, YB and ZB releases 32.07, 16.45 and 30.61 kcal mol−1. These values are interestingly hugely greater than those obtained with pure C24 and show that BC23 is a better adsorbent. Moreover, XB with the lowest value of Eads is found to be the most stable molecular structure, followed by ZB and YB. The value of Eads for the most stable state in the adsorption of TMZ on the B12N12 FLN in the gas phase was reported to be −31.59 kcal mol−2, while that obtained for the adsorption of TMZ on the BC3NT is −18.84 kcal mol−1.32 Accordingly, BC23 is a better material to adsorb TMZ than B12N12 and BC3NT. The negative values of ΔG obtained for the three states simulated in the gas phase interestingly show that the adsorption process is spontaneous under standard conditions, the formation of XB being the most favorable (ΔG = −21.17 kcal mol−1). The B–O interaction between BC23 and organic molecules is thus of paramount importance for the adsorption of the latter. Zoua et al. recently reported a ΔG value of −15.73 kcal mol−1 for the adsorption of juglone on BC23 (using the M05-2X-D3/6-311+G(d,p) theoretical method) via the carbonyl O-atom of juglone. These results emphasize the importance of doping C24 by replacing one atom by boron to improve its properties.
The values of ΔE and ΔG for the formation of XB were also calculated at both B3LYP-D3/6-31+G(d,p) and wB97XD/6-31+G(d,p) theoretical levels. The results summarized in Table 3 show a good agreement between the values found with the three functionals. Indeed, the values of Eads in the gas phase are respectively −30.41 and −28.24 kcal mol−1 with wB97XD and B3LYP-D3 functionals. A similar observation is made for the ΔG values, −24.53 and −22.46 kcal mol−1 being found respectively with these functionals. The proximity between the values of Eads and ΔG obtained with the different functionals proves the reliability of the outcomes. It should be noted that the B–O bond length of XB is also found to be 1.53 Å at both B3LYP-D3/6-31+G(d,p) and wB97XD/6-31+G(d,p) theoretical levels, strengthening the aforementioned reliability.
| M05-2X-D3 | B3LYP-D3 | wB97XD | ||||
|---|---|---|---|---|---|---|
| E ads | ΔG | E ads | ΔG | E ads | ΔG | |
| Gas | −32.07 | −21.17 | −27.24 | −22.46 | −30.41 | −24.53 |
| Water | −29.50 | −23.14 | −24.65 | −19.22 | −30.43 | −23.65 |
3.3.2.3 Topology analysis of the molecular complexes. Knowing that covalent bonds are not the only interactions stabilizing chemical systems, topological analysis is usually applied to deeply scrutinize the structure of molecular systems. The Barder's approach of topology is therefore used herein to identify all interactions between the adsorbent and the adsorbate in the molecular states considered. Indeed, the Bader QTAIM (Quantum Theory of Atoms in Molecules) is a powerful tool for topology analysis containing the type and structure of bonds and intermolecular interactions. It provides good information on all types of inter- and intramolecular interactions like shared interactions (covalent bonds) and noncovalent or weak interactions such as van der Waals (vdW) interactions and hydrogen bonds found between two bonded atoms.48,49 According to this theory, the critical point of the electron density, which can be a minimum point, a maximum point, or a saddle point, can fall into four categories (atomic, bond, ring and cage). The atomic critical point (ACP) represents the geometrical position of an atom or nucleus (other than hydrogen) and geometrically denotes a local maximum point of electron density in all three directions of space. The bond critical point (BCP) indicates a critical point related to a bond or physical or chemical interaction. The ring critical point (RCP) denotes a ring or set of atoms forming a ring. Cage critical points are observed when multiple rings form a cage.50,51 Several crucial parameters obtained from a bond critical point between two or more interacting atoms are of interest when probing the nature and strength of a chemical bond interaction. Some of those parameters are electron density ρ(r), Laplacian of electron density ∇2ρ(r), total energy density h(r), Lagrangian kinetic energy G(r), potential energy density v(r), electron localization function (ELF) η(r), binding energy EL = V(r)/2, etc. Therefore
- ∇2ρ(r) < 0, h(r) < 0 and −G(r)/v(r) < 1 indicate covalent interactions;
- non-covalent interactions (like weak hydrogen bonds, vdW interactions, and electrostatic interactions) are found when ∇2ρ(r) > 0, h(r) > 0 and −G(r)/v(r) > 1;
- partially covalent interactions are characterized by ∇2ρ(r) > 0, h(r) < 0 and 0.5 < −G(r)/v(r) < 1.
ELF results from local excess kinetic energy density, which is attributed to Pauli repulsion. The ELF value is always found between 0 and 1, and when its value is between 0.5 and 1, covalent interactions are identified, whereas ELF < 0.5 is attributed to NCIs.
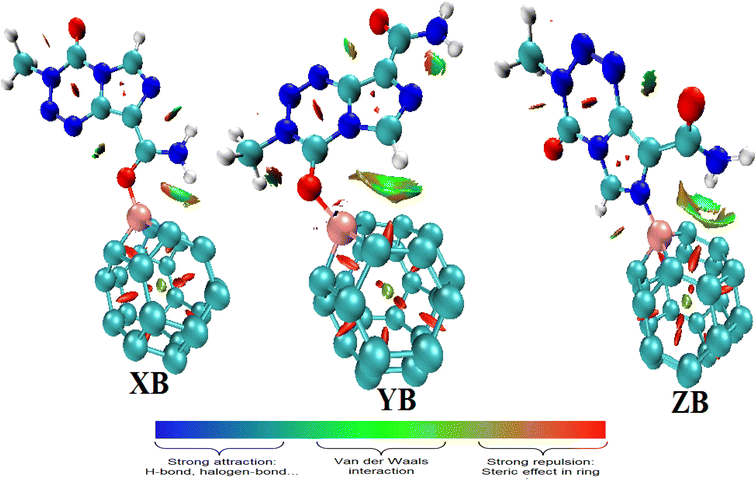
The topological parameters described herein are obtained with the M05-2X functional since the lowest values of adsorption energy are obtained at the M05-2X-D3/6-31+G(d,p) level. The molecular diagrams of the TMZ–BC23 molecular complexes presented in Fig. 5 show that in addition to the B–O/N bond, the systems have non-conventional hydrogen bonds (HBs) between the drug and the cage. One N–H⋯C hydrogen bond is thus evident in XB and ZB, whereas a C–H⋯C interaction is found in YB. Some relevant topological parameters describing those interactions are summarized in Table 4. The B–O/N bonds are all characterized by positive values of ∇2ρ(r) and negative values of the total energy density h(r). Moreover, their values of the ratio −G(r)/v(r) are in the range 0.5–1 a.u., whereas those of the ELF are less than 0.5 a.u. These observations indicate that TMZ and BC23 are linked via a partially covalent interaction like a dative bond in all molecular complexes. The absolute value of the energy E and the total electron density ρ(r) of these interactions follow the same trend and increase in the order: ZB < XB < YB. This means that the B–N bond of YB is the strongest though it has almost the same value of E with XB. The HBs in all complexes are weak since their ∇2ρ(r) > 0 and H(r) > 0. The values of the ratio −G(r)/v(r) all greater than one, as well as those of the ELF lower than 0.1000 a.u. and their energy values clearly corroborate this finding.
| ρ(r), a.u. | ∇2ρ(r), a.u. | h(r), a.u. | −G(r)/v(r), a.u. | η(r), a.u. | E (kcal mol−1) | ||
|---|---|---|---|---|---|---|---|
| XB | B–O | 0.1206 | 0.6021 | −0.0621 | 0.7739 | 0.1367 | −86.19 |
| N–H⋯C | 0.0149 | 0.0527 | 0.0018 | 1.1843 | 0.0494 | −3.02 | |
| YB | B–O | 0.1006 | 0.5181 | −0.0480 | 0.7871 | 0.1103 | −70.77 |
| C–H⋯C | 0.0101 | 0.0354 | 0.0015 | 1.2516 | 0.0330 | −1.85 | |
| ZB | B–N | 0.1259 | 0.4491 | −0.0816 | 0.7036 | 0.1798 | −86.44 |
| N–H⋯C | 0.0146 | 0.0470 | 0.0010 | 1.1034 | 0.0532 | −3.06 |
The QTAIM method was complemented by the reduced density gradient (RDG) function to evaluate the previously mentioned weak interactions. Indeed, the QTAIM lacks accuracy in predicting non-covalent interactions such as vdW interactions, hydrogen bond interactions, and π-stacking interactions. The RDG function is categorized in the context of non-covalent interaction methods, which is a powerful way to analyze the types of intermolecular interactions. The NCI index has the advantage that it allows the visualization of weak interactions in real space by means of 3D isosurfaces. From the color-filled RDG isosurface, different types of regions can be identified by simply examining their colors. The color scale bar presented in Fig. 6 shows that the more blue implies a stronger attractive interaction, whereas attractive vdW forces are depicted by the greenish or bluish surfaces.52 The NCI isosurfaces of the molecular complexes formed between TMZ and pristine BC23 (Fig. 6) confirm the presence of the HBs previously observed. These HBs, characterized by green isosurfaces, are consequently attractive vdW interactions. Apart from these HBs, several other interactions of this type in addition to ring steric repulsions are found to further stabilize the molecular systems.
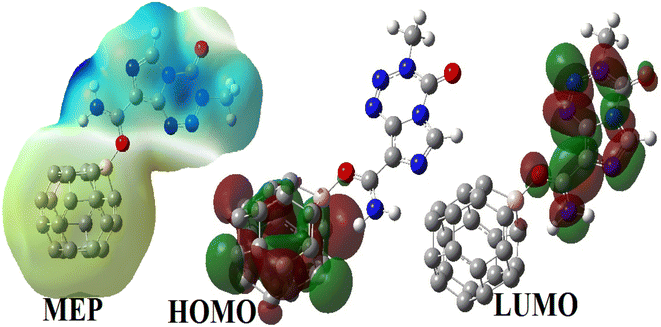
3.3.2.4 Electronic properties. The FMOs of BC23, TMZ and their molecular complexes are evaluated herein in terms of their distribution and energy. This was done to probe the reactivity, electrical conductivity, and stability of the compounds studied. The HOMO and LUMO are the first orbitals that constitute the frontier molecular orbitals. The distribution of the FMOs of all molecular complexes simulated herein are similar, the reason why only that of XB which is the most stable is depicted in Fig. 7. It is observed from Fig. 7 that the HOMO and LUMO of XB are exclusively localized on BC23 and TMZ respectively. This indicates a probable charge transfer from the TMZ moiety to the cage during the formation of the complex. The values of the FMO energy levels as well as their difference Eg are summarized in Table 5. As the structures of BC23 and the simulated complexes are open shell systems, the values of energy level presented are those of alpha orbitals. The table shows an increment in the HOMO energy of the cage from −170.80 eV to −144.78, −154.93 and −154.24 eV respectively in XB, YB and ZB after the adsorption of TMZ. However, the increase in the LUMO energy of the adsorbent upon adsorption of TMZ is slight. These observations are in agreement with the decrease in the Eg value of the cage. Indeed, the formation of XB, YB and ZB leads to a reduction of Eg of the cage by 21.67, 11.80 and 8.58% respectively at the M05-2X-D3/6-31+G(d,p) level. Moreover, the decrease in the Eg value of XB was found to be 20.06 and 50.00% with the wB97XD and B3LYP-D3 functionals respectively. These observations show the good agreement between the Minnesota and the wB97XD functionals. The most stable complex thus interestingly leads to the greatest change in Eg, showing the good sensitivity of BC23 towards TMZ. The adsorption of TMZ was reported to cause changes of 38.09 and 17.72% in the Eg values of B12N12 and Al12N12 respectively at the DFT/M06-2X/6-311G(d,p) level.1 In the same vein, Zhu and coworkers found that the adsorption of TMZ on the external surface of the BC3NT leads to 42.61% change in the Eg value of the NM.31
| TMZ | BC23 | XB | YB | ZB | ||
|---|---|---|---|---|---|---|
| Gas | E HOMO | −197.81 | −170.84 | −144.78 | −154.93 | −154.24 |
| E LUMO | −39.20 | −63.40 | −60.63 | −60.17 | −56.02 | |
| E g | 161.61 | 107.44 | 84.61 | 94.76 | 98.21 | |
| % ΔEg | — | — | 21.67 | 11.80 | 8.58 | |
| DM (Debye) | 3.63 | 0.27 | 13.42 | 5.21 | 8.92 | |
| Water | E HOMO | −192.97 | −163.23 | −150.78 | — | — |
| E LUMO | −35.50 | −56.02 | −48.88 | — | — | |
| E g | 157.47 | 107.21 | 101.90 | — | — | |
| % ΔEg | — | — | 4.94 | — | — | |
| DM (Debye) | 5.51 | 0.56 | 17.02 | — | — | |
However, this parameter was reported to be greatly influenced by the DFT functional used. In investigating the adsorption of juglone on the BC23 FLN, it was found that the Eg of the cage changes by 74.57, 36.20, 45.84 and 41.02% respectively when applying the functionals B3LYP, wB97XD, M05-2X and M06-2X to the 6-311+G(d,p) basis sets.25 Therefore, the 21.67% change observed in this work is very important in evaluating the sensing ability of BC23 since the electrical conductivity (σ) of materials is proportional to the HOMO–LUMO energy difference as shown by eqn (4). In that equation, T is the temperature and kB is the Boltzmann constant. The electrical conductivity is significantly affected by a slight shift in the energy bond gap. Consequently, the electrical conductivity of BC23 interestingly increases after the adsorption of TMZ due to the 21.67% change in the Eg value of the cage, making it suitable to sense the anticancer drug.
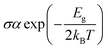 | (4) |
Dipole moment (DM) is also of paramount importance in evaluating the sensing ability of a material. High values of DM generally indicate good reactivity (since nucleophilic and electrophilic sites are far apart) and higher solubility in polar media. Table 5 shows that the DMs of BC23 XB, YB and ZB are respectively 0.27, 13.42, 5.21 and 8.92 D (data obtained with the M05-2X functional). The DM of XB is also found to be 13.21 and 13.03 D with the wB97XD and the B3LYP DFT functionals respectively. Accordingly, the adsorption of TMZ leads to a great increment in the DM of the cage, the most stable molecular complex XB interestingly exhibiting the highest DM. This might be directly related to the density of charge transfer from TMZ to the NC and explains the highest interaction energy found with XB. Indeed, the DM of the complexes is found to be directly proportional to the values of Eint as found in the literature.18 This finding corroborates the good sensing ability previously observed in analyzing the FMO levels, and implies the better solubility of the TMZ–BC23 molecular complex in polar media like water. Moreover, the vector representing the DM of XB, YB and ZB presented in Fig. 8 (along with that of TMZ and BC23) is oriented from the cage to TMZ, indicating that the former is the electron rich site of complexes.
The Hirshfeld atomic charge of the B-atom of the cage is found to decrease from 0.19(e) to 0.10, 0.09 and 0.08(e) in XB, YB and ZB respectively after adsorption. The acidity of this atom is thus reduced. Moreover, the global charge Q(e) of the cage is found to be e −0.64, −0.42 and −0.52e in these respective molecular complexes. The negative values of Q(e) as well as the aforementioned discrepancy in the atomic charge of B clearly describe a charge transfer the TMZ drug to the BC23 cage. XB still exhibits the greatest value of Q(e), followed by ZB. Accordingly, the stability of the molecular complexes is directly proportional to the amount of charge transferred from the adsorbent to the adsorbate. In NBO analysis, the stabilization energy E(2) is probed via second-order perturbation theory and the associated delocalization of charges from the donor (i) to the acceptor (j) is calculated as shown in eqn (5). In this equation, Ei and Ej are the orbital energies of the molecular complexes, and qi and Fij are respectively the donor orbital occupancy and diagonal element of the NBO Fock matrix.14 Many electron density transfers were identified between TMZ and BC23. Herein, only those involving charge transfer from the O/N-atoms of TMZ to the B-atom of the NC are summarized in Table 6. It is clearly observed from the table that the greatest values of E(2) are found in XB, confirming the highest amount of electron density delocalized from the donor to the acceptor in XB and its greatest stability.
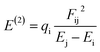 | (5) |
| Donor | Acceptor | E (2) | Donor | Acceptor | E (2) | |
|---|---|---|---|---|---|---|
| XB | LP(O24) | σ*(B) | 1873.07 | LP(O24) | RY*(B) | 108.65 |
| LP(O24) | σ*(B) | 44.81 | LP(O24) | RY*(B) | 206.74 | |
| YB | LP(O25) | σ*(B) | 137.70 | LP(O25) | σ*(B) | 10.55 |
| LP(O25) | σ*(B) | 57.98 | — | — | — | |
| ZB | LP(N2) | σ*(B) | 143.85 | LP(N2) | RY*(B) | 30.40 |
| LP(N2) | RY*(B) | 11.95 | — | — | — |
These results are corroborated by the molecular electrostatic potential (MEP) of the complexes. Indeed, the MEP map of the complex XB (which looks like that of YB and ZB) depicted in Fig. 8 clearly shows that the regions near the vicinity of the pristine have a reddish-yellow colored isosurface, whereas the TMZ moiety is surrounded by a blue isosurface. It turns out from this observation that the cage is an electron rich site while TMZ represents the electrophile site of the complex as predicted by the DM and global Hirshfeld's charge Q(e).
3.4 Effect of solvation
The optimized structures of BC23 and TMZ in water at the M05-2X-D3/6-31+G(d,p), wB97XD/6-31+G(d,p) and 3LYP-D3/6-31+G(d,p) levels of theory revealed no significant change in their geometric parameters. In order to evaluate the effect of that solvent on the adsorption process, the most stable complex XB was also allowed to relax in water. It turns out from the results that though an increment in the Eads is observed, XB remains very stable in water, with an adsorption energy of −36.50, −37.43 and −32.65 kcal mol−1 respectively the DFT functionals M05-2X-D3, wB97XD and B3LYP-D3. Moreover, a discrepancy of about 2 kcal mol−1 is found in the ΔG value for the formation of XB (at M05-2X-D3/6-31+G(d,p)), indicating that the formation of the complex is slightly more spontaneous in water than in the gas phase. The adsorbent–adsorbate interatomic distance (B–O bond length) slightly reduces in water, passing from 1.53 to 1.51 Å, whereas the length of the N–H⋯C hydrogen bond between TMZ and the cage greatly increases in water (from 2.54 in the gas phase to 2.97 Å in solution) irrespective of the functionals. These results indicate a good adsorption ability of BC23 toward TMZ in water. The values of Eads in water for the adsorption of TMZ on B12N12 and Al12N12 were reported to be respectively −26.74 and −42.18 kcal mol−1 at the M06-2X/6-311G(d,p) level.2 The best favorable adsorption capacity of BC23 toward juglone was also obtained in water by Zoua and coworkers.25 The ΔG values of these reactions were found to be −13.20 and −28.89 kcal mol−1 respectively, indicating that the reaction with BC23 is thermodynamically more favorable than that with pristine B12N12.At the M05-2X-D3/6-31+G(d,p) level of theory, the B–C bond length after adsorption of TMZ in water is 1.64–1.66 and 1.63 Å respectively in the 4-MRs and in the 6-MR. These values are similar to those obtained in the gas phase. However, the change in the FMO energy difference in water is only 4.94, 4.21 and 11.15% with the M05-2X-D3, wB97XD and B3LYP-D3 functionals respectively, indicating that BC23 is not sensitive to TMZ in aqueous solution, despite its good adsorption ability. Similar results were recently published by Ndjopme and coworkers. However, an increase in the DM of XB is observed in water, proving the solubility of the complex in that solvent.
4 Conclusion
The main objective of the present study was to evaluate the ability of C24 and BC23 to adsorb the TMZ anticancer drug via the DFT/M05-2X-D3/6-31+G(d,p) theoretical chemistry approach in both gas and aqueous media. The reliability of results was confirmed by calculating the properties of the most stable configuration at DFT/3LYP-D3/6-31+G(d,p) and DFT/wB97XD/6-31+G(d,p) theoretical levels. It came out from this work that: (i) pure pristine C24 is not a suitable adsorbent of TMZ since the Gibbs free energy of adsorption is found to be positive in both media of study; (ii) BC23 can spontaneously form at least three stable molecular complexes with TMZ, the most probable of them involving the O-atom of the amide group of TMZ (with Eads and ΔG values of −40.04 and −21.17 kcal mol−1 at the M05-2X-D3/)-31+G(d,p) level); (iii) the adsorption of TMZ on BC23 involves the transfer of −0.6395e (the value obtained with the Minnesota group functional) from the latter to the former, which is confirmed by the MEP map of XB, NBO analysis and the distribution of its FMOs; (iv) the value of the DM as well as the orientation of its vector corroborate the direction of charge transfer; (v) in addition to the B–O/N bonds, the molecular complexes TMZ-BC23 are further stabilized by a non-conventional HB found between the adsorbent and the adsorbate; (vi) the adsorption of TMZ on the external surface of BC23 is slightly more spontaneous in water than in the gas phase, though the complex is less stable; (vii) the small change in the FMO energy difference of the cage (% ΔE = 4.42, 4.21 and 11.11 respectively found with M05-2X, wB97Xd and B3LYP functionals) in water after the adsorption of TMZ shows that the sensitivity of the cage decreases in aqueous solution. According to our results, BC23 is a better adsorbent of TMZ than B12N12 and BC3NT, and is more sensitive to that drug than Al12N12.Author contributions
Tamafo Fouegue A. D.: conceptualization, investigation, writing-original draft, and software. Zoua V. de P.: investigation, writing draft, and software. Ndjopme Wandji B. L.: investigation and data curation; Ndongo K. G.: investigation and data curation. Abdoul Ntieche R.: supervision and validation. Ghogomu J. N.: supervision and validation.Conflicts of interest
The authors declare that they have no known competing interests regarding the work reported in this paper.Acknowledgements
The authors gratefully acknowledge the research modernization grant to lecturers by the Ministry of Higher Education of Cameroon.References
- J. Zugazagoita, C. Guedes, S. Ponce, I. Ferrer, S. Molina-Pinelo and L. Paz-Ares, Clin. Therapeut., 2016, 38, 1551–1566 CrossRef PubMed
.
- W. B. L. Ndjopme, A. D. Tamafo Fouegue, N. K. Nkungli, N. R. Abdoul and A. Wahabou, R. Soc. Open Sci., 2022, 9, 211650 CrossRef PubMed
.
- A. Hosseinian, V. Esmail and Y. A. Saeideh, J. Clust. Sci., 2017, 28, 2681–2692 CrossRef CAS
.
- M. S. Badiee, A. Morsali and S. A. Beyramabadi, Orient. J. Chem., 2015, 31, 2053–2057 CrossRef CAS
.
- V. P. Zoua, A. D. Tamafo Fouegue, D. M. Bikélé, N. R. Abdoul and A. Wahabou, Int. J. Quantum Chem., 2022, 122, 26843 CrossRef
.
- A. Khalili, T. B. Mohammad and H. H. G. Seyed, Electro Phys. Theor. Chem., 2020, 5, 1829–1836 CAS
.
- A. Khalili, T. B. Mohammad and H. H. G. Seyed, Vietnam J. Chem., 2021, 59, 211–220 CAS
.
- A. Rodrigo, L. Silva, D. F. S. Machado, H. C. B. de Oliveira, L. Ribeiro and D. A. da Silva Filho, Sci. Rep., 2022, 12, 15848 CrossRef PubMed
.
- A. D. Nwagu, H. Louis, H. O. Edet, I. Benjamin, N. V. Osabor and S. A. Adeyinka, Mater. Sci. Semicond. Process., 2023, 157, 107334 CrossRef CAS
.
- M. F. Fellah, Diam. Relat. Mater., 2021, 119, 108593 CrossRef CAS
.
- R. Rahimi, S. Kamalinahad and M. Solimannejad, Mater. Res. Express, 2018, 5, 035006 CrossRef
.
- M. R. Dehghan, S. Ahmadi and Z. M. Kotena, Struct. Chem., 2021, 32, 1949–1960 CrossRef CAS
.
- D. Paul, A. Vaidyanathan, U. Sarkar and B. Chakraborty, Struct. Chem., 2021, 32, 2259–2270 CrossRef CAS
.
- S. Kaviani, D. A. Tayurskii, O. V. Nedopekin and I. Piyanzina, J. Mol. Liq., 2022, 365, 120131 CrossRef CAS
.
- O. Alptekin, B. Sen, A. Savk, U. Ercetin, S. D. Mustafov, M. F. Fellah and F. Sen, Sci. Rep., 2020, 10, 7215–7227 CrossRef CAS PubMed
.
- J. S. Al-Otaibi, S. Y. Mary, N. Acharjee and D. G. Churchill, J. Mol. Model., 2022, 28, 332 CrossRef CAS PubMed
.
- R. Hossain, M. Hasan, S. D. Shamim, T. Ferdous, A. Hossain and F. Ahmed, Comput. Theor. Chem., 2021, 1197, 113156 CrossRef
.
- S. Bibi, S. Ur-rehman, L. Khalid, I. A. Bhatti, H. N. Bhatti, J. Iqbal, F. Q. Bai and H. Zhang, RSC Adv., 2022, 12, 2873 RSC
.
- G. I. Giannopoulos, Nanomater, 2022, 12, 2711 CrossRef CAS PubMed
.
- H. Ma, Y. Hou, H. Fang and A. Sarkar, J. Comput. Electron., 2021, 20, 1065–1071 CrossRef CAS
.
- J. K. Patra, G. Das, L. F. Fraceto, E. V. R. Campos, M. P. Rodriguez-Torres, L. S. Acosta-Torres, L. A. Diaz-Torres, R. Grillo, M. K. Swamy, S. Sharma, S. Habtemariam and H.-S. Shin, J. Nanobiotechnol., 2018, 16, 1–33 CrossRef PubMed
.
- S. K. Debnath and R. Srivastava, Front. Nanosci., 2021, 3, 644564–644586 Search PubMed
.
- M. Mohajeri, B. Behnam and A. Sahebkar, J. Cell. Physiol., 2018, 234, 298–319 CrossRef PubMed
.
- M. Petchmark and V. Ruangpornvisuti, Phys. E Low-dimens. Syst. Nanostruct., 2021, 127, 114506 CrossRef CAS
.
- V. P. Zoua, A. D. Tamafo Fouegue, M. O. Bouba, N. R. Abdoul and A. Wahabou, Comput. Theor. Chem., 2023, 1222, 114077 CrossRef CAS
.
- C. Celaya, L. F. Hernandez-Ayala, F. B. Zamudio, J. A. Vargaz and M. Reina, J. Mol. Liq., 2021, 329, 1–9 CrossRef
.
- B. T. Tomic, C. S. Abraham, S. Pelemis, S. J. Armakovic and S. Armokovic, Phys. Chem. Chem. Phys., 2019, 21, 23329 RSC
.
- S. F. Henry, K. Tracy and C. Hilary, Clin. Cancer Res., 2000, 6, 2585–2597 Search PubMed
.
- J. M. D. Malcolm, L. P. Greg and J. Blair, Am. J. Cancer, 2002, 1, 55–80 CrossRef
.
- O. Raul, P. Gloria and M. Consolacion, Curr. Neuropharmacol., 2021, 19, 513–537 Search PubMed
.
- R. A. Harris, J. Mol. Liq., 2019, 288, 111084 CrossRef CAS
.
- J. Zhu, Z. Lu, X. Jing, X. Wang, Q. Liu and L. Wu, Chem. Pap., 2021, 74, 4525–4531 CrossRef
.
- W. Kohn and L. L. Sham, Phys. Rev., 1965, 140, 1133–1138 CrossRef
.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382 CrossRef PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 1–19 CrossRef PubMed
.
- A. V. Rassolov, A. M. Ratner, J. A. Pople, C. P. Redfern and A. L. Curtiss, J. Comput. Chem., 2001, 22, 976–984 CrossRef
.
- J. S. Binkley, A. J. Pople and J. W. Hehre, J. Am. Chem. Soc., 1980, 102, 939–947 CrossRef CAS
.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS PubMed
.
- J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC
.
- R. F. W. Bader, Atoms in Molecules : A Quantum Theory, Oxford University Press, Ontario, 1990 Search PubMed.
- N. K. Nkungli and J. N. Ghogomu, J. Mol. Model., 2017, 23, 1–20 CrossRef CAS PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision D.01, Gaussian Inc., Wallingford, 2013 Search PubMed
.
-
R. Dennington, T. A. Keith and J. M. Millam, GaussView Version 6, Semichem Inc., Shawnee Mission, KS, USA, 2016 Search PubMed
.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS PubMed
.
- O. Masoomeh, S. Mozhgan and R. S. Hamid, Chin. J. Phys., 2020, 65, 567–578 CrossRef
.
- M. Hurst Jr and M. O. Hurst, ACS Omega, 2018, 3, 1000–1006 CrossRef PubMed
.
- M. D. Mohammadi, H. Y. Abdullahb, V. Kalamsec and A. Chaudharid, Comput. Theor. Chem., 2021, 1204, 113391 CrossRef CAS
.
- H. Louis, T. C. Egemonye, T. O. Unimuke, B. E. Inah, H. O. Edet, E. A. Eno, S. A. Adalikwu and A. S. Adeyinka, ACS Omega, 2022, 7, 34929–34943 CrossRef CAS PubMed
.
- R. F. Bader and C. F. Matta, Found. Chem., 2013, 15, 253–276 CrossRef CAS
.
- S. Howard and T. Krygowski, Can. J. Chem., 1997, 75, 1174–1181 CrossRef CAS
.
- A. D. Tamafo Fouegue, J. H. Nono, N. K. Nkungli and J. N. Ghogomu, Struct. Chem., 2021, 32, 353–366 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2023 |