Ion emission from 1–10 MDa salt clusters: individual charge state resolution with charge detection mass spectrometry†
Matthew S.
McPartlan
,
Conner C.
Harper
 ,
Emeline
Hanozin
,
Emeline
Hanozin
 and
Evan R.
Williams
and
Evan R.
Williams
 *
*
Department of Chemistry, University of California, Berkeley, California 94720-1460, USA. E-mail: erw@berkeley.edu; Tel: +(510) 643-7161
First published on 27th December 2023
Abstract
Salt cluster ions produced by electrospray ionization are used for mass calibration and fundamental investigations into cluster stability and charge separation processes. However, previous studies have been limited to relatively small clusters owing to the heterogeneity associated with large, multiply-charged clusters that leads to unresolved signals in conventional m/z spectra. Here, charge detection mass spectrometry is used to measure both the mass and charge distributions of positively charged clusters of KCl, CaCl2, and LaCl3 with masses between ∼1 and 10 MDa by dynamically measuring the energy per charge, m/z, charge, and mass of simultaneously trapped individual ions throughout a 1 s trapping time. The extent of remaining hydration on the clusters, determined from the change in the frequency of ion motion with time as a result of residual water loss, follows the order KCl < CaCl2 < LaCl3, and is significantly lower than that of a pure water nanodrop, consistent with tighter water binding to the more highly charged cations in these clusters. The number of ion emission events from these clusters also follows this same trend, indicating that water at the cluster surface facilitates charge loss. A new frequency-based method to determine the magnitude of the charge loss resulting from individual ion emission events clearly resolves losses of +1 and +2 ions. Achieving this individual charge state resolution for ion emission events is an important advance in obtaining information about the late stages of bare gaseous ions formation. Future experiments on more hydrated clusters are expected to lead to a better understanding of ion formation in electrospray ionization.
Introduction
Ionic clusters have been widely investigated by mass spectrometry. Atomic gold clusters1–3 and CsI clusters4–6 of the form [(CsI)nCs]+ and [(CsI)nI]− have been produced by laser desorption/ionization over a broad range of sizes (m/z 190–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). These clusters are useful for precise instrument calibration3,4 and fundamental studies of ion stability.5,6 Abundant “magic number” cluster sizes, corresponding to more stable structures have been observed, for example, “cubic-like” atomic arrangements, e.g., n = 13 (3 × 3 × 3) and n = 62 (5 × 5 × 5).5 The abundances of magic number clusters can be enhanced at higher temperatures7 or by activating clusters in tandem MS experiments.8,9 High internal energy can lead to the loss of neutral species that result in abundant more stable core structures.7–10
000). These clusters are useful for precise instrument calibration3,4 and fundamental studies of ion stability.5,6 Abundant “magic number” cluster sizes, corresponding to more stable structures have been observed, for example, “cubic-like” atomic arrangements, e.g., n = 13 (3 × 3 × 3) and n = 62 (5 × 5 × 5).5 The abundances of magic number clusters can be enhanced at higher temperatures7 or by activating clusters in tandem MS experiments.8,9 High internal energy can lead to the loss of neutral species that result in abundant more stable core structures.7–10
Multiply charged clusters consisting of a variety of constituents, including metal atoms,11 ion containing nanodrops,12–14 aqueous droplets,15–18 and biomolecular clusters,19–21 can be readily produced by electrospray ionization (ESI). Multiply charged clusters from a variety of salts have also been produced by ESI,8,9,22–24 with singly charged clusters of CsI with up to ∼700 constituent ions (m/z ∼90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000)23 and unresolved clusters of unknown charge up to m/z ∼150
000)23 and unresolved clusters of unknown charge up to m/z ∼150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 reported.24 Activation of multiply charged clusters can lead to dissociation by loss of one or more neutral constituents, as is the case for singly charged ions, but ionic species can also be lost. At a critical cluster size, both charge and neutral loss processes can be competitive and both processes are observed.25,26 At smaller cluster sizes, charge loss is favored but higher activation energies can promote neutral loss that is often entropically favored.26 A liquid drop model, originally developed as a model for nuclear fission, has been applied to metal clusters.11,27,28 This model includes the cluster surface energy and coulombic repulsion and predicts that cluster fission should occur above a material dependent critical value, defined as (z2/n)c, where z is the cluster charge and n is the number of atoms in the cluster. Critical values for pure metal clusters typically range from 0.97 (Au) to 0.14 (Na).11,28
000 reported.24 Activation of multiply charged clusters can lead to dissociation by loss of one or more neutral constituents, as is the case for singly charged ions, but ionic species can also be lost. At a critical cluster size, both charge and neutral loss processes can be competitive and both processes are observed.25,26 At smaller cluster sizes, charge loss is favored but higher activation energies can promote neutral loss that is often entropically favored.26 A liquid drop model, originally developed as a model for nuclear fission, has been applied to metal clusters.11,27,28 This model includes the cluster surface energy and coulombic repulsion and predicts that cluster fission should occur above a material dependent critical value, defined as (z2/n)c, where z is the cluster charge and n is the number of atoms in the cluster. Critical values for pure metal clusters typically range from 0.97 (Au) to 0.14 (Na).11,28
A key limitation in studying the very large multiply charged salt clusters that can be readily produced by ESI is mass analysis, which is challenging owing to closely spaced m/z values of all the possible charge states and cluster sizes.23,24 The resulting mass spectral complexity is a primary reason why “volatile” salts, such as ammonium acetate or ammonium bicarbonate, are used to provide a high ionic strength environment in native mass spectrometry experiments29 unless very small emitters that limit nonvolatile salt cluster formation and adduction are used.30,31 Charged salt-containing droplets initially generated by electrospray undergo rapid solvent evaporation that increases the strength of the electric field at the droplet surface and can ultimately drive droplet fission. This can occur when the coulombic repulsive forces exceed the adhesive force of the droplet surface tension. The Rayleigh limit (eqn (1)) predicts:
| zR = 8π(ε0γR3)1/2 | (1) |
The dissociation behavior of large salt-containing aqueous nanodrops and drier salt clusters with masses between 1 and 10 MDa (15–32 nm diameter) and ∼50–300 charges have been dynamically measured previously using charge detection mass spectrometry (CDMS).34 CDMS has the advantage that the m/z, charge, and mass of ions are measured on an individual basis, thereby circumventing issues associated with the spectral congestion of heterogeneous samples analyzed using conventional mass spectrometers.18,34–48 This capability has extended the size range of ionic clusters that can be investigated by more than 100-fold. The extent of charging on aqueous nanodrops relative to the Rayleigh limit charge for an aqueous nanodrop depends on the identity of ions contained in the droplet.34 For alkali metal chlorides, there was progressively less charging with increasing alkali metal ion diameter. Both extensively hydrated and more “dry” clusters were investigated. Discrete losses of minimally solvated singly charged ions were reported based on the average value of charge and mass loss measured for thousands of ion dissociation events.34 However, the high uncertainty in any single ion emission event made it difficult to determine conclusively if any of these events were losses of +2 or higher charge state ions.
Here, the dissociation behavior of salt clusters formed from aqueous solutions containing KCl, CaCl2, and LaCl3 is investigated using a method that makes it possible to obtain individual charge state resolution for the discrete emission of +1 and +2 charged species from 1–10 MDa ions. Cluster ion energy, m/z, charge, and mass are measured throughout the entire time that ions are trapped, which can range from 100 ms up to 5+ s.41,43–46,48 These capabilities have previously been used to monitor pure aqueous nanodrops up to 600+ MDa (50–120 nm in diameter) and measure relatively small ion emission events that preceded or followed large fission events.18 These results demonstrate that CDMS is well-suited for investigating the dynamics of large clusters or nanodrops and can enable further insight into the late stages of gaseous cluster ion formation from charged droplets.
Methods
Charge detection mass spectrometry
Experiments were performed using a home-built electrostatic ion trap-based charge detection mass spectrometer. A detailed description of this instrument and operating parameters are given elsewhere.41,43–45 In brief, positive ions are generated by electrospray ionization and are introduced into the instrument where they are confined in a quadrupole ion guide for up to 1 s before being pulsed through a turning quadrupole into an electrostatic cone trap for mass analysis. The frequency and harmonic amplitudes of the signal induced by each ion on a cylindrical detector tube in the center of the trap are used to dynamically determine the m/z, charge, energy per charge, and mass of each trapped ion. A short time Fourier transform (STFT) of the induced time domain signal with a 25 ms window is stepped forward in 5 ms increments. The 25 ms window length was chosen to produce adequate time resolution while limiting adverse peak broadening effects inherent to signals with changing frequencies. The pressure in the electrostatic ion trap region was ∼3 × 10−9 Torr, and ions were trapped for 1 s. In these experiments, there are typically 2–11 ions trapped and measured simultaneously. The electrostatic ion trap and the charge sensitive pre-amplifier were operated at room temperature.Ionic cluster formation
100 mM aqueous solutions of KCl, CaCl2, and LaCl3 were prepared using a Milli-Q Gradient ultrapure water purification system (Millipore, Billerica, MA). Borosilicate nanoelectrospray emitters (1.0 mm outer diameter, 0.78 mm inner diameter, with filament, Part no. BF100-78-10, Sutter Instrument, Novato, CA) were pulled to a tip inner diameter of 1.75 ± 0.11 μm using a Sutter Instrument Flaming/Brown P-87 pipet puller. Emitters were positioned ∼2 mm from the instrument inlet. A positive electrospray voltage of 0.8–1.2 kV was applied to a platinum wire that is in contact with the solution in the emitter and the resulting ions were introduced to the instrument via a modified Z-spray electrospray source (Waters Corp., Milford, MA). A source temperature of 82 °C and pressure of 35 Torr was used to optimize the production and transmission of 1–10 MDa salt clusters with limited hydration. These conditions are softer than typically used conditions for conventional measurements on this instrument that lead to more fully dehydrated gaseous ions. To allow for direct comparison between the different cluster species, all cluster experiments were conducted sequentially and with minimal tuning of instrument parameters beyond adjustment of the electrospray voltage.Results and discussion
An overview of dynamic ion signals in CDMS
The frequency of ion motion in an electrostatic ion trap is given by eqn (2),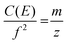 | (2) |
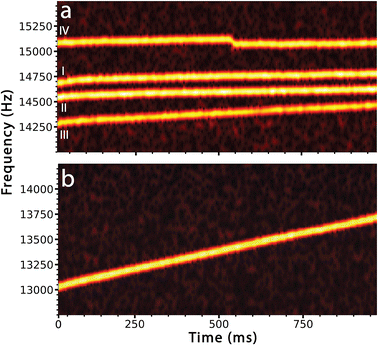
Each of these behaviors is illustrated in Fig. 1 that shows the time-dependent frequency evolution for large ionic clusters that were formed from 100 mM aqueous LaCl3. Softer source conditions were used to maintain some hydration on the majority of these ions. Fig. 1a shows the fundamental frequencies of motion of four ions between 14.0 and 15.5 kHz. These ions were simultaneously trapped along with 6 other ions (frequency traces for these ions are not shown). In these STFT traces, the frequencies of ion motion are continuously monitored throughout the trapping period and the color scale indicates the signal intensity from which ion charge is determined. Ion traces I and II (Fig. 1a) show behavior that is typical for ions that have little remaining hydration. Ions I and II have masses of 4.198 ± 0.042 MDa and 4.516 ± 0.042 MDa with 164.5 ± 1.5 and 173.0 ± 1.3 charges, respectively. These ions do not undergo a measurable change in mass or charge with time but their frequencies increase by 0.072 Hz ms−1 and 0.068 Hz ms−1, respectively. This small frequency increase is consistent with energy loss due to collisions with background gas in the electrostatic ion trap.
Ion III has a similar mass and charge as ions I and II (3.938 ± 0.044 MDa, 143.4 ± 1.4 charges at time t = 0 ms) but the frequency of this ion increases by 0.176 Hz ms−1, much more rapidly than that of the other two ions. The more rapid increase in frequency is due to continuous loss of water molecules from this ion. Mass measurements at the beginning and end of the trapping period indicate that this ion loses ∼16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ± 3490 water molecules, corresponding to an evaporative water loss rate of roughly 17 H2O per ms. Although this cluster has extensive water adduction, the rate of frequency increase and water loss is significantly less than that of a pure aqueous nanodrop of a similar size. The STFT trace for one such charged nanodrop, formed from pure aqueous solution (6.961 ± 0.044 MDa, 213.3 ± 1.4 charges at time t = 0 ms), that does not undergo charge loss or fission is shown in Fig. 1b. The frequency increases at a rate of over 0.697 Hz ms−1, which is roughly an order of magnitude greater than that of the drier clusters I and II. This is due to a larger change in mass from 6.961 ± 0.044 MDa at the start of the trapping period to 6.331 ± 0.044 MDa at the end. This mass loss corresponds to the evaporation of 35
800 ± 3490 water molecules, corresponding to an evaporative water loss rate of roughly 17 H2O per ms. Although this cluster has extensive water adduction, the rate of frequency increase and water loss is significantly less than that of a pure aqueous nanodrop of a similar size. The STFT trace for one such charged nanodrop, formed from pure aqueous solution (6.961 ± 0.044 MDa, 213.3 ± 1.4 charges at time t = 0 ms), that does not undergo charge loss or fission is shown in Fig. 1b. The frequency increases at a rate of over 0.697 Hz ms−1, which is roughly an order of magnitude greater than that of the drier clusters I and II. This is due to a larger change in mass from 6.961 ± 0.044 MDa at the start of the trapping period to 6.331 ± 0.044 MDa at the end. This mass loss corresponds to the evaporation of 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 3500 water molecules at a rate of roughly 35 H2O per ms.
000 ± 3500 water molecules at a rate of roughly 35 H2O per ms.
A sudden drop in frequency characteristic of loss of charge is illustrated for ion IV in Fig. 1a. The frequency of this ion (3.869 ± 0.039 MDa with ∼159 charges) increases slightly (0.067 Hz ms−1), similar to that for ions I and II, which is consistent with loss of energy due to background collisions and minor mass losses over the trapping period. There is an abrupt drop in frequency (−51 Hz) at ∼530 ms. This sudden frequency decrease is due to loss of charge from the ion. This appears to occur gradually over a ∼15 ms period but this is a visual artifact resulting from how these data are processed. The 80 Hz peak base width inherent to the short STFT segments (25 ms), combined with the 5 ms overlapping increment used, results in smoothing of the frequency drop between the frequencies before and after ion emission. However, analysis using longer STFT segments to improve the frequency resolution show that the two frequencies are discrete and can clearly be resolved (see ESI†). The ion that is emitted is not observed directly.
Tracing frequencies of dynamic ions
Automated analysis of multiple, simultaneously trapped ions undergoing rapid solvent evaporation and charge emission events presents a significant challenge. In order to trace the frequencies of ions that undergo rapid frequency changes, a relatively short 25 ms STFT window is used and is stepped forward in 5 ms increments. The first 5 ms of each acquired transient is discarded due to the inclusion of the impulse induced by the large voltage increase on the first cone electrode necessary to ‘close’ the trap.43 For each STFT step, both amplitudes and frequencies for signals that are above a threshold corresponding to ∼25 charges are recorded. These signals are sorted by frequency and are compared to the list of frequencies from the immediately prior STFT step for all but the first step. Each new signal is associated with a signal identified in the previous step that is within ±5 Hz where possible. These data make it possible to compose a trace of ion oscillation frequency as a function of trap time. If no peak in the prior step is within ±5 Hz, a new trace is started. This can occur as a result of a sudden frequency change due to charge emission. This process is continued in each subsequent STFT step for the entire trap time.A filtering process is required to eliminate erroneous ion traces resulting from noise capture associated with the relatively low threshold (∼25 charges) used to ensure robust tracing. Filtering is based on trace duration and slope. Traces shorter than three STFT steps (15 ms) are discarded. Longer ion traces are filtered by their frequency slope to eliminate those that originate from either noise signals or from ion–ion interactions within the trap. Traces that start in the first two STFT steps represent the initial state of each ion after successful trapping. New traces that are accompanied by the disappearance of an initial trace reflect a change in ion properties, such as charge loss. Traces with start and end times that occur within 5 STFT steps of each other are paired. Additionally, the start of the trace to be appended must be within +10 Hz or −1000 Hz of the end of the previous trace. This uneven window was selected because positive ions that lose positive charges undergo rapid and large decreases in frequency whereas frequency increases due to background gas collisions and solvent evaporation are much smaller over the same time period. Ion frequencies that increase above this +10 Hz threshold can occur due to ion–ion interactions.48 Traces that cannot be associated with an initially trapped ion are discarded.
Automated identification of charge emission events
The frequency of ion motion can change due to loss of energy, such as occurs by ion collisions with background gas or by loss of mass or charge. There are also small variations in frequency due to ion–ion interactions.48 In order to distinguish frequency changes due to charge loss from those caused by weak ion–ion interactions, the first derivative with respect to time of each trace of the fundamental frequency of each ion is computed. A 25 ms wide moving average of the first derivative signal stepped forward in 5 ms intervals is then used to smooth the trace. Ion emission events are identified by searching for negative peaks with a magnitude larger than a critical threshold. This threshold is determined by a quadratic function that takes the frequency at which the ion is oscillating into account (see ESI†). This method accounts for the nonlinear relationship between ion energy and oscillation frequency and more accurately identifies charge emission events at higher frequencies where weak ion–ion interactions with larger absolute values of frequency shift would otherwise alias as charge emission events.The STFT frequency traces of each ion that undergoes an identified emission event are divided into segments that are delineated by the time at which the event occurs. Each resulting segment is fit with a linear regression. The total magnitude of frequency loss during an emission event is computed via interpolation from these fit lines to account for ‘rolling off’ at the edges of abrupt frequency changes introduced by the STFT computation.
Analysis of charge emission using amplitude-based method
For ions that undergo a charge emission event, the average amplitude and frequency of each STFT trace segment and that of its associated harmonic trace before and after the emission event is determined. These values are subsequently used to compute the harmonic amplitude ratio (HAR) and ultimately the energy, charge and mass of the ion during each trace segment.41,42 The amplitude computed charge loss is the difference in measured ion charge averaged over all STFT steps that occur before the emission event and those that occur after the emission event. This value has substantial uncertainty because the charge loss is typically smaller than the uncertainty in the ion charge before and after fission. Subtraction of these values that have large uncertainties further compounds this issue. As an example to illustrate this problem, the charge for ion IV in Fig. 1a before charge emission at ∼530 ms is 158.4 ± 1.6 e. After charge emission, the charge is 159.2 ± 2.1 e. Subtraction of these values leads to change in the original charge of the ion of +0.8 ± 2.6 e. A reduction in frequency must correspond to the loss of a positive charge, not the addition of a positive charge to the original ion. Loss of one charge is still consistent with this value within experimental error. Thus, it is not possible to unambiguously determine the charge loss due to emission for these small emission events for any single ion emission event with this extent of measurement error. When measurements for many salt clusters and nanodrops with masses between 1 and 10 MDa (15–32 nm diameter) were made previously, the average value for charge loss was centered around the loss of a single positive charge but the distribution had a full-width at half maximum of ∼5 charges.34 Thus, the uncertainty in these measurements does not provide the resolution necessary to distinguish between a +1 and a +2 charge loss from a single ion emission measurement.Analysis of charge emission using frequency-based method
In order to obtain a more precise value for charge loss in an individual charge loss event, a different procedure was developed to relate the discrete change in frequency characteristic of a charge loss event directly to a change in charge. This can be accomplished using a procedure based on the approximation that the mass loss that accompanies the charge loss event is insignificant relative to the mass of the precursor ion. Prior experimental results on aqueous nanodrops indicate that this approximation should be valid when the charge loss is small.18 For example, loss of a singly charged ion from 2–4 MDa salt-containing aqueous nanodrops with 80–120 charges was accompanied by an unmeasurable mass loss (less than ∼2000 Da).34 Results from molecular dynamics simulations also suggest that singly charged ions that are emitted from small multiply charged water clusters carry away relatively few solvent molecules.10,51,52 Loss of a singly charged ion from a comparable size dry cluster is likely accompanied by an even smaller mass loss.In the frequency-based method, the mass and charge of the ions in each trace segment prior to emission are computed as described above in the amplitude-based method. The mass of the precursor after the emission event is approximated as the mass before the emission event, i.e., mass loss is considered negligible. Similarly, the change in ion energy per charge for a 100+ charged ion undergoing loss of one charge must also be less than 1%. Thus, C(E) in eqn (2) can also be approximated as a constant value throughout the emission event. With these two approximations, the charge loss measurement is decoupled from direct determination of charge via amplitude measurements. In other words, charge loss is determined directly from the change in frequency before and after an emission event. This method is analogous to the method used to determine the mass of a single ion demonstrated with both Fourier-transform ion cyclotron resonance53 and quadrupole ion trap mass spectrometry.54,55 In those experiments, a change in the charge state of an ion of unknown mass is induced or occurs spontaneously. If this occurs by loss or gain of a single charge, then the charge of the original ion can be determined from the two measured m/z values. In contrast, the mass and charge of the single ions in our experiments are directly measured, and the frequency change upon ion emission is used to determine the charge state of the ion that is emitted.
Eqn (2) is shown in a rearranged form in eqn (3), which relates the approximately constant C(E) and m values to the frequencies and charges before (f1; z1) and after the emission event (f2; z2).
| z2f12 = C(E)/m = z1f22 | (3) |
This can be written as a ratio (eqn (4)).
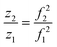 | (4) |
Using the charge value determined for the ion prior to the emission as z1, a value of z2 and ultimately the charge lost during a fission event, i.e., (z1 − z2), can therefore be determined solely by the frequency change associated with charge emission. This significantly improves the resolution obtainable by eliminating large uncertainties associated with the subtraction of two amplitudes that individually have uncertainties greater than ±1 charge.
Characterization of MDa salt clusters
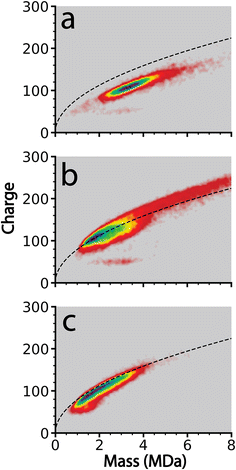
In order to determine the extent to which this frequency-based method improves the resolution of charge loss for ions that are emitted from relatively dry clusters where solvent loss should be small, this method was applied to cluster data acquired from 100 mM aqueous KCl, CaCl2, and LaCl3 solutions. These ions were chosen because they have different charge states but their ionic radii are similar (∼0.15 nm for K+ and ∼0.11 nm for Ca+2 and La+3).56 Instrumental conditions were chosen to obtain large MDa size clusters with limited hydration.Clusters generated from these three solutions were obtained sequentially using identical instrument parameters with only minor differences in ESI potentials necessary to establish and maintain ion current. The size and charge distributions of the resulting salt clusters are shown in the form of two-dimensional charge vs. mass plots in Fig. 2. The clusters are generally between 1 and 6 MDa with the exception of CaCl2, which extends in mass to ∼10 MDa. These higher mass ions are charged above the Rayleigh limit calculated for water clusters of the same mass (dashed black lines in Fig. 2). Charging of the LaCl3 clusters is much closer to the Rayleigh limit whereas charging for KCl is slightly below. The origin of the different extents of charging relative to the Rayleigh limit and hydration for these different ions is unclear and is currently under investigation.
Of these three analytes, LaCl3 clusters underwent the highest number of charge emission events with 4046 events observed from 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117 ions. CaCl2 clusters underwent 2842 emission events from 25
117 ions. CaCl2 clusters underwent 2842 emission events from 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 595 ions. KCl clusters only led to 192 initially recorded emission events from 11
595 ions. KCl clusters only led to 192 initially recorded emission events from 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 368 ions. All of these 192 events were manually reviewed, and it was determined that each event was misidentification of charge loss originating from either complex interferences between overlapping frequencies of two or more ions, or ion–ion interactions. These cases can be distinguished from true charge emission events by examining how the ion trace changes over the remaining trapping time. Patterns of oscillations in ion frequency (weak ion–ion interactions), overlaps in frequency space between two ions (ion–ion spectral interference), or correlated and opposite frequency changes between two simultaneously observed ion traces (stronger ion–ion interaction) are all common examples of phenomena that produce rapid drops in frequency that can be misidentified as charge loss events by the automated data analysis procedure described above.48 The sequential and identical nature of these experiments suggests that other data reported here include a similar proportion of misidentified ion emission events. Less than 2% of total observed ions produced interactions that were mis-identified. A similar fraction of misidentified ion–ion interactions48 are expected in the other datasets and should constitute a minor contribution to the overall statistical analysis of data where many more emission events were recorded, as is the case for CaCl2 and LaCl3.
368 ions. All of these 192 events were manually reviewed, and it was determined that each event was misidentification of charge loss originating from either complex interferences between overlapping frequencies of two or more ions, or ion–ion interactions. These cases can be distinguished from true charge emission events by examining how the ion trace changes over the remaining trapping time. Patterns of oscillations in ion frequency (weak ion–ion interactions), overlaps in frequency space between two ions (ion–ion spectral interference), or correlated and opposite frequency changes between two simultaneously observed ion traces (stronger ion–ion interaction) are all common examples of phenomena that produce rapid drops in frequency that can be misidentified as charge loss events by the automated data analysis procedure described above.48 The sequential and identical nature of these experiments suggests that other data reported here include a similar proportion of misidentified ion emission events. Less than 2% of total observed ions produced interactions that were mis-identified. A similar fraction of misidentified ion–ion interactions48 are expected in the other datasets and should constitute a minor contribution to the overall statistical analysis of data where many more emission events were recorded, as is the case for CaCl2 and LaCl3.
The reason for no observed charge emission events for KCl but many charge emission events for the other two salts may be due to the relative extents of charging of these ions as well as their relative extents of hydration. The charging relative to the Rayleigh limit computed for water for the same mass clusters is less for KCl than the other two salts. This lower coulombic repulsion may contribute to why no emission events were observed for KCl, although other factors, such as slightly lower hydration, may also play a role. Water may be more strongly bound to the higher charge state cations and may facilitate charge emission.
Determining ion hydration from STFT data
The frequencies of dry ions typically increase at a rate between 1 and 10 Hz s−1, depending on their initial frequency, due to energy loss from collisions with background gas. Ions that continuously undergo desolvation increase in frequency at a significantly higher rate due to reduction of mass and the loss of kinetic energy. Highly solvated ions undergoing rapid solvent evaporation can increase in frequency by >100 Hz over the course of a 1 s trapping interval. The frequency change due to energy loss as a result of background collisions is much less than the frequency change associated with loss of both mass and energy from solvent evaporation. Prior results on large aqueous nanodrops indicate that the rate of frequency increase before and after charge emission events, such as droplet fission, is the same.18 This is due to the small mass loss and indicates that the droplet temperature is largely unaffected by charge emission events. The rates of frequency increase before and after charge emission also appear similar in these cluster data, although a detailed statistical analysis was not performed.The ability to extract information about the extent of hydration of individual ions from these CDMS measurements makes it possible to categorize charge emission events based on the extent of precursor ion hydration. Charge emission from nearly dehydrated clusters can be distinguished from those originating from more hydrated clusters or nanodrops. The salt clusters investigated in this study were generated using instrument conditions optimized to produce nearly desolvated clusters. Ions in this condition were chosen specifically to provide insight into charge separation at late stages of droplet evaporation.
Making a direct comparison between ions with different trapping frequencies is complicated due to the nonlinear relationship between frequency and ion m/z. To account for this and compare the extents of ion hydration for the different cluster sizes, histograms of the slope of the fundamental frequency were normalized according to the frequency of each ion using eqn (5),
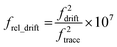 | (5) |
The normalized slope data for all of the dehydrated salt clusters and for pure aqueous nanodrops are shown in Fig. 3. The scaled frequency drift for pure water is centered at ∼7.2. In striking contrast, the scaled frequency drifts for all three salts are significantly lower, well below 0.06. Values below 0.01 are most probable for KCl and CaCl2, with the tail of the distribution extending out to higher values for CaCl2 indicating that CaCl2 clusters are on average more hydrated than KCl clusters. LaCl3 has a maximum ∼0.015 and tails out to even higher values than CaCl2. These results indicate that the average extent of remaining hydration progresses in the order KCl, CaCl2, and LaCl3 and that all three of these ionic clusters have significantly less hydration compared to that of a pure water droplet, i.e., they are at late states of bare cluster ion formation. The higher hydration with increasing cation charge suggests that water is more tightly bound to the higher charge state cations, which also have a higher overall number of anions.14
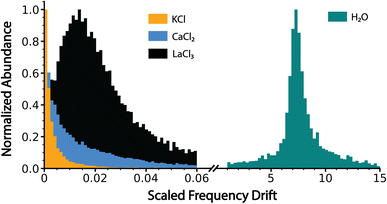 | ||
| Fig. 3 Charge detection mass spectrometry data for KCl, CaCl2, LaCl3 and pure water clusters showing the scaled frequency change (eqn (5) in text) due to energy and mass loss for clusters formed by electrospray ionization of 100 mM aqueous solutions of KCl, CaCl2 and LaCl3 and pure water. Water loss follows the trend KCl < CaCl2 < LaCl3 ⋘ pure water, indicating that these ionic salt clusters are in the late stages of bare cluster formation. | ||
The number of independent ion emission events for a single cluster ion for CaCl2 and LaCl3 shows that there are more ions that undergo 2 or more emission events during the trap period for LaCl3 than for CaCl2 (see ESI†). This suggests that greater extents of hydration are correlated with higher rates of emission events, consistent with the lack of emission events observed for the much drier KCl ions.
Comparing amplitude-based and frequency-based charge loss measurements
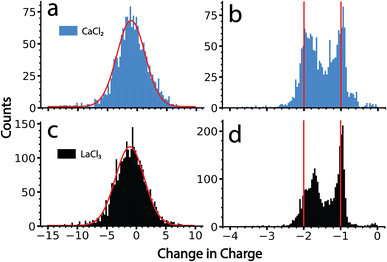
The data for ions from CaCl2 and LaCl3 solutions were processed using the amplitude-only and the frequency-based methods. Results from these two analysis methods are shown in Fig. 4. There is only a single peak with the amplitude-based method for both salts. A Gaussian fit of these data results in a centroid corresponding to an average change in the charge state of −1.0 e and −1.2 e, for CaCl2 and LaCl3 clusters, respectively (Fig. 4a and c). The distributions are reasonably fit by a Gaussian function (shown in red) and the width of this distribution is primarily due to the uncertainty in the charge determination of the precursor before and after emission in the amplitude-only method. Each distribution has nearly an equal population above −1 as it does below this value. Values above −1 are not physically reasonable; zero would correspond to no charge loss and positive values indicate that emission of a negatively charged ion occurred. If this were the case, the frequency would jump up, not down, and would not have been identified as an emission event in the tracing procedure. Heterogeneity in the magnitude of the charge loss also contributes to the width of this distribution. However, no useful information other than an approximation of an ‘average’ charge loss event can be gained owing to the magnitude of the measurement uncertainty. Results obtained here closely match what has been reported previously on similar size clusters and nanodrops.34By comparison, data analyzed using the frequency-based method shows discrete charge emission peaks corresponding to the loss of +1 and +2 charges (Fig. 4b and d), indicating that emission of either a singly charged ion or doubly charged ion can be resolved using this analysis. Emission events between −0.8 and 0 primarily originate from ion frequency interferences that were not filtered out by the dynamically calculated minimum frequency change threshold. All tracing parameters were identical to those used for the amplitude method shown in Fig. 4a and c. Thus, the improved resolution is due to the much lower uncertainty inherent to the frequency-based method for small charge losses. The peak indicating loss of 2 charges is shifted slightly towards the peak corresponding to the loss of 1 charge, which is most likely due to a larger mass loss accompanying the loss of doubly charged ions than that for singly charged ions. Larger mass losses decrease the quality of the approximation of zero mass loss used to obtain these values and result in skewed charge losses. Data showing a change in charge state of −1.8 is consistent with emission of a +2 ion that is accompanied by ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da in mass. Interestingly, there is virtually no loss of +3 ions in the data for LaCl3 despite lanthanum existing as a +3 ion in solution. This indicates that these emission events correspond to ions with one or more counterions. The actual size and composition of the species emitted is not known, but if they are clusters, their masses must be small because this method was still able to achieve individual charge state resolution.
000 Da in mass. Interestingly, there is virtually no loss of +3 ions in the data for LaCl3 despite lanthanum existing as a +3 ion in solution. This indicates that these emission events correspond to ions with one or more counterions. The actual size and composition of the species emitted is not known, but if they are clusters, their masses must be small because this method was still able to achieve individual charge state resolution.
The frequency-based method shows a similar extent of emission of +1 and +2 ions, indicating that pathways for these two processes are competitive for clusters in the size range studied here. The slightly lower average charge loss of ∼1 that was obtained from the amplitude-only method is likely due to the use of a Gaussian fitting function that does not adequately describe subtle skewing of these data toward higher charge losses. This skewing is obfuscated by the high uncertainty associated with the amplitude-only method.
Comparison of (z2/n) values
It is interesting to compare values of (z2/n)c, the critical value above which fission is predicted to occur, obtained previously for metal ions and other small multiply charged clusters to the values determined for the much larger salt clusters presented here. Fig. 5 shows (z2/n) values determined for each of the large salt clusters. These values were determined by approximating the entire mass of the cluster as pure salt with n defined as the number of individual ions in each ionic cluster. KCl, for which no fission events were observed, produces a Gaussian shaped (z2/n) distribution centered at ∼0.13. The critical size must be larger because these ions were not observed to undergo charge loss. A previous study9 has placed the critical size for +2 ions of several salts (NaI, KBr, and CsI) at around n = 18. Values of (z2/n) were not reported, but this critical size for +2 ions corresponds to a (z2/n)c value of ∼0.11, somewhat lower than what we observe for these much larger KCl clusters.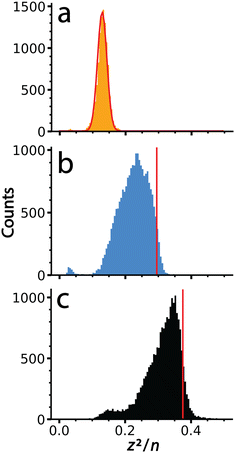 | ||
| Fig. 5 Values of (z2/n) calculated from the mass and charge data shown in Fig. 2 for (a) KCl, (b) CaCl2 and (c) LaCl3. The red line in (a) is a Gaussian fit to these data that is centered at a value of 0.13. Data for (b) and (c) were not fit due to their non-Gaussian peak shapes indicative of ion emission at higher (z2/n) values. Vertical lines, shown in red, were superimposed to indicate the point of half maximum, which are defined as (z2/n)c here. | ||
The (z2/n) distributions for CaCl2 and LaCl3 are not well fit by a Gaussian function because there is an asymmetric cutoff at the upper end of both distributions. This asymmetry and abundant fission events indicate that the edge is due to the critical cluster size as a result of depletion of clusters with higher values by charge emission. The greater extent of asymmetry on the higher values of (z2/n) for LaCl3 compared to CaCl2 is consistent with the greater number of emission events observed for the former. Values of (z2/n)c for CaCl2 and LaCl3 were estimated as the values where this edge was 50% of the peak height, ∼0.30 and ∼0.38, respectively. The increase in (z2/n)c values with cation charge state is consistent with higher stability owing to increased favorable ionic interactions. These values are similar to metal ions and slightly lower than biomolecules where (z2/n)c values of ∼0.47 and ∼0.44 have been reported for multiply protonated clusters of leucine-enkephalin19 and serine,57 respectively. These results demonstrate that cluster stability as modeled by the liquid drop model (z2/n) can be scaled to clusters of unprecedented size, and that stability can be probed using CDMS and the methods described here.
Conclusions
Charge emission from large, multiply charged salt clusters with masses between 1–10 MDa was investigated with charge detection mass spectrometry. The relative extents of hydration can be obtained from the rate at which the fundamental frequency of ion motion in the electrostatic ion trap increases with time. Hydration of these relatively dry ions increased in the order KCl, CaCl2, and LaCl3, consistent with higher water binding energies for more highly charged cations. The propensity for charge emission appears to be related to the extent of residual hydration remaining on the clusters, with more emission events observed for LaCl3 than for CaCl2. No ion emission from KCl, which formed the driest clusters, was observed. Residual water molecules in these clusters must disrupt the ionic bonds near the surface of the cluster and facilitate charge emission. The (z2/n)c values from the liquid drop model are higher for LaCl3 than for CaCl2, consistent with stronger ionic bonds in the former.Direct measurements of cluster charge can be made using the amplitude of the short time Fourier transform trace for each ion. Subtraction of the measured charge before and after an emission event provides a simple method of determining the charge lost in each event. When this method is applied to thousands of ions, the results indicate that the average ion emission event is primarily a loss of a singly charged ion. However, the large uncertainty in these measurements precludes distinguishing the loss of +1 from the loss of +2 charges from individual ions. The new frequency-based method demonstrated here clearly resolves emission of +1 and +2 ions, enabling substantially improved information to be obtained about charge emission pathways from these large clusters. Emission of +3 ions was negligible for LaCl3, indicating that hydrated ions of La+3 reported previously when generated by ESI likely originated from Rayleigh fission of larger droplets that have lower salt concentrations.12,58,59 This frequency-based method for single charge state resolution for ion loss from individual highly charged ions is applicable to any FTMS method, such as Orbitrap-based CDMS. The use of this method to investigate ion formation from nanometer sized aqueous droplets formed by electrospray ionization is under further investigation and we expect these studies will shed new light on the mechanism of how ions are formed in electrospray ionization.
Author contributions
MSM performed experiments, developed software and analyzed results. ERW directed investigations. All authors contributed to the design of experiments, development of the methods, analysis of data and the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the National Science Foundation Division of Chemistry under grant number CHE-2203907 and the Arnold and Mabel Beckman Foundation Postdoctoral Fellowship in Chemical Instrumentation (C. C. H.). Software needed to obtain information about ion fragmentation from individual CDMS ion traces was developed with financial support from the National Institutes of Health (5R01GM139338).References
- L. Schweikhard, P. Beiersdorfer, W. Bell, G. Dietrich, S. Krückeberg, K. Lützenkirchen, B. Obst and J. Ziegler, Hyperfine Interact., 1996, 99, 97–104 CrossRef CAS.
- C. Yannouleas, U. Landman, A. Herlert and L. Schweikhard, Phys. Rev. Lett., 2001, 86, 2996–2999 CrossRef CAS PubMed.
- L. Kolářová, L. Prokeš, L. Kučera, A. Hampl, E. Peňa-Méndez, P. Vaňhara and J. Havel, J. Am. Soc. Mass Spectrom., 2017, 28, 419–427 CrossRef PubMed.
- X. Lou, J. L. J. van Dongen and E. W. Meijer, J. Am. Soc. Mass Spectrom., 2010, 21, 1223–1226 CrossRef CAS PubMed.
- M. E. Castro, D. H. Russell, I. J. Amster and F. W. McLafferty, Anal. Chem., 1986, 58, 483–485 CrossRef CAS PubMed.
- M. A. Baldwin, C. J. Proctor, I. J. Amster and F. W. McLafferty, Int. J. Mass Spectrom. Ion Processes, 1983, 54, 97–107 CrossRef CAS.
- C. N. Stachl and E. R. Williams, J. Phys. Chem. Lett., 2020, 11, 6127–6132 CrossRef CAS PubMed.
- V. H. Wysocki, C. M. Jones, A. S. Galhena and A. E. Blackwell, J. Am. Soc. Mass Spectrom., 2008, 19, 903–913 CrossRef CAS PubMed.
- D. Zhang and R. G. Cooks, Int. J. Mass Spectrom., 2000, 195–196, 667–684 CrossRef.
- L. Konermann and Y. Haidar, Anal. Chem., 2022, 94, 16491–16501 CrossRef CAS PubMed.
- W. A. Saunders, Phys. Rev. A, 1992, 46, 7028–7041 CrossRef PubMed.
- W. A. Donald, M. Demireva, R. D. Leib, M. J. Aiken and E. R. Williams, J. Am. Chem. Soc., 2010, 132, 4633–4640 CrossRef CAS PubMed.
- M. J. DiTucci and E. R. Williams, Chem. Sci., 2017, 8, 1391–1399 RSC.
- S. Heiles, R. J. Cooper, M. J. DiTucci and E. R. Williams, Chem. Sci., 2017, 8, 2973–2982 RSC.
- E. J. Davis and M. A. Bridges, J. Aerosol Sci., 1994, 25, 1179–1199 CrossRef CAS.
- A. Doyle, D. R. Moffett and B. Vonnegut, J. Colloid Sci., 1964, 19, 136–143 CrossRef CAS.
- M. A. Abbas and J. Latham, J. Fluid Mech., 1967, 30, 663–670 CrossRef.
- E. Hanozin, C. C. Harper, M. S. McPartlan and E. R. Williams, ACS Cent. Sci., 2023, 9, 1611–1622 CrossRef CAS PubMed.
- J. C. Jurchen, D. E. Garcia and E. R. Williams, J. Am. Soc. Mass Spectrom., 2003, 14, 1373–1386 CrossRef CAS PubMed.
- S. W. Lee and J. L. Beauchamp, J. Am. Soc. Mass Spectrom., 1999, 10, 347–351 CrossRef CAS.
- A. E. Counterman, A. E. Hilderbrand, C. A. S. Barnes and D. E. Clemmer, J. Am. Soc. Mass Spectrom., 2001, 12, 1020–1035 CrossRef CAS.
- M. Gamero-Castaño and J. Fernández de la Mora, Anal. Chim. Acta, 2000, 406, 67–91 CrossRef.
- F. Sobott, H. Hernández, M. G. McCammon, M. A. Tito and C. V. Robinson, Anal. Chem., 2002, 74, 1402–1407 CrossRef CAS PubMed.
- D. L. Shinholt, S. N. Anthony, A. W. Alexander, B. E. Draper and M. F. Jarrold, Rev. Sci. Instrum., 2014, 86, 113109 CrossRef PubMed.
- T. E. Cooper and P. B. Armentrout, J. Phys. Chem. A, 2009, 113, 13742–13751 CrossRef CAS PubMed.
- R. L. Wong and E. R. Williams, J. Phys. Chem. A, 2003, 107, 10976–10983 CrossRef CAS.
- M. Seidl and M. Brack, Ann. Phys., 1996, 245, 275–310 CAS.
- A. Vieira and C. Fiolhais, Phys. Lett. A, 1996, 220, 231–236 CrossRef CAS.
- A. T. Iavarone, O. A. Udekwu and E. R. Williams, Anal. Chem., 2004, 76, 3944–3950 CrossRef CAS PubMed.
- A. C. Susa, Z. Xia and E. R. Williams, Anal. Chem., 2017, 89, 3116–3122 CrossRef CAS PubMed.
- A. C. Susa, Z. Xia and E. R. Williams, Angew. Chem., Int. Ed., 2017, 56, 7912–7915 CrossRef CAS PubMed.
- L. Rayleigh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1882, 14, 184–186 CrossRef.
- D. Duft, T. Achtzehn, R. Müller, B. A. Huber and T. Leisner, Nature, 2003, 421, 128 CrossRef CAS PubMed.
- C. C. Harper, D. D. Brauer, M. B. Francis and E. R. Williams, Chem. Sci., 2021, 12, 5185–5195 RSC.
- A. G. Elliott, S. I. Merenbloom, S. Chakrabarty and E. R. Williams, Int. J. Mass Spectrom., 2017, 414, 45–55 CrossRef CAS PubMed.
- T. Doussineau, C. Y. Bao, R. Antoine, P. Dugourd, W. Zhang, F. D'Agosto and B. Charleux, ACS Macro Lett., 2012, 1, 414–417 CrossRef CAS PubMed.
- D. Z. Keifer and M. F. Jarrold, Mass Spectrom. Rev., 2017, 36, 715–733 CrossRef CAS PubMed.
- D. Z. Keifer, E. E. Pierson and M. F. Jarrold, Analyst, 2017, 142, 1654–1671 RSC.
- W. H. Benner, Anal. Chem., 1997, 69, 4162–4168 CrossRef CAS.
- B. L. Barney, S. N. Pratt and D. E. Austin, Planet. Space Sci., 2016, 125, 20–26 CrossRef.
- A. G. Elliott, C. C. Harper, H.-W. Lin and E. R. Williams, Analyst, 2017, 142, 2760–2769 RSC.
- C. C. Harper, A. G. Elliott, H.-W. Lin and E. R. Williams, J. Am. Soc. Mass Spectrom., 2018, 29, 1861–1869 CrossRef CAS PubMed.
- C. C. Harper, A. G. Elliott, L. M. Oltrogge, D. F. Savage and E. R. Williams, Anal. Chem., 2019, 91, 7458–7465 CrossRef CAS PubMed.
- A. G. Elliott, C. C. Harper, H.-W. Lin, A. C. Susa, Z. Xia and E. R. Williams, Anal. Chem., 2017, 89, 7701–7708 CrossRef CAS PubMed.
- C. C. Harper, Z. M. Miller, M. S. McPartlan, J. S. Jordan, R. E. Pedder and E. R. Williams, ACS Nano, 2023, 17, 7765–7774 CrossRef CAS PubMed.
- C. C. Harper, Z. M. Miller, H. Lee, A. J. Bischoff, M. B. Francis, D. V. Schaffer and E. R. Williams, Anal. Chem., 2022, 94, 11703–11712 CrossRef CAS PubMed.
- J. S. Jordan, Z. M. Miller, C. C. Harper, E. Hanozin and E. R. Williams, J. Am. Soc. Mass Spectrom., 2023, 34, 1186–1195 CrossRef CAS PubMed.
- C. C. Harper, V. S. Avadhani, E. Hanozin, Z. M. Miller and E. R. Williams, Anal. Chem., 2023, 95, 10077–10086 CrossRef CAS PubMed.
- D. Z. Keifer, A. W. Alexander and M. F. Jarrold, J. Am. Soc. Mass Spectrom., 2017, 28, 498–506 CrossRef CAS PubMed.
- E. E. Pierson, D. Z. Keifer, L. Selzer, L. S. Lee, N. C. Contino, J. C. Y. Wang, A. Zlotnick and M. F. Jarrold, J. Am. Chem. Soc., 2014, 136, 3536–3541 CrossRef CAS PubMed.
- L. Konermann, R. G. McAllister and H. Metwally, J. Phys. Chem. B, 2014, 118, 12025–12033 CrossRef CAS PubMed.
- S. Consta, J. Mol. Struct.: THEOCHEM, 2002, 591, 131–140 CrossRef CAS.
- X. Cheng, Nucleic Acids Res., 1996, 24, 2183–2189 CrossRef CAS PubMed.
- D. M. Bell, C. R. Howder, R. C. Johnson and S. L. Anderson, ACS Nano, 2014, 8, 2387–2398 CrossRef CAS PubMed.
- C. R. Howder, D. M. Bell and S. L. Anderson, Rev. Sci. Instrum., 2014, 85, 014104 CrossRef PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- J. S. Jordan and E. R. Williams, Analyst, 2021, 146, 2617–2625 RSC.
- M. F. Bush, R. J. Saykally and E. R. Williams, Int. J. Mass Spectrom., 2006, 253, 256–262 CrossRef CAS PubMed.
- M. F. Bush, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2008, 130, 9122–9128 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Effects of STFT segment length on time and frequency resolution, computation of dynamic frequency threshold for charge emission events, and frequency of zero, one and multiple ion emission events for single ions. See DOI: https://doi.org/10.1039/d3an01913f |
| This journal is © The Royal Society of Chemistry 2024 |