Phenotypic profiling based on body fluid traces discovered at the scene of crime: Raman spectroscopy of urine stains for race differentiation
Bhavik
Vyas
 a,
Lenka
Halámková
a,
Lenka
Halámková
 b and
Igor K.
Lednev
b and
Igor K.
Lednev
 *a
*a
aDepartment of Chemistry, University at Albany, State University of New York, Albany, NY 12222, USA. E-mail: ilednev@albany.edu
bDepartment of Environmental Toxicology, Texas Tech University, Lubbock, TX 79409, USA
First published on 27th August 2024
Abstract
Modern criminal investigations heavily rely on trace bodily fluid evidence as a rich source of DNA. DNA profiling of such evidence can result in the identification of an individual if a matching DNA profile is available. Alternatively, phenotypic profiling based on the analysis of body fluid traces can significantly narrow down the pool of suspects in a criminal investigation. Urine stain is a frequently encountered specimen at the scene of crime. Raman spectroscopy offers great potential as a universal confirmatory method for the identification of all main body fluids, including urine. In this proof-of-concept study, Raman spectroscopy combined with advanced statistics was used for race differentiation based on the analysis of urine stains. Specifically, a Random Forest (RF) model was built, which allowed for differentiating Caucasian (CA) and African American (AA) descent donors with 90% accuracy based on Raman spectra of dried urine samples. Raman spectra were collected from samples of 28 donors varying in age and sex. This novel technology offers great potential as a universal forensic tool for phenotypic profiling of a potential suspect immediately at the scene of a crime, providing invaluable information for a criminal investigation.
Introduction
Forensic science is the application of scientific principles and techniques to matters of criminal justice, focusing on investigating crimes. Forensic scientists collect, preserve, and analyze evidence to aid in solving these crimes. Key areas of forensic science, such as DNA analysis, toxicology, fingerprint analysis, digital forensics, and trace evidence examination, heavily rely on analytical chemistry.1The analysis of body fluid traces at a crime scene is of paramount importance in forensic investigations.2 Identifying the type of body fluid associated with a specific stain can provide crucial contextual information, helping investigators determine the stain's relevance to the case. Body fluid traces are particularly significant as they can serve as a source of DNA evidence and make a link to a person of interest.3 Alongside fingerprints, DNA is one of the few pieces of physical evidence capable of conclusively identifying an individual.4
Along with DNA profiling, it is important to determine the type of bodily fluid, so that the prosecutor can demonstrate its relevance to the crime. Current forensic methods for body fluid identification are primarily based on enzymatic effects or serology.5 These methods can be time-consuming and destructive, sometimes showing false positive results.6 These limitations are a massive downside when the volume of samples collected at crime scenes is low in quality and/or quantity. In cases with small amounts of evidence, there is a possibility of using up all of the evidence available to identify the body fluid and not having enough remaining for DNA analysis. Forensic investigations aim to prioritize critical testing and get the best possible outcome from the evidence to identify an individual. Ideally, the body fluid trace should be preserved after identification for future tests. Recent literature has discussed that forensic laboratories are dealing with a considerable backlog of DNA evidence because all collected stains are subjected to DNA analysis without a prior body fluid identification.7 Our laboratory3,5 and others8–13 have been working on developing emerging technologies for identifying body fluid traces. SupreMEtric LLC is commercializing a universal, non-destructive test for the confirmatory identification of all main body fluids using Raman spectroscopy (https://www.supremetric.com/).
A corresponding match is required to utilize the results of a DNA test in a criminal investigation. Alternatively, characteristics such as sex and race could be used to create a profile for a person of interest. Developing a suspect profile immediately after the crime scene is discovered could be invaluable for the investigative leads and narrowing down the pool of potential suspects. Our laboratory and others combine vibrational spectroscopy and machine learning for phenotypic profiling based on the analysis of body fluids. Specifically, Raman spectroscopy showed promising results for determining sex based on the analysis of bloodstains14 and saliva,15 race based on bloodstain16 and semen,17 and the age group of the donor based on bloodstains.18 In addition, ATR FTIR of bloodstains was used to determine the sex, race,19 and chronological age of the donor.20
One body fluid of interest for forensic analysis is urine, as it is vital evidence often found at crime scenes of sexual assault cases.3 At other times, urine is commonly discovered on the victims of kidnapping and confinement,21 in drug-related crimes, and on corrections officers after prisoners have thrown urine bombs.22 Forensic investigations aim to identify individuals involved in a crime, whether as the culprit or victim, by employing techniques such as DNA profiling from body fluid traces and fingerprint analysis from crime scenes. Studies have reported that DNA can be extracted from dry urine traces.23,24 However, the challenge in analyzing urine samples lies in the composition, as they are predominantly water and contain minimal cellular components.25 Thus, urine provides little DNA, which can be insufficient for profiling and makes identifying an individual challenging.26 Given these complexities, there is a pressing need for novel methods in forensic science to analyze urine traces accurately and non-destructively.
Urine is a primarily transparent, amber-colored, sterile liquid generated by the kidneys while filtering blood. Humans produce an average of 0.6–2.6 L of urine per day. The generation of urine depends upon the water balance in the body.25 The major components of urine are metabolic byproducts like urea, creatinine, ammonia, creatine, inorganic ions (Na+, K+, Cl−), hippuric acid, citric acid, etc.25 Urine composition can vary depending on the donors’ diet, physical activity, and environment. Various factors affect the concentration of creatinine.27 Creatinine is formed in the body by spontaneous irreversible dehydration of creatine and creatine phosphate from muscle metabolites. The rate of creatinine formation decreases with age. Approx. 2% of the body's creatine is converted to creatinine every 24 hours. Recent studies have shown that the amount of creatinine formed differs among different races because of genetic and biological factors.28 In the context of phenotype profiling based on urine trace evidence, Takakura et al. recently reported a method using Fourier transform infrared (FTIR) spectroscopy combined with multivariate statistics to determine the donor's sex from urine traces.29
The advancement of analytical techniques has significantly enhanced forensic trace evidence analysis, particularly in the context of body fluid identification. Emerging methods, such as advanced liquid chromatography mass spectrometry (LC-MS), X-ray diffraction, next-generation RNA sequencing, nanotechnologies, and lab-on-chip devices, are increasingly employed as presumptive and confirmatory tests.30 Vibrational spectroscopy techniques like Raman spectroscopy and infrared spectroscopy (IR) are gaining popularity in forensic evidence analysis.31–34 These techniques require minimal sample preparation, are highly specific, and offer great sensitivity with non-destructive and rapid analysis.5,35 Specifically, Raman spectroscopy has shown great potential in analyzing various types of forensic trace evidence, providing detailed information about the molecular composition of samples in a non-destructive manner. Examples include paint, hair, ink, fibers, fingerprints, gunshot residues, and body fluid analysis.35–39 Raman spectroscopy also allows for rapid analysis at a crime scene with the help of handheld spectrometers, which are commercially available.40,41 Handheld Raman instruments, such as the TruNarc™ handheld narcotic analyzer from Thermo Fisher Scientific (https://www.thermofisher.com/order/catalog/product/TRUNARC), are designed to be compact and lightweight. These features enhance their portability, allowing forensic experts to easily transport them to crime scenes or other locations requiring on-site forensic analysis. A handheld Raman spectrometer allows for real-time analysis and decision-making, which can be critical in forensic investigations. The addition of advanced chemometrics to spectroscopic techniques makes it a powerful and universal tool for trace evidence analysis.42–46 Chemometrics utilizes the multivariate property of spectral data and can uncover latent relationships of variables. Based on these relationships, it can draw a comprehensive output and, specifically, can provide classifications and identify significant components based on spectral features.47,48
In this proof-of-concept study, we utilize Raman spectroscopy combined with advanced statistical analysis to introduce a novel technique for determining the racial background of donors from dry urine traces. This approach has the potential to enhance the efficiency of suspect identification and streamline forensic investigations.
Materials and methods
A total of 28 human urine samples (14 Caucasian; 14 American of African descent) were purchased from BioIVT, Inc. (Westbury, NY). The donor population was selected to accommodate sex and age variations. Male and female donors were adequately represented in each sample class. The donors ranged in age from 13 to 68 (p > 0.05). All urine samples (1 sample per donor) were stored at −20 °C until sample preparation. Before deposition, the urine samples were thawed and homogenized using a vortex (Heathrow Scientific, Vernon Hills, IL). Aliquots of 10 μL were deposited onto microscope slides covered with aluminum foil to limit substrate interference.49 The samples were kept in a hood for at least 24 hours at room temperature for drying before spectral collection.Instrumentation
All Raman spectra were collected using an inVia Raman Microscope (Renishaw, Inc. Hoffman Estate, IL) using WiRE 3.2 software and equipped with a Leica research-grade microscope. The microscope was outfitted with a 50× objective and a PRIOR automatic mapping stage, which collected spectra from various points of the sample stain. A 785 nm wavelength laser source was used for excitation, with a 1200 g mm−1 grating achieving a spectral resolution of approximately 1.2 cm−1 that was sufficient for this work since the minimum natural bandwidth of the Raman bands of our samples was approximately 15 cm−1. The spectral collection range used for this study was 400–1800 cm−1. A total of 18 spectra per sample were collected by selecting points in a grid pattern, with two 10 s accumulations at each point. A silicon standard was used for the calibration (band at 520 cm−1) prior to daily spectral collection.Statistical data analysis
RF is a robust classification method known for its resilience against outliers and non-normal distributions (e.g., zero-truncated data and extreme value distributions). It can handle large numbers of variables54 even if they are highly correlated55 and can estimate the importance of each predictor (i.e., representative wavenumbers in spectra). RF is a classification and regression machine learning method that constructs an ensemble of numerous de-correlated decision trees.52,54 Each decision tree is trained on a different subset of the data, known as a bootstrap sample, drawn with or without replacement from the original training dataset. The remaining subset of the original dataset serves the out-of-bag (OOB) portion, which will be used as a cross-validation dataset. The OOB error rate is an important metric used to evaluate the cross-validation performance (misclassification rate) of the Random Forest model. It is calculated by aggregating results from all OOB portions and determining differences between the predictions and the actual instances. In a Random Forest, each decision tree is trained on a bootstrapped sample of the original dataset. Consequently, specific data points are excluded or considered “out-of-bag” in each tree. Calculating the OOB error rate involves evaluating each data point in the training set using the trees not trained on that specific data point. This process enables the estimation of the model's performance on unseen data. The predicted output of each out-of-bag data point is compared to its actual output, resulting in the calculation of the error rate as the proportion of misclassified data points. The OOB error rate is typically calculated using the out-of-bag (OOB) samples, which are not included in the training of each decision tree within the Random Forest ensemble. This error rate provides an overall estimation of the model's performance on unseen data. It is important to note that the OOB error rate is specific to Random Forest models and is not a standard evaluation metric for other models.54
We can tune several parameters to optimize the RF model for the intended classification. The first is node size, which determines the depth of the tree build and the number of observations in each node of the classifier tree. Additionally, each node separates the data into two subsets, maximizing their homogeneity concerning the classes (races). The size of this subset is the same for all trees set by the researcher and referred to as “m-try”. To determine the optimal number of trees, we have built multiple Random Forest models with different numbers of trees (n-tree values) and recorded the OOB error rate. Subsequently, we select the number of trees with a stabilized minimum OOB rate. If there are many features in the training dataset, many trees may be necessary to encompass the variance. Hence, big data like spectral datasets will need lots of computing power and time to determine an optimal number of trees. We can use the Gini index feature selection technique for dimensionality reduction, select the most critical spectral feature for the discrimination between classes, and eliminate the spectral noise.56 The GINI index is computed from permuting OOB data and observing how much a prediction error changes when the data for that variable is permuted while all others remain unchanged. The prediction error on the out-of-bag portion of the data for each tree was recorded as an OOB error rate for classification. Gini importance measures the average gain of purity (homogeneity) by splits of a given variable. The more critical the variable, the more it splits labeled nodes into pure single-class nodes. Permuting a vital variable leads to relatively significant decreases in mean Gini importance.
The RF model adopts the Gini index to determine the best-split selection based on spectral features. The OOB sample is used to estimate the prediction error and then to evaluate variable importance. RF assesses the relative importance of the features during the classification process by identifying variables that contribute the most to the analysis.
In addition to predicting outcomes in classification, RF can be applied to the training datasets to select essential variables. RF essentially tries to build homogeneous groups of samples, and RF reveals the features that most strongly influence the formation of these groups. RF allows for estimating the importance of elements used for classification, shedding light on the biological basis of the classification results.
In the tree-building process, a set of randomly chosen variables are considered candidates for each tree split, and the variables that yield the best separation are chosen. For subsequent nodes (partitions) in the tree, another optimal binary division is performed until a leaf (or terminal node) is created, representing a class. This process is repeated to construct other trees with another bootstrap portion from the original dataset. Many bootstrap samples and feature subsets are drawn from the original dataset. Each classification tree is fitted to a bootstrap sample (referred to as the “in-bag” spectra) using the subset features. The spectra not sampled (referred to as the “out-of-bag” spectra OOB) are left for testing, and the model makes the predictions based on these spectra. The predictions for all spectra in the OOB portion are made by traversing down the tree, and final predictions are made by averaging over the forecast of all decision trees. During the Random Forest (RF) construction, the OOB error rate is calculated to estimate predictive performance. The final prediction of the RF is a combination of predictions from all the trees in the ensemble. Each tree predicts a class for spectra, and the entire forest generates the percentage of votes for each class by aggregating results across all trees. Combining trees and their predictions is known as “bagging” and ensures that the trees are de-correlated with each other.
The “bagging” techniques aggregate high-variance trees to enhance prediction accuracy.56 While the RF model randomizes the variable selection during each tree split, making it susceptible to overfitting due to its nature of creating multiple decision trees, using the Gini index for the feature selection mitigates this risk and prevents overfitting and noise at the spectral level.
In the context of a Random Forest model applied to a Raman spectral dataset, the mean decrease Gini (or Gini index) is a measure used to assess the importance of each spectral variable (or feature) in predicting the target variable. The Gini index measures impurity or the extent of class mixing within a decision tree node. The mean decrease Gini provides insight into which spectral variables contribute more to the predictive power of the Random Forest model for the Raman spectral dataset. Variables with higher mean decrease Gini values are typically considered more relevant or influential in distinguishing between different classes or categories within the dataset.57
Results and discussion
The Raman spectra were acquired from all 28 urine samples and were collected using automatic mapping. The mapping techniques collected 18 spectra per sample from different points of urine stain to cover the intrinsic heterogeneity. The average Raman spectra of both races are shown in Fig. 1. The urine spectrum resembles the spectrum of urea and shows some peaks corresponding to creatinine. A strong peak at 1013 cm−1 corresponds to the N–C–N stretching of urea, and minor peaks at 534 cm−1, 549 cm−1, and 1175 cm−1 can be assigned to urea and creatinine.5,26 According to the literature, the small response at 1541 cm−1 can be attributed to the C–N stretching of urea and the C–C stretching of the aromatic ring of acids in the urine.5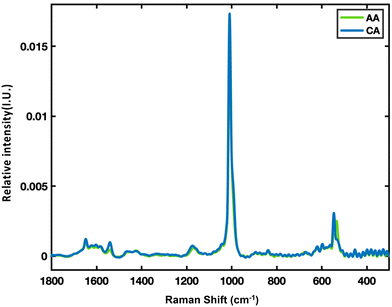 | ||
| Fig. 1 Average Raman spectra of both races: American of African descent (AA, green) and Caucasian American (CA, blue). | ||
There is a small difference between the preprocessed average Raman spectra of AA and CA samples, as evident in Fig. 1. The difference between the mean spectra of AA and CA datasets is shown in Fig. 2, along with one standard spectral deviation for each class. The difference spectrum is within one standard deviation for each class, indicating that the difference is most probably statistically insignificant. Therefore, using individual bands in the Raman spectra cannot identify the donor's race class. Therefore, a statistical analysis of the entire Raman spectra would be needed to classify individual Raman spectra.58
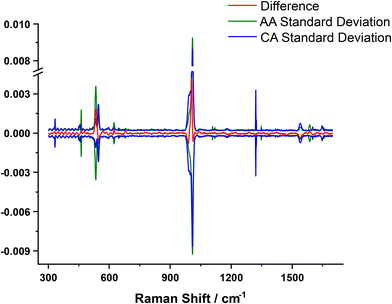 | ||
| Fig. 2 Difference mean Raman spectrum (red) and in-class standard deviations of urine spectra of Caucasian American (blue) and American of African descent (green) classes. | ||
We used 18 samples (9-CA and 9-AA) to create a training dataset for the RF model and left aside ten randomly chosen samples as the test dataset. The randomized selection of test samples ensures that each sample has an equal opportunity to be included in the test set, mitigating potential limitations and biases. After the training data from the 18 donors were processed and the final RF model was built, the remaining spectral data from 10 samples in external validation (test dataset) were analyzed, and their class was predicted to determine the RF's performance.
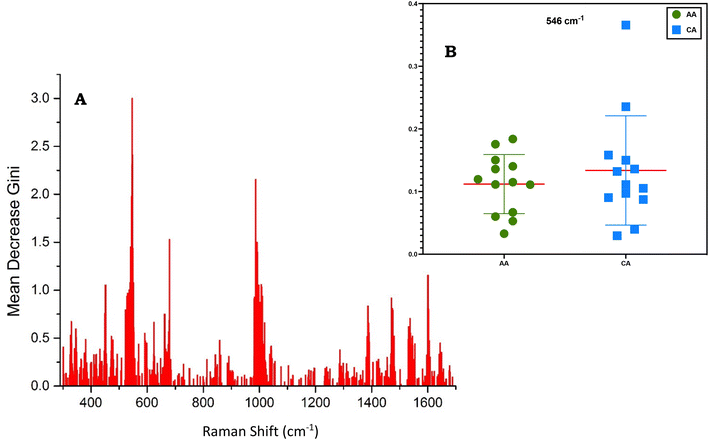
The Gini index (or mean decrease Gini) produced by RF was applied for dimensionality reduction. Specifically, the Gini index selected the most “important spectral features” to build a simpler model. Furthermore, we reran Random Forest, dropping 65% of the least informative features from the model suggested by the Gini index. This step aimed to reduce the Raman spectral region, minimize the inclusion of features that may not significantly contribute to the model's predictive power, and prevent overfitting the model based on data noise. Using the predictors chosen by the Gini index, a new RF model was trained on the entire training dataset comprising 316 spectra. The Mean Gini index helped to select 500 features (wavenumber regions) from the training dataset to build the final model and eliminate noise. Fig. 3A shows the mean decrease in the Gini coefficient as a measure of how each variable contributes to the homogeneity of the nodes in the resulting Random Forest.
Mean decrease Gini values were selected for the critical Raman band of the urine, which is best suited for classifying the two racial groups (Fig. 3A). Raman shifts are 549 cm−1, 780 cm−1, 1013 cm−1, and 1610 cm−1 and can be assigned mostly to creatine, urea, and creatinine.25,26 The literature supports the peak assignment as the creatinine formation rate differs among the races.28 The band at 546 cm−1 has been identified as the most significant based on the Mean Gini index. However, it is noted that the mean and standard deviation values of this band exhibit substantial overlap between the classes (Fig. 3B). Consequently, there is a necessity for a machine learning approach that can leverage all features selected by the Gini index, along with their combinations, to construct an algorithm capable of effectively harnessing the complexity inherent in hyperspectral datasets. This algorithm should be designed to discern donors’ race accurately.
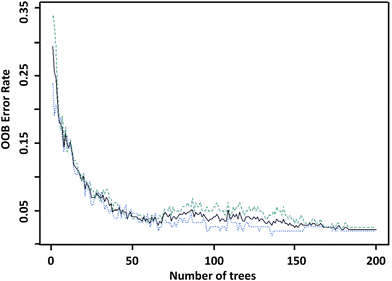
In the next step, we explored how changes in n-tree and m-try affected the OOB error rate. The value of m-try = 12 was obtained using the automatic tuning function in R software (Liaw and Wiener 2001). We also plotted RF models with varying numbers of trees against the corresponding OOB error rate. Fig. 4 shows that after about 200 trees, the error stabilizes and reaches the minimum. Consequently, the final RF model was based on 200 classification trees with twelve variables at each split (m-try). Regarding the node size parameter (the minimum number of observations required to create a terminal node), we kept the default settings of the package (node size = 1), which results in deeper trees with more final nodes.
The final RF model was based on 200 classification trees with 12 variables at each split (m-try). Once the RF model was created, it was used to predict the test dataset of 175 spectra from ten different donors. The OOB error rate is calculated during model training and indicates the model's error approximation.59 This error rate, derived from the prediction accuracy of all other trees, assessed the final RF model's performance. Once the final Random Forest model is trained, it is then applied to the external test dataset to evaluate its performance on completely new and unseen data. The performance of the final model on the test dataset was summarized by the confusion matrix that provides a detailed breakdown of the model's predictions compared to the actual classes in the test dataset.
The OOB error rate of the final RF model was estimated as 2%, corresponding to seven misclassified spectra (Table 1), which indicates a high predictive performance of the constructed RF model. All donors in the training dataset were correctly classified. The mean decrease Gini index for the feature selection helped improve the performance and prediction ability of the Random Forest model by selecting the spectral region that contributes most to the discrimination of two races while eliminating noise and spurious data points. The OOB error rate provided a robust estimation of error, validating the model's effectiveness.
| Type of Random Forest | Classification |
|---|---|
| Number of trees | 200 |
| Number of variables at each split | 12 |
| Node size | 1 |
| OOB estimate of error rate | 2% |
| Confusion matrix (cross validation) | CA (actual) | AA (actual) |
|---|---|---|
| CA (predicted) | 152 | 3 |
| AA (predicted) | 4 | 157 |
| Confusion matrix (external validation) | CA | AA |
|---|---|---|
| CA (predicted) | 84 | 13 |
| AA (predicted) | 3 | 75 |
| External validation (donor level) | CA (actual) | AA (actual) |
|---|---|---|
| CA (predicted) | 5 | 1 |
| AA (predicted) | 0 | 4 |
The OOB method provided very stable prediction results with high prediction accuracy and low error for the cross-validation. However, the cross-validation is performed solely on the training dataset. To determine the model's true performance, we conducted external validation using ten samples that were withheld from the training process and were kept separate from the model during the training phase. In Random Forests (RF), predictions are made by aggregating votes from all decision trees in the ensemble. Each spectrum is classified based on the majority vote, with the class receiving the highest number of votes considered the prediction. Thus, each unknown spectrum is ultimately assigned to one of the races, CA or AA, with a higher classification probability. It means the default 50% threshold was applied to the model's spectral level predictions. A total of 175 spectra from 10 donors were selected for external validation, ensuring they were not used in model training, and were introduced into the final RF model. The classification prediction for the spectra from 10 donors from the external validation dataset is shown in Fig. 5, with the probabilities (per spectrum) to be assigned to class CA. This analysis allowed for the discrimination of CA and AA races with an accuracy of 91% at the spectral level (Table 1). Urine stains display inherent heterogeneity with a non-uniform distribution of components throughout the stain. This heterogeneity results from evaporation, diffusion, and crystallization processes, which impact urine constituents’ concentration and spatial organization. As a result, distinct variations in the Raman spectra are observed across different regions of the stain, highlighting the influence of these processes on the spectroscopic characteristics of urine stains. Spectral misclassification is not an unusual result as not all the Raman spectra collected from urine stains will reflect the characteristic Raman signature of the race intended because of the low concentration regions of the biomarkers in urine stains, as mentioned above. Hence, it is vital to perform sample-level classification using spectral-level prediction with a 50% default threshold. Considering the donor-level predictions with an appropriate threshold (50%), external validation reached 90% accuracy for predicting the class of unknown donors. Nine of ten donors were classified correctly, with most of the spectra assigned to an actual class, thus confirming the method's reliability for this proof-of-concept study of race differentiation based on human urine traces analyzed by Raman spectroscopy.
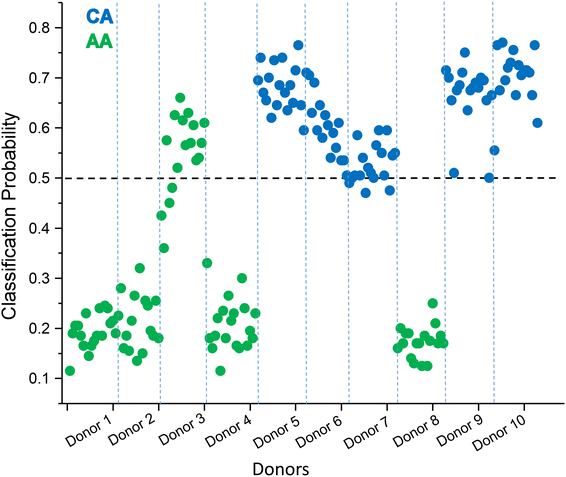 | ||
| Fig. 5 External validation of the RF model. The estimated classification probability for each spectrum is shown. All urine spectra were scored with the likelihood attributed to the CA race. | ||
For this proof-of-concept study, we used 18 samples, each with 18 spectra from different spots, totaling approximately 316 spectra. The high-dimensional nature of Raman spectroscopy, with numerous features per spectrum, compensated for the limited sample size in the calibration dataset. The Random Forests are effective with small datasets,54 and bootstrapping cross-validation with out-of-bag error estimation further supports our model's reliability by training on multiple data subsets and validating with the remaining data.60 Our binary Random Forest model achieved an impressive 90% accuracy on external validation samples, which were completely unknown to the model, demonstrating its robustness. Urine serves as an ultrafiltrate of blood, containing cellular components indicative of genetic and hereditary traits. The results obtained affirm that Raman spectroscopy's selectivity enables the capture of distinct genetic markers present within urine stains found at the crime scene.
Conclusion
A novel analytical technique is highly in demand for the forensic analysis of body fluids. Urine, primarily consisting of water with minimal cellular components, poses challenges for forensic scientists due to the limited abundance of biochemical features. Raman spectroscopy presents a rapid, non-destructive, label-free, and highly sensitive method, which are the fundamental advantages of forensic trace evidence analysis. In this proof-of-concept study, we have demonstrated a novel method for differentiating Americans of African descent and Caucasians using Raman spectroscopy paired with a Random Forest classification model. The optimized RF model could distinguish between Caucasians and African Americans with 90% accuracy at the donor level by correctly identifying the donor's race in 9 out of 10 external validation samples. However, further investigation is required to cover variations such as the time of urine collection, donors’ diet, environmental factors, and medical conditions that can affect the spectral output of urine. This proof-of-concept study included only two racial groups, Caucasian and African American. Future research will utilize a larger donor pool to include a broader range of ethnicities and mixed-race donors. The reliability of our results is supported by external validation, which achieved a 90% accuracy for the nine additional samples that were not included in the training dataset.Author contributions
Conceptualization: I. K. L. and B. V.; data curation: L. H. and B. V.; formal analysis: L. H. and B. V.; investigation: B. V.; methodology: I. K. L. and B. V.; writing – original draft: I. K. L., B. V., and L. H.; writing – review & editing: I. K. L., B. V., and L. H.; supervision: I. K. L.; funding acquisition: I. K. L.; project administration: I. K. L.Data availability
The datasets used and analyzed during the current study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Alexis Weber for proofreading the manuscript. This work was supported in part by the National Science Foundation grant 2304318. I.K.L. acknowledges a Williams-Raycheff endowment.References
- E. Mistek, et al., Toward Locard's Exchange Principle: Recent Developments in Forensic Trace Evidence Analysis, Anal. Chem., 2019, 91(1), 637–654 CrossRef CAS PubMed.
- K. Virkler and I. K. Lednev, Analysis of body fluids for forensic purposes: from laboratory testing to non-destructive rapid confirmatory identification at a crime scene, Forensic Sci. Int., 2009, 188(1–3), 1–17 CrossRef CAS.
- C. K. Muro, et al., Forensic body fluid identification and differentiation by Raman spectroscopy, Forensic Chem., 2016, 1, 31–38 CrossRef CAS.
- R. Li, Forensic Biology: A Subdiscipline of Forensic Science, in Forensic Biology, Abingdon, Oxon, Routledge, 2015, pp. 53–69 Search PubMed.
- B. Vyas, L. Halámková and I. K. Lednev, A universal test for the forensic identification of all main body fluids including urine, Forensic Chem., 2020, 20, 100247 CrossRef CAS.
- K. Virkler and I. K. Lednev, Analysis of body fluids for forensic purposes: From laboratory testing to non-destructive rapid confirmatory identification at a crime scene, Forensic Sci. Int., 2009, 188(1), 1–17 CrossRef CAS PubMed.
- R. A. Wickenheiser, Proactive crime scene response optimizes crime investigation, Forensic Sci. Int. Synergy, 2023, 100325 CrossRef PubMed.
- H. Yang, et al., Body fluid identification by mass spectrometry, Int. J. Legal Med., 2013, 127(6), 1065–1077 CrossRef PubMed.
- E. Hanson, et al., Targeted S5 RNA sequencing assay for the identification and direct association of common body fluids with DNA donors in mixtures, Int. J. Legal Med., 2023, 137(1), 13–32 CrossRef PubMed.
- E. K. Hanson, H. Lubenow and J. Ballantyne, Identification of forensically relevant body fluids using a panel of differentially expressed microRNAs, Anal. Biochem., 2009, 387(2), 303–314 CrossRef CAS PubMed.
- J. Antunes, et al., A data-driven, high-throughput methodology to determine tissue-specific differentially methylated regions able to discriminate body fluids, Electrophoresis, 2021, 42(9–10), 1168–1176 CrossRef CAS PubMed.
- A. Takamura, et al., Soft and Robust Identification of Body Fluid Using Fourier Transform Infrared Spectroscopy and Chemometric Strategies for Forensic Analysis, Sci. Rep., 2018, 8(1), 8459 CrossRef.
- N. Achetib, et al., Specific fluorescent signatures for body fluid identification using fluorescence spectroscopy, Sci. Rep., 2023, 13(1), 3195 CrossRef CAS PubMed.
- A. Sikirzhytskaya, V. Sikirzhytski and I. K. Lednev, Determining Gender by Raman Spectroscopy of a Bloodstain, Anal. Chem., 2017, 89(3), 1486–1492 CrossRef CAS PubMed.
- C. K. Muro, L. de Souza Fernandes and I. K. Lednev, Sex Determination Based on Raman Spectroscopy of Saliva Traces for Forensic Purposes, Anal. Chem., 2016, 88(24), 12489–12493 CrossRef CAS.
- E. Mistek, et al., Race Differentiation by Raman Spectroscopy of a Bloodstain for Forensic Purposes, Anal. Chem., 2016, 88(15), 7453–7456 CrossRef CAS.
- C. K. Muro and I. K. Lednev, Race Differentiation Based on Raman Spectroscopy of Semen Traces for Forensic Purposes, Anal. Chem., 2017, 89(8), 4344–4348 CrossRef CAS.
- K. C. Doty and I. K. Lednev, Differentiating Donor Age Groups Based on Raman Spectroscopy of Bloodstains for Forensic Purposes, ACS Cent. Sci., 2018, 4(7), 862–867 CrossRef CAS.
- E. Mistek, L. Halámková and I. K. Lednev, Phenotype profiling for forensic purposes: Nondestructive potentially on scene attenuated total reflection Fourier transform-infrared (ATR FT-IR) spectroscopy of bloodstains, Forensic Chem., 2019, 16, 100176 CrossRef CAS.
- S. Giuliano, E. Mistek-Morabito and I. K. Lednev, Forensic Phenotype Profiling Based on the Attenuated Total Reflection Fourier Transform-Infrared Spectroscopy of Blood: Chronological Age of the Donor, ACS Omega, 2020, 5(42), 27026–27031 CrossRef CAS.
- T. Nakazono, et al., Dual Examinations for Identification of Urine as Being of Human Origin and for DNA-Typing from Small Stains of Human Urine, J. Forensic Sci., 2008, 53(2), 359–363 CrossRef CAS PubMed.
- G. Rischitelli, et al., The risk of acquiring hepatitis B or C among public safety workers: A systematic review, Am. J. Prev. Med., 2001, 20(4), 299–306 CrossRef CAS PubMed.
- M. Prinz, W. Grellner and C. Schmitt, DNA typing of urine samples following several years of storage, Int. J. Legal Med., 1993, 106(2), 75–79 CrossRef CAS.
- S. Ghatak, R. B. Muthukumaran and S. K. Nachimuthu, A simple method of genomic DNA extraction from human samples for PCR-RFLP analysis, J. Biomol. Tech., 2013, 24(4), 224–231 Search PubMed.
- S. Bouatra, et al., The Human Urine Metabolome, PLoS One, 2013, 8(9), e73076 CrossRef CAS.
- J. Bispo, et al., Correlating the amount of urea, creatinine, and glucose in urine from patients with diabetes mellitus and hypertension with the risk of developing renal lesions by means of Raman spectroscopy and principal component analysis, J. Biomed. Opt., 2013, 18(8), 087004 CrossRef.
- L. Caporossi, et al., A new HPLC-MS/MS method for urinary creatinine determination: Comparison study with Jaffè's method, Urine, 2023, 5, 23–28 CrossRef.
- D. B. Barr, et al., Urinary creatinine concentrations in the U.S. population: implications for urinary biologic monitoring measurements, Environ. Health Perspect., 2005, 113(2), 192–200 CrossRef CAS PubMed.
- A. Takamura, et al., Phenotype Profiling for Forensic Purposes: Determining Donor Sex Based on Fourier Transform Infrared Spectroscopy of Urine Traces, Anal. Chem., 2019, 91(9), 6288–6295 CrossRef CAS.
- L. M. Almehmadi and I. K. Lednev, Stand-off Raman spectroscopy is a promising approach for the detection and identification of bloodstains for forensic purposes, J. Raman Spectrosc., 2024, 55(2), 227–231 CrossRef CAS.
- C. K. Muro, et al., Vibrational Spectroscopy: Recent Developments to Revolutionize Forensic Science, Anal. Chem., 2015, 87(1), 306–327 CrossRef CAS.
- T. Yaseen, D.-W. Sun and J.-H. Cheng, Raman imaging for food quality and safety evaluation: Fundamentals and applications, Trends Food Sci. Technol., 2017, 62, 177–189 CrossRef CAS.
- A. Weber, et al., Innovative Vibrational Spectroscopy Research for Forensic Application, Anal. Chem., 2023, 95(1), 167–205 CrossRef CAS.
- A. Weber, A. Wójtowicz and I. K. Lednev, Post deposition aging of bloodstains probed by steady-state fluorescence spectroscopy, J. Photochem. Photobiol., B, 2021, 221, 112251 CrossRef CAS.
- S. R. Khandasammy, et al., Bloodstains, paintings, and drugs: Raman spectroscopy applications in forensic science, Forensic Chem., 2018, 8, 111–133 CrossRef CAS.
- K. C. Doty, et al., What can Raman spectroscopy do for criminalistics?, J. Raman Spectrosc., 2016, 47(1), 39–50 CrossRef CAS.
- G. McLaughlin and I. K. Lednev, Potential application of Raman spectroscopy for determining burial duration of skeletal remains, Anal. Bioanal. Chem., 2011, 401(8), 2511–2518 CrossRef CAS PubMed.
- M. O. Amin, E. Al-Hetlani and I. K. Lednev, Discrimination of smokers and nonsmokers based on the analysis of fingermarks for forensic purposes, Microchem. J., 2023, 188, 108466 CrossRef CAS.
- S. R. Khandasammy, et al., Identification and highly selective differentiation of organic gunshot residues utilizing their elemental and molecular signatures, Spectrochim. Acta, Part A, 2023, 291, 122316 CrossRef CAS PubMed.
- W. R. de Araujo, et al., Portable analytical platforms for forensic chemistry: A review, Anal. Chim. Acta, 2018, 1034, 1–21 CrossRef CAS PubMed.
- A. Lanzarotta, M. Witkowski and J. Batson, Identification of Opioids and Related Substances using Handheld Raman Spectrometers, J. Forensic Sci., 2020, 65(2), 421–427 CrossRef CAS PubMed.
- A. P. Barber, A. R. Weber and I. K. Lednev, Raman spectroscopy to determine the time since deposition of heated bloodstains, Forensic Chem., 2024, 37, 100549 CrossRef CAS.
- A. Sikirzhytskaya, et al., Raman spectroscopy for the identification of body fluid traces: Semen and vaginal fluid mixture, Forensic Chem., 2023, 32, 100468 CrossRef CAS.
- V. Sikirzhytski, A. Sikirzhytskaya and I. K. Lednev, Advanced statistical analysis of Raman spectroscopic data for the identification of body fluid traces: Semen and blood mixtures, Forensic Sci. Int., 2012, 222(1), 259–265 CrossRef CAS.
- A. Gredilla, et al., Non-destructive Spectroscopy combined with chemometrics as a tool for Green Chemical Analysis of environmental samples: A review, TrAC, Trends Anal. Chem., 2016, 76, 30–39 CrossRef CAS.
- V. Sharma, et al., On the rapid and non-destructive approach for wood identification using ATR-FTIR spectroscopy and chemometric methods, Vib. Spectrosc., 2020, 110, 103097 CrossRef CAS.
- B. K. Lavine and J. Workman, Chemometrics, Anal. Chem., 2013, 85(2), 705–714 CrossRef CAS PubMed.
- B. Vyas, et al., Raman hyperspectroscopy of saliva and machine learning for Sjögren's disease diagnostics, Sci. Rep., 2024, 14(1), 11135 CrossRef CAS PubMed.
- L. Cui, et al., Aluminium foil as a potential substrate for ATR-FTIR, transflection FTIR or Raman spectrochemical analysis of biological specimens, Anal. Methods, 2016, 8(3), 481–487 RSC.
- R. C. Team, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, 2014 Search PubMed.
- A. Liaw and M. Wiener, Classification and Regression by RandomForest, R news, 2002, 2.3, 18–22 Search PubMed.
- J. Lauzon-Gauthier, P. Manolescu and C. Duchesne, The Sequential Multi-block PLS algorithm (SMB-PLS): Comparison of performance and interpretability, Chemom. Intell. Lab. Syst., 2018, 180, 72–83 CrossRef CAS.
- M. L. Barker and W. Rayens, Partial Least Squares For Discrimination, J. Chemom., 2003, 17, 166–173 CrossRef CAS.
- L. Breiman, Random Forests, Mach. Learn., 2001, 45(1), 5–32 CrossRef.
- A. Sarica, A. Cerasa and A. Quattrone, Random Forest Algorithm for the Classification of Neuroimaging Data in Alzheimer’s Disease: A Systematic Review, Front. Aging Neurosci., 2017, 9, 329 CrossRef PubMed.
- C. Strobl, J. Malley and G. Tutz, An introduction to recursive partitioning: Rationale, application, and characteristics of classification and regression trees, bagging, and random forests, Psychol. Methods, 2009, 14(4), 323–348 Search PubMed.
- H. Hong, G. Xiaoling and Y. Hua, Variable selection using Mean Decrease Accuracy and Mean Decrease Gini based on Random Forest, in 2016 7th IEEE International Conference on Software Engineering and Service Science (ICSESS), 2016.
- B. Barton, et al., Chemometrics for Raman Spectroscopy Harmonization, Appl. Spectrosc., 2022, 76(9), 1021–1041 CrossRef CAS PubMed.
- S. Janitza and R. Hornung, On the overestimation of random forest's out-of-bag error, PLoS One, 2018, 13, e0201904 CrossRef PubMed.
- R. Kohavi, A study of cross-validation and bootstrap for accuracy estimation and model selection, in Ijcai, Montreal, Canada, 1995 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |