Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Heavy element incorporation in nitroimidazole radiosensitizers: molecular-level insights into fragmentation dynamics†
Pamela H. W.
Svensson
 *a,
Lucas
Schwob
b,
Oscar
Grånäs
*a,
Lucas
Schwob
b,
Oscar
Grånäs
 a,
Isaak
Unger
a,
Olle
Björneholm
a,
Nicusor
Timneanu
a,
Isaak
Unger
a,
Olle
Björneholm
a,
Nicusor
Timneanu
 a,
Rebecka
Lindblad
a,
Anna-Lydia
Vieli
a,
Vicente
Zamudio-Bayer
a,
Rebecka
Lindblad
a,
Anna-Lydia
Vieli
a,
Vicente
Zamudio-Bayer
 c,
Martin
Timm
c,
Konstantin
Hirsch
c,
Martin
Timm
c,
Konstantin
Hirsch
 c,
Carl
Caleman
c,
Carl
Caleman
 ad and
Marta
Berholts
ad and
Marta
Berholts
 *e
*e
aDepartment of Physics and Astronomy, University of Uppsala, SE-75120 Uppsala, Sweden. E-mail: pamela.svensson@physics.uu.se
bDeutsches Elektronen-Synchrotron DESY, Notkestr. 85, 22607 Hamburg, Germany
cAbteilung für Hochempfindliche Röntgenspektroskopie, Helmholtz Zentrum Berlin für Materialien und Energie, 12489 Berlin-Adlershof, Germany
dCenter for Free-Electron Laser Science, DESY, DE-22607 Hamburg, Germany
eInstitute of Physics, University of Tartu, W. Ostwald 1, EST-50411, Tartu, Estonia. E-mail: marta.berholts@gmail.com
First published on 27th October 2023
Abstract
The present study investigates the photofragmentation behavior of iodine-enhanced nitroimidazole-based radiosensitizer model compounds in their protonated form using near-edge X-ray absorption mass spectrometry and quantum mechanical calculations. These molecules possess dual functionality: improved photoabsorption capabilities and the ability to generate species that are relevant to cancer sensitization upon photofragmentation. Four samples were investigated by scanning the generated fragments in the energy regions around C 1s, N 1s, O 1s, and I 3d-edges with a particular focus on NO2+ production. The experimental summed ion yield spectra are explained using the theoretical near-edge X-ray absorption fine structure spectrum based on density functional theory. Born–Oppenheimer-based molecular dynamics simulations were performed to investigate the fragmentation processes.
1 Introduction
In radiation therapy with X-rays, the damage is mediated to the DNA directly by ionization and indirectly through reactive species formed upon the ionization of water. Here, about two-thirds of all biological damage results from indirect action, while direct effects deal just one-third of the damage.1 The primary objective of radiotherapy is to maximize the dose delivered to the target tumor tissue while minimizing damage to surrounding healthy tissue. One approach to achieving this is through the use of radiosensitizers, which increase the sensitivity of tumor tissue to radiation treatment. The effectiveness of a radiosensitizer is determined by the ratio of the radiation dose required to produce a given biological effect without the radiosensitizer compared to the dose required in its presence. In the treatment of low oxygenated tissue called hypoxia, often found in tumors, nitroimidazoles attracted significant interest.2–5 Nitroimidazoles are a class of electrophilic radiosensitizers. These compounds mimic oxygen actions in radiotherapy and their radiosensitization efficacy was linked to the quantity of NO and/or NO2 fragments generated during ionization.6–8 The fragmentation products of nitroimidazoles, in the same way as oxygen, can attach to DNA radicals formed by ionizing radiation or secondary electrons. This can disrupt DNA repair processes and result in increased DNA damage. This effect is beneficial in radiotherapy as it allows for lower doses of radiation and thus reduces the associated side effects.4,5,7 Additionally, NO was shown to help with the oxygenation of the hypoxic cells.9Despite ongoing investigations of numerous radiosensitizer compounds, interpreting clinical trial results in the context of underlying physical and chemical processes remains challenging. This has hindered the ability to fully comprehend why some radiosensitizers are more effective than others. Therefore, the precise mechanism underlying sensitization is not yet fully understood.
The goal of this study is to investigate on the molecular level how nitroimidazole-based model compounds respond to ionizing radiation by applying near-edge X-ray mass spectrometry (NEXAMS) and quantum mechanical calculations. In the experiment, a heavy element, iodine, was incorporated into nitroimidazoles. The studied molecules are 4-iodo-2-methyl-5-nitroimidazole (INim), 1-ethyl-5-iodo-2-methyl-4-nitroimidazole (EtINim), 2-bromo-5-iodo-4-nitroimidazole (BrINim), and non-iodinated reference 2-methyl-5-nitroimidazole (Nim). The structures of their protonated forms with initial charge +1, as they appear after electrospray ionization, are presented in Fig. 1. The location of the proton was assigned to the N2 site due to its higher proton affinity.10 We change the structure of the non-iodinated sample, referred to as NimH+ by introducing an iodine atom to the C3 site, resulting in INimH+. In addition, there are two variations of INimH+: one involves replacing the methyl group at the C1 site with a bromine atom (BrINimH+), while the other includes adding an ethyl chain to the N1 site (EtINimH+). The purpose of iodine, a high-Z element, is to act as an “antenna” for X-rays during medical irradiation. Specifically, the high photoionization cross section of iodine is exploited to enhance the X-ray absorption efficiency of the nitroimidazoles. The expected net result is twofold: the iodine absorption hotspot locally enhances the radiation dose by generating secondary X-rays, photo- and Auger electrons, all important for efficient DNA strand breaks,11 while nitroimidazole counterpart produces sensitization-relevant species upon fragmentation. In this work, we focus on the latter. The study of the fragmentation of iodinated nitroimidazoles is motivated by promising in vitro results where iodinated samples exhibited better radiosensitization of hypoxic cells at much lower concentrations than their iodine-free ref. 12. The positive effect of localized radiation dose enhancement with iodine in tumors was observed significantly earlier.13,14
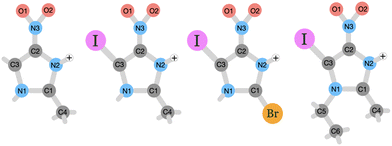 | ||
| Fig. 1 Schematic picture of the studied protonated molecules. From left to right: NimH+, INimH+, BrINimH+, and EtINimH+. | ||
Multiple studies have examined the photoionization and photofragmentation of various isolated nitroimidazoles using techniques such as X-ray photoelectron spectroscopy,15–18 near-edge X-ray absorption fine structure (NEXAFS) spectroscopy,18,19 multiparticle coincidence spectroscopy,16,17,20–24 and mass spectrometry.10,16,17,23,25–29 However, there is a lack of similar investigations specifically focused on halogenated nitroimidazoles, except for a recent study on the gas-phase fragmentation of neutral brominated nitroimidazoles using multiparticle coincidence technique.30 This study demonstrated that the bromination of nitroimidazoles is an effective way of introducing dual functionality to the radiosensitizer model compounds. Notably, the addition of a bromine atom resulted in significant production of reactive Br+ ions and a modest decrease of approximately 15% in the release of nitro group-related species upon dissociation at the C 1s, N 1s, and Br 3d edges. This is in stark contrast to the significant impact of methylation at the N1 site, which reduces the amount of NO+/NO2+ species by approximately 90%.20,22 In this study, we extend the investigations on the fragmentation of halogenated nitroimidazoles to another halogen atom – iodine. Iodine's deeper 1s edge (33.17 keV) compared to bromine (13.47 keV) allows it to absorb higher energy X-rays, potentially leading to more precise radiation delivery to tumor tissues and more energetic Auger electron production causing additional local damage.31 This advantage is particularly beneficial in low-energy radiation treatments like superficial and orthovoltage radiotherapy,32 as well as emerging synchrotron radiation-based photon activation therapies with a focus on low-energy X-rays.33
Here, we explore the influence of the electronic structure of chosen samples on their fragmentation following core excitation and ionization around C 1s, N 1s, O 1s, and I 3d-edges, therefore imitating the dominant secondary processes of X-ray therapy. We focus on the question of whether the incorporation of iodine, affects the electronic environment and thus the production of sensitization-relevant fragments at different photon energies.
2 Method
2.1 Experiment
The near-edge X-ray absorption mass spectrometry (NEXAMS) experiment was performed at the BESSY II synchrotron facility using UE52_PGM beamline with the Ion Trap end-station (Berlin, Germany).34 The samples were introduced into the gas phase by an electrospray ionization (ESI) source in a singly protonated form. A radio frequency ion funnel was used for accumulating and focusing created ions. Next, the ion beam was guided through two consecutive radio frequency hexapole ion guides to a quadrupole mass filter. The mass filter was optimized to let through exclusively protonated parent molecules deflecting ions with lower and higher mass-to-charge ratios (m/z). After that, the ions were sent to the 90° angle deflector for removal of neutral particles from the ion beam. Finally, the protonated parent ions entered the cryogenic linear trap through another quadrupole ion guide. In the trap, ions were irradiated with linearly polarized X-rays in the horizontal direction producing fragments that were then analyzed by a high-transmission reflectron time-of-flight mass spectrometer (RTOF). The nominal m/z range of the spectrometer is about 2–2500. The trap was optimized for fragments in the m/z range of about 38–130, while the parent protonated molecules had m/z of 128 (NimH+), 254 (INimH+), 282 (EtINimH+), and 319 (BrINimH+). This range was selected to have both NO2+ (m/z 46) and I+ (m/z 127) ions present in the mass spectra. No fragments were detected outside of the optimized range. The photon flux was in the order of 1013 ph. s−1.The samples INim, EtINim, BrINim, and Nim were purchased from BLD Pharmatech with 95+%, 97%, 97%, and 99.8% purity, correspondingly. The samples were received in powder form and injected into the experimental chamber from their highly diluted solutions. First, a 5 mM stock solution was prepared with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of water to methanol. Then, 0.1 ml of the stock solution was dissolved in water to reach 98 μM concentration. This solution was then injected through an ESI source into the experimental chamber with a constant flow rate of 0.2 ml h−1.
1 ratio of water to methanol. Then, 0.1 ml of the stock solution was dissolved in water to reach 98 μM concentration. This solution was then injected through an ESI source into the experimental chamber with a constant flow rate of 0.2 ml h−1.
The mass spectra were measured for all samples in their protonated forms across C 1s (275–300 eV), N 1s (395–430 eV), and O 1s (527–542 eV) near-edge regions with 0.1 eV step and 10–15 s acquisition time per step. For iodinated samples also I 3d edge (615–690 eV) was scanned with 0.2 eV step and 10–20 s acquisition time per step. Exceptions apply for the C 1s and N 1s measurements of the INimH+. These measurements were recorded using a narrower photon energy window, specifically 283–298 eV for C 1s and 397–417 eV for N 1s. At the start of the photon energy scans, photon bandwidth at FWHM was 145 meV for C 1s, 250 meV for N 1s, 256 meV for O 1s, and 325 meV for I 3d. The background mass spectrum without X-rays was measured for each scan to be subtracted from the recorded mass spectra. The mass spectra taken at different photon energies were normalized by the photocurrent measured with a calibrated GaAsP diode.
Data was analyzed using custom-made macros in Igor Pro software. Partial ion yield spectra were constructed from the TOF spectra measured as a function of the photon energy for each fragment by integrating the points within a small TOF window containing the peak of interest. The total NEXAMS spectrum is a sum of all the partial ion yield spectra and is an approximation to the total ion yield spectrum.
2.2 Theory
To better understand the electronic structure and fragmentation processes of the studied molecules, Density Functional Theory (DFT) has been used to simulate both NEXAFS spectra and Molecular Dynamics after photoionization. In order to accurately replicate the NEXAFS spectra for the different systems, a geometry optimization was performed using the B3LYP35 functional and def2-TZVPP relativistic basis sets for N, C, H, O, and Br atoms as implemented in the ORCA software.36 I atoms were separately described using the segmented all-electron relativistically contracted (SARC) basis sets with zeroth-order regular approximation (ZORA).37 By employing the TD-DFT38 method we evaluated the transition energies from the C 1s orbital (for all samples) and the N 1s orbital (for NimH+ and INimH+) to all available excited states. Transition probabilities were calculated using the response of the perturbed electron density to electromagnetic radiation within the TD-DFT theory in the ORCA package. The spectra of each chemically distinct atom were individually calculated and then summed to obtain the total spectrum. Subsequently, the total spectrum was adjusted to align with the most prominent characteristics observed in the experimental spectrum.In addition to the NEXAFS calculations, we have performed Born–Oppenheimer molecular dynamics simulations using the Siesta code39 to understand the fragmentation process after photoionization. We have previously employed this methodology in various contexts, including theoretical investigations,40,41 as well as in studies where we compared our simulation results with experimental data.42–44 From the comparison between simulations and the experiment, we could conclude that the relaxation time scales are short enough for the fragmentation to be dominated by the electronic structure of the ground-state geometry.42 This motivates us to use the same approach in the present study. To describe the exchange and correlation effect we used the functional generalized gradient approximation (GGA) as described by Perdew, Burke, and Ernzerhof, and the atomic orbitals were described using Norm-conserving pseudopotentials for all the molecules studied.45,46
As a first step, we conducted a 1 ns simulation in a vacuum environment using the Verlet algorithm. Subsequently, 20 structures were selected from this simulation and utilized as starting geometries for the production run. In the calculations, we focused on the ionization processes dominant during radiotherapy. We studied fragmentation of the INimH with a charge of +3, +4, and +5 possible after ionization and subsequent Auger decay and cascaded Auger decay. The fragmentation of the non-iodinated NimH was studied for the charge +3. During the simulation, we tracked the movement of each atom while allowing the molecules to decompose into fragments over a period of 1 ps with the integration step of 0.5 fs, providing sufficient time for the molecular dynamics to capture the evolution of the system. To determine the breaking point of a bond, we employed the Bond Integrity parameter, which was defined in an earlier study.44 By including the bond distance between atoms and their deviation using the mean bond distances and standard deviation from thermalization runs, one can obtain a value between 0 and 1. A bond can be considered broken if the bond integrity reaches 0.
3 Results
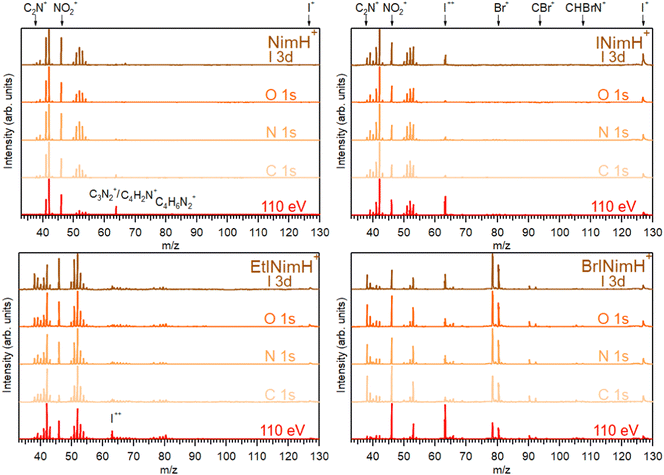
3.1 Summed mass spectra
The mass spectra of the four studied molecules, recorded across the C 1s, N 1s, O 1s, and I 3d edges, are depicted in Fig. 2. For detailed information about the photon energy ranges employed in the measurements, please refer to Section 2.1. To facilitate comparison, a mass spectrum measured at a lower photon energy of 110 eV (upon non-resonant photon absorption in the valence levels) is also included. The summed mass spectra recorded across the above-mentioned edges show minimal fluctuations in resulting fragments within each sample despite variations in the photon energy and therefore in the absorption sites. These fluctuations are primarily observed as slight variations in the intensity of certain fragments. The most significant changes are observed in the mass spectra measured at the photon energy of 110 eV. Here, a notable increase of I++ at m/z 63.5 is detected for all iodinated samples and especially for BrINimH+ and INimH+.Across all spectra, a prominent NO2+ fragment at m/z 46 is observed, accompanied by two sets of peaks clustered around m/z 38–43 and m/z 50–55. For INimH+ and BrINimH+, the second set ends at m/z 54. We attribute these peaks to the ions formed upon the fragmentation of the imidazole ring (see Table 1 for the assignments). In the mass spectra of BrINimH+, there are additional peaks in the lower m/z region attributed to Br++ isotopes at m/z 39.5 and m/z 40.5. The brominated sample has also other Br-containing fragments such as Br+ at m/z 79 and 81, HBr+ at m/z 80 and 82, CBr+ at m/z 91 and 93, and CHBrN+ at m/z 106 and 108 easily identified due to the approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 bromine isotope ratio. All iodinated samples contain I+ at m/z 127 and I++ at m/z 63.5 in their mass spectra.
1 bromine isotope ratio. All iodinated samples contain I+ at m/z 127 and I++ at m/z 63.5 in their mass spectra.
| m/z | NimH+ | INimH+ | EtINimH+ | BrINimH+ |
|---|---|---|---|---|
| 38 | C2N+ | C2N+ | C2N+ | C2N+ |
| 39 | C2HN+ | C2HN+ | C2HN+ | C2HN+ |
| 39.5 | — | — | — | 79Br++ |
| 40 | C2H2N+/CN2+ | C2H2N+/CN2+ | C2H2N+/CN2+ | C2H2N+/CN2+ |
| 40.5 | — | — | — | 81Br++ |
| 41 | C2H3N+/CHN2+ | C2H3N+/CHN2+ | C2H3N+/CHN2+ | CHN2+ |
| 42 | C2H4N+/CH2N2+/CNO+ | C2H4N+/CH2N2+/CNO+ | C2H4N+/CH2N2+/CNO+ | CH2N2+/CNO+ |
| 43 | C2H5N+ | C2H5N+ | C2H5N+ | CHNO+ |
| 46 | NO2+ | NO2+ | NO2+ | NO2+ |
| 50 | C3N+ | C3N+ | C3N+ | C3N+ |
| 51 | C3HN+ | C3HN+ | C3HN+ | C3HN+ |
| 52 | C3H2N+/C2N2+ | C3H2N+/C2N2+ | C3H2N+/C2N2+ | C3H2N+/C2N2+ |
| 53 | C3H3N+/C2HN2 | C3H3N+/C2HN2+ | C3H3N+/C2HN2+ | C2HN2+ |
| 54 | C2H2N2+/C3H4N+/C2NO+ | C2H2N2+/C3H4N+/C2NO+ | C2H2N2+/C3H4N+/C2NO+ | C2H2N2+/C2NO+ |
| 55 | C2H3N2+/C2HNO+/C3H5N+ | — | C2H3N2+/C2HNO+/C3H5N+ | — |
| 62 | — | C4N+ | C4N+ | — |
| 63 | — | C4HN+ | C4HN+ | — |
| 63.5 | — | I++ | I++ | I++ |
| 64 | C3N2+/C4H2N+ | C3N2+/C4H2N+ | C3N2+/C4H2N+ | C3N2+/C4H2N+ |
| 65 | C3HN2+/C4H3N+ | C3HN2+/C4H3N+ | C3HN2+/C4H3N+ | C3HN2+ |
| 66 | C2N3+/C3H2N2+/C4H4N+ | C2N3+/C3H2N2+/C4H4N+ | C2N3+/C3H2N2+/C4H4N+ | C3H2N2+/C2N3+ |
| 67 | C2HN3+/C3H3N2+/C4H5N+ | — | C2HN3+/C3H3N2+/C4H5N+ | — |
| 68 | — | — | C2N2O+/C2H2N3+/C3H4N2+/C4H6N+ | — |
| 69 | — | C2HN2O+/C3H5N2+ | C2HN2O+/C3H5N2+ | C2HN2O+ |
| 76 | — | — | C4N2+ | — |
| 77 | — | — | C4HN2+ | — |
| 78 | — | — | C3N3+/C4H2N2+ | — |
| 79 | — | — | C3HN3+/C4H3N2+ | 79Br+ |
| 80 | — | — | C3N2O+/C3H2N3+/C4H4N2+ | H79Br+ |
| 81 | — | — | C3HN2O+/C3H3N3+/C4H5N2+ | 81Br+ |
| 82 | C4H6N2+ | — | — | H81Br+ |
| 91 | — | — | — | C79Br+ |
| 93 | — | — | — | C81Br+ |
| 106 | — | — | — | CH79BrN+ |
| 108 | — | — | — | CH81BrN+ |
| 127 | — | I+ | I+ | I+ |
The non-iodinated sample, NimH+, has a peak at m/z 64 that corresponds to C3N2+ or/and C4H2N+ and a weak peak at m/z 82 that we attribute to the parent fragment that has lost NO2. The corresponding signal of the parent-NO2 is not visible in the mass spectra of other samples due to the limited mass range explained by the ion trap settings. In the mass spectrum of EtINimH+, there are weak peaks present at the higher m/z 76–81. These peaks arise due to the presence of an ethyl group attached to the nitroimidazole ring. Consequently, upon fragmentation of the ring, heavier carbon-containing fragments are produced (see Table 1).
The most straightforward way to investigate the influence of the iodine addition on the fragmentation is to compare NimH+ and INimH+ samples as these structures are chemically equivalent except for one iodine atom on the latter. The biggest difference is the presence of I+ and I++ ions in the mass spectrum of INimH+. There are subtle differences in the ratios of the peaks located on the left and right sides of the NO2+. Nevertheless, a peak at m/z 42, that could be assigned to C2H4N+, CH2N2+, and/or CNO+ ions, remains dominant for both samples. Please note that for NimH+ and INimH+, this peak was solely assigned to C2H4N+ according to our calculations (see Table 2). The peak at m/z 46 (NO2+) is less intense for the INimH+ in comparison with the dominant peak but becomes stronger at the highest photon energy, copying the behavior of NimH+ (see a mass spectrum recorded at I 3d edge in Fig. 2). The peak at m/z 41, which we assign to the C2H3N+ and/or CHN2+ ions, becomes weaker in the case of the iodinated sample. Other than that, the distribution of the ions remains largely unchanged meaning that the addition of iodine does not drastically alter the fragmentation outcome, apart from adding I+ and I++ ions and lowering the NO2+ ions production.
| m/z | Ions | NimH (%) | INimH (%) | ||
|---|---|---|---|---|---|
| +3 | +3 | +4 | +5 | ||
| 1 | H+ | 30 | 40 | 60 | 80 |
| 12 | C+ | 10 | 15 | 15 | 25 |
| 13 | CH+ | 5 | — | — | — |
| 14 | CH2+ | — | — | — | 15 |
| 15 | CH3+/NH+ | 15 | — | 15 | 5 |
| 16 | O+ | 25 | 25 | 40 | 60 |
| 24 | C2+ | 5 | — | — | — |
| 25 | C2H+ | 10 | — | — | 15 |
| 26 | C2H2+/NC+ | 10 | 10 | 26 | 55 |
| 27 | CHN+ | 25 | 5 | 30 | 30 |
| 28 | CH2N+ | 10 | — | — | — |
| 30 | NO+ | 25 | 25 | 40 | 60 |
| 38 | C2N+ | — | — | 10 | 5 |
| 40 | C2H2N+ | 25 | — | 5 | — |
| 41 | C2H3N+ | — | 5 | — | 5 |
| 42 | C2H4N+ | 40 | 25 | 30 | 40 |
| 46 | NO2+ | 65 | 50 | 55 | 40 |
| 52 | C3H2N+ | — | — | 5 | — |
| 53 | C3H3N+ | — | — | 5 | 15 |
| 54 | C2H2N2+ | 5 | — | — | — |
| 55 | C2H3N2+ | 5 | — | — | — |
| 65 | C3HN2+ | — | — | — | — |
| 66 | C3H2N2+ | 5 | — | — | — |
| 67 | C3H3N2+ | — | — | — | — |
| 80 | C4H4N2+ | — | — | 5 | — |
| 81 | C4H5N2+ | — | 5 | — | — |
| 82 | NimH-NO2+ | 25 | — | — | — |
| 99 | C3H3N2O2+ | 5 | — | — | — |
| 127 | I+ | — | 15 | 50 | 60 |
| 139 | CI+ | — | — | — | 10 |
| 154 | CHIN+ | — | 10 | 5 | 10 |
| 165 | C2IN+ | — | — | 5 | 5 |
| 166 | C2HIN+ | — | 15 | 20 | 15 |
| 206 | C4H3IN2+ | — | — | 5 | — |
| 207 | INim-NO2+ | — | 10 | — | — |
| 208 | INimH-NO2+ | — | 25 | 15 | — |
| 253 | INim+ | — | 20 | — | — |
| 254 | INimH+ | — | — | — | — |
3.2 NEXAMS spectra and NO2+ production
In Section 3.1, the mass spectra demonstrated the summed results obtained across all the measured edges. To gain a deeper understanding of the photon energy-dependent behavior of the produced fragments and examine the possibility of enhancing or inhibiting the production of sensitization-relevant NO2+ ions at specific photon energies, we now focus on the description of the NEXAMS spectra and partial ion yield curves with an emphasis on NO2+ production.Fig. 3 depicts NEXAMS spectra measured for EtINimH+ as an example (see shaded spectra at the bottom) and branching fraction of NO2+ ions for all samples across measured edges. According to the figure, a non-iodinated molecule, NimH+, consistently produces the largest amount of NO2+ ions at all photon energies measured. The percentage varies at different edges and on average grows from C 1s to I 3d from 14% to 18%. Iodinated samples, on the other hand, exhibit similar NO2+ yields, which are approximately 50% lower than that of NimH+ at the N 1s, O 1s, and I 3d edges. At the C 1s edge, the differences between iodinated samples become more pronounced. BrINimH+ produces on average 10.6% of NO2+ ions, INimH+ produces 7.8%, and EtINimH+ produces only 2.0%. Interestingly, there is an increase of 257% in NO2+ ions for EtINimH+ at C 1s starting from 294.5 eV to 300 eV. As can be seen in Fig. S1, presented in the ESI,† NO2+ production increases after the ionization threshold and it becomes the third dominant ion at 298.5 eV. With the exception of BrINimH+, there is an overall increase in NO2+ production from the C 1s edge to the I 3d edge for all samples. However, in the case of BrINimH+, the NO2+ yield decreases from 10.6% at C 1s to 5.7% at I 3d.
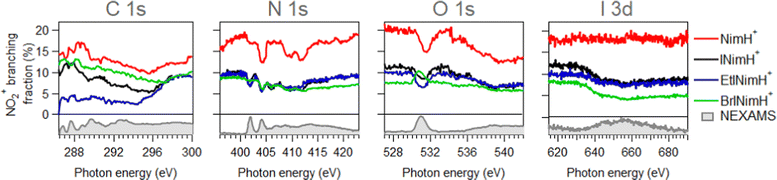 | ||
| Fig. 3 Branching fraction of NO2+ ions across measured edges. Below zero, experimental NEXAMS spectra of EtINImH+ are shown to guide the eye to the resonance positions. | ||
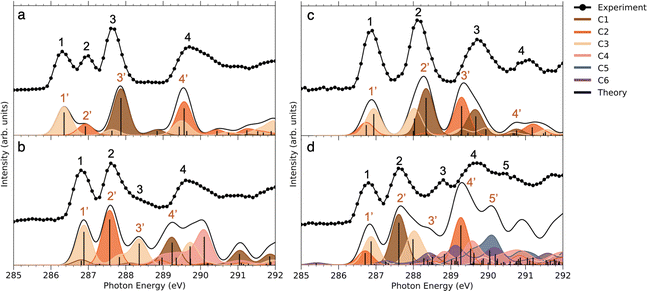
Comparing the C 1s NEXAMS of the iodine-free and iodinated samples, a shift of about 0.5 eV towards higher excitation energies is observed for the iodinated samples indicating a destabilization of the LUMO orbitals by the addition of iodine. For all samples, the first resonance is dominated by the transition 1s → LUMO from the carbon C3, which is bound to the iodine atom, in all systems except in NimH+, where it is bound to hydrogen. If in the case of a non-iodinated sample, this is the only carbon responsible for the first resonance, then in the iodinated samples, a contribution from other carbons is present and is different for different samples. Please refer to Table SI in the ESI† for the assignments of the calculated electronic transitions. In NimH+ and INimH+ (Fig. 4a and b), the second resonance consists mainly of the transitions 1s → LUMO in carbon C2 which is connected to NO2 group. For BrINimH+ and EtINimH+ it is dominated by the 1s → LUMO+1, LUMO transitions from C1 that is connected to bromine or methyl group, respectively. The third resonance is the strongest for NimH+ and predominantly consists of C1 contribution 1s → LUMO+1. For iodinated samples, INimH+ and EtINimH+, the third resonance is mostly C3 contribution 1s → LUMO+2 and 1s → LUMO+1, correspondingly, while for BrINimH+, it is a mixture of C2 1s → LUMO+4 and C1 1s → LUMO+2. As shown in Fig. 3, the structural differences of the samples significantly affect the amount of NO2+ ions produced at C 1s edge. However, all of the samples show the same trend of increasing NO2+ production after the ionization threshold at about 296 eV. Above ionization energy, the contribution from the valence ionization should be taken into account. Possibly, the NO2+ separation pathway is more prominent after valence ionization. More likely, the molecule simply obtains more charge after photoionization and localization of the charge on the carbon atom seems to enhance the NO2+ production. The effect is less visible for N 1s, O 1s, and I 3d edges. In the case of N 1s and O 1s, the charge localizes on the nitro group which could lead to its consequent fragmentation. In the I 3d, a highly charged state is created due to Auger cascades that generally leads to a more vigorous fragmentation.
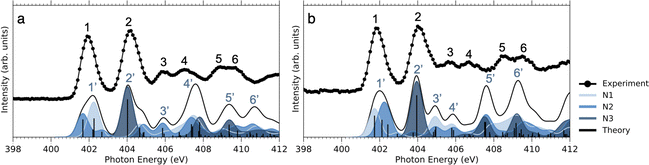
As can be seen in Fig. 3, at the N 1s edge, there are dips in the NO2+ curves coinciding with the resonances in the NEXAMS spectra. The dip appearing at the second resonance is the strongest. Also, dips corresponding to the fifth and sixth resonances are present and are particularly strong in the non-iodinated sample. As Fig. 5 shows, nitro group nitrogen is mainly responsible for these resonances. This indicates that whenever electronic transitions are occurring from the nitro group nitrogen, the NO2+ production is suppressed. There are three main processes that could lead to the reduction in the NO2+ production. First, after photoabsorption, the nitro group can consequently dissociate into smaller fragments such as NO+, O+, and N+. We cannot see the lower masses in the experiment but the calculation predicts the formation of NO+ and O+ ions (see Table 2). The second option is that following electronic relaxation after photoabsorption the nitro group ejects as a neutral. Finally, the most unlikely option is that the bond between the nitro group and the imidazole ring does not dissociate after photoabsorption.
At the O 1s edge, a reduction of the NO2+ ions at the resonance around 531.0 eV is observed for all the samples except for BrINimH+, in which NO2+ production is increased. The behavior observed suggests that there might be different fragmentation pathways leading to the production of NO2+ ions following core excitations of oxygen atoms in the nitro group. These pathways appear to be influenced by the structural differences among the molecules studied. The fact that NO2+ production is increased in the case of BrINimH+ at the O 1s edge suggests that the presence of bromine instead of the methyl group at the C1 site in the molecule could affect the fragmentation process, leading to a different behavior compared to the other studied samples.
3.3 Molecular dynamics
Fig. 6 shows the first four virtual molecular orbitals for the different molecules studied. LUMO is primarily located close to the nitro group in all four molecules, with bonding features between N3 and C2. LUMO+1, LUMO+2, and LUMO+3 all share the weight of the orbitals mainly delocalized at the imidazole ring. Due to the similarity in orbital localization for the different molecules, one would expect the produced fragments by photoabsorption to be created in a similar way, regardless of the addition of heavy atoms or functional groups to the ring, which also can be observed in the overall representation of measured fragments in Fig. 2. The disparity between the LUMO levels, however, would indicate the production of distinctive fragments at increasing photon energies. This is not the case, as seen across the different measured edges in Fig. 2, thus the electronic relaxation occurs before fragmentation, a phenomenon observed in earlier studies.44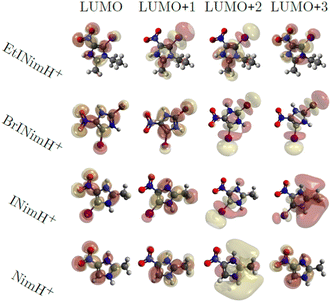 | ||
| Fig. 6 Visualization of molecular orbitals representing the first four unoccupied states using an isovalue of 0.02. | ||
Now we turn to the result of the calculations performed with time-resolved molecular dynamics on NimH+ and INimH+ above the ionization threshold. The charged molecular system is assumed to stay in its electronic ground state at a high temperature and is allowed to freely propagate through the fragmentation process. In relation to the experiment, an electron has been ionized from a 1s or 3d orbital in the protonated molecule causing the emittance of one, two, or three Auger electrons. The produced fragments obtained at the studied charge states are presented in Table 2. We can observe significantly higher rates of low-mass fragments originating from the iodinated sample in contrast to the non-iodinated molecule arising from C–H bond dissociation and thereafter opening of the nitroimidazole ring, a similar behavior recognized in other carbon-based aromatic molecules.47 The channel which leads to an open ring has previously been observed as a high energy path upon NO and NO2 production.48
An interesting feature is a high production of NO+ and NO2+ fragments appearing during irradiation of both iodinated and non-iodinated molecules. The NO+ ion is outside the measurable area in the experiment but is conspicuously produced at 25 to 60% of the simulations depending on the molecule and the charge. Being an important part of the suggested oxygen mimetics mechanism, their rate of production is important to be understood.
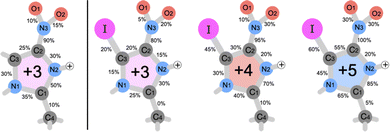
For further analysis of the bond sensitivity in relation to observed fragments, we present the percent of broken bonds between all atoms heavier than hydrogen in Fig. 7. As one can observe, the nitroimidazole ring does, to a large extent, share the bond breaking evenly for the NimH3+ system, supporting the experimental yield observed in Fig. 2. If the charge increases through the Auger cascade, a higher emphasis is laid on the C2–C3 bond and nitrogen bonds connected to C1. In both cases, the N3–C2 bond is close to 100%, leaving this bond to be the weakest in the system. Only small changes in breaking probability can be noticed after introducing an iodine atom to the ring as seen in the percentages for the INim3+ and INim4+ structures. In addition to the production of analogous products, it appears that there might be a potential tendency towards a shorter lifetime of the N3–C2 bond in the iodine-enhanced sample when subjected to irradiation at energies near the I 3d edge (see Table SIII in the ESI†). This could open for a more localized radiation treatment using INim while maintaining sufficiently high NO2+ production. However, it is important to note that these observations may be influenced by low statistics and further studies with larger data sets are required to gain a more comprehensive understanding of the potential impact on the lifetime of the N3–C2 bond due to heavy element incorporation.
4 Conclusion
We have applied ion TOF spectroscopy combined with synchrotron radiation to experimentally study the production of radiosensitization-relevant NO2+ ions in iodinated (INimH+, EtINimH+, BrINimH+) and non-iodinated (NimH+) nitroimidazoles at various photon energies. The key findings are (i) the samples display minimal fluctuations in resulting fragments across C 1s, N 1s, O 1s, and I 3d edges, indicating consistent fragmentation patterns despite variations in absorption sites; (ii) in terms of NO2+ production, the non-iodinated molecule consistently produced the highest amount of NO2+ ions upon core excitation and ionization across all measured edges. The addition of iodine to the sample on average lowered the production of NO2+ ions by about 50% in comparison to the iodine-free nitroimidazole across N 1s, O 1s, and I 3d edges. For the C 1s edge, the amount of produced NO2+ highly depended on the sample and BrINimH+ showed the best result in comparison to NimH+ (lower by 26%), while EtINimH+ demonstrated the worst result (lower by 86%); (iii) electronic transitions from the N 1s with the participation of the nitro group nitrogen result in the suppression of NO2+ production, indicating a strong site-specific fragmentation effect for all samples.We observed similar trends in the fragmentation of iodinated and non-iodinated samples across various photon energies. Although the production of sensitization-relevant NO2+ ions is lower in the iodinated samples, there is a release of I+ and I++ ions, which also could be damaging to the cancerous cells. Therefore, iodinated nitroimidazoles seem to maintain high levels of production of damaging fragments upon fragmentation. Considering the possibility of additional local damage through Auger cascades due to the presence of the heavy atom, halogenation of nitroimidazoles could be a promising strategy for developing more effective radiosensitizers. However, further in vitro investigations are necessary to validate the clinical applicability of these molecules. Moreover, exploring the influence of water, a prominent molecule in cellular environments, on nitroimidazole fragmentation is essential for more accurate comparisons with in vivo conditions.
Author contributions
Conceptualization, MB; experiments, MB, PHWS, IU, LS, ALV; computation and software, PHWS, OG, NT, CC; experimental data analysis, MB, ALV; calculations analysis, PHWS, NT, OG, CC; writing of the manuscript, MB, PHWS; review and editing, OB, VZB, KH, MT, RL, CC, NT, OG; funding acquisition, MB. All authors have read and agreed to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Estonian Research Council grant (MOBTP1013). We acknowledge the BESSY II synchrotron facility for the granted time at the Nanocluster Trap end-station of the UE52_PGM beamline. We acknowledge the Swedish Research Foundation for Strategic Research, the Swedish Research Council (2017-05128, 2018-00740, 2019-03935), the Swedish Research Council via the Röntgen-Ångstöm Cluster, program-oriented funds of the Helmholtz Association. The computations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at Linköping University in the projects 2022/1-36 and 2022/22-597. L. S. acknowledges funding from the Helmholtz Initiative and Networking Fund. This article is based upon work from COST Action CA18212 – Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology).Notes and references
-
H. Murshed, Fundamentals of Radiation Oncology, 3rd edn, 2019 Search PubMed
.
- G. E. Adams, I. R. Flockhart, C. E. Smithen, I. J. Stratford, P. Wardman and M. E. Watts, Radiat. Res., 1976, 67, 9–20 CrossRef CAS
.
- S. Rey, L. Schito, M. Koritzinsky and B. G. Wouters, Adv. Drug Delivery Rev., 2017, 109, 45–62 CrossRef CAS PubMed
.
-
G. H. Harrison and J. Wright, in Cancer Management in Man: Detection, Diagnosis, Surgery, Radiology, Chronobiology, Endocrine Therapy, ed. A. L. Goldson, Springer Netherlands, Dordrecht, 1989, pp. 170–178 Search PubMed
.
- J. F. Fowler, G. E. Adams and J. Denekamp, Cancer Treat. Rev., 1976, 3, 227–256 CrossRef CAS PubMed
.
- A. Zahoor, M. V. Lafleur, R. C. Knight, H. Loman and D. I. Edwards, Biochem. Pharmacol., 1987, 36, 3299–3304 CrossRef CAS PubMed
.
- H. Wang, X. Mu, H. He and X.-D. Zhang, Trends Pharmacol. Sci., 2018, 39, 24–48 CrossRef CAS
.
- B. T. Oronsky, S. J. Knox and J. J. Scicinski, Transl. Oncol., 2012, 5, 66–71 CrossRef PubMed
.
- P. Sonveaux, B. F. Jordan, B. Gallez and O. Feron, Eur. J. Cancer, 2009, 45, 1352–1369 CrossRef CAS
.
- S. Pandeti, L. Feketeová, T. J. Reddy, H. Abdoul-Carime, B. Farizon, M. Farizon and T. D. Märk, RSC Adv., 2017, 7, 45211–45221 RSC
.
-
Radiation Damage in Biomolecular Systems, ed. G. García Gómez-Tejedor and M. C. Fuss, Springer Netherlands, Dordrecht, 2012 Search PubMed
.
- W. Krause, A. Jordan, R. Scholz and J.-L. M. Jimenez, Anticancer Res., 2005, 25, 2145–2151 CAS
.
- R. Santos Mello, H. Callisen, J. Winter, A. R. Kagan and A. Norman, Med. Phys., 1983, 10, 75–78 CrossRef CAS
.
- A. Joubert, M.-C. Biston, C. Boudou, J.-L. Ravanat, T. Brochard, A.-M. Charvet, F. Estève, J. Balosso and N. Foray, Int. J. Radiat. Oncol., Biol., Phys., 2005, 62, 1486–1496 CrossRef CAS PubMed
.
- F. Kajfež, L. Klasinc and V. Šunjić, J. Heterocycl. Chem., 1979, 16, 529–531 CrossRef
.
- P. Bolognesi, A. R. Casavola, A. Cartoni, R. Richter, P. Markus, S. Borocci, J. Chiarinelli, S. Tošić, H. Saadeh, M. Masič, B. Marinković, K. Prince and L. Avaldi, J. Chem. Phys., 2016, 145, 191102 CrossRef CAS PubMed
.
- J. Chiarinelli, A. R. Casavola, M. C. Castrovilli, P. Bolognesi, A. Cartoni, F. Wang, R. Richter, D. Catone, S. Tosic, B. P. Marinkovic and L. Avaldi, Front. Chem., 2019, 7, 1–14 CrossRef
.
- P. Bolognesi, V. Carravetta, L. Sementa, G. Barcaro, S. Monti, P. Manjari Mishra, A. Cartoni, M. C. Castrovilli, J. Chiarinelli, S. Tosic, B. P. Marinkovic, R. Richter and L. Avaldi, Front. Chem., 2019, 7, 151 CrossRef PubMed
.
- L. Feketeová, O. Plekan, M. Goonewardane, M. Ahmed, A. L. Albright, J. White, R. A. J. OHair, M. R. Horsman, F. Wang and K. C. Prince, J. Phys. Chem. A, 2015, 119, 9986–9995 CrossRef
.
- E. Itälä, K. Tanzer, S. Granroth, K. Kooser, S. Denifl and E. Kukk, J. Mass Spectrom., 2017, 52, 770–776 CrossRef
.
- A. Cartoni, A. R. Casavola, P. Bolognesi, M. C. Castrovilli, D. Catone, J. Chiarinelli, R. Richter and L. Avaldi, J. Phys. Chem. A, 2018, 122, 4031–4041 CrossRef CAS
.
- E. Itälä, H. Myllynen, J. Niskanen, J. González-Vázquez, Y. Wang, D. T. Ha, S. Denifl and E. Kukk, J. Phys. Chem. A, 2019, 123, 3074–3079 CrossRef
.
- E. Itälä, J. Niskanen, L. Pihlava and E. Kukk, J. Phys. Chem. A, 2020, 124, 5555–5562 CrossRef
.
- M. Satta, A. R. Casavola, A. Cartoni, M. C. Castrovilli, D. Catone, J. Chiarinelli, S. Borocci, L. Avaldi and P. Bolognesi, ChemPhysChem, 2021, 22, 2387–2391 CrossRef CAS
.
- R. Flammang, J. Elguero, H. Thanh Le, P. Gerbaux and M. Tho Nguyen, Chem. Phys. Lett., 2002, 356, 259–266 CrossRef CAS
.
- K. Tanzer, L. Feketeová, B. Puschnigg, P. Scheier, E. Illenberger and S. Denifl, Angew. Chem., Int. Ed., 2014, 53, 12240–12243 CrossRef CAS PubMed
.
- L. Feketeová, J. Postler, A. Zavras, P. Scheier, S. Denifl and R. A. J. O'Hair, Phys. Chem. Chem. Phys., 2015, 17, 12598–12607 RSC
.
- R. Meißner, J. Kočišek, L. Feketeová, J. Fedor, M. Fárník, P. Limão-Vieira, E. Illenberger and S. Denifl, Nat. Commun., 2019, 10, 2388 CrossRef PubMed
.
- R. Meißner, L. Feketeová, A. Bayer, P. Limão-Vieira and S. Denifl, J. Chem. Phys., 2021, 154, 074306 CrossRef
.
- L. Pihlava, M. Berholts, J. Niskanen, A. Vladyka, K. Kooser, C. StrÅhlman, P. Eng-Johnsson, A. Kivimäki and E. Kukk, Phys. Chem. Chem. Phys., 2023, 25, 13004–13011 RSC
.
- A. Yokoya and T. Ito, Int. J. Radiat. Biol., 2017, 93, 743–756 CrossRef CAS
.
- S. McGregor, J. Minni and D. Herold, J. Clin. Aesthetic Dermatol., 2015, 8, 12–14 Search PubMed
.
- R. Vinit, R. Amit, S. Saurabh, M. Raghvendra, M. Ravindra, P. Piyush, G. Ankur and S. Mahendra, J. Anal. Pharm. Res., 2018, 7, 175–180 Search PubMed
.
- K. Hirsch, J. T. Lau, P. Klar, A. Langenberg, J. Probst, J. Rittmann, M. Vogel, V. Zamudio-Bayer, T. Möller and B. V. Issendorff, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 154029 CrossRef
.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS
.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed
.
- E. van Lenthe, A. van der Avoird and P. E. S. Wormer, J. Chem. Phys., 1998, 108, 4783–4796 CrossRef CAS
.
- E. K. Gross and W. Kohn, Adv. Quantum Chem., 1990, 21, 255 CrossRef CAS
.
- J. M. Soler, E. Artacho, J. D. Gale, A. Garca, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS
.
- O. Grånäs, N. Timneanu, I. Eliah Dawod, D. Ragazzon, S. Trygg, P. Souvatzis, T. Edvinsson and C. Caleman, J. Chem. Phys., 2019, 151, 144307 CrossRef
.
- I. Eliah Dawod, N. Timneanu, A. P. Mancuso, C. Caleman and O. Grånäs, Phys. Chem. Chem. Phys., 2022, 24, 1532–1543 RSC
.
- O. GrÅnäs, A. Mocellin, E. S. Cardoso, F. Burmeister, C. Caleman, O. Björneholm and A. N. de Brito, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 244007 CrossRef
.
- C. Caleman, F. Junior, O. Granas and A. Martin, Crystals, 2020, 10, 585 CrossRef CAS
.
- G. Gopakumar, P. H. Svensson, O. Grånäs, B. Brena, L. Schwob, I. Unger, C.-M. Saak, M. Timm, C. Bülow and M. Kubin,
et al.
, J. Phys. Chem. A, 2022, 126, 1496–1503 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS PubMed
.
- S. Oghbaie, M. Gisselbrecht, E. P. MÅnsson, J. Laksman, C. StrÅhlman, A. Sankari and S. L. Sorensen, Phys. Chem. Chem. Phys., 2017, 19, 19631–19639 RSC
.
- M. Satta, A. R. Casavola, A. Cartoni, M. C. Castrovilli, D. Catone, J. Chiarinelli, S. Borocci, L. Avaldi and P. Bolognesi, ChemPhysChem, 2021, 22, 2387–2391 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp03800a |
| This journal is © the Owner Societies 2024 |