Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tailored anharmonic potential energy surfaces for infrared signatures†
Janine
Hellmers
 ,
Pascal
Czember
and
Carolin
König
,
Pascal
Czember
and
Carolin
König
 *
*
Institut of Physical Chemistry and Electrochemistry, Leibniz University Hannover, Germany. E-mail: carolin.koenig@pci.uni-hannover.de
First published on 25th November 2024
Abstract
Accurately calculated infrared spectra are essential for supporting experimental interpretation, yet full-space anharmonic vibrational structure calculations are only feasible for a limited number of degrees of freedom. Fortunately, characteristic spectroscopic signatures are often dominated by a few key vibrations. We propose a computational protocol specifically tailoring high dimensional anharmonic potential energy surfaces for the accurate and efficient calculation of such spectral signatures with vibrational coupled cluster response theory. Our protocol focuses on the selection of appropriate coordinates for the relevant degrees of freedom and the identification of specific mode-coupling terms for the potential energy surface that require more thorough treatment. This includes applying different levels of electronic structure theory and selecting a restricted set of higher mode-coupling terms (> mode pairs). We validate this protocol on two spectral regions: the fundamental C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations in uracil and the fundamental OH stretchings in catechol. Our findings indicate that the convergence behaviour towards harmonic frequencies in the so-called FALCON algorithm is an effective indicator for the locality character of the relevant degrees of freedom. We find that the C
O stretching vibrations in uracil and the fundamental OH stretchings in catechol. Our findings indicate that the convergence behaviour towards harmonic frequencies in the so-called FALCON algorithm is an effective indicator for the locality character of the relevant degrees of freedom. We find that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretchings in uracil are better described using normal coordinates, while the description with local FALCON coordinates of the OH-stretching vibrations in catechol showed superior performances in VCC spectra calculations. Overall, our protocol offers valuable guidelines for accurate and efficient anharmonic calculation of vibrational spectral signatures.
O stretchings in uracil are better described using normal coordinates, while the description with local FALCON coordinates of the OH-stretching vibrations in catechol showed superior performances in VCC spectra calculations. Overall, our protocol offers valuable guidelines for accurate and efficient anharmonic calculation of vibrational spectral signatures.
1 Introduction
Vibrational spectroscopic tools have been proven indispensable to reveal biomolecular processes on an atomistic level. For instance, difference infrared (IR) spectroscopy can provide unique insights into phenomena such as temporary water wires in rhodopsin.1–4 Also, the proton transfer in the blue light senor using flavin (BLUF) upon light stimuli can be detected by changes in hydrogen-bonding patterns through IR spectroscopy.5 Often, the interpretation of experimental results requires computational aid. However, accurately calculating the vibrational properties of large biomolecular systems poses a formidable computational challenge, especially when anharmonicity or nuclear quantum effects emerge. This is, for instance, evident for spectral regions where hydrogen-bonded stretching vibrations absorb.6,7 Vibrational structure methods offer a route to obtain accurate theoretical descriptions of vibrational wave functions accounting for these effects.8,9 However, full-space treatments of larger molecular systems are impossible by today's means. Fortunately, full interpretation of experimental results is often not necessary: spectral signatures are usually of primary interest, as these and their changes in chemical reactions are often characteristic, such as C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations that are affected by hydrogen bonding. Since the spectral signatures are presumably influenced by only a few degrees of freedom (DOFs), tailoring the computational setup and focusing the computational effort on the region of interest, while applying less accurate but more efficient treatments for the remaining system, is highly desirable.10 The computation of anharmonic IR spectra is rather complex, and finding the best strategy for tailoring the computational setup is not trivial. A successful computation involves several key components: (i) a suitable description of the vibrational DOFs and the selection of the vibrational (sub-)space, (ii) an efficient generation of the potential energy and dipole surfaces, and (iii) the subsequent vibrational wave function calculation. In our work, we focus on tailoring strategies for the first two points. An overview of tailoring strategy ideas for correlated vibrational wave functions is given in ref. 10.
O stretching vibrations that are affected by hydrogen bonding. Since the spectral signatures are presumably influenced by only a few degrees of freedom (DOFs), tailoring the computational setup and focusing the computational effort on the region of interest, while applying less accurate but more efficient treatments for the remaining system, is highly desirable.10 The computation of anharmonic IR spectra is rather complex, and finding the best strategy for tailoring the computational setup is not trivial. A successful computation involves several key components: (i) a suitable description of the vibrational DOFs and the selection of the vibrational (sub-)space, (ii) an efficient generation of the potential energy and dipole surfaces, and (iii) the subsequent vibrational wave function calculation. In our work, we focus on tailoring strategies for the first two points. An overview of tailoring strategy ideas for correlated vibrational wave functions is given in ref. 10.
An important component of tailoring strategies is the choice of vibrational coordinates. One relatively simple, yet previously successful11–14 approach, involves targeting only a subset of vibrational DOFs. For the coordinates, spanning these reduced vibrational spaces, alternative rectilinear coordinates with a more local nature than traditional normal coordinates are advertised.10 These coordinates are known to achieve faster convergence of the n-mode expanded15 potential energy surface (PES).16–22 For instance, some employ so-called localized modes,11,23 while others utilize local normal modes obtained from partial Hessian analysis.12–14 As a prerequisite, localized modes require a full normal mode analysis,22 which can be tedious to generate for large biomolecular systems. In comparison, the partial Hessian analysis requires only diagonalizations of blocks referring to disjoint subsets of atoms. However, the resulting vibrational DOFs include artificial contributions of rotational and translational DOFs and usually lack the description of relative motion.10 In contrast, the so-called flexible adaption of local coordinates of nuclei (FALCON)24 are free of any translational or rotational contributions and can provide coordinates that describe the relative motions of groups of atoms. As in the local monomers approach,22 the construction of FALCON coordinates does not require a full normal mode analysis as a prerequisite. Moreover, the FALCON algorithm can be easily applied to covalently bounded systems and offers a so-called “growing scheme” that successively increases the vibrational subspace. Conceivable starting points for the growing scheme can be a group of atoms, a single atom, or several independent atoms in the molecular system, e.g. (groups of) atoms relevant to the spectroscopic signature of interest. This growing scheme is highly attractive for tailored approaches as it offers a systematic expansion of FALCON-generated vibrational subspaces.10 In this work, this systematic expansion of FALCON-generated vibrational subspaces is pursued for anharmonic vibrational structure calculations for the first time.
The generation of the PES remains, despite the incremental n-mode expansion,15 a large computational bottleneck for systems with many DOFs.16 Besides using local coordinates, a conceivable tailoring strategy for PESs can be realized through multilevel potentials. The exploration of multilevel potentials has remained an ongoing field of research.8,13,16,25–48 In most of these studies, the low-order coupling potentials of the n-mode expansion are described through higher resolutions, e.g. higher electronic structure levels and accurate functional forms. Higher-coupling terms are represented with a lower resolution, e.g. lower electronic structure levels or more approximate functions, for example, with a quartic force field (QFF).28,49 Some studies further describe selected higher-coupling terms on the high level by identifying them with several techniques, e.g. screening measures on low-cost PESs up to four-mode coupling terms.16,35,40,41 For example, Yagi and co-workers28 suggested an inexpensive calculation of indices to determine important mode-coupling terms. In their case, less important coupling terms are recycled at lower resolution, while important coupling terms on the same level are described at higher resolution. In the following, we refer only to the term multilevel instead of multiresolution. In our case, all coupling orders are approximated by the same potential energy function form, where the high and low level rather define the applied level of electronic structure theory. We concentrate on multilevel property surfaces but instead of assigning one electronic structure method to one mode-coupling level, we employ high- and lower-level descriptions for selected sets of modes or mode-coupling terms within the same mode-coupling level. We, hence, do not aim at a good representation of the full vibrational spectrum, but rather of vibrational signatures. For this, a reduced number of mode-coupling terms relevant to the spectroscopic signature of interest are calculated with a higher level of electronic structure theory, while remaining terms with the same coupling order are treated with a lower level of theory.
Another approach to accelerate the PES generation involves the use of fragmented PES calculations.22,50–53 For instance, the Steele group54 recently studied the impact of many-body terms in fragmented PES generations of rather large clathrate-like alkali metal cation hydrates (comprising 20 water molecules). Their findings revealed that higher-order mode-coupling terms are predominantly influenced by one-body contributions. This understanding of vibrational coupling behaviour offers valuable physical insights and presents a promising way to reduce computational costs for larger biomolecular systems. However, this approach lies beyond the scope of the current investigation.
In another study, the same group25 demonstrated the efficacy of combining localized-mode methods23 with multilevel approaches to accelerate the PES generation (non-fragmented) on vibrational-self-consistent field (VSCF) calculations of zero-point and fundamental excitation energies. They first employed a distance-based criterion55 to determine the coupling terms described in the low level. Subsequently, they recalculate the significant mode combinations with a more elaborate high-level electronic description. For the less significant terms, the low-level description is reused. They restrict their approach to mode pair (2MC) terms and do not concentrate the computational effort on a specific spectral region. In contrast to that, we combine local-mode FALCON representations with multilevel techniques to develop a robust strategy for generating PESs for accurate spectroscopic signals. Here, we also take higher-coupling terms (3MC, 4MC) into account and investigate the performance on intensities obtained with correlated mode calculations by vibrational coupled cluster (VCC) theory. By this, we present a reliable protocol for tailored multilevel vibrational structure calculations for spectroscopic signatures. Our protocol involves the investigation of systematically increasing subspaces, obtained through the FALCON growing scheme. Additionally, we systematically enhance the accuracy of property surfaces (PESs and dipole moment surfaces (DMSs)) by incorporating selected higher coupling terms (> mode pairs) to the initial low-level property surface and describe selected coupling terms in the high-level electronic structure theory. We assess our protocol for pyrimidine-2,4(1H,3H)-dione (uracil) within the frequency range of 1600–1900 cm−1, where C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretchings of amid-groups occur, and at the frequency range of 3500–3900 cm−1 for 1,2-dihydroxybenzen (catechol), where OH-stretching vibrations absorb. These spectral signatures serve as representative signatures with anharmonic characters, akin to characteristic spectral signatures in biomolecules. Due to their small system size, uracil and catechol are excellent test models for studying the spectral features common in biomolecular environments. For both molecules, we also compare to experimental spectra. We note, however, that theory–experiment comparison at this accuracy is challenging. The first assessment of the developed protocol in this work assumes molecules in vacuum at 0 K. Obviously, no corresponding experimental results are available. The experiments that are closest to these conditions are presumably vibrational spectra in noble gas matrices, which we have chosen as experimental reference for uracil.56 Also here, however, concentration,57 temperature/annealing58 and matrix effects59 can have a significant impact on the signal's shape, which leads to insecurities in the comparison of the spectra.56 These insecurities are even more pronounced when compared to gas phase spectra, as in the case of catechol. In this work, we, hence, do not expect to exactly reproduce the experimental spectra. The experiment is rather used as a guideline for the validation of the methods developed.
O stretchings of amid-groups occur, and at the frequency range of 3500–3900 cm−1 for 1,2-dihydroxybenzen (catechol), where OH-stretching vibrations absorb. These spectral signatures serve as representative signatures with anharmonic characters, akin to characteristic spectral signatures in biomolecules. Due to their small system size, uracil and catechol are excellent test models for studying the spectral features common in biomolecular environments. For both molecules, we also compare to experimental spectra. We note, however, that theory–experiment comparison at this accuracy is challenging. The first assessment of the developed protocol in this work assumes molecules in vacuum at 0 K. Obviously, no corresponding experimental results are available. The experiments that are closest to these conditions are presumably vibrational spectra in noble gas matrices, which we have chosen as experimental reference for uracil.56 Also here, however, concentration,57 temperature/annealing58 and matrix effects59 can have a significant impact on the signal's shape, which leads to insecurities in the comparison of the spectra.56 These insecurities are even more pronounced when compared to gas phase spectra, as in the case of catechol. In this work, we, hence, do not expect to exactly reproduce the experimental spectra. The experiment is rather used as a guideline for the validation of the methods developed.
After a brief introductory background on the methodology of FALCON coordinates and how multilevel property surfaces are generated in this work, we introduce our computational protocol designed to enhance the efficiency of anharmonic vibrational spectra calculations. This protocol is specifically tailored to capture distinct spectroscopic signatures. After reporting the computational details, we demonstrate the efficiency of our protocol on C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching signatures of the uracil molecule. We continue with the investigation of the spectroscopic signatures originating from OH stretches in catechol. Here, we perform a comprehensive evaluation of FALCON-generated subspaces for subsequent anharmonic calculation and assess the suitability of different choices of underlying rectilinear coordinates for multilevel spectra.
O stretching signatures of the uracil molecule. We continue with the investigation of the spectroscopic signatures originating from OH stretches in catechol. Here, we perform a comprehensive evaluation of FALCON-generated subspaces for subsequent anharmonic calculation and assess the suitability of different choices of underlying rectilinear coordinates for multilevel spectra.
2 Methodology
2.1 FALCON coordinates
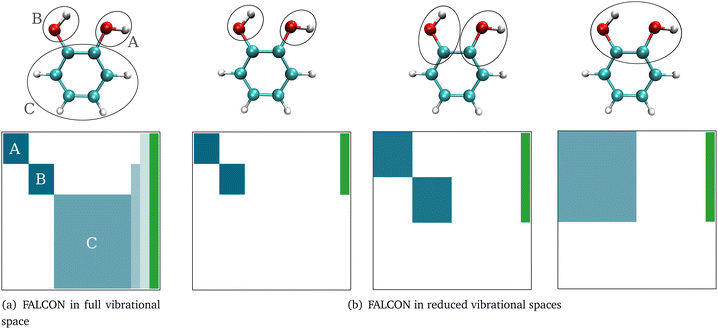
Here, we briefly introduce FALCON coordinates and the related terminology used in this work. For details on the FALCON algorithm, see ref. 24. FALCON coordinates are iteratively constructed rectilinear coordinates with well-defined locality on certain groups of atoms. They are purely vibrational coordinates, free from global translational and rotational contributions. Two different types of local coordinates can be generated: (i) the first option is to employ the FALCON algorithm on the full vibrational space, resulting in spatially local coordinates that describe the intra-group motion, and inter-group coordinates describing relative motion between rigid groups with fixed structures. Generally, intra-group vibrational modes involve only non-zero displacement of the nuclei within this group, while the remaining nuclei have zero displacement. To further illustrate the nature of intra and inter-group FALCON coordinates, the character of these FALCON modes is shown in Fig. 1a. Here, FALCON coordinates spanning the full vibrational space are generated, where the coordinates are kept local to the two OH groups (A) and (B), and the remaining benzene ring (C). The intra-group FALCON coordinates of the two OH groups exhibit the highest degree of locality, followed by the intra-group coordinates of the benzene ring. Further, inter-group coordinates describing the relative motion of (B) ↔ (C) and (BC) ↔ (A) are created with rigid structures of (A)–(C).The second option in the FALCON algorithm is to generate (ii) reduced vibrational spaces with the so-called growing scheme. It systematically expands the vibrational space, starting from user-defined growing seeds. More than one growing seed can be defined as a starting point. The growing seeds refer to an initial group, which are input-defined disjoint (groups of) atoms. The vibrational subspace is expanded iteratively through the fusion of (initial) groups into the groups containing the growing seeds. This fusion is determined by a coupling estimate, for instance, based on the full Hessian. If the full Cartesian Hessian proves to be the bottleneck for the investigated system, a distance-based criterion can be applied, which has been found to yield similar results for small molecules.24 The growing process can be stopped at any iteration step, creating reduced vibrational spaces. The diagonalization of the corresponding reduced mass-weighted Hessian results in quasi-harmonic frequencies and quasi-harmonic modes and are unlike harmonic frequencies and normal modes not directly obtained from the eigenvalues and eigenvectors of the full mass-weighted Hessian. This is exemplarily shown in Fig. 1b. The expansion of the vibrational space starts from the two OH-groups of catechol as growing seeds and each remaining atom of the benzene ring represents one group. In the first fusion step, the two carbon atoms of the benzene ring are fused into the growing group, resulting in a reduced space with six FALCON coordinates and a high degree of locality. In a subsequent fusion, the two groups are merged into one vibrational subspace (right in Fig. 1b), resulting in already rather delocalized twelve FALCON coordinates. If the iteration process is not halted, the growing scheme converges to the full vibrational space with coordinates equivalent to normal coordinates.
2.2 Multilevel potential energy and dipole moment surfaces
The PES V(q1,q2,q3,…,qM) as a function of M vibrational coordinates q1,q2,q3,…,qM can be expressed in terms of a set of approximations8,9,15,60–65| V(1),V(2),…,V(M). | (1) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) m within the restricted mode-coupling60 approximation
m within the restricted mode-coupling60 approximation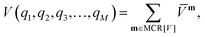 | (2) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) m (or sub-potentials) are functions of only the modes present in the respective MC m. The final set of the MCs included for the PES representation are collected in the mode-combination range (MCR). If all one-, two-, …, M-mode couplings are included in the MCR, the expansion becomes exact. For example, the sub-potentials for one- and two-mode couplings of mode m1 and m2 read
m (or sub-potentials) are functions of only the modes present in the respective MC m. The final set of the MCs included for the PES representation are collected in the mode-combination range (MCR). If all one-, two-, …, M-mode couplings are included in the MCR, the expansion becomes exact. For example, the sub-potentials for one- and two-mode couplings of mode m1 and m2 read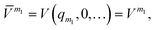 | (3) |
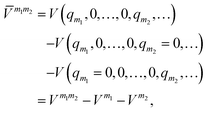 | (4) |
The MCR formalism further enables a multilevel description VML of the underlying potential of the form
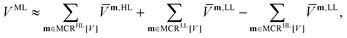 | (5) |
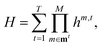 | (6) |
An attractive tool for an efficient black-box calculation of the lower-dimensional sub-potentials in the SOP form represents the adaptive density guided approach (ADGA).26,66,67 Grid points for the sub-potentials are efficiently placed, guided by subsequent vibrational wave function calculations. In comparison to previous studies employing the multilevel variant of the ADGA scheme,16,26,27,68–71 we do not restrict low and high levels to the respective mode-coupling order but rather restrict high- and low-level descriptions to sets of modes tailored to a spectroscopic signature. Our preceding formulation was limited to the energy surface but is equally valid for dipole moment surfaces.
2.3 Computational protocol
Our computational protocol for generating tailored property surfaces for spectral signatures is displayed in Fig. 2. The overall procedure to generate anharmonic IR spectra is presented in the right panel of Fig. 2. Firstly (i), the structure of the investigated system is optimized, followed by the (ii) generation of vibrational coordinates and vibrational (reduced) space. With these modes (iii), the potential energy surface (PES) and dipole moment surface (DMS) operators are generated in a SOP form, followed by the (iv) vibrational wave function calculation. The two steps in the focus are step (ii) and (iii), which are elaborated on the right panel of Fig. 2. These two steps will be explained in detail in the following.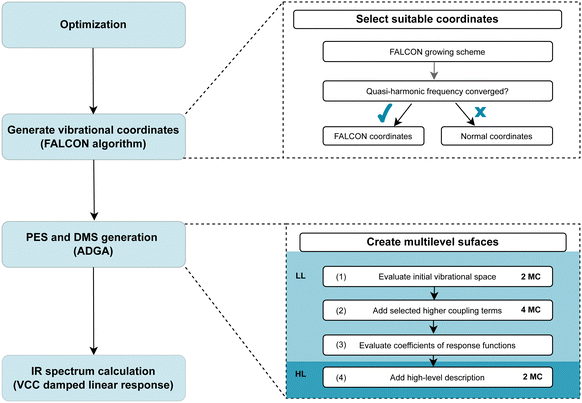 | ||
| Fig. 2 Visualization of the computational protocol suggested for generating tailored multilevel property surfaces for spectral signatures. For more details see explanations in the main text. | ||
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O or OH groups. As explained above, the growing scheme creates reduced vibrational spaces with corresponding quasi-harmonic frequencies. The convergence behaviour of the quasi-harmonic frequencies, referring to the modes of interest, with increasing vibrational space size can guide the selection of the vibrational space and coordinates: rapid convergence for increasing vibrational space size suggests that these FALCON-generated reduced spaces are likely suitable for subsequent anharmonic calculations. For applications of larger molecules, the use of the full vibrational space is unfeasible due to the large number of DOFs. Here, the growing scheme can provide an initial estimate of the vibrational subspace size and assist in identifying which atoms should be considered for spanning the vibrational space.
O or OH groups. As explained above, the growing scheme creates reduced vibrational spaces with corresponding quasi-harmonic frequencies. The convergence behaviour of the quasi-harmonic frequencies, referring to the modes of interest, with increasing vibrational space size can guide the selection of the vibrational space and coordinates: rapid convergence for increasing vibrational space size suggests that these FALCON-generated reduced spaces are likely suitable for subsequent anharmonic calculations. For applications of larger molecules, the use of the full vibrational space is unfeasible due to the large number of DOFs. Here, the growing scheme can provide an initial estimate of the vibrational subspace size and assist in identifying which atoms should be considered for spanning the vibrational space.
3 Computational details
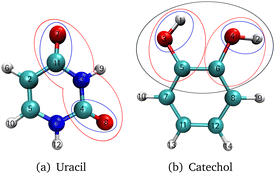
The investigated molecules uracil and catechol (Fig. 3) were optimized using the Gaussian1674 program package employing the B2PLYP75 functional and a Dunning-type correlation consistent triple-ζ basis set76 with augmented77 basis functions (aug-cc-pVTZ). Furthermore, a dispersion correction78 (D3) with Becke–Johnson damping79 (BJ) was added. The SCF convergence threshold was set to tight. The same setting was used for the analytic Hessian calculation. With the Hessian as input, the vibrational coordinates were generated with the program package MidasCpp2022.04.0.80 For the growing scheme of the FALCON algorithm, the initial groups are represented by each atom. As initial growing seeds, we chose for uracil the two oxygen atoms [cf. O7 and O8 in Fig. 3a] of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups. For catechol, the two hydrogen atoms [cf. H1 and H2 in Fig. 3b] from the respective OH-groups were selected. The Hessian-based coupling estimate was chosen as a measure for the order of groups to be fused to the initial growing seeds. The degeneracy threshold was set to 0.0001 a.u. For the catechol molecule, also FALCON coordinates representing the full space were generated. Here, the coordinates are local to three subsets (as depicted in Fig. 1a), representing the two OH groups and the benzene ring, respectively. For all generated FALCON coordinates, the input and output files are provided in the link given in the section “Data availability”. For the uracil molecule, we also investigated reduced spaces spanned by normal coordinates. The coordinates were selected in a way that they capture a similar vibrational behaviour of the equivalent reduced space obtained through FALCON coordinates.
O groups. For catechol, the two hydrogen atoms [cf. H1 and H2 in Fig. 3b] from the respective OH-groups were selected. The Hessian-based coupling estimate was chosen as a measure for the order of groups to be fused to the initial growing seeds. The degeneracy threshold was set to 0.0001 a.u. For the catechol molecule, also FALCON coordinates representing the full space were generated. Here, the coordinates are local to three subsets (as depicted in Fig. 1a), representing the two OH groups and the benzene ring, respectively. For all generated FALCON coordinates, the input and output files are provided in the link given in the section “Data availability”. For the uracil molecule, we also investigated reduced spaces spanned by normal coordinates. The coordinates were selected in a way that they capture a similar vibrational behaviour of the equivalent reduced space obtained through FALCON coordinates.
PESs and DMSs were generated with a locally modified version of the MidasCpp2022.04.080 chemistry program package employing the ADGA.26,67,81 As fit-basis functions polynomial functions are used with a maximum order of eight. For the average vibrational density in the iterative ADGA procedure, a number of six modals per mode were chosen. The basis set number was set to ten B-Spline82 functions with a density of 0.8. Default convergence criterion's of the MidasCpp2022.04.080 version for the ADGA εrel, εabs and ερ were chosen. For the multilevel surfaces, the individual surface operator terms were calculated for each step in the protocol separately and merged afterwards by an in-house python3 library following eqn (5). All single-point (SP) calculations were performed employing ORCA5.0.3.83–85 Two different levels of electronic structure theory were applied. The high level of theory in this work is represented by the B2PLYP-D3BJ/aug-cc-pVTZ level of theory. This choice was inspired as the double hybrid functional B2PLYP75 in conjunction with triple-ζ basis set sizes has shown to yield harmonic frequencies more accurate than other density-functional theory (DFT) approaches while being less computationally demanding as, for instance, coupled cluster calculations.86,87 For anharmonic vibrational structure calculations on proteins, the combination of B3LYP and MP2 has previously been found to be a pragmatic choice.88 Hence, we consider the double hybrid functional B2PLYP that directly combines the named approaches promising for anharmonic calculations on biomolecular systems. The resolution of identity approximation for Coulomb integrals (RI-J)89 and the COSX numerical integration for HF exchange (RI-COSX)90 was used with suiting auxiliary basis sets (def2/J and aug-cc-pVTZ/C for B2PLYP).91 For the low level of theory, we employed r2SCAN-3c92 due to its recommended good-cost accuracy performance.93 For all SP calculations, the SCF convergence threshold was set to tight. All calculated surfaces are listed in the ESI† in Table SI.
The anharmonic vibrational calculations were performed with MidasCpp2023.10.094 targeting all fundamental vibrational excitations, applying VCC damped linear response functions. For the underlying VSCF ground-state wave function calculations a B-Spline basis of 10th order using a primary basis density of 0.8 was chosen. Furthermore, the six lowest VSCF modals per mode were included for the correlation treatment. For the damped linear response calculations, the band-Lanczos algorithm68 was chosen. One technical parameter of the band-Lanczos algorithm is the so-called chain length, which describes the excitation space of the correlated vibrational wave function. Since the full chain length is often not computationally feasible, the user has to ensure a convergence of the chain length. For each VCC IR spectrum in the result section, the convergence of the chain length is ensured (cf. Fig. S2 and S3 in the ESI†). Different excitation levels for the VCC wave function were chosen, ranging from VCC[1] to VCC[4]. The damped linear response functions were calculated at every inverse centimeter for the spectral range of 1600 to 1900 cm−1 and 3500 to 3900 cm−1 for uracil and catechol, respectively. In order to compare the theoretical spectra with the experimental ones, the damping factors for uracil and catechol calculations were set to γ = 2 cm−1 and γ = 13 cm−1, respectively.
All spectra shown in this study are normalized to the maximum peak height of the respective frequency range investigated. The experimental spectrum of uracil56 was extracted using a plot digitizer.95 Presented modes are visualized with the JSindo96 software. Information on explicit runtimes refers to calculations performed on Intel(R) Xeon(R) silver 4316 CPU (2.30 GHz).
4 Results and discussion
4.1 C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) O stretchings signatures in uracil
O stretchings signatures in uracil
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations resulting from reduced vibrational subspaces generated with the FALCON growing scheme. We start from the two oxygen atoms O7 and O8 (Fig. 3a). The fused atoms representing the respective vibrational subspaces are listed in the ESI† in Table SII. The resulting quasi-harmonic frequencies for the two C
O stretching vibrations resulting from reduced vibrational subspaces generated with the FALCON growing scheme. We start from the two oxygen atoms O7 and O8 (Fig. 3a). The fused atoms representing the respective vibrational subspaces are listed in the ESI† in Table SII. The resulting quasi-harmonic frequencies for the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations are displayed in Fig. 4, with the respective harmonic frequencies indicated by dotted lines. Is the reduced space represented by two FALCON coordinates (blue circles in Fig. 3), the quasi-harmonic frequencies deviate strongly from the full harmonic frequency about 36.61 cm−1 and 47.33 cm−1 for the C4
O stretching vibrations are displayed in Fig. 4, with the respective harmonic frequencies indicated by dotted lines. Is the reduced space represented by two FALCON coordinates (blue circles in Fig. 3), the quasi-harmonic frequencies deviate strongly from the full harmonic frequency about 36.61 cm−1 and 47.33 cm−1 for the C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8 and C11
O8 and C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O7 stretching vibration, respectively. Increasing the subspace size, we obtain a converging behaviour towards the full harmonic vibration. However, the harmonic frequencies at normal modes is recovered by a vibrational subspace including 21 modes for the C
O7 stretching vibration, respectively. Increasing the subspace size, we obtain a converging behaviour towards the full harmonic vibration. However, the harmonic frequencies at normal modes is recovered by a vibrational subspace including 21 modes for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O frequency, which is higher in energy (C11
O frequency, which is higher in energy (C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O7). For the quasi-harmonic frequency of C4
O7). For the quasi-harmonic frequency of C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8, full convergence is only reached when all vibrational modes are taken into account. In the harmonic case, tailored FALCON subspaces, hence, appear unsuitable for an adequate alternative representation of the vibrational motion of the two C
O8, full convergence is only reached when all vibrational modes are taken into account. In the harmonic case, tailored FALCON subspaces, hence, appear unsuitable for an adequate alternative representation of the vibrational motion of the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations. Therefore, the full vibrational space (normal modes) is preferable for describing the vibrational motion of the C
O stretching vibrations. Therefore, the full vibrational space (normal modes) is preferable for describing the vibrational motion of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretchings. Hence, we performed anharmonic reduced-space calculations for FALCON and normal coordinates to test our hypothesis.
O stretchings. Hence, we performed anharmonic reduced-space calculations for FALCON and normal coordinates to test our hypothesis.
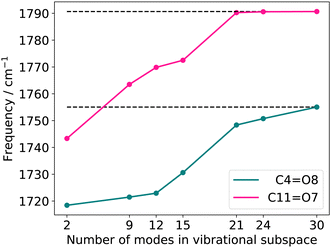 | ||
Fig. 4 Quasi-harmonic frequencies for the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations with increasing vibrational subspace (B2PLYP-D3/aug-cc-pVTZ). The atoms considered in each vibrational subspace are shown in the ESI† in Table SII. O stretching vibrations with increasing vibrational subspace (B2PLYP-D3/aug-cc-pVTZ). The atoms considered in each vibrational subspace are shown in the ESI† in Table SII. | ||
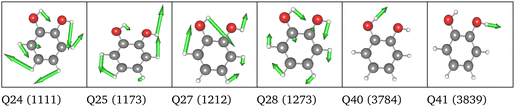
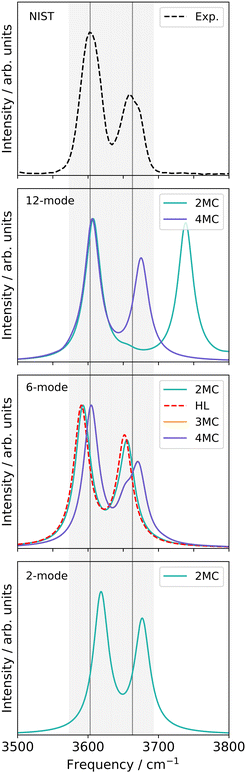
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations (Q24 and Q25 in Fig. S1, ESI†) and the nine-mode space is extended with the modes Q0, Q5, Q9, Q11, Q13, Q18, and Q20 (Fig. S1a, f, j, l, n, s and u, ESI†). All SP calculations were carried out with the low-level method r2SCAN-3c. Further, evaluations of different VCC excitation levels applied on the nine normal mode space (cf. ESI,† Section S2.3.1) suggest, that the coupling order of the potential exerts a higher influence on the calculated infrared spectrum than higher excitations (beyond VCC[2]) in the correlated wave function. Therefore the performance on the 30-mode space and subsequent multilevel calculations are assessed with a VCC[2] level of excitations in the wave function. For comparison, the experimental spectrum in Ar-matrix at 10 K is shown on the bottom panel of Fig. 5. The experimental spectrum exhibits three significant signals within the frequency range of 1600 to 1900 cm−1. According to ref. 56, the first signal around 1703.5–1706.4 cm−1 refers to a combination band, whereas the peak at 1728.2–1733.2 cm−1 and 1761.4–1763.7 cm−1 can be assigned to the fundamental C
O stretching vibrations (Q24 and Q25 in Fig. S1, ESI†) and the nine-mode space is extended with the modes Q0, Q5, Q9, Q11, Q13, Q18, and Q20 (Fig. S1a, f, j, l, n, s and u, ESI†). All SP calculations were carried out with the low-level method r2SCAN-3c. Further, evaluations of different VCC excitation levels applied on the nine normal mode space (cf. ESI,† Section S2.3.1) suggest, that the coupling order of the potential exerts a higher influence on the calculated infrared spectrum than higher excitations (beyond VCC[2]) in the correlated wave function. Therefore the performance on the 30-mode space and subsequent multilevel calculations are assessed with a VCC[2] level of excitations in the wave function. For comparison, the experimental spectrum in Ar-matrix at 10 K is shown on the bottom panel of Fig. 5. The experimental spectrum exhibits three significant signals within the frequency range of 1600 to 1900 cm−1. According to ref. 56, the first signal around 1703.5–1706.4 cm−1 refers to a combination band, whereas the peak at 1728.2–1733.2 cm−1 and 1761.4–1763.7 cm−1 can be assigned to the fundamental C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations, with peak centres at 1731 cm−1 and 1763 cm−1.
O stretching vibrations, with peak centres at 1731 cm−1 and 1763 cm−1.
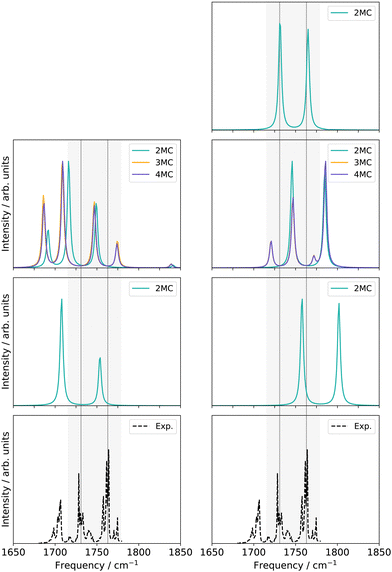 | ||
| Fig. 5 Damped linear response spectra of uracil for the spectral range of 1650–1850 cm−1 on two-mode reduced spaces on a full coupled PES (FVCI), nine-mode reduced space on 2MC, 3MC, and 4MC property surfaces (VCC[4]), and on a 30-mode full space (VCC[2]) for FALCON and normal modes, respectively. The experiment is obtained in an Ar-matix at T = 10 K and taken from ref. 56. The property surfaces are calculated on the r2SCAN-3c level. All peak position values for the calculations can be found in the ESI† in Table SIII. | ||
For the two-mode space in FALCON coordinates on a fully coupled potential (Fig. 5 left panel), the calculated peak positions and intensities (FVCI) significantly diverge from the experimental results: both peaks are red-shifted with a contrary calculated intensity compared to the experiment. Upon expanding the reduced space to nine FALCON modes, the resulting VCC[4] spectrum on 2MC shows a red shift compared to the experimental frequencies, accompanied by the emergence of a third signal around 1692 cm−1. However, the calculated peak heights remain inaccurate in comparison to the experiment. Increasing the coupling level does not improve the agreement with the experiment. Examining the convergence behaviour with growing subspace sizes from the two-mode space to the nine-mode space, we observe a blue shift for the C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8 peak, while a red shift is observed for the C11
O8 peak, while a red shift is observed for the C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O7 fundamental anharmonic peak. Concluding from these results, such FALCON-generated reduced spaces do not appear suitable for appropriately describing the C
O7 fundamental anharmonic peak. Concluding from these results, such FALCON-generated reduced spaces do not appear suitable for appropriately describing the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretches in uracil.
O stretches in uracil.
In the case of the two-mode space spanned by two normal modes (Fig. 5 right panel), the calculated excitation energies obtained from a FVCI calculation show discrepancies of 27 cm−1 and 39 cm−1 when compared to the experimental values for C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8 and C11
O8 and C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O7, respectively. Increasing the vibrational space to nine modes (Fig. 5 right panel), the two peaks of the two-mode space are shifted towards lower frequencies and thereby in closer agreement to the experimental peaks. However, the intensities are still mismatched to the experiment. Increasing the coupling order of the potential to 3MC and 4MC (orange and purple spectrum in Fig. 5), the spectra on these potentials with different coupling orders exhibit identical shapes. Further, we observe a good agreement to the intensity relation, shown in the experiment: a third peak around 1720 cm−1 with a similar height to the experimental peak around 1705 cm−1 appears. This peak refers to a resonance between a combination band and the fundamental C4
O7, respectively. Increasing the vibrational space to nine modes (Fig. 5 right panel), the two peaks of the two-mode space are shifted towards lower frequencies and thereby in closer agreement to the experimental peaks. However, the intensities are still mismatched to the experiment. Increasing the coupling order of the potential to 3MC and 4MC (orange and purple spectrum in Fig. 5), the spectra on these potentials with different coupling orders exhibit identical shapes. Further, we observe a good agreement to the intensity relation, shown in the experiment: a third peak around 1720 cm−1 with a similar height to the experimental peak around 1705 cm−1 appears. This peak refers to a resonance between a combination band and the fundamental C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8 stretching vibration. Increasing the vibrational space to the full vibrational space (30 normal modes), the excitation energies of the two fundamental C
O8 stretching vibration. Increasing the vibrational space to the full vibrational space (30 normal modes), the excitation energies of the two fundamental C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretches agree with the experiment for a 2MC potential. Comparing the peak positions for 2MC coupled potentials of the two-mode, nine-mode, and 30-mode space, we obtain a convergence towards the experiment, but convergence is only reached for the full vibrational space (30 normal modes). We can, hence, conclude, that normal coordinates, in particular the space of all normal coordinates, are a suitable choice for the initial surface, as already indicated by the convergence behaviour of the quasi-harmonic frequencies (Fig. 4). Further, these calculations showed, that higher coupling terms (>2MC) have a high impact on the intensities without impacting the peak positions. Further, the inclusion of three-body terms reveals the appearance of the combination band peak. This can be explained by the fact, that the resonance between the combination band and the fundamental band is itself an interaction of three different modes that necessitates a proper description through a 3MC-coupled PES. Unfortunately, the generation of 3MC coupling terms for 30-modes and the subsequent wave function calculation is already a computational challenge and tailored multilevel property surfaces for these C
O stretches agree with the experiment for a 2MC potential. Comparing the peak positions for 2MC coupled potentials of the two-mode, nine-mode, and 30-mode space, we obtain a convergence towards the experiment, but convergence is only reached for the full vibrational space (30 normal modes). We can, hence, conclude, that normal coordinates, in particular the space of all normal coordinates, are a suitable choice for the initial surface, as already indicated by the convergence behaviour of the quasi-harmonic frequencies (Fig. 4). Further, these calculations showed, that higher coupling terms (>2MC) have a high impact on the intensities without impacting the peak positions. Further, the inclusion of three-body terms reveals the appearance of the combination band peak. This can be explained by the fact, that the resonance between the combination band and the fundamental band is itself an interaction of three different modes that necessitates a proper description through a 3MC-coupled PES. Unfortunately, the generation of 3MC coupling terms for 30-modes and the subsequent wave function calculation is already a computational challenge and tailored multilevel property surfaces for these C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretchings appear as a promising route.
O stretchings appear as a promising route.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8 and C11
O8 and C11![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O7 in comparison to LL1, respectively. Nonetheless, the spectrum correctly represents the intensity ratio, and a third peak around 1718 cm−1 is captured. The resulting spectrum of the merged potential (LL2) lies, hence, between the two single-level spectra [cf. LL1 potential and nine-mode 4MC potential (cf.Fig. 5 right panel)].
O7 in comparison to LL1, respectively. Nonetheless, the spectrum correctly represents the intensity ratio, and a third peak around 1718 cm−1 is captured. The resulting spectrum of the merged potential (LL2) lies, hence, between the two single-level spectra [cf. LL1 potential and nine-mode 4MC potential (cf.Fig. 5 right panel)].
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations in uracil. M refers to the number of modes considered within one electronic structure level. All modes refer to normal coordinates
O stretching vibrations in uracil. M refers to the number of modes considered within one electronic structure level. All modes refer to normal coordinates
| High level | Low level | |
|---|---|---|
| LL1 | 30 M 2MC | |
| LL2 | 9 M 4MC; LL1 | |
| ML1 | 2 M 2MC | LL2 |
| ML2 | 6 M 2MC | ML1 |
 | ||
| Fig. 6 VCC[2] damped linear response spectra of different levels of the employed property surfaces on 30 normal modes of uracil. For further explanations see main text and Table 1. | ||
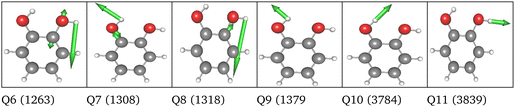
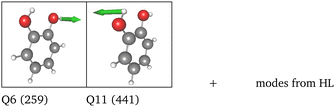
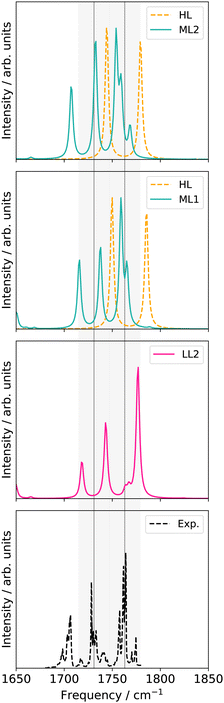
Replacing the most important operator terms through operator terms that are obtained with a more expensive electronic-structure method, appears as a logical next step for an appropriate description of the potential. The two most important modes for the spectral signatures of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O spectral range are the normal coordinates of the C
O spectral range are the normal coordinates of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations. Therefore, we generated a two-mode 2MC coupled high-level potential, where the SPs were calculated on the B2PLYP-D3/aug-cc-pVTZ level and combined it with non-existing terms to the LL2 potential. The merged potential is denoted ML1. The resulting VCC[2] spectrum is depicted in Fig. 6. In comparison to the calculated spectrum on the LL2 potential, we observe a red shift of the ML1. We further observe a good agreement with the experimental data, assuming some uncertainties also in the experiment. Following our protocol, the response functions of the latest low-level potential are analyzed to identify which modes are most significant for the C
O stretching vibrations. Therefore, we generated a two-mode 2MC coupled high-level potential, where the SPs were calculated on the B2PLYP-D3/aug-cc-pVTZ level and combined it with non-existing terms to the LL2 potential. The merged potential is denoted ML1. The resulting VCC[2] spectrum is depicted in Fig. 6. In comparison to the calculated spectrum on the LL2 potential, we observe a red shift of the ML1. We further observe a good agreement with the experimental data, assuming some uncertainties also in the experiment. Following our protocol, the response functions of the latest low-level potential are analyzed to identify which modes are most significant for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching signals and necessitate a high-level description. Both peaks exhibit the strongest mixing with the modes shown in Fig. 7 besides the two C
O stretching signals and necessitate a high-level description. Both peaks exhibit the strongest mixing with the modes shown in Fig. 7 besides the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations (Q24 and Q25 in Fig. 7). The contribution of these modes to the peaks of the response functions at 1743 cm−1 and 1777 cm−1 of the LL2 are displayed in Table 2. For these additional four modes (Q5, Q11, Q13, Q18), we generated a 2MC potential in B2PLYP-D3/aug-cc-pVTZ level of theory (high level) and replaced the respective low-level operator terms in the ML1 potential. The resulting VCC[2] spectrum on this new multilevel potential is labeled with ML2 in Fig. 6. Compared to the ML1 spectrum the intensity of the C4
O stretching vibrations (Q24 and Q25 in Fig. 7). The contribution of these modes to the peaks of the response functions at 1743 cm−1 and 1777 cm−1 of the LL2 are displayed in Table 2. For these additional four modes (Q5, Q11, Q13, Q18), we generated a 2MC potential in B2PLYP-D3/aug-cc-pVTZ level of theory (high level) and replaced the respective low-level operator terms in the ML1 potential. The resulting VCC[2] spectrum on this new multilevel potential is labeled with ML2 in Fig. 6. Compared to the ML1 spectrum the intensity of the C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8 stretching peak increased, and all peaks are slightly red-shifted. Further, a third peak next to the peak referring to C4
O8 stretching peak increased, and all peaks are slightly red-shifted. Further, a third peak next to the peak referring to C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8 appears, which is also shown by the experimental spectrum. This third signal around 1707 cm−1 in the ML2 spectrum originates from a resonance of a combination band from mode Q11 and Q13 (cf.Fig. 7) with the fundamental C
O8 appears, which is also shown by the experimental spectrum. This third signal around 1707 cm−1 in the ML2 spectrum originates from a resonance of a combination band from mode Q11 and Q13 (cf.Fig. 7) with the fundamental C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch Q24. Q11 and Q13 are a symmetric and asymmetric stretch of the uracil ring. It becomes evident, that an accurate description of selected low-order coupling terms significantly improves the spectral shape. Our protocol offers guidance on effectively selecting these terms tailored to the spectroscopic signatures while managing computational costs.
O stretch Q24. Q11 and Q13 are a symmetric and asymmetric stretch of the uracil ring. It becomes evident, that an accurate description of selected low-order coupling terms significantly improves the spectral shape. Our protocol offers guidance on effectively selecting these terms tailored to the spectroscopic signatures while managing computational costs.
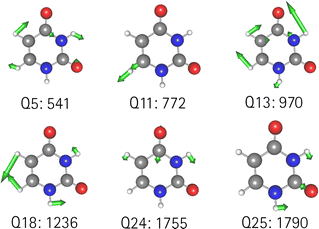 | ||
| Fig. 7 Visualization of the normal modes described in the high level for uracil. The frequency refers to the harmonic frequency in cm−1 obtained with B2PLYP-D3/aug-cc-pVTZ. | ||
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations obtained in the VCC[2] response framework on the LL2 PES. For further information see main text
O stretching vibrations obtained in the VCC[2] response framework on the LL2 PES. For further information see main text
| 1743 cm−1 | 1777 cm−1 | ||
|---|---|---|---|
| Coefficient | Mode(s) | Coefficient | Mode(s) |
| 0.403 | Q241 | 0.780 | Q251 |
| 0.231 | Q111 Q131 | 0.033 | Q111 Q131 |
| 0.120 | Q51 Q181 | 0.019 | Q51 Q181 |
To estimate the computational costs, we examine the number of SP calculations required for the generation of the ML2 PES: for the LL2 PES, which forms the low-level component of the ML2 PES, 211![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 914 SP calculations were required, while the high-level component required 2736 SPs. On average, a single SP calculation for the uracil molecule takes 35 s of CPU time at the low level (r2SCAN-3c) and 373 s of CPU time at the high level (B2PLYP-D3/aug-cc-pVTZ) of theory. Based on this, the estimated total CPU time for these calculations amounts to approximately 100 days. Since these SP calculations can be run in parallel, this results in a total wall time of approximately 2.5 days using 40 cores. In comparison, generating a PES for the full vibrational space of uracil, including 4MC coupling terms, requires an estimated number of 2.7 million SP calculations. A detailed explanation of how this number was determined is available in Section S4 of the ESI.† For the low-level calculations, this corresponds to approximately 1000 days of CPU time, leading to a wall time of around 25 days with 40 cores. For a generation of the PES at the high level only, the immense amount of computing time is even more pronounced, requiring approximately 250 days of wall time with 40 cores. This is 10 times and 100 times the amount of walltime compared to the walltime required by the protocol for a calculation in the low or high level, respectively. This thought experiment highlights that for a high-level PES generation of the full vibrational space of uracil is prohibitively resource-intensive and thereby underlines the efficiency of the proposed protocol.
914 SP calculations were required, while the high-level component required 2736 SPs. On average, a single SP calculation for the uracil molecule takes 35 s of CPU time at the low level (r2SCAN-3c) and 373 s of CPU time at the high level (B2PLYP-D3/aug-cc-pVTZ) of theory. Based on this, the estimated total CPU time for these calculations amounts to approximately 100 days. Since these SP calculations can be run in parallel, this results in a total wall time of approximately 2.5 days using 40 cores. In comparison, generating a PES for the full vibrational space of uracil, including 4MC coupling terms, requires an estimated number of 2.7 million SP calculations. A detailed explanation of how this number was determined is available in Section S4 of the ESI.† For the low-level calculations, this corresponds to approximately 1000 days of CPU time, leading to a wall time of around 25 days with 40 cores. For a generation of the PES at the high level only, the immense amount of computing time is even more pronounced, requiring approximately 250 days of wall time with 40 cores. This is 10 times and 100 times the amount of walltime compared to the walltime required by the protocol for a calculation in the low or high level, respectively. This thought experiment highlights that for a high-level PES generation of the full vibrational space of uracil is prohibitively resource-intensive and thereby underlines the efficiency of the proposed protocol.
4.2 O–H stretching signatures of catechol
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretchings of uracil. Hence, these growing-scheme-generated subspaces are promising for the selection of suitable vibrational coordinates used in subsequent anharmonic structure calculations.
O stretchings of uracil. Hence, these growing-scheme-generated subspaces are promising for the selection of suitable vibrational coordinates used in subsequent anharmonic structure calculations.
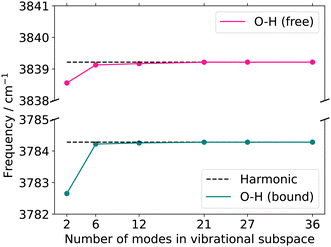 | ||
| Fig. 8 Quasi-harmonic frequencies for the two OH-stretching vibrations with increasing vibrational subspace size (B2PLYP-D3/aug-cc-pVTZ). O–H (bound) refers to the hydrogen-bonded stretching vibration of O3–H1, whereas O–H (free) refers to the hydrogen-bond-accepting stretching vibration of O4–H2. The atoms considered in each vibrational subspace are listed in the ESI† in the Table SIV. The dotted line represents the harmonic frequency at normal modes. | ||
 | ||
| Fig. 9 FVCI, VCC[4] and VCC[3] damped linear response spectra of catechol for the spectral range of 3500–3800 cm−1 on the two-mode (FALCON) reduced-space on full-coupled property surfaces (FVCI), on the six-mode (FALCON) reduced-space on 2MC, 3MC and 4MC property surfaces, and on the twelve-mode (FALCON) reduced space on 2MC, and 4MC property surfaces in comparison to the experiment in gas phase.97 The property surfaces are calculated on the r2SCAN-3c level, if not stated otherwise in the legend (HL). All peak position values for the calculations can be found in Table SV in the ESI.† | ||
The FVCI spectrum on a 2MC potential of the two-mode reduced space (turquoise in Fig. 9) exhibits peaks at 3618 cm−1 and 3677 cm−1 for the bound and free OH stretch, respectively. In the FALCON six-mode space, a spectrum with a 2MC potential exhibits peak positions at 3593 and 3655 cm−1 for the bound and free OH stretch, respectively. These positions are red-shifted by 25 cm−1 and 16 cm−1 with respect to the two-mode space spectrum. The spectral shapes on the 3MC (orange) and 4MC (purple) surfaces yield identical results and are blue-shifted compared to the 2MC potential spectrum. Regarding the calculated peaks of the free OH-stretching vibration, a resonance peak with 3652 and 3672 cm−1 is observed, as indicated by a left-sided shoulder of the peak.
For the twelve-mode space with a 2MC potential, the fundamental OH bound peak is located at 3607 cm−1. This is in agreement with the corresponding peak in the spectrum calculated in the six-mode space with 3MC/4MC coupling terms. In contrast, the peak associated with the free OH stretch (twelve-mode 2MC) shows a significant deviation from the spectra on the two- and six-mode spaces, appearing at 3738 cm−1. Additionally, the two peaks in this spectrum are of equal height, unlike in the spectral shapes of the two- and six-mode space. The spectrum calculation with a potential including 3MC terms resulted in profound convergence issues (cf. Fig. S7h, ESI†) and is, hence, not shown here. Introducing 4MC terms (purple) in the potential of the twelve-mode space, the spectral shape qualitatively aligns with the spectrum of the two- and six-mode space again. The peak position of the free OH stretch appears at 3675 cm−1 aligning with the second resonance peak of the 3MC/4MC six-mode space spectra.
Additionally, an experimental gas-phase spectrum97 is shown on top of Fig. 9. It exhibits two peaks at 3603 cm−1 and 3663 cm−1. The overall shape of the experimental IR spectrum is remarkably well reassembled by the theoretical infrared spectrum on the two-mode space, given the applied approximation in the PES. The peak positions still deviate from the experiment about 15 cm−1 and 14 cm−1 for the bound and free OH stretch, respectively. For the six-mode space, the spectral shapes of the 3MC and 4MC surfaces demonstrate semi-quantitative agreement with the experimental spectrum. The peak position assigned to the bound OH stretch deviates only marginally by 2 cm−1 and 1 cm−1 for the 3MC and 4MC PES, respectively. The experiment also indicates a slight shoulder, however, reversed to the shoulder in the six-mode space. Still, the local description of the OH stretching appears to be remarkably suitable, given the applied level of electronic structure theory. To study the possibility of a fortunate error cancellation arising from the underlying approximation, we calculated the 2MC PES at a higher level using B2PLYP-D3/aug-cc-pVTZ (red in Fig. 9). Notably, we observe a close alignment between the HL and LL spectra, indicating the good performance of the r2SCAN-3c method.
For the twelve-mode space, the inclusion of 4MC terms recovers the numerical stability. This could indicate, that the poor descriptions of the 2MC and 3MC spectra in the twelve-mode space simply can suffer from a non-converged n-mode expanded PES. Still, the twelve-mode space spectrum with 4MC terms performs worse than the spectra of the six-mode space in comparison to experimental data. In a thorough analysis of the 2MC PES, we found two 2MC potential cuts showing conspicuous sharp declines at already small displacements of the corresponding twelve-mode space along the OH-stretch coordinates in conjunction with low-frequency out-of-plane wagging modes (cf. Fig. S10, ESI†). The exclusion of these coupling terms stabilized the response calculations and further yielded frequencies that deviated only one inverse centimeter from both experimental peaks. However, to obtain this minor deviation, the inclusion of the 4MC terms was still necessary. We, hence, believe that these mode-coupling terms between the OH-stretching mode and the out-of-plane modes cause the numerical instabilities in the VCC calculations. This assumption is underlined by earlier work on malonaldehyde.98,99 Here, a similar situation with strong anharmonicity coupling between the in-plane and out-of-plane vibrational motion of the OH groups has been found. These studies also employed rectilinear (normal) coordinates to describe the vibrational motion. Both studies offer the indication that the application of rectilinear stiff coordinates and neglecting rotational and vibrational coupling effects challenge the accurate description of the torsion angular motion of the OH-groups in such systems. Fortunately, such floppy-out-of-plane motions are probably not present in more complex biomolecular systems, as the rotation of the OH-rotation is likely hindered due to solvent molecules or the surrounding environment of the remaining biomolecule.
From the analysis above, we conclude that the OH-stretching modes are better characterized by a rather local nature in the two-mode or six-mode space as (1) their locality character stabilizes the calculation of OH-stretching infrared signals, and (2) they provide very good cost-accuracy ratios.
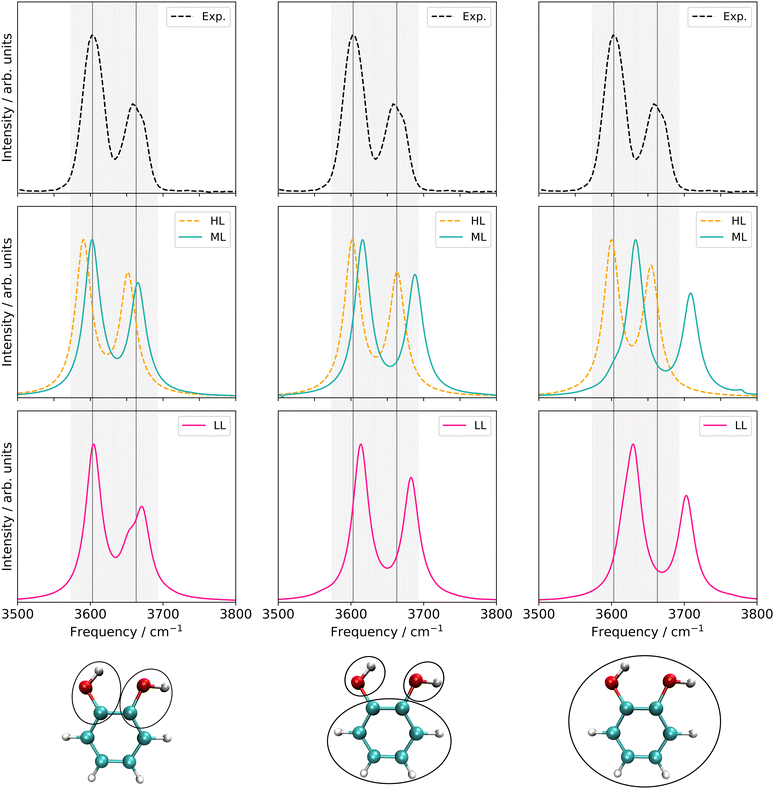 | ||
| Fig. 10 Left panel: VCC[4] damped linear response spectra on different levels of the employed property surfaces of the six-mode FALCON space of catechol. Middle panel: VCC[2] damped linear response spectra of different levels of the employed property surfaces on 36 FALCON modes of catechol. Right panel: VCC[2] damped linear response spectra of different levels of the employed property surfaces on 36 normal modes of catechol. Information about the applied electronic structure method and coupling orders can be found in Table 3. Further, all peak position values can be found in Table SV in the ESI.† | ||
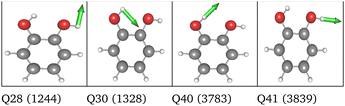
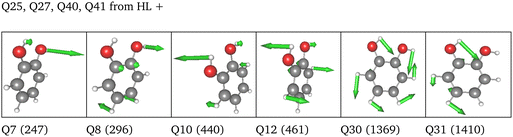
LL PES: the LL PES consists of 2MC terms for the full set of modes, 3MC terms limited to those incorporating at least one of the two OH stretches (Q40/Q41), and 4MC terms for a selected set of modes. The selection of these modes is based on their coupling strength to the OH stretches, estimated on the 2MC LL potential. Due to strong coupling values shown in the space spanned by normal coordinates (cf. Table SVI in the ESI†), a rather large set of ten modes (including the two OH stretches) was chosen. The coupling strength estimates of the FALCON space are by two orders of magnitude smaller than those for normal coordinates (cf. Table SVII in the ESI†). Thus, for the FALCON coordinates only four modes plus the two OH-stretching modes are selected for 4MC terms in the LL of the 36 FC space. Noticeably, all four modes describe inter-group motions of the two OH-groups.
HL PES: the 2MC terms described in the HL were selected by evaluating the coefficients of the response functions referring to the two fundamental OH-stretching peaks. Interestingly, we observed for both spaces relatively small coefficients for mixing vibrational states (cf. Table SVIII in the ESI†). However, the 2MC potential cuts of the LL PES showed instabilities between the out-of-plane wagging and the OH-stretching vibration of the respective OH group (cf. Fig. S14 and S15 in the ESI†). For the normal coordinates, these are the 2MC terms Q7/Q41 and Q10/Q40, and for the FALCON space Q6/Q41 and Q11/Q41. Based on this observation, we included only the modes describing the bending behaviour of the OH groups in conjunction with the OH-stretching modes for the HL. For the FALCON space, these are the bendings Q28 and Q30, whereas for the normal mode space we chose Q24, Q25, Q27, and Q28.
Let us now discuss the performance of the VCC spectra of the LL, HL and ML potential originating from the three different spaces displayed in Fig. 10. For computational efficiency, all response calculations on the full vibrational space were conducted at the VCC[2] level. Analysis of VCC excitation levels in response functions for catechol on the 2MC, 3MC, and 4MC of the FALCON six-mode space (cf. Fig. S9 in the ESI†) reveals that VCC[2] spectra exhibit identical peak positions to VCC[4] spectra, but tend to overestimate the intensity of the free OH peak. The left panel of Fig. 10 shows the results for the reduced space with six FALCON modes as depicted below the graph in this panel. The VCC[4] spectra on LL and HL potential are already extensively discussed above but for better comparison displayed again. On the resulting multilevel spectrum (turquoise), we observe, that the shoulder of the free OH-peak of the LL spectrum disappears for the ML spectrum, resulting in one fundamental peak with semi-quantitative agreement to the experiment. The LL spectrum of the 36 FC space is shown in pink in Fig. 10 middle bottom. It exhibits a similar shape as the experimental data, but the OH-stretching peaks are blue-shifted by 10 cm−1 and 20 cm−1. The ML spectrum almost aligns with the LL spectrum, while the HL spectrum alone (yellow dashed lines) shows surprisingly good agreement with the experiment. While the resulting LL and ML spectra with the 36 NC space exhibit similar shapes to the spectra on 36 FC coordinates, the calculations showed numerical instabilities in chain length convergence (cf. Fig. S7h in the ESI†). The spectrum on the HL potential has red-shifted peaks towards the experiment with frequency values of 3600 cm−1 and 3655 cm−1.
Comparing all multilevel spectra, the spectra calculations on the normal coordinates are the only ones that mitigate numerical instability issues. They further show the largest deviations from the experiment. The reduced-space (6 FC) spectrum from the growing scheme matches the experimental spectrum best. Eye-catching is also the fact, that the HL spectrum of the 36 FC (i.e. four modes on a 2MC PES with B2PLYP-D3/aug-cc-pVTZ) alone achieves excellent agreement with the experiment, in contrast to the respective ML spectrum of 36 FC which deviates slightly more from the experiment. The HL spectrum alone only includes two inter-group coordinates describing the OH-groups’ relative bending motions and two local OH-stretching modes, while the ML PES considers all 36 FALCON coordinates. A larger vibrational space enhances the likelihood of encountering instabilities in the PES, as shown by some 2MC potential cuts. Hence, these pitfall mode combinations can cause these discrepancies.25
We can conclude, that finding a suitable description in rectilinear coordinates for the OH stretchings was not as straightforward as for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretches in the uracil case. Still, our protocol provides highly valuable guidance: we can summarize, that the OH-stretching vibrations are most likely better described by modes localized to a small subset – namely the OH groups themselves – as predicted by the quasi-harmonic frequencies of the growing scheme. This growing scheme also provided suitable FALCON-reduced spaces for the OH stretchings.
O stretches in the uracil case. Still, our protocol provides highly valuable guidance: we can summarize, that the OH-stretching vibrations are most likely better described by modes localized to a small subset – namely the OH groups themselves – as predicted by the quasi-harmonic frequencies of the growing scheme. This growing scheme also provided suitable FALCON-reduced spaces for the OH stretchings.
5 Conclusions
In this work, we proposed a computational protocol for tailoring efficient and at the same time highly accurate calculations of certain spectroscopic signatures in IR-spectroscopy. The protocol consists of two key steps: the selection of suitable coordinates and the generation of the multilevel property surfaces. We evaluated this protocol to two types of spectroscopic signatures: the spectral region of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O fundamental stretchings in uracil and the OH stretchings in catechol.
O fundamental stretchings in uracil and the OH stretchings in catechol.
For the uracil molecule, the protocol successfully yielded a calculated spectrum that closely matches experimental data: the multilevel property surface was generated as a function of normal modes. Reduced spaces in FALCON coordinates appeared unsuitable for anharmonic calculations, which has been correctly predicted by the convergence behaviour of the quasi-harmonic frequencies with increasing vibrational sizes. Moreover, the inclusion of selected higher coupling terms (in the low level) was necessary to reveal Fermi-resonance signals of a combination band and a fundamental C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch.
O stretch.
For the calculation of the OH-stretching spectral signatures of catechol, the protocol suggested a local character of the two OH stretchings from the evaluation of quasi-harmonic frequencies. An underlying reduced-space provided by the FALCON growing scheme algorithm has proven to be well-suited and circumvented instability issues, which occurred in full-space representations. Moreover, we found that including higher coupling terms was more important than high-level treatment of certain coupling terms, highlighting the good performance of the fast r2SCAN-3c semiempirical method.
Overall, we established a protocol that provides reliable guidance while balancing computational cost and accuracy for tailored spectroscopic signatures. However, further practical experience is necessary to develop a robust black-box procedure applicable to larger systems, such as biomolecules. Attractive theories and implementations exist, such as fragment-based potential energy surface generation51,54 or an embedding potential for the vibrational wave function,100 that can be integrated into our protocol to further push the size limitations of these vibrational structure calculations.
Author contributions
J. H. writing – original draft, review, and editing, project administration, data curation, formal analysis, investigation, methodology, validation, visualization, software P. C. writing – review and editing, investigation, validation, formal analysis, software C. K. conceptualization, funding acquisition, validation, supervision, writing – review and editing.Data availability
Data for this article, including the optimized structures of uracil and catechol, all underlying calculated potential energy and dipole moment surfaces, and input and output files for the generation of the FALCON coordinates are available at https://doi.org/10.5281/10.5281/zenodo.14002766.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Deutsche Forschungsgemeinschaft (DFG) through the Emmy Noether Young Group Leader Programme (project 397897341) and an individual research grant (project 523893296). The computations were carried out on the cluster system at the Leibniz University Hannover, Germany, which is funded by the Leibniz University Hannover, the Lower Saxony Ministry of Science and Culture (MWK), and the DFG.Notes and references
- T. Kottke, V. A. Lórenz-Fonfría and J. Heberle, J. Phys. Chem. A, 2017, 121, 335–350 CrossRef CAS PubMed
.
- S. Ito, H. E. Kato, R. Taniguchi, T. Iwata, O. Nureki and H. Kandori, J. Am. Chem. Soc., 2014, 136, 3475–3482 CrossRef CAS PubMed
.
- E. Freier, S. Wolf and K. Gerwert, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11435–11439 CrossRef CAS PubMed
.
- K. Muroda, K. Nakashima, M. Shibata, M. Demura and H. Kandori, Biochemistry, 2012, 51, 4677–4684 CrossRef CAS PubMed
.
- T. Domratcheva, E. Hartmann, I. Schlichting and T. Kottke, Sci. Rep., 2016, 6, 1–14 CrossRef PubMed
.
- T. Fornaro, D. Burini, M. Biczysko and V. Barone, J. Phys. Chem. A, 2015, 119, 4224–4236 CrossRef CAS PubMed
.
- B. Temelso and G. C. Shields, J. Chem. Theory Comput., 2011, 7, 2804–2817 CrossRef CAS PubMed
.
- O. Christiansen, Phys. Chem. Chem. Phys., 2012, 14, 6672–6687 RSC
.
- O. Christiansen, Phys. Chem. Chem. Phys., 2007, 9, 2942–2953 RSC
.
- C. König, Int. J. Quantum Chem., 2021, 121, e26375 CrossRef
.
- P. T. Panek and C. R. Jacob, J. Phys. Chem. Lett., 2016, 7, 3084–3090 CrossRef CAS PubMed
.
- B. Thomsen, T. Kawakami, I. Shigemoto, Y. Sugita and K. Yagi, J. Phys. Chem. B, 2017, 121, 6050–6063 CrossRef CAS PubMed
.
- K. Yagi, K. Yamada, C. Kobayashi and Y. Sugita, J. Chem. Theory Comput., 2019, 15, 1924–1938 CrossRef CAS PubMed
.
- K. Yagi and Y. Sugita, J. Chem. Theory Comput., 2021, 17, 5007–5020 CrossRef CAS PubMed
.
- S. Carter, S. J. Culik and J. M. Bowman, J. Chem. Phys., 1997, 107, 10458–10469 CrossRef CAS
.
- E. L. Klinting, O. Christiansen and C. König, J. Phys. Chem. A, 2020, 124, 2616–2627 CrossRef CAS PubMed
.
- A. Molina, P. Smereka and P. M. Zimmerman, J. Chem. Phys., 2016, 144, 124111 CrossRef PubMed
.
- P. T. Panek and C. R. Jacob, J. Chem. Phys., 2016, 144, 164111 CrossRef PubMed
.
- X. Cheng and R. P. Steele, J. Chem. Phys., 2014, 141, 104105 CrossRef PubMed
.
- B. Thomsen, K. Yagi and O. Christiansen, J. Chem. Phys., 2014, 140, 154102 CrossRef
.
- K. Yagi, M. Keçeli and S. Hirata, J. Chem. Phys., 2012, 137, 204118 CrossRef PubMed
.
- J. M. Bowman, Y. Wang, H. Liu and J. S. Mancini, J. Phys. Chem. Lett., 2015, 6, 366–373 CrossRef CAS PubMed
.
- C. R. Jacob and M. Reiher, J. Chem. Phys., 2009, 130, 084106 CrossRef PubMed
.
- C. König, M. B. Hansen, I. H. Godtliebsen and O. Christiansen, J. Chem. Phys., 2016, 144, 074108 CrossRef PubMed
.
- A. A. Zhanserkeev, E. L. Yang and R. P. Steele, J. Chem. Theory Comput., 2023, 19, 5572–5585 CrossRef CAS PubMed
.
- M. Sparta, M. B. Hansen, E. Matito, D. Toffoli and O. Christiansen, J. Chem. Theory Comput., 2010, 6, 3162–3175 CrossRef CAS PubMed
.
- D. Toffoli, M. Sparta and O. Christiansen, Chem. Phys. Lett., 2011, 510, 36–41 CrossRef CAS
.
- K. Yagi, S. Hirata and K. Hirao, Theor. Chem. Acc., 2007, 118, 681–691 Search PubMed
.
- K. Yagi, S. Hirata and K. Hirao, Phys. Chem. Chem. Phys., 2008, 10, 1781–1788 RSC
.
- K. Yagi and H. Otaki, J. Chem. Phys., 2014, 140, 084113 CrossRef PubMed
.
- J. Liu, J. Yang, X. C. Zeng, S. S. Xantheas, K. Yagi and X. He, Nat. Commun., 2021, 12, 1–10 CrossRef PubMed
.
- G. Rauhut, J. Chem. Phys., 2004, 121, 9313–9322 CrossRef CAS PubMed
.
- G. Rauhut and B. Hartke, J. Chem. Phys., 2009, 131, 014108 CrossRef PubMed
.
- B. Ziegler and G. Rauhut, J. Chem. Phys., 2016, 144, 114114 CrossRef PubMed
.
- B. Ziegler and G. Rauhut, J. Chem. Theory Comput., 2019, 15, 4187–4196 CrossRef CAS PubMed
.
- S. Carter and N. C. Handy, Chem. Phys. Lett., 2002, 352, 1–7 CrossRef CAS
.
- J. A. Tan and J. L. Kuo, J. Chem. Theory Comput., 2018, 14, 6405–6416 CrossRef CAS PubMed
.
- J. A. Tan and J. L. Kuo, J. Chem. Phys., 2021, 154, 134302 CrossRef CAS PubMed
.
- J. A. Tan and J.-L. Kuo, Molecules, 2022, 27, 3198 CrossRef CAS PubMed
.
- D. M. Benoit, J. Chem. Phys., 2004, 120, 562–573 CrossRef CAS PubMed
.
- M. Bounouar and C. Scheurer, Chem. Phys., 2006, 323, 87–101 CrossRef CAS
.
- A. D. Boese and J. M. Martin, J. Phys. Chem. A, 2004, 108, 3085–3096 CrossRef CAS
.
- K. Pflüger, M. Paulus, S. Jagiella, T. Burkert and G. Rauhut, Theor. Chem. Acc., 2005, 114, 327–332 Search PubMed
.
- V. Rodriguez-Garcia, S. Hirata, K. Yagi, K. Hirao, T. Taketsugu, I. Schweigert and M. Tasumi, J. Chem. Phys., 2007, 126, 124303 CrossRef PubMed
.
- T. Hrenar, H. J. Werner and G. Rauhut, Phys. Chem. Chem. Phys., 2005, 7, 3123–3125 RSC
.
- L. Pele and R. B. Gerber, J. Chem. Phys., 2008, 128, 165105 CrossRef PubMed
.
- T. K. Roy and R. B. Gerber, Phys. Chem. Chem. Phys., 2013, 15, 9468–9492 RSC
.
- T. K. Roy and R. B. Gerber, J. Chem. Theory Comput., 2020, 16, 7005–7016 CrossRef CAS PubMed
.
- K. Yagi, K. Hirao, T. Taketsugu, M. W. Schmidt and M. S. Gordon, J. Chem. Phys., 2004, 121, 1383–1389 CrossRef CAS PubMed
.
- M. Riera, C. Knight, E. F. Bull-Vulpe, X. Zhu, H. Agnew, D. G. Smith, A. C. Simmonett and F. Paesani, J. Chem. Phys., 2023, 159, 054802 CrossRef CAS PubMed
.
- D. G. Artiukhin, E. L. Klinting, C. König and O. Christiansen, J. Chem. Phys., 2020, 152, 194105 CrossRef CAS PubMed
.
- D. Madsen, O. Christiansen and C. König, Phys. Chem. Chem. Phys., 2018, 20, 3445–3456 RSC
.
- C. König and O. Christiansen, J. Chem. Phys., 2016, 145, 064105 CrossRef
.
- R. J. Spencer, A. A. Zhanserkeev, E. L. Yang and R. P. Steele, J. Am. Chem. Soc., 2024, 146, 15376–15392 CrossRef CAS PubMed
.
- X. Cheng, J. J. Talbot and R. P. Steele, J. Chem. Phys., 2016, 145, 124112 CrossRef PubMed
.
- A. Y. Ivanov, A. M. Plokhotnichenko, E. D. Radchenko, G. G. Sheina and Y. P. Blagoi, J. Mol. Struct.:THEOCHEM, 1995, 372, 91–100 CAS
.
-
P. Larkin, Infrared and Raman spectroscopy: principles and spectral interpretation, Elsevier, 2017 Search PubMed
.
- S. Coussan, Y. Bouteiller, J. P. Perchard and W. Q. Zheng, J. Phys. Chem. A, 1998, 102, 5789–5793 CrossRef CAS
.
- S. G. Stepanian and L. Adamowicz, Low Temp. Phys., 2020, 46, 155–164 CrossRef CAS
.
- J. Kongsted and O. Christiansen, J. Chem. Phys., 2006, 125, 124108 CrossRef PubMed
.
- D. Toffoli, J. Kongsted and O. Christiansen, J. Chem. Phys., 2007, 127, 204106 CrossRef CAS PubMed
.
- G. C. Schatz, Rev. Mod. Phys., 1989, 61, 669 CrossRef CAS
.
- H. Rabitz and F. Alis, J. Math. Chem., 1999, 25, 197–233 CrossRef CAS
.
- J. O. Jung and R. B. Gerber, J. Chem. Phys., 1996, 105, 10332–10348 CrossRef CAS
.
- K. Yagi, T. Taketsugu, K. Hirao and M. S. Gordon, J. Chem. Phys., 2000, 113, 1005–1017 CrossRef CAS
.
- M. Sparta, I. M. Høyvik, D. Toffoli and O. Christiansen, J. Phys. Chem. A, 2009, 113, 8712–8723 CrossRef CAS PubMed
.
- E. Lund Klinting, B. Thomsen, I. Heide Godtliebsen and O. Christiansen, J. Chem. Phys., 2018, 148, 64113 CrossRef PubMed
.
- I. H. Godtliebsen and O. Christiansen, Phys. Chem. Chem. Phys., 2013, 15, 10035–10048 RSC
.
- I. H. Godtliebsen and O. Christiansen, J. Chem. Phys., 2015, 143, 134108 CrossRef PubMed
.
- B. Thomsen, M. B. Hansen, P. Seidler and O. Christiansen, J. Chem. Phys., 2012, 136, 124101 CrossRef PubMed
.
- P. Seidler, M. Sparta and O. Christiansen, J. Chem. Phys., 2011, 134, 054119 CrossRef PubMed
.
- C. König and O. Christiansen, J. Chem. Phys., 2015, 142, 144115 CrossRef PubMed
.
- P. Seidler, T. Kaga, K. Yagi, O. Christiansen and K. Hirao, Chem. Phys. Lett., 2009, 483, 138–142 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford, CT, 2016 Search PubMed
.
- S. Grimme, J. Chem. Phys., 2006, 124, 34108 CrossRef PubMed
.
- T. H. Dunning and T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS
.
- R. A. Kendall, T. H. Dunning, R. J. Harrison and T. H. Dunning, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- O. Christiansen, I. H. Godtliebsen, E. M. Gras, W. Györffy, M. B. Hansen, M. B. Hansen, E. L. Klinting, J. Kongsted, C. König, S. A. Losilla, D. Madsen, N. K. Madsen, P. Seidler, K. Sneskov, M. Sparta, B. Thomsen, D. Toffoli and A. Zoccante, Molecular Interactions Dynamics And Simulation C++ (MidasCPP) Package, https://gitlab.com/midascpp/midascpp, 2022 Search PubMed.
- M. Sparta, D. Toffoli and O. Christiansen, Theor. Chem. Acc., 2009, 123, 413–429 Search PubMed
.
- D. Toffoli, M. Sparta and O. Christiansen, Mol. Phys., 2011, 109, 673–685 CrossRef CAS
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed
.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed
.
- V. Barone, M. Biczysko and J. Bloino, Phys. Chem. Chem. Phys., 2014, 16, 1759 RSC
.
- M. Biczysko, P. Panek, G. Scalmani, J. Bloino and V. Barone, J. Chem. Theory Comput., 2010, 6, 2115–2125 CrossRef CAS PubMed
.
- T. K. Roy, V. Kopysov, A. Pereverzev, J. Šebek, R. B. Gerber and O. V. Boyarkin, Phys. Chem. Chem. Phys., 2018, 20, 24894–24901 RSC
.
- O. Vahtras, J. Almlöf and M. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518 CrossRef CAS
.
- F. Neese, J. Comput. Chem., 2003, 24, 1740–1747 CrossRef CAS PubMed
.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS
.
- S. Grimme, A. Hansen, S. Ehlert and J.-M. Mewes, J. Chem. Phys., 2021, 154, 064103 CrossRef CAS PubMed
.
- M. Bursch, J.-M. Mewes, A. Hansen and S. Grimme, Angew. Chem., Int. Ed., 2022, 61, e202205735 CrossRef CAS PubMed
.
- O. Christiansen, D. G. Artiukhin, F. Bader, I. H. Godtliebsen, E. M. Gras, W. Györffy, M. B. Hansen, M. B. Hansen, M. G. Højlund, N. Machholdt Høyer, A. Buchgraitz Jensen, E. L. Klinting, J. Kongsted, C. König, D. Madsen, N. K. Madsen, K. Monrad, G. Schmitz, P. Seidler, K. Sneskow, M. Sparta, B. Thomsen, D. Toffoli and A. Zoccante, Molecular Interactions Dynamics And Simulation C++ (MidasCPP) Package, https://gitlab.com/midascpp/midascpp, 2023 Search PubMed.
- W. Digitizer, 2023, https://apps.automeris.io/wpd/.
- K. Yagi, 2022, https://tms.riken.jp/en/research/software/sindo/.
- NIST, 2023, https://webbook.nist.gov/cgi/cbook.cgi?ID=C120809&Units=SI&Mask=80#IR-Spec.
- K. Yagi, T. Taketsugu and K. Hirao, J. Chem. Phys., 2001, 115, 10647–10655 CrossRef CAS
.
- K. Yagi, G. V. Mil’nikov, T. Taketsugu, K. Hirao and H. Nakamura, Chem. Phys. Lett., 2004, 397, 435–440 CrossRef CAS
.
- J. Hellmers and C. König, J. Chem. Phys., 2023, 159, 104108 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: A list of calculated underlying surfaces for the calculated spectra along with the visualization of modes for the applied vibrational spaces in this work and chain length checks ensuring converged damped linear response calculations with the band-Lanczos module. Furthermore, it contains a detailed discussion about the stability of certain potential energy surfaces of catechol and additional information about the multilevel approaches. See DOI: https://doi.org/10.1039/d4cp02916j |
| This journal is © the Owner Societies 2024 |