Sensitivity analysis of aromatic chemistry to gas-phase kinetics in a dark molecular cloud model†
Received
15th August 2024
, Accepted 11th October 2024
First published on 21st October 2024
Abstract
The increasingly large number of complex organic molecules detected in the interstellar medium necessitates robust kinetic models that can be relied upon for investigating the involved chemical processes. Such models require rate coefficients for each of the thousands of reactions; the values of these are often estimated or extrapolated, leading to large uncertainties that are rarely quantified. We have performed a global Monte Carlo and a more local one-at-a-time sensitivity analysis on the gas-phase rate coefficients in a 3-phase dark cloud model. Time-dependent sensitivities have been calculated using four metrics to determine key reactions for the overall network as well as for the cyanonaphthalene molecule in particular, an important interstellar species that is severely under-produced by current models. All four metrics find that reactions involving small, reactive species that initiate hydrocarbon growth have large effects on the overall network. Cyanonaphthalene is most sensitive to a number of these reactions as well as ring-formation of the phenyl cation (C6H5+) and aromatic growth from benzene to naphthalene. Future efforts should prioritize constraining rate coefficients of key reactions and expanding the network surrounding these processes. These results highlight the strength of sensitivity analysis techniques to identify critical processes in complex chemical networks, such as those often used in astrochemical modeling.
1 Introduction
To date, over 300 molecules and ions have been detected in the interstellar medium (ISM), with the number rapidly growing.1 Although such detections confirm the presence of individual molecular species and provide information about their abundances, the chemical processes surrounding these species often remain a mystery. Astrochemical kinetic models are thus typically relied upon to gain information about the underlying chemical pathways.2 Such models simulate the chemical evolution of an interstellar region given a number of input parameters regarding physical conditions and chemical processes.3–6 In larger models this can easily lead to thousands of parameters, all of which must be well-constrained for a robust and reliable model.7 However, the accuracy of these parameters depends on the available observational, experimental, and theoretical data, which is limited.8,9 In particular, astrochemical models are often highly sensitive to the rate coefficients of gas-phase reactions.8,10
The experimental measurement of rate coefficients in general is a time-consuming and difficult task that is further exacerbated by challenges in measuring these values at low temperature in the gas phase. Techniques developed to meet this challenge include ion cyclotron resonance,11 flowing afterglow,12 heavy ion storage rings,13 and CRESU.14 This last technique is able to study ion–neutral and neutral–neutral reactions at temperatures as low as 10 K,15,16 but requires a very large pumping capacity.14 Theoretical treatments also exist for calculating reaction rate coefficients, however, highly-accurate ab initio potential energy surfaces are often needed, as the presence of small barriers can significantly affect calculated rate coefficients.15,17–19 This can become further complicated by the presence of open-shell radicals, which participate in a large portion of reactions relevant to the ISM.19,20 Furthermore, effects such as tunneling and the formation of van der Waals complexes often become significant at low temperatures.15,21 In the absence of low-temperature rate coefficients, either from experiment or theory, values are typically estimated by inspection of similar reactions or by extrapolation of high-temperature values.22 Such estimations are common in astrochemical models but lead to large uncertainties that are often not quantified.8
Sensitivity analysis techniques are frequently applied to complex models to gain an understanding of how uncertainties in input parameters affect output parameters.23,24 The application of sensitivity analysis methods has been extended to a number of research areas including combustion chemistry25 and atmospheric chemistry,26 as well as various astrochemical environments such as the atmospheres of Titan8,27–29 and Neptune,30 protoplanetary disks,31 hot cores,32 diffuse clouds,33 and dark molecular clouds.9,33–36 These studies have primarily focused on using the global sensitivity analysis approach to study simple and abundant molecular species, both comparing abundance uncertainties to observed values and determining key reactions. Over the past decade or more since these initial studies, modeling codes have become more robust and incorporated a wider variety of processes, such as dust grain chemistry.4 Likewise, increasing numbers of detected species and studied reactions requires consistent updates to chemical networks.
A large portion of molecular detections have been made in dark clouds – relatively dense regions of space with low temperatures (∼10 K) yet complex chemical inventories. In particular, the first unambiguous detections of polycyclic aromatic hydrocarbons (PAHs) in the ISM have recently been made toward the Taurus Molecular Cloud 1 (TMC-1).37 PAHs are thought to be abundant throughout the interstellar medium due to ubiquitous spectral features in the infrared and optical/near-infrared.38 These detections suggest formation within the cloud through “bottom-up” processes, yet current astrochemical models dramatically fail to reproduce the observed abundances.37 In this work, we present the application of two sensitivity analysis techniques to a modern astrochemical model of the dark cloud TMC-1. We investigate the effects of rate coefficient uncertainties on modeled abundances of aromatic species and identify their key reactions, as well as compare the suitability of the two different techniques for this purpose.
2 Methodology
2.1 Astrochemical model
A number of modeling codes and chemical networks have been utilized for astrochemical modeling of TMC-1 and other astronomical objects. NAUTILUS,4 UCLCHEM,5 and RATE226 are all publicly available rate-equation codes capable of modeling dark clouds with similar general functionality. The former two codes consider physical and chemical processes on interstellar dust grains, while the latter is gas-phase only. We chose the NAUTILUS modeling code as it is a 3-phase code with a number of features based on experimental and theoretical studies. Dust grains are separated into surface and mantle (bulk ice) phases, with separate reactions for the two phases. A general overview of the model can be seen in Fig. 1. Accretion of gas-phase chemical species onto grain surfaces, desorption of grain species into the gas-phase, and difussion between grain surface and mantle allow for transfer of species between phases. A number of desorption mechanisms are considered including thermal desorption, cosmic-ray stochastic heating, chemical desorption due to reaction exothermicity, and photodesorption via external UV and cosmic-ray induced photons. Dark cloud chemical networks are often based on the KIDA or UMIST databases. We use gas-phase and grain-phase networks based on kida.uva.20147 and Ruaud et al.39 respectively, which have been used extensively in combination with the NAUTILUS code and its predecessors to study dark cloud chemistry.22,40–42 A number of extensions are included based on former works focused on large carbon-chain and aromatic species that have recently been detected in TMC-1.37,43–48 We thus expect our results to be generally applicable to modeling of dark cloud chemistry, while the methods described in the following section are suitable for any kinetic model.
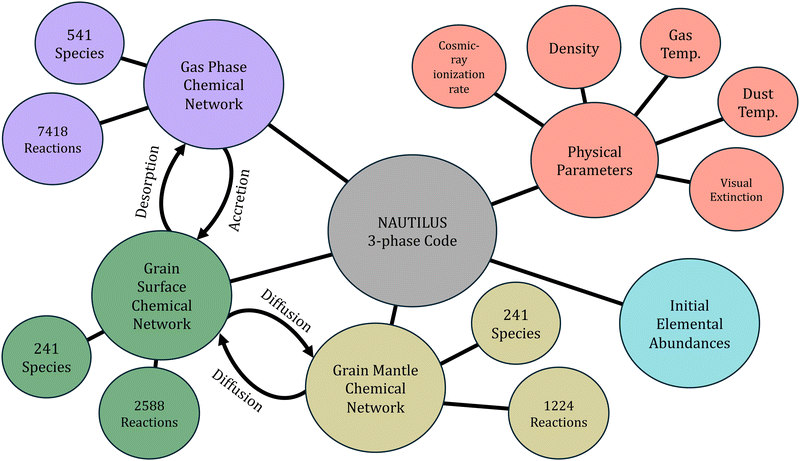 |
| | Fig. 1 A general schematic of the NAUTILUS 3-phase modeling code. This is a rate-equation model that simulates the chemical evolution of an astronomical region given a chemical network, a number of physical parameters, initial abundances, and various numerical parameters. Species and reactions are separated into gas, grain surface, and grain mantle phases with physical processes allowing for transfer between phases. | |
‘Typical’ dark cloud conditions were assumed, namely a gas density of 2 × 104 cm−3,49 a kinetic temperature of 10 K for the gas and dust grains,50 a cosmic-ray ionization rate, ζ, of 1.3 × 10−17 s−1,51 and a visual extinction of 10 mag for external UV photons.52 Chemical desorption was set to 1% efficiency, assuming that 1% of molecules formed on grain surfaces have enough energy to desorb into the gas phase.53 A peak grain temperature of 70 K lasting for 1 × 10−5 s was used for the cosmic-ray heating mechanism as estimated by Hasegawa and Herbst.54 The initial elemental abundances used and their references can be seen in Table 1 and represent the low-metal abundances from Graedel et al.55 with a lower oxygen abundance and a greater sulfur abundance. It has been found that a C/O ratio of 1.1 significantly improves agreement between modeled and observed abundances, particularly for larger hydrocarbons such as unsaturated carbon chains.44,47,56 Data from a recent survey of sulfur-bearing molecules in molecular clouds suggests a depletion factor of 20 relative to the solar abundance, larger than the previously used value.57 We assume that these elements are all initially in atomic form except for hydrogen, which is primarily molecular. All input files used for the model, including the reaction networks and input parameters, are available in a Zenodo repository: https://zenodo.org/doi/10.5281/zenodo.13257328.
Table 1 Initial atomic/molecular abundances referenced to hydrogen nuclei
| Species |
n/nH |
Ref. |
Species |
n/nH |
Ref. |
| H2 |
0.499 |
Ruaud et al.4 |
F |
6.68 × 10−9 |
Neufeld et al.58 |
| He |
0.09 |
Wakelam and Herbst59 |
Cl |
1.00 × 10−9 |
Graedel et al.55 |
| C |
1.70 × 10−4 |
Jenkins60 |
Si |
8.00 × 10−9 |
Graedel et al.55 |
| N |
6.20 × 10−5 |
Jenkins60 |
Na |
2.00 × 10−9 |
Graedel et al.55 |
| O |
1.55 × 10−4 |
Xue et al.44 |
Mg |
7.00 × 10−9 |
Graedel et al.55 |
| S |
7.50 × 10−7 |
Fuente et al.57 |
Fe |
3.00 × 10−9 |
Graedel et al.55 |
| P |
2.00 × 10−10 |
Graedel et al.55 |
|
|
|
2.2 Monte Carlo analysis
Previous sensitivity analyses of gas-phase rate coefficients in astrochemical kinetic models, including those of dark molecular clouds, have primarily made use of the Monte Carlo (MC) approach.8,9,27,29–35,61 In this method, each rate coefficient is selected randomly from an assigned uncertainty distribution, typically a log-normal distribution centered on the nominal value. A large number of iterations are then performed to obtain a statistical spread of abundances.30 Spearman rank correlation coefficients (RCCs) can then be calculated for every rate coefficient-abundance pair. This value is a measure of the monotonic correlation between two variables; essentially how often an increase is observed in both variables simultaneously.62 The reactions with large RCCs can be considered as the reactions whose rate coefficient uncertainties most contribute to uncertainties in modeled abundances, and thus the reactions for which further constraint of rate coefficient would be most beneficial.8 As a global method, the Monte Carlo approach takes into account the entire range of rate coefficient uncertainty and preserves coupling between rate coefficients.23,28,63
In practice, determining uncertainty distributions for a large number of rate coefficients is a difficult task, particularly when many of them are based on chemical intuition or extrapolation of high-temperature data. Thorough statistical analysis of uncertainties, requiring expertise in the techniques used to obtain these values, has only been performed for a small fraction of reactions present in astrochemical networks.8,35 As such, we choose to make a blanket assumption and use uncertainties of a factor of 2.0 for every rate coefficient. This factor of 2.0 is the assumed default for most reactions in astrochemical networks and databases.30,34,35 We also choose to use log-uniform distributions, as they may be more appropriate when uncertainty is not well quantified.25 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations of the model were thus performed and RCCs for every species-reaction pair were calculated for 13 time-points between 4.5 × 104 and 1.1 × 106 years. Monte Carlo analyses with 5000, 15
000 iterations of the model were thus performed and RCCs for every species-reaction pair were calculated for 13 time-points between 4.5 × 104 and 1.1 × 106 years. Monte Carlo analyses with 5000, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and 20
000, and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations were also performed to test the convergence.
000 iterations were also performed to test the convergence.
2.3 One-at-a-time analysis
In contrast to the global Monte Carlo approach, local sensitivity analysis methods may be used to calculate or estimate the local derivative surrounding the nominal value. As such, these techniques take a calculus-based approach to determining sensitivity rather than a statistical approach.23,64 The simplest approach is the one-at-a-time (OAT) method, also called the finite differences or brute force method.23,28,65 This consists of running the model a number of times, where in each iteration one rate coefficient is slightly perturbed while the others are kept constant. Sensitivity coefficients are often calculated according to the equation:| | 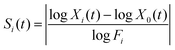 | (1) |
Here Xi(t) is one of the 20 abundances at time t from the ith factor of change, X0(t) is the nominal abundance of the given species at time t, Fi is the ith factor of change, and Si(t) is the resulting sensitivity coefficient.28 While this approach has a number of benefits such as being simple and easy to interpret and providing quantitative information, it is often not applicable to nonlinear models where the local derivative is not representative of the greater uncertainty range.
The application of local sensitivity analysis to astrochemical models is somewhat limited. An OAT approach has been applied to hot-core32 and dark cloud34 networks where key reactions were identified based on sensitivity coefficients using either individual rate coefficient uncertainties or an assumed factor of two as the factor of perturbation. Dobrijevic et al.28 applied a number of sensitivity analysis techniques to a photochemical network of Titan's atmosphere, finding that key reactions identified by OAT and MC techniques can differ significantly when there is non-linearity in the model as a result of large uncertainties in rate coefficients. However, this problem may be bypassed through the use of multiple change factors sampled over a larger range of uncertainty, a variation on the Morris method.63,66 We perform an OAT analysis using 20 factors of change from 0.5 to 2.0 that are equally spaced in log-scale, assuming a factor of two uncertainty in all rate coefficients as with the MC analysis. For each of the 7418 reactions in our gas-phase network, 20 iterations of the model are performed. In each iteration, the rate coefficient of that reaction is multiplied by one of the 20 change factors, and the resulting modeled abundances of all species are collected at the same 13 time points as the MC analysis. Combined with the nominal, unmodified network this results in 21 abundances for every combination of species, reaction, and time. Three sensitivity metrics are calculated from these sets of 21 abundances. The first, hereafter referred to as SC, uses eqn (1) to determine an absolute sensitivity coefficient for each factor of change and averages them for a mean sensitivity coefficient. The other two are based on standard deviation, either dividing by the mean abundance to obtain a relative standard deviation (RSD) or calculating standard deviation using log-scale abundances (log SD). Directionality of the correlation is then included by fitting a linear regression to the abundances as a function of change factor and multiplying the three sensitivity metrics by the sign of the slope.
3 Results & discussion
3.1 Overall network
The sensitivities of the overall network to individual reactions were calculated as the average absolute sensitivities of all species in the network to each reaction. This procedure was repeated for the four aforementioned metrics and for three time points of interest. Reactions were then ranked by decreasing average sensitivity to determine key reactions. The chosen time points for comparison are 106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, 314
500, 314![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400, and 541
400, and 541![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 years, and will be referred to as 1 × 105, 3 × 105, and 5 × 105 years respectively for simplicity. Astrochemical models often agree that the age of TMC-1 seems to be between 105 and 106 years based on comparison to observations, however the exact point within this range is not known. These selected time points thus represent a range of suggested chemical ages, with the later time of 5 × 105 generally providing the best agreement between our model and observations of larger hydrocarbons.44,47,48 Hereafter we refer to the rank of a reaction as its importance, with the highest rank reaction being the most important. For the purpose of comparison, we generally show the top 10 reactions, denoted as key reactions, unless otherwise specified. This is a somewhat arbitrary cutoff as there is no strict definition on what constitutes a “key” reaction but is adequate for identifying predominant reactions and comparing these reactions across different metrics and time points. Full reactions lists sorted by average sensitivity metric can be found in the Zenodo repository: https://zenodo.org/doi/10.5281/zenodo.13257328.
100 years, and will be referred to as 1 × 105, 3 × 105, and 5 × 105 years respectively for simplicity. Astrochemical models often agree that the age of TMC-1 seems to be between 105 and 106 years based on comparison to observations, however the exact point within this range is not known. These selected time points thus represent a range of suggested chemical ages, with the later time of 5 × 105 generally providing the best agreement between our model and observations of larger hydrocarbons.44,47,48 Hereafter we refer to the rank of a reaction as its importance, with the highest rank reaction being the most important. For the purpose of comparison, we generally show the top 10 reactions, denoted as key reactions, unless otherwise specified. This is a somewhat arbitrary cutoff as there is no strict definition on what constitutes a “key” reaction but is adequate for identifying predominant reactions and comparing these reactions across different metrics and time points. Full reactions lists sorted by average sensitivity metric can be found in the Zenodo repository: https://zenodo.org/doi/10.5281/zenodo.13257328.
Fig. 2 shows the top 10 reactions for the overall network at 5 × 105 years for all three OAT metrics, ordered by average relative standard deviation. All three metrics agree very well in terms of the reactions identified as key reactions and the relative ordering, with only minor differences in ranking for the bottom two reactions. Additionally, the three metrics agree well in terms of relative magnitude for the sensitivity metrics. The cosmic-ray ionization of molecular hydrogen,
is consistently the most important reaction by a significant margin, with the average sensitivity of the next most important reaction only being ∼a third of this value. This reaction is the limiting step to formation of H
3+, which subsequently donates a proton to C or O to initiate hydrocarbon and oxygen chemistry respectively. This reaction also has a strong positive influence on atomic hydrogen abundance, likely due to the reaction H
2 + H
2+ → H + H
3+ that quickly follows. As a result, the abundances of many protonated and saturated species increase significantly as the cosmic ray ionization rate of H
2 increases. It is important to note that the uncertainty in this rate, along with all other chemical processes involving cosmic rays, can be thought of as a combination of physical uncertainty in the cosmic-ray flux through this region (established through the input parameter
ζ) and uncertainty in the efficiency of the chemical process, including uncertainty in photodissociation/photoionization cross-section.
31,67 As we are altering the rates of individual cosmic-ray processes and not the parameter
ζ, we are investigating the latter source of uncertainty. In the case of
reaction (2), this arises primarily due to uncertainty in the rate of ionization
via secondary electrons, which depends on the gas composition.
68,69
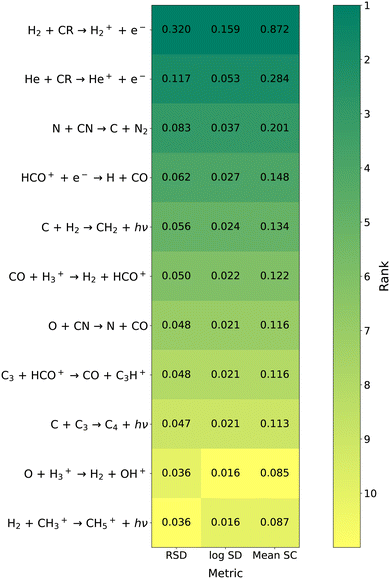 |
| | Fig. 2 Heat map of key reactions according to the three OAT metrics at 5 × 105 years for the overall network. All reaction within the top 10 with any of the three metrics are shown. The shading of each cell corresponds to the reaction's rank, with the exact sensitivity metric also given. Reactions ranked #11 or lower are given the lightest shading. | |
The top 10 reactions for the overall network at 1 × 105, 3 × 105, and 5 × 105 years according to the RSD and RCC metrics are shown in Fig. 3. Comparison of key reactions at different time points provides information about how the chemistry evolves as a function of time. The key reactions identified agree well between the OAT and MC methods at all times despite using different definitions of sensitivity. Thus the reaction rates that are correlated with the abundances of many species are generally the same rates for which changes lead to large deviations in abundances of many species. Previous comparison of a number of sensitivity analysis techniques on a small model of Titan's atmosphere found that OAT and MC methods agree well when uncertainties are small, but as uncertainties grow large the agreement can worsen.28 The authors attribute this to nonlinear behavior that cannot be observed with local methods, and thus suggest that global techniques such as MC should be preferred for uncertainty analysis. The strong agreement between MC and OAT over a larger range of variation may indicate that the use of multiple change factors is able to capture nonlinear behavior, which will be discussed later. It also suggests that coupling between rate coefficients, which is preserved through the MC method but not the OAT method, is not very significant.
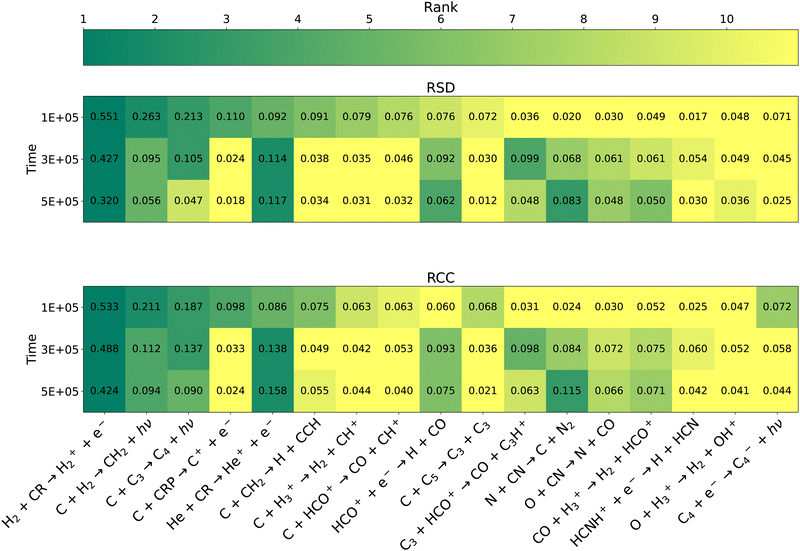 |
| | Fig. 3 Heat map of key reactions according to the RSD metric (top) and RCC metric (bottom) for the overall network. All reaction within the top 10 at any of the 3 time points with either metric are shown. The shading of each cell corresponds to the reaction's rank, with the exact sensitivity metric also given. Reactions ranked #11 or lower are given the lightest shading. | |
Over this range of times, reaction (2) is consistently the most important reaction by a large margin. At 1 × 105 years the remaining key reactions are dominated by reactions involving atomic carbon. As identified in a previous sensitivity analysis by Wakelam et al.,34 many of these are “early-stage” reactions at the beginning of hydrocarbon growth. The authors also highlight the reaction of atomic carbon with C3, attributing the influence of this reaction to the catalytic conversion of C and O into CO via the reaction
As time progresses the magnitude of sensitivities generally decreases, suggesting that the network is approaching a steady-state solution and thus becoming less susceptible to individual changes in reaction rates. In particular the importance of reactions involving atomic carbon drastically decrease as it is converted into more complex molecules, although its reactions with H
2 and C
3 remain important. A number of reactions involving formation and destruction of HCO
+ become important at later time, likely due to its role in protonating neutral species such as carbon-chain species. The protonation of C
3 specifically is a critical step for forming C
3H
n species as well as larger hydrocarbons. The cosmic-ray ionization of helium and the reaction
notably increase in sensitivity as a function of time. The former process is the limiting step to C
+ and atomic oxygen formation
via the reaction
These species react with C
mH and C
mH
2 hydrocarbons that are abundant at later times. Silicon-containing molecules also appear to be highly sensitive to the helium cosmic-ray ionization rate, possibly due to the enhanced production of organo-silicon compounds.
Reaction (4) has been previously investigated as a major mechanism for partitioning elemental nitrogen into N
2. We also find that a number of large, more-saturated hydrocarbons such as C
10H
8, C
6H
6, and C
9H
5+ are highly sensitive to this rate. Additionally, there is a strong negative correlation between this rate and the abundance of atomic carbon at later times, despite this being a significant formation mechanism for atomic carbon. This seems to suggest that this reaction has a role in the partitioning of elemental carbon into its reactive, atomic form that is a building block for large hydrocarbons.
For several of these reactions that have been studied experimentally and theoretically, Wakelam et al.35 compiled this data into datasheets along with recommended rate coefficients and uncertainties. The rate coefficient for the reaction
has been measured a number of times at room temperature, however the temperature dependence of this reaction is unknown. To our knowledge, the reactions
have not been studied experimentally or theoretically and presently use estimated values. Likewise, the majority of the presented ion–neutral reactions do not have experimentally determined constants, although these rates can often be well-predicted by capture theories.
70 Further constraining the rates of these critical reactions will be significantly beneficial toward creating more robust models of molecular clouds.
3.2 Cyanonaphthalene
While the determination of key reactions for the overall network provides information about which processes are generally important due to their effects on a large number of species, a more useful application of sensitivity analysis results may be to study the key reactions for certain species of interest. As the number of detected species grow, more and more of which are larger complex organic molecules, the challenge of modeling these species and understanding the critical pathways to their formation grows as well. Here in particular, we turn our interest toward the PAHs 1- and 2-cyanonaphthalene, which we will hereafter refer to as C10H7CN. These species, along with indene71 and cyanoindene,72 are the only PAHs unambiguously detected in the interstellar medium.37 Previous modeling work has been unable to reproduce the observed abundances by a large margin. However, it is unknown whether the discrepancy arises from missing pathways, underestimated rate coefficients, or both, as well as where in the network these missing pathways or underestimated rates may be.
In Fig. 4, the time-dependent abundances of C10H7CN for all 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MC iterations are plotted, while Table 2 contains the corresponding statistical information for C10H7CN and some precursor species. As molecular complexity increases the spread of abundances does as well. This is consistent with the increased rate coefficient uncertainty propagated as the amount of reactions necessary to form these species increases. It is evident that a factor of 2 uncertainty in all reactions is not enough to account for the observed abundance of C10H7CN, as the MC iteration with the maximum abundance model still under-produces this species by almost two and a half orders of magnitude compared to its TMC-1 observed value. This is not entirely surprising given the large discrepancies between the nominal model and observations; however it does indicate that much larger uncertainties and/or missing reactions are responsible. We thus turn our attention to the reactions identified as key processes for C10H7CN by sensitivity analysis to understand critical processes and areas of the network for future study.
000 MC iterations are plotted, while Table 2 contains the corresponding statistical information for C10H7CN and some precursor species. As molecular complexity increases the spread of abundances does as well. This is consistent with the increased rate coefficient uncertainty propagated as the amount of reactions necessary to form these species increases. It is evident that a factor of 2 uncertainty in all reactions is not enough to account for the observed abundance of C10H7CN, as the MC iteration with the maximum abundance model still under-produces this species by almost two and a half orders of magnitude compared to its TMC-1 observed value. This is not entirely surprising given the large discrepancies between the nominal model and observations; however it does indicate that much larger uncertainties and/or missing reactions are responsible. We thus turn our attention to the reactions identified as key processes for C10H7CN by sensitivity analysis to understand critical processes and areas of the network for future study.
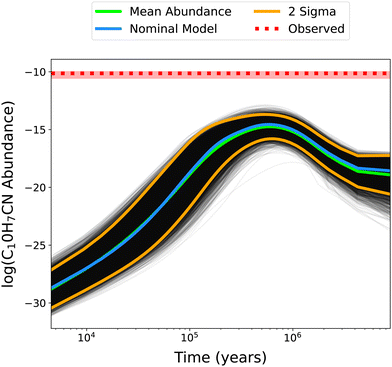 |
| | Fig. 4 Abundances of C10H7CN as a function of time for each of the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MC iterations. The mean abundance curve is shown in green, along with the nominal model (no changes to rate coefficients) in blue and the 2σ distribution in yellow. The dotted red line indicates the observed TMC-1 abundance, with the shaded region signifying the 1σ error. 000 MC iterations. The mean abundance curve is shown in green, along with the nominal model (no changes to rate coefficients) in blue and the 2σ distribution in yellow. The dotted red line indicates the observed TMC-1 abundance, with the shaded region signifying the 1σ error. | |
Table 2 Statistical analysis of MC abundances (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations) for select species at 5 × 105 years
000 iterations) for select species at 5 × 105 years
| Species |
Mean abundance |
+2σ |
−2σ |
Max abundance |
Min abundance |
Observed abundance |
| C10H7CN |
1.73 × 10−15 |
2.05 × 10−14 |
1.46 × 10−16 |
1.43 × 10−13 |
3.04 × 10−19 |
7.35 × 10−11 |
| C10H8 |
5.96 × 10−14 |
7.54 × 10−13 |
4.72 × 10−15 |
5.78 × 10−12 |
8.52 × 10−17 |
— |
| C6H5 |
1.04 × 10−10 |
5.76 × 10−10 |
1.88 × 10−11 |
2.08 × 10−9 |
9.62 × 10−13 |
— |
| CH2CCH |
1.39 × 10−10 |
3.78 × 10−10 |
5.08 × 10−11 |
1.03 × 10−9 |
2.03 × 10−11 |
1.00 × 10−8 |
3.2.1 Key reactions and their rate coefficients.
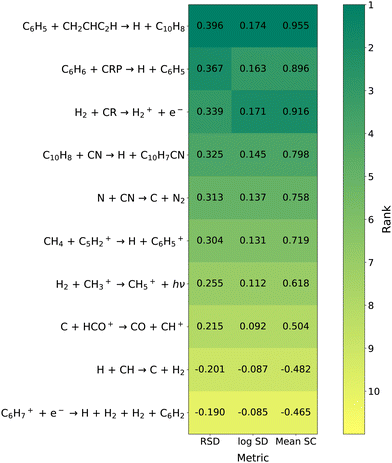
The top 10 reactions ranked by sensitivity of C10H7CN according to the three OAT metrics at 5 × 105 years can be seen in Fig. 5. Fig. 6 displays these reactions at three select time points according to relative standard deviation and rank correlation coefficients. As with the overall network there is strong agreement between all four metrics. We continue to refer to the ranking of a reaction as its importance, in this section specifically the importance to C10H7CN. The cosmic-ray ionization of H2 is by far the most important reaction at 1 × 105 and 3 × 105 years. At 5 × 105 years there are a number of sensitivities of similar magnitude and this is no longer the case.
 |
| | Fig. 5 Heat map of key reactions according to the three OAT metrics at 5 × 105 years for C10H7CN. All reaction within the top 10 with any of the three metrics are shown. The shading of each cell corresponds to the reaction's rank, with the exact sensitivity metric also given. Reactions ranked #11 or lower are given the lightest shading. | |
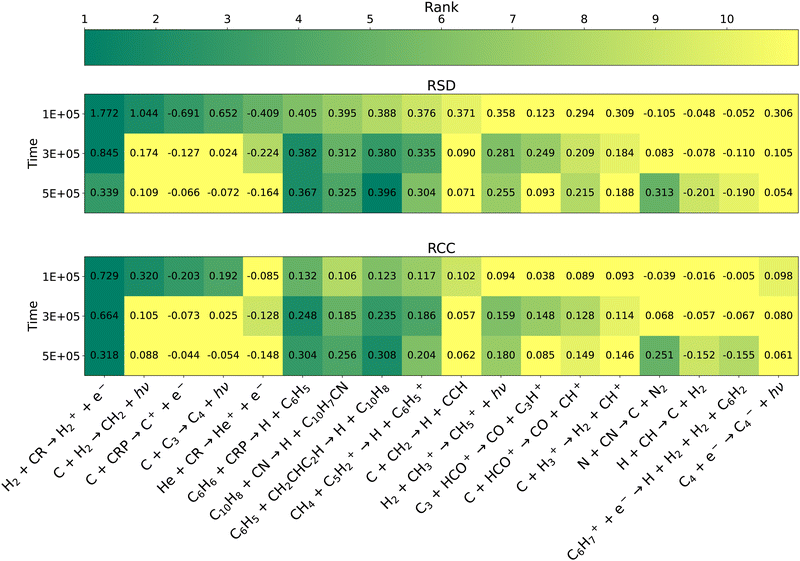 |
| | Fig. 6 Heat map of key reactions according to the RSD metric (top) and RCC metric (bottom) for C10H7CN. All reaction within the top 10 at any of the 3 time points with either metric are shown. The shading of each cell corresponds to the reaction's rank, with the exact sensitivity metric also given. Reactions ranked #11 or lower are given the lightest shading. | |
These key reactions are a mix of “early-stage” hydrocarbon reactions, many of which dominate at early times and are also important to the overall network, and “late-stage” aromatic reactions. Reaction network diagrams centered on aromatic and C3Hn chemistry are showcased in Fig. 7 and 8 respectively. The reactions of C with H2, C3, and CH2 have strong positive correlations with C10H7CN abundance as these reactions drive formation of C3–C5 hydrocarbons that are aromatic precursors as can be seen in these figures. Conversely, the cosmic-ray induced photoionization of C and cosmic-ray ionization of He have strong negative correlations with C10H7CN abundance as the conversion of C to C+ and reaction of C3 with He+ disrupt the formation of these species. The reactions involving aromatic species primarily consist of ring-formation of the phenyl cation (C6H5+) from acyclic hydrocarbons
| | | CH4 + C5H2+ → H + C6H5+, | (9) |
the formation of phenyl radical (C
6H
5) and the subsequent formation of naphthalene (C
10H
8)
via the HAVA mechanism
73,74| | | C6H6 + CRP → H + C6H5 | (10) |
| | | C6H5 + CH2CHC2H → H + C10H8, | (11) |
and direct formation of C
10H
7CN itself
| | | C10H8 + CN → H + C10H7CN. | (12) |
The direct formation of benzene from the dissociative recombination of C
6H
7+ does not appear in
Fig. 6 but is ranked 11th according to the RSD metric and 13th according to the RCC metric at 5 × 10
5 years. This reaction is fast and dominates the production of benzene; however the relative importance of this process along with the competing product channel to form C
6H
2 suggests the branching ratios of these channels appear to have a moderate effect on the abundance of benzene and subsequent species.
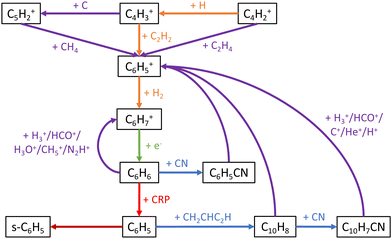 |
| | Fig. 7 Major chemical reactions leading to formation of aromatic species in our network. A blue arrow indicates a neutral–neutral reaction, an orange arrow radiative association, a green arrow dissociative-recombination, a purple arrow ion–neutral, a red arrow photodissociation, and a brown arrow adsorption onto grains. CRP stands for cosmic-ray induced photons, and the prefix ‘s-’ designates a grain-adsorbed species. | |
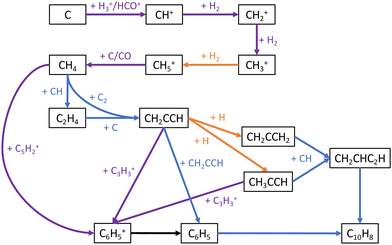 |
| | Fig. 8 Major chemical reactions leading from atomic carbon to the formation of CH4, C3 hydrocarbons, and six-membered rings. A blue arrow indicates a neutral–neutral reaction, an orange arrow radiative association, and a purple arrow ion–neutral. The black arrow leading from C6H5+ to C6H5 is meant to show that pathways exist from the former to the latter, the exact ones being showcased in Fig. 7. | |
At later times, the relative importance of reactions involving atomic carbon generally decreases as was the case for the overall network. Of the reactions that rise in importance, three of them,
| | | H2 + CH3+ → CH5+ + hν | (15) |
are part of the pathway from atomic carbon to methane as visible in
Fig. 8. As shown, methane is a key precursor to the aromatic cation C
6H
5+ as well as C
3 hydrocarbons that participate in the formation of aromatic species. The reaction
displays a negative correlation with C
10H
7CN abundance due to depletion of CH. In
Fig. 8, it can be seen that this radical reacts with isomers of C
3H
4 to form vinylacetylene (CH
2CHC
2H), a key component of the HAVA mechanism. Additionally, the relative importance of the four previously mentioned aromatic reactions increases from 1 × 10
5 years to 5 × 10
5 years as simple carbon-containing species are converted into more complex hydrocarbons. Finally, we again note that
reaction (4) becomes significantly more sensitive with time, becoming the 5th most important reaction to C
10H
7CN at 5 × 10
5 years. As mentioned previously, we suspect this may be due to this reaction's affect on the partitioning of carbon into larger hydrocarbons that are precursors to aromatic species. Notably, the strong positive correlation between C
10H
7CN abundance and the rate of this reaction further suggests that this is the predominant effect. If removal of CN was as or more important we would expect this correlation, and those of many other CN-containing species, to be negative.
Of the four aromatic reactions that the C10H7CN abundance is highly sensitive to, none of them have been studied experimentally at low temperature. The rate prefactor for reaction (10) comes from the high-temperature network of Harada et al.,75 with the 154 nm branching ratios from Kislov et al.76 corresponding to the internal UV field expected in dense clouds.67 Rate coefficients for cosmic-ray induced photoprocesses are typically calculated as a function of the H2 cosmic-ray ionization rate, the photodissociation/photoionization cross section of the molecule of interest, the total absorption cross section, and the induced UV spectrum,77 although the particular details of this calculation are not provided. More recent calculations by Heays et al.67 using updated cross sections yielded general agreement within a factor of 2 as well as some large deviations for specific molecules/atoms. Updated calculations have not yet been performed on C6H6. Reaction (11) presently uses a rate coefficient of 2.5 × 10−10 cm3 s−1 and a branching ratio of 100% according to variational transition state theory and Rice–Ramsperger–Kessel–Marcus (RRKM) calculations at 100 K and zero pressure respectively.73 Follow-up RRKM calculations at zero pressure and 60 K included radiative stabilization of intermediates, finding that the inclusion of this mechanism could favor the formation of unimolecular products over the C10H8 + H channel.78 The direct formation of C10H7CN (reaction (12)) was estimated to occur with a rate near the collision rate as it is a reaction between an unsaturated hydrocarbon and a neutral radical where the difference in ionization energy of the former and electron affinity of the latter is less than 8.75 eV.37,79 CRESU measurements at 15 K of the analogous reaction between C6H6 and CN resulted in a rate coefficient of 5.4 × 10−10 cm3 s−1, indicating that the rate of reaction with C10H8 could be larger than the currently used value. Finally, reaction (9) originates from Herbst and Leung80 with an overall rate coefficient of 1.0 × 10−9 cm3 s−1 and 80/20 branching ratios for the H/H2 elimination channels estimated from Anicich and Huntress.81 In addition to uncertainties in the overall rate, which may be better estimated by capture theory,70 it is unknown whether this is a viable mechanism to formation of the cyclic C6H5+ isomer. This product channel, which requires breaking and forming a large number of bonds, is likely in competition with formation of acyclic products and its status as the dominant channel is debatable.
3.2.2 Completeness of the network.
Beyond the determination of individual rate coefficients that should be further constrained, the identification of key reactions provides information about areas of the network that are incomplete. As shown in Fig. 7 and 8, a number of ring-formation mechanisms to form the first six-membered aromatic ring, primarily C6H5+, exist in the network. These include [4 + 2] reactions proposed by McEwan et al.82 as well as a number of [3 + 3] reactions suggested by Herbst and Leung.80 The sensitivity analysis results clearly indicate that reaction (9), a [5 + 1] mechanism involving methane, is the most important of these. The next most important ring-forming reaction is| | | C2H2 + C4H3+ → C6H5+ + hν. | (17) |
Despite potential energy surface calculations confirming that this radiative association should be barrierless and efficient,83 it is only rank #31 in terms of importance to C10H7CN. The remaining ring-formation mechanisms of C6H5+ are significantly less important with ranks of #161 or lower. Direct formation of C6H684| | | CCH + CH2CHCHCH2 → H + C6H6 | (18) |
and of C6H585,86| | | CH2CCH + CH2CCH → C6H5 + H | (19) |
are found to be even less important to C10H7CN abundance with ranks of #1116 and #976 respectively. There is a notable drop-off in reaction significance once neutral hydrocarbons with 3 or more hydrogen atoms (C2H3, C2H4, CH2CCH, CH3CCH) or hydrocarbon cations with 4 or more hydrogen atoms (C4H4+) are involved. The exception is reaction (9) involving CH4, the simplest saturated hydrocarbon that is efficiently formed from a chain of ion–molecule reactions from CH+ to CH5+ followed by proton donation to CO87 as shown in Fig. 8. This trend suggests a larger problem in the network regarding limited production of more-saturated hydrocarbons that are needed for ring-formation. A large portion of detected TMC-1 molecules and ions have historically been unsaturated hydrocarbons and their derivatives; however, a number of recent detections have found high abundances of more-saturated species that cannot be reproduced by current astrochemical models.88–92 In particular, the propargyl radical (CH2CCH) has been detected in this cloud with a large abundance.93 This species is thought to play a central role in the formation of six-membered aromatic rings from smaller hydrocarbons as indicated in Fig. 8, however the inability of the model to reproduce the observed abundance results in little contribution from CH2CCH to ring-formation.48 Likewise, the abundance of C10H7CN is not highly sensitive to any reaction directly involving CH2CCH nor is the observed abundance of CH2CCH reproduced in any of the Monte Carlo iterations. This indicates that even within a factor of two variation the present pathways to CH2CCH and other C3 hydrocarbons from C1 and C2 hydrocarbons are inadequate, and other mechanisms should be explored.
Hydrogenation of C3Hn+ species via reaction with H2 has been found to proceed efficiently from C3+ to C3H+ followed by radiative association to C3H3+ based on low temperature ion trap experiments.94 C3H and C3H2 can subsequently be formed by dissociative recombination of C3H3+.95,96 Further hydrogenation to C3H4+ was found to be slow with rate coefficients on the order of 1.0 × 10−14 cm3 s−1. Calculations on the radiative associations of C3H3+ and C3H5+ with H2 have shown sizeable barriers in the entrance channels.97 Similarly, selected ion flow tube experiments at room temperature were not able to detect a reaction between C3H3+ and H, establishing an upper limit of 3.0 × 10−12 cm3 s−1 for the rate coefficient.98 The problem of missing information regarding C3 and larger hydrocarbons has also been discussed in the context of modeling chemistry in Titan's atmosphere, with a number of radiative association reactions proposed.29 Rate coefficients for these processes were determined based on a semi-empirical fit to previous calculations using capture rates and densities of states. These reactions are able to efficiently form more-saturated hydrocarbons such as C3H3 and C3H6 but have uncertainties in rate coefficients of a factor of 30 or larger. Grain-surface hydrogenation of C3 up to C3H8 through consecutive additions of H has been found to be quickly produce C3Hn molecules on dust grains,22,99 although additional parameters such as binding energies and efficiency of nonthermal desorption become significant for such processes. An alternative pathway involving radiative attachment of an electron followed by associative detachment with H exists for C4 and larger carbon chains
| | | CmH− + H → CmH2 + e−. | (23) |
Rate coefficients for
reactions (20) for 4 ≤
m ≤ 9 and
(22) for 2 ≤
m ≤ 8 have been determined using statistical calculations
100 and phase-space theory respectively.
101 Room temperature rate coefficients have been measured for
reactions (21) and (23) for a number of carbon-chain lengths using a flowing afterglow-selected ion flow tube.
102 This mechanism presently does not extend beyond C
mH
2 hydrocarbons, possibly due to competition with dissociative attachment. There is a clear need for future work regarding gas-phase formation of more-saturated hydrocarbons, particularly C
3H
n species with
n ≥ 3 that can participate in ring-formation.
It can be seen in Fig. 7 that the remaining aromatic reactions that C10H7CN is highly sensitive to are the three final steps leading from C6H6 to C10H7CN through C6H5 and C10H8. Given that the two most important reactions to C10H7CN involve C6H5, this radical appears to be the major limiting species toward formation of PAHs in the network. C6H5 is predominately formed by cosmic-ray induced photodissociation of C6H6, with direct ring-formation from CH2CCH recombination inefficient as previously discussed. Alternative H-abstraction mechanisms for C6H6 such as reaction with H, OH, CH3, and C2H5 all have sizeable barriers.103–105 Once C6H5 is formed, only 3% or less of it reacts with CH2CHC2H to form C10H8. Due to a lack of reaction with interstellar cations, the vast majority of C6H5 adsorbs onto dust grains where it is essentially trapped. Inclusion of additional destruction mechanisms would limit the amount of C6H5 trapped on dust grains but also the amount available in the gas-phase, thus it may be that mechanisms other than the HAVA mechanism are required to produce PAHs in dark clouds. For example, potential energy surface calculations of the reactions
| | | C6H6 + C4H3+ → H + C10H8+ | (24) |
| | | C6H6+ + 2C2H → C10H8+ | (25) |
| | | C6H5+ + 2C2H2 → C10H9+ | (26) |
indicate that C
10H
8+ and C
10H
9+ may be formed from barrierless ion–molecule processes involving a six-membered ring,
106,107 although experiments on this latter reaction find a small barrier for the second addition of C
2H
2 and the formation of an adduct with a four-membered ring rather than a protonated naphthalene structure.
108 Likewise, C
10H
7+ can rapidly undergo radiative association with H
2 to form C
10H
9+.
109,110 Neutral C
10H
8 may then be formed by charge transfer of C
10H
8+ or dissociative recombination of C
10H
9+.
111,112 In combustion chemistry, ion-based mechanisms to soot formation involving C
3H
3+ have been proposed, with a number of cyclic ions such as C
7H
7+, C
9H
7+, C
9H
9+, C
10H
8+, and C
10H
9+ detected as products.
113–115 Considering the wide variety of ion–molecule reactions that may be involved in interstellar aromatic chemistry and the large rate coefficients of these processes at low temperatures, further expansion and refinement of the aromatic network with a focus on these processes should be another priority for future work.
The incompleteness of the network can also be seen by comparing the magnitude of C10H7CN sensitivities in Fig. 6 to those of the average sensitivities in Fig. 3. The fact that C10H7CN is significantly more sensitive to rate coefficients at these times compared to the average species may be a consequence of it being the largest and most chemically ‘complex’ species in the network. A long sequence of reactions including carbon-chain growth, ring-formation, and the HAVA mechanism are required for it to be formed. Once C10H7CN is formed, its destruction mechanisms are limited to reaction with abundant cations (H+, He+, H3+, HCO+, C+, and H3O+) or adsorption onto dust grains. The former mechanism is assumed to yield C6H5+, which can reform C10H7CN. The result is that any increase to reactive flux along the chain of reactions leading to C10H7CN accumulates in the abundance of this species, making it a kinetic sink. Other processes such as subsequent HAVA to form larger PAHs, or ethynyl addition are likely competing processes that are not currently included in the network. Extension of the aromatic network should thus encompass such reactions and extend beyond C10H8 and C10H7CN.
3.2.3 Model linearity.
In Fig. 9, the abundance of C10H7CN at 5 × 105 years as a function of change in rate coefficient from the OAT analysis is shown for its key reactions according to the RSD metric. As can be seen, there is a near-linear relationship between C10H7CN abundance and change in rate coefficient for many of these reactions, particularly for the rank 1 reaction (10). It is clear that the relationship between the rate of reaction rank 3 (which turns out to be reaction (2), the cosmic-ray ionization of hydrogen), is highly nonlinear and non-monotonic. Decreasing this rate coefficient below the nominal value leads to a strong exponential decrease in C10H7CN abundance. Conversely, increasing this rate coefficient above the nominal value results in a stationary point of peak C10H7CN abundance corresponding to a change factor of ∼1.6, after which C10H7CN abundance begins decreasing. This is likely due to competition between hydrocarbon growth and destruction, both of which proceed via ion–neutral reactions initiated by H3+ formation. A greater rate of H2 cosmic-ray ionization allows complex hydrocarbons to be formed more quickly and to a greater degree, after which destruction via reaction with ions such as H3+, HCO+, and N2H+ take over. The ability of our OAT analysis to capture this relationships and assign appropriately large sensitivity coefficients shows that the use of multiple change factors enables the acquisition of quantitative, reaction-specific sensitivities over a wide range of variations.
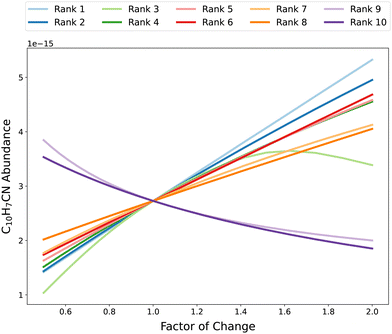 |
| | Fig. 9 Abundances of C10H7CN at 5 × 105 years as a function of factor of change in rate constant for the top 10 reactions according to the RSD metric. Each dot represents an abundance when the rate coefficient of the corresponding reaction has been multiplied by some factor, with the color of the dot representing the degree of change. There are 21 factors of change ranging from 0.5 to 2. | |
4 Conclusion
We have performed Monte Carlo and one-at-a-time sensitivity analyses of a 3-phase dense cloud astrochemical model containing a number of complex organic molecules, including aromatic species. By using multiple factors of change for the one-at-a-time analysis, a larger parameter space can be explored and nonlinear relationships can be discovered. The resulting sensitivities agree well with those determined statistically via the Monte Carlo approach. We find that reactions involved in the initiation of interstellar chemistry through the formation of small reactive species, particularly those responsible for carbon-chain growth, have the greatest average effect on modeled abundances. Between 1 × 105 and 5 × 105 years, the likely age range of TMC-1, the absolute sensitivities and their relative orderings can change significantly. A general decrease in sensitivity metrics with time suggests the approach of a steady-state solution, with reactions involving atomic carbon becoming relatively less important at later times due to increasing complexity of carbon-containing species. Several of these key reactions still use estimated rate coefficients with large uncertainties, and as such more accurate values would significantly benefit the model. Likewise, the use of sensitivity analysis techniques allows us to reveal interesting behavior in the model even for reactions with well-constrained rate coefficients, such as the nonlinear relationship between the rate of reaction of N with CN and the abundance of atomic carbon.
Application of these results to the PAH cyanonaphthalene reveals that it is notably sensitive to four particular aromatic reactions: (1) the ring-formation of C6H5+ from C5H2+ and CH4, (2) the photo-dissociation of benzene to C6H5via the cosmic-ray induced UV field and (3) its subsequent reaction with CH2CHC2H to form naphthalene, and (4) direct formation of cyanonaphthalene via a CN-addition H-elimination mechanism. Consequently the major bottlenecks to C10H7CN formation appear to be formation of both the first and second aromatic ring. A lack of experimental data and robust calculations casts significant uncertainty on the rates of these reactions. It is also unclear whether the reaction between CH4 and C5H2+ is a viable pathway to C6H5+, as well as to what degree radiative stabilization competes with the bimolecular product channel for the formation of C10H8 from the HAVA mechanism. Due to these uncertainties these reactions appear to be good candidates for future experimental and theoretical kinetic and mechanistic studies. Likewise, the high sensitivity of C10H7CN to these reactions suggests that the network may be incomplete in these areas. Alternate pathways to the first six-membered ring are hindered by inefficiencies in formation of more-saturated C3 and C4 hydrocarbons, possibly due to missing hydrogenation mechanisms such as radiative association with H2 or dissociative attachment. Additional ion–neutral routes to form the second aromatic ring may be feasible and rapid under TMC-1 conditions considering their general lack of activation barriers and rate coefficients near the collision rate. The identification of key reactions and incomplete regions of chemistry provides valuable insight for future work on improving kinetic models of dark molecular clouds. Additionally, these methods are broadly applicable to other areas of astrochemical modeling, as well as to fields such as combustion chemistry and atmospheric chemistry where kinetic models are also extensively used.
Author contributions
ANB: conceptualization, methodology, investigation, formal analysis, data curation, visualization, and writing – original draft. CX: methodology and software. TVV: conceptualization, supervision, and project administration. BAM: conceptualization, resources, supervision, and project administration. All authors contributed to writing – review and editing.
Data availability
The NAUTILUS modeling code used is an open-source code that can be found at https://forge.oasu.ubordeaux.fr/LAB/astrochem-tools/pnautilus. The raw sensitivity analysis data, resulting sensitivity metrics, model inputs, and a data analysis Jupyter notebook are located in the Zenodo repository: https://doi.org/10.5281/zenodo.13257329.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We thank Dr Valentine Wakelam for use of the NAUTILUS v1.1 code. A. N. B acknowledges support from the National Science Foundation Grant Number 2141064. B. A. M. and C. X. gratefully acknowledge support of National Science Foundation grant AST-2205126.
Notes and references
- B. A. McGuire, Astrophys. J., Suppl. Ser., 2022, 259, 30 CrossRef.
- E. Herbst and W. Klemperer, Astrophys. J., 1973, 185, 505–534 CrossRef.
- R. T. Garrod, Astrophys. J., 2013, 765, 60 CrossRef.
- M. Ruaud, V. Wakelam and F. Hersant, Mon. Not. R. Astron. Soc., 2016, 459, 3756–3767 CrossRef.
- J. Holdship, S. Viti, I. Jiménez-Serra, A. Makrymallis and F. Priestley, Astron. J., 2017, 154, 38 CrossRef.
- T. J. Millar, C. Walsh, M. V. D. Sande and A. J. Markwick, Astron. Astrophys., 2024, 682, A109 CrossRef.
- V. Wakelam, J.-C. Loison, E. Herbst, B. Pavone, A. Bergeat, K. Béroff, M. Chabot, A. Faure, D. Galli, W. D. Geppert, D. Gerlich, P. Gratier, N. Harada, K. M. Hickson, P. Honvault, S. J. Klippenstein, S. D. L. Picard, G. Nyman, M. Ruaud, S. Schlemmer, I. R. Sims, D. Talbi, J. Tennyson and R. Wester, Astrophys. J., Suppl. Ser., 2015, 217, 20 CrossRef.
- E. Hébrard, M. Dobrijevic, P. Pernot, N. Carrasco, A. Bergeat, K. M. Hickson, A. Canosa, S. D. Le Picard and I. R. Sims, J. Phys. Chem. A, 2009, 113, 11227–11237 CrossRef PubMed.
- V. Wakelam, E. Herbst, J. L. Bourlot, F. Hersant, F. Selsis and S. Guilloteau, Astron. Astrophys., 2010, 517, A21 CrossRef.
- M. Agúndez and V. Wakelam, Chem. Rev., 2013, 113, 8710–8737 CrossRef PubMed.
- T. B. McMahon and J. L. Beauchamp, Rev. Sci. Instrum., 1972, 43, 509–512 CrossRef.
- D. B. Dunkin, F. C. Fehsenfeld, A. L. Schmeltekopf and E. E. Ferguson, J. Chem. Phys., 1968, 49, 1365–1371 CrossRef.
- W. D. Geppert, R. Thomas, A. Ehlerding, F. Hellberg, F. Österdahl, M. Af Ugglas and M. Larsson, Int. J. Mass Spectrom., 2004, 237, 25–32 CrossRef.
- B. R. Rowe, G. Dupeyrat, J. B. Marquette and P. Gaucherel, J. Chem. Phys., 1998, 80, 4915 CrossRef.
- I. R. Cooke and I. R. Sims, ACS Earth Space Chem., 2019, 3, 1109–1134 CrossRef.
- B. M. Hays, D. Gupta, T. Guillaume, O. Abdelkader Khedaoui, I. R. Cooke, F. Thibault, F. Lique and I. R. Sims, Nat. Chem., 2022, 14, 811–815 CrossRef.
- D. C. Clary, Annu. Rev. Phys. Chem., 1990, 41, 61–90 CrossRef.
- I. W. M. Smith, Angew. Chem., Int. Ed., 2006, 45, 2842–2861 CrossRef.
- J. Ma, H. Guo and R. Dawes, Phys. Chem. Chem. Phys., 2012, 14, 12090–12093 RSC.
- A. N. Morozov and A. M. Mebel, Phys. Chem. Chem. Phys., 2020, 22, 6868–6880 RSC.
- Y. Georgievskii and S. J. Klippenstein, J. Phys. Chem. A, 2007, 111, 3802–3811 CrossRef PubMed.
- J.-C. Loison, M. Agúndez, V. Wakelam, E. Roueff, P. Gratier, N. Marcelino, D. N. Reyes, J. Cernicharo and M. Gerin, Mon. Not. R. Astron. Soc., 2017, 470, 4075–4088 CrossRef PubMed.
- H. Rabitz, M. Kramer and D. Dacol, Annu. Rev. Phys. Chem., 1983, 34, 419–461 CrossRef.
- A. Saltelli, J. Geophys. Res.: Atmos., 1999, 104, 3789–3793 CrossRef.
- C. W. Gao, M. Liu and W. H. Green, Int. J. Chem. Kinet., 2020, 52, 266–282 CrossRef.
- A. M. Thompson and R. W. Stewart, J. Geophys. Res.: Atmos., 1991, 96, 13089–13108 CrossRef.
- N. Carrasco, O. Dutuit, R. Thissen, M. Banaszkiewicz and P. Pernot, Planet. Space Sci., 2007, 55, 141–157 CrossRef.
- M. Dobrijevic, E. Hébrard, S. Plessis, N. Carrasco, P. Pernot and M. Bruno-Claeys, Adv. Space Res., 2010, 45, 77–91 CrossRef.
- E. Hébrard, M. Dobrijevic, J. C. Loison, A. Bergeat, K. M. Hickson and F. Caralp, Astron. Astrophys., 2013, 552, A132 CrossRef.
- M. Dobrijevic and J. Parisot, Planet. Space Sci., 1998, 46, 491–505 CrossRef.
- A. I. Vasyunin, D. Semenov, T. Henning, V. Wakelam, E. Herbst and A. M. Sobolev, Astrophys. J., 2008, 672, 629–641 CrossRef.
- V. Wakelam, F. Selsis, E. Herbst and P. Caselli, Astron. Astrophys., 2005, 444, 883–891 CrossRef.
- A. I. Vasyunin, A. M. Sobolev, D. S. Wiebe and D. A. Semenov, Astron. Lett., 2004, 30, 566–576 CrossRef.
- V. Wakelam, J.-C. Loison, E. Herbst, D. Talbi, D. Quan and F. Caralp, Astron. Astrophys., 2009, 495, 513–521 CrossRef.
- V. Wakelam, I. W. M. Smith, E. Herbst, J. Troe, W. Geppert, H. Linnartz, K. Öberg, E. Roueff, M. Agúndez, P. Pernot, H. M. Cuppen, J. C. Loison and D. Talbi, Space Sci. Rev., 2010, 156, 13–72 CrossRef.
- J. Heyl, T. Lamberts, S. Viti and J. Holdship, Mon. Not. R. Astron. Soc., 2023, 520, 503–512 CrossRef.
- B. A. McGuire, R. A. Loomis, A. M. Burkhardt, K. L. K. Lee, C. N. Shingledecker, S. B. Charnley, I. R. Cooke, M. A. Cordiner, E. Herbst, S. Kalenskii, M. A. Siebert, E. R. Willis, C. Xue, A. J. Remijan and M. C. McCarthy, Science, 2021, 371, 1265–1269 CrossRef.
- A. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337 CrossRef.
- M. Ruaud, J. C. Loison, K. M. Hickson, P. Gratier, F. Hersant and V. Wakelam, Mon. Not. R. Astron. Soc., 2015, 447, 4004–4017 CrossRef CAS.
- T. H. G. Vidal, J.-C. Loison, A. Y. Jaziri, M. Ruaud, P. Gratier and V. Wakelam, Mon. Not. R. Astron. Soc., 2017, 469, 435–447 CrossRef.
- D. Navarro-Almaida, R. L. Gal, A. Fuente, P. Rivière-Marichalar, V. Wakelam, S. Cazaux, P. Caselli, J. C. Laas, T. Alonso-Albi, J. C. Loison, M. Gerin, C. Kramer, E. Roueff, R. Bachiller, B. Commerçon, R. Friesen, S. García-Burillo, J. R. Goicoechea, B. M. Giuliano, I. Jiménez-Serra, J. M. Kirk, V. Lattanzi, J. Malinen, N. Marcelino, R. Martín-Domènech, G. M. M. Caro, J. Pineda, B. Tercero, S. P. Treviño-Morales, O. Roncero, A. Hacar, M. Tafalla and D. Ward-Thompson, Astron. Astrophys., 2020, 637, A39 CrossRef.
- S. Doddipatla, G. R. Galimova, H. Wei, A. M. Thomas, C. He, Z. Yang, A. N. Morozov, C. N. Shingledecker, A. M. Mebel and R. I. Kaiser, Sci. Adv., 2021, 7, eabd4044 CrossRef.
- B. A. McGuire, A. M. Burkhardt, S. Kalenskii, C. N. Shingledecker, A. J. Remijan, E. Herbst and M. C. McCarthy, Science, 2018, 359, 202–205 CrossRef PubMed.
- C. Xue, E. R. Willis, R. A. Loomis, K. L. K. Lee, A. M. Burkhardt, C. N. Shingledecker, S. B. Charnley, M. A. Cordiner, S. Kalenskii, M. C. McCarthy, E. Herbst, A. J. Remijan and B. A. McGuire, Astrophys. J. Lett., 2020, 900, L9 CrossRef.
- B. A. McGuire, A. M. Burkhardt, R. A. Loomis, C. N. Shingledecker, K. L. K. Lee, S. B. Charnley, M. A. Cordiner, E. Herbst, S. Kalenskii, E. Momjian, E. R. Willis, C. Xue, A. J. Remijan and M. C. McCarthy, Astrophys. J. Lett., 2020, 900, L10 CrossRef.
- M. C. McCarthy, K. L. K. Lee, R. A. Loomis, A. M. Burkhardt, C. N. Shingledecker, S. B. Charnley, M. A. Cordiner, E. Herbst, S. Kalenskii, E. R. Willis, C. Xue, A. J. Remijan and B. A. McGuire, Nat. Astron., 2021, 5, 176–180 CrossRef.
- R. A. Loomis, A. M. Burkhardt, C. N. Shingledecker, S. B. Charnley, M. A. Cordiner, E. Herbst, S. Kalenskii, K. L. K. Lee, E. R. Willis, C. Xue, A. J. Remijan, M. C. McCarthy and B. A. McGuire, Nat. Astron., 2021, 5, 188–196 CrossRef.
- A. N. Byrne, C. Xue, I. R. Cooke, M. C. McCarthy and B. A. McGuire, Astrophys. J., 2023, 957, 88 CrossRef CAS.
- R. L. Snell, W. D. Langer and M. A. Frerking, Astrophys. J., 1982, 255, 149–159 CrossRef CAS.
- P. Pratap, J. E. Dickens, R. L. Snell, M. P. Miralles, E. A. Bergin, W. M. Irvine and F. P. Schloerb, Astrophys. J., 1997, 486, 862 CrossRef CAS.
- L. Spitzer, Jr. and M. G. Tomasko, Astrophys. J., 1968, 152, 971 CrossRef.
- M. Rodríguez-Baras, A. Fuente, P. Riviére-Marichalar, D. Navarro-Almaida, P. Caselli, M. Gerin, C. Kramer, E. Roueff, V. Wakelam, G. Esplugues, S. García-Burillo, R. L. Gal, S. Spezzano, T. Alonso-Albi, R. Bachiller, S. Cazaux, B. Commercon, J. R. Goicoechea, J. C. Loison, S. P. Treviño-Morales, O. Roncero, I. Jiménez-Serra, J. Laas, A. Hacar, J. Kirk, V. Lattanzi, R. Martín-Doménech, G. Muñoz-Caro, J. E. Pineda, B. Tercero, D. Ward-Thompson, M. Tafalla, N. Marcelino, J. Malinen, R. Friesen and B. M. Giuliano, Astron. Astrophys., 2021, 648, A120 CrossRef.
- R. T. Garrod, V. Wakelam and E. Herbst, Astron. Astrophys., 2007, 467, 1103–1115 CrossRef.
- T. I. Hasegawa and E. Herbst, Mon. Not. R. Astron. Soc., 1993, 261, 83–102 CrossRef.
- T. E. Graedel, W. D. Langer and M. A. Frerking, Astrophys. J., Suppl. Ser., 1982, 48, 321–368 CrossRef.
- U. Hincelin, V. Wakelam, F. Hersant, S. Guilloteau, J. C. Loison, P. Honvault and J. Troe, Astron. Astrophys., 2011, 530, A61 CrossRef.
- A. Fuente, P. Rivière-Marichalar, L. Beitia-Antero, P. Caselli, V. Wakelam, G. Esplugues, M. Rodríguez-Baras, D. Navarro-Almaida, M. Gerin, C. Kramer, R. Bachiller, J. R. Goicoechea, I. Jiménez-Serra, J. C. Loison, A. Ivlev, R. Martín-Doménech, S. Spezzano, O. Roncero, G. Muñoz-Caro, S. Cazaux and N. Marcelino, Astron. Astrophys., 2023, 670, A114 CrossRef.
- D. A. Neufeld, M. G. Wolfire and P. Schilke, Astrophys. J., 2005, 628, 260 CrossRef.
- V. Wakelam and E. Herbst, Astrophys. J., 2008, 680, 371 CrossRef.
- E. B. Jenkins, Astrophys. J., 2009, 700, 1299 CrossRef.
- V. Wakelam, E. Herbst, F. Selsis and G. Massacrier, Astron. Astrophys., 2006, 459, 813–820 CrossRef.
- C. Spearman, Am. J. Psychol., 1904, 15, 72–101 CrossRef.
-
Global sensitivity analysis: the primer, ed. A. Saltelli, Wiley, Chichester, West Sussex, 2008 Search PubMed.
- A. Saltelli, M. Ratto, S. Tarantola and F. Campolongo, Chem. Rev., 2005, 105, 2811–2828 CrossRef PubMed.
- T. Turányi, Reliab. Eng. Syst. Saf., 1997, 57, 41–48 CrossRef.
- M. D. Morris, Technometrics, 1991, 33, 161–174 CrossRef.
- A. N. Heays, A. D. Bosman and E. F. V. Dishoeck, Astron. Astrophys., 2017, 602, A105 CrossRef.
- A. E. Glassgold and W. D. Langer, Astrophys. J., 1973, 186, 859 CrossRef.
- A. Dalgarno, M. Yan and W. Liu, Astrophys. J., Suppl. Ser., 1999, 125, 237 CrossRef.
- T. Su and W. J. Chesnavich, J. Chem. Phys., 1982, 76, 5183–5185 CrossRef.
- A. M. Burkhardt, K. L. K. Lee, P. B. Changala, C. N. Shingledecker, I. R. Cooke, R. A. Loomis, H. Wei, S. B. Charnley, E. Herbst, M. C. McCarthy and B. A. McGuire, Astrophys. J. Lett., 2021, 913, L18 CrossRef.
- M. L. Sita, P. B. Changala, C. Xue, A. M. Burkhardt, C. N. Shingledecker, K. L. K. Lee, R. A. Loomis, E. Momjian, M. A. Siebert, D. Gupta, E. Herbst, A. J. Remijan, M. C. McCarthy, I. R. Cooke and B. A. McGuire, Astrophys. J. Lett., 2022, 938, L12 CrossRef.
- D. S. N. Parker, F. Zhang, Y. S. Kim, R. I. Kaiser, A. Landera, V. V. Kislov, A. M. Mebel and A. G. G. M. Tielens, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 53–58 CrossRef PubMed.
- R. I. Kaiser and N. Hansen, J. Phys. Chem. A, 2021, 125, 3826–3840 CrossRef.
- N. Harada, E. Herbst and V. Wakelam, Astrophys. J., 2010, 721, 1570 CrossRef.
- V. V. Kislov, T. L. Nguyen, A. M. Mebel, S. H. Lin and S. C. Smith, J. Chem. Phys., 2004, 120, 7008–7017 CrossRef.
- R. Gredel, S. Lepp, A. Dalgarno and E. Herbst, Astrophys. J., 1989, 347, 289 CrossRef.
- A. M. Mebel, A. Landera and R. I. Kaiser, J. Phys. Chem. A, 2017, 121, 901–926 CrossRef PubMed.
- I. W. M. Smith, A. M. Sage, N. M. Donahue, E. Herbst and D. Quan, Faraday Discuss., 2006, 133, 137–156 RSC.
- E. Herbst and C. M. Leung, Astrophys. J., Suppl. Ser., 1989, 69, 271 CrossRef.
- V. G. Anicich and W. T. Huntress, Jr., Astrophys. J., Suppl. Ser., 1986, 62, 553 CrossRef.
- M. J. McEwan, G. B. I. Scott, N. G. Adams, L. M. Babcock, R. Terzieva and E. Herbst, Astrophys. J., 1999, 513, 287 CrossRef.
- R. Peverati, P. P. Bera, T. J. Lee and M. Head-Gordon, Astrophys. J., 2016, 830, 128 CrossRef.
- B. M. Jones, F. Zhang, R. I. Kaiser, A. Jamal, A. M. Mebel, M. A. Cordiner and S. B. Charnley, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 452–457 CrossRef PubMed.
- J. A. Miller and S. J. Klippenstein, J. Phys. Chem. A, 2003, 107, 7783–7799 CrossRef.
- L. Zhao, W. Lu, M. Ahmed, M. V. Zagidullin, V. N. Azyazov, A. N. Morozov, A. M. Mebel and R. I. Kaiser, Sci. Adv., 2021, 7, eabf0360 CrossRef.
- E. Herbst, Int. Rev. Phys. Chem., 2017, 36, 287–331 Search PubMed.
- N. Marcelino, J. Cernicharo, M. Agúndez, E. Roueff, M. Gerin, J. Martín-Pintado, R. Mauersberger and C. Thum, Astrophys. J., 2007, 665, L127 CrossRef.
- P. Gratier, L. Majumdar, M. Ohishi, E. Roueff, J. C. Loison, K. M. Hickson and V. Wakelam, Astrophys. J., Suppl. Ser., 2016, 225, 25 CrossRef.
- J. Cernicharo, M. Agúndez, C. Cabezas, N. Marcelino, B. Tercero, J. R. Pardo, J. D. Gallego, F. Tercero, J. A. López-Pérez and P. D. Vicente, Astron. Astrophys., 2021, 647, L2 CrossRef PubMed.
- J. Cernicharo, R. Fuentetaja, C. Cabezas, M. Agúndez, N. Marcelino, B. Tercero, J. R. Pardo and P. D. Vicente, Astron. Astrophys., 2022, 663, L5 CrossRef.
- I. R. Cooke, C. Xue, P. B. Changala, H. T. Shay, A. N. Byrne, Q. Y. Tang, Z. T. P. Fried, K. L. K. Lee, R. A. Loomis, T. Lamberts, A. Remijan, A. M. Burkhardt, E. Herbst, M. C. McCarthy and B. A. McGuire, Astrophys. J., 2023, 948, 133 CrossRef.
- M. Agúndez, N. Marcelino, C. Cabezas, R. Fuentetaja, B. Tercero, P. D. Vicente and J. Cernicharo, Astron. Astrophys., 2022, 657, A96 CrossRef.
- I. Savić and D. Gerlich, Phys. Chem. Chem. Phys., 2005, 7, 1026–1035 RSC.
- G. Angelova, O. Novotny, J. B. A. Mitchell, C. Rebrion-Rowe, J. L. Le Garrec, H. Bluhme, A. Svendsen and L. H. Andersen, Int. J. Mass Spectrom., 2004, 235, 7–13 CrossRef.
- J. L. McLain, V. Poterya, C. D. Molek, D. M. Jackson, L. M. Babcock and N. G. Adams, J. Phys. Chem. A, 2005, 109, 5119–5123 CrossRef PubMed.
- Z. Lin, D. Talbi, E. Roueff, E. Herbst, N. Wehres, C. A. Cole, Z. Yang, T. P. Snow and V. M. Bierbaum, Astrophys. J., 2013, 765, 80 CrossRef.
- G. B. I. Scott, D. A. Fairley, C. G. Freeman, M. J. McEwan, N. G. Adams and L. M. Babcock, J. Phys. Chem. A, 1997, 101, 4973–4978 CrossRef.
- K. M. Hickson, V. Wakelam and J.-C. Loison, Mol. Astrophys., 2016, 3–4, 1–9 Search PubMed.
- R. Terzieva and E. Herbst, Int. J. Mass Spectrom., 2000, 201, 135–142 CrossRef CAS.
- E. Herbst and Y. Osamura, Astrophys. J., 2008, 679, 1670 CrossRef CAS.
- C. Barckholtz, T. P. Snow and V. M. Bierbaum, Astrophys. J., 2001, 547, L171 CrossRef CAS.
- D. L. Baulch, C. T. Bowman, C. J. Cobos, R. A. Cox, Th. Just, J. A. Kerr, M. J. Pilling, D. Stocker, J. Troe, W. Tsang, R. W. Walker and J. Warnatz, J. Phys. Chem. Ref. Data, 2005, 34, 757–1397 CrossRef CAS.
- H.-X. Zhang, S. I. Ahonkhai and M. H. Back, Can. J. Chem., 1989, 67, 1541–1549 CrossRef.
- D. Hou and X. You, Phys. Chem. Chem. Phys., 2017, 19, 30772–30780 RSC.
- C. W. Bauschlicher Jr and A. Ricca, Chem. Phys. Lett., 2000, 326, 283–287 CrossRef.
- P. Ghesquière and D. Talbi, Chem. Phys. Lett., 2013, 564, 11–15 CrossRef.
- A.-R. Soliman, A. M. Hamid, P. O. Momoh, M. S. El-Shall, D. Taylor, L. Gallagher and S. A. Abrash, J. Phys. Chem. A, 2012, 116, 8925–8933 CrossRef PubMed.
- V. Le Page, Y. Keheyan, V. M. Bierbaum and T. P. Snow, J. Am. Chem. Soc., 1997, 119, 8373–8374 CrossRef.
- T. P. Snow, V. Le Page, Y. Keheyan and V. M. Bierbaum, Nature, 1998, 391, 259–260 CrossRef PubMed.
- D. K. Bohme, Chem. Rev., 1992, 92, 1487–1508 CrossRef CAS.
- V. Le Page, Y. Keheyan, T. P. Snow and V. M. Bierbaum, J. Am. Chem. Soc., 1999, 121, 9435–9446 CrossRef CAS.
- G. Baykut, F. W. Brill and J. R. Eyler, Combust. Sci. Technol., 1986, 45, 233–243 CrossRef CAS.
- K. C. Smyth, S. G. Lias and P. Ausloos, Combust. Sci. Technol., 1982, 28, 147–154 CrossRef CAS.
- N. G. Adams, L. D. Mathews and J. David Osborne, Faraday Discuss., 2010, 147, 323–335 RSC.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Ci
Xue
a,
Troy
Van Voorhis
a and
Brett A.
McGuire
*a,
Ci
Xue
a,
Troy
Van Voorhis
a and
Brett A.
McGuire
 *ab
*ab
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations of the model were thus performed and RCCs for every species-reaction pair were calculated for 13 time-points between 4.5 × 104 and 1.1 × 106 years. Monte Carlo analyses with 5000, 15
000 iterations of the model were thus performed and RCCs for every species-reaction pair were calculated for 13 time-points between 4.5 × 104 and 1.1 × 106 years. Monte Carlo analyses with 5000, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and 20
000, and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations were also performed to test the convergence.
000 iterations were also performed to test the convergence.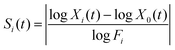
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, 314
500, 314![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400, and 541
400, and 541![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 years, and will be referred to as 1 × 105, 3 × 105, and 5 × 105 years respectively for simplicity. Astrochemical models often agree that the age of TMC-1 seems to be between 105 and 106 years based on comparison to observations, however the exact point within this range is not known. These selected time points thus represent a range of suggested chemical ages, with the later time of 5 × 105 generally providing the best agreement between our model and observations of larger hydrocarbons.44,47,48 Hereafter we refer to the rank of a reaction as its importance, with the highest rank reaction being the most important. For the purpose of comparison, we generally show the top 10 reactions, denoted as key reactions, unless otherwise specified. This is a somewhat arbitrary cutoff as there is no strict definition on what constitutes a “key” reaction but is adequate for identifying predominant reactions and comparing these reactions across different metrics and time points. Full reactions lists sorted by average sensitivity metric can be found in the Zenodo repository: https://zenodo.org/doi/10.5281/zenodo.13257328.
100 years, and will be referred to as 1 × 105, 3 × 105, and 5 × 105 years respectively for simplicity. Astrochemical models often agree that the age of TMC-1 seems to be between 105 and 106 years based on comparison to observations, however the exact point within this range is not known. These selected time points thus represent a range of suggested chemical ages, with the later time of 5 × 105 generally providing the best agreement between our model and observations of larger hydrocarbons.44,47,48 Hereafter we refer to the rank of a reaction as its importance, with the highest rank reaction being the most important. For the purpose of comparison, we generally show the top 10 reactions, denoted as key reactions, unless otherwise specified. This is a somewhat arbitrary cutoff as there is no strict definition on what constitutes a “key” reaction but is adequate for identifying predominant reactions and comparing these reactions across different metrics and time points. Full reactions lists sorted by average sensitivity metric can be found in the Zenodo repository: https://zenodo.org/doi/10.5281/zenodo.13257328.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MC iterations are plotted, while Table 2 contains the corresponding statistical information for C10H7CN and some precursor species. As molecular complexity increases the spread of abundances does as well. This is consistent with the increased rate coefficient uncertainty propagated as the amount of reactions necessary to form these species increases. It is evident that a factor of 2 uncertainty in all reactions is not enough to account for the observed abundance of C10H7CN, as the MC iteration with the maximum abundance model still under-produces this species by almost two and a half orders of magnitude compared to its TMC-1 observed value. This is not entirely surprising given the large discrepancies between the nominal model and observations; however it does indicate that much larger uncertainties and/or missing reactions are responsible. We thus turn our attention to the reactions identified as key processes for C10H7CN by sensitivity analysis to understand critical processes and areas of the network for future study.
000 MC iterations are plotted, while Table 2 contains the corresponding statistical information for C10H7CN and some precursor species. As molecular complexity increases the spread of abundances does as well. This is consistent with the increased rate coefficient uncertainty propagated as the amount of reactions necessary to form these species increases. It is evident that a factor of 2 uncertainty in all reactions is not enough to account for the observed abundance of C10H7CN, as the MC iteration with the maximum abundance model still under-produces this species by almost two and a half orders of magnitude compared to its TMC-1 observed value. This is not entirely surprising given the large discrepancies between the nominal model and observations; however it does indicate that much larger uncertainties and/or missing reactions are responsible. We thus turn our attention to the reactions identified as key processes for C10H7CN by sensitivity analysis to understand critical processes and areas of the network for future study.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations) for select species at 5 × 105 years
000 iterations) for select species at 5 × 105 years









