Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spin dynamics phenomena of a cerium(III) double-decker complex induced by intramolecular electron transfer†
Kana
Kobayashi
a,
Michiyuki
Suzuki
a,
Tetsu
Sato
a,
Yoji
Horii
b,
Takefumi
Yoshida
c,
Brian. K.
Breedlove
a,
Masahiro
Yamashita
 ad and
Keiichi
Katoh
ad and
Keiichi
Katoh
 *e
*e
aDepartment of Chemistry, Graduate School of Science, Tohoku University, 6-3, Aramaki-Aza-Aoba, Aoba-ku, Sendai, Miyagi 980-8578, Japan
bDepartment of Chemistry, Faculty of Science, Nara Women's University, Kitauoya Higashimachi, Nara 630-8506, Japan
cCluster of Nanomaterials, Graduate School of Systems Engineering, Wakayama University, 930 Sakae-Dani, Wakayama, 640-8510, Japan
dSchool of Chemical Science and Engineering, Tongji University, Siping Road 1239, Shanghai 200092, P. R. China
eDepartment of Chemistry, Graduate School of Science, Josai University, 1-1, Keyakidai, Sakaddo, Saitama 350-0295, Japan. E-mail: kkatoh@josai.ac.jp
First published on 18th April 2024
Abstract
Switchable spin dynamic properties in single-molecule magnets (SMMs) via an applied stimulus have applications in single-molecule devices. Many SMMs containing heavy lanthanoid ions with strong uniaxial magnetic anisotropy have been reported to exhibit SMM characteristics in the absence of an external magnetic field. On the other hand, SMMs containing light lanthanoid cerium(III) (Ce3+) ions exhibit field-induced slow magnetic relaxation. We investigated the chemical conversion of a diamagnetic Ce4+ ion (4f0) to a paramagnetic Ce3+ ion (4f1) in Ce-phthalocyaninato double-decker complexes (TBA+[Ce(obPc)2]− (1) and TBA+[Ce(Pc)2]− (2)) which exhibit field-induced SMM behaviour due to a 4f1 system. The phthalocyaninato ligands with electron-donating substituents (obPc2− = 2,3,9,10,16,17,23,24-octabutoxyphthalocyaninato) in 1 have a significant effect on the valence state of the Ce ion, which is reflected in its magnetic properties due to the mixed valence state of the Ce ion. Given that Ce double-decker complexes with π-conjugated ligands undergo intramolecular electron transfer (IET) to the Ce ion mixed valence state, characterised by a mixture of 4f0 and 4f1 configurations, we examined the dynamic disorder inherent in IET influencing magnetic relaxation.
Introduction
Single-molecule magnets (SMMs) are possible candidates for bits in ultra-high-density memory devices and qubits in quantum computers (QC).1–3 SMMs are basically ‘single domain magnets’ since the magnetic interactions between molecules can be ignored due to the fixed number of metal ions and well-ordered magnetic structures.4 Furthermore, SMMs show slow magnetic relaxation rates and quantum tunnelling of the magnetisation (QTM) in a single molecule due to the nature of the electronic structures, which is different from bulk magnets. To make SMMs practical for QC and quantum information processing (QIP),5,6 the energy barrier for spin reversal (Ueff) and fast QTM processes must be controlled.6–9 In crystals, the degenerate orbitals of d and f electrons forming the electronic states reflect the ligand field (LF). As a result, the LF directly influences the uniaxial magnetic anisotropy. Several groups have recently reported the rational molecular design of lanthanoid(III) (Ln3+)-based SMMs, which have distinctive features, including slow magnetic relaxation and QTM.11–18 Although many articles and reviews show that molecular design is essential for SMM behaviour, controlling the magnetic relaxation pathway is still challenging.19–22Since SMM properties are rooted in large uniaxial magnetic anisotropies, it is effective to use heavy Ln3+ ions, such as Tb3+, Dy3+, and Er3+ ions, for high-performance SMMs.23 However, cerium(III) (Ce3+) SMMs with a 4f1 electron configuration have been reported.24–40 In 2013, Kajiwara and co-workers pointed out that the shape of the charge density distribution of a Ce3+ ion was oblate, which is the same as those of Tb3+ (4f8) and Dy3+ (4f9) ions.17,24,41 Therefore, the total angular momentum J in the axial direction of the main axis of the Ce3+ ion is stabilised in the axial LF, and SMM behaviour occurs. In the Ce3+ ion ground state of J = 5/2, 6 (= 2J + 1) levels are degenerate (2F5/2, S = 1/2, L = 3, J = 5/2, gJ = 6/7), and the energy is split by adding an LF, meaning a Kramers doublet (KD) structure remains. However, whether the KD term (|MJ| = 5/2, 3/2, and 1/2) has the lowest energy depends on the LF. Ce3+ complexes have an energy gap between the ground state and the first excited state, which has been reported to be ca. 20 cm−1 and are wide enough to prevent spin reversal.24–40 However, the magnetic relaxation of Ce3+ type SMMs occurs via a Raman process below 10 K.35,42,43 The spin state of the 4f1 electron is the origin of the slow magnetic relaxation phenomenon. In addition, since the stable isotopes of Ce (isotopic nuclides 140Ce, 142Ce, 138Ce, and 136Ce) have no nuclear spin, investigating the magnetic relaxation phenomena, including the ground state and excited state, will provide important insights into the molecular design of Ce-based SMMs.44,45
In Ce compounds with sandwich structures, like cerocene and phthalocyaninato multiple-decker complexes, where Ce is sandwiched by π-conjugated ligands, the valence state of the Ce ion may be in an intermediate electronic state between trivalent (Ce3+) and tetravalent (Ce4+).25,46–48 Precise determination of the valence state of Ce ions in a mixed valence state has been attempted using various methods, including X-ray absorption near edge structure (XANES) and cyclic voltammetry (CV).48–50 However, the determination of the valence state of a Ce ion still has many uncertainties, and it has been reported that its valence state can change depending on the influence of the substituents attached to the ligands.
From the viewpoint of magnetic switching properties, the total angular momentum of Ce3+ ions is J = 5/2, and Ce3+ compounds are paramagnetic with a 4f1 configuration. On the other hand, the total angular momentum of Ce4+ ions with a 4f0 configuration is J = 0, making it diamagnetic. In this sense, Ce4+-phthalocyaninato (Pc2−) double-decker complexes (Ce(Pc)2) are best suited for magnetic switching since Ce4+(4f0) ⇌ Ce3+(4f1) occurs easily (Fig. 1). We studied the Ce3+ ion (4f1) spin dynamics via an intramolecular electron transfer (IET) between the Ce3+ ion and the Pc ligands of Ce–Pc double-decker complexes (TBA+[Ce(obPc)2]− (1) and TBA+[Ce(Pc)2]− (2)) (TBA+ = tetrabutylammonium, obPc2− = 2,3,9,10,16,17,23,24-octabutoxyphthalocyaninato, Pc2− = phthalocyaninato). Moreover, we focused on the effects of IET on the magnetic relaxation process due to the dynamic disorder of the molecular structures.
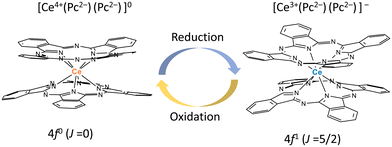 | ||
| Fig. 1 Schematic illustration of redox-active Ce4+-phthalocyaninato double-decker complex Ce(Pc)2, which has magnetic switching due to ease of reduction/oxidation of the Ce ion. | ||
Experimental
All reagents were purchased from Wako Pure Chemical Industries, Ltd, TCI, Strem Chemicals, Inc., and Sigma-Aldrich Co. LLC and used without further purification. Complexes 1 and 2 were prepared according to previously reported literature procedures.48,51–53Synthesis of TBA+[Ce(obPc)2]− (1)
Neutral Ce(obPc)2 was synthesised as follows. Ce(OAc)3·H2O (335 mg, 1.0 mmol), and 1,8-diazabicyclo[5,4,0]undec-7-ene (DBU) (1 mL) and 4,5-dibutoxyphthalonitrile (2125 mg, 7.8 mmol) were added to 1-hexanol (20 mL). The solution was refluxed under argon for 24 h. After cooling, the obtained solid was purified by using column chromatography (C-200 silica gel, Wako) with chloroform (CHCl3) as the eluent. The cerium double-decker complex Ce(obPc)2 (obPc2− = 2,3,9,10,16,17,23,24-octabutoxyphthalocyaninato) was obtained from the dark green band by removing the solvent. Green needle-like crystals of Ce(obPc)2 were obtained recrystallised by layering a dichloromethane solution with n-hexane (964 mg, 0.41 mmol, yield 41%). Single crystals suitable for X-ray diffraction analysis were obtained by diffusing ethanol into a chloroform solution. ESI-MS: m/z: 2318.07 [M]+ (calcd 2318.90) Anal. calcd (%) for C128H160N16O16Ce: C; 66.30, H; 6.96, N; 9.66 found. C; 66.30, H; 6.89, N; 9.62.The reduced cerium(III) double-decker complex TBA+[Ce(obPc)2]− (1) (TBA+ = tetrabutylammonium) was prepared by adding Ce(obPc)2 (82 mg, 0.035 mmol) and 1.6 mL of hydrazine monohydrate (N2H4·H2O) to 16 mL of dimethyl sulfoxide (DMSO), heating to boiling with a heat gun, and sonicating for 30 min until the neutral form green completely disappeared, resulting in the solution turning blue, which is the colour of anionic [Ce(obPc)2]−. Since the redox potential of the Ce4+/Ce3+ couple is higher than the redox potential of N2H4·H2O, Ce4+ ions can be reduced to Ce3+ ions with N2H4·H2O. Tetrabutylammonium bromide (TBA·Br) (500 mg) dissolved in 5.0 mL of DMSO was added to the above solution; upon slow diffusion, a light blue solid precipitated out. A light blue solid of 1 was obtained (67 mg, 0.026 mmol, yield 75%). MALDI-MS: m/z: 2318.12 [M]+ (calcd 2318.90) Anal. Calcd (%) for: C144H196N17O16Ce·H2O: C; 67.05, H; 7.74, N; 9.23 found. C; 66.97, H; 7.74, N; 9.20.
The following was performed to obtain a single crystal. A mixture of Ce(obPc)2 (0.78 mg), DMSO (0.58 mL), and N2H4·H2O (0.02 mL) was heated at 120 °C for 1 h, affording a blue solution of the anionic double-decker complex ([Ce(obPc)2]−). After cooling to room temperature, the undissolved solids were removed using a membrane filter. Slow diffusion of the anionic double-decker solution into a DMSO solution of TBA·Br (0.4 M) afforded plate-like crystals of 1.
Synthesis of TBA+[Ce(Pc)2]− (2)
Ce(Pc)2 was synthesized using the method reported in ref. 53:“A mixture of 1,2-dicyanobenzene (2150 mg, 16.8 mmol), Ce(NH4)2(NO3)6 (500 mg, 0.912 mmol), and DBU (1.5 mL) in 150 mL of 1-hexanol was refluxed for 20 h. The solution was allowed to cool to room temperature and then filtered. The precipitate was washed with CHCl3 and then dried in the air. The crude purple product was extracted with ten 200 mL portions of CHCl3. The green extracts were combined, concentrated, and purified using column chromatography (C-200 silica gel, Wako) with CHCl3 as the eluent. The green fraction, which was the first fraction, was collected while being careful not to contaminate with the H2Pc. The green fraction was concentrated, and n-hexane was added until the compound precipitated (600 mg, 0.515 mmol, 57%). Deep green needle-like crystals were obtained by diffusing n-hexane into a chloroform solution. ESI-MS: m/z 1164.20 [M+] (calcd.1164.21)”.53
The cerium(III) double-decker complex TBA+[Ce(Pc)2]− (2) was prepared by adding Ce(Pc)2 (78 mg, 0.067 mmol) and 1.2 mL of N2H4·H2O to 30 mL of DMSO, heating to boiling with a heat gun, and sonicating for 30 min until the green neutral form completely disappeared to afford a blue solution, which is the colour of the anionic form [Ce(Pc)2]−. TBA·Br (600 mg) was added to the above solution, and then the solution was heated with a heat gun and sonicated for 30 min. After adding 300 mL of distilled water and leaving it overnight, the resulting blue solid of 2 was collected by using suction filtration and recrystallised by liquid–liquid diffusion using acetone/n-hexane to obtain a purple block-like crystalline solid (73.5 mg, 0.0522 mmol, yield 78%). Elemental analysis calcd (%) for C80H68N17Ce: C 68.26, H 4.87, N 16.92; found: C 67.63, H 4.87, N 16.59.
X-ray crystal structure analysis
A single crystal was mounted on a loop rod coated with Paratone-N (HAMPTON RESEARCH). Data were collected on a Rigaku Saturn 724+ CCD diffractometer with graphite monochromated Mo κα radiation (λ = 0.71075 Å) at T = 233 ± 2 K for 1 and T = 100 ± 2 K for 2. An empirical absorption correction based on azimuthal scans of several reflections was applied. The data were corrected for Lorentz and polarization effects. All non-hydrogen atoms were refined anisotropically using a least-squares method, and hydrogen atoms were fixed at calculated positions and refined using a riding model. SHELXL (2014/7 and 2018/3) was used for structure refinement, and the structure was expanded using Fourier techniques.Powder X-ray diffraction (PXRD) patterns of crushed polycrystalline samples of 1 were acquired using Bruker X-ray diffractometer (D2 PHASER) operated at 30 kV and 10 mA using a low-background sample holder in the diffraction angle (2θ) range of 3°–60° in steps of 0.02° at 1 s per step. PXRD patterns for crushed crystalline samples of 2 loaded into capillaries (diameter: 0.8 mm, length: 80 mm, Hilgenderg) with the mother liquor were collected at 298 K using a Rigaku X-ray diffractometer (AFC-7R/LW) operated at 50 kV and 300 mA in the 2θ range of 3°–60° in steps of 0.02° and at 2 s per step. Visualization and analysis of the crystal structure and PXRD patterns were simulated from the single crystal data by using Mercury 4.0.
Physical property measurements
Electrospray ionization mass spectroscopy and elemental analyses were performed at the Research and Analytical Centre for Giant Molecules, Tohoku University. Ultraviolet–visible-near infrared (UV-vis-NIR) spectra for chloroform solutions were acquired on a JASCO V-670 spectrophotometer in a quartz cell with a pathlength of 1 cm at 298 K. Infrared (IR) spectra were acquired on a JASCO FT/IR-6600 and FT/IR-6100V in a KBr matrix at 298 K.Electrochemistry (cyclic voltammetry (CV) and differential pulse voltammetry (DPV)) was performed using an ALS/HCH Model 620D electrochemical analyser. A 0.1 M TBA·PF6 (tetrabutylammonium hexafluorophosphate) dichloromethane solution was used as the supporting electrolyte. A glassy carbon (3 mm diameter) electrode was used as a working electrode, Pt wire was used as a counter electrode, and Ag/AgCl was used as a reference electrode.
X-ray absorption fine structure (XAFS) measurements were conducted on sample pellets (4 mmϕ) in the BL9A beamline of the Photon Factory (2.5 GeV, 450 mA), operated by the High Energy Accelerator Research Organization (KEK), under proposals 2017P016 and 2019G117. The X-rays were monochromatized with a Si(111) water-cooled double crystal monochromator (resolution: ΔE/E ≈ 2 × 10−4 (9 keV)). A Ni-coated double flat mirror was used to reduce the higher harmonics. Chromium foil was employed to calibrate the Ce LIII-edge. The XAFS data was processed using the ATHENA program.54 Deconvolution analysis of XANES spectrum was performed based on the literature.55,56
Magnetic susceptibility measurements were performed on Quantum Design SQUID magnetometers MPMS-XL, MPMS-3, and PPMS ACMS system. Direct current (dc) measurements were performed in the temperature (T) range of 1.8–300 K and dc magnetic fields (H) of −70 to 70 kOe. Alternating current (ac) measurements were performed in the ac frequency (ν) range of 1–1000 Hz with an ac field amplitude of 3 Oe in the presence of an H for 1 (zero to 3 kOe) and 2 (zero to 16 kOe) and the ν range of 10–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz with an ac field amplitude of 3 Oe in the presence of a dc field 750 Oe for 2 by using an ACMS. Measurements were performed on randomly oriented powder samples, placed in gel capsules and fixed with n-eicosane to prevent them from moving during measurements. Using Pascal's constants, all data were corrected for the sample holder, n-eicosane, and diamagnetic contributions from the molecules.
000 Hz with an ac field amplitude of 3 Oe in the presence of a dc field 750 Oe for 2 by using an ACMS. Measurements were performed on randomly oriented powder samples, placed in gel capsules and fixed with n-eicosane to prevent them from moving during measurements. Using Pascal's constants, all data were corrected for the sample holder, n-eicosane, and diamagnetic contributions from the molecules.
Theoretical calculations
Calculations using a complete active space self-consistent field (CASSCF) method with spin–orbit (SO) coupling (CASSCF-SO) were performed using the ORCA 5.0.357 program with the basis set SARC2-DKH-QZVP58 for the Ce ion, SARC-DKH-TZVP59 for N donor atoms, and DKH-def2-SVP59 for non-coordinating atoms. The molecular geometry of the [Ce(Pc)2]− unit was taken from the crystal structure and used for the calculations without geometry optimization. For the calculations on [Ce(obPc)2]−, the butoxy groups were replaced with methoxy groups to reduce the computational costs. The positions of the methoxy protons were optimized at the B3LYP-D3BJ/Def2-SVP level60–62 using Y as the metal centre. Seven of the doublet states were mixed with SO coupling. The number of the doublet states corresponds to the number of cases where one electron is present in any of the seven f orbitals. The SINGLE_ANISO module was used to convert the CASSCF-SO results into the wavefunctions in terms of MJ and to calculate the transition magnetic moment among the ligand field sublevels.Results and discussion
Structural characterisations
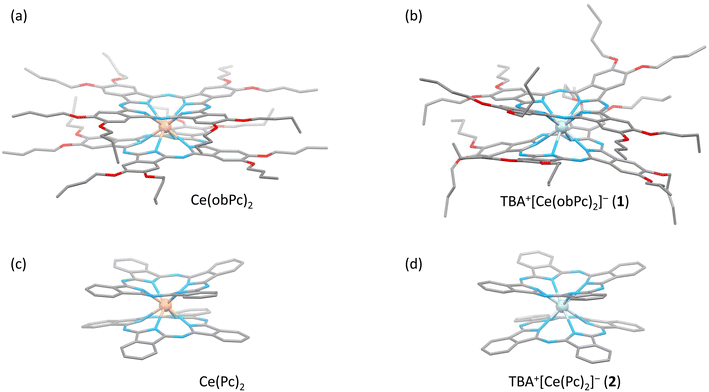
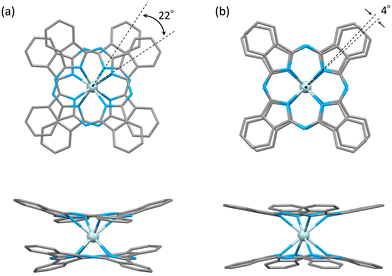
The characteristics of SMMs are related to their crystal structures, and the coordination environment of the metal centre is particularly important. Therefore, we analysed the crystal structures of 1 and 2 (Fig. 2 and 3). In Fig. 2, the structures of the neutral (a and c) and reduced complexes (b and d) were significantly different due to the Ce ionic radius (trivalent: 1.14 Å and tetravalent: 0.96 Å). The structures of neutral complexes are shown in Fig. S1 and S3.† In addition, the ionic radius of the Ce ion in Ce(Pc)2 is intermediate between those of Ce3+ and Ce4+ ions (1.01 Å).63,64Complex 1 has a butoxy group in the Ce(obPc)2 unit and a butyl group in the counter ion TBA+, and the alkyl chains should be disordered around room temperature. Initially, we obtained the diffraction pattern at 120 K but could not obtain enough reflection spots for structural analysis. Therefore, when we compared the lattice constants at 253 K (a = 33.8093, b = 11.2719, c = 36.7273, α = 90.0000, β = 95.3320, γ = 90.0000) and 120 K (a = 34.8002, b = 11.2341, c = 69.9285, α = 90.0000, β = 96.3154, γ = 90.0000), we found that the c-axis was about twice as long at 120 K, and we could confirm a decrease in symmetry. Since we were able to obtain sufficient reflection spots at 233 K, we performed structural analysis and found that 1 was in the monoclinic space group I2/a, and the alkyl chains of [Ce(obPc)2]− unit and TBA+ unit were disordered (Fig. S2 and Table S1†). The presence of the butoxy groups of the [Ce(obPc)2]− unit causes the Pc ligand to have a significantly distorted structure, such as saddle-shaped distortion. The stacking angle (φ) between the two Pc2− ligands was determined to be ca. 22° (Fig. 3a). Thus, the Ce3+ sites in 1 have distorted SP or SAP geometries. The Ce3+ ions are spaced between the two Pc2− ligands with distances of 3.16 Å from the mean plane of the four Niso of the two Pc2− ligands. Crystal-packing diagrams of 1 are shown in Fig. S2.† The intermolecular Ce⋯Ce distance along the b axis was determined to be 11.3 Å, and Ce⋯Ce distance along the a and c axes were determined to be over 16.9 Å. Each molecule of 1 along the b axis is rather well separated from neighbouring molecules due to the alkyl chains of the [Ce(obPc)2]− unit and TBA+ counter ion. However, the structure from the microcrystalline PXRD data at 293 K and simulated from X-ray single crystallographic data at 253 K for 1 almost overlap. At the same time, some polymorphs are present due to the temperature dependence of the diffraction pattern (Fig. S3†).
Complex 2, shown in Fig. 3b, crystallized in the tetragonal space group P4/ncc. It has a square prismatic (SP, quasi-D4h) coordination environment, which is the same structure previously reported by Hückstädt et al. (Table S2,† CCDC 148306).522 has a Ce3+ ion between two Pc2− ligands and is coordinated with TBA+ as a counter ion. φ between the two Pc2− ligands was determined to be ca. 4°. Thus, the Ce3+ site in 2 has a slightly distorted SP geometry. The Ce3+ ion is spaced between the two Pc2− ligands with distances of 3.16 Å from the mean plane of the four Niso of the two Pc2− ligands. Crystal-packing diagrams of 2 are shown in Fig. S5.† The intermolecular Ce⋯Ce distances along the a and c axes were determined to be 12.13 and 11.24 Å, respectively. Each molecule of 2 along the c axis is rather well separated from neighbouring molecules due to the TBA+ counter ion. Furthermore, PXRD patterns for 2 at 293 K are similar to those simulated from X-ray single crystallographic data at 100 K (Fig. S6†).
The coordination environments of neutral and reduced from the crystal structures are significantly different (Fig. 2, 3, S1 and S4†). Since the ionic radius changes depending on the Ce valence state, the Ce–Niso average distance is 2.432 Å for Ce(obPc)2 and 2.418 Å for Ce(Pc)2. On the other hand, it is 2.528 Å for 1 and 2.542 Å for 2 due to the changes in the ionic radii.63,64 Considering the LF in the context of the oblate charge density distribution of the Ce3+ ion with MJ = ±5/2, both 1 and 2 exhibit uniaxial magnetic anisotropies with either SAP and/or SP geometries. Therefore, 1 and 2 should exhibit SMM characteristics.24 However, referring to the ab initio calculations on single ion Ce3+ complexes by Singh et al., zero-field SMM behaviour is unlikely to occur in the D4d/4h geometry of 1 and 2.29 Thus, based on the crystal structure data, we conducted a computational chemistry approach to investigate the presence of uniaxial anisotropy (details will be explained in the following section on magnetic measurements and theoretical calculations).
Electronic structure characterisations
In Ce(Pc)2, the tetravalent Ce state can be changed to the trivalent state since the Ce3+ to Ce4+ oxidation midpoint potential is relatively low.65–68 On the other hand, Ce–Pc triple-decker complexes in which Ce3+ ions are stable can be oxidised to the Ce4+ state.47,69 Both oxidation states of these complexes are stable in solution, and the complexes in either oxidation state can be isolated as solids. Since Ce4+/3+ ions of Ce multiple-decker complexes can undergo electrochemical and chemical oxidation–reduction, switchable metal centres [4f0 (nonmagnetic) ⇌ 4f1 (paramagnetic)] are possible. Several examples of switching between SMMs and paramagnetic properties and spin dynamics phenomena by using the redox process of the metal ion and ligands have been reported.7,67–83 Therefore, since Ce–Pc multiple-decker complexes can be reversibly switched from diamagnetic to paramagnetic/SMMs, they are attractive for use as switches.In both CV and DPV, Ce(obPc)2 showed five redox waves (Fig. S7-1 and S7-2, Tables S3-1 and S3-2†). Ce(obPc)2 undergoes one more redox process than Tb(obPc)2 does because the Ce ion is redox-active, unlike the Tb ion. The five redox waves observed for Ce(obPc)2 have also been observed for other Ce double-decker complexes.48,49 From the redox properties of Ce(Pc)2, Red1 of the Ce(obPc)2 was attributed to the Ce4+/Ce3+ couple.48,49,84
Fig. S8-1† shows a UV-vis-NIR absorption spectrum of Ce(obPc)2. Absorption bands were observed at 357, 476, 649, and 688 nm. The absorption at 357 nm is the Soret band, and the absorptions at 649 nm and 688 nm were attributed to the Q bands. In addition, the broad absorption band at 476 nm was assigned to a ligand-to-metal charge transfer (LMCT) transition from the Pc ligand to the Ce4+ ion.47,69 On the other hand, when Ce(obPc)2 was reduced with hydrazine monohydrate, the bands shifted slightly. The Soret band was at 354 nm, and the Q band was at 642 nm. The LMCT band (448 nm) observed for Ce(obPc)2 was also observed for 1 due to the mixed valence of the Ce4+/3+ ion with IET between the Ce3+ ion and the Pc ligand. On the other hand, the LMCT band was not observed for 2 due to the Ce3+ ion, indicating the effects of the Ce4+ ion in the complex (Fig. S8-2†). Considering the charge balance of the [Ce(obPc)2]− unit, no radicals are generated in the reduced Pc ligands (Fig. S8-1†).47 The anionic state of the Pc ligands was estimated to be [Ce3+(obPc2−)(obPc2−)]− and [Ce4+(obPc2.5−)(obPc2.5−)]−, respectively. The absence of the intervalence(IV) absorption band in the near-infrared region above 1200 nm indicates that there are no π radicals on the Pc ligands (Fig. S8-1 and S8-2†). On the other hand, when Ce(obPc)2 is oxidised by one electron, it becomes cationic, [Ce4+(obPc)˙−(obPc)2−]+, and an IV absorption band is observed in the near-infrared region (Fig. S8-3†).47 In other words, spectroscopic measurements clearly show that no radicals are present on the Pc ligands of the [Ce(obPc)2]− unit in 1. From the spectrum, the reduced form [Ce3+(obPc)2−(obPc)2−]− could be prepared using hydrazine monohydrate. Ce(Pc)2 can also be reduced using the same method to synthesise [Ce(Pc)2]−. In other words, it is possible to synthesise 1 and 2 by chemical reduction (refer to the Experimental section).
It has been reported that the vibrational mode around 880 cm−1 in the IR spectrum is sensitive to the ionic radius of lanthanoids.63 For Ce(Pc)2, it is 883 cm−1, but the band is at 878 cm−1 for 2. In addition, pyrrole stretching (1300–1350 cm−1) and isoindole stretching (1370–1484 cm−1) are sensitive to the ionic radius of lanthanoid ions, and we confirmed that they were shifted for Ce(Pc)2 and 2 (Fig. S9-1 and S9-2†).85 On the other hand, the peak near 880 cm−1 for the vibration mode of Ce(obPc)2 and 1 was not shifted. However, the isoindole stretching frequencies were different, reflecting the oxidation state of the Ce ions (Fig. S9-3 and S9-4†).
For neutral Ce(Pc)2, the IET of [Ce4+(Pc)2−(Pc)2−] ⇌ [Ce3+(Pc)˙−(Pc)2−] occurs because the energy level of the Ce3+ ion 4f1 orbital is very close to the energy level of the Pc˙− frontier orbital (Fig. S10†).48,63 Furthermore, for Ce[(15C5)4Pc]2 ((15C5)4Pc = bis-[tetra-(15-crown-5)-phthalocyaninato]) Langmuir monolayers, molecular orientation-induced IET has been observed.86 Recently, findings indicate the mitigation of IET in Ce(Pc)2 upon adsorption onto an Au(111) substrate, thereby enabling the discernment of the [Ce3+(Pc)˙−(Pc)2−] state. This observation implies that IET can be regulated through the manipulation of the interface.53,87
XAFS allows element-selective measurements, from which information on the local structure and electronic states can be obtained. XAFS spectra are analysed in the energy region from the absorption edge, divided into XANES (from the absorption edge to about 50 eV) and EXAFS (from the XANES region to about 1000 eV). In particular, XANES spectra provide information on the electronic and geometric structures of X-ray absorbing atoms. We measured XANES spectra to investigate the electronic states of several types of Ce-based compounds (Fig. 4). When analysing XANES spectra, the simplest evaluation method is the fingerprint method, which estimates the electronic state and geometric structure by measuring the Ce(Pc)2 based complexes and evaluating the degree of spectral matching. Therefore, we compared the spectra with previously reported analogous compounds and estimated the valence state of the Ce ions.48
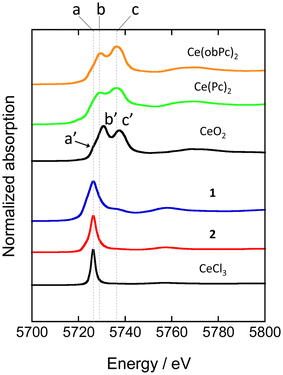 | ||
| Fig. 4 Ce LIII-edge XANES spectra of reference materials (CeO2 and CeCl3) and Ce(Pc)2 based complexes. See ESI for the assignment of each peak. | ||
XANES spectra of neutral and reduced Ce(Pc)2 derivatives were acquired to clarify the valence state of the Ce ion in 1, the energy difference between 2p and 5d levels of the electronic states of Ce3+ and Ce4+ ions is different by ca. 10 eV.88 Ce LIII-edge spectra of 1 and 2 are shown in Fig. 4, together with those of reference samples CeO2 and CeCl3. A white-line peak for the Ce3+ state appears at 5726 eV (labeled as a), which is associated with the 2p → 4f15d dipole-allowed transition.55,56,89 For 1 and 2, a white-line peak appeared at 5726 eV at the same energy as the white line of CeCl3. However, the feature in spectra of 1 and 2 was slightly broader than that of CeCl3. In addition, the absorption labeled c (5736 eV, 2p → 4f05d transition) in the spectrum of 1 is probably due to the influence of the electron-donating alkoxy substituents, as pointed out by Bian et al.48 Peak c was not observed in the spectrum of unsubstituted 2. On the other hand, the two absorption energies observed for Ce(Pc)2 and Ce(obPc)2 were at lower energies than that of CeO2 (labeled a′, b′ and c′ in Fig. 4).48 These absorbance energy shifts are due to differences in the coordination environments and electronic structures.
The mixed valence state of Ce ion has been reported to be the Ce double-decker complexes.48,63,87 The characteristics of the valence state for the Ce double-decker complexes are shown in Tables S4-1 and S4-2.† Table S4-2† shows the results of estimating the ratio of Ce3+ and Ce4+ ions using a Gaussian function from XANES spectrum (Fig. S11†). From the analysis, 2 has 1 mol of Ce3+ ions, and 1 has ca. 0.8 mol of Ce3+ ions with ca. 0.2 mol of Ce4+ ions. The spectral shape, absorption energy, and relative intensity of XANES spectra reflect the electronic structures, which have the weight of orbital mixing between the Ce ion and the ligands. The IET indicates that the f orbital of 1 is mixed with the obPc2 ligands. The valence state of the Ce ion in each compound is reflected in the magnetic properties (vide infra).
Static-field magnetic properties
From the dc measurements, Ce(obPc)2 and Ce(Pc)2 exhibited diamagnetic properties above 10 K. For Ce(obPc)2, a diamagnetic response was generated at 1.8 K (Fig. S12†). On the other hand, the field dependence of the magnetisation (M–H) for powder samples of Ce(Pc)2 exhibits paramagnetic properties at 2 K (Fig. S13†). Here, focusing on the IET, both Ce(obPc)2 and Ce(Pc)2 are in Ce4+/Ce3+ mixed valence states, with the paramagnetic signature observed for Ce(Pc)2 indicative of a higher ratio of Ce3+ in comparison to Ce(obPc)2 (Fig. S10 and Table S4-2†).63Fig. 5a and b show the magnetic susceptibilities (χM) of 1 and 2 in the temperature (T) range of 1.8–300 K in an H of 5 kOe. For clarity, we first show the results for 2, which has 1 mol of Ce3+ ions (Fig. 5b). The value of χMT of 2 at room T was 0.68 cm3 K mol−1, which is lower than the value for one free isolated Ce3+ ion (0.8 cm3 K mol−1, 2F5/2, gJ = 6/7). The gradual decrease in χMT mainly originates from LF effects, such as the thermal depopulation of the Stark sublevels. This behaviour has been reported for other Ce3+ complexes.25,35 The field dependence of the magnetisation (M–H) on powder samples of 2 was measured at 1.8 K (Fig. 5d and S14†). The theoretical saturated magnetisation (Msat) value of completely oriented Ce3+ ions (1 mol) with uniaxial anisotropic and ground KDs of MJ = ±5/2 was 2.14NμB [Msat = gJ (6/7) × MJ (5/2)]. However, Msat for 2 was 1.03NμB which is close to the expected Msat of a randomly oriented Ce3+ ion (1 mol) with uniaxial anisotropy (Msat = 1/2gJMJ = 1.07NμB). In addition, using a pseudo-spin Seff = 1/2 approximation approach for Msat of 2 at 1.8 K, Msat (= 1/2gZeffSeff) was determined to be 1NμB using gZeff ≈ 4 from the CASSCF calculations (Table S5†). The T dependence of χMT and H dependence of M data for 2 were used to determine the magnetic properties using the PHI software package with the LFPs (Table S6†) from CASSCF calculations.90 Experimental results could be explained using the parameters obtained from the theoretical calculations (c.f. Theoretical calculation section).
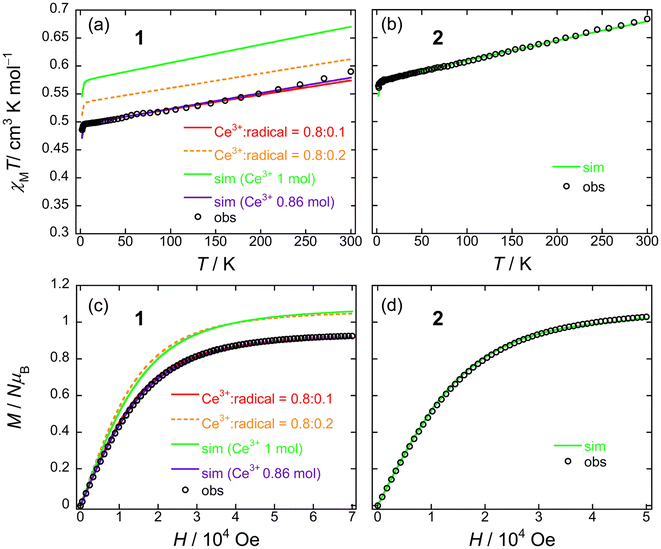 | ||
| Fig. 5 T dependence of χMT for powder samples of (a) 1 and (b) 2 obtained in the T range of 1.8–300 K in an H of 5 kOe. Field dependence of the magnetisation (M–H) measured on powder samples of (c) 1 and (d) 2 at 1.8 K. The solid lines were simulated by using the PHI software package (see main text and Fig. S15†). The ligand field parameters (LFPs) of 1 and 2 were obtained by using CASSCF calculations (see main text). | ||
On the other hand, 1 exhibits a mixed valence state with Ce3+ (ca. 0.8 mol) and Ce4+ ions (ca. 0.2 mol) as determined by using XANES analysis (Table S4†). Therefore, the χMT value of 1 is smaller than that of 2 (1 mol of Ce3+ system) in the T range used (Fig. 5a). In addition, the Msat value of 1 is smaller than that of 2 (Fig. 5c). The T dependence of χMT and H dependence of the M data for 1 were used to determine the magnetic properties by using the PHI software package with the LFPs (Table S6†) from CASSCF calculations (c.f. Theoretical calculation section).90 First, when we performed a simulation on 1 with 1 mol of Ce3+ ion, it had similar behaviour to 2, and the differences reflect the LFPs (Fig. 5a and c: green solid lines). The results of this simulation differ significantly in the theoretical values on the vertical axis compared to the experimental values. Therefore, we performed a simulation with the net abundance ratio of Ce3+ ion in 1 with 0.86 mol, and we were able to nearly reproduce the experimental values (Fig. 5a and c: violet solid lines). This is effective when assuming Ce3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce4+ = 0.8
Ce4+ = 0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 based on XANES spectrum analysis (Table S4-2†) and attributing magnetic properties to the Ce3+ component. On the other hand, the orange dashed line represents the results of the simulation with [Ce3+(obPc)2−(obPc)2−]−
0.2 based on XANES spectrum analysis (Table S4-2†) and attributing magnetic properties to the Ce3+ component. On the other hand, the orange dashed line represents the results of the simulation with [Ce3+(obPc)2−(obPc)2−]−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Ce4+(obPc)2−(obPc)˙3−]− = Ce3+
[Ce4+(obPc)2−(obPc)˙3−]− = Ce3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) radical = 0.8
radical = 0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 based on XANES spectrum analysis (Table S4-2†). However, this did not reproduce the experimental data (Fig. 5a and c). The experimental values were nearly reproduced by the red solid line (Ce3+
0.2 based on XANES spectrum analysis (Table S4-2†). However, this did not reproduce the experimental data (Fig. 5a and c). The experimental values were nearly reproduced by the red solid line (Ce3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) radical = 0.8
radical = 0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1). The simulation results of the M–H curve are presented in Fig. S15.† A χMT value for the radical (S = 1/2) of 0.375 cm3 K mol−1 was used in the simulation. In these simulations, the Ce3+ and radical components are added together. Considering the XANES spectrum and magnetic propeties of the neutral species (Table S4-2 and Fig. S13†) and the simulation results of the M–H curve (Fig. S15†), the magnetisation value of the radicals in the [Ce4+(obPc)2−(obPc)˙3−]− unit resulting from IET are lower than the ratio obtained from the XANES spectrum. However, it is currently unknown how stable the [Ce4+(obPc)2−(obPc)˙3−]− state, which results from IET, is.
0.1). The simulation results of the M–H curve are presented in Fig. S15.† A χMT value for the radical (S = 1/2) of 0.375 cm3 K mol−1 was used in the simulation. In these simulations, the Ce3+ and radical components are added together. Considering the XANES spectrum and magnetic propeties of the neutral species (Table S4-2 and Fig. S13†) and the simulation results of the M–H curve (Fig. S15†), the magnetisation value of the radicals in the [Ce4+(obPc)2−(obPc)˙3−]− unit resulting from IET are lower than the ratio obtained from the XANES spectrum. However, it is currently unknown how stable the [Ce4+(obPc)2−(obPc)˙3−]− state, which results from IET, is.
Both 1 and 2 have uniaxial magnetic anisotropy, and the origin is the Ce3+ ion with ground KDs of MJ = ±5/2. The magnetic behaviour can be reproduced with the LFP obtained from CASSCF calculations. By considering the net abundance ratio of the Ce3+ ion from XANES spectral analysis (Table S4†), it is possible to understand the magnetic behaviour of 1. In comparison to the Tb3+ system, the coordination environments of 1 and 2 are markedly different, but there are no drastic differences in their magnetic behaviours.91 In other words, the presence of structural polymorphs of 1 is thought to have little effect on the T dependence of the χMT values and the M–H properties.
Dynamic magnetic properties
The ac magnetic susceptibilities of powder samples of 1 and 2 were acquired. The in-phase (χ′M) and out-of-phase (χ′′M) signals were ν dependent in the range of 1–1000 Hz in different T ranges. No ν dependence was observed down to 2 K in an H of zero, indicating that 1 and 2 undergo slow magnetic relaxation phenomena in an H ≠ 0 (Fig. S16†).To investigate the magnetic relaxation properties of 1 and 2, ν dependent measurements were performed in the ν range of 1–1000 Hz at 4 K (Fig. S17 for 1 and Fig. S18† for 2). When an H was not applied, no ac signal was observed. This is the same behaviour as that reported for other Ce3+ complexes, indicating that QTM is dominant.24–40 However, when an H > 0 Oe was applied, field-induced slow magnetic relaxation behaviour was observed for 1 and 2. To determine the slow magnetic single relaxation processes of 1 and 2, we analysed the data by using a generalised Debye model (eqn (S1)–(3)†) to estimate τ.92Fig. 6a shows the H dependence of τ. These results confirm that QTM is suppressed in an H and that a direct process is enhanced. Since QTM is suppressed when an H is applied, τ becomes slow with an increase in H and reaches a maximum (τmax). The magnetic field (Hτmax) at which the τ values of 1 and 2 exhibit the lowest rate is 250 Oe for 1 and 750 Oe for 2. In addition, the τ for 1 is approximately twice as slow as that of 2 (Fig. S19†). τ is almost constant between 100 and 3000 Oe due to the Raman process. Above 4000 Oe, τ ∝ H−n with n = 4 due to the Kramers Ce3+ ion, suggesting that the direct process is promoted (eqn (1)).
| τ−1 = a1/(1 + a2H2) + bH4T + c | (1) |
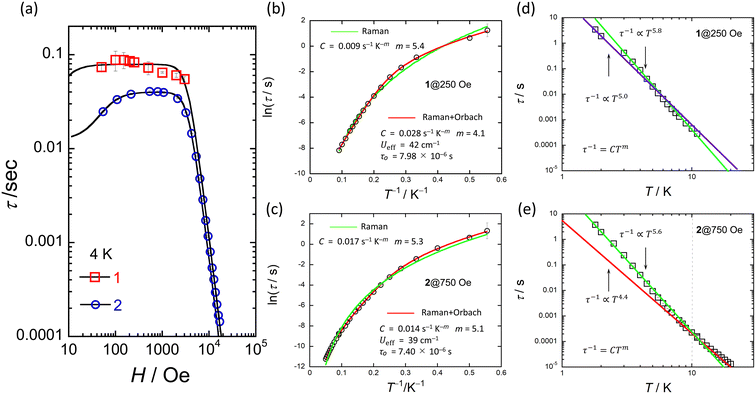 | ||
| Fig. 6 (a) H dependence of τ for 1 and 2 at 4 K obtained from χ′′Mversus ν plots (Fig. S17 and S18†). Black solid lines were fitted by using eqn (1). (b) and (c) shows the T dependence of τ of 1 and 2 in the appropriate H obtained from χ′′Mversus ν plots (Fig. S20 and S21†). Red solid lines were fitted by using eqn (2). Green solid lines were fitted by using τ−1 = CTm. (d) and (e) shows the logarithmic representation of τ below 10 K of 1 and 2 in each appropriate H. Solid lines were fitted by using τ−1 = CTm. The best fits were obtained for the experimental data using the parameters described in the inset of figures (b–e), respectively. | ||
To investigate the slow magnetic relaxation phenomena in detail, we prepared χ′M and χ′′Mversus ν plots. We analysed the data by using a generalized Debye model (eqn (S1)–(S3)†) to estimate τ for 1 in an H of 250 Oe and 2 in an H of 750 Oe (Fig. S20 for 1 and S21† for 2). For 1, a T range of 1.8–11 K and a ν range of 1–1000 Hz were used, and for 2, a T range of 1.8–20 K and a ν range of 1–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz were used (Fig. S21 and S22†). Fig. 6b and c show the T dependences of τ of 1 and 2 (Fig. S23†). The Ueff values of 1 and 2 were estimated from an Arrhenius plot (τ versus T−1) to be 42 cm−1 (60 K) and 40 cm−1 (58 K) with τ0 values of 7.98 × 10–6 s and 7.40 × 10−6 s, respectively. C was determined to be 2.8 × 10–2 s−1 K−m (m = 4.1) for 1 and 1.4 × 10–2 s−1 K−m (m = 5.1) for 2 from Arrhenius plots using eqn (2), where the first and second terms denote Raman and Orbach processes.93
000 Hz were used (Fig. S21 and S22†). Fig. 6b and c show the T dependences of τ of 1 and 2 (Fig. S23†). The Ueff values of 1 and 2 were estimated from an Arrhenius plot (τ versus T−1) to be 42 cm−1 (60 K) and 40 cm−1 (58 K) with τ0 values of 7.98 × 10–6 s and 7.40 × 10−6 s, respectively. C was determined to be 2.8 × 10–2 s−1 K−m (m = 4.1) for 1 and 1.4 × 10–2 s−1 K−m (m = 5.1) for 2 from Arrhenius plots using eqn (2), where the first and second terms denote Raman and Orbach processes.93
| τ−1 = CTm +τ−10exp(−Ueff/kBT) | (2) |
The Ueff (≈40 cm−1) and τ0 (≈10−6 s) values of 1 and 2 are larger than those of related Ce3+ SMMs.24–30,33–40 Therefore, we must consider another magnetic relaxation process instead of an Orbach process due to the small number of phonons below 10 K. The energy gap between the ground state and the first excited state estimated from CASSCF calculations, which will be explained later, was approximately 900 cm−1, which is one order of magnitude larger than the Ueff estimated from the T dependence of τ. From the results of the CASSFC calculations, it is necessary to consider under-barrier Raman processes.35,42,43 It is possible to reproduce the T dependence of τ considering the Raman process (τ ∝ Tm; m = 5.4 for 1 and 5.3 for 2) (Fig. 6b and c). In addition, we found a linear relationship from the logarithmic representation of τ versus T plot for 1, which suggests that the magnetic relaxation mechanism may be a Raman process (Fig. 6d and e).93 A linear relationship at T < 10 K can be reproduced when m = 5.0–5.8. It has been reported that m can take values from 1 to 6 for Raman processes involving optical-acoustic phonons.94 In addition, the vibrational energy barriers (UR) of 1 and 2 were estimated to be ca. 40 cm−1.19–22 Thus, we are considering measuring the vibrational modes in the terahertz region. The Raman process of Ce3+-based single-ion SMM is summarised in Table 1.30,95
| Complexes | Coordination number and/or pseudo-symmetry | H/Oe | C/s−1 K−m | m/s−1 | Direct | Ref. |
|---|---|---|---|---|---|---|
| TBA[Ce(obPc)] (1) | 8-Coordinate sandwich saddle-shaped distorted D4h or D4d | 250 | 0.009 | 5.4 | — | This work |
| TBA[Ce(Pc)] (2) | 8-Coordinate sandwich D4h | 750 | 0.017 | 5.3 | — | This work |
| [CeCd3(Hquinha)3(n-Bu3PO)2I3]·3EtOH·2H2O | 8-Coordinate hexagonal bipyramidal D6h | 1500 | — | 6.9 | — | 35 |
| [Ce(fdh)3(bpy)] (fdh = 1,1,1-fluoro-5,5-dimethyl-hexa-2,4-dione) | 8-Coordinate paddle-wheel shape | 2000 | 0.4 | 6 | — | 39 |
| [Ce(NO3)3L] (L = tBuPO(NHiPr)2) | 9-Coordinate muffin-like structure | 200 | 1.44 | 6.8 | 99.5 | 40 |
| [Ce0.29La0.71(NO3)3L3] | 30 | 0.8 | 7.55 | 306.5 | 40 | |
| [Ce(18-crown-6) (Cl4Cat) (NO3)] (X4Cat = tetrahalocatecholate) | 10-Coordinate sphenocorona D6h | 1500 | 1.22 | 5 (fixed) | — | 42 |
| [Ce(18-crown-6) (Br4Cat) (NO3)] | 10-Coordinate sphenocorona D6h | 800 | 1.87 | 5 (fixed) | — | 42 |
| [Ce(Cpttt)2{(C6F5-κ1-F)B(C6F5)3}] (Cpttt = C5H2tBu3-1,2,4) | Bent-metallocene structure | 1000 | 0.0308 | 5.4 | — | 43 |
| [Ce(Cpttt)2(Cl)] | Bent-metallocene structure | 1000 | 0.00475 | 6.5 | — | 43 |
From the T and H dependences of τ, 1 and 2 exhibit field-induced SMM characteristics. As reported by Singh et al., it is clear that 1 and 2 do not exhibit magnetic relaxation characteristics without an H.29 In addition, the magnetic relaxation phenomenon of 1 is accompanied by IET with spin-phonon coupling because the ionic radius of the Ce ion changes between 1.14 Å (trivalent) and 0.96 Å (tetravalent). The ionic radius of the Ce ion in Ce(Pc)2 is 1.01 Å, which is intermediate between those for Ce3+ and Ce4+ ions in the 8-coordinate system.63,64 Since the ionic radius obtained from X-ray structure analysis is an averaged value, we performed XAFS, which is effective for separating and observing local structures and electronic states in an element selective manner. In addition, the timescale of IET is slower than the measurement time of XAFS (≈10−17 s). From spectroscopic measurements, the holes generated within the Ce double-decker complex are delocalized across the two ligand systems on both vibrational (10−13 s) and electronic (10−15 s) timescales.96 In other words, this timescale is related to the electron transfer rate between the Ce ion and the Pc ligands. In addition, the timescale of valence fluctuations for Ce4+/3+ ions, which is on the order of 10−13 s, changes with the molecular vibration (phonon frequency (ω)).97 The dynamic disorder with ω in SMMs mainly depends on the intramolecular vibrations. Therefore, we should consider the influence of IET with dynamic disorder and phonon coupling on the magnetic relaxation phenomena in addition to spin-phonon interactions (Fig. 7).98 In this case, since the τ of 1 is nearly twice as slow as that of 2, the influence of IET cannot be ignored.
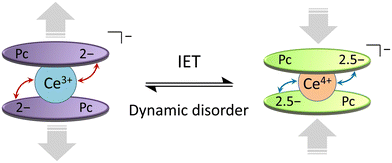 | ||
| Fig. 7 Schematic illustration of the intramolecular electron transfer (IET) in [Ce(obPc)2]− unit of 1 with the dynamic disorder (see main text). | ||
On the other hand, since the Ce⋯Ce distance between molecules is more than 10 Å, we believe that Ce⋯Ce interactions do not influence the magnetic properties of 1 and 2. Therefore, magnetically diluted samples with non-magnetic isostructural complexes were not tested. For Tb3+ and Dy3+ complexes, magnetic dilution is possible with the isostructural Y3+ complex. However, since the structures of 1, 2, and the Y3+ complex are significantly different due to the different ionic radii, magnetic dilution is impossible.64 On the other hand, La3+ ions (4f0: 1.16 Å) have approximately the same ionic radius of Ce3+ ions (4f1: 1.14 Å) and is nonmagnetic, meaning isostructural TBA+[La(obPc)2]− and TBA+[La(Pc)2]− complexes should form. Thus, it should be possible to dilute 1 and 2 magnetically.40 In addition, although structural polymorphism is thought to have little effect on the SMM properties of 1 and 2, we plan to investigate this point in detail with Ce(Pc)2-based complexes in several coordinating environments.
The origin of the uniaxial magnetic anisotropy of 1 and 2 and the magnetic relaxation phenomenon will be discussed in the next section via ab initio calculations (vide infra).
Theoretical studies on the magnetic anisotropy and spin dynamics mechanism
To gain insight into the magnetic structures of [Ce(obPc)2]− for 1 and [Ce(Pc)2]− for 2, CASSCF calculations were performed using the crystal structure coordinates without TBA+. The ground doublet of [Ce(obPc)2]− and [Ce(Pc)2]− was composed of 99.2% and 98.5% of MJ = ±5/2, respectively, confirming the axial magnetic anisotropy (Table S5†). The magnetic easy axis of [Ce(obPc)2]− and [Ce(Pc)2]− coincides with the quasi-C4 axis, which is consistent with the oblate electron density of the Ce3+ ion stabilised by the axial ligand fields of the Pc2− ligands (Fig. S24†). However, the small difference in the composition of MJ = ±5/2 of the ground doublet results in the difference in the gz values of the ground doublet (4.01 for [Ce(obPc)2]− and 3.96 for [Ce(Pc)2]−). The magnitude of the LF splitting for [Ce(obPc)2]− is greater than that for [Ce(Pc)2]− due to the larger axial component of the LFPs (B20 and B40) for [Ce(obPc)2]− (Table S6†). The first excited KDs of [Ce(obPc)2]− and [Ce(Pc)2]− were located at 955 and 921 cm−1, respectively (Fig. S25-1, S25-2, and Table S7†). These energy values are much larger than the Ueff values expected from the experimental ac magnetic measurements (Fig. 6b and c). In other words, the magnetic relaxations via an excited LF level (Orbach process and thermally assisted QTM) do not occur in the relaxation mechanism (see dynamic magnetic properties). The magnetic dipolar transition moment of the ground doublet of [Ce(obPc)2]− (0.151) is smaller than that of [Ce(Pc)2]− (0.202) due to the better axiality of [Ce(obPc)2]− as shown by the larger gz value (Table S5-3†). In other words, the magnetic relaxations driven by a transversal component of the internal magnetic field (QTM) are suppressed for [Ce(obPc)2]− and not for [Ce(Pc)2]−, consistent with the slower τ and small Hτmax values of 1 compared to 2.30 From theoretical investigations on Ce3+-based SMMs reported by Singh et al., D4d/4h geometries are unfavourable for axial magnetic anisotropy.29 However, Ce3+–Pc double-decker complexes shown here have strong axial magnetic anisotropy, although their point group symmetries are classified as D4d/4h. There is no contradiction between our results and previous theoretical investigations because the axial magnetic anisotropy is due to the position of the negative charges on the axis rather than the point group symmetry. In the Ce3+–Pc double-decker complexes, the coordinating N atoms gather in the axial position of the Ce3+ ion due to the small cavity of the Pc2− ligands compared with the Ce3+ ion, enhancing the axial ligand field.Conclusions and perspectives
In this study, we clarified the influence of IET on spin-phonon coupling for magnetic relaxation behaviour.99 We focused on the fact that orbital mixing between Ce ions and π-conjugated planar ligands causes the IET and selected Ce–Pc-based double-decker compounds for this work.We investigated the chemical conversion of the diamagnetic Ce4+ forms (4f0) Ce(obPc)2 and Ce(Pc)2 into the paramagnetic Ce3+ forms (4f1) 1 and 2, both of which exhibit field-induced SMM behaviour. In particular, the Ce ion in 1 undergoes the mixed valence states of Ce4+/Ce3+via IET between the Ce ion and the Pc ligands. On the other hand, the valence state of the Ce ion in 2 is trivalent without IET. The valence states of the Ce ion in each compound are reflected in the magnetic properties. Since the magnetic relaxation time (τ) of 1 is nearly twice as slow as that of 2, the dynamic disorder is expected due to the mixed valence states of Ce4+/Ce3+. From the magnetic field dependence of the spin dynamics, the appropriate magnetic field of 1 with IET is 250 Oe, which is smaller than that of 2 (750 Oe) without IET. If the magnetic field can be reduced by controlling the IET, it should be possible to prepare Ce-based SMMs without an external magnetic field.
The Ce4+/Ce3+ mixed valence states due to IET can be controlled by changing the type of electron-donating groups and controlling the orbital mixing between the Ce ion and the ligands. In other words, it would be possible to control the valence state of the Ce ions by separating the frontier orbitals of the Pc ligands from the 4f1 orbital of the Ce3+ ion.48 The above concepts apply not only to the mononuclear Ce–Pc double-decker complexes but also to dinuclear Ce–Pc multiple-decker complexes.47,69 For example, an advantage of dinuclear Ce complexes is that the valence state of each Ce ion can be changed separately by changing the number of porphyrinoids ligands inserted between the Ce ions.99 In addition, we have synthesised Ce–Pc multiple-decker complexes with up to seven layers of Pc ligands with four Cd2+ ions in between the Ce ions (quadruple- to septuple-decker complexes).100,101 The modulation of the spin dynamics via supramolecular chemistry holds promise for realizing Ce SMMs. Furthermore, proton switching,102 dimerization,103–105 fullerene co-crystals,106 and one-dimensional expansion approaches10,107 by regulating the coordination geometries and intermolecular interactions are conceivable.108 The spin dynamics of a Ce ion can be altered by adjusting the interactions between conduction electrons (holes) due to molecular orbital overlap53 and the interactions between frontier orbitals and Ce f orbitals induced by the distortions of the π-conjugated porphyrinoids with electron-donating substituents.
In addition, we will use these Ce complexes to investigate the control of the spin dynamics due to IET. The Ce(Pc)2 system exhibits a distinctive feature wherein IET occurs between the Ce ion and Pc ligands, thus manifesting its intricate electronic configuration. In contrast, mixed valence states have been documented for numerous metal complexes and inorganic compounds. To the best of our knowledge, instances of IET occurring between other Ln ions and Pc ligands have not been reported. However, the electron transfer between Ln ions and radical ligands significantly influences the magnetic properties.109–112 In other words, diverse valence states owing to electron transfer between Ln ions and ligands are possible. Thus, Ln ion-based SMMs exhibiting mixed valence states can be synthesised through judicious molecular design. Furthermore, this paper was centred on the investigation of the IET phenomenon in its reduced form [Ce(obPc)2]−. However, from the analysis of the electronic spectra, in solution, cationic [Ce(obPc)2]+ forms through the one-electron oxidation of 1, whereas a radical species concurrently forms on the Pc ligands. Our ongoing research endeavours will further explore the intricacies of electron transfer dynamics between Ce4+ and Pc˙− ligands, extending our inquiry into solid state environments. By applying IET to the spin dynamics of Ce porphyrinoid-based complexes, it will be possible to investigate the effects of dynamic disorder on SMM properties.
Author contributions
K. K. designed the study and the main conceptual ideas and supervised the project. K. K., M. S., T. S. Y. H., T. Y., and K. K. collected and analysed the data. All authors aided in interpreting the results and prepared the manuscript. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by a Grant-in-Aid for Scientific Research (C) (grant no. 21K05010, no. 15K05467), Grant-in-Aid for Young Scientists (B) (grant no. 24750119), Grant-in-Aid for Scientific Research (S) (grant no. 20225003) from JSPS KAKENHI, CREST (JPMJCR12L3) from JST. The X-ray absorption fine structure was collected on the BL9A beamline in the Photon Factory of the High Energy Accelerator Research Organization (KEK, proposal no. 2017P016, 2019G117). Y. H. acknowledges Prof. Takashi Kajiwara (Nara Women's University) for computational resources and PXRD measurements.References
- L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186 CrossRef CAS PubMed
.
- M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793 CrossRef CAS PubMed
.
- J. Tejada, E. M. Chudnovsky, E. del Barco, J. M. Hernandez and T. P. Spiller, Nanotechnology, 2001, 12, 181–186 CrossRef CAS
.
-
D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006 Search PubMed
.
- C. J. Wedge, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. Mcinnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204-1–107204-5 CrossRef PubMed
.
- G. Aromí, D. Aguilà, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537–546 RSC
.
- W. Wernsdorfer, N. Aliaga-Alcalde, D. N. Hendrickson and G. Christou, Nature, 2002, 416, 406–409 CrossRef PubMed
.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542 CrossRef CAS PubMed
.
- F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449 CrossRef CAS PubMed
.
- K. Katoh, S. Yamashita, N. Yasuda, Y. Kitagawa, B. K. Breedlove, Y. Nakazawa and M. Yamashita, Angew. Chem., Int. Ed., 2018, 57, 9262–9267 CrossRef CAS PubMed
.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed
.
- F. Habib and M. Murugesu, Chem. Soc. Rev., 2013, 42, 3278–3288 RSC
.
- H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1–33 CrossRef CAS
.
- S. T. Liddle and J. Van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC
.
- P. Zhang, Y. N. Guo and J. Tang, Coord. Chem. Rev., 2013, 257, 1728–1763 CrossRef CAS
.
- J. L. Liu, Y. C. Chen and M. L. Tong, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC
.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC
.
- C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E. S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202 CrossRef CAS PubMed
.
- A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nat. Commun., 2017, 8, 14620 CrossRef PubMed
.
- L. Gu and R. Wu, Phys. Rev. Lett., 2020, 125, 117203-1–117203-6 CrossRef PubMed
.
- Y. Ma, Y. Zhai, Q. Luo, Y. Ding and Y. Zheng, Angew. Chemie Int. Ed., 2022, 61, e202206022 CrossRef CAS PubMed
.
- L. Scherthan, R. F. Pfleger, H. Auerbach, T. Hochdörffer, J. A. Wolny, W. Bi, J. Zhao, M. Y. Hu, E. E. Alp, C. E. Anson, R. Diller, A. K. Powell and V. Schünemann, Angew. Chem., Int. Ed., 2020, 59, 8818–8822 CrossRef CAS PubMed
.
- K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952–17957 CrossRef CAS PubMed
.
- S. Hino, M. Maeda, K. Yamashita, Y. Kataoka, M. Nakano, T. Yamamura, H. Nojiri, M. Kofu, O. Yamamuro and T. Kajiwara, Dalton Trans., 2013, 42, 2683–2686 RSC
.
- J. J. Le Roy, I. Korobkov, J. E. Kim, E. J. Schelter and M. Murugesu, Dalton Trans., 2014, 43, 2737–2740 RSC
.
- S. Hino, M. Maeda, Y. Kataoka, M. Nakano, T. Yamamura and T. Kajiwara, Chem. Lett., 2013, 42, 1276–1278 CrossRef CAS
.
- C. Takehara, P. L. Then, Y. Kataoka, M. Nakano, T. Yamamura and T. Kajiwara, Dalton Trans., 2015, 44, 18276–18283 RSC
.
- T. Shi, Y. Xu, M.-X. Li, C.-M. Liu, E. N. Nfor and Z.-X. Wang, Polyhedron, 2020, 188, 114695 CrossRef CAS
.
- S. K. Singh, T. Gupta, L. Ungur and G. Rajaraman, Chem. – Eur. J., 2015, 21, 13812–13819 CrossRef CAS PubMed
.
- F. A. Mautner, F. Bierbaumer, R. C. Fischer, À. Tubau, S. Speed, E. Ruiz, S. S. Massoud, R. Vicente and S. Gómez-Coca, Inorg. Chem., 2022, 61, 11124–11136 CrossRef CAS PubMed
.
- E. Regincós Martí, A. B. Canaj, T. Sharma, A. Celmina, C. Wilson, G. Rajaraman and M. Murrie, Inorg. Chem., 2022, 61, 9906–9917 CrossRef PubMed
.
- J. Mayans, L. Tesi, M. Briganti, M. E. Boulon, M. Font-Bardia, A. Escuer and L. Sorace, Inorg. Chem., 2021, 60, 8692–8703 CrossRef CAS PubMed
.
- C. Takehara, P. L. Then, Y. Kataoka, M. Nakano, T. Yamamura and T. Kajiwara, Dalton Trans., 2015, 44, 18276–18283 RSC
.
- A. Ben Khélifa, M. S. Belkhiria, G. Huang, S. Freslon, O. Guillou and K. Bernot, Dalton Trans., 2015, 44, 16458–16464 RSC
.
- Q.-W. Li, R.-C. Wan, Y.-C. Chen, J.-L. Liu, L.-F. Wang, J.-H. Jia, N. F. Chilton and M.-L. Tong, Chem. Commun., 2016, 52, 13365–13368 RSC
.
- H. Wada, S. Ooka, T. Yamamura and T. Kajiwara, Inorg. Chem., 2017, 56, 147–155 CrossRef CAS PubMed
.
- C. P. Burns, X. Yang, S. Sung, J. D. Wofford, N. S. Bhuvanesh, M. B. Hall and M. Nippe, Chem. Commun., 2018, 54, 10893–10896 RSC
.
- A. Upadhyay, K. R. Vignesh, C. Das, S. K. Singh, G. Rajaraman and M. Shanmugam, Inorg. Chem., 2017, 56, 14260–14276 CrossRef CAS PubMed
.
- M. X. Xu, Y. S. Meng, J. Xiong, B. W. Wang, S. Da Jiang and S. Gao, Dalton Trans., 2018, 47, 1966–1971 RSC
.
- S. K. Gupta, S. Shanmugan, T. Rajeshkumar, A. Borah, M. Damjanović, M. Schulze, W. Wernsdorfer, G. Rajaraman and R. Murugavel, Dalton Trans., 2019, 48, 15928–15935 RSC
.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed
.
- E. Rousset, M. Piccardo, M. E. Boulon, R. W. Gable, A. Soncini, L. Sorace and C. Boskovic, Chem. – Eur. J., 2018, 24, 14768–14785 CrossRef CAS PubMed
.
- J. Liu, D. Reta, J. A. Cleghorn, Y. X. Yeoh, F. Ortu, C. A. P. Goodwin, N. F. Chilton and D. P. Mills, Chem. – Eur. J., 2019, 25, 7749–7758 CrossRef CAS PubMed
.
- E. Moreno-Pineda, M. Damjanović, O. Fuhr, W. Wernsdorfer and M. Ruben, Angew. Chem., Int. Ed., 2017, 56, 9915–9919 CrossRef CAS PubMed
.
- A. L. Wysocki and K. Park, J. Phys.: Condens. Matter, 2020, 32, 274002 CrossRef CAS PubMed
.
- N. M. Edelstein, P. G. Allen, J. J. Bucher, D. K. Shuh, C. D. Sofield, N. Kaltsoyannis, G. H. Maunder, M. R. Russo and A. Sella, J. Am. Chem. Soc., 1996, 118, 13115–13116 CrossRef CAS
.
- T. H. Tran-Thi, T. A. Mattioli, D. Chabach, A. D. Cian and R. Weiss, J. Phys. Chem., 1994, 98, 8279–8288 CrossRef CAS
.
- Y. Bian, J. Jiang, Y. Tao, M. T. M. Choi, R. Li, A. C. H. Ng, P. Zhu, N. Pan, X. Sun, D. P. Arnold, Z. Y. Zhou, H. W. Li, T. C. W. Mak and D. K. P. Ng, J. Am. Chem. Soc., 2003, 125, 12257–12267 CrossRef CAS PubMed
.
- H. Isago, J. Porphyrins Phthalocyanines, 2014, 18, 762–770 CrossRef CAS
.
- M. D. Walter, C. H. Booth, W. W. Lukens and R. A. Andersen, Organometallics, 2009, 28, 698–707 CrossRef CAS
.
- K. Takahashi, M. Itoh, Y. Tomita, K. Nojima, K. Kasuga and K. Isa, Chem. Lett., 1993, 22, 1915–1918 CrossRef
.
- H. Hückstädt, A. Tutaß, M. Göldner, U. Cornelissen and H. Homborg, Z. Anorg. Allg. Chem., 2001, 627, 485–497 CrossRef
.
- I. Saiful, M. I. Hossain, K. Katoh, M. Yamashita, R. Arafune, S. M. Fakruddin Shahed and T. Komeda, J. Phys. Chem. C, 2022, 126, 17152–17163 CrossRef CAS
.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed
.
- A. Bianconi, A. Marcelli, H. Dexpert, R. Karnatak, A. Kotani, T. Jo and J. Petiau, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 806–812 CrossRef CAS PubMed
.
- J. El Fallah, S. Boujana, H. Dexpert, A. Kiennemann, J. Majerus, O. Touret, F. Villain and F. Le Normand, J. Phys. Chem., 1994, 98, 5522–5533 CrossRef CAS
.
- F. Neese, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS
.
- D. Aravena, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2016, 12, 1148–1156 CrossRef CAS PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- P. J. Stephen, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef
.
- H. Isago and M. Shimoda, Chem. Lett., 1992, 147–150 CrossRef CAS
.
- R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, A32, 751–767 CrossRef CAS
.
- G. Ostendorp, H. W. Rotter and H. Homborg, Z. fur Naturforsch. – B J. Chem. Sci., 1996, 51, 567–573 CrossRef CAS
.
- J. W. Buchler and M. Nawra, Inorg. Chem., 1994, 33, 2830–2837 CrossRef CAS
.
- J. K. Duchowski and D. F. Bocian, J. Am. Chem. Soc., 1990, 112, 8807–8811 CrossRef CAS
.
- M. Safarpour Haghighi, C. L. Teske and H. Homborg, Z. Anorg. Allg. Chem., 1992, 608, 373–380 Search PubMed
.
- J. W. Buchler, M. Kihn-Botulinski, A. de Cian, J. Fischer, R. Weiss and H. Paulus, J. Am. Chem. Soc., 1986, 108, 3652–3659 CrossRef CAS
.
- S. Fortier, J. J. Le Roy, C.-H. Chen, V. Vieru, M. Murugesu, L. F. Chibotaru, D. J. Mindiola and K. G. Caulton, J. Am. Chem. Soc., 2013, 135, 14670–14678 CrossRef CAS PubMed
.
- A. I. Gaudette, I.-R. Jeon, J. S. Anderson, F. Grandjean, G. J. Long and T. D. Harris, J. Am. Chem. Soc., 2015, 137, 12617–12626 CrossRef CAS PubMed
.
- J. Tong, S. Demeshko, M. John, S. Dechert and F. Meyer, Inorg. Chem., 2016, 55, 4362–4372 CrossRef CAS PubMed
.
- B. S. Dolinar, S. Gómez-Coca, D. I. Alexandropoulos and K. R. Dunbar, Chem. Commun., 2017, 53, 2283–2286 RSC
.
- X. Zhu, S. Su, W. Cao, Y. Wen, S. Hu, X. Wu and T. Sheng, Dalton Trans., 2017, 46, 7267–7272 RSC
.
- G. N. Newton, S. Yamashita, K. Hasumi, J. Matsuno, N. Yoshida, M. Nihei, T. Shiga, M. Nakano, H. Nojiri, W. Wernsdorfer and H. Oshio, Angew. Chem., Int. Ed., 2011, 50, 5716–5720 CrossRef CAS PubMed
.
- N. Ishikawa, M. Sugita, N. Tanaka, T. Ishikawa, S. Y. Koshihara and Y. Kaizu, Inorg. Chem., 2004, 43, 5498–5500 CrossRef CAS PubMed
.
- M. Gonidec, E. S. Davies, J. Mcmaster and D. B. Amabilino, J. Am. Chem. Soc., 2010, 1756–1757 CrossRef CAS PubMed
.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239 CrossRef CAS PubMed
.
- D. E. Freedman, D. M. Jenkins, A. T. Iavarone and J. R. Long, J. Am. Chem. Soc., 2008, 130, 2884–2885 CrossRef CAS PubMed
.
- L. Norel, M. Feng, K. Bernot, T. Roisnel, T. Guizouarn, K. Costuas and S. Rigaut, Inorg. Chem., 2014, 53, 2361–2363 CrossRef CAS PubMed
.
- C. M. Dickie, A. L. Laughlin, J. D. Wofford, N. S. Bhuvanesh and M. Nippe, Chem. Sci., 2017, 8, 8039–8049 RSC
.
- A. Nava, L. Rigamonti, E. Zangrando, R. Sessoli, W. Wernsdorfer and A. Cornia, Angew. Chem., Int. Ed., 2015, 54, 8777–8782 CrossRef CAS PubMed
.
- I.-R. Jeon, J. G. Park, D. J. Xiao and T. D. Harris, J. Am. Chem. Soc., 2013, 135, 16845–16848 CrossRef CAS PubMed
.
- E. N. Tarakanova, O. A. Levitskiy, T. V. Magdesieva, P. A. Tarakanov, V. E. Pushkarev and L. G. Tomilova, New J. Chem., 2015, 39, 5797–5804 RSC
.
- F. Lu, M. Bao, C. Ma, X. Zhang, D. P. Arnold and J. Jiang, Spectrochim. Acta, Part A, 2003, 59, 3273–3286 CrossRef PubMed
.
- S. L. Selektor, A. V. Shokurov, V. V. Arslanov, Y. G. Gorbunova, K. P. Birin, O. A. Raitman, F. Morote, T. Cohen-Bouhacina, C. Grauby-Heywang and A. Y. Tsivadze, J. Phys. Chem. C, 2014, 118, 4250–4258 CrossRef CAS
.
- J. Granet, M. Sicot, B. Kierren, S. Lamare, F. Chérioux, F. Baudelet, Y. Fagot-Revurat, L. Moreau and D. Malterre, Nanoscale, 2018, 10, 9123–9132 RSC
.
- J. F. Herbst and J. W. Wilkins, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 1689–1701 CrossRef CAS
.
- W. Li, S. Yamada, T. Hashimoto, T. Okumura, R. Hayakawa, K. Nitta, O. Sekizawa, H. Suga, T. Uruga, Y. Ichinohe, T. Sato, Y. Toyama, H. Noda, T. Isobe, S. Takatori, T. Hiraki, H. Tatsuno, N. Kominato, M. Ito, Y. Sakai, H. Omamiuda, A. Yamaguchi, T. Yomogida, H. Miura, M. Nagasawa, S. Okada and Y. Takahashi, Anal. Chim. Acta, 2023, 1240, 340755 CrossRef CAS PubMed
.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed
.
- K. Katoh, B. K. Breedlove and M. Yamashita, Chem. Sci., 2016, 7, 4329–4340 RSC
.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, I, 341–351 CrossRef
.
-
A. Abragam and B. Bleaney, Electron paramagnetic resonance of transition ions, Oxford University Press, 2012 Search PubMed
.
- A. Singh and K. N. Shrivastava, Phys. Status Solidi, 1979, 95, 273–277 CrossRef CAS
.
- A. Borah and R. Murugavel, Coord. Chem. Rev., 2022, 453, 214288 CrossRef CAS
.
- J. K. Duchowski and D. F. Bocian, J. Am. Chem. Soc., 1990, 112, 3312–3318 CrossRef CAS
.
- G. Liang, M. Croft, D. C. Johnston, N. Anbalagan and T. Mihalisin, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 5302–5309 CrossRef CAS PubMed
.
- H. A. Mook and R. M. Nicklow, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 1656–1662 CrossRef CAS
.
- The concept shown here was reported in the Grants-in-Aid for Scientific Research (C) (No. 21K05010) project in 2021. Principal Investigator: Dr Keiichi Katoh, Title: High-speed control of the magnetisation of single-molecule magnets via fluctuation of the valence state of rare earth elements. https://kaken.nii.ac.jp/grant/KAKENHI-PROJECT-21K05010/.
- Y. Horii, M. Damjanović, M. R. Ajayakumar, K. Katoh, Y. Kitagawa, L. Chibotaru, L. Ungur, M. Mas-Torrent, W. Wernsdorfer, B. K. Breedlove, M. Enders, J. Veciana and M. Yamashita, Chem. – Eur. J., 2020, 26, 8621–8630 CrossRef CAS PubMed
.
-
K. Kobayashi, Single-molecule magnet properties of light rare earth Ce(III) phthalocyaninato multiple-decker complexes, M.Sc. Dissertation, Tohoku university, Japan, 2016 Search PubMed
.
- Y. Horii, Y. Horie, K. Katoh, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2018, 2, 565–574 CrossRef PubMed
.
- Y. Horii, K. Katoh, B. K. Breedlove and M. Yamashita, Chem. Commun., 2017, 53, 8561–8564 RSC
.
- T. Morita, M. Damjanović, K. Katoh, Y. Kitagawa, N. Yasuda, Y. Lan, W. Wernsdorfer, B. K. Breedlove, M. Enders and M. Yamashita, J. Am. Chem. Soc., 2018, 140, 2995–3007 CrossRef CAS PubMed
.
- Y. Horii, S. Kishiue, M. Damjanović, K. Katoh, B. K. Breedlove, M. Enders and M. Yamashita, Chem. – Eur. J., 2018, 4320–4327 CrossRef CAS PubMed
.
- K. Katoh, N. Yasuda, M. Damjanović, W. Wernsdorfer, B. K. Breedlove and M. Yamashita, Chem. – Eur. J., 2020, 26, 4805–4815 CrossRef CAS PubMed
.
- T. Sato, B. K. Breedlove, M. Yamashita and K. Katoh, Angew. Chem., Int. Ed., 2021, 60, 21179–21183 CrossRef CAS PubMed
.
- A. G. Martynov, Y. Horii, K. Katoh, Y. Bian, J. Jiang, M. Yamashita and Y. G. Gorbunova, Chem. Soc. Rev., 2022, 51, 9262–9339 RSC
.
- A. A. Trifonov, I. A. Borovkov, E. A. Fedorova, G. K. Fukin, J. Larionova, N. O. Druzhkov and V. K. Cherkasov, Chem. – Eur. J., 2007, 13, 4981–4987 CrossRef CAS PubMed
.
- I. L. Fedushkin, O. V. Maslova, A. G. Morozov, S. Dechert, S. Demeshko and F. Meyer, Angew. Chem., Int. Ed., 2012, 51, 10584–10587 CrossRef CAS PubMed
.
- M. A. Hay and C. Boskovic, Chem. – Eur. J., 2021, 27, 3608–3637 CrossRef CAS PubMed
.
- M. A. Dunstan, A. S. Manvell, N. J. Yutronkie, F. Aribot, J. Bendix, A. Rogalev and K. S. Pedersen, Nat. Chem., 2024, 2, 1–8 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2332889 for Ce(obPc)2 and 2332908 for 1. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt00436a |
| This journal is © The Royal Society of Chemistry 2024 |