First-principles-based microkinetic modeling of methanol steam reforming over Cu(111) and Cu(211): structure sensitive activity and selectivity†
Xinyi
Zhang
and
Bo
Yang
 *
*
School of Physical Science and Technology, ShanghaiTech University, 393 Middle Huaxia Road, Shanghai 201210, China. E-mail: yangbo1@shanghaitech.edu.cn
First published on 24th September 2024
Abstract
The development of hydrogen energy is widely recognized as a key approach to addressing the energy and carbon emission challenges. Methanol steam reforming is a promising hydrogen production scheme that can provide high-purity hydrogen. In this work, we studied the primary reaction mechanisms of methanol steam reforming over the Cu(111) and Cu(211) surfaces using density functional theory (DFT) calculations and microkinetic simulations. A detailed kinetic perspective on the reaction mechanism, which is often overlooked in previous research that relies solely on DFT calculations, is provided in the current work. Our findings reveal that under typical experimental conditions, the dominant mechanism on the Cu(111) surface is the methyl formate mechanism, while the H2COO dehydrogenation mechanism is dominant on Cu(211). The activity over the Cu(111) surface was slightly higher than that over Cu(211). Based on the degree of rate control analysis results, a reaction rate equation was derived to quantitatively explain the trend of activity under different operating conditions. It was also found that CO2 selectivity was significantly higher over Cu(211) than over the Cu(111) surface. Furthermore, based on the Wulff construction scheme, copper nanoparticle models with different sizes were constructed, and a detailed structure sensitivity study was executed. This comprehensive investigation sheds light on the mechanisms of methanol steam reforming reactions over the Cu(111) and Cu(211) surfaces, providing essential insights for the design of high-performance catalysts for hydrogen production.
1. Introduction
As the urgency of the energy crisis intensifies and environmental pollution worsens, the search for novel energy sources is more pressing than ever.1–3 Hydrogen, a high-energy-density, clean and renewable secondary energy source, is widely regarded as a crucial alternative to fossil fuels.4–6 It can be produced through various methods, including methane steam reforming, coal gasification, electrolysis of water, and biological methods.7 However, the first two methods still rely on fossil fuel as raw material, and the third method requires substantial energy input.8 Therefore, exploring a new approach to produce hydrogen with high efficiency and minimal pollution is of the utmost importance.Methanol serves as an ideal substrate for producing hydrogen due to its simple molecular structure and easy accessibility.9 It can be derived from various renewable sources. For instance, it can be produced through the pyrolysis of biomass, which includes components such as cellulose, hemicelluloses, and lignin,10 or through the thermal gasification of biomass.11 There are three primary methods to produce hydrogen with methanol, i.e., (1) methanol decomposition, (2) oxidative methanol steam reforming, and (3) methanol steam reforming:
| CH3OH → CO + 2H2 | (1) |
| CH3OH + ½O2 → CO2 + 2H2 | (2) |
| CH3OH + H2O → CO2 + 3H2 | (3) |
Among the three methods mentioned above, methanol steam reforming (MSR) holds promise for producing hydrogen due to its high yield of H2 and significant selectivity towards CO2.12 This selectivity towards CO2 is crucial for further hydrogen utilization,13 because even minuscule amounts of carbon monoxide (CO) can be harmful under many circumstances, necessitating an exceptionally pure and CO-free hydrogen source.
In order to design new catalysts that enhance the activity of MSR and increase selectivity towards CO2, it is essential to understand the detailed reaction mechanism. Cu-based catalysts are predominantly used for MSR due to their high activity and selectivity.14 The current mainstream view proposes three mechanisms for MSR over Cu, with the first step in each mechanism being the dehydrogenation of methanol to form methoxy.12,14 One of the three mechanisms is the water gas shift (WGS) mechanism.15–17 This mechanism involves the decomposition of methanol to CO, which further reacts with water vapor to yield CO2. However, studies have shown that CO cannot react with water vapor in the presence of methanol, despite the WGS reaction being highly active on Cu-based catalysts.18
An alternative mechanism was proposed by Takezawa, which involves formaldehyde reacting with hydroxyl or oxygen adsorbed on the catalyst surface to produce intermediates such as HCOOH, HCOO, and H2COO.19 These species are further dehydrogenated and eventually converted to CO2 and H2. This mechanism is referred to as the H2COO dehydrogenation mechanism.
Takezawa also proposed the methyl formate mechanism suggesting that formaldehyde reacts with methoxy to form methyl formate, which is then hydrolyzed and dehydrogenated to form CO2.20 Jiang21 and Peppley22 established a kinetic model based on this mechanism, and their results were highly consistent with experimental data, indicating that the methyl formate mechanism is likely responsible for MSR. However, methyl formate is generally produced at a lower proportion of water vapor and cannot be detected in the gas phase or on the surface of the catalyst under MSR conditions.23 Although it has been demonstrated that the rate of methyl formate hydrolysis to CO2 is approximately 30 times faster than that of the overall MSR reaction, which implies that the absence of methyl formate may be due to its hydrolysis occurring too rapidly to be observed, the fact that methyl formate is not directly observed in experiments still raises questions about the authenticity of this proposed mechanism.20
Despite extensive research on the mechanism of MSR over Cu, this topic remains contentious. Given the inherent challenges in experimentally elucidating the actual reaction mechanism of MSR, computational simulation methods, such as first-principles calculations, have become vital in providing complementary and often more detailed information about the reaction mechanism.
Regarding the methyl formate mechanism, the work of Lin et al.24 calculated the energy of each intermediate and transition state involved in this mechanism on the Cu(111) surface and found that the methyl formate mechanism is energetically favored. This process was shown to have a lower effective activation energy than the overall MSR reaction, which is consistent with the experimental observation that the steam reforming of methyl formate is faster than the MSR reaction. Lin et al. also found that the hydrolysis process of methyl formate may not be able to effectively compete with the desorption of methyl formate. Therefore, they concluded that the methyl formate route is not a competitive mechanism on the Cu(111) surface. While their study focused primarily on the energetics over the Cu(111) surface, the exact reaction mechanism over different facets of the copper catalyst and the identification of the most active facet still remain unknown. Thus, it would be valuable to compare their results with a comprehensive microkinetic study over both the Cu(111) and Cu(211) facets.
In the present study, a comprehensive analysis was conducted. We employed density functional theory (DFT) calculations to determine the energies of surface species on the Cu(111) and Cu(211) facets, based on the establishment of a complex reaction network. Furthermore, detailed microkinetic analysis was also performed to gain deeper insights into the reaction system. The dominant reaction pathway under each set of reaction conditions was determined from the reaction network under different operating conditions. The activity of the MSR reaction, CO2 selectivity, and the detailed reaction mechanisms were also systematically studied and compared on both the Cu(111) and Cu(211) surfaces.
2. Methods
2.1 DFT calculations
All the DFT calculations performed in this study were carried out using the Vienna Ab initio Simulation Package (VASP.5.4) and the projector augmented wave (PAW) method.25–27 The Bayesian error estimation functional with van der Waals correlation (BEEF-vdW) exchange–correlation functional was employed,28 which can account for long-range dispersion forces and has been widely used in the simulation of surface catalytic reactions.29–37 The plane-wave basis set had a cutoff energy of 500 eV, and the convergence criteria were set to 1 × 10−4 eV for energy and 0.05 eV Å−1 for the force on each relaxed atom. The 3 × 3 Cu(111) slab model consisted of 5 atomic layers, with the atoms in the top 2 layers allowed to relax during the optimization process. For the 3 × 4 Cu(211) slab model, there were 12 atomic layers, and the atoms in the top 3 layers were allowed to relax during the optimization. The Brillouin zone was sampled using a 4 × 4 × 1 Monkhorst–Pack k-point grid with Methfessel-Paxton smearing of 0.1 eV for the Cu(111) surface,38 and a 4 × 2 × 1 k-point grid for the Cu(211) surface.The transition states were determined using the constrained minimization method.39,40 This approach allows for the identification of a transition state when the force on the relaxed atom diminishes and the energy is maximized along the reaction coordinate but minimized with respect to all remaining degrees of freedom. The constrained minimization method has been developed for more than twenty years and is widely used by many groups and verified by frequency calculations.41–44 All transition states were verified by vibrational frequency analysis, and the obtained vibrational frequencies were also used to calculate the associated free energies. The adsorption enthalpy of CO over Cu(111) calculated by DFT data is −0.656 eV. According to the adsorption energy measured experimentally (−0.549 eV),45 the gas-phase energy of molecular CO was corrected by −0.107 eV. The reaction free energy of methanol steam reforming calculated by CatMAP under 298 K temperature and standard pressure is −0.3177 eV. The energy of gaseous CO2 was corrected by 0.278 eV to align with the experimental value46 (−0.0397 eV) of the Gibbs free energy of reaction for the methanol steam reforming reaction.
2.2 Microkinetic modeling
The reaction kinetics of the MSR process were analyzed using the CatMAP package developed by Nørskov's group.47 This Python-based simulation package applies the mean-field approximation to obtain the kinetic results of surface catalytic reactions. According to the experimental conditions, simulations were performed at 5% CH3OH conversion, with a temperature range of 498–598 K and a total pressure of 1 bar. The steam-to-methanol partial pressure ratios (S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M) were set to 1
M) were set to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and 1
3, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 to investigate the variation of the reaction mechanism under different S
4 to investigate the variation of the reaction mechanism under different S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios. In this study, the variation in the S
M ratios. In this study, the variation in the S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratio was achieved by altering the partial pressure of water vapor, while keeping the partial pressure of methanol constant at 0.15 bar, the remaining composition was inert gas. The partial pressure of the inert gas was adjusted to compensate for the varying partial pressure of water vapor, ensuring that the sum of the partial pressures of all gaseous species remains constant. The free energies of the surface species and transition states were calculated using the following equation:
M ratio was achieved by altering the partial pressure of water vapor, while keeping the partial pressure of methanol constant at 0.15 bar, the remaining composition was inert gas. The partial pressure of the inert gas was adjusted to compensate for the varying partial pressure of water vapor, ensuring that the sum of the partial pressures of all gaseous species remains constant. The free energies of the surface species and transition states were calculated using the following equation: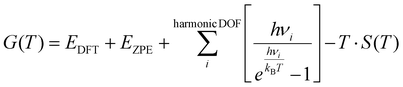 | (4) |
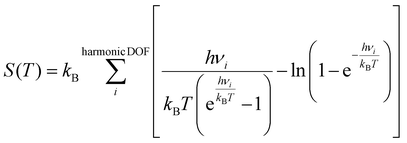 | (5) |
The free energies of the gaseous species were determined by the equation:
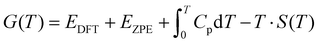 | (6) |
The degree of rate control (DRC) analysis method developed by the Campbell group49,50 was also employed in this study. The DRC value quantifies the effect of changing the free energy of a surface intermediate or transition state on the overall reaction rate. Specifically, the DRC value Xi for the considered intermediate or transition state i can be obtained using the following equation:
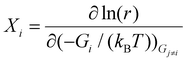 | (7) |
3. Results and discussion
3.1 Reaction network of the MSR process
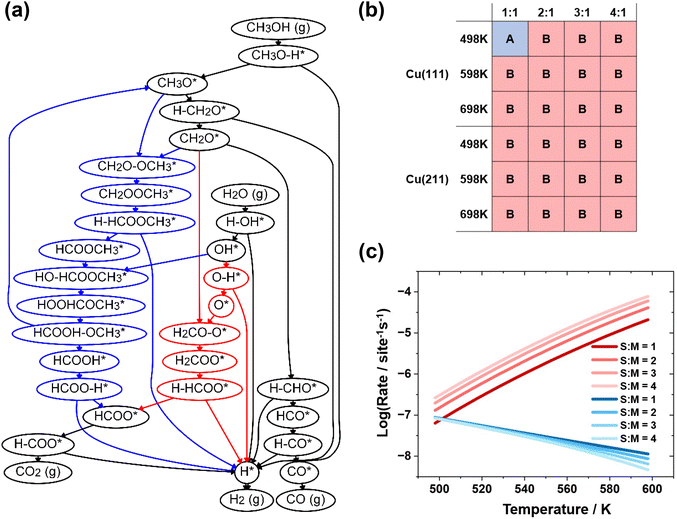
In the present study, a complex reaction network was established, consisting of 24 surface intermediates, 51 transition states, 5 gaseous species, and 54 elementary steps. A full reaction network containing all surface species can be found in the ESI.† We found that the reaction network includes most of the intermediates considered in previously published theoretical works,24,51–55 including intermediates and transition states for the methyl formate pathway, the H2COO dehydrogenation pathway, and the water–gas shift pathway. The energies of all possible reaction intermediates and transition states involved in the networks were calculated for further analysis, and the activation free energies and reaction free energies for each elementary step are listed in the ESI as Table S1.†3.2 Dominant reaction pathways for MSR
Microkinetic simulations were conducted using the established reaction network on the Cu(111) and Cu(211) surfaces at the temperatures and pressures employed in experiments, specifically 498 to 598 K and 1 bar. The dominant reaction pathways were identified under these conditions through running the microkinetic simulations and removing the elementary steps with the lowest reaction rates iteratively, as introduced in our previous work.56 In this previous work, a systematic description of the algorithm for reaction network generation and pruning was provided, using the concept also proposed by our group.57 The dominant reaction pathways for MSR are merged into a pruned reaction network shown in Fig. 1(a), where the elementary steps and surface species unique to pathways A and B are shown in blue and red, respectively. Fig. 1(b) presents the dominant reaction pathway under different conditions over the Cu(211) and Cu(111) surfaces. The reaction energies and activation energy for the elementary steps involved in the dominant pathways are provided in Table 1. The configurations for the intermediates and transition states in the elementary steps are presented in the ESI as Fig. S1.†| Elementary steps | Cu(111) | Cu(211) | ||
|---|---|---|---|---|
| E a/eV | ΔE/eV | E a/eV | ΔE/eV | |
| 2* + CH3OH(g) → CH3O* + H* | 1.03 | −0.31 | 1.03 | −0.36 |
| H2O(g) + 2* → OH* + H* | 1.20 | −0.17 | 1.14 | −0.35 |
| OH* + * → O* + H* | 1.82 | 0.63 | 1.76 | 0.94 |
| CH3O* + * → H* + CH2O* | 1.42 | 0.99 | 1.28 | 1.10 |
| CH2O* + O* → H2COO* + * | −0.15 | −0.66 | 0.04 | −0.99 |
| H2COO* + * → HCOO* + H* | 0.89 | −0.79 | 0.96 | −0.73 |
| HCOOH* + * → HCOO* + H* | 0.71 | −0.39 | 0.69 | −0.66 |
| HCOO* + * → CO2(g) + H* + * | 1.19 | 0.70 | 1.52 | 1.14 |
| CH2O* + * → HCO* + H* | 0.96 | 0.38 | 1.00 | 0.28 |
| HCO* + * → CO* + H* | 0.31 | −0.75 | 0.38 | −0.42 |
| CH2O* + CH3O* → CH2OOCH3* + * | 0.24 | −0.43 | 0.10 | −0.57 |
| CH2OOCH3* + * → HCOOCH3* + H* | 1.01 | 0.02 | 1.17 | 0.32 |
| HCOOCH3* + OH* → HOOHCOCH3* + * | 0.56 | 0.27 | 0.70 | 0.23 |
| HOOHCOCH3* + * → HCOOH* + CH3O* | 0.37 | −0.29 | 0.38 | −0.10 |
| H* + H* → H2(g) + 2* | 0.96 | 0.27 | 0.95 | 0.15 |
| CO* → CO(g) + * | — | 0.55 | — | 0.50 |
Analysis of the pruned reaction network shown in Fig. 1(a) reveals that pathway A is consistent with the methyl formate mechanism proposed by Takezawa,20 while pathway B resembles the H2COO dehydrogenation mechanism. Our results indicate that the methyl formate mechanism only exists at low temperatures and low S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios, which is consistent with the experimental observations.23 Since both mechanisms start with the O–H bond breaking of methanol, followed by the dehydrogenation of methoxide to form formaldehyde, the main difference arises from the two elementary steps: CH2O* + O* → H2COO* + * and CH2O* + CH3O* → CH2OOCH3* + *.
M ratios, which is consistent with the experimental observations.23 Since both mechanisms start with the O–H bond breaking of methanol, followed by the dehydrogenation of methoxide to form formaldehyde, the main difference arises from the two elementary steps: CH2O* + O* → H2COO* + * and CH2O* + CH3O* → CH2OOCH3* + *.
Fig. 1(c) shows the variation of reaction rates at different temperatures. It can be seen that at low temperatures, the elementary step of formaldehyde reacting with methoxy is dominant, while at higher temperatures, the oxidation of formaldehyde is dominant. The rates of these two elementary steps exhibit a crossing behavior at a specific temperature, and this temperature is lower when the S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratio is higher. This trend coincides with the observed change in the dominant mechanism. To further validate this trend, we also performed microkinetic simulations at an S
M ratio is higher. This trend coincides with the observed change in the dominant mechanism. To further validate this trend, we also performed microkinetic simulations at an S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratio of 0.1, and the result (see Fig. S2 in the ESI†) is consistent with the observed trend, demonstrating the self-consistency of our findings.
M ratio of 0.1, and the result (see Fig. S2 in the ESI†) is consistent with the observed trend, demonstrating the self-consistency of our findings.
3.3 Activity over Cu(111) and Cu(211)
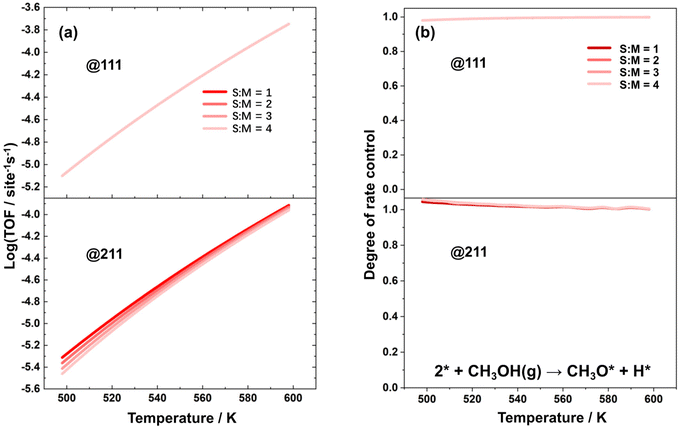
Microkinetic simulations were further conducted to analyze the impact of reaction conditions on the overall reaction activity. Specifically, simulations were performed on the Cu(111) and Cu(211) surfaces at varied temperatures ranging from 498 K to 598 K and S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios from 1 to 4. The reaction rate and the degree of rate control for methanol conversion were analyzed, as depicted in Fig. 2(a) and (b), respectively. The sum of the DRC coefficients under all conditions are provided in the ESI as Fig. S5.† The value of this sum fluctuates around 1 within the tolerance of numerical error. It was found that the elementary step of the dehydrogenation of methanol to form methoxy is the rate-controlling step under all reaction conditions, and therefore, its rate can be considered equal to the TOF for the methanol steam reforming process.
M ratios from 1 to 4. The reaction rate and the degree of rate control for methanol conversion were analyzed, as depicted in Fig. 2(a) and (b), respectively. The sum of the DRC coefficients under all conditions are provided in the ESI as Fig. S5.† The value of this sum fluctuates around 1 within the tolerance of numerical error. It was found that the elementary step of the dehydrogenation of methanol to form methoxy is the rate-controlling step under all reaction conditions, and therefore, its rate can be considered equal to the TOF for the methanol steam reforming process.
We derived a rate equation for the MSR reaction, as expressed in the following equation:
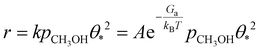 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios. This suggests that it is reasonable to represent the TOF with the reaction rate of the dehydrogenation of methanol to form methoxy, which will greatly simplify the further analysis.
M ratios. This suggests that it is reasonable to represent the TOF with the reaction rate of the dehydrogenation of methanol to form methoxy, which will greatly simplify the further analysis.
The derived rate equation demonstrates that the overall reaction activity is determined by several key factors, including the activation free energy of the dehydrogenation of methanol to form methoxy, the reaction temperature, the coverage of free active sites, and the partial pressure of methanol. Additionally, the free energy remains unchanged with variations in the S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratio. As a result, at a specific temperature and over a particular catalyst surface, the reaction activity becomes a function of the coverage of free active sites. Fig. 3 illustrates the logarithm of coverage of free active sites under different reaction conditions.
M ratio. As a result, at a specific temperature and over a particular catalyst surface, the reaction activity becomes a function of the coverage of free active sites. Fig. 3 illustrates the logarithm of coverage of free active sites under different reaction conditions.
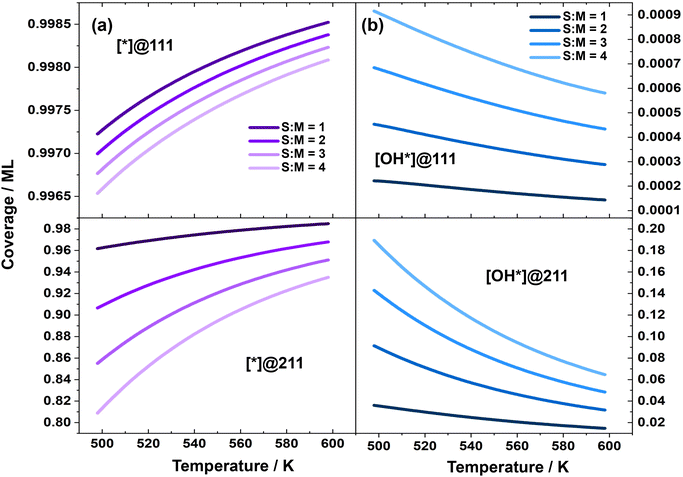 | ||
Fig. 3 (a) Coverage of free site; (b) logarithm of coverage of surface OH species over Cu(111) and Cu(211), in the MSR reaction, as a function of temperature with different S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios. M ratios. | ||
As shown in Fig. 2(a), the TOF over the Cu(111) surface remains relatively constant across different S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios. However, over the Cu(211) surface, the TOF decreases significantly with higher S
M ratios. However, over the Cu(211) surface, the TOF decreases significantly with higher S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios. This observation aligns with the fact that the coverage of free active sites remains nearly constant under different S
M ratios. This observation aligns with the fact that the coverage of free active sites remains nearly constant under different S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios over Cu(111), but decreases substantially with higher S
M ratios over Cu(111), but decreases substantially with higher S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios over Cu(211).
M ratios over Cu(211).
To further investigate the reason for the decrease in the coverage of free active sites with increasing S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios, we examined the coverage of all surface species. Our analysis revealed that surface-adsorbed OH is the dominant species over these two surfaces. Therefore, we focused our study on the coverage of OH. Fig. 3 demonstrates that the change in OH coverage under different S
M ratios, we examined the coverage of all surface species. Our analysis revealed that surface-adsorbed OH is the dominant species over these two surfaces. Therefore, we focused our study on the coverage of OH. Fig. 3 demonstrates that the change in OH coverage under different S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios is minor over Cu(111), but significant over Cu(211). According to the energies of the elementary steps, the reaction Gibbs free energy of H2O + * → OH* + ½H2 is 0.24 eV higher over Cu(111) than over Cu(211), which may explain why OH* prefers to adsorb on the Cu(211) surface. The increasing coverage of OH* with higher S
M ratios is minor over Cu(111), but significant over Cu(211). According to the energies of the elementary steps, the reaction Gibbs free energy of H2O + * → OH* + ½H2 is 0.24 eV higher over Cu(111) than over Cu(211), which may explain why OH* prefers to adsorb on the Cu(211) surface. The increasing coverage of OH* with higher S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios is likely due to the higher water partial pressure, which leads to an elevated rate of H2O dehydrogenation and subsequently results in a higher surface OH coverage. These are further supported by the detailed derivation for the coverage of free sites and their relations with the reaction order and apparent activation energies as shown in the ESI.†
M ratios is likely due to the higher water partial pressure, which leads to an elevated rate of H2O dehydrogenation and subsequently results in a higher surface OH coverage. These are further supported by the detailed derivation for the coverage of free sites and their relations with the reaction order and apparent activation energies as shown in the ESI.†
The activity over different catalyst surfaces is a function of both the free site coverage and the activation free energy at a particular temperature. Fig. S4 in the ESI† displays that the activation free energy of the dehydrogenation of methanol to form methoxy is slightly higher over the Cu(211) surface than over the Cu(111) surface. Additionally, Fig. 3 shows that the free site coverage is generally lower over the Cu(211) surface, which contributes to the fact that the activity over the Cu(111) surface is slightly higher than over the Cu(211) surface. Notably, the TOF over both surfaces at 498 K is on the order of magnitude of 10−5 per s per site, which is quite low. This result is consistent with the experimental observations that the maximum TOF based on surface sites of the MSR reaction over polycrystalline Cu foil is too low to be readily detected.58
3.4 Product selectivity and structure sensitivity
The CO2 selectivity is another crucial property to consider for the MSR process, as CO is a poisonous byproduct that can deactivate the catalysts used in downstream hydrogen utilization. The selectivity of CO2 under different reaction conditions over each catalyst surface is plotted in Fig. 4. The results indicate that the selectivity of CO2 is higher over the Cu(211) surface than over the Cu(111) surface. In the research conducted by Li and co-workers,59 CO2 selectivity over Cu(111) ranges from approximately 10% to 40%, while over Cu(211) it varies from 60% to 90% at temperatures between 500 K and 600 K, the temperature range considered in our work. Meanwhile, our study reports a CO2 selectivity ranges from 0 to 40% over Cu(111) and from 75% to 80% over Cu(211), which aligns closely with the findings presented by Li and co-workers. Over both surfaces, the selectivity increases with increasing S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratio. Furthermore, we found that although the activity of the MSR reaction over the Cu(111) surface is slightly higher than over the Cu(211) surface, the low CO2 selectivity over the Cu(111) surface makes it less advantageous for further application in hydrogen production. Thus, it would be insightful to study the structure sensitivity of the catalytic performance to determine the optimal facet for practical applications. It should be noted that we selected these two surfaces because they represent typical surface step and flat sites that are extensively studied in the majority of theoretical and surface science works. Consequently, our comparison focuses solely on the preference between these two sites.
M ratio. Furthermore, we found that although the activity of the MSR reaction over the Cu(111) surface is slightly higher than over the Cu(211) surface, the low CO2 selectivity over the Cu(111) surface makes it less advantageous for further application in hydrogen production. Thus, it would be insightful to study the structure sensitivity of the catalytic performance to determine the optimal facet for practical applications. It should be noted that we selected these two surfaces because they represent typical surface step and flat sites that are extensively studied in the majority of theoretical and surface science works. Consequently, our comparison focuses solely on the preference between these two sites.
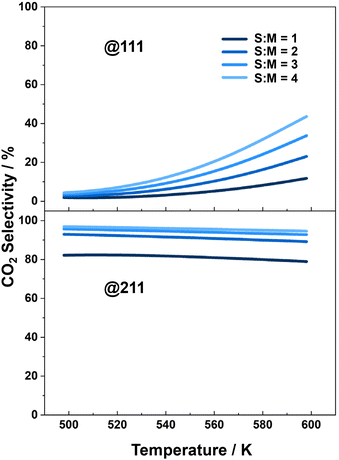 | ||
Fig. 4 CO2 selectivity over Cu(111) and Cu(211), in MSR reaction, as a function of temperature, with different S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios. M ratios. | ||
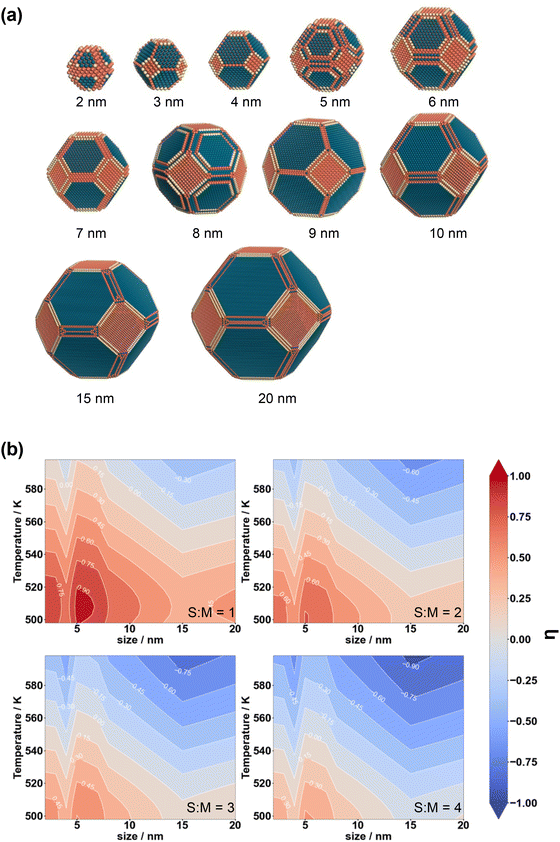
To study the structure sensitivity of the MSR reaction, we constructed Cu nanoparticle models with different sizes according to the Wulff construction method, and the corresponding structures are presented in Fig. 5(a). We then accurately determined the number of both Cu(111) and Cu(211) surface sites. In order to assess the catalyst performance more comprehensively, we employed the formation rate of CO2 as a metric of activity, as it can effectively capture both the activity of reactant consumption and the selectivity of CO2 production. The logarithm of the ratio of the CO2 formation rates over different S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios, temperatures, and nanoparticle sizes, denoted as η, was calculated using the following formula:
M ratios, temperatures, and nanoparticle sizes, denoted as η, was calculated using the following formula:
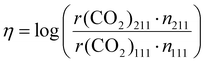 | (9) |
The results are presented in Fig. 5(b). According to Fig. 5(b), a positive value of the logarithm of the ratio indicates a greater contribution from the Cu(211) facet. In most scenarios, the Cu(211) facet exhibits a more substantial contribution than the Cu(111) facet. The figure reveals that at lower S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios, lower temperatures, and smaller particle sizes, the CO2 yield over the Cu(211) facet is notably higher compared to that over the Cu(111) facets.
M ratios, lower temperatures, and smaller particle sizes, the CO2 yield over the Cu(211) facet is notably higher compared to that over the Cu(111) facets.
4. Conclusions
In this study, we investigated the trends of reaction activity, product selectivity, and mechanism selectivity under various reaction conditions over both the Cu(111) and Cu(211) surfaces. Throughout the study, the reaction mechanism over the Cu(211) surface was found to be the H2COO mechanism. In contrast, over the Cu(111) surface, both the methyl formate and H2COO mechanisms were observed, with the former occurring only at low temperatures and low S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios. These findings are consistent with the available experimental observations. The reaction activity over the Cu(111) surface was slightly higher than over the Cu(211) surface. Since the rate-controlling transition state for the entire reaction could be identified through the DRC analysis, we were able to derive a rate equation that can quantitatively explain the trend of activity under different reaction conditions. Furthermore, we found that the CO2 selectivity was significantly higher over the Cu(211) surface than over the Cu(111) surface. The copper nanoparticle models of different sizes built based on the Wulff construction scheme make the calculations of the amounts of the (211) and (111) surface sites for each nanoparticle possible. After carrying out a detailed structure sensitivity study, we found that at lower S
M ratios. These findings are consistent with the available experimental observations. The reaction activity over the Cu(111) surface was slightly higher than over the Cu(211) surface. Since the rate-controlling transition state for the entire reaction could be identified through the DRC analysis, we were able to derive a rate equation that can quantitatively explain the trend of activity under different reaction conditions. Furthermore, we found that the CO2 selectivity was significantly higher over the Cu(211) surface than over the Cu(111) surface. The copper nanoparticle models of different sizes built based on the Wulff construction scheme make the calculations of the amounts of the (211) and (111) surface sites for each nanoparticle possible. After carrying out a detailed structure sensitivity study, we found that at lower S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratios, lower temperatures, and smaller particle sizes, the CO2 yield over the (211) facet is higher compared to that over the (111) facet. This finding will be instructive for the future design of improved catalysts.
M ratios, lower temperatures, and smaller particle sizes, the CO2 yield over the (211) facet is higher compared to that over the (111) facet. This finding will be instructive for the future design of improved catalysts.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (22072091, 22322302) and National Key Research and Development Program of China (2022YFA1503804). We thank the HPC Platform of ShanghaiTech University and Shanghai Supercomputer Center for computing time.References
- G. E. Halkos and E.-C. Gkampoura, Renewable Sustainable Energy Rev., 2021, 144, 110981 CrossRef.
- L. Li, W. Zeng, M. Song, X. Wu, G. Li and C. Hu, Catalysts, 2022, 12, 244 CrossRef CAS.
- Y. Pan and F. Dong, Technol. Forecast. Soc. Change, 2022, 176, 121475 CrossRef.
- H. Wang, in Waste to Renewable Biohydrogen, Elsevier, 2023, pp. 195–210 Search PubMed.
- X. Wang, S. Bi, J. Zhang and H. Tao, Catalysts, 2022, 12, 204 CrossRef CAS.
- M. Oikawa, Y. Kojiya, R. Sato, K. Goma, Y. Takagi and Y. Mihara, Int. J. Hydrogen Energy, 2022, 47, 1319–1327 CrossRef CAS.
- M. Yue, H. Lambert, E. Pahon, R. Roche, S. Jemei and D. Hissel, Renewable Sustainable Energy Rev., 2021, 146, 111180 CrossRef.
- I. Dincer, Int. J. Hydrogen Energy, 2012, 37, 1954–1971 CrossRef CAS.
- J. Zhao, R. Shi, Z. Li, C. Zhou and T. Zhang, Nano Sel., 2020, 1, 12–29 CrossRef.
- D. Güllü and A. Demirbaş, Energy Convers. Manage., 2001, 42, 1349–1356 CrossRef.
- T. Chmielniak and M. Sciazko, Appl. Energy, 2003, 74, 393–403 CrossRef CAS.
- D. R. Palo, R. A. Dagle and J. D. Holladay, Chem. Rev., 2007, 107, 3992–4021 CrossRef CAS.
- A. D. Le and B. Zhou, J. Power Sources, 2008, 182, 197–222 CrossRef CAS.
- S. Sá, H. Silva, L. Brandão, J. M. Sousa and A. Mendes, Appl. Catal., B, 2010, 99, 43–57 CrossRef.
- J. Amphlett, M. Evans, R. Mann and R. Weir, Can. J. Chem. Eng., 1985, 63, 605–611 CrossRef CAS.
- H. Kobayashi, N. Takezawa and C. Minochi, Chem. Lett., 1976, 5, 1347–1350 CrossRef.
- E. Santacesaria and S. Carra, Appl. Catal., 1983, 5, 345–358 CrossRef CAS.
- D. R. Palo, R. A. Dagle and J. D. Holladay, Chem. Rev., 2007, 107, 3992–4021 CrossRef CAS PubMed.
- N. Takezawa and N. Iwasa, Catal. Today, 1997, 36, 45–56 CrossRef CAS.
- K. Takahashi, N. Takezawa and H. Kobayashi, Appl. Catal., 1982, 2, 363–366 CrossRef CAS.
- C. Jiang, D. Trimm, M. Wainwright and N. Cant, Appl. Catal., A, 1993, 97, 145–158 CrossRef CAS.
- B. A. Peppley, J. C. Amphlett, L. M. Kearns and R. F. Mann, Appl. Catal., A, 1999, 179, 31–49 CrossRef CAS.
- Y. Choi and H. G. Stenger, Appl. Catal., B, 2002, 38, 259–269 CrossRef CAS.
- S. Lin, D. Xie and H. Guo, ACS Catal., 2011, 1, 1263–1271 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1993, 47, 558 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758 CrossRef CAS.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter, 2012, 85, 235149 CrossRef.
- H. Wu and B. Yang, Appl. Surf. Sci., 2023, 614, 156116 CrossRef CAS.
- P. Wu and B. Yang, Catal. Sci. Technol., 2019, 9, 6102–6113 RSC.
- D. Xu, P. Wu and B. Yang, J. Phys. Chem. C, 2019, 123, 8959–8966 CrossRef CAS.
- K. Yang and B. Yang, J. Phys. Chem. C, 2018, 122, 10883–10891 CrossRef CAS.
- W. Zhu and B. Yang, J. Phys. Chem. C, 2021, 125, 18743–18751 CrossRef CAS.
- F. Studt, F. Abild-Pedersen, J. B. Varley and J. K. Nørskov, Catal. Lett., 2013, 143, 71–73 CrossRef CAS.
- S. Gautier, S. N. Steinmann, C. Michel, P. Fleurat-Lessard and P. Sautet, Phys. Chem. Chem. Phys., 2015, 17, 28921–28930 RSC.
- A. J. Medford, J. Sehested, J. Rossmeisl, I. Chorkendorff, F. Studt, J. K. Nørskov and P. G. Moses, J. Catal., 2014, 309, 397–407 CrossRef CAS.
- H. Thirumalai and J. R. Kitchin, Surf. Sci., 2016, 650, 196–202 CrossRef CAS.
- M. Methfessel and A. Paxton, Phys. Rev. B: Condens. Matter, 1989, 40, 3616 CrossRef CAS PubMed.
- A. Alavi, P. Hu, T. Deutsch, P. L. Silvestrelli and J. Hutter, Phys. Rev. Lett., 1998, 80, 3650 CrossRef CAS.
- A. Michaelides, Z.-P. Liu, C. Zhang, A. Alavi, D. A. King and P. Hu, J. Am. Chem. Soc., 2003, 125, 3704–3705 CrossRef CAS.
- M. Cieplak, M. Henkel, J. Karbowski and J. R. Banavar, Phys. Rev. Lett., 1998, 80, 3654 CrossRef CAS.
- L. Liu, B. McAllister, H. Ye and P. Hu, J. Am. Chem. Soc., 2006, 128, 4017–4022 CrossRef CAS.
- B. Yang, X.-Q. Gong, H.-F. Wang, X.-M. Cao, J. J. Rooney and P. Hu, J. Am. Chem. Soc., 2013, 135, 15244–15250 CrossRef CAS PubMed.
- X.-P. Wu and X.-Q. Gong, J. Am. Chem. Soc., 2015, 137, 13228–13231 CrossRef CAS PubMed.
- J. Wellendorff, T. L. Silbaugh, D. Garcia-Pintos, J. K. Nørskov, T. Bligaard, F. Studt and C. T. Campbell, Surf. Sci., 2015, 640, 36–44 CrossRef CAS.
- X. Fu, W. Shen, T. Yao and W. Hou, Physical Chemistry, Higher Education Press, 2005 Search PubMed.
- A. J. Medford, C. Shi, M. J. Hoffmann, A. C. Lausche, S. R. Fitzgibbon, T. Bligaard and J. K. Nørskov, Catal. Lett., 2015, 145, 794–807 CrossRef CAS.
- C. H. Shomate, J. Phys. Chem., 1954, 58, 368–372 CrossRef CAS.
- C. A. Wolcott, A. J. Medford, F. Studt and C. T. Campbell, J. Catal., 2015, 330, 197–207 CrossRef CAS.
- C. T. Campbell, ACS Catal., 2017, 7, 2770–2779 CrossRef CAS.
- Y.-X. Wang, H.-L. Zhang, P. An, H.-S. Wu and J.-F. Jia, J. Phys. Chem. C, 2021, 125, 20905–20918 CrossRef CAS.
- X.-K. Gu and W.-X. Li, J. Phys. Chem. C, 2010, 114, 21539–21547 CrossRef CAS.
- S. Lin, D. Xie and H. Guo, J. Phys. Chem. C, 2011, 115, 20583–20589 CrossRef CAS.
- Z.-J. Zuo, L. Wang, P.-D. Han and W. Huang, Int. J. Hydrogen Energy, 2014, 39, 1664–1679 CrossRef CAS.
- S. Lin, R. S. Johnson, G. K. Smith, D. Xie and H. Guo, Phys. Chem. Chem. Phys., 2011, 13, 9622–9631 RSC.
- T. Gu, B. Wang, S. Chen and B. Yang, ACS Catal., 2020, 10, 6346–6355 CrossRef CAS.
- B. Wang, S. Chen, J. Zhang, S. Li and B. Yang, J. Phys. Chem. C, 2019, 123, 30389–30397 CrossRef CAS.
- L. Mayr, X. Shi, N. Köpfle, B. Klötzer, D. Y. Zemlyanov and S. Penner, J. Catal., 2016, 339, 111–122 CrossRef CAS.
- S.-S. Wang, X.-K. Gu, H.-Y. Su and W.-X. Li, J. Phys. Chem. C, 2018, 122, 10811–10819 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt01808g |
| This journal is © The Royal Society of Chemistry 2024 |