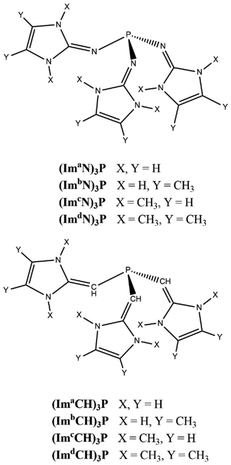
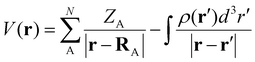Beyond the triple bond: unlocking dinitrogen activation with tailored superbase phosphines†
Vilakkathala U.
Krishnapriya
ab and
Cherumuttathu H.
Suresh
 *bc
*bc
aChemical Science and Technology Division, CSIR-National Institute of Interdisciplinary Science and Technology, Thiruvananthapuram – 695019, Kerala, India
bResearch Centre, University of Kerala, Thiruvananthapuram, 695034, Kerala, India. E-mail: sureshch@gmail.com; sureshch@niist.res.in
cSrinivasa Ramanujan Institute for Basic Sciences, Kerala State Council for Science Technology and Environment, Kottayam, 686501, Kerala, India
First published on 4th November 2024
Abstract
Activating atmospheric dinitrogen (N2), a molecule with a remarkably strong triple bond, remains a major challenge in chemistry. This theoretical study explores the potential of superbase phosphines, specifically those decorated with imidazolin-2-imine ((ImN)3P) and imidazolin-2-methylidene ((ImCH)3P) to facilitate N2 activation and subsequent hydrazine (H2NNH2) formation. Using density functional theory (DFT) at the M06L/6-311++G(d,p) level, we investigated the interactions between these phosphines and N2. Mono-phosphine–N2 complexes exhibit weak, noncovalent interactions (−0.6 to −7.1 kcal mol−1). Notably, two superbasic phosphines also form high-energy hypervalent complexes with N2, albeit at significantly higher energies. The superbasic nature and potential for the hypervalency of these phosphines lead to substantial N2 activation in bis-phosphine–N2 complexes, where N2 is “sandwiched” between two phosphine moieties through hypervalent P–N bonds. Among the phosphines studied, only (ImN)3P forms an exothermic sandwich complex with N2, stabilized by hydrogen bonding between the ImN substituents and the central N2 molecule. A two-step, exothermic hydrogen transfer pathway from (ImN)3P to N2 results in the formation of a bis-phosphine–diimine (HNNH) sandwich complex. Subsequent hydrogen transfer leads to the formation of a bis-phosphine–hydrazine (H2NNH2) complex, a process that, although endothermic, exhibits surmountable activation barriers. The relatively low energy requirements for this overall transformation suggest its potential feasibility under the optimized conditions. This theoretical exploration highlights the promise of superbase phosphines as a strategy for metal-free N2 activation, opening doors for the development of more efficient and sustainable nitrogen fixation and utilization methods.
Introduction
Nitrogen, the most abundant element in the Earth's atmosphere, is vital for almost all organisms. Yet, these organisms cannot use this nitrogen directly, and hence, the activation of nitrogen is an essential process.1–3 The high dissociation energy and the high HOMO–LUMO gap make the activation of dinitrogen under ambient temperature and pressure conditions extremely challenging.4 Dinitrogen (N2) is very unreactive due to its strong NN triple bond and even today, the celebrated Haber process is the only non-natural way to activate this bond to produce useful nitrogenous compounds.5–8 The Haber process makes use of catalysts that accelerate the cleavage of the N–N bond and the process involves the reaction between hydrogen and nitrogen at a moderately elevated temperature and high pressure. Such a process is very energy intensive, whereas N2 fixation occurs under mild conditions naturally in some microorganisms by using the nitrogenase enzyme. The nitrogenase enzyme contains an Fe–Mo–S cluster complex, known as MoFe nitrogenase, where N2 binds and gets reduced to ammonia.9–12 While numerous studies have investigated the mechanism of N2 activation by nitrogenase, the precise molecular details remain elusive.13–19The presence of vacant and filled d orbitals of appropriate energy and symmetry of transition metal complexes allows them to accept and back-donate the electron density with N2. This back-bonding weakens the highly stable N–N triple bond and is able to perform N2 activation. Main group elements, lacking such d orbitals, have traditionally been less effective in N2 activation. However, recent research has challenged this view, demonstrating the potential of metal-free catalysts for this crucial process. Extensive efforts have led to the development of various catalysts for N2 activation, including those based on transition metals (Fe, Mo, Au, etc.), main group metals (Bi, Si, etc.), and, more recently, metal-free systems.20–29 In the past three years, electrochemical ammonia production by main group metal-based catalysts has attracted greater attention in the field of N2 activation.6,30–33 While innovative approaches like electrochemical ammonia production and (photo)electrocatalysis have shown promise, progress has been hampered by reproducibility issues.34
Despite the predominance of metal-based catalysts, metal-free systems are gaining interest. In 2017, Bettinger et al. reported the photochemical extrusion of dinitrogen using phenylborylene under matrix isolation conditions.35 Braunschweig et al. reported that dinitrogen can easily be reduced by using borylene.36 Their work provides a pivotal moment in the scenario of dinitrogen activation using p-block elements and also offers that main group elements are also able to contribute in dinitrogen activation. Recently, p-block half-metal boron was found to be useful for the activation of N2.37 Among s-block elements, Li shows reactivity with N2 because of its extreme reduction potential.38,39 In 2021, Frenking et al. reported that low-valent Ca complexes can reduce dinitrogen.39 The exceptional durability and activity of metal-free catalysts, coupled with their economic and environmental benefits, underscore the importance of their development. Consequently, there is a growing emphasis on the design and synthesis of novel metal-free catalysts for N2 activation.
Very recently, Suresh and Krishnapriya40 showed the remarkable electron-donating properties of the moieties imidazolin-2-imine (ImN–), its methyl derivative (Im′N–), imidazolin-2-methylidene (ImCH–) and its methyl derivative (Im′CH–). These moieties substituted to benzene, pyridine, N-heterocyclic carbene and phosphine led to the design of extremely electron-rich ligands. Fareed and Suresh also showed that substitution of such moieties on the phenyl ring (Fig. 1b and c) can lead to more than a 4-fold increase in cation–π interaction energy compared to benzene.41 Dielmann et al. synthesized a variety of ImN-decorated extremely electron-rich phosphines.42 Such nonionic phosphorus(III) ligands showed superior electron donating ability to any other known phosphines in chemistry and they are described as a new class of superbases. Dielmann et al. investigated their unique electron-releasing character to describe their capability to capture and cleave CO2 molecules.43 With their superior electron-donating ability towards a core structure, these moieties are promising candidates in homogeneous catalysis, offering innovative possibilities for creating auxiliary ligands and advancing catalysis research.
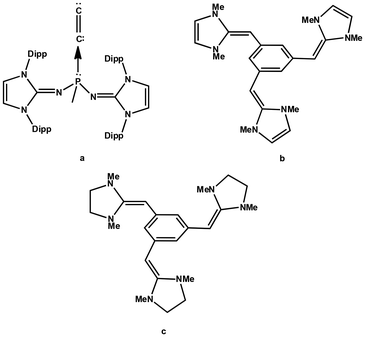 | ||
| Fig. 1 (a) C2 complex of the phosphine ligand synthesized by Leung et al. in 2021. (b) and (c) The cation–π receptors proposed by Fareed and Suresh in 2011. | ||
Recently, the diatomic molecule C2 has been structurally characterized by Leung et al. as a monoligated complex with the formula (ImaN)2(CH3)PC2 (Fig. 1a), where the N center of the imidazolidin-2-iminato groups (ImaN) is adorned with the bulky R group 2,6-diisopropylphenyl.44 Leung et al.'s discovery of a C2 complex of phosphine suggests an unprecedented reaction in chemistry and the driving force of this reaction could be attributed to the incredible electron-donating properties of the ImaN substituent which creates an extremely electron-rich phosphorus center in chemistry. The analysis of the electronic structure of (ImaN)2(CH3)PC2 with quantum chemical methods suggested the formation of the ligand-to-C2 (L → C2) coordination bond which induced a large charge migration from P towards C2. Despite the fact that ImCH- or Im'CH-based systems are yet to be synthesized, theoretical studies from our group suggest that phosphines decorated with these substituents are highly electron rich and they would behave as superbases (Fig. 2).
The focus of this study is on the metal-free N2 activation reactions facilitated by the superbases of (ImN)3P and (ImCH)3P types. The study will assess the electron richness of these ligands and investigate the formation of both L → N2 and L → N2 ← L complexes. We anticipate that the ability of phosphorus to achieve a hypervalent state will be key to the N2 activation process.
The molecular electrostatic potential (MESP) is a valuable tool in computational chemistry for visualizing and understanding the distribution of the electron density within a molecule.45–47 It provides insights into the regions of electrophilic and nucleophilic reactivities, intermolecular interactions, and the nature of chemical bonding.48–51 In this study, MESP topological analysis is employed to assess the electron richness of superbase ligands and to visualize changes in electron density distribution during the N2 activation process.
Computational methodology
All the computational calculations have been carried out with density functional theory (DFT) using Gaussian16 suites of programs.52 All the ligands and complexes were optimized using the DFT method M06L/6-311++G(d,p).53 Vibrational frequency analysis has been carried out to ensure that all of the optimized strictures correspond to the local minima containing only positive vibrational frequencies. The energy difference between the complexes and the individual molecules optimized at the same level of theory is considered as the interaction energy of the complex. The self-consistent reaction field (SCRF) approach with the solvation model density (SMD) method was used to calculate the solvation-corrected energy change and free energy change. Non-polar acetonitrile was employed as the solvent for the calculation. Natural bond orbital (NBO) analysis54,55 was employed to interpret bonding.The MESP topological analysis was performed on the optimized geometries at the M06L/6-311++G(d,p) level of theory using the ‘cube’ and ‘potential’ keywords in Gaussian16. The MESP V(r) at any point with respect to the position vector r is defined as follows:
Results and discussion
MESP analysis of phosphines
Fig. 3 illustrates the depiction of Vmin in the lone pair region of P in MESP isosurface plots for a representative set of PR3 ligands. Considering the Vmin of PH3 of –23.6 kcal mol−1 as a reference point, the higher negative Vmin of −39.0 kcal mol−1 observed for PMe3 suggests that the methyl substitution on P leads to an increase in electron density around the lone pair region of P.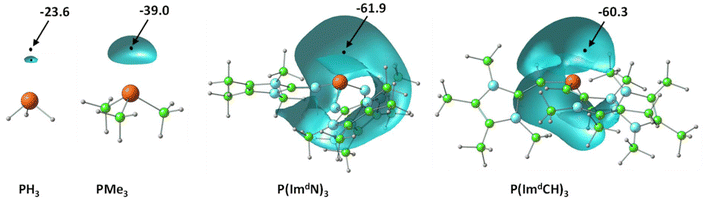 | ||
| Fig. 3 Representation of the MESP isosurfaces of a set of phosphines at −20 kcal mol−1. Vmin values are given in kcal mol−1. Color code: blue, N; green, C; grey, H; rust brown, P. | ||
The introduction of imidazolin-2-imine (ImN–) and imidazolin-2-methylidene (ImCH–) moieties has been proposed as a strategy to design highly electron-rich substrates and ligands, leading to the classification of such ligands as superbases.40,60 Compared to PMe3, the superbases constructed through substitution with ImN–, Im′N–, ImCH–, and Im′CH– exhibit a notable increase in the magnitude of Vmin. For example, considering the Vmin values (Table 1), P(ImdN)3 emerges as the most electron-rich, demonstrating a 2.6-fold higher magnitude for Vmin compared to PH3, highlighting its exceptional electron richness. Previous studies have suggested that this new class of superbase phosphine ligands possesses an electron-donating ability comparable to that of N-heterocyclic carbenes.40
| Phosphine | V min | Phosphine | V min |
|---|---|---|---|
| PH3 | −23.6 | P(ImdN)3 | −61.9 |
| PMe3 | −39.0 | P(ImaCH)3 | −50.8 |
| P(ImaN)3 | −47.6 | P(ImbCH)3 | −59.2 |
| P(ImbN)3 | −52.7 | P(ImcCH)3 | −59.6 |
| P(ImcN)3 | −56.8 | P(ImdCH)3 | −60.3 |
Mono-phosphine–N2 complexes
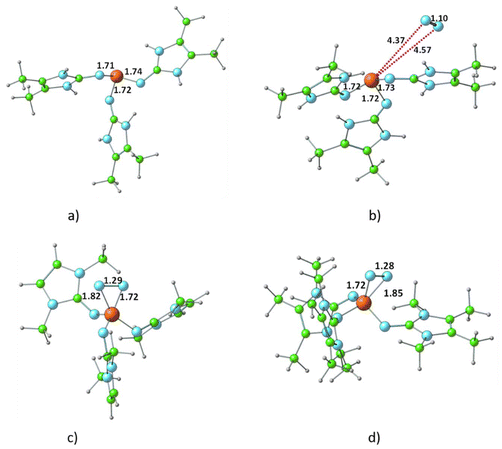
The optimized structure of all R3P⋯N2 complexes showed that the interaction of N2 with phosphine is very weak, characterized as van der Waals-type interactions with P⋯N distances spanning from 3.44 to 4.43 Å. The respective interaction energies (Table S1†) fall within the range −0.6 to −7.1 kcal mol−1, with the weakest observed for the H3P⋯N2 complex and the strongest for the (ImbN)3P⋯N2 complex. As a representative example, the optimized structure of (ImbN)3P⋯N2 is shown in Fig. 4. Comparison with the free (ImbN)3P ligand confirms that this weak N2 complexation does not significantly perturb the phosphine's structure.We further investigated complex formation involving a direct bond between the phosphorus of PR3 and the nitrogen of N2. Among all phosphines studied, only P(ImcN)3 and P(ImdN)3 showed the formation of such complexes with N2. These complexes, denoted as (ImcN)3P–N2 and (ImdN)3P–N2, are also depicted in Fig. 4. It is evident from the P–N distances that the P center forms bonds with five N centers, establishing the complex as a hypervalent phosphorus system. Notably, two of these P–N bonds are significantly shorter than those in free PR3, while another two exhibit nearly identical distances. Only one P–N bond is elongated by approximately 0.1 Å compared to free phosphine. The N–N distance of 1.28 Å clearly indicates substantial dinitrogen activation due to the hypervalent bonding with the phosphine ligand. However, the energetics suggest that both (ImcN)3P–N2 and (ImdN)3P–N2 are high-energy systems, lying 70.1 and 65.9 kcal mol−1, respectively, above free phosphine and N2. Therefore, their formation under ambient conditions is unlikely.
Bis-phosphine–N2 complexes
Fig. 5 presents the representative structures of bis-phosphine–N2 complexes: Me3P–NN–PMe3 and (ImaN)3P–NN–P(ImaN)3. Notably, Me3P–NN–PMe3 is 49.7 kcal mol−1 higher in energy, whereas (ImaN)3P–NN–P(ImaN)3 is 18.1 kcal mol−1 lower in energy (ΔE) compared to free phosphines and N2. In contrast, the formation of H3P–NN–PH3 is endothermic by 87.4 kcal mol−1. This highlights the crucial role of the superbase character of P(ImaN)3 in enhancing the ligand's affinity for bonding with N2. All bis-phosphine–N2 complexes feature P–N bond formation from both ligands (Table 2). The P–NN distances fall within the range of 1.59–1.65 Å, significantly shorter than the typical range for a P–N single bond (1.70–1.77 Å). This suggests considerable double bond character in the P–NN bonds, implying hypervalency at the P center. Additionally, the N–N distances range from 1.43 to 1.49 Å, approaching that of an N–N single bond. These data underscore the strength of the newly formed P–NN bonds, leading to a significant activation of the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond, effectively reducing it to an N–N single bond.
N triple bond, effectively reducing it to an N–N single bond.
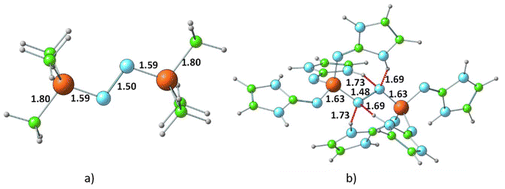 | ||
| Fig. 5 Optimized structures of the dinitrogen bonded complexes of (a) PMe3 and (b) P(ImaN)3 ligands. Bond distances and N⋯HN hydrogen bond distances are shown in Å. | ||
| Complex | ΔE | ΔG | D P–N1 | D P–N2 | D N–N |
|---|---|---|---|---|---|
| H3P–NN–PH3 | 87.4 | 111.2 | 1.59 | 1.59 | 1.46 |
| Me3P–NN–PMe3 | 49.7 | 72.4 | 1.59 | 1.59 | 1.50 |
| (ImaN)3P–NN–P(ImaN)3 | −13.3 | 18.5 | 1.63 | 1.63 | 1.48 |
| (ImbN)3P–NN–P(ImbN)3 | −18.1 | 18.4 | 1.61 | 1.62 | 1.47 |
| (ImcN)3P–NN–P(ImcN)3 | 13.5 | 51.0 | 1.61 | 1.61 | 1.47 |
| (ImdN)3P–NN–P(ImdN)3 | 2.6 | 42.3 | 1.60 | 1.62 | 1.46 |
| (ImaCH)3P–NN–P(ImaCH)3 | 5.1 | 35.2 | 1.65 | 1.65 | 1.49 |
| (ImbCH)3P–NN–P(ImbCH)3 | 41.1 | 68.1 | 1.61 | 1.62 | 1.46 |
| (ImcCH)3P–NN–P(ImcCH)3 | 22.1 | 53.1 | 1.64 | 1.64 | 1.43 |
| (ImdCH)3P–NN–P(ImdCH)3 | 20.2 | 55.4 | 1.63 | 1.63 | 1.44 |
The energetics of the mono- and bis-phosphine complexes, summarized in Fig. 6, clearly demonstrate the superior N2 activation capability of phosphine superbases bearing ImN-type substituents on phosphorus compared to those with ImCH-type substituents. Notably, the formation of (ImaN)3P–NN–P(ImaN)3 and (ImbN)3P–NN–P(ImbN)3 is exothermic, releasing 13.3 and 18.1 kcal mol−1, respectively. This favorable energetic profile can be attributed to the additional stabilization provided by four N–H⋯N hydrogen bonds that surround the central N2 unit (Fig. 5b), a feature unique to these systems possessing N–H bonds.
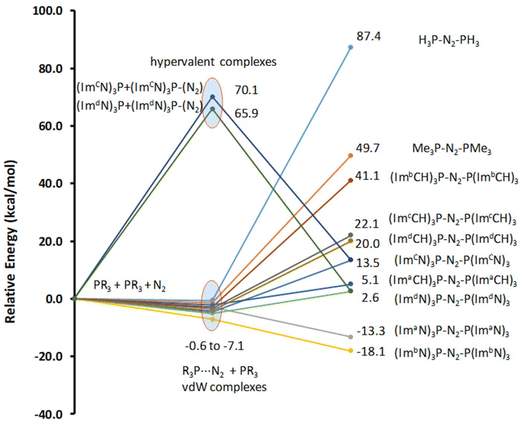 | ||
| Fig. 6 Relative energies of the mono phosphine and bis-phosphine complexes with N2. Energy data are given in kcal mol−1. | ||
In the bis-phosphine–N2 complex, dinitrogen is positioned between two phosphine moieties, forming two P–N bonds. This arrangement significantly alters the bonding environment at both the phosphorus and nitrogen centers. For instance, the three P–N bonds in P(ImaN)3 contract from 1.74, 1.71, and 1.72 Å to 1.69, 1.65, and 1.65 Å in the (ImaN)3P–NN–P(ImaN)3 complex, signifying stronger P–N bonds in the complex. Moreover, the two newly formed P–N bonds with N2 exhibit an even shorter bond length of 1.63 Å. These structural data unequivocally demonstrate that all five P–N bonds in the hypervalent bis-phosphine–N2 complex are substantially stronger than a typical P–N single bond. In essence, the remarkable hypervalent P–N bonding facilitates the activation of the N2 triple bond, effectively reducing it to an N–N single bond.
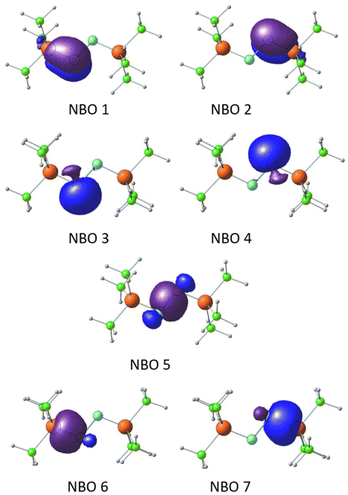
The P–N bonding in the bis-phosphine–N2 complex was further elucidated through NBO analysis, using Me3P–NN–PMe3 as a representative case. NBOs reveal that the N centers adopt an sp2 hybridized state (Fig. 7). Degenerate NBOs 1 and 2, depicted in Fig. 7, represent π-bonds between P and N, arising from the interaction of the lone pair on N (the ‘p’ orbital not involved in sp2 hybridization) with the Rydberg ‘d’ orbitals of the P center. This π-bonding interaction is predominantly contributed by the N center (89%), with the remaining contribution from the P center. Similarly, the degenerate NBOs 3 and 4 correspond to sp2 hybrid lone pair orbitals on each N centers. The NBO 5 describes the N–N σ-bond formed from the sp2 hybrid orbitals on the N centers. The degenerate NBOs 6 and 7 depict the σ-bonding orbitals between the third sp2 hybrid orbital of the N center and primarily the 3s orbital of the P center.
NBO analysis and the observed N–N bond lengths collectively confirm the reduction of the N–N bond to a single bond character in the bis-phosphine–N2 complexes. The calculated energy required for homolytic fission of Me3P–NN–PMe3 into two Me3P–N˙ radical fragments (66.1 kcal mol−1) and the analogous process for (ImaN)3P–NN–P(ImaN)3 (75.3 kcal mol−1) reveal a dramatic weakening of the N–N bond compared to its strength in dinitrogen (226 kcal mol−1). This substantial decrease in bond strength underscores the remarkable activation of N2 achieved through the formation of these hypervalent sandwich complexes with superbase phosphines.
The subsequent investigation, focusing on further N2 activation, will exclusively consider (ImaN)3P–NN–P(ImaN)3 due to its exothermic formation and the presence of stabilizing N–H⋯N hydrogen bonds.
Formation of the diimine complex (ImaN′)3P–NHNH–P(ImaN′)3
Within the (ImaN)3P–NN–P(ImaN)3 complex, two of the four NN⋯HN hydrogen bonds are notably shorter (by 0.039 Å), suggesting the potential for further N2 activation. This activation is realized through the transfer of a hydrogen atom involved in one of these shorter hydrogen bonds to the NN unit, yielding the NNH⋯N hydrogen-bonded intermediate (ImaN′)3P–NNH–P(ImaN)3. The (ImaN′)3P ligand represents the “hydrogen abstracted” state of the original (ImaN)3P ligand. This hydrogen transfer proceeds via the transition state ts1, characterized by the partial formation of an NN–H bond concurrent with the rupturing of the original H–N bond. The resulting intermediate, (ImaN′)3P–NNH–P(ImaN)3, features four hydrogen bonds surrounding the ‘NNH’ unit (Fig. 8). Subsequent activation of the N–N bond occurs through another hydrogen transfer involving the shortest of these hydrogen bonds (HNN⋯HN, 1.638 Å), leading to the transition state ts2. The final product is a sandwich complex of diimine (HNNH) with the phosphine ligand (ImaN′)3P, namely (ImaN′)3P–HNNH–P(ImaN′)3.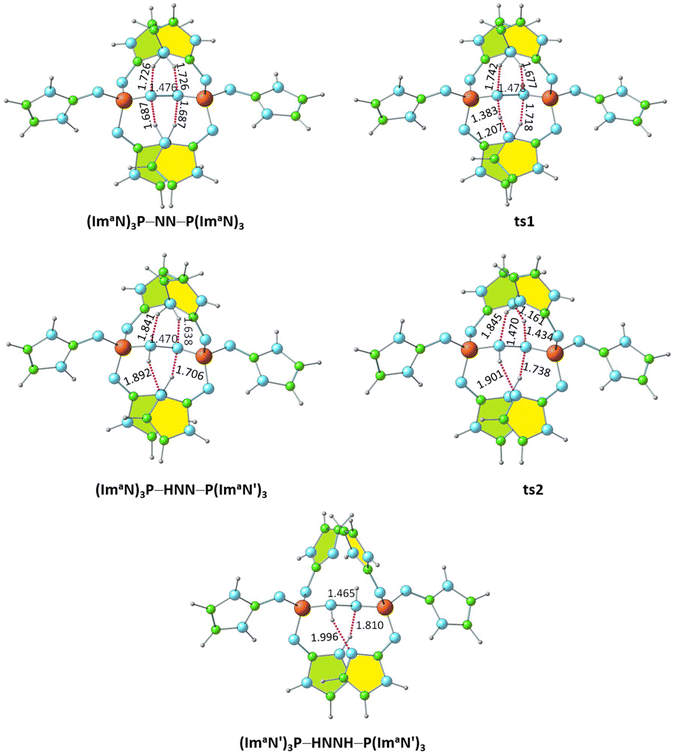 | ||
| Fig. 8 Optimized structures of the products and transition states for the formation of the diimine complex (ImaN′)3P–HNNH–P(ImaN′)3. P–N and N–N distances are shown in Å. | ||
The solvation energy-incorporated energy profile diagram for the hydrogen transfer within the (ImaN)3P–NN–P(ImaN) complex, leading to the activated diimine product (ImaN′)3P–HNNH–P(ImaN′)3, is presented in Fig. 9. This process involves two exothermic (and exergonic) hydrogen transfer steps. The initial hydrogen transfer, exothermic by 6.1 kcal mol−1, proceeds through ts1 with an activation energy of only 2.6 kcal mol−1. The resulting intermediate, (ImaN′)3P–NNH–P(ImaN)3, then undergoes a second hydrogen transfer via ts2. This step, with an activation barrier of 1.0 kcal mol−1, is even more exothermic, releasing 14.1 kcal mol−1. Overall, the reaction is exothermic by 20.2 kcal mol−1. When considering the free energy profile, both steps appear virtually barrierless, and the formation of the diimine complex (ImaN′)3P-NHNH-P(ImaN′)3 is exergonic by 18.0 kcal mol−1.
| (ImaN′)3P–HNNH–P(ImaN′)3 → 2 (ImaN′)3P–HN˙ | (1) |
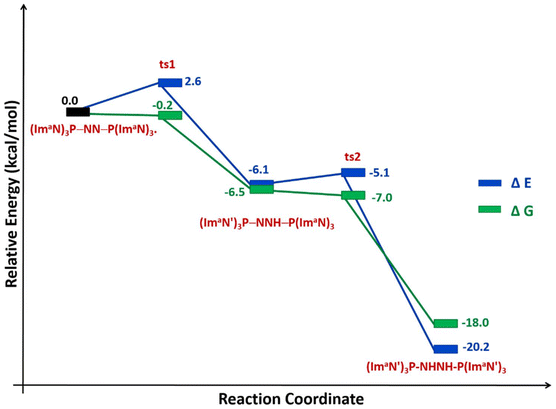 | ||
| Fig. 9 Reaction energy profile diagram for hydrogen transfer occurs in (ImaN)3P–NN–P(ImaN)3 to form the diimine complex (ImaN′)3P–HNNH–P(ImaN′)3. | ||
The N–N bond strength of the diimine complex (ImaN′)3P–HNNH–P(ImaN′)3 was evaluated through the energetics of reaction (1). Cleavage of the N–N bond, yielding the radical (ImaN′)3P–HN˙, requires a dissociation energy of 45.6 kcal mol−1, highlighting the significant activation of the N–N bond. Notably, the N–N bond in the diimine is weakened by 29.7 kcal mol−1 compared to that observed in the dinitrogen complex (ImaN)3P–NN–P(ImaN)3.
Hydrazine complex (ImaN′′)3P–H2NNH2–P(ImaN′′)3
Further activation of the N–N bond in the diimine complex can lead to the formation of a hydrazine complex, (ImaN′′)3P–H2NNH2–P(ImaN′′)3, via hydrogen transfer reactions (Fig. 10). Here, the (ImaN′′)3P ligand represents the “hydrogen abstracted” state of the (ImaN′)3P ligand. The N–H⋯N hydrogen bond (1.810 Å) observed in (ImaN′)3P–HNNH–P(ImaN′)3 is considered for the initial hydrogen transfer reaction. This process proceeds through the transition state ts3, yielding the intermediate (ImaN′′)3P–H2NNH–P(ImaN′′)3.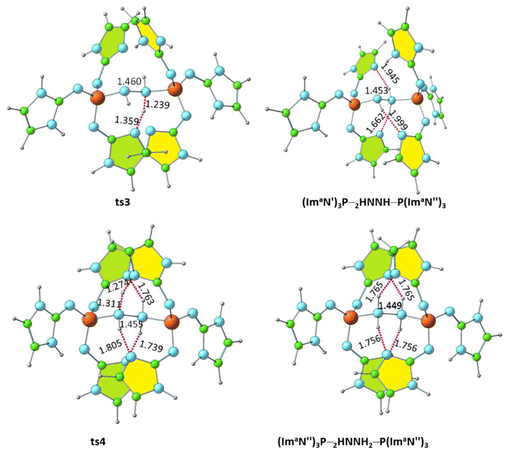 | ||
| Fig. 10 Optimized structures of the products and transition states for the formation of the hydrazine complex (ImaN′′)3P–H2NNH2–P(ImaN′′)3. P–N and N–N distances are shown in Å. | ||
The solvation-corrected energy and free energy profiles (Fig. 11) reveal that this reaction has an activation energy of 8.6 kcal mol−1 and an activation free energy of 6.7 kcal mol−1. It is also endothermic by 7.0 kcal mol−1 and endergonic by 9.8 kcal mol−1.
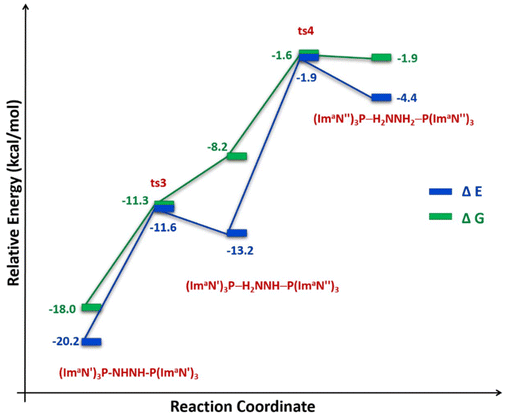 | ||
| Fig. 11 Reaction energy profile diagram for hydrogen transfer occurs in (ImaN′)3P–HNNH–P(ImaN′)3 to form the hydrazine complex (ImaN′′)3P–H2NNH2–P(ImaN′′)3. | ||
A subsequent hydrogen transfer within the intermediate (ImaN′′)3P–HNNH2–P(ImaN′)3 leads to the hydrazine complex (ImaN′′)3P–H2NNH2–P(ImaN′′)3via ts4. This step exhibits activation energies of 11.3 kcal mol−1 (energy) and 6.6 kcal mol−1 (free energy). Overall, the formation of the hydrazine complex from the diimine complex is endothermic by 15.8 kcal mol−1 and endergonic by 16.1 kcal mol−1. However, both the activation energy and activation free energy are readily surmountable under ambient conditions.
We also modelled the dissociation of both (ImaN′′)3P ligands from the hydrazine complex (ImaN′′)3P–H2NNH2–P(ImaN′′)3 to generate the hydrazine H2NNH2. Since two P–N bonds are cleaved in this dissociation, a stepwise dissociation is considered. The first P–N bond dissociation (reaction (2)) occurs with an energy change of 30.9 kcal mol−1 and a free energy change of 15.2 kcal mol−1. The second P–N bond dissociation, releasing hydrazine (reaction (3)), occurs from (ImaN′′)3P–H2NNH2 and has an energy change of 28.7 kcal mol−1 and a free energy change of 12.4 kcal mol−1.
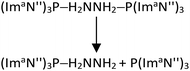 | (2) |
| (ImaN′′)3P–H2NNH2 → (ImaN′′)3P + H2NNH2 | (3) |
Comparing the energy profiles for diimine formation (Fig. 9) and hydrazine formation (Fig. 11) reveals that the diimine complex is both a kinetically and thermodynamically favoured product. However, the transformation from the diimine complex to the hydrazine complex, while endothermic, remains feasible due to its relatively low barrier of 18.3 kcal mol−1. Furthermore, by strategically manipulating reaction conditions such as temperature, pressure, and reactant/product concentrations in accordance with Le Châtelier's principle, the equilibrium can be shifted to favour the formation of hydrazine, despite its thermodynamically less favoured nature.
Conclusions
This study presents a novel approach for N2 activation using superbase phosphines, specifically (ImN)3P. By leveraging the exceptional electron-donating ability of these newly designed ligands, we demonstrate a metal-free pathway for efficient N2 activation, overcoming the challenges posed by the strong N–N triple bond.DFT calculations at the M06L/6-311++G(d,p) level reveal that bis-phosphine complexes, forming hypervalent sandwich structures with N2, exhibit the most promising N2 activation. This activation is driven by the formation of strong P–N bonds with double bond character and a concomitant weakening of the N–N bond, as evidenced by structural and bonding analyses. The superbasic nature of the ImN-type substituents on the phosphine ligands plays a crucial role in enhancing their affinity for N2 and stabilizing the resulting complexes.
We propose a two-step hydrogen transfer pathway for the (ImN)3P–N2–P(ImN)3 sandwich complex, leading to the exothermic formation of a diimine intermediate with a significantly weakened N–N bond. Further hydrogen transfer results in the formation of a hydrazine complex, a process that, while endothermic, exhibits surmountable activation barriers.
This research underscores the potential of ImN-type superbase phosphine ligands in facilitating nitrogen activation and transformation. The ability to controllably convert dinitrogen into more reactive intermediates like diimine and hydrazine opens new avenues for the design of metal-free catalytic systems for nitrogen fixation and other applications in chemical synthesis. Experimental validation of these computational findings is the next crucial step in realizing the potential of this novel approach.
Author contributions
The manuscript was written through the contributions of all authors. All authors have read and approved the final version of the manuscript.Data availability
The data supporting this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
VUK gratefully acknowledges the research fellowship (No. KSCSTE/972/2018-FSHP-MAIN) provided by the Kerala State Council for Science, Technology and Environment (KSCSTE), Kerala, India. CHS and VUK would also like to express their appreciation for the support received from the IT service unit of both CSIR-NIIST and CSIR-4PI institutes. Additionally, CHS extends his thanks to CSIR-NIIST for the opportunity to work on deputation assignment at SRIBS.References
- M. D. Fryzuk, J. B. Love, S. J. Rettig and V. G. Young, Science, 1997, 275, 1445–1447 CrossRef.
- S. D. Minteer, P. Christopher and S. Linic, ACS Energy Lett., 2018, 4, 163–166 CrossRef.
- S. F. McWilliams, D. L. Broere, C. J. Halliday, S. M. Bhutto, B. Q. Mercado and P. L. Holland, Nature, 2020, 584, 221–226 CrossRef.
- V. Krewald, Dalton Trans., 2018, 47, 10320–10329 RSC.
- S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Nat. Catal., 2018, 1, 490–500 CrossRef.
- G. Qing, R. Ghazfar, S. T. Jackowski, F. Habibzadeh, M. M. Ashtiani, C.-P. Chen, M. R. Smith III and T. W. Hamann, Chem. Rev., 2020, 120, 5437–5516 CrossRef PubMed.
- L. Wang, M. Xia, H. Wang, K. Huang, C. Qian, C. T. Maravelias and G. A. Ozin, Joule, 2018, 2, 1055–1074 CrossRef.
- C. J. M. van der Ham, M. T. M. Koper and D. G. H. Hetterscheid, Chem. Soc. Rev., 2014, 43, 5183–5191 RSC.
- F. Neese, Angew. Chem., Int. Ed., 2006, 45, 196–199 CrossRef.
- B. E. Smith, R. L. Richards and W. E. Newton, Catalysts for nitrogen fixation: nitrogenases, relevant chemical models and commercial processes, Springer Science & Business Media, 2004 Search PubMed.
- G. Schwarz, R. R. Mendel and M. W. Ribbe, Nature, 2009, 460, 839–847 CrossRef.
- K. M. Lancaster, M. Roemelt, P. Ettenhuber, Y. Hu, M. W. Ribbe, F. Neese, U. Bergmann and S. DeBeer, Science, 2011, 334, 974–977 CrossRef PubMed.
- B. M. Barney, H.-I. Lee, P. C. Dos Santos, B. M. Hoffman, D. R. Dean and L. C. Seefeldt, Dalton Trans., 2006, 2277–2284 RSC.
- B. M. Barney, T.-C. Yang, R. Y. Igarashi, P. C. Dos Santos, M. Laryukhin, H.-I. Lee, B. M. Hoffman, D. R. Dean and L. C. Seefeldt, J. Am. Chem. Soc., 2005, 127, 14960–14961 CrossRef.
- L. C. Seefeldt, B. M. Hoffman and D. R. Dean, Annu. Rev. Biochem., 2009, 78, 701–722 CrossRef.
- R. Y. Igarashi, M. Laryukhin, P. C. Dos Santos, H.-I. Lee, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, J. Am. Chem. Soc., 2005, 127, 6231–6241 CrossRef.
- F. Studt and F. Tuczek, J. Comput. Chem., 2006, 27, 1278–1291 CrossRef PubMed.
- H. Broda, S. Hinrichsen and F. Tuczek, Coord. Chem. Rev., 2013, 257, 587–598 CrossRef.
- B. M. Hoffman, D. R. Dean and L. C. Seefeldt, Acc. Chem. Res., 2009, 42, 609–619 CrossRef PubMed.
- c. T. Bazhenova and A. Shilov, Coord. Chem. Rev., 1995, 144, 69–145 CrossRef.
- C. Ling, X. Niu, Q. Li, A. Du and J. Wang, J. Am. Chem. Soc., 2018, 140, 14161–14168 CrossRef CAS PubMed.
- A. Shilov, Russ. Chem. Bull., 2003, 52, 2555–2562 CrossRef CAS.
- K. Arashiba, Y. Miyake and Y. Nishibayashi, Nat. Chem., 2011, 3, 120–125 CrossRef CAS PubMed.
- R. R. Schrock, Nat. Chem., 2011, 3, 95–96 CrossRef CAS PubMed.
- M. Yuki, H. Tanaka, K. Sasaki, Y. Miyake, K. Yoshizawa and Y. Nishibayashi, Nat. Commun., 2012, 3, 1254 CrossRef.
- T. Mondal, W. Leitner and M. Hölscher, Dalton Trans., 2024, 53(18), 7890–7898 RSC.
- M. Lan, N. Zheng, X. Dong, C. Hua, H. Ma and X. Zhang, Dalton Trans., 2020, 49, 9123–9129 RSC.
- Y. Zhou, X. Yu, X. Wang, C. Chen, S. Wang and J. Zhang, Electrochim. Acta, 2019, 317, 34–41 CrossRef CAS.
- P. Avenier, X. Solans-Monfort, L. Veyre, F. Renili, J.-M. Basset, O. Eisenstein, M. Taoufik and E. A. Quadrelli, Top. Catal., 2009, 52, 1482–1491 CrossRef CAS.
- N. Cao, Z. Chen, K. Zang, J. Xu, J. Zhong, J. Luo, X. Xu and G. Zheng, Nat. Commun., 2019, 10, 2877 CrossRef.
- G. F. Chen, S. Ren, L. Zhang, H. Cheng, Y. Luo, K. Zhu, L. X. Ding and H. Wang, Small Methods, 2019, 3, 1800337 CrossRef.
- Y. Liu, Y. Su, X. Quan, X. Fan, S. Chen, H. Yu, H. Zhao, Y. Zhang and J. Zhao, ACS Catal., 2018, 8, 1186–1191 CrossRef.
- F. Lü, S. Zhao, R. Guo, J. He, X. Peng, H. Bao, J. Fu, L. Han, G. Qi and J. Luo, Nano Energy, 2019, 61, 420–427 CrossRef.
- H. Iriawan, S. Z. Andersen, X. Zhang, B. M. Comer, J. Barrio, P. Chen, A. J. Medford, I. E. L. Stephens, I. Chorkendorff and Y. Shao-Horn, Nat. Rev. Dis. Primers, 2021, 1, 56 CrossRef.
- K. Edel, M. Krieg, D. Grote and H. F. Bettinger, J. Am. Chem. Soc., 2017, 139, 15151–15159 CrossRef PubMed.
- M.-A. Légaré, G. Bélanger-Chabot, R. D. Dewhurst, E. Welz, I. Krummenacher, B. Engels and H. Braunschweig, Science, 2018, 359, 896–900 CrossRef.
- S. N. Shirodkar, C. A. Sayou Ngomsi and P. Dev, ACS Appl. Electron. Mater., 2023, 5, 1707–1714 CrossRef.
- T.-T. Liu, D.-D. Zhai, B.-T. Guan and Z.-J. Shi, Chem. Soc. Rev., 2022, 51, 3846–3861 RSC.
- B. Rösch, T. Gentner, J. Langer, C. Färber, J. Eyselein, L. Zhao, C. Ding, G. Frenking and S. Harder, Science, 2021, 371, 1125–1128 CrossRef.
- V. U. Krishnapriya and C. H. Suresh, Organometallics, 2023, 42, 571–580 CrossRef.
- F. B. Sayyed and C. H. Suresh, J. Phys. Chem. A, 2011, 115, 9300–9307 CrossRef.
- J. J. Chi, T. C. Johnstone, D. Voicu, P. Mehlmann, F. Dielmann, E. Kumacheva and D. W. Stephan, Chem. Sci., 2017, 8, 3270–3275 RSC.
- F. Buss, P. Mehlmann, C. Mück-Lichtenfeld, K. Bergander and F. Dielmann, J. Am. Chem. Soc., 2016, 138, 1840–1843 CrossRef.
- T.-F. Leung, D. Jiang, M.-C. Wu, D. Xiao, W.-M. Ching, G. P. Yap, T. Yang, L. Zhao, T.-G. Ong and G. Frenking, Nat. Chem., 2021, 13, 89–93 CrossRef PubMed.
- C. H. Suresh, G. S. Remya and P. K. Anjalikrishna, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1601 Search PubMed.
- S. R. Gadre and R. N. Shirsat, Electrostatics of atoms and molecules, Universities Press, 2000 Search PubMed.
- P. Politzer and D. G. Truhlar, Chemical applications of atomic and molecular electrostatic potentials: reactivity, structure, scattering, and energetics of organic, inorganic, and biological systems, Springer Science & Business Media, 2013 Search PubMed.
- C. H. Suresh and S. Anila, Acc. Chem. Res., 2023, 56, 1884–1895 CrossRef.
- J. Tomasi, in Quantum Theory of Chemical Reactions: 1: Collision Theory, Reactions Path, Static Indices, Springer, 1979, pp. 191–228 Search PubMed.
- B. Galabov and P. Bobadova-Parvanova, J. Phys. Chem. A, 1999, 103, 6793–6799 CrossRef.
- C. H. Suresh and N. Koga, Inorg. Chem., 2002, 41, 1573–1578 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, Chem. Phys., 2006, 125, 194101 Search PubMed.
- F. Weinhold and C. R. Landis, Chem. Educ. Res. Pract., 2001, 2, 91–104 RSC.
- F. Weinhold, Discovering chemistry with natural bond orbitals, John Wiley & Sons, 2012 Search PubMed.
- P. Politzer and J. S. Murray, Theor. Chem. Acc., 2002, 108, 134–142 Search PubMed.
- S. R. Gadre, S. A. Kulkarni and I. H. Shrivastava, J. Chem. Phys., 1992, 96, 5253–5260 CrossRef.
- N. Mohan, C. H. Suresh, A. Kumar and S. R. Gadre, Phys. Chem. Chem. Phys., 2013, 15, 18401–18409 RSC.
- N. Mohan and C. H. Suresh, J. Phys. Chem. A, 2014, 118, 1697–1705 CrossRef PubMed.
- M. A. Wuensche, P. Mehlmann, T. Witteler, F. Buss, P. Rathmann and F. Dielmann, Angew. Chem., Int. Ed., 2015, 54, 11857–11860 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt02703e |
| This journal is © The Royal Society of Chemistry 2024 |