High efficiency graphene–silicon hybrid-integrated thermal and electro-optical modulators

Abstract

Graphene modulators are considered a potential solution for achieving high-efficiency light modulation, and graphene–silicon hybrid-integrated modulators are particularly favorable due to their CMOS compatibility and low cost. The exploitation of graphene modulator latent capabilities remains an ongoing endeavour to improve the modulation and energy efficiency. Here, high-efficiency graphene–silicon hybrid-integrated thermal and electro-optical modulators are realized using gold-assisted transfer. We fabricate and demonstrate a microscale thermo-optical modulator with a tuning efficiency of 0.037 nm mW⁻¹ and a high heating performance of 67.4 K μm³ mW⁻¹ on a small active area of 7.54 μm² and a graphene electro-absorption modulator featuring a high speed data rate reaching 56 Gb s⁻¹ and a low power consumption of 200 fJ per bit. These devices show superior performance compared to the state of the art devices in terms of high efficiency, low process complexity, and compact device footage, which can support the realization of high-performance graphene–silicon hybrid-integrated photonic circuits with CMOS compatibility.

---

New concepts

Graphene–silicon hybrid integration holds promise for efficient light modulation in integrated photonic circuits. Yet, the pursuit of solutions that facilitate significant advancements in terms of efficiency and speed remains a topic of immense interest and significance in silicon-based graphene modulator research. Simultaneously achieving low power consumption and a compact device footprint is crucial for enabling tightly packed, energy-efficient photonic circuits suitable for high-speed optical interconnects and computing. In this study, graphene–silicon integration modulators based on both thermo-optic and electro-absorption effects were realized utilizing gold-assisted transfer methods. Benefiting from clean interfaces and low contact resistance, the graphene–silicon integration platform enabled by gold-assisted transfer supports high-performance optical modulation, demonstrating modulation with enhanced efficiency and greater speed. Therefore, the proposed graphene–silicon hybrid integrated modulators are expected to revolutionize our understanding of how to explore the potential of graphene for realizing large-scale integrated photonic circuits with low power consumption and high speeds.

Introduction

Silicon on insulator (SOI) technology has become an attractive platform for high-efficiency photonic and opto-electronic applications due to its complementary metal-oxide-semiconductor (CMOS) compatibility, low-complexity fabrication processes, and low-cost manufacturing techniques.¹ However, the efficiency and speed of SOI-based optical modulators are limited by the intrinsic properties of silicon. In particular, being a centrosymmetric crystal, modulation of absorption and the phase of the incident electromagnetic field via an external electric field (Pockels effect or Kerr effect) in silicon is challenging. Possible routes to indirectly modify light–matter interactions in silicon include doping and structural modifications.² Furthermore, the plasma dispersion effect in silicon facilitates electro-optical modulation in waveguides.³ However, the limited bandwidth in silicon electro-optical modulators poses challenges for practical applications, such as communication networks and optical computing, requiring higher information capacity and faster processing speed. Therefore, the development of hybrid-integrated devices on the SOI platform is highly desirable and has considerable technological relevance.^4–6

In this context, graphene is arguably the most promising candidate for integrated opto-electronics.⁷ In the last two decades, graphene has been the subject of intense research, which led to the realization of micro-scale optoelectronic devices^8–10 with advanced functionalities, such as linear and nonlinear optical modulators,^11–15 photodetectors,¹⁶ light emitters,¹⁷ gas sensors¹⁸ and gates for logic operations,¹⁹ thanks to its remarkable electrical and optical properties.^20–23 Particularly, the exploitation of graphene latent capabilities remains an ongoing endeavour. To date, graphene modulators based on the SOI platform are still regarded as one of the most promising candidates for large scale photonic systems.^24,25 There are mainly two mechanisms that can be exploited to realize graphene-based light modulators: the thermo-optic (TO) effect and the electro-absorption (EA) effect. Graphene heaters have been proven to be highly efficient in TO modulators, thanks to their low optical absorption²⁶ and high thermal conductivity. Taking advantage of the TO effect, graphene has been incorporated into various waveguide structures such as Mach–Zehnder interferometers,^27,28 micro-ring resonators,^29,30 and photonic crystal nanocavities^31,32 to achieve energy-efficient light modulation. On the other hand, graphene EA modulators can convert electric signals into a modulation of the light intensity, enabling effective amplitude modulation. Various graphene EA modulators have been developed, including graphene–silicon,³³ suspended graphene,³⁴ double-layer graphene^35–37 (DLG), and graphene-based hybrid plasmonics,³⁸ each exhibiting pros and cons. Although a lot of work has been conducted, there are still challenges to achieve high efficiency and low power consumption hindered by the high contact resistance, leading to the slow development of practical solutions in many key applications. The exploration of high efficiency graphene–silicon hybrid-integrated modulators is highly desirable.

In this work, by utilizing the gold-assisted transfer method, the contact resistances are further reduced; consequently, high performance thermal and electro-optical modulators are achieved with enhanced efficiency, lower power consumption, and expanded bandwidth. We first demonstrated a TO modulator based on a silicon micro-ring structure (Q ∼ 67000) with a graphene heater integrated onto it. Due to the efficient thermal tunability of the refractive index via an external electric field, a heating efficiency as high as 67.4 K μm³ mW⁻¹ has been demonstrated over a small active area of 7.54 μm². At the same time, the device possesses high modulation speed with 10–90% rise and fall response times of 4.85 and 5.55 μs, respectively. These results are significantly faster compared to those of metal TO modulators, which typically exhibit response times of a few milliseconds.^39,40 We further realized a graphene EA modulator based on the same architecture as the TO modulator, where we simply replaced AlO_x with a HfO₂ dielectric layer. This device demonstrates a high 3 dB bandwidth of up to 26.8 GHz and a high data rate reaching 56 Gb s⁻¹ with a power consumption of 200 fJ per bit. The proposed devices provide a feasible solution to support large-scale high-performance photonic systems and pave the way for future optical communication and sensing applications.

Results and discussion

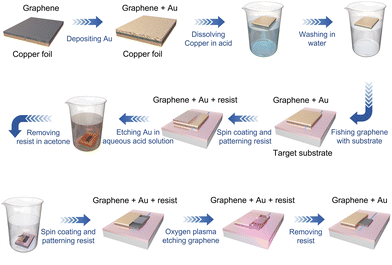
Gold-assisted transfer method

The conventional wet-transfer method, which is currently the standard approach for the fabrication of opto-electronic devices, employs the polymethyl-methacrylate polymer (PMMA) or other organic compounds as the supporting layer.^41,42 There are some remarkable improvements with this method but the removal of the supporting layer is generally necessary with organic procedures such as acetone steam.^43–45 However, due to the strong chemical adsorption between graphene and organic compounds, complete removal of organic residues is usually impossible,⁴⁶ leading to poor metal–graphene contact and performance degradation. Another approach for the fabrication of graphene based opto-electronic devices is the dry-transfer method but it suffers from low yield and is incapable of wafer-scale fabrication. For both of our devices, we employed the gold-assisted transfer process, as shown schematically in Fig. 1. Compared to other graphene transfer methods, the gold-assisted method, which utilizes gold films instead of PMMA as the supporting layer, provides simplified fabrication and low contact resistances.^47,48 The process begins with the deposition of a gold supporting layer onto a commercially available single-layer graphene (SLG) sample grown on a copper foil. Subsequently, the copper substrate undergoes etching by floating it on an ammonium persulfate solution for a duration of 4 hours. Once the copper etching process is completed, the gold-SLG film is carefully transferred into a beaker containing deionized (DI) water and then carefully lifted onto the target substrate. After ensuring the complete drying of the transferred film, any excess gold is removed using an aqueous acid solution, while the excess graphene films are etched through oxygen plasma. The graphene layers in our devices exhibit a surface resistance of approximately 700 Ω □⁻¹ and a contact resistance of approximately 0.3 Ω mm (see Supplementary Note 1 for more details, ESI†).

Fig. 1 Gold-assisted transfer method. The process begins with the deposition of an Au supporting layer on a commercially available SLG sample grown on copper foil. Then the copper substrate is completely etched by placing it in ammonium persulfate solution for 4 hours. Once the copper etching is complete, the Au-SLG film is transferred in a beaker with DI water and then lifted onto the target substrate. After complete drying, the excess Au and graphene films are removed using aqueous acid solution and oxygen plasma etching, respectively.

Graphene TO modulators

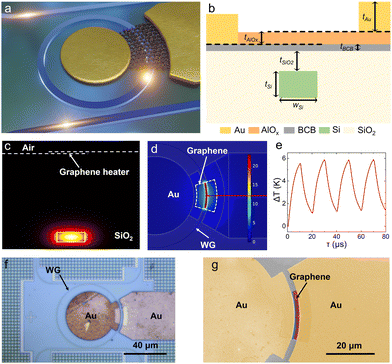
Thermo-optic modulators are highly attractive for applications such as switching and routing. The simple structural design, compact footprint, and cost-effectiveness render TO modulators highly attractive for a variety of applications, particularly in the realm of low-cost and low-frequency modulation, such as in low-frequency switching arrays and tunable filters. Additionally, their ease of manufacturing and substantial process tolerance can enhance yield, surpassing those achievable with electro-optic modulation schemes based on alternative effects. Fig. 2a shows a sketch of the graphene TO micro-ring modulator. The resonator consists of a micro-ring with a radius of 30 μm and a gap of 200 nm coupled with two bus waveguides. Four grating couplers are used for coupling the signal light into and out of the chip. This configuration is highly sensitive to small changes in the effective refractive index (n_eff) of the mode. Fig. 2b shows the cross-section view of the device. As depicted in Fig. 2b, a buried waveguide with a cross-section of 220 nm × 480 nm was used to guide single-mode transverse electric (TE) light. The simulated electric field distribution of the guided mode is shown in Fig. 2c. On top of the waveguide, a 10 nm layer of benzocyclobutene (BCB) was spin-coated to enhance the adhesion ability of the substrate with graphene sheets and thus facilitate the transfer of high-quality SLG. Furthermore, a SLG/AlO_x/SLG structure, consisting of two single layer graphene sheets with a 20 nm AlO_x spacer, is designed on top. The SLG/AlO_x/SLG structure overlaps above the resonator, forming an arc along the ring with a central angle of 30 degrees and a width of ∼1.5 μm above the resonator. Two gold electrodes were formed on both SLG sheets on each side of the waveguide to form a micro-heater. Ohmic heating is generated in the SLG due to a potential difference between the gold electrodes, leading to a temperature increase on the silicon waveguide.

Fig. 2 The graphene TO modulator. (a) 3D illustration of the graphene TO micro-ring modulator. (b) Cross-section of the device. The white dashed line shows the graphene sheets. (c) Waveguide TE-mode profile distribution simulated through finite-different time-domain simulation. (d) Temperature rise distribution across the x–y plane for ∼1 mW power dissipated in the proposed device. (e) Si waveguide transient temperature rise at the point indicated with the red arrow. (f) Optical microscopy image of the device. Scale bar, 40 μm. (g) False-color SEM image of the device. Scale bar, 20 μm.

To verify the thermal conduction performance during the heating process, the temperature distribution of the proposed device was simulated with the 3D finite element method using the COMSOL transient heat transfer module. Simulations were performed assuming thermal conductivities of 5000 W m⁻¹ K⁻¹ for graphene, 301 W m⁻¹K⁻¹ for Au contacts, 131 W m⁻¹ K⁻¹ for Si waveguide and substrates, 1.12 W m⁻¹ K⁻¹ for glass substrates and 30 W m⁻¹ K⁻¹ for AlO_x. For the top boundary of the device, free convection to ambient air with a heat transfer coefficient of h₁ = 15 W m⁻² K⁻¹ was assumed. For the bottom part, we assumed loose contact with a metal holder, with a heat transfer coefficient of h₂ = 150 W m⁻² K⁻¹. Graphene layers are modeled as infinitesimally thin films. The heat dissipated in the device is distributed according to the resistance of each constituent element, i.e., the overlapping and non-overlapping area of the graphene layers, the AlO_x thin layer resistance and the contact resistances, considering their respective electrical resistance values (see Supplementary Note 4, ESI†). The power is dissipated in a pulsed manner, assuming a total of 4 applied pulses, each with a 10 μs pulse width and a 20 μs pulse period. All the geometric aspects of the simulations were set up according to the device used in our experiments. Fig. 2d shows the temperature rise distribution across the x–y plane at its peak value, i.e., at the center of the 4th pulse assuming a total of ∼1 mW power deposited in the configuration, i.e., 1 V applied bias. Fig. 2e shows the transient temperature rise of the waveguide below the graphene layers. We extracted the transient solution of temperature at the point indicated by the red arrow in the waveguide for different applied voltages. In the micro-heater system, the resistance within the AlO_x layer serves to augment heating efficiency, while the exceptional thermal conductivity inherent in graphene facilitates rapid switching speeds.

The buried silicon waveguide was fabricated through typical lithography and dry-etching processes on a commercial SOI wafer with a 220 nm thick top silicon layer and a 2 μm thick SiO₂ buried oxide layer. Then the SLG/AlO_x/SLG layers were assembled (see Methods for details) and carefully aligned with the micro-ring using the gold-assisted transfer technique, as already discussed in details. Fig. 2f shows a microscope image of the fabricated device, where the ring resonator and gold contacts can be seen clearly, while Fig. 2g shows the scanning electron microscope (SEM) images of the fabricated device, in which the top and bottom SLG (red and blue) overlap above the buried ring waveguide. The TE-polarized light is coupled from the fiber to the waveguide using the input grating coupler. By applying a bias voltage to the micro-heater, the waveguide underneath is heated, leading to variations in the effective index of the transmission mode. Applying a bias voltage to the micro-heaters heats the underlying waveguide, resulting in the modulation of the effective index for the transmission mode. Consequently, these index variations result in a shift of the resonance peak in the transmission spectrum of the device. In turn, this allows for a large modulation of the light transmission at a fixed selected wavelength, such as 1550 nm, finally leading to efficient TO modulation.

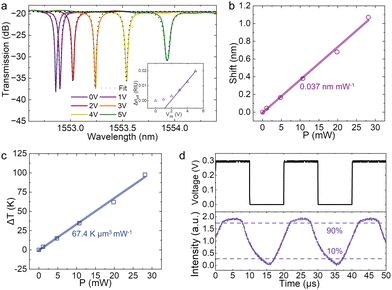
We first characterized the I–V properties of the graphene TO modulator and measured a total resistance of 1.16 kΩ (see Supplementary Note 4, ESI†). The static electro-optic response of the device is measured using the experimental setup shown in the Methods section and the free spectral range (FSR) and extinction ratio (ER) are approximately 3 nm and 19 dB, respectively (see Supplementary Note 2, ESI†). As shown in Fig. 3a, by increasing the external bias voltage applied to the graphene micro-heater, we observed a red shift of the resonance peak due to the TO effect, as discussed above. The wavelength shifts of the resonance peak relative to the voltages of 1, 2, 3, 4 and 5 V are 0.04, 0.2, 0.4, 0.7 and 1.1 nm, respectively. We numerically fit the experimental measurements with a Lorentzian function, as shown by the black dot lines in Fig. 3a. The inset in Fig. 3b shows the change in the n_eff with respect to the bias voltage. The estimated refractive indices at bias voltages of 0, 1, 2, 3, 4 and 5 V are 2.3933, 2.3941, 2.393, 2.4003, 2.4059 and 2.4131, respectively (see Supplementary Note 3, ESI†). As the voltage is increased, localized heating occurs, leading to changes in the coupling state within the micro-ring resonator and the quality-factor of the device reduced gradually.

Fig. 3 Electro-optic response of the graphene TO modulator. (a) Transmission spectra (colors) for various applied bias voltages (0–5 V). The inset shows the change in the effective refractive index in the active area as a function of the bias voltages. (b) Wavelength shift of the resonance peaks as a function of the input electrical power to graphene. (c) Temperature change in the silicon resonator as a function of the input power to graphene. (d) Normalized output intensity from the through port at a rectangular bias signal (1.85–2.15 V) at 50 kHz to graphene.

Fig. 3b presents the shifts in the resonance peaks as a function of the electrical tuning power, from which we extract a tuning efficiency of 0.037 nm mW⁻¹ by linear fitting, which can be improved by further reducing the thickness of the top oxide layer, thus bringing the graphene closer to the waveguide. This translates into a power of 81 mW required to obtain one FSR shift. We define the normalized tuning efficiency as the reciprocal of the product of tuning power needed for one FSR shift and the active area and thus obtain 1.63 W⁻¹ μm⁻², considering the small active area of 7.54 μm² of our device.

Next, we studied the heating performance of the graphene heater, which dissipates electrical power into heat above the silicon micro-ring resonator, using a commercial finite-element solver. Taking into account the TO coefficient of silicon at 1550 nm (∼dn/dT = 1.8 × 10⁻⁴ K⁻¹), the refractive index of silicon at different temperatures can be calculated, after which the corresponding n_eff of the waveguide mode can be calculated. By fitting the extracted n_eff with the measured one (inset in Fig. 3a), the produced temperature changes (ΔT) in the silicon waveguide are determined as a function of the electrical power, as shown in Fig. 3c. The ΔT increases linearly with increasing electrical power, and the heating efficiency, which corresponds to the conversion efficiency from electrical power to Joule heating, can be estimated as 67.4 K μm³ mW⁻¹, considering the slope of the fitted line in Fig. 3b (3.39 K mW⁻¹) and the volume of the resonator (19.9 μm³).^28,29

Furthermore, we conducted real-time optical waveform measurements to quantify the dynamical electro-optical response of the graphene TO modulator. The normalized signal output from the through port is plotted in violet in Fig. 3d by driving the device with a square waveform electrical signal at 50 kHz (black curve). The modulated signal intensity was detected using a photodetector and recorded using an oscilloscope. The output signal responded to the input signal with 10–90% rise and fall times of 4.85 and 5.55 μs, respectively, which indicates that our device is faster than the previous metal TO micro-ring modulators reported.

In Table 1, we have shown a comprehensive comparison of the performances of our device with those of previously reported state-of-the-art TO modulators. Our graphene TO modulator has distinct advantages in terms of heating efficiency and normalized tuning efficiency compared to other graphene TO modulators (ref. 29 and 30). In addition, our experimental results confirm that graphene TO modulators exhibit higher efficiency and speed compared to TO modulators based on metal heaters (ref. 39 and 40).

Table 1 Performance of graphene TO modulators

Device structure	Rise time (μs)	Fall time (μs)	Tuning efficiency (nm mW^−1)	Heating efficiency (K μm^3 mW^−1)	Normalized tuning efficiency (W^−1 m^−2)
a This work.
Graphene micro-ring resonator^a	4.85	5.55	0.037	67.4	1.63
Graphene micro-ring resonator^30	3.0	3.6	0.33	8.8	0.2
Graphene racetrack resonator^29	1.2	3.6	0.24	7.66	0.67
NiCr–Au micro-ring resonator^40	1500	2000	0.054	N/A	N/A
Ti racetrack resonator^39	9	6	0.91	N/A	N/A

---

Graphene EA modulator

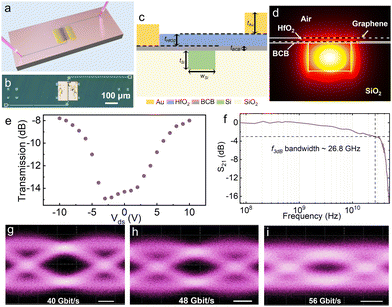
As discussed, the response time of TO modulators is usually in the range of microseconds, ultimately limited by the heat dissipation process. EA modulators can achieve a significantly faster switching time (∼ns) thanks to the high mobility of graphene, well-suited for high-speed applications. In our device, by simply replacing the conducting AlO_x spacer with insulating HfO₂, we realized graphene EA modulators suitable for high-speed applications. The sketch and cross-sectional view of the fabricated graphene EA modulator are displayed in Fig. 4a and c. A buried waveguide with a thickness of t_Si = 220 nm and a width of w_Si = 450 nm was employed to guide TE light around 1550 nm. In addition to the waveguide fabrication process, the silicon wafer undergoes chemical mechanical polishing to planarize the oxide layer, thus bringing the waveguide closer to graphene. Then the SLG/HfO₂/SLG structure was fabricated on top of the waveguide using the gold-assisted transfer method described in the previous section, which ensured high quality of graphene along with low impurities and high quality interfaces. The thickness of the HfO₂ dielectric layer is set to be 30 nm. A thinner dielectric layer decreases the modulation voltage and increases the device capacitance simultaneously, resulting in a reduction in both device speed and power consumption. Meanwhile, reducing the thickness of this layer also leads to a lower breakdown voltage. The length of the SLG/HfO₂/SLG stacks is set to be 180 μm. Fig. 4d shows the simulated electrical field distribution of the guided mode, which illustrates that most of the optical power is confined in the waveguide core and only a small portion of the light (∼1.1%) is evanescently coupled to the graphene layers. The structure configuration of our device can be clearly seen from the optical microscope image in Fig. 4b.

Fig. 4 The graphene EA modulator. (a) 3D illustration of the graphene EA modulator. (b) Optical microscope image of the device. Scale bar, 100 μm. (c) Cross-section of the device. The black dashed line shows the graphene sheets. (d) Waveguide TE-mode profile distribution. (e) Corresponding transmission at 1550 nm as a function of applied bias voltages. (f) Measured electro-optical S₂₁ frequency response of the EA modulator when the bias voltage is 3 V. (g)–(i), NRZ eye diagrams generated at data rates of 40, 48, and 56 Gb s⁻¹. The white scale bar corresponds to 5 ps.

We measured the static electro-optic response of the EA modulator using the experimental setup described above. The modulation efficiency is determined to be 1.3 dB V⁻¹ at 4 V (Fig. 4e). To confirm the high-speed capabilities of the graphene EA modulator, we conducted small signal measurements to determine its electro-optical bandwidth, as illustrated in Fig. 4f. A bias tee is used to combine a 3 V DC bias with a radio frequency (RF) signal provided by a photonic network analyzer (PNA), which is then fed to the graphene EA modulator with a GS probe. The output light was amplified by an erbium-doped fiber amplifier and filtered by an optical tunable filter. Finally, it was transmitted to the PNA for detection and processing. The measured S₂₁ frequency response indicates that the 3 dB bandwidth of our device is 26.8 GHz. The high-speed data transmission potential of the EA modulator is further verified by transmission measurements. A 2 V peak-to-peak 2¹⁵−1 pseudo-random binary sequence signal was generated by an arbitrary waveform generator with a DC bias of 3 V. Fig. 4g depicts the eye diagrams of non-return-to-zero (NRZ) signals generated at data rates of 56 Gb s⁻¹. Disregarding the parasitic capacitance, we achieved an energy efficiency of approximately ∼200 fJ per bit for the graphene EA modulator, with a measured capacitance (C) of ∼200 fF and a voltage swing (V_AC) of ∼2.2 V. This energy efficiency demonstrates the potential of our graphene EA modulator for high-speed and low-power applications.

Table 2 provides a summary of our results and a comparison with other graphene EA modulators. Our graphene EA modulator exhibits notable advantages compared to other graphene EA modulators listed in Table 2 in terms of modulation depth and speed. Compared to devices utilizing mechanical exfoliation of graphene (ref. 46), our device offers the capability to transfer large-area CVD graphene onto substrates enabling efficient and cost-effective production of graphene-based devices (Supplementary Note 1, ESI†). The bandwidth of the device can be further optimized by increasing the quality of the oxide layer, which can also lead to improvements in the overall device performance.

Table 2 Performance of the graphene EA modulators

Device structure	Insertion loss (dB μm^−1)	Modulation depth (dB)	Band-width (GHz)	Data rate (Gb s^−1)	Power consumption (fJ per bit)
a This work.
DLG^a	0.025	7.1	26.8	56	200
DLG^37	0.092	3	29	50	N/A
DLG^49	0.13	4	39	40	160
SLG^35	0.076	5	5.9	10	350
SLG^33	N/A	3.6	1	N/A	N/A

---

Conclusions

In summary, we proposed high efficiency graphene integrated photonic modulators based on the gold-assisted transfer method. Thanks to the high quality transfer method, our devices clearly display performances, surpassing those of the state-of-the-art devices. In particular, we demonstrated a graphene TO micro-ring modulator with a compact active area of 7.54 μm² exhibiting a wavelength tuning efficiency of 0.037 nm mW⁻¹ and a high heating efficiency of 67.4 K μm³ mW⁻¹ which indicates the high conversion efficiency from electrical power to temperature rise in the waveguide. Next, by replacing the oxide layer, we demonstrated a graphene EA modulator with a high data rate reaching 56 Gb s⁻¹ and a low power consumption of 200 fJ per bit. The realized devices display high efficiency, high speed, small footprint, low energy consumption and CMOS-compatibility, and thus they hold great potential for large-scale production of micro-scale integrated opto-electronic devices, with foreseeable applications in the fields of optical communications, neural networks, biosensing, and LIDAR.

Methods

Device fabrication

The waveguides were fabricated using a photo-lithography process by a CMOS foundry. A 10 nm layer of BCB is spin-coated on top to planarize and promote adhesion of the surface. Commercially available SLG (BGI) grown on copper foil via CVD are transferred using the gold-assisted transfer method. The gold supporting layer is deposited on the surface of a SLG sample and then it is placed in a solution of 1 g of ammonium persulfate (1 g diluted in 40 mL of DI water) to etch the copper substrate. Once the copper etching is complete, the gold-SLG film is transferred into a beaker with DI water to wash off the residual etchant. After three repetitions of cleaning, the gold-SLG film was transferred onto the target substrate and allowed to dry. Subsequently, graphene was lithographically patterned followed by wet etching with acid solution and oxygen plasma etching respectively to define active channels. After depositing a dielectric layer on top through atomic layer deposition, we repeated the graphene-transfer process to construct the SLG/dielectric/SLG structure. After the transfer processes, the chip was baked at 90 °C for 4 hours to ensure the complete removal of residual water between the graphene and the substrate.

Experimental setup

The transmission spectra under different voltages were measured with the measurement system shown in Supplementary Note 6 (ESI†). Two probes were utilized to establish contact with the electrodes, allowing the application of an electrical signal from a source meter to the device under test (DUT) through gold electrodes. The input light in the TE mode, generated from a tunable laser source, was carefully polarization controlled and launched into the chip using a grating coupler subsequently. The modulated light was collected by coupling the output light back into an optical fiber connected to an optical power meter.

Author contributions

J. W. conceived the idea for the project. J. W., Z. N., J. L., G. S. and E. L. supervised the work. X. W. and T. Z. designed the devices. Y. W., Z. C. and Z. L. fabricated the devices. X. W., S. D., E. L., O.G. and G. S. performed the simulations. X. W., Y. X. and L. L. measured devices. X. W. performed data analysis and drafted the manuscript. All authors have contributed to the manuscript and given approval to the final version.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge funding from the National Key Research and Development Program of China (2019YFB2205303), the National Natural Science Foundation of China (62205054, 62375051, and 62225404), the Natural Science Foundation of Jiangsu Province (BK20210207 and BK20222007), Fundamental Research Funds for the Central Universities, and Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the Collaborative Research Center (CRC) 1375 “NOA”, project C4.

References

1. S. Y. Siew, B. Li, F. Gao, H. Y. Zheng, W. Zhang, P. Guo, S. W. Xie, A. Song, B. Dong, L. W. Luo, C. Li, X. Luo and G.-Q. Lo, J. Light. Technol., 2021, 39, 4374–4389.
2. R. Soref, IEEE J. Sel. Top. Quantum Electron., 2006, 12, 1678–1687.
3. Q. Xu, S. Manipatruni, B. Schmidt, J. Shakya and M. Lipson, Opt. Express, 2007, 15, 430.
4. Z. Xie, T. Zhao, X. Yu and J. Wang, Small, 2024, 2311621.
5. M. Zhang, L. Yang, X. Wu and J. Wang, Research, 2023, 6, 0206.
6. L. R. Chen, J. Wang and C. Fang, Acta Electonica Sin., 2022, 50, 2233–2241.
7. Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50.
8. M. Romagnoli, V. Sorianello, M. Midrio, F. H. L. Koppens, C. Huyghebaert, D. Neumaier, P. Galli, W. Templ, A. D’Errico and A. C. Ferrari, Nat. Rev. Mater., 2018, 3, 392–414.
9. N. Youngblood, Y. Anugrah, R. Ma, S. J. Koester and M. Li, Nano Lett., 2014, 14, 2741–2746.
10. E. Heidari, H. Dalir, F. M. Koushyar, B. M. Nouri, C. Patil, M. Miscuglio, D. Akinwande and V. J. Sorger, Nanophotonics, 2022, 11, 4011–4016.
11. R. Amin, J. K. George, H. Wang, R. Maiti, Z. Ma, H. Dalir, J. B. Khurgin and V. J. Sorger, APL Photonics, 2021, 6, 120801.
12. M. A. Giambra, V. Mišeikis, S. Pezzini, S. Marconi, A. Montanaro, F. Fabbri, V. Sorianello, A. C. Ferrari, C. Coletti and M. Romagnoli, ACS Nano, 2021, 15, 3171–3187.
13. B. S. Lee, A. P. Freitas, A. Gil-Molina, E. Shim, Y. Zhu, J. Hone and M. Lipson, arXiv, preprint, 2020, arXiv:2011.08832.
14. C. Wu, S. Brems, D. Yudistira, D. Cott, A. Milenin, K. Vandersmissen, A. Maestre, A. Centeno, A. Zurutuza, J. Van Campenhout, C. Huyghebaert, D. Van Thourhout and M. Pantouvaki, Laser Photonics Rev., 2023, 17, 2200789.
15. G. Soavi, G. Wang, H. Rostami, D. G. Purdie, D. De Fazio, T. Ma, B. Luo, J. Wang, A. K. Ott, D. Yoon, S. A. Bourelle, J. E. Muench, I. Goykhman, S. Dal Conte, M. Celebrano, A. Tomadin, M. Polini, G. Cerullo and A. C. Ferrari, Nat. Nanotechnol., 2018, 13, 583–588.
16. X. Gan, R.-J. Shiue, Y. Gao, I. Meric, T. F. Heinz, K. Shepard, J. Hone, S. Assefa and D. Englund, Nat. Photonics, 2013, 7, 883–887.
17. T.-H. Han, Y. Lee, M.-R. Choi, S.-H. Woo, S.-H. Bae, B. H. Hong, J.-H. Ahn and T.-W. Lee, Nat. Photonics, 2012, 6, 105–110.
18. T. Tan, Z. Yuan, H. Zhang, G. Yan, S. Zhou, N. An, B. Peng, G. Soavi, Y. Rao and B. Yao, Nat. Commun., 2021, 12, 6716.
19. Y. Li, N. An, Z. Lu, Y. Wang, B. Chang, T. Tan, X. Guo, X. Xu, J. He, H. Xia, Z. Wu, Y. Su, Y. Liu, Y. Rao, G. Soavi and B. Yao, Nat. Commun., 2022, 13, 3138.
20. X. Du, I. Skachko, A. Barker and E. Y. Andrei, Nat. Nanotechnol., 2008, 3, 491–495.
21. M. Massicotte, G. Soavi, A. Principi and K.-J. Tielrooij, Nanoscale, 2021, 13, 8376–8411.
22. O. Dogadov, C. Trovatello, B. Yao, G. Soavi and G. Cerullo, Laser Photonics Rev., 2022, 16, 2100726.
23. A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902–907.
24. C. Qiu, H. Zeng and Y. Su, Natl. Sci. Open, 2022, 1, 20220031.
25. Y. Liao, G. Feng, H. Zhou, J. Mo, H. J. Sun and S. H. Zhou, IEEE Photonics Technol. Lett., 2018, 30, 661–664.
26. H. Li, Y. Anugrah, S. J. Koester and M. Li, Appl. Phys. Lett., 2012, 101, 111110.
27. Y. Sun, Y. Cao, Y. Yi, L. Tian, Y. Zheng, J. Zheng, F. Wang and D. Zhang, RSC Adv., 2017, 7, 39922–39927.
28. L. Yu, D. Dai and S. He, Appl. Phys. Lett., 2014, 105, 251104.
29. S. Nakamura, K. Sekiya, S. Matano, Y. Shimura, Y. Nakade, K. Nakagawa, Y. Monnai and H. Maki, ACS Nano, 2022, 16, 2690–2698.
30. D. Schall, M. Mohsin, A. A. Sagade, M. Otto, B. Chmielak, S. Suckow, A. L. Giesecke, D. Neumaier and H. Kurz, Opt. Express, 2016, 24, 7871.
31. S. Yan, X. Zhu, L. H. Frandsen, S. Xiao, N. A. Mortensen, J. Dong and Y. Ding, Nat. Commun., 2017, 8, 14411.
32. Z. Xu, C. Qiu, Y. Yang, Q. Zhu, X. Jiang, Y. Zhang, W. Gao and Y. Su, Opt. Express, 2017, 25, 19479.
33. M. Liu, X. Yin, E. Ulin-Avila, B. Geng, T. Zentgraf, L. Ju, F. Wang and X. Zhang, Nature, 2011, 474, 64–67.
34. A. Phatak, Z. Cheng, C. Qin and K. Goda, Opt. Lett., 2016, 41, 2501.
35. Y. Hu, M. Pantouvaki, J. Van Campenhout, S. Brems, I. Asselberghs, C. Huyghebaert, P. Absil and D. Van Thourhout, Laser Photonics Rev., 2016, 10, 307–316.
36. Z. Cheng, X. Zhu, M. Galili, L. H. Frandsen, H. Hu, S. Xiao, J. Dong, Y. Ding, L. K. Oxenløwe and X. Zhang, Nanophotonics, 2020, 9, 2377–2385.
37. M. A. Giambra, V. Sorianello, V. Miseikis, S. Marconi, A. Montanaro, P. Galli, S. Pezzini, C. Coletti and M. Romagnoli, Opt. Express, 2019, 27, 20145.
38. D. Ansell, I. P. Radko, Z. Han, F. J. Rodriguez, S. I. Bozhevolnyi and A. N. Grigorenko, Nat. Commun., 2015, 6, 8846.
39. P. Dong, W. Qian, H. Liang, R. Shafiiha, N.-N. Feng, D. Feng, X. Zheng, A. V. Krishnamoorthy and M. Asghari, Opt. Express, 2010, 18, 9852.
40. X. Liu, P. Ying, X. Zhong, J. Xu, Y. Han, S. Yu and X. Cai, Opt. Lett., 2020, 45, 6318.
41. M. Onodera, S. Masubuchi, R. Moriya and T. Machida, Jpn. J. Appl. Phys., 2020, 59, 010101.
42. A. Montanaro, W. Wei, D. De Fazio, U. Sassi, G. Soavi, P. Aversa, A. C. Ferrari, H. Happy, P. Legagneux and E. Pallecchi, Nat. Commun., 2021, 12, 2728.
43. X. Gao, L. Zheng, F. Luo, J. Qian, J. Wang, M. Yan, W. Wang, Q. Wu, J. Tang, Y. Cao, C. Tan, J. Tang, M. Zhu, Y. Wang, Y. Li, L. Sun, G. Gao, J. Yin, L. Lin, Z. Liu, S. Qin and H. Peng, Nat. Commun., 2022, 13, 5410.
44. Y.-M. Seo, W. Jang, T. Gu, H.-J. Seok, S. Han, B. L. Choi, H.-K. Kim, H. Chae, J. Kang and D. Whang, ACS Nano, 2021, 15, 11276–11284.
45. H. Van Ngoc, Y. Qian, S. K. Han and D. J. Kang, Sci. Rep., 2016, 6, 33096.
46. X. Liang, B. A. Sperling, I. Calizo, G. Cheng, C. A. Hacker, Q. Zhang, Y. Obeng, K. Yan, H. Peng, Q. Li, X. Zhu, H. Yuan, A. R. Hight Walker, Z. Liu, L. Peng and C. A. Richter, ACS Nano, 2011, 5, 9144–9153.
47. Y. Wu, X. Zou, M. Sun, Z. Cao, X. Wang, S. Huo, J. Zhou, Y. Yang, X. Yu, Y. Kong, G. Yu, L. Liao and T. Chen, ACS Appl. Mater. Interfaces, 2016, 8, 25645–25649.
48. R. S. Sundaram, M. Steiner, H.-Y. Chiu, M. Engel, A. A. Bol, R. Krupke, M. Burghard, K. Kern and P. Avouris, Nano Lett., 2011, 11, 3833–3837.
49. H. Agarwal, B. Terrés, L. Orsini, A. Montanaro, V. Sorianello, M. Pantouvaki, K. Watanabe, T. Taniguchi, D. V. Thourhout, M. Romagnoli and F. H. L. Koppens, Nat. Commun., 2021, 12, 1070.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nh00160e

‡ These authors contributed equally to this work.

---