A self-assembled metallo-macrocycle two-qubit spin system

Abstract

A self-assembled, charge-neutral dicopper(II) metallo-macrocycle with a near degenerate singlet–triplet ground state is a prototype molecular two-qubit system. The weakly-coupled spin centres delivered a long phase memory time of 5.4 μs, and each spin can be selectively switched using an applied potential providing a convenient means to modulate the quantum levels.

---

Paramagnetic molecules have been at the forefront of the exploration of physical phenomena that will ultimately lead to the realisation of quantum computing.^1,2 Although not inherently primed to feature in a functioning device, examination of coordination complexes bearing an unpaired electron has provided significant advancement in the key design criteria for the basic component, the qubit. This includes an examination of the spin dynamics measured via the spin–lattice (T₁) and phase memory (T_M) relaxation lifetimes that govern qubit operation, where providing a rigid framework that isolates the spin host,³ eliminating the nuclear spin bath,^4,5 and phonon effects,⁶ have greatly improved performance. In addition, paramagnetic molecules have executed elementary quantum logic through manipulation of electronic states using microwaves,⁷ and electrical or optical tiggers.^8–10

More recent molecular prototypes have delivered multi-qubit systems wherein spin centres are brought together in chemical entities that modulates their interaction,¹¹ delivering the requirements for more sophisticated operations such as error correction and quantum simulation.¹² Exemplary work from Winpenny¹³ and Aromí¹⁴ have produced elegant supramolecular assemblies with two or more paramagnetic centres where electron spins can be addressed independently at selected microwave frequencies, known as g-engineering. The alternative method to generating a multi-level system is to tap into an available hyperfine manifold known as a qudit,¹⁵ neatly exemplified by [Yb(trensal)] with its 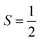ground state and 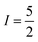nuclear spin of ¹⁷³Yb.¹⁶ Combining these two motifs for developing multi-spin molecules, we have investigated the spin dynamics in a self-assembled copper metallo-macrocycle, [Cu₂(L)₂] ([1]; Fig. 1), which combines two 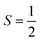Cu^II centres each bearing an 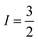manifold. The Cu^II ions are linked through a dithiocarbamate chelate affording a highly covalent square planar geometry, devoid of deleterious nuclear spins, which enforces an intermetallic separation that gives weak spin coupling. Moreover the complex can be oxidised and therein electrically switched between two, one or no unpaired spins, providing additional versatility hitherto unexplored for multi-spin supramolecular qubits.

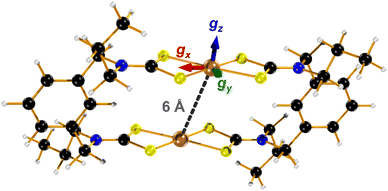Fig. 1 Molecular structure of two-fold symmetric [1] showing the interspin distance and orientation of the principal g-values (Cu, bronze; S, canary; N, indigo; C, onyx; H, alabaster).

The synthesis of [1] is carried out in a two-step process. The bis-amine precursor to the dithiocarbamate ligand is formed by treating α,α′-dibromo-m-xylene with excess isopropylamine, and isolated as a colourless oil. Subsequent deprotonation by triethylamine followed by addition of carbon disulfide produces the bis-dithiocarbamate. Addition of an equimolar amount of a copper salt gave microcrystalline [1], which is mildly soluble in chlorinated solvents and acetonitrile, sparingly soluble in aromatics, and insoluble in alcohols and alkanes. The IR spectrum exhibits the signature ν(C–N) and ν(C–S) stretches at 1446 and 964 cm⁻¹, respectively, of the dithiocarbamate moiety.¹⁷ The electronic spectrum displays a ligand-field transition at 606 nm and ligand-to-metal charge transfer band at 432 nm. The intensity of these features is exactly twice that of the calibrant compound [Cu(dbdtc)₂] (dbdtc = N,N-dibenzyl-dithiocarbamate; Fig. S1, ESI†). The cyclic voltammogram of [1] showed two reversible one-electron transfer waves at −0.063 V and +0.110 V, respectively (Fig. S2, ESI†). These processes represent successive oxidation of the complex to give [1]¹⁺ and diamagnetic [1]²⁺.¹⁸ The reversibility is aided by the preservation of planarity at the Cu centres, and the close separation of oxidative waves of 170 mV underpins their electronic communication. A reduction process at E_pa = −1.194 V is irreversible due to the inability of the metallo-macrocycle to give the tetrahedral geometry preferred by Cu^I.¹⁹

Magnetic susceptibility measurements for [1] show a temperature independent magnetic moment from 25–290 K, yielding a value of μ_eff = 2.54 μ_B at room temperature (Fig. S4, ESI†). Below 25 K the value decreases to ca. 1.7 μ_B due to exchange coupling between Cu^II centres and intermolecular interactions within the powder sample. The room temperature magnetic moment confirms the presence of two Cu^II ions (cf. spin-only value of 2.45 μ_B). Fitting of the susceptibility using the standard Heisenberg–Dirac–van Vleck Hamiltonian, Ĥ = −2JS₁·S₂ + μ_BgSH, yielded g = 2.077 and J = −0.9 cm⁻¹, describing a pair of antiferromagnetically coupled Cu^II ions. The accuracy of these spin-Hamiltonian parameters was aided by simultaneous fitting of variable field magnetisation measurements (Fig. S5, ESI†). The exchange coupling constant denotes a weak interaction between the two Cu^II centres, consistent with the lengthy through-bond and through-space coupling pathways.

In the absence of diffraction-quality single crystals, a structure of [1] was obtained by geometry optimisation at the BP86 level of theory. The result was a two-fold symmetric molecule with identical CuS₄ centres that are coplanar (Table S4, ESI†). The average Cu–S distance is in excellent agreement with other dicopper metallo-macrocycles, as are the dithiocarbamate bite angles and tetrahedralisation about the metal ion. The Cu⋯Cu distance at 5.96 Å is slightly longer than the experimental value of 5.42 Å,²⁰ but the crystal structure is influenced by lattice packing excluded from the optimisation. The CuS₄ plane makes an angle of 40.6° to the Cu⋯Cu vector, a parameter added to the exchange coupling matrix for the EPR simulation (vide infra). The electronic structure is described by a broken-symmetry (BS) solution with one unpaired electron in b_1g magnetic orbital localised at each CuS₄ site giving a near singlet–triplet ground state (Fig. S14, ESI†). This is the Cu–S σ* orbital with 49% Cu d character, underpinning the high covalency of this system. The exchange coupling constant is estimated at J_calcd = −0.09 cm⁻¹, a consequence of the negligible overlap of the magnetic orbitals where spin propagation is through the inefficient σ bonding pathway. The Mulliken spin density analysis shows one unpaired electron at each CuS₄ site with the majority (60%) resident on sulfur (Fig. S15, ESI†). The highly covalent in-plane bonding provided by the dithiocarbamate results in the long spin–lattice relaxation lifetime. The magnitude of the exchange interaction is evident in the fluid solution EPR spectrum. The seven-line hyperfine pattern stems from the coupling of two Cu^II centres each with 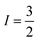nuclear spin from the 100% abundant ^63,65Cu isotopes (Fig. S6, ESI†). Given the near singlet–triplet ground state, the spectrum was simulated for S = 1 and gave g_iso = 2.042 and A_iso = 35 × 10⁻⁴ cm⁻¹. The corresponding fluid solution spectrum of [Cu(dbdtc)₂] yielded gave g_iso = 2.043 and A_iso = 74 × 10⁻⁴ cm⁻¹, values synonymous with Cu^II bis-dithiocarbamates (Fig. S7, ESI†). This gives a benchmark hyperfine coupling for a single CuS₄ centre, which being double the value for [1], confirms J ≫ A (Fig. S8).

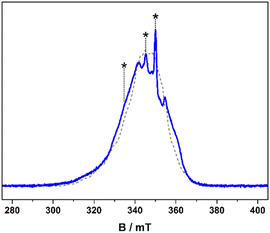
The frozen solution spectrum displays a complicated hyperfine pattern that stems from weakly coupled Cu^II ions (Fig. S9, ESI†). Unlike the fluid solution measurement, the weak coupling produces extensive singlet–triplet mixing of the ground state, leading to the appearance of the “forbidden” half-field signal. The complicated line broadening is due to the inherent flexibility of [1] that leads to inhomogeneity in the linewidth, which is impossible to include in the simulation as it results from g-, A- and J-strain. Within this limitation, the simulation has been achieved using the geometry-optimised structure as the starting point, which is two-fold symmetric giving equivalent Cu^II sites (Fig. 1). The computed Cu⋯Cu distance of 5.96 Å and the relative orientation of each CuS₄ coordination plane to the Cu⋯Cu vector at ϕ = 40.6° are included in the dipolar matrix (Jd). The principal g- and A-values were taken from the spectrum of [Cu(dbdtc)₂] (Fig. S10, ESI†), the isotropic exchange constant from magnetic susceptibility, and these were systematically varied along with the Cu⋯Cu distance and angle ϕ to achieve a match with the spectral width (Fig. S11, ESI†). Such approximations are necessary for simulation of spectra for molecules with weak coupling between multiple spin centres.²¹ The best result gave g = (2.03, 2.03, 2.10) and A = (30, 30, 160) × 10⁻⁴ cm⁻¹, applied to both the allowed transitions and the half-field signal (Table 1). The degree of axiality is consistent with all known Cu^II bis-dithiocarbamates and the average values match the isotropic ones.²² With Cu⋯Cu fixed at 6 Å, the angle of each CuS₄ plane to this vector was increased to ϕ = 58°. The best fit gave J = +0.1 cm⁻¹, describing a ferromagnetic coupling between the Cu^II ions, which accords with spin propagation through an even number of bonds brough about by the meta-substituted aromatic linker.²³ This is different to J = −0.9 cm⁻¹ from susceptibility, as powder samples will often give an intermolecular coupling that overrides a smaller intramolecular exchange interaction. Nevertheless, both estimates of J underscore the extensive singlet–triplet mixing in the ground state.

Table 1 Experimental and calculated EPR spin-Hamiltonian parameters

Parameter	Experimental	Calculated^a
a From ZORA-PBE0 DFT calculations. b 〈g〉 = (gx + gy + gz)/3. c Rhombicity, Rg = (gy − gx)/(gz − gx). d g-anisotropy, Δg = gz − gx. e In units 10^−4 cm^−1. f 〈A〉 = (Ax + Ay + Az)/3. g In units cm^−1. h Angle between Cu⋯Cu vector and CuS4 mean plane.
g x	2.03	2.026
g y	2.03	2.034
g z	2.10	2.097
〈g〉^b	2.053	2.052
R g	0	0.113
Δg^d	0.07	0.071
A xx	30	−42.9
A yy	30	−43.6
A zz	160	−132.6
〈A〉^e^f	73.3	−73.0
J	+0.1	−0.09
ϕ	58°	41°

---

The electronic structure of [1] has been verified through accurate calculation of the spin-Hamiltonian parameters. Noticeably the calculated g-values are very close to those used in the simulation with the same anisotropy and small rhombicity provided by the acute bite angle of the dithiocarbamate ligand (Table 1). Given the two-fold symmetry of the metallo-macrocycle, the Cu^II sites are identical, and the orientation of the g-matrix is the same for both with g_z perpendicular to the CuS₄ plane, and g_x bisecting the dithiocarbamate ligand (Fig. 1). This orientation perfectly matches the results obtained from single-crystal EPR studies of Cu^II dithiocarbamates.²⁴ Hyperfine coupling constants obtained via the DFT method are generally less accurate as is the case here but the degree of axiality replicates that seen experimentally.

The spin relaxation properties, parameterised by T₁ and T_M, were investigated for [1] at a field position corresponding to the most intense signal in the electron spin echo (ESE)-detected spectrum at 350 mT (Fig. 2). The solvent system was a 4 : 1 mixture of CDCl₃/Cl₃CCN, which was chosen as the compound retains its glass at the measurement temperature as well as being devoid of nuclear spins.⁸ Inversion recovery data were collected to assess the temperature dependence of the spin–lattice relaxation between 5 and 50 K (Fig. 3). The curves are modelled with a biexponential function that yielded values for the fast (T_1,f) and slow (T_1,s) relaxation processes, assigned to spectral diffusion and spin–lattice relaxation times, respectively. Overall the T_1,s decreases by an order of magnitude from 25.1 ms at 5 K to 2.5 ms at 50 K. The magnitude of T₁ is similar to other bimetallic molecular spin qubits, and considerably longer than T_M.^1,4,9,25 The decay of the Hahn echo also follows a biexponential profile, giving a phase memory time of 5.35 μs at 5 K that is essentially invariant up to 20 K (Fig. 3). The relaxation time improves by ca. 10% when the field position is shifted to 346 mT coinciding with a component of the A_zz hyperfine interaction, but then decreases by a similar amount when the field is moved further from the echo maximum. The absence of a field dependent trend is derived from the near degenerate singlet–triplet ground state. The decline above 20 K is a consequence of the coupling between the spin centres as T₁ remains thee orders of magnitude longer at 50 K, though ligand protons will contribute to the decoherence. This is a different outcome to a related dicopper(II) complex where the T₁ and T_M approach parity at this temperature.⁹

Fig. 2 ESE-detected EPR spectrum (blue line) and simulation (dashed line) of a 0.5 mM solution of the [1] in 4 : 1 CDCl₃/Cl₃CCN recorded at 10 K. Asterisks indicate field positions for relaxation measurements.

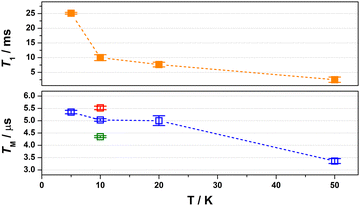Fig. 3 Comparison of the temperature dependence of T₁ (top) and T_M (bottom) relaxation times for [1] diluted in 4 : 1 CDCl₃/Cl₃CCN recorded at B₀ = 350 mT. Field dependence of the T_M relaxation.

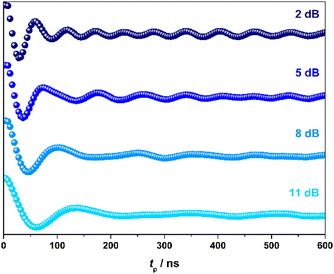
To demonstrate coherent spin control, echo-detected nutation experiments were performed by applying a microwave pulse of duration t_p to produce Rabi-like oscillations between two states that correspond to arbitrary superpositions of the electron spin (Fig. 4). The physical origin is confirmed by the linear dependence of the oscillation frequency (Ω_R) with the applied microwave amplitude (B₁), which was varied by selecting microwave attenuations of 2, 5, 8 and 11 dB (Fig. S19, ESI†). Changes in the oscillations were observed at t_p > 400 ns that derive from interaction with ligand protons and are independent of the microwave attenuation.²⁶

Fig. 4 Variable power nutation measurements for [1] in 4 : 1 CDCl₃/Cl₃CCN at 10 K and 350 mT.

This dicopper(II) metallo-macrocycle affords enviable phase memory times for a multi-level molecular qubit. The system is addressable where an applied potential can switch individual spin centres “on” and “off”, and access different entanglement opportunities. The major advantage of this bis-dithiocarbamate linker is the ease with which it can be synthetically modified to afford a tuneable system. Such adaptations include extending the aromatic backbone to modulate the spin coupling, mixing metal ions to give separately addressable spins, and expand the number of spin centres by provide additional coordination sites via the alkyl group of the amine. Focus will now be directed towards exploring the chemical space to deliver options aimed at overcoming the current bottleneck that is the physical implementation of quantum logic.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. S. Sproules, in Electron Paramagnetic Resonance, ed. V. Chechik and D. M. Murphy, The Royal Society of Chemistry, Cambridge, UK, 2017, vol. 25, pp. 61.
2. A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301.
3. S. Sproules, Dalton Trans., 2021, 50, 4778.
4. K. Bader, M. Winkler and J. van Slageren, Chem. Commun., 2016, 52, 3623.
5. (a) M. J. Graham, C. Yu, M. Krzyaniak, M. R. Wasieleski and D. E. Freedman, J. Am. Chem. Soc., 2017, 139, 3196; (b) C. Yu, M. J. Graham, J. M. Zadrozny, J. Niklas, M. Krzyaniak, M. R. Wasieleski, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 14678.
6. M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2017, 139, 4338.
7. (a) S. Nakazawa, S. Nishida, T. Ise, T. Yoshino, N. Mori, R. Rahimi, K. Sato, Y. Morita, K. Toyota, D. Shiomi, M. Kitagawa, H. Hara, P. Carl, P. Höfer and T. Takui, Angew. Chem., Int. Ed., 2012, 51, 9860; (b) G. Wolfowicz and J. J. L. Morton, eMagRes, 2016, 5, 1515.
8. J. McGuire, H. N. Miras, E. Richards and S. Sproules, Chem. Sci., 2019, 10, 1483.
9. J. Salinas Uber, M. Estrader, J. Garcia, P. Lloyd-Williams, A. Sadurní, D. Dengler, J. van Slageren, N. F. Chilton, O. Roubeau, S. J. Teat, J. Ribas-Ariño and G. Aromí, Chem. – Eur. J., 2017, 23, 13648.
10. S. L. Bayliss, D. W. Laorenza, P. J. Mintun, B. D. Kovos, D. E. Freedman and D. D. Awschalom, Science, 2020, 370, 1309.
11. (a) J. M. Arndur, K. R. Mullin, M. J. Waters, D. Puggioni, M. K. Wojnar, M. Gu, L. Sun, P. H. Oyala, J. M. Rondinelli and D. Freedman, Chem. Sci., 2022, 13, 7034; (b) I. Pozo, Z. Huang, F. Lombardi, D. I. Alexandropoulos, F. Kong, M. Slota, I. Tkach, M. Bennati, J.-R. Deng, W. Stawski, P. N. Horton, S. J. Coles, W. K. Myers, L. Bogani and H. L. Anderson, Chemistry, 2024, 10, 299; (c) D. Ranieri, F. Santanni, A. Privitera, A. Albino, E. Salvadori, M. Chiesa, F. Totti, L. Sorace and R. Sessoli, Chem. Sci., 2023, 14, 61.
12. (a) M. Atzori, A. Chiesa, E. Morra, M. Chiesa, L. Sorace, S. Carretta and R. Sessoli, Chem. Sci., 2018, 9, 6183; (b) A. Chiesa, F. Petiziol, E. Macaluso, S. Wimberger, P. Santini and S. Carretta, AIP Adv., 2021, 11, 025134.
13. (a) S. Lockeyer, A. J. Fielding, G. F. S. Whitehead, G. A. Timco, R. E. P. Winpenny and E. J. L. McInnes, J. Am. Chem. Soc., 2019, 141, 14633; (b) C. J. Rogers, D. Asthana, A. Brookfield, A. Chiesa, G. A. Timco, D. Collison, L. S. Natrajan, S. Carretta, R. E. P. Winpenny and A. M. Bowen, Angew. Chem., Int. Ed., 2022, 61, e202207947.
14. (a) D. Aguilà, O. Roubeau and G. Aromí, Dalton Trans., 2021, 50, 12045; (b) D. Maniaki, D. Garay-Ruiz, L. A. Barrios, D. O. T. A. Martins, D. Aguilà, F. Tuna, D. Reta, O. Roubeau, C. Bo and G. Aromí, Chem. Sci., 2022, 13, 5574.
15. S. Chicco, G. Allodi, A. Chiesa, E. Garlatti, C. D. Buch, P. Santini, R. De Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2024, 146, 1053.
16. (a) R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. S. Pedersen, R. De Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2018, 140, 9814; (b) K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801.
17. G. Hogarth, Prog. Inorg. Chem., 2005, 53, 71.
18. (a) J. Cookson, E. A. L. Evans, J. P. Maher, C. J. Serpell, R. L. Paul, A. R. Cowley, M. G. B. Drew and P. D. Beer, Inorg. Chim. Acta, 2010, 363, 1195; (b) M. E. Padilla-Tosta, O. D. Fox, M. G. B. Drew and P. D. Beer, Angew. Chem., Int. Ed., 2001, 40, 4235.
19. A. R. Hendrickson, R. L. Martin and N. M. Rohde, Inorg. Chem., 1976, 15, 2115.
20. P. D. Beer, N. Berry, M. G. B. Drew, O. D. Fox, M. E. Padilla-Tosta and S. Patell, Chem. Commun., 2001, 199.
21. (a) M. Atzori, S. Benci, E. Morra, L. Tesi, A. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731; (b) I. Borilovic, P. J. Alonso, O. Roubeau and G. Aromí, Chem. Commun., 2020, 56, 3139.
22. A. V. Ivanov, E. V. Korneeva, B. V. Bukvetskii, A. S. Goryan, O. N. Antzutkin and W. Forsling, Russ. J. Coord. Chem., 2008, 34, 59.
23. C. Riplinger, J. P. Y. Kao, G. M. Rosen, V. Kathirvelu, G. R. Eaton, S. S. Eaton, A. Kutateladze and F. Neese, J. Am. Chem. Soc., 2009, 131, 10092.
24. S. A. Al'tshuler, R. Kirmse and B. V. Solov'ev, J. Phys. C: Solid State Phys., 1975, 8, 1907.
25. K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304.
26. S. R. Hartmann and E. L. Hahn, Phys. Rev., 1962, 128, 2042.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental procedures for synthesis, and physical and computational methods; electronic spectra; cyclic voltammetry; magnetometry; cw and pulsed EPR spectra and data analysis; orbital and spin density plots. See DOI: https://doi.org/10.1039/d4cc03859b

---