Open Access Article
Open Access ArticleGenesys-Cat: automatic microkinetic model generation for heterogeneous catalysis with improved Bayesian optimization†
Yannick Ureel ,
Lowie Tomme,
Maarten K. Sabbe
,
Lowie Tomme,
Maarten K. Sabbe and
Kevin M. Van Geem
and
Kevin M. Van Geem *
*
Laboratory for Chemical Technology, Department of Materials, Textiles and Chemical Engineering, Ghent University, Technologiepark 125, 9052 Gent, Belgium. E-mail: Kevin.VanGeem@UGent.be
First published on 2nd January 2025
Abstract
Developing complex microkinetic models for heterogeneous catalysis is a cumbersome task, often lacking accuracy if proper kinetic properties are unknown. Therefore, a novel rule-based microkinetic model generator for heterogeneous catalysis called Genesys-Cat is presented. Genesys-Cat automatically generates an elementary reaction network based on user-defined reaction families. One of the main advantages of Genesys-Cat is the determination of kinetic properties based on a limited set of experimental data when ab initio data is absent. Genesys-Cat employs an improved, highly efficient Bayesian optimization algorithm to estimate accurate kinetic properties with limited computational and experimental effort. In this way, computationally and experimentally efficient, accurate microkinetic models (R2 = 0.89–0.99) can be generated for a wide range of processes involving heterogeneous catalysts. Genesys-Cat facilitates the automatic generation of gas and surface-phase mechanisms in parallel, which is compatible with standard reactor model simulators like Chemkin and Cantera. The benefits of our approach are demonstrated in the catalytic cracking of iso-octane for three different zeolites, while our model generator is also applicable to conventional metal catalysts. The obtained microkinetic models identify the dominant reaction pathways and can be employed for rational catalyst and reactor design.
1. Introduction
Chemical kinetic models predict conversion, product yields, and heat consumption and allow the assessment of dominant reaction pathways under various conditions.1 The predictions of these models can be employed for the optimization of process conditions,2,3 reactor or catalyst design,4–6 or environmental and life-cycle analysis and plant design.7 The more fundamental these validated kinetic models are, the more insight they provide into the reaction mechanism, the more reliable their predictions are for a wide range of process conditions, and, hence, the more valuable they are. Microkinetic models consider only elementary reactions and do not lump species together. These reaction networks can be generated manually for processes with a limited number of reactions, but for many real-life processes, this is unfeasible. In processes like steam cracking,8,9 pyrolysis,10–12 catalytic cracking,13,14 combustion15 and others, hundreds to thousands of elementary reactions can occur.16 Therefore, numerous automated network generators have been developed that have in common that they determine all relevant elementary reactions based on a set of reaction families that describe all possible reactions a molecule undergoes in the respective chemical process. A wide range of automated microkinetic model generators have been developed in the past decades, such as NETGEN,17 ReNGeP,18 RMG,19,20 Genesys,21 and RING.22 These mechanism generators are either rule-based or rate-based. In rule-based generators, the defined reaction families entirely determine the reaction network. On the other hand, rate-based generators calculate the production rate of species and only add the involved reactions to the network if the production rate is above a certain threshold.The previously discussed reaction network generators have been developed predominantly for gas- or liquid-phase reactions and do not consider the presence of a catalyst. Nevertheless, catalytic reactions comprise 90% of all chemical processes.23 When generating reaction networks for catalytic processes, most network generators, such as ReNGeP, only consider one phase and do not consider the catalyst explicitly.18 RMG improved on this and integrated the catalytic network generator RMG-cat to facilitate rate-based reaction network generation of catalytic networks, explicitly considering the catalyst.24,25 Recently, it was demonstrated how RMG can be used to generate an optimal microkinetic model considering the correlated uncertainty of the employed quantum chemical properties.26 A disadvantage of this approach, however, is that accurate kinetics for the catalytic reactions are required to generate the reaction network because of the rate-based algorithm. These accurate kinetic properties are often lacking for catalytic reactions, as quantum chemical ab initio data is computationally expensive to acquire and does not always reach chemical accuracy (within 4 kJ mol−1 margin of error).27 Typically, the uncertainty in density functional theory calculations amounts to 20–40 kJ mol−1.28 Hence, the single-event microkinetic (SEMK) modeling approach is still popular for modeling complex catalytic processes.29 Within the SEMK approach, constant kinetic properties are assumed for every reaction family with eventual corrections for symmetry and Brønsted–Evans–Polanyi relations. They are often determined by regressing them with experimental data.30 While the fitted kinetic properties do not always reflect reality, this is often a necessary approximation due to a lack of accurate kinetic properties. Microkinetic models based on SEMK typically employ network generations using Boolean relation matrices, representing molecules by a matrix.31–33 This approach lacks interpretability, flexibility, and compatibility with other chemo-informatic tools. A more intuitively interpretable model is obtained by representing molecules in reaction families by SMARTS or Smiles in automated microkinetic model generators.34 Moreover, the constraints on reactants and products are more easily defined, making it more flexible, and the use of chemoinformatic packages like RDKit or CDK35,36 makes it more compatible with chemoinformatic tools such as machine learning for thermodynamic property prediction.
In this work, we have developed a new rule-based automated catalytic microkinetic model generator coupled with improved Bayesian optimization for kinetic property estimation. Using a rule-based network generator for catalytic processes is of high value for modeling these reactions, as has been demonstrated for metal-catalyzed processes.37,38 Estimating accurate kinetic properties based on quantum chemical predictions is challenging due to the lack of available data. Therefore, rate-based microkinetic models like RMG estimate kinetics based on the Brønsted–Evans–Polanyi relation or reaction similarity with the existing kinetic library.24 This often works for common metal catalysts if there is a close match between the library and the reaction to estimate. However, this methodology often fails with zeolites or more complex catalysts as the similarity is lacking. This makes a rule-based network generator less error-prone as the elementary reactions added do not require an estimation of the kinetics. Kinetic properties must be estimated after the reaction network has been generated and thermodynamic properties are determined. Most microkinetic models employ a combination of the Rosenbrock39 or gradient-based Levenberg–Marquardt algorithm40 to fit their kinetic parameters to the experimental data.41 One disadvantage of these optimizers is that they do not guarantee finding the global optimum and require a large number of function evaluations. Depending on the complexity of the reactor and microkinetic models, this can limit the optimization of the parameters. Therefore, an improved Bayesian optimization algorithm is proposed in this work. A global optimum can be found with a minimum of function evaluations by employing Bayesian optimization. Using an automated, rule-based kinetic model generator coupled with Bayesian optimization enables us to quickly obtain a fundamental catalytic kinetic model with a minimum of simulation effort and experimental data. These models can yield valuable insights into catalytic reaction pathways and how to improve selectivities or activities. To illustrate these capabilities, a case study on the cracking of iso-octane in three different zeolites is performed.
2. Materials and methodology
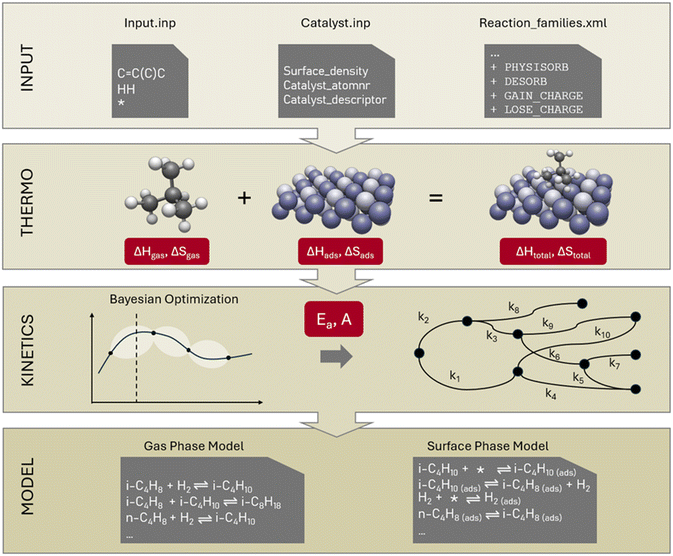
The automated catalytic microkinetic model generator is a branch of the in-house developed gas-phase kinetic model generator “Genesys”. Therefore, we have named the catalytic model generator “Genesys-Cat” and will refer to it as such throughout the manuscript. In the method section, we will focus on the extensions made on Genesys for catalytic model generation and will only provide a basic description of its inner workings. Genesys generates microkinetic models in four steps: it reads the input (discussed in the upcoming section 2.1), generates the reaction network (section 2.2), assigns thermodynamic properties (section 2.3), and determines the kinetic properties of all reactions (section 2.4). The extensions of these steps for Genesys-Cat will be discussed in the following sections. Fig. 1 presents an overview of the Genesys-Cat workflow and the added extensions to model catalytic reactions, which will be discussed throughout the method section. For further detailed information, the reader is referred to the original work on Genesys.212.1. Input
The process reactants have to be supplied to “Input.inp,” which is a similar input file as for gas-phase models, where the Smiles of the reactants are given, only with the catalyst dummy atom added, represented by a “*” in Fig. 1. As Genesys is based on the Java package CDK,35,36 the catalyst must be represented by a chemical element to allow reactions to occur. The most appropriate representation depends on the type of catalyst. In the case of metal catalysts, this can be the most abundantly present metal. The consideration of multiple active sites where adsorbates interact across the different surfaces is also supported, even though, in traditional modeling, this is not common.In addition to the “Input.inp” file, a catalyst input file must be generated to specify to Genesys-Cat that a catalyst is present. This file contains the name of the catalyst, the surface site density, and the atom number of the chemical element representing the catalyst. Apart from this formal representation of the catalyst by an element, the catalyst input file can optionally contain simple kinetic catalyst descriptors, which can be used later to calculate kinetic properties. For example, in zeolite chemistry, the protonation enthalpy is often used to represent the effect of acidity and added to the activation energies of certain scission reactions.31,42
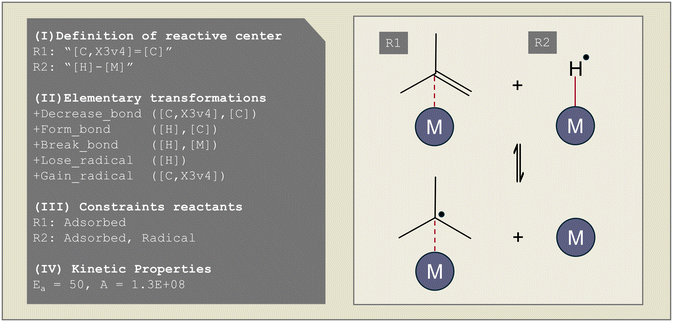
2.2. Network generation
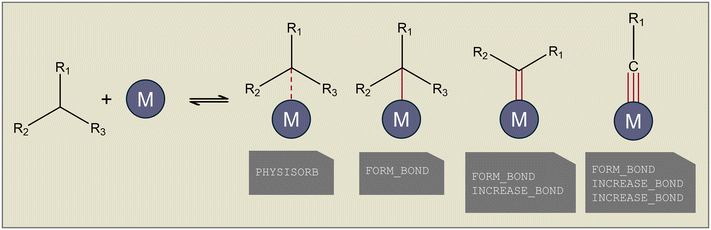
As Genesys is a rule-based microkinetic model generator, a reaction family file has to be specified to define the different elementary reactions that occur. Reaction families consist, in general, of four parts, as illustrated in Fig. 2: (I) the definition of the atoms and bonds in SMARTS notation, which are the reactive center(s), (II) the recipe of elementary transformations these reactive centers undergo upon reaction, (III) constraints upon the reactants and products formed, (IV) the kinetics of the reaction. The possible elementary transformations and constraints are extended in Genesys-Cat to properly generate catalytic reaction networks.The main difference between gas-phase and surface reactions from a conceptual network generation point of view is the occurrence of adsorption. However, in catalysis, adsorption is not the simple formation of a bond between a molecule and the catalyst, as a distinction has to be made between physisorption and chemisorption. Physisorption is a delocalized bond between the adsorbate and adsorbent that differs from the localized single, double, or triple bonds in chemisorption. The distinction between physisorption and chemisorption allows for a more accurate thermochemistry calculation, as a distinction can be made between a weaker physical interaction or a stronger chemical bond. Therefore, as presented at the top of Fig. 1, in Genesys-Cat, two new elementary transformations are defined as “physisorb” and “desorb” for the physisorption step and its reverse reaction. For this, a new type of delocalized bond is defined in the CDK package. Chemisorption is also allowed in Genesys-Cat with single, double, and triple bonds, which is already described by the original gas-phase model generator Genesys, as shown in Fig. 3. The network generation guarantees the site balance by maintaining the number of active sites within every reaction. The total number of active sites is specified in reactor model solvers like Chemkin and Cantera,43 where a catalyst site density and catalyst surface area are provided.
 | ||
| Fig. 3 Different types of adsorption bonds incorporated in Genesys-Cat with the corresponding elementary transformation below. | ||
In addition to adsorption, catalytic species can have charges, such as, for example, in cracking chemistry where the zeolite acid site donates a proton and ionizes hydrocarbons to carbonium and carbenium ions.44–46 This is opposed to gas-phase reactions of hydrocarbons where no ionized molecules are formed. Therefore, an additional constraint is defined to verify the charge of a molecule. In addition, two elementary transformations, “gain_charge” and “lose_charge”, are defined, which allow reactive atoms to gain and lose charges.
One advantage of Genesys-Cat being a branch of Genesys and not an entirely new code is that it allows simultaneous generation of gas-phase and surface-phase reactions and interaction of both phases. For example, the parallel generation of gas-phase and surface-phase reactions is important in high-temperature catalytic reactions where side reactions can occur in the high-temperature gas phase. In ESI,† a hypothetical kinetic model for thermal and catalytic cracking of 1-butene comprising both gas- and surface-phase reactions is provided to illustrate Genesys-Cat's capabilities. A list of the employed reaction families is available in the ESI.† To generate a mechanism with coupled gas- and surface-phase reactions, the same input files can be used as in a conventional catalytic reaction system. The sole input file requiring modification is the reaction family file. This file specifies both gas- and surface-phase reaction families, with constraints applied to the reactants to indicate whether a given reactant is adsorbed onto a catalyst surface. During reaction network generation, Genesys-Cat automatically determines whether or not a generated reaction occurs on a surface and should be written to the surface- or gas-phase mechanism. Other processes comprising both gas- and surface-phase reactions include methane pyrolysis,47–49 oxidative dehydrogenation of ethane or propane to ethylene or propylene,50–52 catalytic combustion,53–55 and catalytic pyrolysis of biomass or plastic waste at severe temperatures.56,57 Most common reactor models, such as Chemkin or Cantera, can solve multiphase models. Therefore, the generated microkinetic model by Genesys-Cat is compatible with Chemkin and can be readily converted to Cantera compatible formats.
2.3. Thermodynamic properties
After the reaction network has been generated and all products are determined, thermodynamic properties must be assigned to all reactants and products. For gas-phase molecules, Genesys uses the extensive quantum chemical library, group additivity, and machine learning models to determine accurate enthalpies of formation, entropies, and heat capacities. These properties are all represented by NASA polynomials to account for the temperature dependencies following the Chemkin and Cantera format. In this way, chemically accurate (within 4 kJ mol−1) thermodynamic properties are attained for gas-phase molecules.58–60The thermodynamics of adsorbed species follow the same hierarchy, where the quantum chemical library is first screened, and statistical models are used to predict the enthalpy of formation, standard molar entropy, and heat capacity albeit in the form of NASA-polynomials. Most thermodynamic libraries of adsorbed species consider metal catalyst sites such as platinum alloys,61 bimetallic alloys,62,63 or metal–organic frameworks.64 Genesys-Cat relies on predictive models for thermochemical property prediction when the adsorbed compound is absent in the library. For this, the gas-phase properties are calculated to which an adsorption enthalpy or entropy is added. Therefore, the dummy atom representing the catalyst is removed, and the InChI of the corresponding gas-phase molecule is determined. Then adsorption corrections are added to the gas-phase properties. Today different models exist to predict mainly the adsorption enthalpy of a wide range of (bi)metallic catalysts.65–68 As Genesys-Cat is specifically developed with the purpose of generating catalytic mechanisms for zeolites, the developed models by De Moor et al.69 and Nguyen et al.70 are incorporated for the prediction of the adsorption enthalpy and entropy of alkanes and alkenes respectively. This allows the fast and accurate determination of the hydrocarbon thermochemistry in four common zeolite frameworks: FAU, MFI, BEA, and MOR. The accuracy of these adsorption corrections is typically between 10–20 kJ mol−1, which is worse than that of gas-phase species due to the employed quantum chemical methods.69
2.4. Kinetic properties
The kinetic parameter estimation in microkinetic catalytic models based on experimental data is common practice.32,41,71,72 This is because accurate quantum chemical ab initio data is often lacking, as quantum chemical methods in catalysis are either highly expensive or lack sufficient accuracy to achieve chemical accuracy.28,73 Within the SEMK approach, kinetic properties are often kept constant within one reaction family. Certain reactions are assumed to be in quasi-equilibrium as they go orders of magnitude faster than other rate-determining steps. The leftover critical kinetic parameters are then commonly determined by minimizing the residuals between the experimental and estimated quantities, such as molar flowrates, mole/mass fractions, and yields of the relevant molecules. The preliminary microkinetic model must be solved with a reactor model based on the experimental setup to estimate these quantities. As mentioned, common algorithms to minimize the residuals and determine the kinetic parameters are the Rosenbrock algorithm, Levenberg–Marquardt algorithm, or genetic algorithms.74 However, Levenberg–Marquardt is a gradient-based algorithm, making it expensive to evaluate as it has to compute the gradient at every time step, and it is prone to be stuck in local optima, which is detrimental to the performance of the obtained microkinetic model. Therefore, their performance highly depends on the initial guess of the kinetic parameters. Genetic algorithms are excellently suited for finding a global optimum but require a lot of function evaluations to converge, making them computationally expensive.
When designing a Bayesian optimization algorithm, two parameters are essential for its performance: the Gaussian process kernel and the acquisition function. The Gaussian process kernel determines the covariance function of the objective function to learn.76 In essence, this kernel determines the “shape” of the surrogate model. The most common kernel employed in Bayesian optimization is the radial basis function (RBF). Further, the acquisition function determines the next query, which is the next set of kinetic parameters to evaluate. This acquisition function is optimized (typically maximized) to determine the next query by balancing both exploration (discovering the objective function) and exploitation (selecting a query with a low objective function value). The most commonly used acquisition function is the expected improvement (EI) function which maximizes the expected value that a query will improve upon the current optimum.
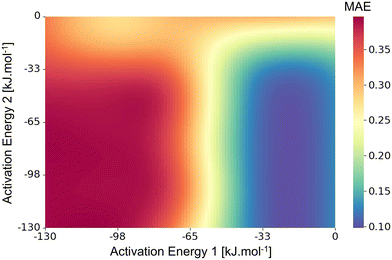
For usage in Genesys-Cat, an improved Bayesian optimization is proposed compared to the common combination of an RBF-kernel and EI acquisition function. In this improved optimization algorithm, adaptations were made to both the kernel and the acquisition function. The objective function typically spans a wide range in values with areas where conversions are properly estimated but the product selectivities are not optimally determined and areas where the conversions are over- or underestimated. This results in typically two plateaus, separated by a steep gradient, as visualized in Fig. 4. Evidently, the Bayesian optimization should be able to reach adequate conversions and selectivities even though these effects occur at a different length scale. While the conversion varies slowly at long length scales with the resulting two patterns, the product selectivities vary faster at lower length scales and more subtly affect the objective function. Therefore, two kernels are combined to represent this behavior. The rational quadratic kernel (RQ) is employed to represent the effect of the conversion, while the Matérn-kernel (ν = 3/2) allows for less smooth behavior and captures the impact of changing selectivities.
Inspired by the work of Hoffman et al.,77 a combination of acquisition functions is employed. While the original hedge algorithm proposed by Hoffman et al. was found to be suboptimal, a combination of expected improvement and minimization of the Gaussian process surrogate model was performed by iterating at every run. Expected improvement balances exploration and exploitation while minimizing the Gaussian process (surrogate model) purely exploits. In every iteration, the other acquisition function is called. In this way, the Bayesian optimization quickly converges to the relevant range as it is more exploitative, exploring less of the entire field but converging faster to an optimum than regular expected improvement. It also identifies sooner when it falsely predicts a parameter combination to be promising. Note that the Bayesian optimization algorithm uses a Chemkin model as input and can hence be independently used of Genesys-Cat.
All Bayesian optimization strategies were initialized with 50 random function evaluations. The acquisition functions were optimized using a differential evolution algorithm, after which this optimum was employed as input for a minimization based on the L-BFGS-B algorithm as implemented in SciPy. The Gaussian processes were implemented with the Scikit-learn package.78
2.5. Case-study: catalytic cracking of iso-octane
A case study was performed on the catalytic cracking of iso-octane to demonstrate the benefits of Genesys-Cat coupled with the improved Bayesian optimization algorithm. Experimental data from three different zeolites were gathered, and an automatically generated microkinetic model was constructed.| Zeolite (topology) | T (K) | piC8 (kPa) | W/FiC8 (kgcat s mol−1) | Conversion (mol%) | Number of experiments |
|---|---|---|---|---|---|
| LZY20 (FAU) | 748 | 6–8 | 8–80 | 17–60 | 15 |
| CBV720 (FAU) | 723–748 | 3–8 | 14–132 | 21–52 | 14 |
| CBV760 (FAU) | 723–748 | 3–8 | 13–215 | 4–33 | 15 |
For the kinetic properties, the activation energies were taken from molecular dynamic calculations81,82,84–89 as specified in Table 2, while the pre-exponential factors were determined via the proposed Bayesian optimization algorithm. The protonation and isomerization reactions were considered in quasi-equilibrium, and the activation entropy and enthalpy were set to zero. Consequently, twelve parameters were left to optimize with Bayesian optimization. In general, limiting the dimensionality of the optimization problem to 20 dimensions is advised.75 The minimized objective function was the absolute sum of the residual mole fraction of all relevant species, as presented by eqn (1). The optimized parameters were the activation entropies, as these scale more linearly with the objective function, unlike a direct regression of the pre-exponential factors. As activation energies are more widely available and more accurately determined by static quantum chemical calculations,90 it was decided to regress the activation entropies and acquire the activation energy from the literature. The employed parameter ranges for the activation entropy are reported in Table S2 in the ESI.† Eqn (2) presents the link between the activation entropies (Δ‡S) and the pre-exponential factors (A), with kb the Boltzmann constant, h the Planck constant, and R the universal gas constant. However, when activation entropies are available while activation energies are unknown, it is also possible to estimate the activation entropies with Bayesian optimization instead of the activation energies. When both the activation energies and entropies are unknown, estimating one of them is still advisable. This is because the activation energies and entropies are highly correlated, hampering a simultaneous estimation of both. If an educated initial guess of the kinetic parameters is available, one can include this parameter combination in the initial data to guide the Bayesian optimization. The latter is not done for the presented case study.
| Ea [kJ mol−1] | Ea [kJ mol−1] | ||
|---|---|---|---|
| a Extrapolated from protolytic scission (p) and (s). | |||
| Physisorption | 0 | Protonation81,82 | 20 |
| Intramolecular H-/Me-shift85,86 | 15 | PCP-branching85 | 35 |
| Protolytic scission (p)84 | 180 | β-Scission (p)88 | 85 |
| Protolytic scission (s)89 | 140 | β-Scission (s,s)82 | 75 |
| Protolytic scission (t)a | 110 | β-Scission (s,t)82,88 | 67 |
| Hydride-transfer (s)87 | 52 | β-Scission (t,s)82 | 70 |
| Hydride-transfer (t)87 | 52 | β-Scission (t,t)82 | 53 |
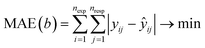 | (1) |
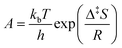 | (2) |
Reactor simulations were performed using Chemkin reactor models. The recycle electro-balance reactor could be modeled as a continuously stirred tank reactor (CSTR). The governing equations for the CSTR, eqn (3) and (4), are solved for steady-state to find the appropriate output. The molar flow rate of compound i is denoted by Fi, with F0i the inlet composition. The rate of production per mass of catalyst is represented by Ri, with W the catalyst mass. τ represents the mean residence time in the reactor, and surface species are denoted by i*, with Ci* the molar concentration per mass of catalyst.
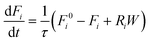 | (3) |
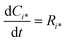 | (4) |
3. Results and discussion
3.1. Automatic network generation
The obtained reaction network by Genesys-Cat is entirely dependent on the defined reaction families and product and reactant constraints. To demonstrate the flexibility of Genesys-Cat, three different reaction networks, with three distinct product constraints, are presented employing the 23 reaction families as defined in section 2.5.2. Here we varied the maximum number of carbon atoms between 8 and 12, and the maximum number of double bonds between 1 and 2. From Table 3 it is clear that varying the product constraints profoundly affects the obtained reaction network size. To maintain numerical stability when solving the kinetic model and limit computation time, it is important not to exaggerate the size and complexity of the reaction network. For this reason, it is important to be knowledgeable about the modeled process and to know which products are relevant to consider.| Network no. | Max. carbon atoms | Max. double bonds | No. species | No. reactions |
|---|---|---|---|---|
| 1 | 8 | 1 | 104 | 561 |
| 2 | 12 | 1 | 232 | 1251 |
| 3 | 12 | 2 | 325 | 1760 |
As no species with two double bonds and more than 8 carbon atoms were experimentally detected, a reaction network consisting of 104 species and 561 reversible reactions, including the physisorption reactions, was selected. As all considered reactions are reversible, the kinetic model is thermodynamically consistent. Table 4 provides a more detailed overview of the number of reactions per type of reaction family.
| Reaction family | No. reactions |
|---|---|
| Physisorption | 54 |
| Protonation | 18 |
| Protolytic scission | 48 |
| β-Scission | 12 |
| Intramolecular H-shift | 14 |
| Intramolecular Me-shift | 14 |
| Intermolecular hydride-transfer | 401 |
3.2. Evaluation of Bayesian optimization strategies
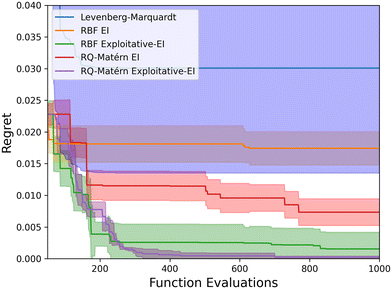
Five different optimization strategies have been tested for optimizing the kinetic parameters. The Levenberg–Marquardt algorithm is compared to four Bayesian optimization algorithms: the RBF-kernel with the EI acquisition function (RBF EI), the RBF-kernel with EI and surrogate model optimization (RBF Exploitative-EI), the combined RQ-Matérn kernel with EI (RQ-Matérn EI), and the improved strategy combining different kernels and EI with surrogate model optimization (RQ-Matérn Exploitative-EI). As a benchmark case, we have employed the experimental data of the LZY20 zeolite, with all runs repeated five times. For the Levenberg–Marquardt algorithm, random initial guesses were taken within the parameter range reported in Table S2.† Fig. 5 presents the “Regret” with an increasing number of experiments for all analyzed algorithms. “Regret” is defined as the difference between the current and global optimum.The Levenberg–Marquardt algorithm is highly dependent on the initial guess, resulting in a high standard deviation on the optimizer performance. The Levenberg–Marquardt algorithm quickly converges to a local optimum after less than 300 function evaluations, resulting in the worst kinetic model of those regressed in this study. The default Bayesian optimization strategies with EI improve upon the gradient-based Levenberg–Marquardt algorithm but do not converge towards a clear optimum after 1000 runs. The RBF-kernel has difficulties capturing the objective function, resulting in little improvement. The RQ-Matérn-kernel was better suited to represent the objective function but only slowly converges towards the optimal combination of kinetic parameters. However, a faster convergence to the optimum was reached by combining EI with surrogate model optimization (Exploitative EI). By using this acquisition function with the default RBF-kernel, a faster initial convergence is found, but it generally fails to capture the smaller intricacies of the objective function, as was discussed in Fig. 4. Therefore, by combining the RQ-kernel and Matérn-kernel with a more exploitative-based acquisition function a fast conversion to the identified optimum was found. In this way, even though 12 kinetic parameters are optimized simultaneously, the kinetic model can be optimized with only around 500 model evaluations, improving upon default Bayesian optimization strategies. The exploitative EI acquisition function results in a fast convergence toward the perceived optimum. At the same time, the adapted RQ-Matérn kernel enables the Gaussian process to capture the fine details of the objective function, resulting in an improved performance. This implies that more complex kinetic models and reactor models can be employed to optimize the kinetic parameters. Consequently, detailed catalytic microkinetic models can be quickly and automatically generated with minimal experimental and computational effort.
The optimal Bayesian optimization strategy, especially the kernel, depends on the objective function and type of optimization problem. Due to the nature of the objective function and complex reaction network used in this work, the RQ-Matérn kernel is found to be optimal. However, when adapting this objective function or moving to less complex, smaller reaction systems, other kernels such as the RBF might perform better. Nevertheless, the RQ-Matérn kernel is likely to be an optimal configuration for optimizing many complex reaction networks as the objective function in this work is well-accepted and often used. The employed acquisition function (exploitative EI) is less case-dependent and will outperform the regular EI in many multidimensional optimization problems, quickly identifying regions of the design space where the model is falsely confident. However, in simple kinetic models with less than ∼20 molecules involved, the Gaussian process will not be falsely confident in regions of the design space, making regular EI ideally suited. Therefore, it is advised to start with the default RBF EI configuration to optimize simple catalytic models and move towards the RQ-Matérn Exploitative EI algorithm for more complex systems.
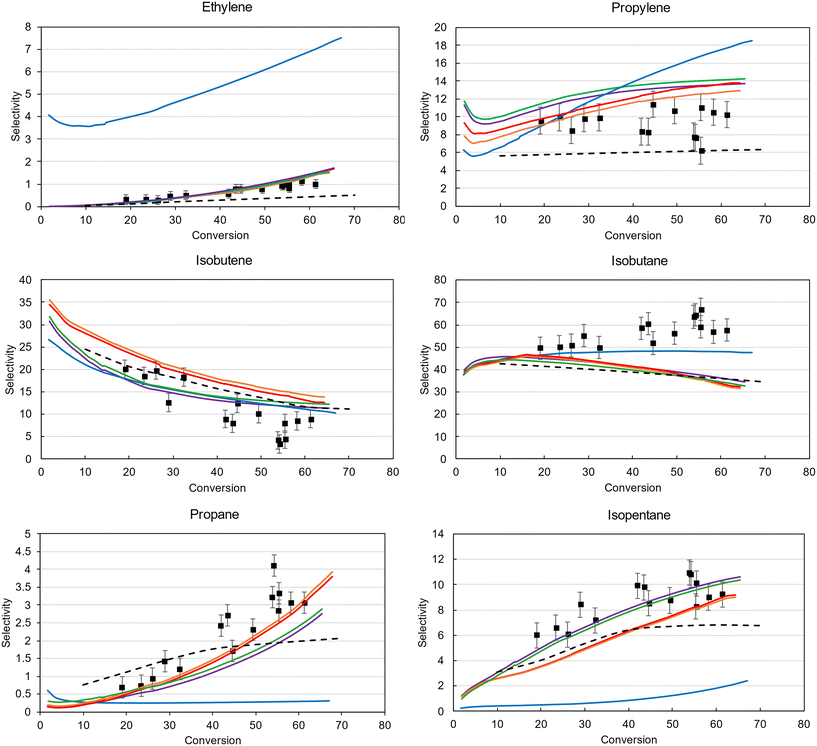
To further illustrate the benefits of the improved Bayesian optimization algorithm implemented in Genesys-Cat, the model predictions for the six most important products are shown in Fig. 6. The experimental data and standard deviation is depicted by the black markers and error bars. While the Levenberg–Marquardt model properly captures the isobutene and isobutane selectivities, which are the main products, it completely fails to predict the selectivity of the side products. This as the local optimizer cannot refine the objective function once it has reached the local optimum. The Bayesian optimization strategies are much better at predicting the selectivities of all products as they are more explorative. While the final model (purple model Fig. 6) predicts the isobutane selectivity worse than the locally optimized model, it predicts all other products much better, resulting in a decrease in residuals, as shown in Fig. 5. As also observed in Fig. 5, the discrepancy is limited between the final models optimized by RBF Exploitative-EI (green) and the improved Bayesian optimization (purple) after 1000 function evaluations. The reason for this trade-off stems from the SEMK approximation as will be elaborated on later. The final solution of the most efficient optimizer, RQ-Matérn Exploitative-EI, properly predicts the main and side products and has reached this solution at least twice as fast as the other algorithms considered.
In Fig. 6, a comparison between the Genesys-Cat-based models and a literature reference model91 has been made. This reference kinetic model has been developed on the same experimental data, with similar reaction families but with different thermodynamic and kinetic properties.91 The difference in modeled selectivities between this reference kinetic model and the Genesys-Cat models is the most profound for propylene, propane, and isopentane. The superior performance of Genesys-Cat mainly stems from the improved accuracy of the employed thermodynamic properties and estimated kinetic properties.
3.3. Kinetic models iso-octane cracking
Three different kinetic models have been developed for the three different zeolites employed for the catalytic cracking of iso-octane. The resulting pre-exponential factors for the LZY20 zeolite, obtained by Bayesian optimization, are presented in Table 5. The optimized pre-exponential factors of the other two zeolites are supplied in ESI† Table S3 and S4.| A [s−1] | A [s−1] | ||
|---|---|---|---|
| a [l mol−1 s−1]. | |||
| Physisorption (alkanes) | 1.81 101a | Physisorption (alkenes) | 3.15 102a |
| Protolytic scission (p) | 5.23 106 | β-Scission (p) | 4.75 107 |
| Protolytic scission (s) | 7.86 105 | β-Scission (s,s) | 3.78 107 |
| Protolytic scission (t) | 8.86 105 | β-Scission (s,t) | 1.63 1011 |
| Hydride-transfer (s) | 2.14 104 | β-Scission (t,s) | 1.12 109 |
| Hydride-transfer (t) | 4.78 106 | β-Scission (t,t) | 1.59 109 |
The obtained pre-exponential factors are in line with what is chemically intuitively expected. As mentioned, the pre-exponential factor is determined by the activation entropy. This activation entropy is expected to be more negative for the protolytic scission than the β-scission as the protolytic scission starts from a loosely bound physisorbed reactant compared to a more strictly bound chemisorbed carbenium ion for the β-scission. Additionally, across the different β-scission modes, the pre-exponential also varies. Similarly to what is found in literature, the β-scission (s,s) mode has a more negative activation entropy than the (s,t) mode.92 This is because the former mode's formed tertiary products and transition state are more stable and move further away from the zeolite framework. This results in a higher entropy of the (s,t) transition state compared to the (s,s) transition state and, hence, a lower activation entropy for the β-scission (s,t) mode. The activation entropy is higher with a tertiary reactant because the tertiary reactant is more loosely bound to the zeolite framework than the secondary reactant. Hence, the β-scission (t,s) and (t,t) pre-exponential factor is lower than that of the (s,t) mode.
The significance of the regression was determined with an F-test, which proved the significance of all models as specified in Table 6. The tabulated F-values are 1.81 proving the significance of all obtained microkinetic models.
| F-Value | R2 | |
|---|---|---|
| LZY20 | 260 | 0.92 |
| CBV720 | 173 | 0.89 |
| CBV760 | 2118 | 0.99 |
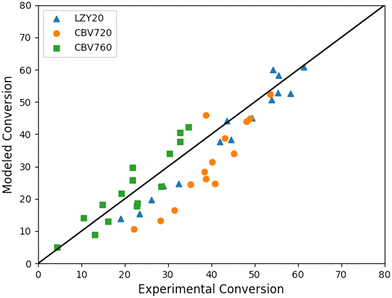
Fig. 7 shows a parity plot of the experimental and simulated conversions of iso-octane. This parity plot proves the proper activity prediction for all zeolites in a wide range of process conditions varying both temperature and space–time. Fig. S1 in the ESI† shows no deviation trend between the modeled and experimental conversion with varying temperatures.
In addition to the activity, Fig. 8 presents the molar selectivity profile in function of conversion of the different zeolites. The four most important products are presented: isobutene, isobutane, propylene and ethylene. For clarity of the figure, the error bars on the experimental data are left out. The selectivities of all other products are presented in ESI† Fig. S2 and S3. The trends of all main products are well-predicted at all conversions, apart from isobutane and propylene at higher conversions. This likely stems from a chain length dependency of the hydride-transfer reactions, which is not considered in the model due to the SEMK approach. This chain length dependency is also shown in Fig. 6, where a trade-off is found between accurately predicting the propane and isopentane, or isobutane selectivity which are all products predominantly formed by the hydride-transfer. Subsequent fitting of the thermochemical adsorption properties did not improve the accuracy of the predictions, and was therefore not included in the final model.
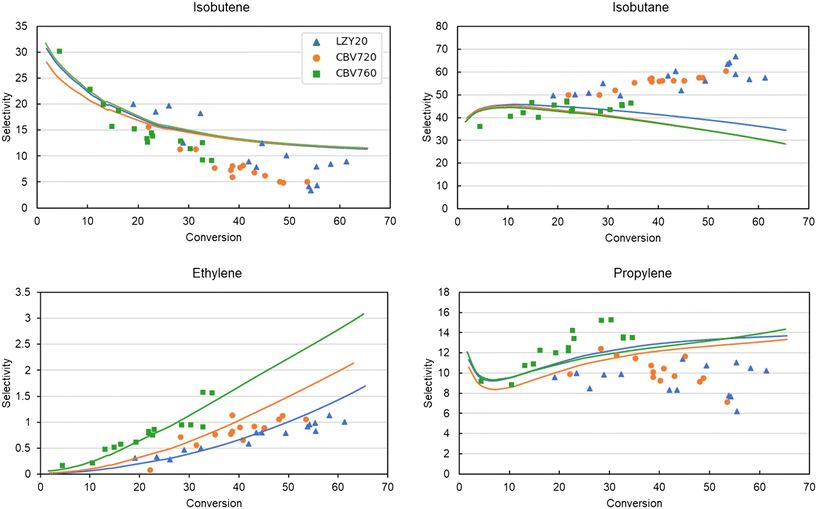 | ||
| Fig. 8 Experimental (markers) vs. modeled (lines) selectivities of the main cracking products of iso-octane in LZY20, CBV720, and CBV760 as a function of conversion. | ||
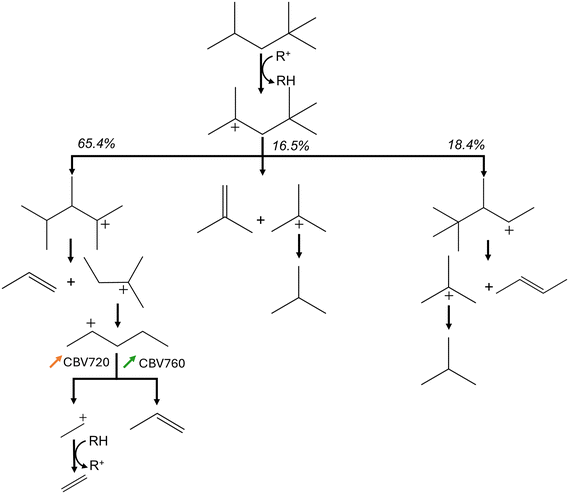
Even though the kinetic parameters are regressed towards experimental data and not determined via quantum chemical data, the obtained microkinetic models provide fundamental insights. This is demonstrated by the wide range of process conditions and zeolites for which the activity and selectivity are adequately modeled. In addition, the obtained kinetic parameters agree with chemical intuition and literature, as previously argued. One of the advantages of microkinetic models is that they allow further insight to identify the dominant reaction pathways. Fig. 9 presents the predicted dominant reaction pathways of iso-octane cracking in LZY20. The most important reactions have been identified using the Chemkin reaction path analyzer, where the three most important reaction steps for iso-octane were selected, followed by the most important reactions for every subsequently formed product. The most important rate-determining step here are hydride-transfer reactions as expected for the large pores in FAU. In addition, the relative changes in reaction rate for CBV720 and CBV760 compared to LZY20 are presented. In CBV720 and CBV760 an increase in reaction rate for the β-scission (p) and hydride-transfer (s) reactions were found. This results in a slight increase in selectivity towards ethylene and propane. As a result, the isobutene also drops slightly due to the increased hydride-transfer reaction rates.
The increase in β-scission (p) likely stems from a higher concentration of strong acid sites in the CBV760 and CBV720 catalysts compared to LZY20. Unfortunately, only the total concentration of acid sites is available for these catalysts, and no distinction is made between strong and weak acid sites. As this is historical experimental data and the employed catalysts are no longer available, no further zeolite characterization can be performed. Nevertheless, the Si/Al ratio is higher for CBV760 and CBV720, which generally corresponds to stronger acid sites as the distance between the acid sites is larger.93 In addition to this, the higher share of hydride-transfer (s) reactions can be linked to the higher micropore volume in CBV760 and CBV720. The bimolecular hydride-transfer reaction has a voluminous transition state making it favorable in highly microporous volume.
It should be stressed that this approach reduces both the computational and experimental burden. Unlike pure machine learning models, a limited set of experimental data is required to estimate the kinetic parameters accurately. On the other hand, while this approach employs a first-principles-based reaction network and thermodynamic properties, it is currently unfeasible for kinetic properties due to the computational intensity of the required quantum chemical calculations. In this way, one can quickly obtain a detailed microkinetic model, valid in a wide range of conditions, to get further insight into the kinetics of the catalytic reactions. These models can then be employed for further catalyst design or in computational fluid dynamic calculations to optimize reactor design and process conditions.
4. Conclusion
The new rule-based kinetic model generator Genesys-Cat for heterogeneous catalysis was presented. By extending the existing kinetic model generator Genesys for catalytic reactions, an efficient model generator is obtained that can generate gas and surface-phase mechanisms in parallel, which are compatible with Chemkin and Cantera. While the assignment of thermodynamic properties is based on similar methods as Genesys, Bayesian optimization is employed to estimate kinetic properties. Determining all kinetic properties for complex catalytic processes via ab initio calculations is unfeasible. Therefore, our improved Bayesian optimization reduces the computational burden and improves upon commonly used optimizers such as the Levenberg–Marquardt algorithm. To demonstrate the efficiency of this methodology, three kinetic models were developed for the iso-octane cracking across three different zeolites. The obtained microkinetic models accurately predicted the zeolites' activity and selectivity, with R2-values between 0.89–0.99 for the different models, and allowed further insight into the dominant reaction pathways for all three zeolites. Genesys-Cat can be employed on many different catalytic processes and even complements high-throughput screening of catalysts as it quickly generates accurate microkinetic models based on experimental data. In this way, the generated microkinetic models facilitate both rational catalyst and reactor design.Data availability
The data supporting this article including reaction families, catalyst properties, obtained kinetic properties, and additional insights into the model predictions are included in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
Yannick Ureel and Lowie acknowledge financial support from the Fund for Scientific Research Flanders (FWO Flanders) through the doctoral fellowship grant 1185822N and 1159825N.References
- R. Van de Vijver, N. M. Vandewiele, P. L. Bhoorasingh, B. L. Slakman, F. Seyedzadeh Khanshan, H. H. Carstensen, M. F. Reyniers, G. B. Marin, R. H. West and K. M. Van Geem, Int. J. Chem. Kinet., 2015, 47, 199–231 CrossRef CAS.
- S. G. Davis, A. V. Joshi, H. Wang and F. Egolfopoulos, Proc. Combust. Inst., 2005, 30, 1283–1292 CrossRef.
- B. R. Hough, D. T. Schwartz and J. Pfaendtner, Ind. Eng. Chem. Res., 2016, 55, 9147–9153 CrossRef CAS.
- A. H. Motagamwala and J. A. Dumesic, Chem. Rev., 2021, 121, 1049–1076 CrossRef CAS PubMed.
- Y. Wu, K. E. Taylor, N. Biswas and J. K. Bewtra, J. Chem. Technol. Biotechnol., 1999, 74, 519–526 CrossRef CAS.
- M. A. Pacheco and C. G. Dassori, Chem. Eng. Commun., 2002, 189, 1684–1704 CrossRef CAS.
- T. Cordero-Lanzac, A. Ramirez, A. Navajas, L. Gevers, S. Brunialti, L. M. Gandía, A. T. Aguayo, S. M. Sarathy and J. Gascon, J. Energy Chem., 2022, 68, 255–266 CrossRef CAS.
- M. K. Sabbe, K. M. Van Geem, M.-F. Reyniers and G. B. Marin, AIChE J., 2011, 57, 482–496 CrossRef CAS.
- K. M. Van Geem, M.-F. Reyniers, G. B. Marin, J. Song, W. H. Green and D. M. Matheu, AIChE J., 2006, 52, 718–730 CrossRef CAS.
- S. Wang, G. Dai, H. Yang and Z. Luo, Prog. Energy Combust. Sci., 2017, 62, 33–86 CrossRef.
- C. A. Pappijn, N. Vin, F. H. Vermeire, R. Van de Vijver, O. Herbinet, F. Battin-Leclerc, M.-F. Reyniers, G. B. Marin and K. M. Van Geem, Fuel, 2020, 275, 117744 CrossRef CAS.
- F. H. Vermeire, R. De Bruycker, O. Herbinet, H.-H. Carstensen, F. Battin-Leclerc, G. B. Marin and K. M. Van Geem, Fuel, 2017, 208, 779–790 CrossRef CAS.
- T. von Aretin, S. Schallmoser, S. Standl, M. Tonigold, J. A. Lercher and O. Hinrichsen, Ind. Eng. Chem. Res., 2015, 54, 11792–11803 CrossRef CAS.
- S. Standl, M. Tonigold and O. Hinrichsen, Ind. Eng. Chem. Res., 2017, 56, 13096–13108 CrossRef CAS.
- H. J. Curran, P. Gaffuri, W. J. Pitz and C. K. Westbrook, Combust. Flame, 2002, 129, 253–280 CrossRef CAS.
- T. Lu and C. K. Law, Prog. Energy Combust. Sci., 2009, 35, 192–215 CrossRef CAS.
- L. J. Broadbelt, S. M. Stark and M. T. Klein, Ind. Eng. Chem. Res., 1994, 33, 790–799 CrossRef CAS.
- G. G. Martens and G. B. Marin, AIChE J., 2001, 47, 1607–1622 CrossRef CAS.
- M. Liu, A. G. Dana, M. S. Johnson, M. J. Goldman, A. Jocher, A. M. Payne, C. A. Grambow, K. Han, N. W. Yee, E. J. Mazeau, K. Blondal, R. H. West, C. F. Goldsmith and W. H. Green, J. Chem. Inf. Model., 2021, 61, 2686–2696 CrossRef CAS PubMed.
- C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Comput. Phys. Commun., 2016, 203, 212–225 CrossRef CAS.
- N. M. Vandewiele, K. M. Van Geem, M.-F. Reyniers and G. B. Marin, Chem. Eng. J., 2012, 207, 526–538 CrossRef.
- S. Rangarajan, A. Bhan and P. Daoutidis, Comput. Chem. Eng., 2012, 45, 114–123 CrossRef CAS.
- C. H. Bartholomew and R. J. Farrauto, Fundamentals of industrial catalytic processes, John Wiley & Sons, 2011 Search PubMed.
- C. F. Goldsmith and R. H. West, J. Phys. Chem. C, 2017, 121, 9970–9981 CrossRef CAS.
- K. Blondal, J. Jelic, E. Mazeau, F. Studt, R. H. West and F. Goldsmith, Ind. Eng. Chem. Res., 2019, 58, 17682–17691 CrossRef CAS.
- B. Kreitz, P. Lott, F. Studt, A. J. Medford, O. Deutschmann and C. F. Goldsmith, Angew. Chem., Int. Ed., 2023, 62, e202306514 CrossRef CAS.
- B. Ruscic, Int. J. Quantum Chem., 2014, 114, 1097–1101 CrossRef CAS.
- J. Wellendorff, T. L. Silbaugh, D. Garcia-Pintos, J. K. Nørskov, T. Bligaard, F. Studt and C. T. Campbell, Surf. Sci., 2015, 640, 36–44 CrossRef CAS.
- J. W. Thybaut and G. B. Marin, J. Catal., 2013, 308, 352–362 CrossRef CAS.
- T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217 CrossRef CAS.
- J. W. Thybaut, G. B. Marin, G. V. Baron, P. A. Jacobs and J. A. Martens, J. Catal., 2001, 202, 324–339 CrossRef CAS.
- C. S. Laxmi Narasimhan, J. W. Thybaut, G. B. Marin, P. A. Jacobs, J. A. Martens, J. F. Denayer and G. V. Baron, J. Catal., 2003, 220, 399–413 CrossRef CAS.
- I. R. Choudhury, K. Hayasaka, J. W. Thybaut, C. S. Laxmi Narasimhan, J. F. Denayer, J. A. Martens and G. B. Marin, J. Catal., 2012, 290, 165–176 CrossRef CAS.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- E. L. Willighagen, J. W. Mayfield, J. Alvarsson, A. Berg, L. Carlsson, N. Jeliazkova, S. Kuhn, T. Pluskal, M. Rojas-Chertó, O. Spjuth, G. Torrance, C. T. Evelo, R. Guha and C. Steinbeck, J. Cheminf., 2017, 9, 33 Search PubMed.
- C. Steinbeck, C. Hoppe, S. Kuhn, M. Floris, R. Guha and L. E. Willighagen, Curr. Pharm. Des., 2006, 12, 2111–2120 CrossRef CAS.
- V. Streibel, H. A. Aljama, A.-C. Yang, T. S. Choksi, R. S. Sánchez-Carrera, A. Schäfer, Y. Li, M. Cargnello and F. Abild-Pedersen, ACS Catal., 2022, 12, 1742–1757 CrossRef CAS.
- T. Gu, B. Wang, S. Chen and B. Yang, ACS Catal., 2020, 10, 6346–6355 CrossRef CAS.
- H. Rosenbrock, Comput. J., 1960, 3, 175–184 CrossRef.
- D. W. Marquardt, J. Soc. Ind. Appl. Math., 1963, 11, 431–441 CrossRef.
- J. Van Belleghem, C. Ledesma, J. Yang, K. Toch, D. Chen, J. W. Thybaut and G. B. Marin, Appl. Catal., A, 2016, 524, 149–162 CrossRef CAS.
- J. W. Thybaut and G. B. Marin, Chem. Eng. Technol., 2003, 26, 509–514 CrossRef CAS.
- D. G. Goodwin, H. K. Moffat, I. Schoegl, R. L. Speth and B. W. Weber, Cantera: An Object-oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes (3.0.0), Zenodo, 2023, DOI:10.5281/zenodo.8137090.
- W. O. Haag, R. M. Dessau and R. M. Lago, in Studies in Surface Science and Catalysis, Elsevier, 1991, vol. 60, pp. 255–265 Search PubMed.
- J. S. Buchanan, J. G. Santiesteban and W. O. Haag, J. Catal., 1996, 158, 279–287 CrossRef CAS.
- S. M. Babitz, B. A. Williams, J. T. Miller, R. Q. Snurr, W. O. Haag and H. H. Kung, Appl. Catal., A, 1999, 179, 71–86 CrossRef CAS.
- S. R. Patlolla, K. Katsu, A. Sharafian, K. Wei, O. E. Herrera and W. Mérida, Renewable Sustainable Energy Rev., 2023, 181, 113323 CrossRef CAS.
- I. W. Wang, R. A. Dagle, T. S. Khan, J. A. Lopez-Ruiz, L. Kovarik, Y. Jiang, M. Xu, Y. Wang, C. Jiang and S. D. Davidson, Catal. Sci. Technol., 2021, 11, 4911–4921 RSC.
- D. A. Kutteri, I. W. Wang, A. Samanta, L. Li and J. Hu, Catal. Sci. Technol., 2018, 8, 858–869 RSC.
- L. Ye, X. Duan and K. Xie, Angew. Chem., Int. Ed., 2021, 60, 21746–21750 CrossRef CAS PubMed.
- Z. Geng, Y. Zhang, H. Deng, S. Wang and H. Dong, Chem. Eng. Res. Des., 2023, 195, 235–246 CrossRef CAS.
- M. Nadjafi, Y. Cui, M. Bachl, A. Oing, F. Donat, G. Luongo, P. M. Abdala, A. Fedorov and C. R. Müller, ChemCatChem, 2023, 15, e202200694 CrossRef CAS.
- Q. Zhu, H. Li, Y. Wang, Y. Zhou, A. Zhu, X. Chen, X. Li, Y. Chen and H. Lu, Catal. Sci. Technol., 2019, 9, 6638–6646 RSC.
- Y. Yang, G. Wang, P. Zheng, F. Dang and J. Han, Catal. Sci. Technol., 2020, 10, 2452–2461 RSC.
- R. Qiu, W. Wang, Z. Wang and H. Wang, Catal. Sci. Technol., 2023, 13, 2566–2584 RSC.
- M. S. Abbas-Abadi, Y. Ureel, A. Eschenbacher, F. H. Vermeire, R. J. Varghese, J. Oenema, G. D. Stefanidis and K. M. Van Geem, Prog. Energy Combust. Sci., 2023, 96, 101046 CrossRef.
- E. Pütün, Energy, 2010, 35, 2761–2766 CrossRef.
- M. K. Sabbe, F. De Vleeschouwer, M.-F. Reyniers, M. Waroquier and G. B. Marin, J. Phys. Chem. A, 2008, 112, 12235–12251 CrossRef CAS PubMed.
- M. K. Sabbe, M. Saeys, M.-F. Reyniers, G. B. Marin, V. Van Speybroeck and M. Waroquier, J. Phys. Chem. A, 2005, 109, 7466–7480 CrossRef CAS.
- Y. Ureel, F. H. Vermeire, M. K. Sabbe and K. M. Van Geem, Chem. Eng. J., 2023, 472, 144874 CrossRef CAS.
- J. A. Esterhuizen, B. R. Goldsmith and S. Linic, Chem, 2020, 6, 3100–3117 CAS.
- K. T. Winther, M. J. Hoffmann, J. R. Boes, O. Mamun, M. Bajdich and T. Bligaard, Sci. Data, 2019, 6, 1–10 CrossRef.
- O. Mamun, K. T. Winther, J. R. Boes and T. Bligaard, Sci. Data, 2019, 6, 1–9 CrossRef CAS.
- F. L. Oliveira, C. Cleeton, R. N. B. Ferreira, B. Luan, A. H. Farmahini, L. Sarkisov and M. Steiner, Sci. Data, 2023, 10, 230 CrossRef CAS PubMed.
- M. Andersen and K. Reuter, Acc. Chem. Res., 2021, 54, 2741–2749 CrossRef CAS PubMed.
- W. Xu, M. Andersen and K. Reuter, ACS Catal., 2021, 11, 734–742 CrossRef CAS.
- O. Mamun, K. T. Winther, J. R. Boes and T. Bligaard, npj Comput. Mater., 2020, 6, 1–11 CrossRef.
- V. Fung, G. Hu, P. Ganesh and B. G. Sumpter, Nat. Commun., 2021, 12, 88 CrossRef CAS.
- B. A. De Moor, M.-F. O. Reyniers, O. C. Gobin, J. A. Lercher and G. B. Marin, J. Phys. Chem. C, 2011, 115, 1204–1219 CrossRef CAS.
- C. M. Nguyen, B. A. De Moor, M.-F. Reyniers and G. B. Marin, J. Phys. Chem. C, 2011, 115, 23831–23847 CrossRef CAS.
- S. Matera, W. F. Schneider, A. Heyden and A. Savara, ACS Catal., 2019, 9, 6624–6647 CrossRef CAS.
- S. K. Rao, R. Imam, K. Ramanathan and S. Pushpavanam, Ind. Eng. Chem. Res., 2009, 48, 3779–3790 CrossRef CAS.
- J. E. Sutton, W. Guo, M. A. Katsoulakis and D. G. Vlachos, Nat. Chem., 2016, 8, 331 CrossRef CAS PubMed.
- T.-Y. Park and G. F. Froment, Comput. Chem. Eng., 1998, 22, S103–S110 CrossRef CAS.
- P. I. Frazier, arXiv, 2018, preprint, arXiv:1807.02811, DOI:10.48550/arXiv.1807.02811.
- C. E. Rasmussen and C. K. I. Williams, Gaussian processes for machine learning, MIT Press, Massachusetts Institute of Technology, 2006 Search PubMed.
- M. Hoffman, E. Brochu and N. De Freitas, 2011.
- F. Pedregosa, V. Michel, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, J. Vanderplas, D. Cournapeau, F. Pedregosa, G. Varoquaux, A. Gramfort, B. Thirion, O. Grisel, V. Dubourg, A. Passos, M. Brucher and É. Duchesnay, Scikit-learn: Machine Learning in Python, 2011 Search PubMed.
- R. Van Borm, A. Aerts, M.-F. Reyniers, J. A. Martens and G. B. Marin, Ind. Eng. Chem. Res., 2010, 49, 6815–6823 CrossRef CAS.
- H. Beirnaert, R. Vermeulen and G. Froment, in Studies in Surface Science and catalysis, Elsevier, 1994, vol. 88, pp. 97–112 Search PubMed.
- P. Cnudde, K. De Wispelaere, J. Van der Mynsbrugge, M. Waroquier and V. Van Speybroeck, J. Catal., 2017, 345, 53–69 CrossRef CAS.
- P. Cnudde, K. De Wispelaere, L. Vanduyfhuys, R. Demuynck, J. Van der Mynsbrugge, M. Waroquier and V. Van Speybroeck, ACS Catal., 2018, 8, 9579–9595 CrossRef CAS PubMed.
- Y. Ureel, F. H. Vermeire, M. K. Sabbe and K. M. Van Geem, Ind. Eng. Chem. Res., 2022, 62, 223–237 CrossRef.
- J. Van der Mynsbrugge, A. Janda, S. Mallikarjun Sharada, L.-C. Lin, V. Van Speybroeck, M. Head-Gordon and A. T. Bell, ACS Catal., 2017, 7, 2685–2697 CrossRef CAS.
- J. Rey, P. Raybaud, C. Chizallet and T. S. Bučko, ACS Catal., 2019, 9, 9813–9828 CrossRef CAS.
- J. Rey, A. Gomez, P. Raybaud, C. Chizallet and T. Bučko, J. Catal., 2019, 373, 361–373 CrossRef CAS.
- S. Borghèse, M. Haouas, J. Sommer and F. Taulelle, J. Catal., 2013, 305, 130–134 CrossRef.
- J. Rey, C. Bignaud, P. Raybaud, T. Bučko and C. Chizallet, Am. Ethnol., 2020, 132, 19100–19104 Search PubMed.
- H. Krannila, W. O. Haag and B. C. Gates, J. Catal., 1992, 135, 115–124 CrossRef CAS.
- C. J. Cramer, Essentials of computational chemistry: theories and models, John Wiley & Sons, Chichester, England, 2013 Search PubMed.
- R. Van Borm, M. F. Reyniers and G. B. Marin, AIChE J., 2012, 58, 2202–2215 CrossRef CAS.
- M. N. Mazar, S. Al-Hashimi, M. Cococcioni and A. Bhan, J. Phys. Chem. C, 2013, 117, 23609–23620 CrossRef CAS.
- A. T. Smith, P. N. Plessow and F. Studt, J. Phys. Chem. C, 2021, 125, 16508–16515 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: S1. Considered reaction families S2. Catalyst properties for iso-octane cracking S3. Parameter ranges of the activation entropy estimation S4. Pre-exponential factors of the CBV720 and CBV760 Kinetic Model S5. Reaction families for coupled gas and surface phase mechanism of thermal and catalytic 1-butene cracking S6. Residual conversion with varying temperature S7. Experimental and predict molar selectivities of other products. See DOI: https://doi.org/10.1039/d4cy01344a |
| This journal is © The Royal Society of Chemistry 2025 |