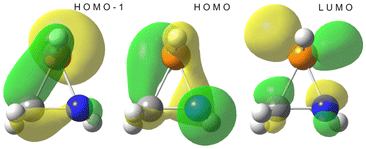A “phosphorus derivative” of aziridines: on the importance of ring strain energy and three heteropolar bonds in azaphosphiridines

Abstract

Compared to aziridines, azaphosphiridines, which formally result from the replacement of a carbon atom by phosphorus, have been much less studied. In this work, accurate values for one of the most prominent properties, the ring strain energy (RSE), have been theoretically examined for a wide range of azaphosphiridine derivatives. Strongly related aspects of interest for developing the use of azaphosphiridines in heteroatom and polymer chemistry are ring opening reactions and polymerisations, the latter facilitated by their significantly high RSE. While methyl groups have little influence on the RSE, complexation with different metal moieties increases the RSE in all cases, and an increase was also found upon oxidation to the corresponding P-oxides and other σ⁵λ⁵-P derivatives. The highest RSE was found for the P-protonated azaphosphiridinium cation and azaphosphiridines with exocyclic double bonds. A correlation of the RSEs with the relaxed force constants of the endocyclic ring bonds and AIM-derived parameters in the ring critical points, such as the electron density, ρ(r), and the Lagrangian of the kinetic energy, G(r), was found. A relatively low barrier to P–C bond cleavage via nucleophilic attack of MeNH₂ on phosphorus points to the possibility of ring-opening polymerisation.

---

Introduction

σ³λ³-Azaphosphiridines III can be considered as formally derived from aziridines¹I (Fig. 1) by replacing the carbon with phosphorus, its ‘carbon copy’.² Aziridines is a very important class of compounds that are present in natural products, APIs (active pharmaceutical ingredients) and polymers.³ The use of aziridines as formal precursors allows chemists to utilise their existing knowledge of aziridine synthetic utility and biological⁴ or medical⁵ applications while exploring the unique reactivity and functionality imparted by the incorporation of phosphorus. This formal transformation opens the door to a wide range of applications in fields such as medicinal chemistry, materials science and catalysis.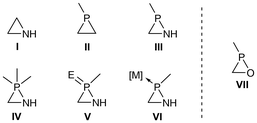

Fig. 1 Three-membered heterocycles I–VII (E = O, S, NR; [M] = BR₃, M(CO)₅; M = Cr, Mo, W; external lines denote ubiquitous substituents).

On the other hand, the incorporation of a NH unit in phosphirane II results in the formation of σ³λ³-azaphosphiridines III.^6,7 In this context, σ refers to the coordination number, while λ refers to the number of electrons involved in bonding at the phosphorus atom. These compounds are fascinating in the realm of phosphorus-based heterocycles due to their potential reactivity based on the three distinct degrees of polarisation in their endocyclic bonds and significantly increased ring strain energy (RSE) for III ⁸ (vide infra). These characteristics render III intriguing candidates for potential applications in ring-opening polymerisations.

The chemistry of uncomplexed or higher P-coordination index azaphosphiridine made significant advances in the 1970s and 1980s.⁹ In particular, in 1973 the first σ⁵λ⁵-azaphosphiridines IV were successfully synthesised by reacting the azine of hexafluoroacetone with different phosphorus derivatives.¹⁰ Subsequently, Niecke reported the synthesis of the σ⁴λ⁵-azaphosphiridine P-imine V using the reaction between diazomethane and a bis(imino)phosphorane.¹¹ The synthesis of σ⁴λ⁵-azaphosphiridine P-sulphides V was also achieved using two different protocols.¹² In the first, a thioxophosphorane was employed, which underwent a reaction with tert-butyl azide, resulting in the formation of the azaphosphiridine through photochemically induced nitrogen extrusion. In the second approach, the synthesis of V is achieved through the reaction of a phosphorane and diazomethane, with a thermally promoted nitrogen removal step. The first free σ³λ³-azaphosphiridine III was also prepared by Niecke through a thermally induced valence isomerization of an imino(methylene)phosphorane.⁷ Years later, Majoral devised another strategy for the synthesis of III using two equivalents of lithium amide, which reacted with phosphaalkenes to yield the detectable phosphaguanidines that spontaneously converted to the corresponding heterocycles,¹³ but no further research was published afterwards. Subsequently, azaphosphiridine P-oxides were proposed as intermediates in the base-induced rearrangement of α-halophosphonamidates. However, in no case could the three-membered heterocycle be isolated.^14–17 The development of the chemistry of terminal phosphinidene metal complexes also led to the preparation of azaphosphiridine complexes VI ^18,19via reaction with imines.²⁰ The development of the Li/Cl phosphinidenoid complex methodology^21,22 enabled broader access to new complexed azaphosphiridine complexes through the reaction with imines¹⁸ or carbodiimides.^23,24 In the latter case, the iminoazaphosphiridine stands out for its remarkable reactivity towards the activation of small molecules, such as phenyl isocyanate, carbon dioxide, carbon monoxide, elemental sulfur or isocyanides.^24,25 In particular, the reaction with CO₂ was subjected to detailed study, which revealed that it behaves as a masked FLP system and responds to the presence of the reagent as a stimulus.

The only other related P-heterocycle with three different polar bonds that has been the subject of greater investigation are σ³λ³-oxaphosphiranes VII, which also display a high RSE.²⁶ Although compounds III and VII possess a comparable core structure, one of the principal anticipated benefits of azaphosphiridines is their elevated basicity, which is attributed to the presence of nitrogen. This should enhance their nucleophilic character towards both hard and soft electrophilic centres at the N and P ring atoms, respectively. Furthermore, azaphosphiridines are anticipated to exhibit enhanced versatility with regard to functionalisation, thereby facilitating their potential utilisation in subsequent applications.

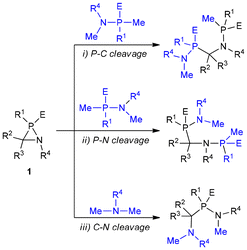
A computational study of these heterocycles III–VI is essential to further investigate their structural and electronic properties. Lammertsma was first to undertake a theoretical investigation of azaphosphiridines. Utilising isodesmic reactions, he estimated the RSE of the unsubstituted azaphosphiridine to be approximately 26.5 kcal mol⁻¹, which was considerably higher than that of phosphirane (21.4 kcal mol⁻¹) but slightly lower than the RSE of aziridine (28.2 kcal mol⁻¹).²⁷ The aforementioned values were recalculated years later using the more reliable homodesmotic reactions, resulting in 23.7, 19.9 and 27.6 kcal mol⁻¹ for these three rings, respectively.¹⁹ This high RSE value prompted the computational study of the ring-opening reactions in the parent heterocycle.²⁷ The cleavage of the endocyclic P–C and C–N bonds are endothermic processes, with the former being slightly more favoured both kinetically and thermodynamically. Conversely, the cleavage of the P–N bond is a slightly exergonic process with a high TS (transition state) which additionally involves a migration of a hydrogen from C to P. Therefore, the only feasible process with an accessible energy barrier is the breaking of the endocyclic P–C bond. Complexation to one unit of W(CO)₅ was shown to have negligible effect on the energies of these opening reactions.

Years later, Espinosa Ferao and Streubel conducted a more detailed analysis of the potential energy surfaces of a small but representative set of decomplexed azaphosphiridines,⁸ and a notable variation in the RSE, increasing from 22.6 to 38.0 kcal mol⁻¹, was observed when moving from the parent compound of III to the oxidized form VI (E = O). One year later, the same authors found that complexation of the azaphosphiridine to one Cr(CO)₅ unit did not result in a significant change in the RSE value.⁸ Furthermore, RSE values of 50.58 and 52.2 kcal mol⁻¹ were found for the E and Z isomers of 3-imino-azaphosphiridine P–W(CO)₅, respectively, indicative of a super strained ring that may explain their enhanced reactivity.

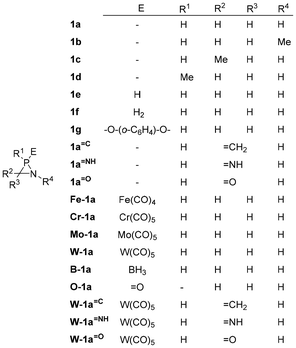
Notwithstanding the aforementioned investigations, a significant knowledge gap remained with regard to the effects of substituents. Consequently, a comprehensive study of the RSEs for a diverse range of azaphosphiridines was undertaken to gain further insights. This study systematically examines the RSE of a series of azaphosphiridines with different substituents (Fig. 2), as they are a priori excellent candidates for polymerisation reactions and exhibit analogy with aziridines and with the recently studied oxaphosphiranes.²⁸ Thus, the unsubstituted azaphosphiridine 1a has been included together with those differently substituted with methyl groups in the three positions as well as cationic azaphosphiridinium species. Additionally, complexed azaphosphiridines in which the phosphorus LP (lone pair) is involved in coordinative bonding and, hence, typically protected by Fe(CO)₄, Cr(CO)₅, Mo(CO)₅ and W(CO)₅, as well as with borane, have been investigated. Furthermore, oxidised species such as the P-oxide and the pentacoordinated P(V) derivative, as well as functionalisation with different exocyclic unsaturations at carbon, have been included in the study. Finally, the objective is to examine the potential correlation between RSE and the electronic or structural intrinsic properties of the system in order to arrive to some reactivity predictions.

Fig. 2 Parent and differently substituted or functionalized azaphosphiridines 1 studied.

Results and discussion

Estimation of RSE

Ring strain is a distinctive attribute of small rings, as this spring load serves as the driving force behind their transformation into open chain (or ring-enlarged) products. Moreover, it exerts influence over other properties, including the stereochemical stability of σ³λ³-pnictogen atoms in small rings.²⁹ It should be noted that the RSE cannot always be separated from other unwanted contaminations (e.g. σ-aromaticity and ring atoms rehybridisation).³⁰ However, it was calculated for the investigated azaphosphiridines using appropriate homodesmotic reactions (Scheme 1). Homodesmotic reactions (reaction class 4 or “RC4”) represent the second to last category in a hierarchy of increasingly precise processes, due to the conservation of larger fragments, as outlined in a recent classification and redefinition of the types of reactions used in thermo-chemistry.³¹ The RSE was obtained by averaging the opposite of the energy value (including a zero-point energy correction) for the three RC4-type endocyclic bond cleavage reactions: one P–C bond (reaction i), one P–N bond (reaction ii) and one C–N bond (reaction iii). It should be noted that, after appropriate selection of the reagents, the first two reactions are identical (same reagents and products).

Scheme 1 Homodesmotic reactions used for the estimation of the RSEs of 1.

Table 1 presents the calculated RSE values for all compounds. For purposes of comparison, the values obtained at the DLPNO-CCSD(T)/def2-QZVPP(ecp) level and at the B97-3c optimisation level (in brackets) have been included. While the latter are an acceptable estimate, they include in some cases (Fe-1a) absolute variations of up to 2.6 kcal mol⁻¹. Firstly, it can be noted that the level used here (DLPNO-CCSD(T)/def2-QZVPP//B97-3c) is in good agreement with the DLPNO-CCSD(T)/def2-TZVPP//BP86/def2-TZVP level that was used to calculate the RSE reported for the parent azaphosphiridine 1a (23.7 kcal mol⁻¹).⁸ Furthermore, there is a satisfactory correlation with the estimated value of 26.2 kcal mol⁻¹ derived through the additive method, which considers bond contributions to ring strain (6.18, 11.42 and 8.65 kcal mol⁻¹ for P–C, P–N and C–N bonds, respectively) while the additive estimation using atomic contributions yields a value of 21.9 kcal mol⁻¹ (8.65, 10.22 and 3.07 kcal mol⁻¹ for C, N and P atoms, respectively).³²

Table 1 Ring strain energies (RSEs) (kcal mol⁻¹) calculated for compounds 1 at the DLPNO-CCSD(T)/def2-QZVPP(ecp) level (values obtained at the B97-3c optimisation level in brackets)

Compound	RSE	Compound	RSE
1a	24.4 (24.8)	Fe-1a	32.1 (34.7)
1b	23.2 (22.9)	Cr-1a	30.4 (31.3)
1c	24.4 (24.1)	Mo-1a	30.8 (32.0)
1d	24.4 (24.0)	W-1a	31.7 (31.5)
1e	53.0 (53.1)	B-1a	34.3 (34.0)
1f	27.8 (27.9)	O-1a	38.9 (38.6)
1g	34.1 (34.3)	W-1a^=C	41.04 (40.5)
1a^=C	33.8 (32.4)	W-1a^=NH	45.0 (43.6)
1a^=NH	37.3 (34.8)	W-1a^=O	46.9 (45.4)
1a^=O	40.3 (38.1)	1a·H^+	23.1 (24.3)

---

Secondly, the introduction of a methyl group at either carbon or phosphorus results in a negligible change in the RSE value. However, at nitrogen, a slight decrease in RSE is observed (from 24.4 to 23.2 kcal mol⁻¹). P-complexation with an Fe(CO)₄ group has been observed to increase the RSE by almost 8 kcal mol⁻¹, a result that is consistent with that observed for oxaphosphiranes.²⁸ Nevertheless, complexation with Cr(CO)₅, Mo(CO)₅ and W(CO)₅ yields RSE values of 30.4, 30.8 and 31.7 kcal mol⁻¹, respectively, with a maximum value of 34.3 kcal mol⁻¹ observed in the case of complexation with BH₃. The oxidation of the parent compound to the P-oxide (σ⁴λ⁵-P) O-1a also results in an increase to 38.9 kcal mol⁻¹, which exhibits the same trend reported for oxaphosphiranes.²⁸ In contrast, the azaphosphiridine with a σ⁵λ⁵-P centre 1f exhibited a comparatively lower value of 27.8 kcal mol⁻¹. The introduction of exocyclic unsaturations on the ring carbon of the azaphosphiridines, namely =CH₂, =NH and =O, resulted in a considerable increase in RSE in all cases, reaching values of 41.0, 45.0 and 46.9 kcal mol⁻¹, respectively (Table 1). These results demonstrate a clear trend of =CH₂ < =NH < =O, as already reported for oxaphosphiranes.²³

P-protonated azaphosphiridinium 1e is the derivative with the highest RSE of all species studied herein, as was the case for the oxaphosphiranium cation for the oxygen analogues.²⁸ This could be due to the absence of the phosphorus lone pair, which would provide the well-known ring strain relaxation mechanism by increasing the ‘p’ character of the atomic orbitals involved in endocyclic bonds.³³ However, it is expected that the most basic centre of azaphosphiridine 1a is the N atom, due to the high reluctance of the P atom to acquire the required sp³ hybridisation in the corresponding protonated species. Indeed, at the working level of theory, the P-to-N proton shift from 1e to the N-protonated species 1a·H⁺ was calculated to be very exergonic (ΔG = −22.8 kcal mol⁻¹), with a moderate barrier (ΔG^‡ = 30.6 kcal mol⁻¹) for the intramolecular process, thus suggesting a preferred intermolecular pathway (not computed). The N atom of 1a is expected to be somewhat more basic than the most strained aziridine (reported pK_b = 6.02).³⁴ The resulting 1a·H⁺ derivative displays slightly lower RSE than the corresponding conjugate base 1a (Table 1).

In contrast, the high RSE of the σ⁵λ⁵-spiro-azaphosphiridine 1g does not correlate with the particularly low value reported for the related σ⁵λ⁵-spiro-oxaphosphirane (9.03 kcal mol⁻¹).³⁵ This can be tentatively explained by the lower apicophilicity of the NH group in comparison to O, which resulted in a slightly distorted square pyramidal geometry for 1g (τ₅ = 0.178), in contrast to the trigonal bipyramidal structure observed for the σ⁵λ⁵-spiro-oxaphosphirane.

Relationship between RSEs and geometrical parameters

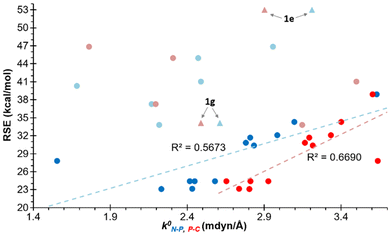
The potential correlation between the calculated RSEs and a number of electronic and structural properties is a key focus of the study. The relationship between the relaxed force constants (k⁰) of the endocyclic bonds and angles of the different azaphosphiridines was initially investigated. A handful of studies have been published that correlate the RSE with the relaxed force constants of endocyclic bonds. For instance, this has been demonstrated in the case of three-membered rings containing a single heteroatom³³ as well as for oxaphosphiranes and derivatives.^36–38 However, in the case of the aza-phosphiridines 1 that were studied, no good overall correlations were found for all compounds for any of the endocyclic bonds or angles. Nevertheless, a significant correlation (R² = 0.8344) was identified with the relaxed constants of the C–N endocyclic bond when derivative 1e was excluded (Fig. 3). On the other hand, some correlation was found for derivatives with complexed and uncomplexed exocyclic double bonds (R² = 0.4033) especially when 1a^=C was excluded from the correlation.

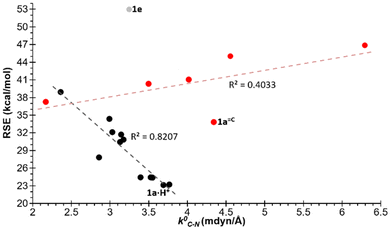Fig. 3 Plot of the RSEs (kcal mol⁻¹) versus the relaxed force constants of the C–N bonds. In red are compounds with exocyclic unsaturations and in grey 1e excluded from the correlation.

It can be observed that compounds with exocyclic double bonds exhibit the highest relaxed force constant for the endocyclic C–N bond. This is attributed to the contribution of resonance structures, which endow them with a partial double bond character. Such a phenomenon is particularly evident in compounds W-1a^=C, W-1a^=NH and W-1a^=O (Scheme 2).

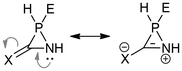Scheme 2 Resonance structures of azaphosphiridines with exocyclic unsaturations. X = CH₂, NH, O; E = LP, W(CO)5.

Similarly, an acceptable correlation was identified for the endocyclic N–P bonds (R² = 0.5673) when excluding derivatives 1e and 1g and those with exocyclic unsaturations (Fig. 4). The distinct behaviour of the latter is a logical consequence of the significant delocalisation of the lone pair (LP) of the ring N atom across the exocyclic position in these enamine, amide or amidine groups. This results in the acquisition of a significant electronic deficiency on the endocyclic N atom adjacent to the P atom, due to the participation of the aforementioned resonance structures (Scheme 2). The relative importance of this phenomenon increases with the electronegativity of the exocyclic heavy atom, following the order C < N < O. Similarly, for the endocyclic P–C bonds, an even stronger correlation (R² = 0.6690) was identified, whereby only compounds with exocyclic =NH and =O unsaturations were excluded (Fig. 3).

Fig. 4 Plot of the RSEs (kcal mol⁻¹) versus the relaxed force constants of the P–N (blue) and P–C bonds (red). In light blue and light red circles are compounds with exocyclic unsaturations, and with light triangles 1e and 1g excluded from the correlation.

The relationship between RSE and geometric parameters, including endocyclic bond distances and angles, was also examined. Thus, significant correlations were uncovered between RSEs and endocyclic C–N bond distances (Fig. S1†). For the complexed and uncomplexed azaphosphiridines with exocyclic bonds, excellent R² values were found when represented separately (R² = 0.9796 and 0.9999, respectively). For the remaining azaphosphiridines, an acceptable correlation of R² = 0.6530 between the variables was found with cationic species 1e being excluded from the correlation. The notable reduction in C–N bond distances observed in compounds with exocyclic double bonds can be attributed to their partial C=N double bond character, which is influenced by the participation of resonance structures (Scheme 2). Again, the importance of these structures increases with the electronegativity of the exocyclic heavy atom. Similarly, an excellent correlation was observed for the endocyclic N–P bond distances (R² = 0.7489) when the six compounds with exocyclic unsaturations were excluded (Fig. S1†). Ultimately, the correlation with the P–C endocyclic bond distances was somewhat weaker (R² = 0.6575) after excluding compounds containing the =NH and =O unsaturations (Fig. S1†).

On the other hand, for the case of endocyclic bond angles, a natural correspondence with the distances of the opposite bond is observed. Therefore, no meaningful correlation was identified for the C–N–P angle (Fig. S2†). However, as observed for the P–C bond distance (Fig. S1c†), the correlation strengthens when derivatives bearing exocyclic C=NH, C=CH₂ and C=O groups are excluded. Additionally, compound 1f was excluded from all correlations. Similarly, the P-centred bond angle correlations could be grouped into three categories, as observed for the opposite C–N bond distances (see the ESI†). Good correlations were obtained in all three cases (Fig. S2†). Finally, regarding the P–C–N angle, a similar pattern emerges as observed for the P–N opposite bond distance (Fig. 4). That is, the compounds exhibit two distinct trends, depending on whether they present (R² = 0.881) or not (R² = 0.634) exocyclic unsaturations (Fig. S2†).

Relationship between RSEs and electronic parameters

The relationship between the RSE and other electronic properties, such as the HOMO and LUMO energies, was then investigated. Nevertheless, no satisfactory correlation was identified. It was hypothesised that this could be due to the potential anti-aromaticity of derivatives with exocyclic double bonds. To this end, the aromaticity of the 1a^=C, 1a^=NH and 1a^=O was investigated. This was conducted by plotting isochemical shielding contour plots (ISCP), in which the σ_zz values (zz components of the magnetic shielding tensor) in the z = ±2 Å plane, parallel to the xy plane (the plane where the ring is situated) are represented (Fig. 5), as recently shown for similar³² or differrent³⁹ cyclic species. The observation of low −NICS_zz values in the aforementioned plane above the ring region serves to demonstrate the low aromaticity of the system.

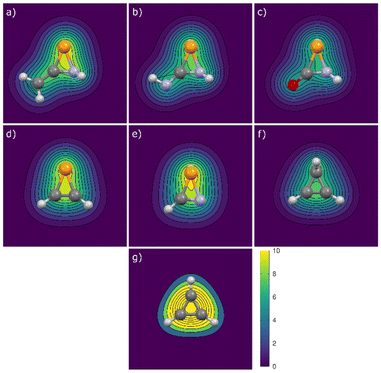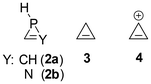
Fig. 5 ISCP of σ_zz (ppm) in the plane parallel to the xy (ring) plane at ±2 Å (average) for compounds (a) 1a^=C, (b) 1a^=NH, (c) 1a^=O, (d) 2a, (e) 2b, (f) 3 and (g) 4.

These results were compared with those obtained for the derivatives without exocyclic double bonds, 2a and 2b, as well as with cyclopropene 3 and the cyclopropenyl cation 4 (Fig. 6). It is evident that the cyclopropenyl cation (4) exhibits the most pronounced aromatic character among the three-membered rings displayed (Fig. 5g; the corresponding anion 4⁻ is shown in Fig. S3†). As anticipated, cyclopropene 3 exhibits nonaromatic characteristics, whereas the unsaturated compounds 2 demonstrate the long-range effects of the substantial diatropic current generated by the lone pair on the phosphorus atom, along with a minor contribution from the C=Y unsaturation (the sole one present in cyclopropene 3). The latter components are only discernible in the contour maps of derivatives 1a^=C, 1a^=NH and 1a^=O (Fig. 5).

Fig. 6 Selected model three-membered rings 2a,b, 3 and 4 for the aromaticity study.

Relationship between RSEs and QTAIM-derived properties

Some noteworthy correlations were identified between the parameters derived from Bader's QTAIM (Quantum Theory of Atoms-in-Molecules) theory^40,41 and the RSE. The correlation between the RSE and the electron density at the RCPs (ring critical points) was particularly strong (R² = 0.9533) after removal of the derivatives with exocyclic unsaturations (1a^=C, 1a^=NH, 1a^=O, W-1a^=C, W-1a^=NH and W-1a^=O) from the representation (Fig. 7a). The latter are grouped in two distinct subsets (complexed and uncomplexed, as in the previous cases), also demonstrating a significant inverse correlation. In these subsets, the RSE increases with decreasing electron density in the RCPs in the order CH₂ > NH > O. Similarly, a rather strong correlation (R² = 0.8496) was found with the Lagrangian of the kinetic energy density G(r) in the RCPs, again removing the compounds with exocyclic unsaturations that correlate with each other with an inverse trend (Fig. 7b). This is in accordance with previous findings in the literature.⁴² A somewhat weaker correlation (R² = 0.5176) was identified with the Lagrangian of the kinetic energy density per electron, G(r)/ρ(r), that was reported to display stronger linear correlation with RSE for other three-membered rings.⁴³ Here, again, the subset of compounds with exocyclic unsaturations showed an inverse trend (Fig. S4†).

Fig. 7 Plot of the RSEs versus (a) ρ(r)_RCP and (b) G(r)_RCP for the azaphosphiridines 1. Compounds excluded from the general correlation are uncomplexed (green) and complexed (red) species with exocyclic double bond.

Study of the nucleophile-induced ring-opening mechanism in azaphosphiridines

The azaphosphiridine ring is a poor nucleophile due to its low energy, essentially N-centred HOMO (−8.22 eV), but a good electrophile because of its low-lying phosphorus p-type LUMO (0.62 eV), with a predominant lobe at the P–C bond side of the P atom (i.e., almost opposite to the ring N atom), as observed for the parent compound 1a (Fig. 8). Furthermore, the combination of predominantly P-centred filled (HOMO−1) and vacant (LUMO) orbitals suggests the potential for a singlet phosphinidene-type reactivity while being masked as part of azaphosphiridines, as recently proposed for oxaphosphiranes.⁴⁴

Fig. 8 Computed (B3LYP/def2-TZVP) Kohn–Sham HOMO−1, HOMO and LUMO isosurfaces (0.06 au) for 1a.

The LUMO of oxaphosphiranes was shown to exert a pivotal influence on the approach of an incoming nucleophile,⁴⁵ which ultimately resulted in the initial formation of an encounter complex.²⁸ Similarly, in the case of azaphosphiridines, the LUMO (mostly representing the σ-hole that corresponds to σ*(P–N), as shown in Fig. S5†) directs the approach of methylamine, resulting in the formation of the encounter complex 1a·(MeNH₂) (Fig. 9). The BCP for the N⋯P interaction is situated approximately at the midpoint of the bond path, as evidenced in the contour plot for the Laplacian of the electron density, ∇²ρ (Fig. 9).

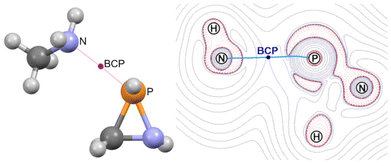Fig. 9 Computed (B3LYP-D4/def2-TZVP) structure (left) for the encounter complex 1a·(MeNH₂) and contour plot for the Laplacian of the electron density (B3LYP/def2-TZVPP) at the NPN plane (right).

The most intense valence shell charge concentration (VSCC) band for the donor (D) atom, in this case N, and the shallow one for the acceptor (P) atom are located in the respective atomic basins, that is to say, at both sides of the BCP (Fig. 3). This feature is quantified by means of the adimensional parameter relative charge concentration band position,⁴⁶τ_VSCC, defined as τ_VSCC = r(VSCCD)·r(VSCCP)/d², where r(VSCC) is the (signed) position (in Å) of the VSCC band in the bond path axis relative to the BCP and ‘d’ is the internuclear distance. In the case of the encounter complex 1a·(MeNH₂), the relatively high negative τ_VSCC value, together with the small positive ∇²ρ (Table 2), suggests that it should be classified as a van der Waals complex.⁴⁶ This conclusion is further supported by the relatively long D⋯P distance and low Wiberg bond index (WBI). Additionally, it displays a moderate interaction energy, predominantly characterised by an electron transfer from the lone pair at the donor (N) atom to the endocyclic σ*(P–N) orbital, as predicted by the second-order perturbation theory (SOPT) (Table 2). Similar weak interactions (Table 2) and ∇²ρ patterns (Fig. 10) are found for the van der Waals complexes of 1a with either MeOH or PMe₃. The latter complex is reminiscent of the van der Waals P⋯P complexes formed between an oxaphosphirane and PMe₃ at either side of the ring P atom, which have recently been reported.⁴⁵ The van der Waals complex with 1,3-dimethyl-imidazol-2-ylidene (NHC^Me2) was found to be somewhat stronger than the other complexes, with the chloride complex exhibiting the greatest strength. This was evidenced by the shorter distances, higher bond orders and stronger interaction energies (Table 2).

Fig. 10 Computed (B3LYP/def2-TZVPP//B3LYP-D4/def2-TZVP) variation of the Laplacian of the electron density at the central part of the donor-phosphorus normalized bond path in encounter complexes 1a·(nucleophile), for Cl⁻ (green), MeOH (red), MeNH₂ (blue), NHC^Me2 (grey) and PMe₃ (orange).

Table 2 Parameters related to the strength of the interaction of the P atom in van der Waals complexes of 1a with different nucleophiles

Nucleophile	d	WBI	∇ ^2 ρ	τ VSCC	E int ^c	E SOPT ^c
a Å. b e Å^−5. c kcal mol^−1.
Cl^−	2.761	0.226	1.220	−0.049	−10.9	22.2
MeOH	3.053	0.019	0.863	−0.095	−1.6	1.8
MeNH2	2.966	0.044	0.940	−0.082	−1.9	4.1
NHC^Me2	2.800	0.137	0.975	−0.069	−4.0	10.5
PMe3	3.296	0.069	0.637	−0.067	−2.7	4.1

---

The case of methyl amine serves to illustrate the two-fold effect of the initial van der Waals complex formation. Firstly, it increases the population of both endocyclic σ*(P–N)/σ*(P–C) orbitals (0.024/0.018 and 0.046/0.019e in 1a and 1a·(MeNH₂), respectively), thereby weakening the corresponding bonds (WBI_P–N/P–C = 0.891/0.960 and 0.844/0.955 for 1a and 1a·(MeNH₂), respectively). Secondly, it also increases the Lagrangian kinetic energy density per electron, G(r)/ρ(r), at the ring critical point (0.977 and 1.001 au, for 1a and 1a·(MeNH₂), respectively), which has been demonstrated to correlate with an increase in the RSE within a set of structurally related rings.⁴⁶

Furthermore, the use of parent azaphosphiridine (1a) and its κP-W(CO)₅ complex (W-1a) demonstrates that an approaching of the donor atom of the nucleophile to either the P or C ring atoms results in the promotion of P–C bond cleavage. Therefore, the energetically favourable ring opening reactions with methylamine MeNH₂ of these azaphosphiridine derivatives (Scheme 3), due to their high RSEs, were investigated. The initial reaction resulted in the formation of the opening product 5, occurring via an exergonic process (ΔG° = −9.2 kcal mol⁻¹) with a moderate activation barrier (ΔG^‡ = 33.5 kcal mol⁻¹) (Fig. 11). Conversely, the reaction of the complex initially yielded the intermediate compound W-6 (not observed in the case of uncomplexed azaphosphiridine), which exhibited a higher activation barrier (ΔG^‡ = 41.4 kcal mol⁻¹). Subsequently, the migration of hydrogen to phosphorus produced compound W-5 exergonically. For comparison purpose, the attack of methylamine on the acyclic analogues 7 and W-7 was also studied. First, the attack on 7 furnishes an ion pair intermediate (whose energy was computed as the sum of the two isolated ions) in a very endergonic process with high activation barrier (ΔG^‡ = 63.7 kcal mol⁻¹). Similarly, the attack of MeNH₂ on W-7 leads to the formation of compounds 10 and W-11 in an endergonic process with a high activation barrier (ΔG^‡ = 59.3 kcal mol⁻¹). The intermediates that result from the reactions of both the cyclic and acyclic uncomplexed derivatives with methylamine are not stable, and thus do not represent energy minima. This is because the negative charge on P is not stabilised to the same extent as in the case of the complexed analogues, which are stable and could be characterised computationally as minima. The final exothermicity values (expressed in zero point-corrected energies) for the opening reactions of azaphosphiridines 1a and W-1a (ΔE_ZPE = −20.2 and −21.7 kcal mol⁻¹, respectively) (Fig. S6†) roughly match the RSE of each ring at the level of calculation employed (the overall process is a lower quality isodesmic reaction, RC3).

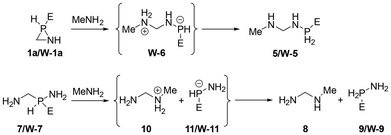Scheme 3 Methyl amine-mediated P–C bond cleavage in parent (1a) and W(CO)₅ complexed (W-1a) azaphosphiridine and model acyclic analogues 7 and W-7.

Fig. 11 Computed (DLPNO-CCSD(T)/def2-TZVPP) Gibbs free energy profile for the MeNH₂-mediated P–C bond cleavage reactions depicted in Scheme 3: 1a (black); W-1a (grey); 7a (red); W-7 (blue).

Computational details

DFT calculations were performed with the ORCA program⁴⁷ All geometry optimizations were run in redundant internal coordinates in the gas phase, with tight convergence criteria and using Grimme's functional B97-3c.⁴⁸ For the mechanistic study depicted in Scheme 3 and the van der Waals complexes 1a·(nucleophile), optimizations were performed employing the B3LYP^49,50 functional together with the RIJCOSX algorithm,⁵¹ the 2010 Grimme's semiempirical atom-pair-wise London dispersion correction (DFT-D4)⁵² and the Ahlrichs segmented def2-TZVP basis set.⁵³ Harmonic frequency calculations verified the nature of ground states or TS having all real (positive) frequencies or only one imaginary frequency, respectively. Relaxed force constants were computed as the reciprocals of the diagonal elements C_ii of the compliance matrix, which resulted upon inversion of the Hessian matrix in nonredundant internal coordinates.^54–57 From these optimized geometries, all reported data were obtained by means of single-point (SP) calculations using the more polarized def2-QZVPP^58,59 basis set. Reported energies were corrected for the zero-point vibrational term or the Gibbs energy correction at the optimization level and obtained by means of the recently developed near-linear scaling domain-based local pair natural orbital (DLPNO) method⁶⁰ to achieve coupled cluster theory with single, double, and perturbative triple excitations (CCSD(T)).⁶¹ Interaction energies in van der Waals complexes were computed using the double-hybrid-meta-GGA functional PWPB95⁶² with Grimme's semiempirical atom-pair-wise correction (DFT-D3)⁶³ and the def2-QZVPP basis set. Properties derived from the topological analysis of the electronic density were obtained with the Multiwfn program.⁶⁴ Grid points for calculation of NICS-related properties and the isochemical shielding contour were done with GNU Octave scripts.⁶⁵ Isochemical shielding contour plots were computed in a plane parallel to the ring (xy) plane, at 2 Å distance, taking a grid of 10 201 equispaced points from −4.00 to +4.00 Å in 0.08 Å intervals in both x and y directions from the ring centroids.

Conclusions

The accurate RSEs of a wide variety of various substituted and/or functionalised, azaphosphiridine derivatives have been calculated using appropriate homodesmotic reactions. It has been observed that ring substitution with methyl groups hardly influences the RSE values. On the other hand, complexation to different metal or boron units, oxidation to the P-oxide or a σ⁵λ⁵-P-derivative and/or the presence of exocyclic unsaturations at the ring C atom increased the RSE in all cases, and the P-protonated azaphosphiridinium cation shows the highest RSE.

The acceptable correlation of the RSEs with the relaxed force constants of the endocyclic bonds and AIM-derived parameters such as the electron density, ρ(r), and the Lagrangian of the kinetic energy, G(r) at the ring critical points is noteworthy. It is important to highlight that the exergonicity and the relatively low barrier to the cleavage of the P–C bond by MeNH₂, underlines the effect of the RSE as a driving force for the ring-opening of azaphosphiridines, especially in comparison to acyclic analogues. This could pave the way for their use in polymerisation reactions.

Author contributions

Conceptualization, A. E. F. and R. S.; methodology, A. G. A. and A. R. P.; validation, A. E. F. and R. S.; formal analysis, investigation, A. G. A., A. R. P. and A. E. F.; resources, A. E. F. and R. S.; data curation, A. E. F. and R. S.; writing – review and editing, A. E. F., A. G. A. and A. R. P.; supervision, A. E. F. and R. S. All authors have read and agreed to the published version of the manuscript.

Data availability

Theoretical results and computed structures.

The data that support the findings of this study are openly available in ESI† of this manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to the Servicio de Cálculo Científico – University of Murcia for computational resources. A. G. A. is indebted to the University of Bonn for a three-month research stay.

References

1. H. J. Dequina, C. L. Jones and J. M. Schomaker, Chem, 2023, 9, 1658–1701.
2. K. B. Dillon, F. Mathey and J. F. Nixon, Phosphorus: The Carbon Copy: From Organophosphorus to Phospha-organic Chemistry, Wiley, 1998.
3. T. Gleede, L. Reisman, E. Rieger, P. C. Mbarushimana, P. A. Rupar and F. R. Wurm, Polym. Chem., 2019, 10, 3257–3283.
4. C. Dank and L. Lelo, Org. Biomol. Chem., 2023, 21, 4553–4573.
5. G. S. Singh, Mini-Rev. Med. Chem., 2016, 16, 892–904.
6. E. Niecke, A. Seyer and D.-A. Wildbredt, Angew. Chem., 1981, 93, 687–688.
7. N. Dufour, A. M. Caminade and J. P. Majoral, Tetrahedron Lett., 1989, 30, 4813–4814.
8. A. Espinosa and R. Streubel, Chem. – Eur. J., 2011, 17, 3166–3178.
9. A. García Alcaraz, A. Espinosa Ferao and R. Streubel, Dalton Trans., 2021, 50, 7324–7336.
10. K. Burger, J. Fehn and W. Thenn, Angew. Chem., Int. Ed. Engl., 1973, 12, 502–503.
11. E. Niecke and W. Flick, Angew. Chem., Int. Ed. Engl., 1975, 14, 363–364.
12. E. Niecke, J. Böske, B. Krebs and M. Dartmann, Chem. Ber., 1985, 118, 3227–3240.
13. M. J. P. Harger and A. Williams, Tetrahedron Lett., 1986, 27, 2313–2314.
14. M. J. P. Harger and A. Williams, J. Chem. Soc., Perkin Trans. 1, 1989, 563–569.
15. J. Fawcett, M. J. P. Harger, D. R. Russell and R. Sreedharan-Menon, J. Chem. Soc., Chem. Commun., 1993, 1826–1828.
16. M. J. P. Harger and R. Sreedharan-Menon, J. Chem. Soc., Perkin Trans. 1, 1997, 527–532.
17. M. J. P. Harger and R. Sreedharan-Menon, J. Chem. Soc., Perkin Trans. 1, 1998, 211–216.
18. S. Fankel, H. Helten, G. Von Frantzius, G. Schnakenburg, J. Daniels, V. Chu, C. Müller and R. Streubel, Dalton Trans., 2010, 39, 3472–3481.
19. R. Streubel, J. M. Villalba Franco, G. Schnakenburg and A. Espinosa Ferao, Chem. Commun., 2012, 48, 5986–5988.
20. R. Streubel, A. Ostrowski, H. Wilkens, F. Ruthe, J. Jeske and P. G. Jones, Angew. Chem., Int. Ed. Engl., 1997, 36, 378–381.
21. A. Özbolat, G. Von Frantzius, J. M. Pérez, M. Nieger and R. Streubel, Angew. Chem., Int. Ed., 2007, 46, 9327–9330.
22. A. Schmer, P. Junker, A. Espinosa Ferao and R. Streubel, Acc. Chem. Res., 2021, 54, 1754–1765.
23. J. M. Villalba Franco, T. Sasamori, G. Schnakenburg, A. Espinosa Ferao and R. Streubel, Chem. Commun., 2015, 51, 3878–3881.
24. J. M. Villalba Franco, G. Schnakenburg, T. Sasamori, A. Espinosa Ferao and R. Streubel, Chem. – Eur. J., 2015, 21, 9650–9655.
25. J. M. Villalba Franco, G. Schnakenburg, A. Espinosa Ferao and R. Streubel, Dalton Trans., 2016, 45, 13951–13956.
26. O. Krahe, F. Neese and R. Streubel, Chem. – Eur. J., 2009, 15, 2594–2601.
27. T. P. M. Goumans, A. W. Ehlers, M. J. M. Vlaar, S. J. Strand and K. Lammertsma, J. Organomet. Chem., 2002, 643–644, 369–375.
28. A. Espinosa Ferao, A. Rey Planells and R. Streubel, Eur. J. Inorg. Chem., 2021, 2021, 348–353.
29. A. Espinosa Ferao and A. García Alcaraz, New J. Chem., 2020, 44, 8763.
30. J. F. Gonthier, S. N. Steinmann, M. D. Wodrich and C. C. Corminboeuf, Chem. Soc. Rev., 2012, 41, 4671–4687.
31. S. E. Wheeler, K. N. Houk, P. V. R. Schleyer and W. D. Allen, J. Am. Chem. Soc., 2009, 131, 2547–2560.
32. A. Espinosa Ferao and A. Rey Planells, Chem. – Eur. J., 2023, 29, e202302243.
33. A. Rey Planells and A. Espinosa Ferao, Inorg. Chem., 2020, 59, 11503–11513.
34. J. B. Sweeney, Chem. Soc. Rev., 2002, 31, 247–258.
35. J. Faßbender, N. Volk, A. García Alcaraz, S. Balasubramaniam, A. Espinosa Ferao and R. Streubel, Chem. Commun., 2022, 59, 1285–1288.
36. C. Schulten, G. Von Frantzius, G. Schnakenburg, A. Espinosa and R. Streubel, Chem. Sci., 2012, 3, 3526–3533.
37. A. Espinosa and R. Streubel, Chem. – Eur. J., 2012, 18, 13405–13411.
38. R. Streubel, C. Murcia-García, G. Schnakenburg and A. Espinosa Ferao, Organometallics, 2015, 34, 2676–2682.
39. A. Espinosa Ferao, Eur. J. Inorg. Chem., 2024, 27, e202300641.
40. R. F. W. Bader, in Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990.
41. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
42. A. Bauzá, D. Quiñonero, P. M. Deyà and A. Frontera, Chem. Phys. Lett., 2012, 536, 165–169.
43. A. Espinosa Ferao, Tetrahedron Lett., 2016, 57, 5616–5619.
44. N. Volk, A. García Alcaraz, S. Balasubramaniam, J. Heumann, G. Schnakenburg, A. Espinosa Ferao and R. Streubel, Dalton Trans., 2024, 53, 19351–19359.
45. A. García Alcaraz, A. Espinosa Ferao and R. Streubel, New J. Chem., 2024, 48, 20119–20125.
46. A. Espinosa Ferao, A. García Alcaraz, S. Zaragoza Noguera and R. Streubel, Inorg. Chem., 2020, 59, 12829–12841.
47. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
48. J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104.
49. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
50. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
51. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109.
52. E. Caldeweyher, J. M. Mewes, S. Ehlert and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 8499–8512.
53. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
54. W. J. Taylor and K. S. Pitzer, J. Res. Natl. Bur. Stand., 1947, 38, 1.
55. J. C. Decius, J. Chem. Phys., 1963, 38, 241–248.
56. K. Brandhorst and J. Grunenberg, ChemPhysChem, 2007, 8, 1151–1156.
57. K. Brandhorst and J. Grunenberg, Chem. Soc. Rev., 2008, 37, 1558–1567.
58. A. Schäfer, C. Huber, R. Ahlrichs, A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
59. D. Feller, J. Comput. Chem., 1996, 17, 1571–1586.
60. C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101–134113.
61. J. A. Pople, M. Head-Gordon, K. Raghavachari, J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975.
62. (a) L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309; (b) L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688.
63. (a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154119; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
64. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
65. J. W. Eaton, D. Bateman, S. Hauberg and R. Wehbring, GNU Octave version 8.2.0 manual: a high-level interactive language for numerical computations, 2023.

---

Footnote

† Electronic supplementary information (ESI) available: Other computational results and calculated structures. See DOI: https://doi.org/10.1039/d4dt03117b

---