Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetism and electrical and thermal transport in the natural Fe1−xMnxWO4 (x = 0.2) mineral from Potosí, Bolivia†
Dmytro Skachko a,
Bohdan Kundys
a,
Bohdan Kundys b,
Volodymyr Levytskyi
b,
Volodymyr Levytskyi a,
Esteban Zuñiga-Puelles
a,
Esteban Zuñiga-Puelles a,
Andreas Leithe-Jasper
a,
Andreas Leithe-Jasper c and
Roman Gumeniuk
c and
Roman Gumeniuk *a
*a
aInstitut für Experimentelle Physik, TU Bergakademie Freiberg, Leipziger Straße 23, 09599 Freiberg, Germany. E-mail: roman.gumeniuk@physik.tu-freiberg.de
bUniversité de Strasbourg, CNRS, Institut de Physique et Chimie des Matériaux de Strasbourg, UMR 7504, Strasbourg F-67000, France
cMax-Planck-Institut für Chemische Physik fester Stoffe, Nöthnitzer Straße 40, 01187 Dresden, Germany
First published on 5th March 2025
Abstract
The composition of a natural single crystalline specimen from the province of Potosí in Bolivia is found to be Fe0.8Mn0.2WO4. It crystallizes with the primitive monoclinic NiWO4 structure type [space group P2/c, a = 4.74751(6) Å, b = 5.71335(7) Å, c = 4.96847(5) Å, β = 90.15(1)°]. Magnetic susceptibility and specific heat capacity measurements indicated that the mineral undergoes multiple magnetic transitions: TN1 ≈ T\,cpN1 = 67(1) K, TN2 = 28(3) K, and T\,cpN2 = 8(1) K. The reduced magnetic entropy of ≈R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 upon the high-temperature antiferromagnetic ordering suggests the failure of the simplified LS-coupling scheme in the description of the magnetism. Fe0.8Mn0.2WO4 is characterized by enlarged electrical resistivity showing an exponential decrease with temperature for T > 300 K, from which an energy gap of 310 meV is deduced. The well-pronounced maximum occurring in the phononic thermal conductivity just below the TN1 is described by the Debye–Callaway model, indicating the dominance of phonon scattering on defects as well as umklapp processes.
3 upon the high-temperature antiferromagnetic ordering suggests the failure of the simplified LS-coupling scheme in the description of the magnetism. Fe0.8Mn0.2WO4 is characterized by enlarged electrical resistivity showing an exponential decrease with temperature for T > 300 K, from which an energy gap of 310 meV is deduced. The well-pronounced maximum occurring in the phononic thermal conductivity just below the TN1 is described by the Debye–Callaway model, indicating the dominance of phonon scattering on defects as well as umklapp processes.
1 Introduction
Mixed Fe1−xMnxWO4 tungstates play an important role in the development of supercapacitors and photoluminescent-, photocatalytic- and electrode materials for lithium-ion batteries.1–8 As a result, investigations into their magnetic, electrochemical and photoluminescence properties have become a prominent area of scientific inquiry. Nevertheless, despite the increased interest in this class of materials, several crystallochemical, magnetic, thermodynamic points remain less clear.Given that both the ternary FeWO4 (ferberite) and MnWO4 (huebnerite) as well as quaternary Fe1−xMnxWO4 (wolframite) tungstates occur as natural minerals, their crystal structures have been the subject of extensive investigation since the nineteenth century.9 They were shown to crystallize with a monoclinic (space group P2/c) wolframite (NiWO4) structure type.9,10 Such an arrangement foresees d-elements to reside within the condensed distorted [O6] octahedra, a hypothesis that is both crystallographically and chemically plausible. Nevertheless, the existence of a small monoclinic distortion (angle β ≈ 90°) has prompted a number of reinvestigations.1,4,9 One of the most recent ones confirming the questionable β found that the FeWO4 structure is indeed characterized by partial occupancy of the normally empty [O4]-tetrahedral voids.4 Obviously, the nature of the chemical disorder in quaternary Fe1−xMnxWO4 remains unknown due to the neighboring positions of the d-element constituents in the periodic table. Importantly, no phase transition for the natural FeWO4 is observed up to 20 GPa.1
Magnetic measurements indicated that FeWO4 orders antiferromagnetically at TN = 75 K and reveals anisotropic properties due to the magneto-crystalline anisotropy of the Fe2+ ions. Such a behavior is explained by the super-exchange interactions occurring via O2−-ions along distinct paths between neighboring Fe2+ ions.11 The change of the magnetic entropy ΔSmag = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 (gas constant R = 8.314 J mol−1 K−1) for FeWO4 upon the transition was deduced from the specific heat measurements and it is again in line with the 2+ oxidation state of iron ions (i.e., it corresponds to the total spin angular momentum S = 2).9 On the other hand, MnWO4 is characterized by a much more complex magnetic structure, including three transitions at TN of 13.5 K, 12.3 K and 8 K, respectively. The low temperature antiferromagnetic phases were shown to possess incommensurately modulated structures.12,13 Interestingly, both quaternary Fe1−xMnxWO4 ferberite and hubnerite always reveal magnetic behavior reminiscent of those of MnWO4. Some attempts to construct magnetic phase diagrams for them are made in ref. 11 and 14.
5 (gas constant R = 8.314 J mol−1 K−1) for FeWO4 upon the transition was deduced from the specific heat measurements and it is again in line with the 2+ oxidation state of iron ions (i.e., it corresponds to the total spin angular momentum S = 2).9 On the other hand, MnWO4 is characterized by a much more complex magnetic structure, including three transitions at TN of 13.5 K, 12.3 K and 8 K, respectively. The low temperature antiferromagnetic phases were shown to possess incommensurately modulated structures.12,13 Interestingly, both quaternary Fe1−xMnxWO4 ferberite and hubnerite always reveal magnetic behavior reminiscent of those of MnWO4. Some attempts to construct magnetic phase diagrams for them are made in ref. 11 and 14.
The reported electrical resistivities [ρ(T)] for both FeWO4 and MnWO4 are large, varying in the range of Ω m–kΩ m, which are characterized by an exponential decrease with temperature. The increased conductivity in FeWO4 at RT is believed to be related to the presence of a small admixture of Fe3+ ions, which triggers electron hopping along and between the chains in the [001]-direction.15 On the other hand, higher ρ(T) in MnWO4 is explained by small and large polaron hopping for LT- and HT-regimes, respectively.16 Now, in mixed Fe1−xMnxWO4 tungstates, characterized by the presence of Mn2+ ions, it is believed that the latter do not block the electron hopping paths and thus, the interchain electron transfer is possible.15
The Seebeck coefficients [α(T)] of FeWO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4,7,15,17 and MnWO4
4,7,15,17 and MnWO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 are large and positive in the whole studied temperature range, assuming the dominance of hole-like conduction mechanisms. The decrease in the values of α(T) (i.e., they vary between 140 μV K−1 and 350 μV K−1 at RT depending on the synthesis route) in FeWO4 is explained by the increase of Fe3+-impurity ion concentration.4
16 are large and positive in the whole studied temperature range, assuming the dominance of hole-like conduction mechanisms. The decrease in the values of α(T) (i.e., they vary between 140 μV K−1 and 350 μV K−1 at RT depending on the synthesis route) in FeWO4 is explained by the increase of Fe3+-impurity ion concentration.4
The energy band gaps of ≈2 eV (ref. 8 and 18–20) and ≈2.6 eV (ref. 7, 18 and 20) for FeWO4 and MnWO4, respectively, were estimated by spectroscopic measurements and further confirmed by the simulations within density functional theory. The high-pressure studies revealed that the energy gap of FeWO4 can be suppressed to 1.56 eV at 16 GPa (ref. 1) and to 2.08 eV at 10 GPa for MnWO4.21
Magnetic studies have been conducted on quaternary natural Fe1−xMnxWO4 (x ≈ 0.2) minerals sourced from Portugal and Mexico.22 However, a comprehensive analysis of their electrical and thermal transport properties remains unavailable. In this work, we provide a combined investigation of the structural and physical properties of the Fe0.8Mn0.2WO4 single-crystalline specimen sourced from the Potosí province in Bolivia.
2 Experimental
The studied specimen is a natural single crystal of the Fe1−xMnxWO4 composition belonging to the group of wolframite minerals and originating from the Potosí province in Bolivia, which is known for the excellent quality of such minerals.23The specimen was characterized by powder X-ray diffraction performed using a Huber G670 Guinier camera (CuKα1 radiation, λ = 1.54056 Å). Phase analysis was performed using the WinXpow software package24 and Rietveld refinement was performed using WinCSD.25 Single-crystal diffraction [SCXRD, a STOE STADIVARI diffractometer (MoKα radiation, λ = 0.71073 Å) equipped with a Dectris Pilatus300K detector] was performed on a crystal mechanically extracted from the crushed sample.
The supplementary crystallographic data for Fe0.8Mn0.2WO4 are deposited under CCDC 2425342.†
The surface of the polished wolframite embedded in a conductive resin was investigated using a scanning electron microscope (SEM) (Jeol JSM − 7800F) equipped with an energy dispersive X-ray spectrometer (EDXS) Quantax 400 EDXS system from Bruker. Such an analysis indicated the (Fe,Mn)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W relationship in the main phase to be 1
W relationship in the main phase to be 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with an oxygen content of ≈70 at%. Recalculating further the Fe and Mn contents, we deduced the Fe0.80(3)Mn0.20(3)W1.00(3)O4 chemical composition for the studied wolframite. Besides the main phase, the investigated specimen contained an admixture of SnO2 and CuFeS2 (Fig. 1), which was not visible in the measured PXRD patterns.
1 with an oxygen content of ≈70 at%. Recalculating further the Fe and Mn contents, we deduced the Fe0.80(3)Mn0.20(3)W1.00(3)O4 chemical composition for the studied wolframite. Besides the main phase, the investigated specimen contained an admixture of SnO2 and CuFeS2 (Fig. 1), which was not visible in the measured PXRD patterns.
Temperature (1.8–300 K) and magnetic field (0–7 T) dependencies of magnetic susceptibility, specific heat capacity and thermal conductivity were measured by the corresponding options of DynaCool-12 from Quantum Design. High temperature (450–600 K) electrical resistivity and Seebeck coefficients were obtained using an ULVAC ZEM-3 device. Due to the highly insulating nature of the sample for T < 450 K, electrical resistivity was additionally measured using an AC method at 100 kHz with an Agilent Precision LCR meter, Model E4980A.
3 Results and discussion
3.1 Crystal structure
All reflections collected for Fe0.8Mn0.2WO4 from the single crystal XRD experiment were indexed within the monoclinic lattice with the unit cell parameters a = 4.7466(9) Å, b = 5.711(1) Å, c = 4.969(1) Å and β = 90.21(3)°. The analysis of the extinction conditions indicated l = 2n for h0l and 00l indices and thus, two possible space groups (SG) P2/c or Pc. In the first step we have chosen the centrosymmetric one to find a structural model. By applying direct methods four atomic positions were located as shown in Table 1. The preliminary refinement cycle converged with a low reliability factor RF = 0.033, indicating the correctness of the obtained model. Performing further extinction correction and refining anisotropic displacement parameters (ADP), RF was reduced to 0.014. Crystallographic details of this refinement together with the final values of atomic coordinates and equivalent displacement parameters are collected in Table 1. The obtained ADPs are shown in Table 2. Since Fe and Mn are neighboring elements in the periodic table, reasonable refinement of their statistical mixture is rather impossible. Therefore, the composition of the crystal was fixed to the results from EDX analysis.| Method | Single crystal | Powder |
|---|---|---|
| a Obtained from PXRD and used for single crystal refinement.b M is a statistical mixture of (0.8Fe + 0.2Mn) in accordance with EDX analysis. | ||
| Unit cell parametersa | ||
| a (Å) | 4.74751(6) | |
| b (Å) | 5.71335(7) | |
| c (Å) | 4.96847(5) | |
| β (°) | 90.15(1) | |
| V (Å3) | 134.76(2) | |
| Calculated density ρ (g cm−3) | 7.48(1) | |
| Radiation, λ (Å) | MoKα, 0.71073 | CuKα1, 1.54056 |
| Absorption coeff. (mm−1) | 50.40 | 122.1 |
| Scan step (°); N (images) | 1° (ω-scans); 1414 | 0.005 |
| Maximal 2Θ (°) | 76.47 | 100.41 |
| Minimal h, k, l | −6, −9, −8 | 0, 0, −4 |
| Maximal h, k, l | 8, 9, 8 | 4, 5, 5 |
| Crystal size, μm3 | 20 × 40 × 96 | |
| Absorption correction | Multiscan | |
| Tmax/Tmin | 0.376/0.187 | |
| N (hkl) measured | 6523 | 156 |
| N (hkl) unique | 739 | |
| Rint/Rσ | 0.066/0.026 | |
| N (hkl) observed | 6316 | |
| Observation criterion | F(hkl) ≥ 4σ(F) | |
| Refined parameters | 33 | 22 |
| Extinction coefficient | 0.0389(8) | |
| Goodness of fit, S | 1.03 | 1.01 |
| RF(RI); RW(RP) | 0.014/0.015 | 0.056; 0.103 |
| Residual peaks (e− Å−3) | −0.41/0.50 | −0.57/0.73 |
M in 2f (1/2 y 3/4), y, Beq/iso![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
0.3253(2), 0.70(1) | 0.3278(3), 1.05(1) |
| d(M−2O1), d(M–2O2) | 2.069(3), 2.140(3) | 2.064(4), 2.171(5) |
| d(M–2O2), d(M–2M) | 2.190(3), 3.1869(8) | 2.248(5), 3.169(2) |
| W in 2e (0 y 1/4), y, Beq/iso | 0.18021(4), 0.484(4) | 0.1798(1), 1.13(1) |
| d(W–2O2), d(W–2O1) | 1.789(3), 1.913(3) | 1.736(4), 1.909(5) |
| d(W–2O1), d(W–2W) | 2.129(3), 3.2267(2) | 2.142(4), 3.2237(5) |
| O1 in 4g (xyz), x, y | 0.2129(6), 0.1059(5) | 0.2119(9), 0.1101(7) |
| z, Beq/iso | 0.9351(5), 0.70(4) | 0.934(1), 0.90(2) |
| O2 in 4g (xyz), x, y | 0.2536(6), 0.3757(5) | 0.2363(9), 0.3830(8) |
| z, Beq/iso | 0.3933(6), 0.75(5) | 0.379(1), 0.96(2) |
As one can see from Table 2, the B11 displacement parameter for the heavy W-atom is by a factor of ≈1.4 larger than B22 and B33. This fact together with the partial occupancy by Fe and W of the additional tetrahedral voids reported in ref. 4 prompted us to check the possibility of the latter scenario in the studied wolframite. For these purposes, we performed differential Fourier synthesis before refining ADPs. It indicated an additional electronic density of +2.85 e− Å−3 localized at the 4g [0.041(2) 0.176(2) 0.2470(6)] crystallographic site, which is just a split position to the available W in 2e (Table 1). This observation brought us to the conclusion that the model proposed in ref. 4 cannot be applied to the natural wolframite. We assume instead that the enlarged B11 for Fe0.8Mn0.2WO4 is most probably due to mechanical stress in the microcrystal appearing after crushing the initial sample – an effect discussed in more detail elsewhere.26–29
The obtained structural model from single crystal XRD was used to refine the powder XRD data, which converged with low reliability factors. The atomic coordinates and displacement parameters are collected in Table 1. The experimental, theoretical and differential profiles for it are depicted in Fig. 2. Importantly, the hkl reflections with h ≠ 0 and l ≠ 0 are found to reveal a clear split. It is visible in the inset to Fig. 2, where some of these peaks are presented in comparison with the (230) one. Such an indication of the monoclinic distortion can sometimes remain invisible, as it is the case in the sample observed in ref. 4.
 | ||
| Fig. 2 Powder XRD patterns for Fe0.8Mn0.2WO4. Inset: indexing of the selected reflections. A clear split is visible for those with h ≠ 0 and l ≠ 0, confirming the monoclinic distortion. | ||
The refined unit cell parameters (Table 1) agree well with the predictions made for Fe1−xMnxWO4 tungstates on the basis of the XRD investigations of some natural minerals.6 The strongest deviation of ≈0.2% is observed for the a-parameter and thus, deducing from Fig. 5 in ref. 6, the Mn-content for the compound studied here would be x = 0.38. However, one can see from the study6 that the data obtained for x < 0.5 (e.g., available in ref. 4, 30 and 31) strongly deviate from the proposed linear x(V)-dependence. For this reason, the higher Mn-content in our mineral is rather unlikely.
The refined interatomic distances in the crystal structure of Fe0.8Mn0.2WO4 (Table 1) agree well with the sums of ionic radii of the corresponding ions [r(Fe2+) = 0.82 Å, r(Mn2+) = 0.91 Å, and r(O2−) = 1.32 Å].32 The maximal shortenings of Fe–O and W–O contacts do not exceed 3.3% and 7.8%, respectively, and agree well with the earlier reports.4,31
The structural peculiarities of the NiWO4 type are widely discussed in the literature.4,10,31,33 It is considered as consisting of [FeO6]- (distorted due to the Jahn–Teller effect) and [WO6]-octahedra sharing their edges and forming zigzag chains along the [001] direction. Also, along the [100] direction, filled octahedra alternate with the empty ones, thus possessing common trigonal faces and being organized in columns (Fig. 3a). Such a close packing of octahedra gives rise to interstitial tetrahedral voids. They can become partially filled (Fig. 3b), as has been shown on the basis of combined single crystal XRD, TEM and SEM studies in ref. 4. Alternatively, one could consider the crystal structure of FeWO4 to be consisting of trigonal puckered nets formed by oxygen atoms extending in the bc-plane and being at x ≈ 0.25 and 0.75, respectively (Fig. 3c). In the free space in-between, the planar trigonal nets (not shown in Fig. 3c) formed by W6+ (x = 0) and Fe2+ (x = 1/2) are incorporated. Such a layered presentation, however, has less chemical meaning due to the absence of bonding Fe–Fe, W–W and O–O contacts in the studied structure.
 | ||
| Fig. 3 (a) Arrangement of filled and empty octahedra in FeWO4 (NiWO4 type). (b) Structural model with partially filled tetrahedra (the full occupancy is shown) proposed for FeWO4 in ref. 4. (c) Arrangement of the puckered trigonal nets W6+ and Fe2+ ions in-between (for more details, see the text). | ||
3.2 Magnetic susceptibility
The temperature dependence of reciprocal magnetic susceptibility χ−1(T) for Fe0.8Mn0.2WO4 is depicted in Fig. 4. In the T-range of 130–300 K, it perfectly fits the Curie–Weiss law χ−1 = (T − ΘCW)/C. The Weiss temperature ΘCW = −19(1) K and the effective magnetic moment obtained from such a fit agree well with those reported for pure FeWO4.34,35 The somewhat smaller ΘCW value [−19(1) K instead of −27 K] can be explained by the relatively narrow T-range in which our fit was performed.
obtained from such a fit agree well with those reported for pure FeWO4.34,35 The somewhat smaller ΘCW value [−19(1) K instead of −27 K] can be explained by the relatively narrow T-range in which our fit was performed.
With the lowering temperature, Fe0.8Mn0.2WO4 undergoes an antiferromagnetic (AF) transition at TN1 = 67(1) K, in agreement with ref. 36, and further changes its magnetic structure at TN2 = 28(3) K. As one can see from inset a to Fig. 4, the value of TN1 nicely fits that of TN from Mn-content dependence, confirming the correctness of the chemical composition (established from EDX) of the studied mineral. Additionally, almost no and very weak field dependencies are observed for TN1 and TN2, respectively (inset b to Fig. 4). All these findings agree well with the earlier reports about complex magnetic phase formation in Fe1−xMnxWO4, which is caused by the various superexchange couplings between adjacent Mn–Mn, Fe–Fe, and Mn–Fe-ions via one or two intervening oxygen ions.1,11,34
3.3 Specific heat
The temperature dependence of specific heat capacity cp(T) for Fe0.8Mn0.2WO4 in different magnetic fields in comparison with the synthetic ternary FeWO4 and phonon reference compound ZnWO4 (both these data are taken from ref. 9) is depicted in Fig. 5. In agreement with magnetic susceptibility (inset b to Fig. 4) no suppression of AF with increasing field is observed. Also, expectedly, the anomaly due to the antiferromagnetic ordering at T\,cpN1 = 66(1) K in the studied mineral is shifted towards a lower T (inset to Fig. 4). | ||
| Fig. 5 Temperature dependencies of specific heat capacity in different magnetic fields for Fe0.8Mn0.2WO4 together with the literature data for FeWO4 and ZnWO4.9 | ||
Subtracting further the phonon reference, we obtained the electronic specific heat for Fe0.8Mn0.2WO4. Presenting it in cel/T(T) mode and integrating it, we obtained the temperature evolution of the magnetic entropy  . As one can see from Fig. 6, a value slightly larger than R
. As one can see from Fig. 6, a value slightly larger than R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln3 can be reached upon the transition. Obviously, it is much lower than the theoretical expectations for Fe2+ (S = 2) or Fe3+ (S = 5/2) ions given as ΔSmag = R
ln3 can be reached upon the transition. Obviously, it is much lower than the theoretical expectations for Fe2+ (S = 2) or Fe3+ (S = 5/2) ions given as ΔSmag = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2S + 1) = R
ln(2S + 1) = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln5 and R
ln5 and R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln6, respectively. On the other hand, assuming the influence of the crystal electric field effect on Fe-ions, and thus electronic configurations with S = 1 or 3/2, one could also deduce the entropies R
ln6, respectively. On the other hand, assuming the influence of the crystal electric field effect on Fe-ions, and thus electronic configurations with S = 1 or 3/2, one could also deduce the entropies R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln3 and R
ln3 and R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln4, respectively. It is noteworthy that the reduced total spin angular momenta should also indicate much lower effective magnetic moments disagreeing with our experiment. All these hints towards the failure of the simplified classical LS-coupling scheme in the description of the complex magnetic behavior in Fe0.8Mn0.2WO4. Importantly, as it is also clearly visible from Fig. 4 in ref. 37, ΔSmag upon the HT-magnetic transition in the pristine MnWO4 is well below R
ln4, respectively. It is noteworthy that the reduced total spin angular momenta should also indicate much lower effective magnetic moments disagreeing with our experiment. All these hints towards the failure of the simplified classical LS-coupling scheme in the description of the complex magnetic behavior in Fe0.8Mn0.2WO4. Importantly, as it is also clearly visible from Fig. 4 in ref. 37, ΔSmag upon the HT-magnetic transition in the pristine MnWO4 is well below R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln6. Even more, this value does not reach up to 30 K. Besides that, a well pronounced and broadened (i.e., due to the cation mixture) anomaly at T\,cpN2 ≈ 10(1) K in our sample becomes especially clearly visible in the cel/T(T) presentation (inset to Fig. 6). It perfectly overlaps with the antiferromagnetic anomalies at TN1 = 13.4 K, TN2 = 12.5 K and TN3 = 7.4 K in MnWO4,38,39 stressing additionally the complexity of the magnetic structure of Fe0.8Mn0.2WO4.
ln6. Even more, this value does not reach up to 30 K. Besides that, a well pronounced and broadened (i.e., due to the cation mixture) anomaly at T\,cpN2 ≈ 10(1) K in our sample becomes especially clearly visible in the cel/T(T) presentation (inset to Fig. 6). It perfectly overlaps with the antiferromagnetic anomalies at TN1 = 13.4 K, TN2 = 12.5 K and TN3 = 7.4 K in MnWO4,38,39 stressing additionally the complexity of the magnetic structure of Fe0.8Mn0.2WO4.
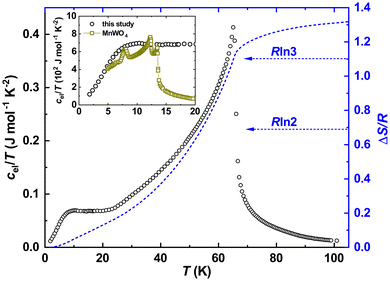 | ||
| Fig. 6 Temperature dependence of the electronic specific heat of Fe0.8Mn0.2WO4 in the cel/T(T) presentation (left black scale) together with the temperature evolution of the magnetic entropy near an antiferromagnetic transition. Inset: low-temperature dependencies of cel/T(T) for Fe0.8Mn0.2WO4 together with the literature data for MnWO4.37 The latter were divided by 20 for better visualization. | ||
3.4 Electrical and thermal transport
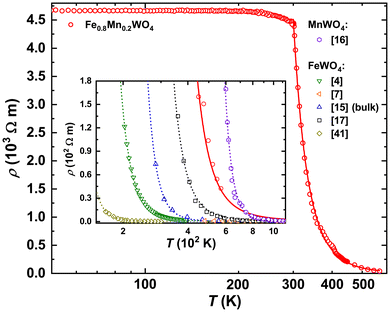
The temperature dependence of electrical resistivity ρ(T) for Fe0.8Mn0.2WO4 is depicted in the inset to Fig. 7. It increases exponentially with decreasing temperature down to ≈300 K and then saturates, reaching the ρ ≈ 4.8 kΩ m value. In the whole studied range, it is by ≈3–5 orders of magnitude higher than ρ(T) reported for CuFeS2 (i.e., an impurity phase in our sample),40 thus confirming the purity of the studied specimen.Its comparison with the ρ(T) of undoped FeWO4 and MnWO4 is presented in Fig. 7. As it is seen therein, all these dependencies can be nicely described by the Arrhenius approximation given as ρ = ρ0eEg/KbT, where Eg is the energy gap. Interestingly, the latter value for FeWO4 is reported to vary in a broad range of 150–260 meV.4,15–17,41,42 Since the authors of ref. 4, 15 and 41 performed their studies on single crystalline materials obtained from chemical vapor transport reactions and in ref. 16 and 17 bulk samples were studied, one has to conclude on the extreme sensitivity of ρ(T) to any even minor impurities.
As it is discussed in ref. 41 and 43, Mn2+-ions in Fe1−xMnxWO4 do not block the electron hopping paths, thus allowing charge carrier transfer also between chains, which results in the enhancement of ρ(T). In agreement with this report, Fe0.8Mn0.2WO4 reveals both higher electrical resistivity (Fig. 7) and an energy gap value of Eg = 310 meV (to be able to compare our value with the previously reported one, we performed an Arrhenius fit for the temperature range of 480–560 K). Importantly, the latter value is smaller than Eg = 705 meV of MnWO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 and larger than those observed for FeWO4 (see the discussion above). Fitting ρ(T) in the whole measured range of 300–560 K, one would obtain Eg = 247 meV for Fe0.8Mn0.2WO4, clearly breaking the trend visible in Fig. 7. It is noteworthy that the band gap values deduced from ρ(T) are always underestimated and the true Eg values for MnWO4 and FeWO4 deduced from spectroscopic measurements are 2.6–3 eV (ref. 7 and 18) and 2 eV,18,19,44 respectively.
16 and larger than those observed for FeWO4 (see the discussion above). Fitting ρ(T) in the whole measured range of 300–560 K, one would obtain Eg = 247 meV for Fe0.8Mn0.2WO4, clearly breaking the trend visible in Fig. 7. It is noteworthy that the band gap values deduced from ρ(T) are always underestimated and the true Eg values for MnWO4 and FeWO4 deduced from spectroscopic measurements are 2.6–3 eV (ref. 7 and 18) and 2 eV,18,19,44 respectively.
The Seebeck coefficients of thermopower α(T) of all Fe1−xMnxWO4-specimens studied up to now are positive in the whole temperature range, thus assuming the dominance of the hole-like conduction mechanism therein. Also, the α(T) of single crystalline FeWO4 decreases nearly linearly with increasing temperature,4,15,17 whereas for a bulk sample, an increase is reported14 (Fig. 7). This is again an indication of the sensitivity of thermopower to the samples’ crystallinity, similar to that discussed above for ρ(T) dependencies. Interestingly, the α(T) of polycrystalline FeWO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 and MnWO4
14 and MnWO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 (not shown in Fig. 8) reveal a change in the slope at a certain temperature, which is explained in both cases by the increase of the charge carrier mobilities. In line with these observations, the α(T) of single crystalline Fe0.8Mn0.2WO4 decreases linearly with T. In the temperature range of ≈450–600 K, it is also the largest one [seemingly, the α(T) of MnWO4 would become larger for T > 650 K].
16 (not shown in Fig. 8) reveal a change in the slope at a certain temperature, which is explained in both cases by the increase of the charge carrier mobilities. In line with these observations, the α(T) of single crystalline Fe0.8Mn0.2WO4 decreases linearly with T. In the temperature range of ≈450–600 K, it is also the largest one [seemingly, the α(T) of MnWO4 would become larger for T > 650 K].
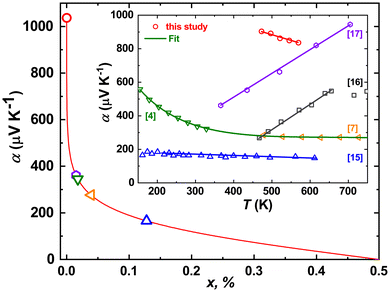 | ||
Fig. 8 Seebeck coefficient α300 K as a function of holes (Fe3+) per Fe-site concentration (x) calculated from the Heikes equation (eqn (1)). Inset: temperature dependence of the Seebeck coefficient of thermopower α(T) for Fe0.8Mn0.2WO4 in comparison with FeWO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4,7,15,16 and MnWO4 4,7,15,16 and MnWO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 samples of different origins. 17 samples of different origins. | ||
Assuming now the α(T) of Fe0.8Mn0.2WO4 to remain linear down to 300 K and the applicability of the simplified Heikes equation (i.e., considering the degeneracy factors gA and gB to be equal)45–47 given as:
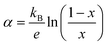 | (1) |
The temperature dependence of thermal conductivity κ(T) for Fe0.8Mn0.2WO4 is presented in Fig. 9. It is high for 5 K < T < 50 K (e.g., by a factor of ≈3 higher than those of the high quality pyrite crystal48) and reveals a well pronounced maximum at Tmax ≈ 12 K, which corroborates the good crystallinity and high quality of the sample. For T > 100 K, κ(T) slightly increases almost linearly with temperature, which most probably occurs due to radiation heat losses (inset to Fig. 9).49,50 Interestingly, two anomalies can be observed: (i) the increase of κph(T) that begins at TN1 = 67(1) K and (ii) an irregular behavior visible at T\,cpN2 ≈ 8(1) K, in line with the specific heat measurements.
 | ||
| Fig. 9 Temperature dependence of thermal conductivity κ(T) for Fe0.8Mn0.2WO4 together with the fit to eqn (2). Inset: deviation of experimental data from the theoretical expectation due to radiation heat losses. | ||
Since electrical resistivity for the studied mineral at 300 K is expected to be ≈12 kΩ m, the electronic component of κ(T), in accordance with the Wiedemann–Franz law, would be κel(300 K) = L0T/ρ = 6.1 × 10−10 W m−1 K−1 (L0 = 2.44 × 10−8 W Ω K−2 is the Lorenz number). Comparing this κel with the values in Fig. 9, one can conclude that the κ(T) of Fe0.8Mn0.2WO4 is completely dominated by phonons (i.e., κph), and thus, obeys the Debye–Callaway model51 given as:
 | (2) |
| τtot−1 = τB−1 + τPD−1 + τN−1 + τU−1 | (3) |
The parameter ΘD in eqn (2) denotes the Debye temperature of Fe0.8Mn0.2WO4. It is rather impossible to deduce it from the above described cp(T); therefore we fitted the specific heat data for ZnWO4 taken from ref. 9 in the T-range of 3–20 K to the cp(T) = γT + βT3 + δT5 ansatz, thus obtaining the Sommerfeld coefficient γ = 7.1(9) mJ mol−1 K−2, β = 0.11(9) mJ mol−1 K−4 [corresponds to ΘD (ZnWO4) = 477(3) K] and δ = 4.1(9) × 10−4 mJ mol−1 K−6. To obtain an approximate Debye temperature of Fe0.8Mn0.2WO4, the value above was multiplied by [Mr(ZnWO4)/Mr(Fe0.8Mn0.2WO4)]1/2 = 1.016, where Mr is the corresponding molar mass. Having now ΘD (Fe0.8Mn0.2WO4) = 485 K, we further calculate the velocity of sound for the studied mineral vS = 3726 m s−1 using eqn (4) (therein nat = 8.97 × 1028 m−3 is the concentration of atoms per unit cell volume).
 | (4) |
Introducing the ΘD and vS values in eqn (2), we fit κ(T) in the temperature range of 1.8–106 K (Fig. 9) with an overall reliability factor R2 = 0.993. The obtained parameters and their standard deviations are summarized in Table 3.
| τ−1 | Equation | Ci | Units for Ci |
|---|---|---|---|
| τB−1 | vS/C1 | 2.7(1) | [10−4 m] |
| τPD−1 | C2x4T4 | 183(4) | — |
| τN−1 | C3xT3 | 5.96(9) | [105 s−1 K−3] |
| τU−1 | C4x2T3e(−ΘD/3T) | 3.9(5) | [106 s−1 K−3] |
As one can see, the C1 coefficient indicates a rather large grain boundary size in agreement with the excellent microstructural quality of the studied single crystalline specimen. The C2 parameter, which is due to the point defects (i.e., Mn-doping and/or the Fe3+-holes), is approximately one order of magnitude smaller than single crystalline PbS52 and polycrystalline indium thiospinels.53 In the HT-range, we observe the contribution of both normal-(C3) and umklapp (C4) phonon–phonon processes, as expected for single crystalline materials.
The discrepancies between the fit and experiment observed in the LT-region just below the maximum could be attributed to the features present in cp(T) (Fig. 5). To shed light on this problem, measurements performed on different samples with the same microstructure (i.e., equal or similar τB and τPD) are necessary. Interestingly, the further mismatch of fit to eqn (4) to the experiment appears for T > TN1 = 67(1) K. Obviously, to explain the κ(T) behavior for the temperature range of 70–100 K, perturbation density functional theory (pDFT) calculations combined with additional experiments aiming at the estimation of phonon dispersions in Fe0.8Mn0.2WO4 are required.
4 Conclusions
Combined X-ray powder diffraction (PXRD) and energy dispersive X-ray spectroscopic (EDXS) studies confirmed the natural crystal from the wolframite group originating from the Potosí province in Bolivia to be of high quality containing only local inclusions of chalcopyrite and some silicates. Its chemical formula was found to be Fe1−xMnxWO4 (x = 0.2). Further single crystal and powder XRD experiments confirmed the mineral to crystallize with the monoclinic wolframite structure type. A slight monoclinic distortion is clearly evidenced by the split of hkl reflections with h ≠ 0 and l ≠ 0 in the PXRD patterns.The measurements of the temperature and field-dependent magnetic susceptibility for Fe1−xMnxWO4 (x = 0.2) indicated an effective magnetic moment close to that expected for Fe2+ ions. A complex magnetic structure with transitions at TN1 = 67(1) K and TN2 = 28(3) K is also in line with the earlier studied quaternary wolframites. Further confirmation of this complexity is deduced from specific heat measurements revealing anomalies at T\,cpN1 = 66(1) K and T\,cpN2 = 8(1) K. It is noteworthy that the reduced magnetic entropy of ≈R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (instead of R
3 (instead of R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln5) upon the HT transition indicates the failure of the simplified LS-coupling scheme in the description of the magnetism in the studied mineral.
ln5) upon the HT transition indicates the failure of the simplified LS-coupling scheme in the description of the magnetism in the studied mineral.
The electrical resistivity of Fe1−xMnxWO4 (x = 0.2) increases exponentially upon decreasing temperature reaching a saturation value of ρ ≈ 4.8 kΩ m below 300 K. The high-temperature energy gap of 310 meV, deduced from the exponential decrease with temperature, is expectedly closer to FeWO4 (150–260 meV) than to MnWO4 (710 meV).
The measured thermal conductivity slightly decreases with decreasing temperature down to TN1 ≈ 66(1) K and then overcomes a huge maximum centered at Tmax ≈ 12 K, revealing some additional anomaly at T\,cpN2 ≈ 8(1) K. Assuming it to be dominated by the phonon processes [the electronic contribution to κ(T) is found to be ≈10−10 W m−1 K−1], the Debye–Callaway model was applied. Such a fit indicated enlarged grain boundary sizes, enhanced defect concentration and the dominance of umklapp processes in the studied single crystal.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The QD DynaCool-12 measurement system was acquired within the DFG project 422219907. We thank S. Kostmann and U. Burkhardt for performing EDX characterization of our sample and H. Borrmann, E. Meier and A. Schwarzer for their assistance during XRD measurements. V. L. is grateful to DFG for financial support (project 467257848).References
- D. Diaz-Anichtchenko, J. E. Aviles-Coronado, S. López-Moreno, R. Turnbull, F. J. Manjón, C. Popescu and D. Errandonea, Inorg. Chem., 2024, 63, 6898–6908 CrossRef CAS PubMed.
- O. Fabelo, J. Gonzalez-Platas, S. Savvin, P. Botella and D. Errandonea, J. Appl. Phys., 2024, 136, 175901 CrossRef CAS.
- S. G. Altendorf, D. Takegami, A. Meléndez-Sans, C. F. Chang, M. Yoshimura, K. D. Tsuei, A. Tanaka, M. Schmidt and L. H. Tjeng, Phys. Rev. B, 2023, 108, 085119 CrossRef CAS.
- A. Maignan, M. Schmidt, Y. Prots, O. I. Lebedev, R. Daou, C.-F. Chang, C.-Y. Kuo, Z. Hu, C.-T. Chen, S.-C. Weng, S. G. Altendorf, L.-H. Tjeng and Y. Grin, Chem. Mater., 2022, 34, 789–797 CrossRef CAS.
- M. Assis, A. C. Tello, F. S. Abud, P. Negre, L. K. Ribeiro, R. A. Ribeiro, S. H. Masunaga, A. E. Lima, G. E. Luz Jr, R. F. Jardim, A. B. Silva, J. Andrés and E. Longo, Appl. Surf. Sci., 2022, 600, 154081 CrossRef CAS.
- D. A. Umbsaar and S. M. Antao, Minerals, 2021, 12, 42 CrossRef.
- R. Schuler, F. Bianchini, T. Norby and H. Fjellvåg, ACS Appl. Mater. Interfaces, 2021, 13, 7416–7422 CrossRef CAS PubMed.
- B. Huang and J. N. Hart, Phys. Chem. Chem. Phys., 2020, 22, 1727–1737 RSC.
- W. G. Lyon and E. F. Westrum, J. Chem. Thermodyn., 1974, 6, 763–780 CrossRef CAS.
- R. O. Keeling, Acta Crystallogr., 1957, 10, 209–213 CrossRef CAS.
- E. García-Matres, N. Stüßer, M. Hofmann and M. Reehuis, Eur. Phys. J. B, 2003, 32, 35–42 CrossRef.
- G. Lautenschläger, H. Weitzel, T. Vogt, R. Hock, A. Böhm, M. Bonnet and H. Fuess, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 6087–6098 CrossRef PubMed.
- I. Urcelay-Olabarria, J. M. Perez-Mato, J. L. Ribeiro, J. L. García-Muñoz, E. Ressouche, V. Skumryev and A. A. Mukhin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 014419 CrossRef.
- H. Obermayer, H. Dachs and H. Schröcke, Solid State Commun., 1973, 12, 779–784 CrossRef CAS.
- E. Schmidbauer, U. Schanz and F. J. Yu, J. Phys.: Condens. Matter, 1991, 3, 5341–5352 CrossRef CAS.
- R. Bharati, R. Singh and B. Wanklyn, J. Phys. Chem. Solids, 1982, 43, 641–644 CrossRef CAS.
- R. Bharati, Y. P. Yadava and R. A. Singh, J. Mater. Sci. Lett., 1983, 2, 808–810 CrossRef CAS.
- T. Ejima, T. Banse, H. Takatsuka, Y. Kondo, M. Ishino, N. Kimura, M. Watanabe and I. Matsubara, J. Lumin., 2006, 119–120, 59–63 CrossRef CAS.
- S. Rajagopal, V. Bekenev, D. Nataraj, D. Mangalaraj and O. Khyzhun, J. Alloys Compd., 2010, 496, 61–68 CrossRef CAS.
- K. Hoang, Phys. Rev. Mater., 2017, 1, 024603 CrossRef.
- D. Errandonea and J. Ruiz-Fuertes, Crystals, 2018, 8, 71 CrossRef.
- R. Guillen and J. R. Regnard, Phys. Chem. Miner., 1985, 12, 246–254 CrossRef CAS.
- T. Birkett, Can. Mineral., 2003, 41, 1296–1297 CrossRef.
- STOE Powder Software, WinXPow (version 2), STOE and Cie GmbH, Darmstadt, 2001 Search PubMed.
- L. Akselrud and Y. Grin, J. Appl. Crystallogr., 2014, 47, 803–805 CrossRef CAS.
- P. J. Withers, Rep. Prog. Phys., 2007, 70, 2211–2264 CrossRef.
- N. Rossini, M. Dassisti, K. Benyounis and A. Olabi, Mater. Des., 2012, 35, 572–588 CrossRef.
- P. Withers and H. Bhadeshia, Mater. Sci. Technol., 2001, 17, 355–365 CrossRef CAS.
- A. Nezu, H. Matsuzaka and R. Yokoyama, Rigaku J., 2014, 30, 4–12 CrossRef.
- C. Escobar, H. Cid-Dresdner, P. Kittl and I. Dümler, Am. Mineral., 1971, 56, 489–498 CAS.
- D. Ülkü, Z. Kristallogr. Krist., 1967, 124, 192–219 CrossRef.
- J. Emsley, The Elements, Clarendon Press, Oxford, 3rd edn, 1998 Search PubMed.
- M. Almeida, L. Cavalcante, C. Morilla-Santos, P. L. Filho, A. Beltrán, J. Andrés, L. Gracia and E. Longo, Mater. Charact., 2012, 73, 124–129 CrossRef CAS.
- H. Weitzel, Solid State Commun., 1969, 7, 1249–1252 CrossRef CAS.
- M. A. P. Almeida, L. S. Cavalcante, C. Morilla-Santos, C. J. Dalmaschio, S. Rajagopal, M. S. Li and E. Longo, CrystEngComm, 2012, 14, 7127–7132 RSC.
- Y.-X. Zhou, H.-B. Yao, Q. Zhang, J.-Y. Gong, S.-J. Liu and S.-H. Yu, Inorg. Chem., 2009, 48, 1082–1090 CrossRef CAS PubMed.
- C. P. Landee and E. F. Westrum, J. Chem. Thermodyn., 1976, 8, 663–674 CrossRef CAS.
- C. P. Landee, J. Westrum and F. Edgar, AIP Conf. Proc., 1976, 29, 445–446 CrossRef CAS.
- C. M. N. Kumar, Y. Xiao, P. Lunkenheimer, A. Loidl and M. Ohl, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235149 CrossRef.
- P. Wyżga, M. Bobnar, C. Hennig, A. Leithe-Jasper, T. Mori and R. Gumeniuk, Z. Anorg. Allg. Chem., 2017, 643, 858–863 CrossRef.
- K. Sieber, K. Kourtakis, R. Kershaw, K. Dwight and A. Wold, Mater. Res. Bull., 1982, 17, 721–725 CrossRef CAS.
- Y. Noda, M. Shimada, M. Koizumi and F. Kanamaru, J. Solid State Chem., 1979, 28, 379–384 CrossRef CAS.
- K. Sieber, H. Leiva, K. Kourtakis, R. Kershaw, K. Dwight and A. Wold, J. Solid State Chem., 1983, 47, 361–367 CrossRef CAS.
- W. S. Choi, K. Taniguchi, S. J. Moon, S. S. A. Seo, T. Arima, H. Hoang, I.-S. Yang, T. W. Noh and Y. S. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205111 CrossRef.
- J. Robert, R. Heikes and R. W. Ure, Thermoelectricity: Science and Engineering, Interscience Publishers, New York - London, 1961 Search PubMed.
- J.-S. Zhou and J. B. Goodenough, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, R15002–R15004 CrossRef CAS.
- P. M. Chaikin and G. Beni, Phys. Rev. B, 1976, 13, 647–651 CrossRef CAS.
- E. Zuñiga-Puelles, R. Cardoso-Gil, M. Bobnar, I. Veremchuk, C. Himcinschi, C. Hennig, J. Kortus, G. Heide and R. Gumeniuk, Dalton Trans., 2019, 48, 10703–10713 RSC.
- K. A. Borup, J. de Boor, H. Wang, F. Drymiotis, F. Gascoin, X. Shi, L. Chen, M. I. Fedorov, E. Müller, B. B. Iversen and G. J. Snyder, Energy Environ. Sci., 2015, 8, 423–435 RSC.
- Thermal transport option user's manual, Quantum design, Inc. 6325 Lusk Blvd., San Diego, CA, USA technical report, 2002.
- T. M. Tritt, Thermal Conductivity: Theory, Properties, and Applications, Springer New York, NY, 2004 Search PubMed.
- E. Zuñiga-Puelles, V. Levytskyi, A. Özden, T. Gürel, N. Bulut, C. Himcinschi, C. Sevik, J. Kortus and R. Gumeniuk, Phys. Rev. B, 2023, 107, 195203 CrossRef.
- E. Zuñiga-Puelles, A. Özden, V. Pacheco, L. Akselrud, R. Cardoso-Gil, A. Straßheim, P. Wyżga, C. Himcinschi and R. Gumeniuk, J. Alloys Compd., 2024, 976, 173055 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2425342. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5dt00332f |
| This journal is © The Royal Society of Chemistry 2025 |