Moiré metasurfaces with tunable near-infrared-I chiroptical responses for biomolecular chirality discrimination†
Mengjia
Cen
abc,
Jiawei
Wang
 abc,
Ming
Cheng
abc,
Ming
Cheng
 abc,
Ziyan
Lei
abc,
Ye
Li
abc,
Zhenming
Wang
abc,
Xueqian
Zhao
abc,
Zixuan
Wu
abc,
Huanian
Zhang
abc,
Ziyan
Lei
abc,
Ye
Li
abc,
Zhenming
Wang
abc,
Xueqian
Zhao
abc,
Zixuan
Wu
abc,
Huanian
Zhang
 *de and
Yan Jun
Liu
*de and
Yan Jun
Liu
 *abc
*abc
aDepartment of Electrical and Electronic Engineering, Southern University of Science and Technology, Shenzhen 518055, China. E-mail: yjliu@sustech.edu.cn
bState Key Laboratory of Optical Fiber and Cable Manufacture Technology, Southern University of Science and Technology, Shenzhen 518055, China
cShenzhen Engineering Research Center for High Resolution Light Field Display and Technology, Southern University of Science and Technology, Shenzhen 518055, China
dZhejiang Lingkang Medical Equipment Co., Ltd, Wenling, 317500, China. E-mail: huanian_zhang@163.com
eSchool of Physics and Optoelectronic Engineering, Shandong University of Technology, Zibo, 255049, China
First published on 2nd December 2024
Abstract
Manipulating circular dichroism in chiral metasurfaces has been increasingly important for a wide range of polarization-sensitive photonic applications. However, simple methods for presenting chiral nanostructures with tunable and considerable chiroptical responses in the near-infrared-I regime remains underexplored. Herein, two sheets of suspended symmetric bilayer metagratings fabricated via single-step electron beam lithography are stacked into a moiré metasurface with its circular dichroism value reaching up to 20.9°. The chirality of the moiré metasurface can be fully tuned in terms of both its sign and magnitude by adjusting the in-plane angle between the two twisted sheets of metagratings. The multilayered design is accessible to the coupling of hybridized plasmons for governing the chiroptical properties in the near-infrared-I regime. The ratio between the resonance wavelength and the grating period is about 1.65, which is much lower compared to that in most existing moiré metasurfaces with strong chiroptical responses. Furthermore, the superchiral fields in the inter-sheet region are further exploited for label-free enantiodiscrimination with ultrahigh sensitivity of 10.17 nm fmol−1 mm2. The proposed moiré metasurfaces with strong near-infrared-I chirality hold great potential for supporting polarization engineering and biomolecular detection, paving a way for advanced applications in medical diagnosis, biomedical imaging, and display technologies.
1. Introduction
Arranged in defined lattices with subwavelength nanostructures, metasurfaces can strongly interact with incident light to modulate its phase, amplitude, and polarization.1 Upon breaking the mirror symmetry, metasurfaces become chiral, exhibiting chiroptical responses like circular dichroism (CD) due to polarization-dependent light–matter interactions.2–6 Beacuse of their capability of boosting chiroptical responses, chiral metasurfaces have attracted tremendous attention for various promising applications, including chiral molecular sensing,7–11 enantioselection,12–16 spin-dependent emission,17–19 information encryption and storage,20,21 and holographic displays.22,23 Numerous periodic nanostructure designs and diverse fabrication techniques have been developed to break mirror symmetry and achieve chiral nanostructures accordingly, such as planarized asymmetric patterns,24–26 three-dimensional chiral structures,27–30 kirigami structures,31 twisted stacking bilayer metasurfaces,32–34 and structures with extrinsic chirality.35,36 With these progressions, current research has been focusing more on gaining locally addressable tunability in chiral metasurfaces for manipulating polarization and multiplexing applications. Combined with phase-change materials,37–39 magneto-optical materials,40 liquid crystals,41–44 mechanical deformation,45 and biochemical reconfiguration,46,47 active control of the CD magnitude or spectral position can be realized. Nevertheless, achieving the chirality reversion of metasurfaces continues to be a challenge.As an essential characteristic of optical devices in practical applications, the working wavelength is of great importance. The near-infrared-I (NIR-I) window plays a crucial role in bioimaging, fluorescence detection, environmental monitoring, and short-distance telecommunications, where its deep penetration, minimal scattering and low heat damage ability is leveraged.48,49 Since most existing chiral metasurfaces often rely on complex fabrication techniques, sophisticated geometries, and precise alignments, it is not easy to fabricate chiral metasurfaces composed of subwavelength-sized nanostructures to obtain strong chiroptical responses in the NIR-I regime. Thus, chiral metasurfaces with tunable and responsive optical chirality in the NIR-I regime are relatively scarce compared to those with tunable and responsive optical chirality in longer wavelength ranges, such as the NIR-II, mid-infrared and terahertz regimes. CD reversion designs combining strong chiroptical responses in the NIR-I regime are desirable for further applications. Twisted stacking moiré metasurfaces with active and static layers show natural advantages of altering CD signs and eliminating the process of layer alignment.50 In contrast to chiral metasurfaces based on intrinsic chiral structures or site-specific rotation of subassemblies, moiré metasurfaces are not inherently chiral. When the in-plane angle between the lattice directions of the two twisted achiral layers is not 0° or 90°, the mirror symmetry is broken, and the inherent chirality of moiré metasurfaces can be achieved. Although the optical chirality of moiré metasurfaces can be tuned by changing the twisted angle, most of them are developed above NIR-I wavelengths or have weak chiroptical performance in visible and NIR-I regimes.51–54
Herein, we introduce a moiré metasurface that allows reversible post-fabrication manipulation of the strong chiroptical responses in the NIR-I regime. The moiré metasurface consists of two sheets of suspended bilayer metagratings in a twisted stacking arrangement. In the suspended bilayer metagratings, the top and bottom grating layers, which are spaced by an Si3N4 membrane, are self-aligned via a single-step electron beam lithography (EBL) process, hence simplifying the fabrication of bilayer metasurfaces. The moiré metasurface exhibits CD reaching up to 20.9° at a wavelength of about 825 nm. Changing the angle between the two twisted sheets of bilayer metagratings, the chirality of the moiré metasurface can be switched in terms of both its sign and magnitude. The multilayered design allows coupling of hybridized plasmons, which lie at higher energy levels, thus decreasing the ratio between the resonance wavelength and the grating period. The superchiral fields in inter-sheet regions are studied for the physical mechanism behind the CD signals. We further demonstrate that the plasmonic moiré metasurface could be used for label-free enantiodiscrimination with an ultrahigh sensitivity of 10.17 nm fmol−1 mm2. Our proposed approach provides an alternative route to simultaneously control the CD sign and magnitude with strong chiroptical responses in the NIR-I regime, hence holding great potential in medical diagnosis, biomedical imaging, and display technologies.
2. Results and discussion
2.1 Chiral arrangement of moiré metasurfaces
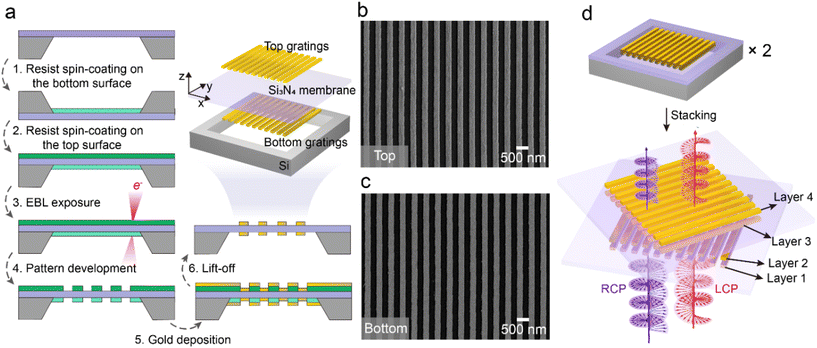
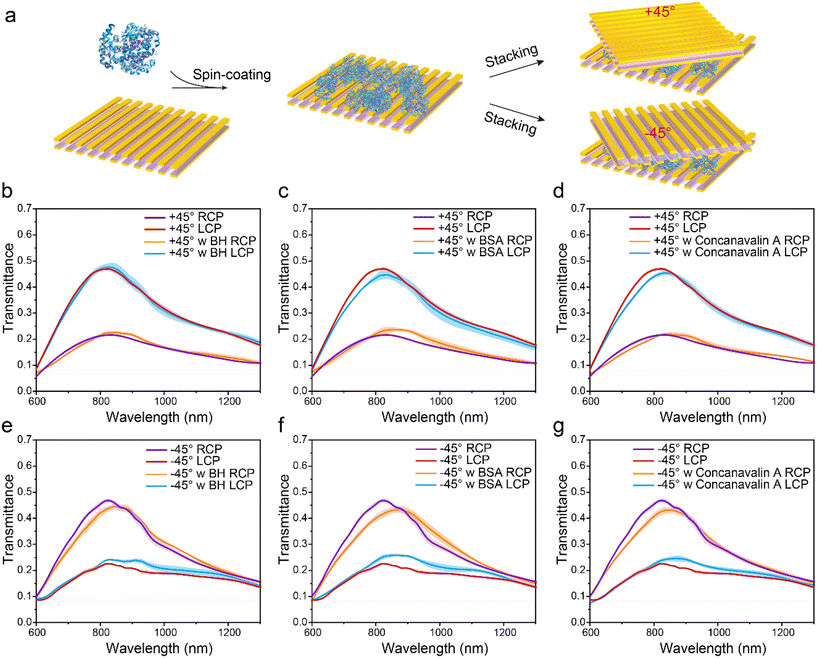
The building blocks of the moiré metasurface are two identical sheets of suspended bilayer metagratings. A schematic of the suspended bilayer metagratings with their processing steps is presented in Fig. 1a. The suspended bilayer metagratings consist of two symmetric gold metagratings spaced by an Si3N4 membrane. The Si3N4 membrane serves as not only a supporting layer for both top and bottom metagratings but also an interlayer for confining gap plasmons.55 The single-step EBL process eliminates alignment errors in the fabrication of bilayer metagratings, creating a simple self-aligned metal–insulator–metal structural configuration. The scanning electron microscopy (SEM) images of the top and bottom surfaces of the suspended bilayer metagratings are shown in Fig. 1b and c, respectively. The period and width of the metagratings are 500 nm and 250 nm, respectively. The thicknesses of the Si3N4 membrane and metagratings are 50 nm and 30 nm, respectively. Without a substrate, the suspended bilayer metagratings are considered as a symmetric structure along the light propagation direction. As shown in Fig. 1d, by stacking two such sheets at a certain in-plane twisted angle, the chiral arrangement is accomplished. The lattice asymmetry of multilayered metagratings along the light propagation direction induces chiroptical responses. These grating layers are designated 1–4 along the propagation direction of the normally incident light for the sake of clear descriptions.2.2 Characterization of chiroptical responses
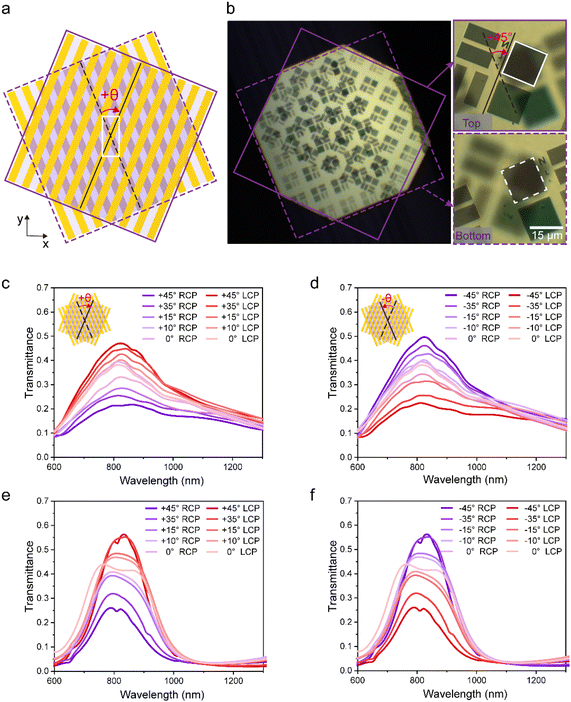
As shown in Fig. 2a, the bottom and top sheets of suspended bilayer metagratings are indicated by the violet dashed and solid squares, respectively. Their relative in-plane twisted angle θ determines the handedness of the moiré metasurface. The relative clockwise and counterclockwise rotations of the top and the bottom sheets correspond to positive and negative values of θ, respectively. The area framed by the white line is a unit cell of the moiré metasurface. The photographs of the moiré metasurface with θ = +45° under a 100× objective lens are presented in Fig. 2b. In the right-hand panel, the metagrating area highlighted by the white solid and dashed squares on the top and bottom sheets are overlapped, corresponding to Fig. 2a. Detailed SEM images of the bilayer nanostructures are shown in Fig. S1.† The value of θ can be changed by in situ restacking, allowing active control of the chiral arrangement to manipulate chiroptical responses. We experimentally characterized the chiroptical responses of the moiré metasurface with the twist angle θ changing from 45° to 0°, while the transmittance spectra under incident right- and left-handed circularly polarized (RCP and LCP) light are illustrated in Fig. 2c and d. The polarization-dependent resonance is located at the wavelength of 825 nm within the NIR-I regime. As θ changes from +45° to 0°, the LCP light transmittance gradually decreases, while the RCP one increases accordingly. Opposite trends occur when θ changes from −45° to 0°. At present, we do not have an effective way to achieve a specific gap distance. In Fig. S2,† we use the simulation approach to evaluate the gap distance. Numerically simulated transmittance spectra (see Fig. 2e and f) show results similar to the experimentally measured ones with an estimated gap distance of 200 nm. The discrepancy between the experimentally measured and simulated spectra could be possibly attributed to fabrication errors, the small measurement area (5 μm × 5 μm), the estimated gap distance from simulations, and incoherent incident light used in our experiments. In addition, Fig. S3† shows measured and simulated chiral-component transmittance of the +45°-arranged moiré metasurface. As can be seen, the output cross-polarization of RCP is the dominant part, meaning that the incident RCP light converts to LCP light upon interaction with the +45°-arranged moiré metasurface. The co-polarized output of the LCP light is higher than the cross-polarized part. The disparity of the transmittance for RCP and LCP light incidence implies the chiroptical responses of the moiré metasurfaces.Furthermore, for a clearer illustration of the chiroptical responses of the designed moiré metasurface, we re-write the relationship to CD as CDT with respect to transmittance,56–59
| CDT = TRCP − TLCP | (1) |
2.3 Near-field analyses of the optical chirality
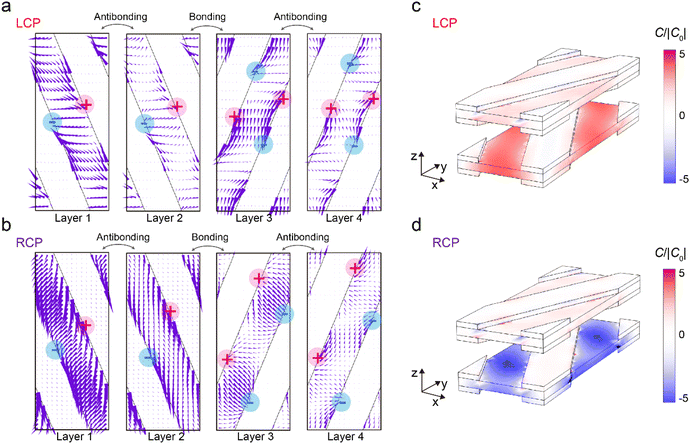
To reveal the origin of the optical chirality in the moiré metasurface, we carried out near-field analyses of a moiré unit cell based on full-wave electromagnetic simulations. Fig. 4a and b show the simulated charge distributions and normalized surface currents on each metagrating layer of the +45°-arranged moiré metasurface at the wavelength of 837 nm under LCP and RCP light incidence, respectively. When the normally incident light impinges on the bottom metagrating layer, complex hybridized plasmonic modes are excited in the four grating layers. As revealed in Fig. 4a and b, the similar surface current vector fields on layer 1 and layer 2 are related to the symmetry charge distributions, indicating the antibonding mode between these two layers. A bonding mode between layer 2 and layer 3 is supported by the counterpropagating currents. Co-propagating currents occur between layer 3 and layer 4, leading to an antibonding mode. In general, the antibonding mode generating repulsion forces lies at a higher energy level compared to the bonding mode. Thus, the charge maps with two antibonding modes elucidate a shorter resonance wavelength in the multilayered moiré metasurfaces, showing different plasmonic modes compared to other bilayer moiré metasurfaces.7,50,60 The ratio between the resonance wavelength and the grating period is 1.65. As shown in Table S1,† the ratios in most reported moiré metasurfaces with strong CD are larger than 3, hindering the realization of chiroptical responses in the NIR-I regime due to the difficulty of fabricating delicate nanostructures within a small grating period. We simulated transmittance spectra of the +45°-arranged moiré metasurface composed of two sheets of single-layer metagratings, as shown in Fig. S5.† As expected, the chiroptical responses are relatively weak in the NIR-I regime while quite strong at a wavelength of 2000 nm. The plasmonic modes in the two-layer metagratings lie at the low energy level. The ratio between the resonance wavelength and the grating period is about 4. In addition, the normalized current vectors indicate charge densities in the metagratings. Layer 3 and layer 4 have relatively weak surface currents under RCP light illumination but strong ones under LCP light illumination, which corresponds to the polarization-selected transmittance in the moiré metasurfaces.To evaluate the light–matter interactions at the near field, we further calculated the superchiral field C, which is written as:61–63
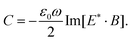 | (2) |
Here ε0 is the free-space permittivity, ω is the angular frequency, and E and B denote the local electric and magnetic fields, respectively. The enhancement of the superchiral field is derived as C/|C0|, where C0 is the value obtained under circularly polarized light without metagratings.61 The sign of C helps with figuring out the different handedness of local fields. The positive and negative signs indicate the LCP and RCP fields, respectively. As illustrated in Fig. 4c and d, the superchiral fields at 837 nm of the +45°-arranged moiré metasurface are highly handedness-dependent for the incident light. Under LCP light incidence, the moiré metasurface is governed by the LCP superchiral field, as shown in Fig. 4c. Comparatively, in Fig. 4d, under RCP light incidence, the bottom and top sheets of the bilayer metagratings illustrate the RCP and LCP superchiral fields, respectively, indicating the cross-polarization conversion. The distinct superchiral fields in the inter-sheet region enable different chiral light–matter interactions near the moiré metasurface, which is promising for enhancing the interaction with chiral biomolecules.
2.4 Enhanced CD measurements of chiral biomolecules
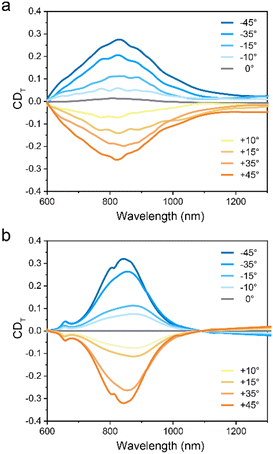
The exposed intense superchiral fields in the inter-sheet region are sufficiently sensitive to detect the chiral structures of biomolecules, such as the secondary structures of proteins. As a proof-of-concept, we further exploited our moiré metasurfaces to discriminate the structural chirality of chiral biomolecules using three kinds of well-studied proteins: bovine hemoglobin (BH), bovine serum albumin (BSA) and concanavalin A. As Fig. 5a illustrates, we stacked ±45°-arranged moiré metasurfaces for strong chiral light–matter interaction. Before stacking, a monolayer of protein was spin-coated on the bottom sheet of the moiré metasurface. Taking advantage of the reconfigurable design, the same kind of protein was added only once for both measurements in ±45°-arranged moiré metasurfaces. The transmittance spectra with and without protein-coating are shown in Fig. 5b–g. The error bands are calculated from the standard deviation with six measurements. On the −45°-arranged moiré metasurface, the wavelength shifts are induced with the presence of proteins. In addition, the peak transmittance decreases for the RCP light illumination but increases for the LCP light after protein-coating (see Fig. 5e–g). Comparatively, on the +45°-arranged moiré metasurface, the wavelength shifts and the peak transmittance changes are not as apparent as in the cases of the −45°-arranged moiré metasurface.To achieve much more straightforward observations, we further calculated the CDT, accordingly, as presented in Fig. 6. Both the wavelength shifts and the peak transmittance changes are specific to the handedness of the moiré metasurface. We also calculated the CD in degrees (see Fig. S6†), in which the transmittance has similarly changing trend as the one observed in CDT spectra. However, the wavelength shifts shown in Fig. S6† are not so obvious due to the wide bandwidth. Therefore, we use CDT spectra for chirality detection in our experiments. The chirality of the proteins can be determined by the dissymmetry in spectral shift, which is defined as:64
| ΔΔλ = Δλ−45° − Δλ+45° | (3) |
| ΔCDT = (CDT@−45°P − CDT@−45°) + (CDT@+45°P − CDT@+45°) | (4) |
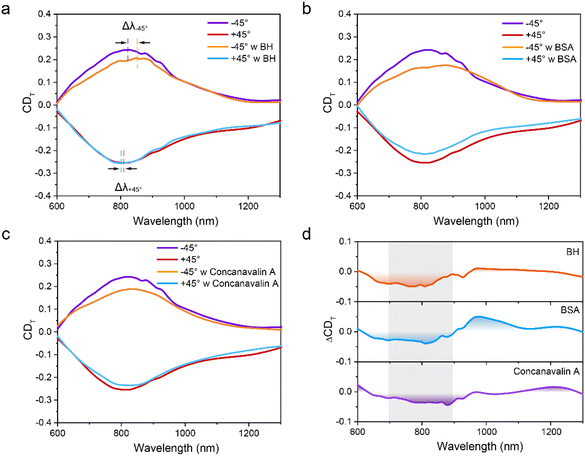 | ||
| Fig. 6 (a–c) CDT spectra for the ±45°-arranged moiré metasurfaces with and without (a) BH, (b) BSA and (c) concanavalin A, respectively. (d) Calculated protein-induced ΔCDT. | ||
3. Conclusions
In summary, we have demonstrated an active, plasmonic moiré metasurface with NIR-I chiroptical responses for label-free chirality detection of biomolecules. The moiré metasurface is constructed by stacking two twisted sheets of suspended bilayer metagratings spaced by an Si3N4 membrane, which are prepared via single-step of EBL exposure. The top and bottom metagratings are symmetric and self-aligned. CD reaching up to 20.9° can be achieved in the moiré metasurface at a wavelength of 825 nm. More importantly, both the sign and the magnitude of CD in the moiré metasurface can be actively and conveniently manipulated by changing the stacking angle between the two twisted sheets of suspended bilayer metagratings. The multilayered design facilitates the excitation of hybridized plasmonic modes within the shorter wavelength range, hence resulting in a relatively small ratio between the resonance wavelength and the grating period and further relaxation of the fabrication difficulties. The inter-sheet region in our moiré metasurfaces features a unique exposed area with strongly enhanced superchiral fields, which can be further exploited for chirality discrimination of biomolecules. As a proof-of-concept, three proteins with the same handedness, namely BH, BSA and concanavalin A, have been successfully discriminated with sensitivities of about 1.83, 10.17, and 1.03 nm fmol−1 mm2, respectively. Our proposed moiré metasurfaces with active control of both the sign and magnitude of CD via their twisted arrangement could serve as important platforms for medical diagnosis, biomedical imaging, and display technologies.4. Materials and methods
4.1 Moiré metasurface fabrication
As shown in Fig. 1, the bilayer metagratings were supported by a commercially available Si3N4 membrane (CleanSiN, China) with a thickness of 50 nm. The top and bottom surfaces of the Si3N4 membrane were subjected to a hydrophilic treatment for uniform spin-coating. First, the bottom surface was coated with 120 nm of AR-P 6200.05 resist (5% solids content) (Allresist, Germany). Then the top surface was coated with 200 nm of AR-P 6200.09 resist (9% solids content) (Allresist, Germany). The baking temperature and time for both top and bottom resists were 150 °C and 60 s. A single-step EBL process with an exposure dose of 300 C cm−2 was carried out for pattern writing. The acceleration voltage was 80 kV and the beam current was set to 2 nA. Due to the single-step EBL fabrication, the top and bottom metagratings are perfectly self-aligned. Gold layers were subsequently deposited on both sides after pattern development. After a lift-off process using the remover AR 600-71 (Allresist, Germany), suspended symmetric bilayer metagratings are obtained. Finally, the moiré metasurface is constructed by stacking two twisted sheets of suspended bilayer metagratings.4.2 Preparation of chemicals
The BH was purchased from Aladdin. The BSA and concanavalin A were obtained from Sigma-Aldrich. These three proteins were all dissolved in Tris/HCl buffer solution (PH = 7) at a concentration of 1 mg ml−1. The protein solutions were spin-coated on the top surface of the bottom suspended bilayer metagratings at 2000 rpm, forming an ∼10 nm-thick layer that was confirmed by a surface profiler (KLA-Tencor, P-7). After each measurement, the metasurfaces were soaked in the Tris/HCl buffer solution for 2 h to completely dissolve the protein. Then, the metasurfaces were rinsed with the Tris/HCl buffer solution. Deionized water was used to remove excess residues. After drying, the metasurfaces were cleaned by ultraviolet ozone for 25 min. With this thorough cleaning, we recorded the spectra of BH, BSA and concanavalin A on the moiré metasurfaces in sequence.4.3 Optical characterization
The in situ optical transmittance spectra were recorded via a microspectrophotometer system (CRAIC 20/30PV). Unpolarized broadband light (70 W xenon lamp, Olympus) was sequentially passed through a broadband linear polarizer (Thorlabs, WP25M-UB, 250–4000 nm) and a quarter-wave plate (QWP, Thorlabs, SAQWP05M-1700, 600–2700 nm) to convert it into either LCP or RCP light as the incident beam. A 100× objective lens (NA = 0.8) was used to collect transmitted light. This light was then guided to both the imaging camera and the spectrometer through a beam splitter. The camera was used to perform in situ measurements. In the light path to the spectrometer, an aperture was used to select the measurement area. In our experiments, the measurement area was 5 μm × 5 μm.4.4 Numerical simulation
To calculate transmittance spectra, the finite-difference time-domain (FDTD) method was used in this work. The wavelength-dependent refractive indices of gold and Si3N4 were based on the data from our previous work.54 A moiré unit of the stacked and twisted bilayer metagratings was simulated with periodic boundary conditions along the x-axis and y-axis and a perfectly matched layer along the z-axis (i.e., the light propagation direction). A uniform mesh size of 2 nm in all three dimensions was used to cover the region of structures. To calculate the surface currents and superchiral fields, we used COMSOL Multiphysics software, which is based on the finite element method. The refractive indices, boundary conditions, and propagation directions were set to be the same as those in the FDTD method. The superchiral fields were derived more conveniently by calculating the geometrical model using the volume method.Author contributions
Y. J. L. conceived the project and designed the experiment. M. C. and J. W. fabricated samples. M. C. carried out the measurements. M. C. performed simulations and wrote the manuscript. Y. J. L. supervised the project. All authors completed data analysis, discussed the results, and contributed to the final manuscript.Data availability
The data that support the findings of this work are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by the National Key R&D Program of China (Grant No. 2022YFA1203702), the National Natural Science Foundation of China (Grant No. 62075093), the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2024A1515010415), the Shenzhen Science and Technology Innovation Commission (Grant No. JCYJ20220818100413030), the Shenzhen Development and Reform Commission (Grant No. XMHT20220114005), the Opening Fund of the State Key Laboratory of Optoelectronics & Materials and Technologies (Sun Yat-sen University) (Grant No. OEMT-2024-KF-04), the High Level of Special Funds from the Southern University of Science and Technology (Grant No. G030230001 and G03034K004), and Graduate Education Innovation Grants from the Southern University of Science and Technology (Grant No. 202401002). The authors acknowledge the assistance of staff at the SUSTech Core Research Facilities.References
- N. Yu and F. Capasso, Nat. Mater., 2014, 13, 139–150 CAS.
- Y. Tang and A. E. Cohen, Phys. Rev. Lett., 2010, 104, 163901 Search PubMed.
- M. Hentschel, M. Schäferling, X. Duan, H. Giessen and N. Liu, Sci. Adv., 2017, 3, e1602735 Search PubMed.
- H. He, M. Cen, J. Wang, Y. Xu, J. Liu, W. Cai, D. Kong, K. Li, D. Luo, T. Cao and Y. J. Liu, ACS Appl. Mater. Interfaces, 2022, 14, 53981–53989 CAS.
- J. Mun, M. Kim, Y. Yang, T. Badloe, J. Ni, Y. Chen, C. W. Qiu and J. Rho, Light Sci. Appl., 2020, 9, 139 CrossRef CAS PubMed.
- Z. Wang, F. Cheng, T. Winsor and Y. Liu, Nanotechnology, 2016, 27, 412001 CrossRef PubMed.
- Z. Wu, X. Chen, M. Wang, J. Dong and Y. Zheng, ACS Nano, 2018, 12, 5030–5041 CrossRef CAS PubMed.
- Y. Zhao, A. N. Askarpour, L. Sun, J. Shi, X. Li and A. Alù, Nat. Commun., 2017, 8, 14180 Search PubMed.
- R. Knipper, V. Kopecký, U. Huebner, J. Popp and T. G. Mayerhöfer, ACS Photonics, 2018, 5, 3238–3245 CrossRef CAS.
- J. Garciá-Guirado, M. Svedendahl, J. Puigdollers and R. Quidant, Nano Lett., 2018, 18, 6279–6285 CrossRef.
- J. García-Guirado, M. Svedendahl, J. Puigdollers and R. Quidant, Nano Lett., 2020, 20, 585–591 CrossRef.
- E. Hendry, T. Carpy, J. Johnston, M. Popland, R. V. Mikhaylovskiy, A. J. Lapthorn, S. M. Kelly, L. D. Barron, N. Gadegaard and M. Kadodwala, Nat. Nanotechnol., 2010, 5, 783–787 Search PubMed.
- Y. Shi, T. Zhu, T. Zhang, A. Mazzulla, D. P. Tsai, W. Ding, A. Q. Liu, G. Cipparrone, J. J. Sáenz and C. W. Qiu, Light: Sci. Appl., 2020, 9, 62 Search PubMed.
- R. Jin, X. Zhang, P. Huo, Z. Cai, Y. Lu, T. Xu and Y. Liu, Phys. Rev. Lett., 2024, 133, 86901 Search PubMed.
- M. L. Solomon, J. Hu, M. Lawrence, A. García-Etxarri and J. A. Dionne, ACS Photonics, 2019, 6, 43–49 Search PubMed.
- L. Mao, P. Cheng, K. Liu, M. Lian and T. Cao, Nanoscale Adv., 2022, 4, 1617–1652 Search PubMed.
- M. Cotrufo, C. I. Osorio and A. F. Koenderink, ACS Nano, 2016, 10, 3389–3397 Search PubMed.
- O. Aftenieva, M. Schnepf, B. Mehlhorn and T. A. F. König, Adv. Opt. Mater., 2021, 9, 2001280 CrossRef CAS.
- M. Cen, J. Liu, J. Wang, Y. Li, W. Cai, M. Cheng, D. Kong, X. Tang, T. Cao, Y. Q. Lu and Y. J. Liu, ACS Nano, 2024, 18, 20556–20566 Search PubMed.
- K. Chen, G. Ding, G. Hu, Z. Jin, J. Zhao, Y. Feng, T. Jiang, A. Alù and C. W. Qiu, Adv. Mater., 2020, 32, 1906352 CrossRef CAS.
- Y. Xie, P. Yang, L. Deng, Z. Feng, J. Li, C. Zhang, X. Tang, C. Li, J. Li, L. Xu, D. Zhang, X. Chen and G. Zou, Adv. Opt. Mater., 2022, 10, 2102197 Search PubMed.
- Y. Chen, X. Yang and J. Gao, Light: Sci. Appl., 2018, 7, 84 Search PubMed.
- Z. Yin, Y. Shi, M. Cen, T. Cao, C. Xu, D. Luo, G. Li and Y. J. Liu, Sci. Bull., 2021, 66, 1518–1524 Search PubMed.
- J. Li, D. Wu, C. W. Qiu, J. Ni, S. Liu, G. Hu, Y. Hu, Z. Lao, Q. Zhang, S. Dong and J. Chu, ACS Nano, 2021, 15, 2893–2900 Search PubMed.
- G. Palermo, M. Rippa, D. M. Aceti, A. Guglielmelli, L. Valente, D. Sagnelli, A. D'Avino, B. Guilcapi, N. Maccaferri, L. Petti and G. Strangi, Nano Lett., 2024, 24, 10202–10209 Search PubMed.
- W. Chen, Z. Wang, M. V. Gorkunov, J. Qin, R. Wang, C. Wang, D. Wu, J. Chu, X. Wang, Y. Kivshar and Y. Chen, Nano Lett., 2024, 24, 9643–9649 CrossRef CAS PubMed.
- J. Dixon, M. Lawrence, D. R. Barton and J. Dionne, Phys. Rev. Lett., 2021, 126, 123201 CrossRef CAS.
- S. Rajamani, D. Simeone, A. Pecora, M. Manoccio, G. Balestra, A. H. Bayramov, N. T. Mamedov, A. Passaseo, G. Gigli, D. M. Tobaldi, V. Tasco, M. Esposito, A. Cola and M. Cuscunà, Adv. Mater. Technol., 2024, 9, 2301250 Search PubMed.
- M. Esposito, V. Tasco, F. Todisco, M. Cuscunà, A. Benedetti, D. Sanvitto and A. Passaseo, Nat. Commun., 2015, 6, 6484 CrossRef CAS PubMed.
- Y. Tang, Y. Liang, J. Yao, M. K. Chen, S. Lin, Z. Wang, J. Zhang, X. G. Huang, C. Yu and D. P. Tsai, Laser Photonics Rev., 2023, 17, 2200597 Search PubMed.
- S. Qiao, X. Zhang, Q. Liang, Y. Wang, C.-Y. Ji, X. Li, L. Jiang, S. Feng, H. Guo and J. Li, Photonics Res., 2024, 12, 218 CrossRef.
- D. Frese, Q. Wei, Y. Wang, L. Huang and T. Zentgraf, Nano Lett., 2019, 19, 3976–3980 Search PubMed.
- J. Bai and Y. Yao, ACS Nano, 2021, 15, 14263–14274 Search PubMed.
- K. Tanaka, D. Arslan, S. Fasold, M. Steinert, J. Sautter, M. Falkner, T. Pertsch, M. Decker and I. Staude, ACS Nano, 2020, 14, 15926–15935 Search PubMed.
- L. Mao, K. Liu, S. Zhang and T. Cao, ACS Photonics, 2020, 7, 375–383 CrossRef CAS.
- E. Plum, X. X. Liu, V. A. Fedotov, Y. Chen, D. P. Tsai and N. I. Zheludev, Phys. Rev. Lett., 2009, 102, 1–4 Search PubMed.
- F. Neubrech, M. Hentschel and N. Liu, Adv. Mater., 2020, 32, 1905640 CrossRef CAS PubMed.
- F. Ding, Y. Yang and S. I. Bozhevolnyi, Adv. Opt. Mater., 2019, 7, 1801709 Search PubMed.
- X. Sha, K. Du, Y. Zeng, F. Lai, J. Yin, H. Zhang, B. Song, J. Han, S. Xiao, Y. Kivshar and Q. Song, Sci. Adv., 2024, 10, eadn9017 Search PubMed.
- I. Zubritskaya, N. Maccaferri, X. Inchausti Ezeiza, P. Vavassori and A. Dmitriev, Nano Lett., 2018, 18, 302–307 Search PubMed.
- S. Yin, D. Xiao, J. Liu, K. Li, H. He, S. Jiang, D. Luo, X. W. Sun, W. Ji and Y. J. Liu, IEEE Photonics J., 2018, 10, 4600909 CAS.
- D. Xiao, Y. J. Liu, S. Yin, J. Liu, W. Ji, B. Wang, D. Luo, G. Li and X. W. Sun, Opt. Express, 2018, 26, 25305 Search PubMed.
- S. Yin, W. Ji, D. Xiao, Y. Li, K. Li, Z. Yin, S. Jiang, L. Shao, D. Luo and Y. J. Liu, Opt. Commun., 2019, 448, 10–14 Search PubMed.
- J. Li, P. Yu, S. Zhang and N. Liu, Nat. Commun., 2020, 11, 3574 Search PubMed.
- H. T. Lin, Y. Y. Hsu, P. J. Cheng, W. T. Wang, S. W. Chang and M. H. Shih, Nanoscale Adv., 2022, 4, 2428–2434 Search PubMed.
- X. Duan, S. Kamin, F. Sterl, H. Giessen and N. Liu, Nano Lett., 2016, 16, 1462–1466 CrossRef CAS PubMed.
- M. Matuschek, D. P. Singh, H. H. Jeong, M. Nesterov, T. Weiss, P. Fischer, F. Neubrech and N. Liu, Small, 2018, 14, 1702290 Search PubMed.
- M. Yang, S. Qiu, E. Coy, S. Li, K. Załęski, Y. Zhang, H. Pan and G. Wang, Adv. Mater., 2022, 34, 2106314 CrossRef CAS.
- C. Li and Q. Wang, ACS Nano, 2018, 12, 9654–9659 CrossRef CAS.
- B. Lyu, Y. Li, Q. Jia, H. Li, G. Yang, F. Cao, S. Kou, D. Liu, T. Cao, G. Li and J. Shi, Laser Photonics Rev., 2023, 17, 2201004 CrossRef.
- P. T. Probst, M. Mayer, V. Gupta, A. M. Steiner, Z. Zhou, G. K. Auernhammer, T. A. F. König and A. Fery, Nat. Mater., 2021, 20, 1024–1028 CrossRef CAS PubMed.
- Z. Han, F. Wang, J. Sun, X. Wang and Z. Tang, Adv. Opt. Mater., 2023, 11, 2301022 CrossRef CAS.
- M. K. Chen, J. C. Zhang, C. W. Leung, L. Sun, Y. Fan, Y. Liang, J. Yao, X. Liu, J. Yuan, Y. Xu, D. P. Tsai and S. W. Pang, Nanophotonics, 2023, 12, 2479–2490 Search PubMed.
- Y. Liu, Z. Wu, P. S. Kollipara, R. Montellano, K. Sharma and Y. Zheng, ACS Nano, 2021, 15, 6448–6456 CAS.
- M. Cen, J. Wang, J. Liu, Y. Li, W. Cai, D. Kong, D. Luo, T. Cao and Y. J. Liu, Photonics, 2022, 9, 980 Search PubMed.
- Z. Li, Y. Jiang, W. Liu, Y. Zhang, H. Cheng, J. Li, J. Tian and S. Chen, Appl. Phys. Lett., 2023, 122, 181702 Search PubMed.
- B. Frank, X. Yin, M. Schäferling, J. Zhao, S. M. Hein, P. V. Braun and H. Giessen, ACS Nano, 2013, 7, 6321–6329 Search PubMed.
- W. Ye, X. Yuan, C. Guo, J. Zhang, B. Yang and S. Zhang, Phys. Rev. Appl., 2017, 7, 054003 Search PubMed.
- A. B. Khanikaev, N. Arju, Z. Fan, D. Purtseladze, F. Lu, J. Lee, P. Sarriugarte, M. Schnell, R. Hillenbrand, M. A. Belkin and G. Shvets, Nat. Commun., 2016, 7, 12045 CAS.
- J.-G. Yun, S.-J. Kim, H. Yun, K. Lee, J. Sung, J. Kim, Y. Lee and B. Lee, Opt. Express, 2017, 25, 14260 CAS.
- M. Schäferling, D. Dregely, M. Hentschel and H. Giessen, Phys. Rev. X, 2012, 2, 031010 Search PubMed.
- J. Mun, M. Kim, Y. Yang, T. Badloe, J. Ni, Y. Chen, C. W. Qiu and J. Rho, Light: Sci. Appl., 2020, 9, 139 Search PubMed.
- K. Yao and Y. Liu, Nanoscale, 2018, 10, 8779–8786 Search PubMed.
- Z. Wu and Y. Zheng, Adv. Opt. Mater., 2017, 5, 1700034 Search PubMed.
- C. Y. Lin, C. C. Liu, Y. Y. Chen, K. Y. Chiu, J. De Wu, B. L. Lin, C. H. Wang, Y. F. Chen, S. H. Chang and Y. C. Chang, ACS Appl. Mater. Interfaces, 2021, 13, 1152–1157 Search PubMed.
- M. Cen, J. Wang, J. Liu, H. He, K. Li, W. Cai, T. Cao and Y. J. Liu, Adv. Mater., 2022, 34, 2203956 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr03952a |
| This journal is © The Royal Society of Chemistry 2025 |