Open Access Article
Open Access ArticleSemiclassical description of nuclear quantum effects in solvated and condensed phase molecular systems
Riccardo
Conte
 *,
Giacomo
Mandelli
*,
Giacomo
Mandelli
 ,
Giacomo
Botti
,
Giacomo
Botti
 ,
Davide
Moscato
,
Davide
Moscato
 ,
Cecilia
Lanzi
,
Cecilia
Lanzi
 ,
Marco
Cazzaniga
,
Marco
Cazzaniga
 *,
Chiara
Aieta
*,
Chiara
Aieta
 * and
Michele
Ceotto
* and
Michele
Ceotto
 *
*
Dipartimento di Chimica, Università degli Studi di Milano, via Golgi 19, Milano, 20133, Italy. E-mail: riccardo.conte1@unimi.it; marco.cazzaniga@guest.unimi.it; chiara.aieta@unimi.it; michele.ceotto@unimi.it
First published on 3rd December 2024
Abstract
In this perspective we deal with the challenge of investigating nuclear quantum effects in solvated and condensed phase molecular systems in a computationally affordable way. To this end, semiclassical methods are promising theoretical approaches, as we demonstrate through vibrational spectroscopy and reaction kinetics. We show that quantum vibrational features can be found in hydrates of carbonyl compounds and microsolvated amino acids, and we report quantum estimates of the low-temperature reaction rate constant of a unimolecular reaction taking place in a noble-gas matrix. The hallmark of semiclassical methods is their ability to include nuclear quantum effects into classical molecular dynamics simulations. For this reason, unlike other popular methods, semiclassical approaches are able to account also for real-time quantum contributions and are expected to point out the importance of nuclear quantum effects in complex systems for a wider range of chemical properties.
Introduction
One of the recurrent debates in chemistry concerns whether or not nuclear quantum effects (NQEs) play an important role in solvated and condensed phase systems. There are indeed clues to support either thesis. For instance, we know that zero point energy (ZPE) is typically larger and larger as the dimensionality of the system increases and is present even at 0 K. This makes it one of the most relevant and influential among NQEs. However, common sense is that NQEs are washed out by the environment in solvated and condensed phase systems, so a classical interpretation may be thought to be everything one needs.The topic could be elusive because nuclear quantum effects are sometimes neither very large nor show up in a clear and distinct way compared to classical properties. Vibrational spectroscopy is a good example. Being related to transitions between vibrational quantum states, vibrational spectroscopy is a purely quantum mechanical topic. However, despite the clear theoretical differences behind classical and quantum estimates of vibrational frequencies,1 quantum ones can be often approximated to a good degree, especially when looking at fundamental transitions, using their classical counterparts.
The topic is also much debated due to the large dimensionality of the systems to be studied. Computer simulations are key in helping the interpretation of unclear experimental results or in making predictions under conditions not accessible to the experiment, but theoretical approaches able to fully describe quantum effects are challenging to implement in a computationally affordable way. Furthermore, some phenomena, molecular reactivity being one of them, are intrinsically dynamical, and the development of accurate and computationally efficient quantum approaches in a time-dependent framework is a hard task.
Purely quantum mechanical approaches, such as the split operator technique,2 are suitable to tackle only low-dimensional systems. Therefore, in the field of nuclear quantum dynamics, many efforts have been made to introduce and develop techniques that accurately describe the quantum dynamics of larger and larger systems. Path integral molecular dynamics (PIMD),3–5 the strictly related ring polymer molecular dynamics (RPMD),6–9 and centroid molecular dynamics (CMD)8,10,11 have been often used to investigate complex and large dimensional systems both in gas and condensed phases. Currently, they arguably are the most manageable methods to describe NQEs in large dimensional systems. A recent review of these methods can be found in ref. 12. However, even if they perform an efficient quantum sampling of the thermal (Boltzmann) operator they do not satisfactorily approximate real-time quantum effects. For these reasons, PIMD based methods are very effective in describing thermodynamic and structural properties, but other approaches may be preferable for spectroscopy and kinetics calculations.
A very powerful technique able to take into account real-time propagation is the multiconfiguration time-dependent Hartree (MCTDH) method.13 MCTDH can be applied to a single or several coupled potential energy surfaces (PESs) and it has been successfully employed to investigate various properties of complex systems including the spectroscopy of water clusters,14 reaction rates,15 and electron transfer dynamics.16 However, a sum-of-product form of the electronic Hamiltonian is required, which hinders applications to large dimensional systems. Efforts to ease the issue have been proposed, remarkably with the multi-layer MCTDH technique.17,18
The open quantum systems family of methods is another kind of approach which is gaining recognition and has potential to describe NQEs in complex systems. Even if starting from models, these methods have been adopted to investigate strong vibrational coupling,19 excited state proton transfer,20 proton transfer and proton tunneling in DNA.21
Here we show that semiclassical (SC) dynamics methods can deal with the quantum description of solvated and condensed phase systems and place them in perspective as an effective protocol for routine quantum mechanical studies of solvated and condensed phase systems. SC approaches are based on an effective stationary phase approximation to Feynman's path integral formulation of quantum mechanics. This approximation allows one to add quantum effects on top of evolution of classical trajectories.22–24 No particular form of the PES is required, so they can be implemented “on-the-fly”. Furthermore, classical trajectories are computationally affordable also for very large dimensional systems, so SC methods are naturally shaped to investigate nuclear quantum effects in such systems.25,26 The SC field is a very active one and it is still nowadays being advanced from the point of view of both theory and applications.27–45
In this perspective, we will first show that NQEs featured in the vibrational spectroscopy of microsolvated systems can be detected using the semiclassical initial value representation (SCIVR) or its divide-and-conquer (DC SCIVR) version introduced and implemented by our group.46 Some pioneering results in the field of microsolvation, that we propose also here, were obtained for protonated glycine tagged with hydrogen molecules.47 Furthermore, a new full-dimensional SCIVR calculation concerning specific combination bands found in hydrates of carbonyl compounds by a recent experiment will be reported. We start from microsolvation because simulations of microsolvated systems can extend our knowledge of the solvation process by pointing out the role of each vibrational mode. Then, we will move to reactive systems and present some new results of a reaction taking place in a noble-gas matrix. Calculation of the thermal reaction rate constant will be performed by means of the semiclassical transition state theory (SCTST),48,49 largely advanced in recent years by our group.50–52
Finally, in our conclusive remarks, we will briefly anticipate some of the future work in the field. For instance, the nuclear-electronic orbital (NEO) technique is an established method able to include some nuclei, usually protons, in the quantum description of the system.53–55 By Fourier transforming the time-dependent proton dipole moment obtained from the time-evolved proton density one can get an estimate of vibrational frequencies of modes involving the protons and coupled heavier nuclei.56 Ongoing studies by one of us aim at advancing theoretical vibrational spectroscopy and simulation of dynamical phenomena by connecting SC methods to the NEO quantum description of the proton-electronic structure.
We move now to a brief introduction to the computational methodologies employed in the reported calculations. The reader interested in a deeper understanding of the theory behind the adopted methodologies will find plenty of details and discussions in the suggested references.
Semiclassical initial value representation methods for calculation of vibrational power spectra
For vibrational spectroscopy calculations we adopt the semiclassical initial value representation approach. The physical observable calculated with SCIVR is the vibrational density of states I(E), which has the characteristic to be peaked at the energy levels of the vibrational Hamiltonian. Consequently, quantum frequencies of vibration can be obtained as differences among the final and start energy levels involved in the vibrational transitions. For instance, fundamental frequencies are calculated as differences between the energy levels of the excited vibrational state and the zero-point energy.Dealing with large molecular systems, a divide-and-conquer semiclassical initial value representation approach is usually (but not always) needed to get a sizable spectroscopic signal. DC SCIVR allows one to perform SCIVR calculations in reduced dimensionality subspaces, while keeping the underlying classical trajectory full dimensional. The additional computational cost is related to the determination of the best subspace partition to minimize the loss of accuracy which the calculation suffers mainly in the second order quantum fluctuations. Furthermore, DC SCIVR requires calculation of a projected potential along the dynamics.46 The DC-SCIVR working formula is
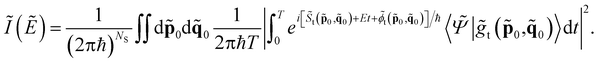 | (1) |
To use eqn (1) one has to perform ab initio classical molecular dynamics in full dimensionality by evolving for a time T a set of classical trajectories determined by initial conditions (![[p with combining tilde]](https://www.rsc.org/images/entities/b_char_0070_0303.gif) 0,
0, ![[q with combining tilde]](https://www.rsc.org/images/entities/b_char_0071_0303.gif) 0) in the phase space and driven by forces obtained from the PES of the system. The tilde symbol means that the calculation is performed in a subspace of dimensionality NS.
0) in the phase space and driven by forces obtained from the PES of the system. The tilde symbol means that the calculation is performed in a subspace of dimensionality NS. ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) indicates the reduced-dimensionality classical action along the trajectory, and
indicates the reduced-dimensionality classical action along the trajectory, and ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) is a phase obtained from a combination of subspace position and momentum derivatives with respect to initial conditions along the trajectory.
is a phase obtained from a combination of subspace position and momentum derivatives with respect to initial conditions along the trajectory. ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) and
and ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) are fundamental in describing NQEs such as ZPEs or anharmonic overtones and combination bands.
are fundamental in describing NQEs such as ZPEs or anharmonic overtones and combination bands.
In the case of high-dimensional systems, such as solvated or condensed-phase ones, an analytical PES is not available and the dynamics is computationally affordable only for a single trajectory. The methodology is still effective, provided the reference quantum state (|〉![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) ), involved in the overlap with a time-evolved coherent state |
), involved in the overlap with a time-evolved coherent state |![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) t(
t(![[p with combining tilde]](https://www.rsc.org/images/entities/b_char_0070_0303.gif) 0,
0,![[q with combining tilde]](https://www.rsc.org/images/entities/b_char_0071_0303.gif) 0)〉, is chosen in a tailored way.57 In cases where a full dimensional SCIVR calculation is doable, i.e., a sizable spectroscopic signal can be obtained in spite of the dimensionality of the system, eqn (1) is still valid with Ns = Nvib, i.e., the total number of vibrational degrees of freedom. The tilde symbols are no longer present since quantities are full dimensional ones, and the full potential is used instead of the projected one.
0)〉, is chosen in a tailored way.57 In cases where a full dimensional SCIVR calculation is doable, i.e., a sizable spectroscopic signal can be obtained in spite of the dimensionality of the system, eqn (1) is still valid with Ns = Nvib, i.e., the total number of vibrational degrees of freedom. The tilde symbols are no longer present since quantities are full dimensional ones, and the full potential is used instead of the projected one.
Semiclassical transition state theory (SCTST) for calculation of reaction rate constants
For the kinetic calculations, a classical estimate of the thermal kinetic constant at temperature T of the generic R → P reaction, proceeding through a transition state indicated by the ‡ symbol, is provided by the well-known classical transition state theory formula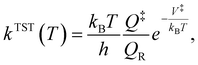 | (2) |
To get a quantum estimate of the kinetic constant, we employ SCTST. SCTST is able to describe accurately quantum features which largely impact the value of the kinetic constant, such as tunneling (more accurately in the shallow tunneling regime), and is able to account for anharmonic couplings between the reactive mode and the other molecular modes. The working formula we employ for SCTST is48
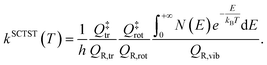 | (3) |
In eqn (3) the partition functions have been divided into their translational, rotational, and vibrational components. N(E) is the semiclassical cumulative reaction probability. While analytical expressions exist for translational and rotational partition functions, SCTST allows one to evaluate N(E) and QR,vib starting from the estimate of anharmonic constants for the normal modes at the transition state, which is performed in a perturbative fashion, and density of states for reactants and transition state, which is performed by a Monte-Carlo procedure based on the Wang–Landau algorithm.58 Both calculations of anharmonic constants and vibrational density of states are computationally intensive tasks, which hamper application of SCTST to large dimensional systems. Development work by our group has permitted us to overcome these issues by introducing and implementing algorithms for parallel computing architectures and thus paving the way to the calculation of kinetic constants for solvated systems.50,51,59
Demonstration of importance of NQEs in (micro-)solvated systems
We present the results of some simulations pointing out the importance of NQEs in (micro-)solvated and condensed phase systems. The simulations concern the vibrational spectroscopy of two micro-solvated systems and the kinetics of the VI → I conformer interconversion of glycine in the condensed phase environment of a noble-gas atom matrix. The main goal is to show that such systems exhibit quantum properties and sizable NQEs are present.Vibrational spectroscopy of (micro-)solvated species
We start from a past investigation in which we found a substantial NQE in the vibrational spectrum of protonated glycine microsolvated by three hydrogen molecules.47 We performed computations on the system employing harmonic, quasi-classical, and semiclassical methods. The level of electronic structure was chosen to be DFT-B3LYP/aVDZ in agreement with previous studies on protonated glycine.60 Such a level of electronic structure allows the calculation to be performed in a few days using twenty Intel Xeon E5-2660v3 2.6 GHz cpu cores. The ab initio “on-the-fly” dynamics was evolved for a total of about 600 fs, and further computational details can be found in ref. 47. Fig. 1 summarizes the results.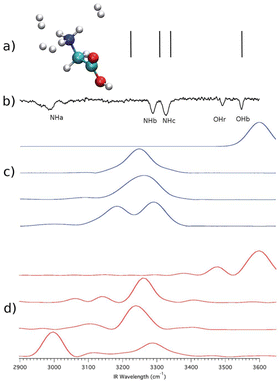 | ||
| Fig. 1 Vibrational spectra for protonated glycine microsolvated by three H2 molecules. Panel (a): harmonic estimates. Panel (b): the experimental spectrum; Panel (c): the quasi-classical trajectory method results; Panel (d): DC-SCIVR calculation. This figure has been reproduced from ref. 47 with permission from the Royal Society of Chemistry, copyright 2018. | ||
The high-frequency vibrational spectrum in Fig. 1 is characterized by the OHb signal and the signals of the three NH stretches (NHa, NHb, and NHc). It is clear that scaled harmonic estimates – vertical lines in panel (a) – are not satisfactory in describing the experiment reported in panel (b). In the harmonic case, anharmonicity has been artificially enforced by introduction of a multiplicative scaling factor. Therefore, anharmonicity is inaccurately accounted for and quantum effects are missing. A more accurate description of anharmonicity is given by the quasi-classical simulation of panel (c). Quasi-classical methods return anharmonic classical estimates of frequencies starting from harmonically quantized initial conditions.61 However, the ND3+ rotor interacts with the three hydrogen molecules leading to the quantum mechanical effect known as quantum interference, which influences the vibrational levels right above and below the rotational barrier and it is therefore responsible for the red shift of the NHa signal. The NQE appears in the form of an additional shift in the signal of the NHa stretch compared to the quasi-classical estimate. Only the DC-SCIVR calculation shown in panel (d) was able to reproduce this quantum effect which is distinctive of one of the fundamental frequencies of vibration. The trajectories employed in the quasi-classical trajectory and semiclassical calculations were the same. A simulation was made for each of the 4 signals and results are reported on 4 different lines in panels (c) and (d). The experimental OHr feature refers to a different conformer of protonated glycine, which is accessible to the experiment but not of interest here.
We notice that anharmonicity, by itself, is not an NQE and it just refers to deviations from the harmonic behavior. A certain amount of anharmonicity can indeed be found by means of the quasi-classical trajectory method, which is not suitable to reproduce NQEs since it is based on classical molecular dynamics of nuclei and the Fourier transform of a classical velocity autocorrelation function. Conversely, a semiclassical approach employing the same trajectories is able to reproduce correctly the experimental findings pointing out, based on the difference from the classical estimate, the presence of a nuclear quantum effect involving the NHa stretch.
Quantum interference requires that suitable interactions between two or more particles are in place. In this case, the interference nature of the quantum effect is revealed by the fact that when protonated glycine is tagged by a single H2 molecule the quantum effect is no longer present (see ref. 47). Furthermore, the purely nuclear nature of this effect has also been demonstrated in ref. 47. Upon deuteration of the ND3+ rotor (ND3+) the quantum effect disappears and classical and quantum calculations return the same frequency estimates.
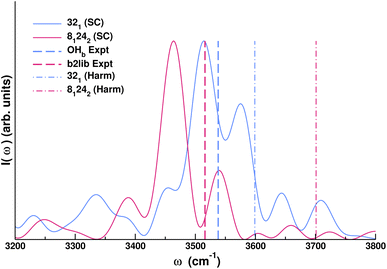
Quantum features in vibrational spectra are certainly not limited to fundamental transitions. They also involve combination bands and overtones. Classical estimates of the vibrational frequency of such spectral features generally return simply the sum of the single transition frequencies they are made of in a harmonic-like fashion, with deviations possible if the modes are involved in Fermi resonances. However, a proper quantum treatment is necessary since NQEs manifest themselves in the form of a shift of combination bands and overtones compared to classical estimates. A remarkable example is given by monohydrated carbonyl compounds, for which a rather universal resonance between the hydrogen-bonded OH stretch of the water molecule (OHb) and the combination band (b2lib) made of the water bending overtone (b2) and a libration mode (lib) has been detected in recent experiments.62 One peculiarity of the carbonyl–water interaction is that the frequency of the hydrogen bonded OH stretch is lowered at most to a value of 3500 cm−1. Simulation of such a system with detection of the b2lib combination band is very challenging for any theoretical method. Here, we employ SCIVR for the case of acetone monohydrate.
We find out that a full-dimensional SCIVR approach is feasible for the acetone monohydrate system using the DFT-B3LYP-D3BJ/def2-TZVPD level of electronic theory. The ab initio “on-the-fly” dynamics of the trajectory is about 600 fs long. Fig. 2 reports the spectrum in the 3200–3800 cm−1 range, corroborating experimental findings. In our simulation, following a well-established setup in SCIVR calculations, we have started from initial conditions of the dynamics characterized by a harmonic quantum of excitation in the water bending mode while the lowest frequency modes not involved in the b2lib combination bands were given no initial energy.
The harmonic estimate for the fundamental OHb stretch is at 3599 cm−1 and the one for the b2lib combination band is at 3701 cm−1. Harmonic frequencies are in inverse order compared to the experiment, so the common scaling procedure for harmonic frequencies is useless. Remarkably, the semiclassical calculation is able to reproduce both signals in the experimental order and with a very good accuracy given the level of electronic structure theory employed (density functional theory). This can be better appreciated from the frequency estimates reported in Table 1.
| Mode | Harmonic | Semiclassical | Experiment |
|---|---|---|---|
| b2lib | 3701 | 3464 | 3516 |
| OHb | 3599 | 3514 | 3538 |
The calculation demonstrates that SCIVR techniques are able to obtain quantum frequency estimates of such complicated systems, opening up the possibility to thoroughly investigate the presence (or absence) of this particular resonance in generic monohydrated systems.63 This interaction between the fundamental OHb stretch and the b2lib combination band is ubiquitous for a water solvated system and it requires the description of NQEs since a combination band is involved. These results pose the question of whether NQEs of the same kind may also be present in a fully solvated system. To this purpose, one needs an effective computational method, like an SC approach, to point out NQEs and prove their contribution.
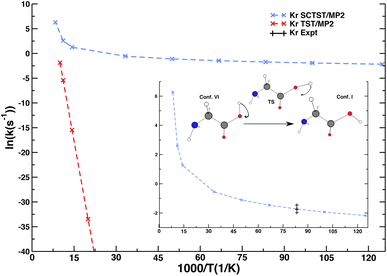
Kinetics of glycine conformer interconversion in a noble-gas matrix
Besides spectroscopy, low-temperature chemical kinetics is another example of NQE importance in condensed phase systems. We present an original SCTST result for the rate constant of glycine interconversion from conformer VI to conformer I (the global minimum of glycine) taking place in a Krypton matrix. Conformer VI is quite elusive, and even at very low temperature and under dark conditions it converts to conformer I with a short lifetime. These considerations together with glycine deuteration studies suggested that the contribution of NQEs, in particular tunneling, is fundamental to explain this fast interconversion. The calculation of the lifetime of glycine conformer VI has been tackled in the past for the isolated molecule only.52,64 However, reference experiments were performed in a matrix of noble gas,65 and one may wonder if the presence of the matrix environment could play a role in this reaction, since half-life times are slightly different for different matrices, and, most of all, calculations for the isolated molecule were one order of magnitude or more off the experimental data. In a recent calculation,52 some of us showed that our SCTST implementation in the gas phase was able to improve the accuracy of the calculated half-life time of conformer VI, but SCTST calculations at a high electronic structure theory level for the isolated molecule were still a factor of three off the experimental data. Here, we employ a novel computational setup, which describes glycine quantum mechanically and includes the effect of the matrix using ONIOM-EE.66 Specifically, we adopt the MP2/aug-cc-pVDZ level of electronic structure for the glycine molecule and the ONIOM-EE Universal Force Field (UFF) for the matrix. More details will be available in a dedicated paper currently under drafting. We show in Fig. 3 that SCTST calculations of glycine interconversion (VI → I) rates (from which the lifetime of conformer VI is calculated) are doable also accounting explicitly for the Krypton matrix producing a result in very good agreement with the experiment. Conversely, a classical transition state theory calculation completely misses the quantum tunneling effect, which is dominant in this system.Our multidimensional SCTST approach explicitly includes the contribution of the Krypton matrix showing that the matrix presence may play an important role in determining the outcome of a kinetic rate constant calculation, even when the matrix is constituted by noble gas atoms. In this case, SCTST calculations combined with other approaches, often employed for modeling the solvent with excellent outcome, such as the polarizable continuum model (PCM)67 or a solvation model based on density (SMD),68 could not provide the same level of accuracy of our atomistic description. The possibility of an explicit treatment of the matrix will allow us to study NQEs on tunneling rates from different environments and eventually study with similar approaches liquid phase solvation.
Conclusions and outlook
Results for vibrational spectroscopy have been presented with a focus on NQEs related to micro-solvation. Studies such as those on monohydrate compounds allow for a better understanding of hydrogen bonding.69 In addition, semiclassical methods have already been employed to scale up these kinds of investigations to study larger clusters70 and fully solvated systems.71 SCIVR approaches have been shown to be accurate and computationally affordable provided they are associated with an efficient level of electronic structure. In the future, the main perspective in the field is to come up with a complete SCIVR description of spectroscopy and thermal rate constants of solvated systems.As for vibrational spectroscopy, results reported in a recent study on time average semiclassical IR spectroscopy are promising for future innovative investigations of this kind, which will allow for reliable assignments of complex experimental signals and better interpretation of molecular interactions.72 Furthermore, the recent interface of semiclassical spectroscopy methods with the ORCA suite of codes, performed by two of us, has increased the applicability of our semiclassical approaches and will permit further studies on b2lib resonance in monohydrates to be undertaken for a possible dedicated publication.
Another perspective in the semiclassical spectroscopy field is represented by facing the vibrational problem from a different point of view. It is possible to go beyond the Born–Oppenheimer approximation by treating selected nuclei (usually protons) quantum mechanically on the same footing as electrons. This is at the heart of the NEO methods and is expected to describe more accurately quantum effects involving specific nuclei such as protons in proton transfer reactions.54 However, the remaining nuclei play a fundamental role in vibrational spectroscopy and proton transfer processes and a classical description of them is not always satisfactory. Current work performed by one of us aims at providing a semiclassical description of heavier atoms coupled to protons described by NEO to improve the outcome of calculations and yield a better description of vibrational dynamics and proton transfer phenomena.
Combining the two methods would make it possible to exploit the strengths of both: NEO describes the proton at a full quantum level and it is able to account for tunneling, which is hard to describe with real-time semiclassical dynamics.73 Semiclassical dynamics is able to recover delocalization of heavy nuclei and account for anharmonicity in spectroscopy calculations at the cost of classical dynamics simulations.28,30 Therefore, it would be possible to better compute full anharmonic vibrational spectra, accounting for signals associated with combination bands, resonances, fundamental transitions, and also tunneling splittings.
As for chemical kinetics, we have shown that condensed phase SCTST calculations of reactions occurring in gas matrices are doable. In particular, we have introduced the case of glycine interconversion in a Krypton matrix. One would expect that interactions of the molecule with a noble-gas matrix would be irrelevant, but this is not the case when looking at the lifetime of glycine conformer VI. A more complete investigation, including comparisons with results for the isolated molecule and calculations for several types of matrices will be presented in a future paper currently under drafting.
Finally, we notice that SCTST is a member of the family of transition state theory methods, so accuracy of kinetic rate constant calculations can be improved by inclusion of real-time quantum effects in the semiclassical treatment. The theory underlying this approach has already been developed by two of us starting from an original semiclassical approximation to the thermal flux–flux autocorrelation function tested on model systems.74 Since the approach returned improved results compared to the most popular approaches, future work will aim at further developing this technique and applying it to real reactive molecular systems in full dimensionality.
Data availability
Data can be obtained upon reasonable request to one of the corresponding authors.Author contributions
Riccardo Conte: conceptualization, supervision, methodology, investigation, funding acquisition, writing original draft and review. Giacomo Mandelli: methodology, investigation, review. Giacomo Botti: methodology, investigation, review. Davide Moscato: methodology, review. Cecilia Lanzi: methodology, review. Marco Cazzaniga: conceptualization, supervision, methodology, investigation, review. Chiara Aieta: conceptualization, supervision, methodology, investigation, funding acquisition, review. Michele Ceotto: conceptualization, supervision, methodology, investigation, funding acquisition, review.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We thank Prof. Sharon Hammes-Schiffer for insightful comments. R. C. thanks Università degli Studi di Milano for funding under project PSR2022_DIP_005_PI_RCONT. C. A. thanks Università degli Studi di Milano for funding under project PSR2022_DIP_005_PI_CAIET and the European Commission for support through a Marie Curie “Global” Fellowship for the project “NEOSC” (Grant Agreement No. 101106284—NEOSC—HORIZON-MSCA-2022-PF-01). M. C. acknowledges financial support from the European Research Council (Grant Agreement No. (647107)—SEMICOMPLEX—ERC-2014-CoG under the European Union's Horizon 2020 and No. 101081361—SEMISOFT—ERC-2022-POC2 under the Horizon Europe research and innovation programme). Authors Davide Moscato and Cecilia Lanzi are currently PhD candidates at Università degli Studi di Milano with research interests in non-adiabatic semiclassical dynamics and spectroscopy of biomolecular systems (D. M.) and theoretical and applied development of semiclassical infra-red spectroscopy (C. L.).References
- R. Conte, C. Aieta, G. Botti, M. Cazzaniga, M. Gandolfi, C. Lanzi, G. Mandelli, D. Moscato and M. Ceotto, Theor. Chem. Acc., 2023, 142, 53 Search PubMed
.
- T. Taha and M. Ablowitz, J. Comput. Phys., 1984, 55, 203–230 CrossRef
.
-
R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals, McGraw-Hill, 1965 Search PubMed
.
- D. Marx and M. Parrinello, J. Chem. Phys., 1996, 104, 4077–4082 CrossRef CAS
.
- S. Habershon, G. S. Fanourgakis and D. E. Manolopoulos, J. Chem. Phys., 2008, 129, 074501 CrossRef PubMed
.
- I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2005, 122, 084106 CrossRef
.
- T. E. Markland and D. E. Manolopoulos, J. Chem. Phys., 2008, 129, 024105 CrossRef PubMed
.
- A. Witt, S. D. Ivanov, M. Shiga, H. Forbert and D. Marx, J. Chem. Phys., 2009, 130, 194510 CrossRef PubMed
.
- N. Ananth, J. Chem. Phys., 2013, 139, 124102 CrossRef
.
- E. Geva, Q. Shi and G. A. Voth, J. Chem. Phys., 2001, 115, 9209–9222 CrossRef CAS
.
- T. Fletcher, A. Zhu, J. E. Lawrence and D. E. Manolopoulos, J. Chem. Phys., 2021, 155, 231101 CrossRef CAS PubMed
.
- S. C. Althorpe, Annu. Rev. Phys. Chem., 2024, 75, 397–420 CrossRef CAS PubMed
.
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 CrossRef CAS
.
- O. Vendrell, F. Gatti and H.-D. Meyer, Angew. Chem., Int. Ed., 2007, 46, 6918–6921 CrossRef CAS
.
- R. van Harrevelt, G. Nyman and U. Manthe, J. Chem. Phys., 2007, 126, 084303 CrossRef
.
- Y. Xie, J. Zheng and Z. Lan, J. Chem. Phys., 2015, 142, 084706 CrossRef PubMed
.
- H. Wang and M. Thoss, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef CAS
.
- U. Manthe, J. Chem. Phys., 2008, 128, 164116 CrossRef
.
- L. P. Lindoy, A. Mandal and D. R. Reichman, Nat. Commun., 2023, 14, 2733 CrossRef CAS
.
- B. Le Dé, S. Huppert, R. Spezia and A. W. Chin, J. Chem. Theory Comput., 2024, 20, 8749–8766 CrossRef PubMed
.
- L. Slocombe, M. Sacchi and J. Al-Khalili, Commun. Phys., 2022, 5, 109 CrossRef CAS
.
- F. Grossmann and A. L. Xavier, Phys. Lett. A, 1998, 243, 243–248 CrossRef CAS
.
- W. H. Miller, Mol. Phys., 2002, 100, 397–400 CrossRef CAS
.
-
E. Pollak, in The Semiclassical Initial Value Series Representation of the Quantum Propagator, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 259–271 Search PubMed
.
- W. H. Miller, J. Phys. Chem. A, 2001, 105, 2942–2955 CrossRef CAS
.
- X. Liu and J. Liu, Mol. Phys., 2018, 116, 755–779 CrossRef CAS
.
- T. Begušić and J. Vaníček, J. Chem. Phys., 2020, 153, 024105 CrossRef
.
- C. Aieta, M. Micciarelli, G. Bertaina and M. Ceotto, Nat. Comm., 2020, 11, 4384 CrossRef
.
- M. Werther, S. L. Choudhury and F. Großmann, Int. Rev. Phys. Chem., 2020, 40, 81–125 Search PubMed
.
- C. Aieta, G. Bertaina, M. Micciarelli and M. Ceotto, J. Chem. Phys., 2020, 153, 214117 CrossRef CAS PubMed
.
- M. Gandolfi, A. Rognoni, C. Aieta, R. Conte and M. Ceotto, J. Chem. Phys., 2020, 153, 204104 CrossRef CAS
.
- M. Dutra, S. Wickramasinghe and S. Garashchuk, J. Phys. Chem. A, 2020, 124, 9314–9325 CrossRef CAS
.
- V. M. Freixas, A. J. White, T. Nelson, H. Song, D. V. Makhov, D. Shalashilin, S. Fernandez-Alberti and S. Tretiak, J. Phys. Chem. Lett., 2021, 12, 2970–2982 CrossRef CAS PubMed
.
- G. Botti, C. Aieta and R. Conte, J. Chem. Phys., 2022, 156, 164303 CrossRef CAS PubMed
.
- K. Polley and R. F. Loring, J. Chem. Phys., 2022, 156, 124108 CrossRef CAS PubMed
.
- S. Malpathak, M. S. Church and N. Ananth, J. Phys. Chem. A, 2022, 126, 6359–6375 CrossRef CAS PubMed
.
- M. Dutra, S. Garashchuk and A. V. Akimov, Int. J. Quant. Chem., 2023, 123, e27078 CrossRef CAS
.
- S. Upadhyayula and E. Pollak, J. Phys. Chem. Lett., 2023, 14, 9892–9899 CrossRef CAS
.
- J.-X. Zeng, S. Yang, Y.-C. Zhu, W. Fang, L. Jiang, E.-G. Wang, D. H. Zhang and X.-Z. Li, J. Phys. Chem. A, 2023, 127, 2902–2911 CrossRef CAS PubMed
.
- R. Moghaddasi Fereidani and J. Vanicek, J. Chem. Phys., 2024, 160, 044113 CrossRef CAS
.
- R. Conte, C. Aieta, M. Cazzaniga and M. Ceotto, J. Phys. Chem. Lett., 2024, 15, 7566–7576 CrossRef CAS
.
- E. Fallacara, F. Finocchi, M. Cazzaniga, S. Chenot, S. Stankic and M. Ceotto, Angew. Chem., Int. Ed., 2024, e202409523 CAS
.
- L. Bonnet, Chem. Phys. Lett., 2024, 851, 141459 CrossRef CAS
.
- C. A. Myers, K. Miyazaki, T. Trepl, C. M. Isborn and N. Ananth, J. Chem. Phys., 2024, 161, 084114 CrossRef CAS
.
- E. Pollak, J. Chem. Phys., 2024, 160, 150902 CrossRef CAS
.
- M. Ceotto, G. Di Liberto and R. Conte, Phys. Rev. Lett., 2017, 119, 010401 CrossRef
.
- F. Gabas, G. Di Liberto, R. Conte and M. Ceotto, Chem. Sci., 2018, 9, 7894–7901 RSC
.
- R. Hernandez and W. H. Miller, Chem. Phys. Lett., 1993, 214, 129–136 CrossRef CAS
.
-
J. Barker, T. L. Nguyen, J. F. Stanton, C. Aieta, M. Ceotto, F. Gabas, T. J. D. Kumar, C. G. L. Li, L. L. Lohr, A. Maranzana, N. F. Ortiz, J. M. Preses, J. M. Simmie, J. A. Sonk and P. J. Stimac, Multiwell Software Suite, 2024 Search PubMed
.
- C. Aieta, F. Gabas and M. Ceotto, J. Chem. Theory Comput., 2019, 15, 2142–2153 CrossRef CAS PubMed
.
- G. Mandelli, C. Aieta and M. Ceotto, J. Chem. Theory Comput., 2022, 18, 623–637 CrossRef CAS
.
- G. Mandelli, L. Corneo and C. Aieta, J. Phys. Chem. Lett., 2023, 14, 9996–10002 CrossRef CAS
.
- S. P. Webb, T. Iordanov and S. Hammes-Schiffer, J. Chem. Phys., 2002, 117, 4106–4118 CrossRef CAS
.
- S. Hammes-Schiffer, J. Chem. Phys., 2021, 155, 030901 CrossRef CAS
.
- S. M. Garner, S. Upadhyay, X. Li and S. Hammes-Schiffer, J. Phys. Chem. Lett., 2024, 15, 6017–6023 CrossRef CAS
.
- L. Zhao, A. Wildman, Z. Tao, P. Schneider, S. Hammes-Schiffer and X. Li, J. Chem. Phys., 2020, 153, 224111 CrossRef CAS PubMed
.
- M. Ceotto, S. Atahan, G. F. Tantardini and A. Aspuru-Guzik, J. Chem. Phys., 2009, 130, 234113 CrossRef PubMed
.
- C. Aieta, F. Gabas and M. Ceotto, J. Phys. Chem. A, 2016, 120, 4853–4862 CrossRef CAS
.
- F. Angiolari, G. Mandelli, S. Huppert, C. Aieta and R. Spezia, Chem.–Eur. J., 2024, e202401000 CrossRef CAS
.
- R. Wu and T. B. McMahon, J. Am. Chem. Soc., 2007, 129, 4864–4865 CrossRef CAS PubMed
.
- C. Qu and J. M. Bowman, J. Phys. Chem. Lett., 2018, 9, 2604–2610 CrossRef CAS PubMed
.
- T. L. Fischer, T. Wagner, H. C. Gottschalk, A. Nejad and M. A. Suhm, J. Phys. Chem. Lett., 2021, 12, 138–144 CrossRef CAS
.
- P. R. Rablen, J. W. Lockman and W. L. Jorgensen, J. Phys. Chem. A, 1998, 102, 3782–3797 CrossRef CAS
.
- C. Qu, P. L. Houston, R. Conte, A. Nandi and J. M. Bowman, J. Phys. Chem. A, 2021, 125, 5346–5354 CrossRef CAS PubMed
.
- G. Bazsó, G. Magyarfalvi and G. Tarczay, J. Phys. Chem. A, 2012, 116, 10539–10547 CrossRef
.
- L. W. Chung, H. Hirao, X. Li and K. Morokuma, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 327–350 CAS
.
- F. Lipparini, G. Scalmani, B. Mennucci, E. Cancès, M. Caricato and M. J. Frisch, J. Chem. Phys., 2010, 133, 014106 CrossRef
.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 Search PubMed
.
- T. L. Fischer, M. Bödecker, S. M. Schweer, J. Dupont, V. Lepère, A. Zehnacker-Rentien, M. A. Suhm, B. Schröder, T. Henkes and D. M. Andrada,
et al.
, Phys. Chem. Chem. Phys., 2023, 25, 22089–22102 Search PubMed
.
- A. Rognoni, R. Conte and M. Ceotto, Chem. Sci., 2021, 12, 2060–2064 Search PubMed
.
- D. Moscato, G. Mandelli, M. Bondanza, F. Lipparini, R. Conte, B. Mennucci and M. Ceotto, J. Am. Chem. Soc., 2024, 146, 8179–8188 Search PubMed
.
- C. Lanzi, C. Aieta, M. Ceotto and R. Conte, J. Chem. Phys., 2024, 160, 214107 Search PubMed
.
- R. Conte, A. Aspuru-Guzik and M. Ceotto, J. Phys. Chem. Lett., 2013, 4, 3407–3412 CAS
.
- C. Aieta and M. Ceotto, J. Chem. Phys., 2017, 146, 214115 CrossRef PubMed
.
| This journal is © The Royal Society of Chemistry 2025 |