Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamical arrest for globular proteins with patchy attractions†
Maxime J.
Bergman
 a,
Tommy
Garting
a,
Tommy
Garting
 a,
Cristiano
De Michele
a,
Cristiano
De Michele
 b,
Peter
Schurtenberger
b,
Peter
Schurtenberger
 *ac and
Anna
Stradner
*ac and
Anna
Stradner
 ac
ac
aDivision of Physical Chemistry, Department of Chemistry, Lund University, PO Box 124, SE-221 00 Lund, Sweden. E-mail: peter.schurtenberger@fkem1.lu.se
bDipartimento di Scienze, Università degli Studi Roma Tre, Via della Vasca Navale 84, Roma, Italy
cLINXS Institute of Advanced Neutron and X-ray Science, Scheelevägen 19, SE-223 70 Lund, Sweden
First published on 8th January 2025
Abstract
Attempts to use colloid science concepts to better understand the dynamic properties of concentrated or crowded protein solutions are challenging due to the fact that globular proteins generally have heterogeneous surfaces that result in anisotropic or patchy contributions to their interaction potential. This is particularly difficult when targeting non-equilibrium transitions such as glass and gel formation in concentrated protein solutions. Here we report a systematic study of the reduced zero shear viscosity ηr of the globular protein γB-crystallin, an eye lens protein that plays a vital role in vision-related phenomena such as cataract formation or presbyopia, and compare the results to the existing structural and dynamic data. Combining two different tracer particle-based microrheology methods allows us to precisely locate the line of kinetic arrest within the phase diagram and characterize the functional form of the concentration and temperature dependence of ηr. We show that while our results qualitatively confirm the existing view that this protein can be reasonably well described using a coarse-grained picture of a patchy colloid with short range attractions, there are a number of novel findings that cannot easily be understood with the existing simple colloid models. We demonstrate in particular the complete failure of an extended law of corresponding states for a description of the temperature dependence of the arrest line, and discuss the role that transient clusters play in this context.
1. Introduction
Protein phase behavior and the existence of liquid–liquid phase separation in protein solutions and mixtures have entered again into the focus of the life sciences and biophysics community.1 For example, Klosin et al. have investigated how the cell ensures minimal effect from protein concentration fluctuations, caused by the stochasticity of protein expression.2 They hypothesized that protein concentrations in the cytosol are kept constant via compartmentalization of excess protein, driven by phase separation. These authors were indeed able to demonstrate that liquid droplets, formed through phase separation, can effectively reduce expression noise for their engineered protein system. Evidently, equilibrium phenomena such as liquid–liquid phase separation can underlie intra-cellular control mechanisms.3 However, non-equilibrium processes such as dynamical arrest could threaten protein regulation: if an arrest occurs during phase separation, the resultant phases will contain significantly different protein concentrations than anticipated.4Recent evidence that phase transitions in living cells may represent an important mechanism in cellular organization has spurred renewed interest in exploring analogies to colloid solutions. Liquid–liquid phase separation has been studied extensively in the past, often driven by its connection to the occurrence of so-called protein condensation diseases.5,6 Initially, protein phase behavior was found to have clear analogies to colloids interacting with short range attractions. A key observation was for example that the location of the binodal and spinodal in protein solutions was also following the so-called extended law of corresponding states (ELCS).7,8 The ELCS provides a convenient link between the reduced second virial coefficient 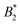 as a measure of the interaction strength obtained at low concentrations and the predicted phase separation at high concentrations.9 In combination with isotropic potentials such as for example a combination of excluded volume repulsion and short range attractions, and applying a non-equilibrium self-consistent generalized Langevin equation theory, this approach has been able to reproduce the experimentally observed interplay between liquid–liquid phase separation and dynamical arrest in protein solutions quite successfully.10 However, despite the considerable insight provided by the ELCS combined with isotropic colloid models, this theoretical framework was subsequently found to be limited in application: proteins often have heterogeneous surfaces leading to anisotropic and patchy interactions, and recent efforts have revealed that patchy colloid models harbour more predictive power when it comes to static properties of protein solutions.11–14 Moreover, it was also found that more refined interaction models that include attractive patches and/or shape anisotropy are particularly important for a correct description of the dynamic properties of protein solutions.3 Unfortunately, there exists only limited information on the effects of patchy interactions on dynamic properties and the related non-equilibrium liquid–solid transitions. Furthermore, achieving a structure-based assignment of the location of patches and their interaction potential remains difficult, and requires for example a more refined coarse-graining strategy that starts from a molecular description of the protein.15,16
as a measure of the interaction strength obtained at low concentrations and the predicted phase separation at high concentrations.9 In combination with isotropic potentials such as for example a combination of excluded volume repulsion and short range attractions, and applying a non-equilibrium self-consistent generalized Langevin equation theory, this approach has been able to reproduce the experimentally observed interplay between liquid–liquid phase separation and dynamical arrest in protein solutions quite successfully.10 However, despite the considerable insight provided by the ELCS combined with isotropic colloid models, this theoretical framework was subsequently found to be limited in application: proteins often have heterogeneous surfaces leading to anisotropic and patchy interactions, and recent efforts have revealed that patchy colloid models harbour more predictive power when it comes to static properties of protein solutions.11–14 Moreover, it was also found that more refined interaction models that include attractive patches and/or shape anisotropy are particularly important for a correct description of the dynamic properties of protein solutions.3 Unfortunately, there exists only limited information on the effects of patchy interactions on dynamic properties and the related non-equilibrium liquid–solid transitions. Furthermore, achieving a structure-based assignment of the location of patches and their interaction potential remains difficult, and requires for example a more refined coarse-graining strategy that starts from a molecular description of the protein.15,16
Attractive patches appear to be responsible for an arrest transition at much lower protein concentrations than typically found for classical colloids interacting primarily through centrosymmetric interaction potentials, and arrest seems to be linked to the formation of transient clusters or networks.17–20 Progress is currently limited by the lack of information available on the influence of patchy attractions on macroscopic flow properties in solutions of globular proteins such as the zero shear viscosity. This is not only crucial in our strive for understanding dynamic processes in the cellular environment, but also important in current attempts to develop high concentration biological formulations for drug delivery, amongst others. Patchy protein–protein interactions can lead to a dramatic increase of the viscosity of such formulations even at moderate volume fractions due to the formation of transient clusters, thus strongly impinging syringeability.15
Here we focus on the lens protein γB-crystallin, which is known to exhibit liquid–liquid phase separation, with a critical concentration around ccrit ≈ 220–240 mg mL−1, or a critical volume fraction of ϕcrit ≈ 0.15–0.17.17,21,22γB-crystallin is known to play a key role for example in cataract formation and presbyopia.5,18,23–25 This connection between liquid–liquid phase separation in solutions of eye lens proteins and the formation of cataracts has led to a systematic study of the phase diagram of this protein.11,17,21,22,26–28 The application of coarse-grained colloid models such as hard spheres with short range attractions, patchy colloids or hard ellipsoids with short range attractions resulted in fairly good agreement with the experimentally determined static properties of γB-crystallin solutions.11,17,26 However, subsequent studies also revealed that the dynamic properties of γB-crystallin solutions are much more complex and cannot be reproduced with simple colloid models based on isotropic interaction potentials.18
The dynamic properties of γB-crystallin solutions have so far mainly been investigated by dynamic light scattering (DLS) and neutron spin echo spectroscopy (NSE), both characterizing collective diffusion at different characteristic time and length scales.17,18,29 DLS looks at collective diffusion on length scales of a few hundred nanometers, which for concentrations around the critical concentration is dominated completely by critical slowing down, resulting in a strong temperature and concentration dependence.17,29 At higher concentrations, DLS reveals the presence of a large noncritical background contribution that results in an unusual logarithmic rather than exponential decay of the intermediate scattering function (ISF), presumably due to the combined effects of critical slowing down and an approaching arrest transition.17 NSE probes dynamics at nanometre length scales and the results show a dramatic reduction in collective cage diffusion around the nearest neighbor distance for increasing concentration. This observation, combined with the estimate of the location of the arrest line based on the indication of non-ergodicity in DLS, suggests that the dynamical arrest is driven by the formation of transient clusters and networks created by attractive patches rather than an isotropic potential.17,18 Unfortunately, we currently lack information on the concentration and temperature dependence of the solution viscosity as a direct measure of the macroscopic flow properties of γB-crystallin solutions.
Therefore we now extend the existing dynamical information by probing the zero shear viscosity of γB-crystallin for several temperatures using two passive microrheology techniques, combined with a new approach for preparing highly concentrated and solid-like samples.30 These results are compared to repulsive and attractive colloid models, where we find that the concentration dependence of the reduced viscosity ηr = η0/ηs, where η0 is the zero shear viscosity of the protein solution and ηs that of the solvent, follows a power law characteristic of isotropically attractive spheres – although a clear signature of the attractive patches can be observed in the early onset of the arrest transition. Surprisingly, the observed concentration dependence of ηr appears independent of temperature. The arrest line is thus also temperature-independent above the binodal, even though interactions between γB-crystallins have already been shown to change significantly in this temperature range.8 Moreover, a weak contribution to ηr close to the critical point arises from critical behavior, which does not appear to follow the laws of universality, hinting at additional contributions to the viscosity. We finally formulate a scenario harmonizing our current findings with previous conclusions and discuss a possible generalization of these results to other proteins interacting via patchy interactions. Our findings are important not only to better understand the cellular environment, but also to improve the formulation of high concentration biopharmaceuticals.
2. Results and discussion
In order to gauge the macroscopic flow properties of γB-crystallin, a large number of protein solutions were prepared, covering a broad range of volume fractions (0.035 ≤ ϕ ≤ 0.25) and temperatures (20 °C ≤ T ≤ 35 °C), where we profited from a novel evaporation technique to achieve protein volume fractions beyond the arrest transition. Tracer particles were added to γB-crystallin samples, and their motion was recorded using DLS-based and MPT-based (multiple particle tracking) microrheology. The latter technique relies on tracking the individual fluorescent tracer particles using videos created with confocal laser scanning microscopy (CLSM), whereas the former rests on the light scattering caused by tracers (see Materials and Methods section for further information). The concentration and temperature range were chosen based on the previously published experimental state diagram (Fig. 1a, adapted from ref. 17), in order to cover conditions where the samples are in the previously located fluid phase above the critical temperature Tcrit, and extending to the estimated location of the arrest line. Within the chosen temperature range, earlier static light scattering (SLS) and DLS measurements have demonstrated a dramatic variation of the isothermal compressibility and the dynamic correlation length describing the decay of long wavelength concentration fluctuations by almost two orders of magnitude, in particular close to the critical isochore at ϕcrit.17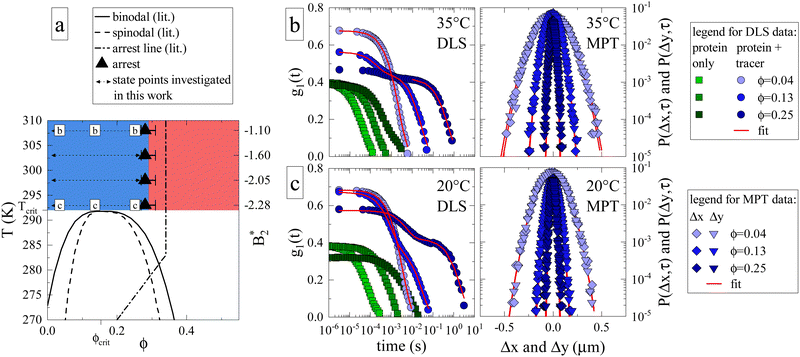 | ||
Fig. 1 (a) Adaptation of the state diagram for γB17 with added results from the current work. This previous work determined the binodal (solid line), spinodal (dashed line) and arrest line (dashed dotted line). We now add the range of state points investigated in this work (arrows) and the position of the arrest transition based on the MCT-like power law (triangles) and evaporation experiments (horizontal bars). Also indicated are the state points shown in panels (b) and (c). The measured values of the reduced second virial coefficient 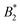 are shown on the right figure axis at the corresponding temperatures (from ref. 8). (b) Representative experimental data of three samples at 35 °C for DLS (left) and MPT (right) measurements. The DLS panel displays the field correlation function g1(t) for protein samples with (blue circles) or without (green squares) embedded tracer particles. Red lines represent the fit to the protein + tracer mixtures. A decimated number of data points is shown for clarity, with the full curve shown in Fig. S1 (ESI†). The MPT panel depicts the Van Hove function, which indicates the range of movement for the tracer particles in both x- and y-direction (diamonds and downwards triangles), with corresponding Gaussian fits (red lines). (c) Same type of data as shown in panel (b) but for samples measured at 20 °C, close to Tcrit. are shown on the right figure axis at the corresponding temperatures (from ref. 8). (b) Representative experimental data of three samples at 35 °C for DLS (left) and MPT (right) measurements. The DLS panel displays the field correlation function g1(t) for protein samples with (blue circles) or without (green squares) embedded tracer particles. Red lines represent the fit to the protein + tracer mixtures. A decimated number of data points is shown for clarity, with the full curve shown in Fig. S1 (ESI†). The MPT panel depicts the Van Hove function, which indicates the range of movement for the tracer particles in both x- and y-direction (diamonds and downwards triangles), with corresponding Gaussian fits (red lines). (c) Same type of data as shown in panel (b) but for samples measured at 20 °C, close to Tcrit. | ||
We first determine how the proximity to the critical point (ϕcrit = 0.154, Tcrit ≈ 19 °C)17 and the related critical opalescence and critical slowing down experienced by the protein solution affects the microrheological methodology. For this reason, Fig. 1b displays typical results from microrheology measurements taken at 35 °C, i.e. far away from Tcrit, and Fig. 1c showcases data at 20 °C. Each panel includes three state points: ϕ = 0.04 < ϕcrit, ϕ = 0.13 ≈ ϕcrit and ϕ = 0.25 > ϕcrit. In the DLS-based approach, the field autocorrelation function g1(t) is obtained from the measured intensity autocorrelation function g2(t), which depends on the scattering emanating from both the protein and the tracers. In MPT, the probability of a tracer displacement is expressed using the Van Hove function. Both microrheology approaches clearly display a retardation of tracer motion (blue symbols in Fig. 1b and c) with increasing protein volume fraction, indicated in DLS as a shift to longer decay times while in MPT as a narrowing of the displacement distribution.
Whereas the MPT method provides consistent results, regardless of the location of the state point, this is different for DLS-based microrheology. Here the increased scattering due to protein critical behavior clearly complicates the analysis of the DLS tracer data at any given temperature. In the diluted regime, there is no significant contribution from protein scattering. The decay of g1(t) is dominated by the tracer signal, resulting in a single, easily analysed decay (light blue circles, Fig. 1b and c). However, close to ϕcrit critical scattering increases the protein signal, and a critical slowing down moves the corresponding decay from the protein solution to much larger decay times. This is illustrated by DLS measurements on pure protein samples (green squares, Fig. 1b and c). The effect on g1(t) as measured on protein plus tracer mixtures (medium blue circles, Fig. 1b and c) is therefore not surprising: the overall g1(t) exhibits two decay processes, which nearly merge. The first is associated with the temporal decay of critical protein concentration fluctuations and the second originates from the tracer diffusion. We attempt to enhance the tracer signal by using sufficiently high tracer particle concentrations to effectively drown out the intrinsic protein scattering contribution to g1(t), with any possible multiple scattering suppressed by the use of a so-called 3D DLS technique.31 Regardless, the overlap between the two scattering contributions mitigates accurate analysis of the tracer decay and the thus obtained values of ηr carry a larger uncertainty.
Protein contributions to scattering and g1(t) remain significant beyond ϕcrit. At high temperatures, the two parts of the decay are sufficiently separated to analyse the tracer motion only (Fig. 1b, dark blue circles). At temperatures close to Tcrit, the interplay between critical slowing down and approaching dynamical arrest leads to the previously mentioned unusual logarithmic decay of g1(t),17 which is not easily analyzed (Fig. 1c, dark blue circles). Evidently, DLS measurements close to either ϕcrit or Tcrit are impacted tremendously by (general) critical protein behavior. In contrast, MPT-based microrheology relies on fluorescence, and is not at all affected by the increased scattering contribution of the proteins. Using DLS-based microrheology to explore the flow properties of protein solutions in the vicinity of a critical point could thus lead to an overestimation of ηr and suggest a large, additional critical contribution to the zero shear viscosity, which is however not apparent in the MPT data (see also Fig. S1 and S2 for further illustration, ESI†).
Having established the appropriate methodology for measuring ηr for γB-crystallin solutions over the required concentration and temperature range, we next present the results from the four concentration series at all temperatures 20 ≤ T ≤ 35 °C (Fig. 2). All ηr values superimpose on a single curve within the experimental uncertainty, and no effect of temperature on the functional dependence can be seen, indicating a temperature-independent approach to and location of the arrest transition around ϕg ≈ 0.28. Good correspondence is found between the data points from the two techniques when omitting the DLS-based data around the critical concentration, confirming our previous conclusions on the broad applicability of such microliter-based techniques for protein characterization.30
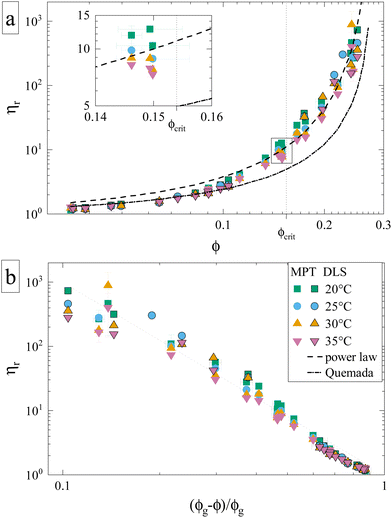 | ||
| Fig. 2 Reduced sample viscosities at four different temperatures obtained using DLS (framed symbols) and MPT (unframed symbols), ranging from just above the critical temperature (20 °C) to 35 °C. The lines indicate fits, either to the Quemada expression for hard spheres (dashed-dotted) or a power law used for attractive spheres (dashed) with an exponent γ = 3.1 and ϕg = 0.28 (see text). Both panels contain the same data represented in a different way, and the legend applies to both. (a) ηr plotted versus volume fraction ϕ. Inset: Close-up of datapoints at ϕcrit, which are (partially) shown in Fig. 4. (b) ηr plotted versus the reduced volume fraction ε = (ϕg − ϕ)/ϕg, which allows for a better comparison to the power law. | ||
Such an absence of temperature dependence for the concentration dependence of ηr and for the location of the arrest line ϕg of γB-crystallin is quite unexpected. Previous work revealed that γB-crystallin is an attractive system with a pronounced T-dependence of the reduced second virial coefficient 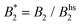 , where B2 is the second virial coefficient of the protein and Bhs2 that of a reference hard sphere system.8 The ELCS asserts a connection between
, where B2 is the second virial coefficient of the protein and Bhs2 that of a reference hard sphere system.8 The ELCS asserts a connection between 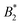 and the location of the binodal and spinodal.9 Recently, it has successfully been extended to include the dependence of non-equilibrium phenomena, such as an arrest line, on
and the location of the binodal and spinodal.9 Recently, it has successfully been extended to include the dependence of non-equilibrium phenomena, such as an arrest line, on 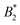 .32 Indeed, comparable work for synthetic colloids with short range attractions have reported a change of the arrest transition from 0.18 ≤ ϕg ≤ 0.36 upon a change of temperature or
.32 Indeed, comparable work for synthetic colloids with short range attractions have reported a change of the arrest transition from 0.18 ≤ ϕg ≤ 0.36 upon a change of temperature or 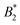 by
by 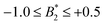 .32 In addition, a recent simulation study showcases that the ELCS also applies to patchy particles: the binodals of particles with the same patch distribution, but different types of patches, collapse when plotted as a function of
.32 In addition, a recent simulation study showcases that the ELCS also applies to patchy particles: the binodals of particles with the same patch distribution, but different types of patches, collapse when plotted as a function of 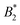 .33,34 In our case,
.33,34 In our case, 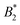 increases from
increases from 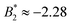 at 20 °C to
at 20 °C to 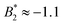 at 35 °C,8 but against expectations we observe no measurable change in ϕg (see Fig. 1). This T-independence of ϕg is reminiscent of effective hard spheres rather than attractive particles, but of course the observed values of ϕg are much too low for an effective hard sphere behavior.
at 35 °C,8 but against expectations we observe no measurable change in ϕg (see Fig. 1). This T-independence of ϕg is reminiscent of effective hard spheres rather than attractive particles, but of course the observed values of ϕg are much too low for an effective hard sphere behavior.
An attempt to fit the concentration dependence of the reduced viscosity with classical hard sphere models such as Quemada,35 Krieger–Dougherty,36 Mooney37 as well as a modified Vogel–Fulcher–Tammann (VFT)38,39 description also clearly fails. Such (empirical) models have been used with varying success, especially in combination with the introduction of an effective size to approximate the protein as a quasi-spherical colloid. Yet, the viscosity behavior of γB-crystallin is clearly affected by attractions, as none of the aforementioned models yielded a satisfying agreement, with Quemada shown as an example (Fig. 2a, dashed-dotted line).
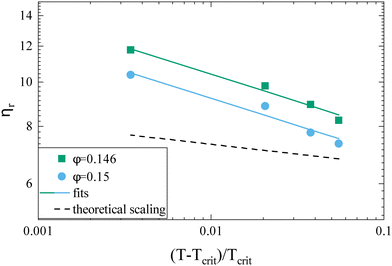
Theoretical work on hard sphere and attractive systems using mode coupling theory (MCT) and computer simulations predicts a power-law dependency of the reduced viscosity ηr ∼ ε−γ in the vicinity of the arrest transition, where ε is a reduced order parameter defined as ε = (Xg − X)/Xg, with X given either by the volume fraction ϕ or the strength of the attraction.40 The value of γ then depends on the interaction between particles, with γ = 2.8 for hard spheres, and values γ ≥ 3 for attractive particles.40,41 The viscosity data obtained for γB-crystallin solutions is indeed well reproduced at higher concentrations with a power law exponent γ = 3.1 ± 0.1 when using ϕg = 0.28 (see Fig. 2a, dashed line). The range over which this power law appears to be valid is surprisingly large. While for the hard sphere-like eye lens protein α-crystallin an MCT-like power law with an exponent of γ = 2.8 was found to reproduce the data only for ε ≤ 0.13,42 here the data follows a power law over a much more extended range ε ≤ 0.6 (Fig. 2b). Similar differences were also found in the simulation study, with a validity of the power law for ε ≤ 0.07 for hard spheres and ε ≤ 0.34 for attractive particles.40
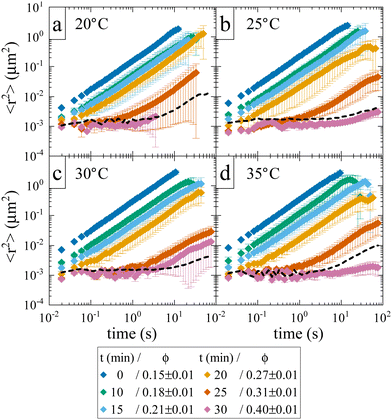
While the location of the arrest line has so far only relied on an analysis of the concentration dependence of the reduced viscosity, here we now confirm the existence of an arrested solid-like state at volume fractions ϕ > ϕg using evaporation experiments. This allows us to directly probe volume fractions beyond ϕg with MPT-based microrheology that are not accessible using standard sample preparation procedures for dense protein solutions. In an earlier work,30 we demonstrated the efficiency of such an experiment to obtain otherwise inaccessible volume fractions. Although the evaporation procedure results in a somewhat heterogeneous concentration profile within the sample cell, this can be taken care of by ensuring that confocal measurements are performed at several different locations within the sample. Fig. 3 shows the average MSD of tracers as a function of evaporation period or average volume fraction ϕ. We see the expected slowing down of the tracer diffusion with increasing ϕ and the formation of a completely arrested sample at around ϕg ≈ 0.27–0.31. In the arrested samples any apparent residual motion of the tracer particles is due to macroscopic collective drift (Fig. S3, ESI†), primarily caused by the instrument (black dashed line in Fig. 3). The resulting location of the arrest transition is indicated in Fig. 1 by horizontal bars and is in good agreement with the value of ϕg ≈ 0.28 obtained from the power law fit to the viscosity data, and at slightly lower volume fractions than what was previously reported in the literature based on DLS measurements.17
While the overall functional form of the concentration dependence of ηr appears independent of temperature, a closer look at the MPT-based microrheology nevertheless indicates a systematic weak temperature dependence at concentrations close to the critical concentration ϕcrit (Fig. 2a, inset and Fig. S4 in the ESI†). In phase-separating systems, ηr encompasses a non-critical component ηnoncrit as well as a critical component ηcrit. The power law-like approach to the arrest, as discussed previously, describes ηnoncrit. Any observed divergence from this power law at concentrations close to ϕcrit should thus correspond to the critical contribution ηcrit. Universal scaling laws for binary fluids dictate that upon approaching the critical point, ηcrit scales as ηcrit ∼ ξ−xη, where ξ is the correlation length, related to the reduced temperature εT = (T − Tcrit)/Tcrit by a similar scaling relation ξ ∼ εT−ν.43,44 Using literature values xη = 0.068 and ν = 0.63, this results in an asymptotic scaling law of ηcrit ∼ εT−0.043. Rather than the theoretical exponent 0.043, we instead find experimentally a value of 0.12 ± 0.02 for volume fractions in the vicinity of ϕcrit (Fig. 4), suggesting another, unknown contribution to the zero shear viscosity. Clearly, the possible existence of additional contributors to the zero shear viscosity in the vicinity of a critical point invites further research. Following the viscosity along a critical isochore requires measurements over a large range of temperatures with high accuracy and resolution. The temperature control in our MPT microrheology experiment is unfortunately not good enough for such a study, so there is obviously a need for future experiments. Nevertheless, our results indicate a possibly stronger temperature effect than what one would expect from a comparison with simple fluids.
We are thus confronted with a number of findings that partly seem contradictory. On the one hand, typical for attractive and patchy systems, γB-crystallin solutions show an arrest transition at a low volume fraction ϕg ≈ 0.28. Starting as low as ϕ = 0.13, the concentration dependence of ηr can be described with an MCT-like power law with an exponent γ = 3.1 ± 0.1 that is slightly higher than the value for hard spheres (2.8), in agreement with simulation data for weakly attractive colloids.40,41 On the other hand, we find no measurable temperature dependence of the location of the arrest transition ϕg, despite the fact that the reduced second virial coefficient 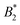 varies considerably across the temperature range.8 This indicates an effective hard sphere- or hard ellipsoid-like behavior, despite the fact that all existing structural and dynamic properties are in agreement with a short range attractive and patchy potential.11,17,18 This is also in line with the earlier findings for proteins undergoing an arrested spinodal decomposition.4,10 These studies demonstrated that the binodal and spinodal for liquid–liquid phase separation would follow an extended law of corresponding states, i.e.
varies considerably across the temperature range.8 This indicates an effective hard sphere- or hard ellipsoid-like behavior, despite the fact that all existing structural and dynamic properties are in agreement with a short range attractive and patchy potential.11,17,18 This is also in line with the earlier findings for proteins undergoing an arrested spinodal decomposition.4,10 These studies demonstrated that the binodal and spinodal for liquid–liquid phase separation would follow an extended law of corresponding states, i.e.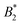 could be used as an effective temperature to rescale the experimental phase boundaries obtained for different solution conditions. However, the location of the arrest line within the unstable region of the phase diagram was determined rather by the contact value of the potential and would not rescale with
could be used as an effective temperature to rescale the experimental phase boundaries obtained for different solution conditions. However, the location of the arrest line within the unstable region of the phase diagram was determined rather by the contact value of the potential and would not rescale with 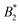 .4,10
.4,10
At present we can only speculate about this peculiar arrest behavior. We currently believe that the arrest transition is caused by transient clusters formed by the attractive patches. These transient (and polydisperse) clusters are characterized by an open structure with low internal density. While the patch attraction leads to the formation of such clusters, the clusters themselves behave as effective hard spheres, driving the observed glass transition at ϕg ≈ 0.28. In a recent simulation study, the existence of such transient clusters was proposed in order to explain the cage diffusion behavior of γB-crystallin.18 Cage diffusion is represented by the short time collective diffusion coefficient Ds(q*) measured at a q-value q*, corresponding to the nearest neighbor peak position in S(q). Measured over a comparable temperature range as used in this study, Bucciarelli et al. found that cage diffusion was not affected by temperature, but rather exhibited a dramatic slowing down upon increased γB-crystallin concentration. This concentration-induced impact on cage diffusion was shown to be best reproduced with a patchy attractive model introducing transient clusters.18 A similar model has recently been shown to reproduce the strong concentration dependence in concentrated solutions of self-assembling monoclonal antibodies, where opposite charges on different parts of the antibody would create attractive patches as a driving force for self-assembly.15
The importance of patchy attractions in determining short- and long-time dynamic properties is further illustrated in Fig. 5. Here we compare experimental results for the concentration dependence of the inverse of the relative viscosity 1/ηr and the normalised short-time cage diffusion coefficient DSc(q*)/D0 with the predictions for the reduced long-time self diffusion coefficient DLs/D0 from computer simulations based on a model of attractive ellipsoids. This colloid model had previously been shown to quantitatively reproduce static properties such as the temperature and concentration dependence of the osmotic compressibility or the location of the binodal for liquid–liquid phase separation.17,45
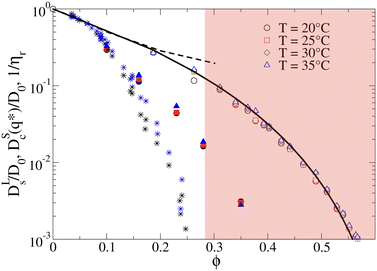 | ||
| Fig. 5 The inverse of the reduced viscosity 1/ηrversus volume fraction ϕ for two temperatures T = 20 °C (black stars) and T = 35 °C (blue stars), respectively, and the concentration dependence of the normalised short-time cage diffusion coefficient DSc(q*)/D0 (data taken from ref. 17) for three temperatures T = 20 °C (black filled circles), T = 25 °C (red filled squares) and T = 35 °C (blue filled triangles). Also shown are the results from computer simulations of weakly attractive hard ellipsoids with dimensions mimicking γB-crystallin. The data for the normalized long-time self diffusion coefficient DLs/D0 are given by the open symbols for 4 different temperatures (T = 20 °C (open black circles), T = 25 °C (open red squares), T = 30 °C (open green diamonds), T = 35 °C (open blue triangles)) and are well-reproduced by a power law of the form DLs/D0 = [(ϕg − ϕ)/ϕg]γ (solid line), with ϕg = 0.66 and γ = 3.7. Also shown are the results from simulations for weakly attractive ellipsoids including hydrodynamic interactions for DSc(q*)/D0 taken from ref. 45 given by the black dashed line. The red shaded region indicates macroscopic arrest. | ||
The simulations and the underlying model of weakly attractive ellipsoids with dimensions closely resembling γB-crystallin are described in more detail in the Materials and Methods section. As shown in Fig. 5, we see that the resulting values for DLs/D0 are well described by a power law of the form DLs/D0 = [(ϕg − ϕ)/ϕg]γ, with ϕg = 0.66 and γ = 3.7 (see also Fig. S5 in the ESI†). The simulations thus indicate an arrest transition at ϕg ≈ 0.66, and there appears to be no measurable temperature dependence. This is close to the location of the arrest transition for hard ellipsoids with an axial ratio of around 2 found from computer simulations and experiments,46,47 and indicates that the weak attraction that drives phase separation and reproduces the structural properties such as the osmotic compressibility has only a weak influence on the long-time dynamic properties such as DLs/D0 and ηr. Arrest appears to be driven primarily by excluded volume interactions instead.
A similar discrepancy between the model predictions based on computer simulations for weakly attractive spheres or ellipsoids and the experimental observations was previously reported also for the short-time cage diffusion coefficient DSc(q*)/D0,18,45 where the data are also included in Fig. 5. While the simulations predict a concentration dependence that initially follows the behavior of DLs/D0 and then shows a weaker ϕ-dependence at higher concentrations, the experimental data shows a dramatic decrease with increasing ϕ already at low volume fractions. Moreover, DSc(q*)/D0 remains non-zero even in the arrested region, i.e. local short-time structural cage relaxations still occur for ϕ > ϕg. It has previously been suggested that this dramatic slowing down of DSc(q*)/D0 is the result of patchy attractions leading to the formation of large transient clusters already at low ϕ-values.18 Computer simulations of patchy particles at comparable values of 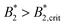 , where
, where 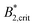 is the value of
is the value of 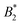 at the critical temperature, demonstrated that these large clusters can become space-filling already at relatively low ϕ-values, resulting in a correspondingly strongly reduced DSc(q*)/D0. However, while these transient clusters also strongly influence the zero shear viscosity, the strength of the patch–patch attraction results in an estimated bond life time τb ≈ 200 ns that is presumably short compared to the longest stress relaxation time linked to the zero shear viscosity, and thus microscopic dynamical arrest occurs at higher concentrations.18
at the critical temperature, demonstrated that these large clusters can become space-filling already at relatively low ϕ-values, resulting in a correspondingly strongly reduced DSc(q*)/D0. However, while these transient clusters also strongly influence the zero shear viscosity, the strength of the patch–patch attraction results in an estimated bond life time τb ≈ 200 ns that is presumably short compared to the longest stress relaxation time linked to the zero shear viscosity, and thus microscopic dynamical arrest occurs at higher concentrations.18
What still remains unclear in such a scenario is why the arrest line appears to be independent of temperature, even though the underlying overall attraction, as indicated by 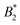 , becomes stronger at lower temperatures. We have studied γB-crystallins at relatively high ionic strength, and thus one possible cause could lie in the subtle interplay between different attractive components of the overall interaction potential: on the one hand, a rather weakly attractive isotropic potential (primarily caused by van der Waals attraction) and on the other hand, more strongly attractive patches that could arise either from oppositely charged or hydrophobic patches on the γB surface.18,48 If these attractive patches are for example due to hydrophobic interactions, they would lose strength at lower temperatures. At the same time, an overall
, becomes stronger at lower temperatures. We have studied γB-crystallins at relatively high ionic strength, and thus one possible cause could lie in the subtle interplay between different attractive components of the overall interaction potential: on the one hand, a rather weakly attractive isotropic potential (primarily caused by van der Waals attraction) and on the other hand, more strongly attractive patches that could arise either from oppositely charged or hydrophobic patches on the γB surface.18,48 If these attractive patches are for example due to hydrophobic interactions, they would lose strength at lower temperatures. At the same time, an overall 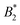 could still signal stronger overall attraction due to the increasing isotropic contribution. The ratio of the strength of attraction between patches and the isotropic contribution would then also decrease and lead to a change in character for the system. At elevated temperatures, patch attractions would drive cluster formation, which dominates the dynamic properties measured by NSE and microrheology and determines the location of the arrest line. At lower temperatures where patch interactions are smaller, the arrest would follow the typical behavior of particles with isotropic short range attractions. This view is corroborated by previous work, which has demonstrated that at temperatures significantly below the critical temperature Tcrit, the arrest line is located in the spinodal region of the phase diagram and shows indeed a significant temperature dependence as expected for an isotropic attractive potential (see Fig. 1).17 However, while there are indeed several hydrophobic patches at the protein surfaces, γB-crystallin at pH 7.1 also has several charge patches with opposite sign.49 Since an increase in temperature also will change the solvent dielectric constant, the Debye screening length and thus the charge distribution and the electrostatic patch–patch interaction, this could also result in an unexpected temperature dependence of the corresponding patch–patch attraction for oppositely charged patches.
could still signal stronger overall attraction due to the increasing isotropic contribution. The ratio of the strength of attraction between patches and the isotropic contribution would then also decrease and lead to a change in character for the system. At elevated temperatures, patch attractions would drive cluster formation, which dominates the dynamic properties measured by NSE and microrheology and determines the location of the arrest line. At lower temperatures where patch interactions are smaller, the arrest would follow the typical behavior of particles with isotropic short range attractions. This view is corroborated by previous work, which has demonstrated that at temperatures significantly below the critical temperature Tcrit, the arrest line is located in the spinodal region of the phase diagram and shows indeed a significant temperature dependence as expected for an isotropic attractive potential (see Fig. 1).17 However, while there are indeed several hydrophobic patches at the protein surfaces, γB-crystallin at pH 7.1 also has several charge patches with opposite sign.49 Since an increase in temperature also will change the solvent dielectric constant, the Debye screening length and thus the charge distribution and the electrostatic patch–patch interaction, this could also result in an unexpected temperature dependence of the corresponding patch–patch attraction for oppositely charged patches.
3. Conclusion
Using tracer particle-based microrheology methods we were able to report the first experimental investigation of the reduced zero-shear viscosity ηr of γB-crystallin solutions over a large volume fraction and temperature range. These measurements have allowed us to precisely locate the arrest line, and compare the concentration and temperature dependence of ηr with other structural and dynamic properties of γB-crystallin. Our results have confirmed the already existing view that this protein can be reasonably well described using a coarse-grained picture of a (patchy) colloid with short range attractions. We observe a measurable critical contribution ηcrit to ηr in the vicinity of the critical point, in line with the previously characterized divergence of the static and dynamic correlation length measured by light scattering, although the experimentally determined exponent of the corresponding scaling law ηr ∼ εT−(0.12±0.02) is considerably larger than the value predicted for classical binary fluids. On the other hand, the overall concentration dependence of ηr appears to be independent of T, in contrast to the large-scale gradient diffusion measured by DLS that is strongly dominated by critical behavior, but similar to the previously reported short time cage diffusion coefficient measured by NSE. The concentration dependence of ηr is well described by an MCT-like power law over a surprisingly large range of volume fractions, and the magnitude of the exponent in this power law is comparable to what has been found in theoretical studies of colloids with short range attractions. Apparently, while attractive patches cause a dramatic slowing down of cage diffusion, and move the arrest transition to quite low volume fractions, the resulting functional form that describes the concentration dependence of ηr seems rather insensitive to microstructural details.There remain some puzzling findings that are not easily understood within this colloid picture. A strongly varying 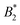 above the critical temperature, juxtaposed by a temperature independent location of ϕg, clearly does not follow the frequently postulated use of an extended law of corresponding states also for non-equilibrium properties such as kinetic arrest.32 Obviously dynamic quantities such as short time cage diffusion and viscosity are much more strongly influenced by local details of the interaction potential and the local microstructure than the phase behavior. There is clearly a need for further studies of the link between interaction anisotropy, the formation of transient clusters and their consequences for these dynamic properties. For proteins, this also needs to be linked to the molecular structure and its dependence on the solution properties. We believe that this is not only of fundamental interest for the colloid community, but has consequences for diverse communities such as cell biology or pharmaceutical formulation science, where an ability to predict the existence and location of an arrest transition would be extremely important.
above the critical temperature, juxtaposed by a temperature independent location of ϕg, clearly does not follow the frequently postulated use of an extended law of corresponding states also for non-equilibrium properties such as kinetic arrest.32 Obviously dynamic quantities such as short time cage diffusion and viscosity are much more strongly influenced by local details of the interaction potential and the local microstructure than the phase behavior. There is clearly a need for further studies of the link between interaction anisotropy, the formation of transient clusters and their consequences for these dynamic properties. For proteins, this also needs to be linked to the molecular structure and its dependence on the solution properties. We believe that this is not only of fundamental interest for the colloid community, but has consequences for diverse communities such as cell biology or pharmaceutical formulation science, where an ability to predict the existence and location of an arrest transition would be extremely important.
On a more technical level, our study also allows us to draw some conclusions about the potential and limits of these tracer particle-based microrheology techniques. They obviously have significant advantages when compared with classical rheometrical measurements. Traditional rheological measurements of low shear viscosity for low concentration protein solutions are often suffering from artefacts caused by the amphiphilic properties of many proteins, which tend to form a viscoelastic film at liquid–air or liquid–solid interfaces, while measurements at high protein concentrations become prohibitive due to the rather large sample volumes required. This is not the case for tracer particle-based microrheology, which can be performed using DLS and/or MPT. Our study has now provided additional insights into their use in concentrated protein solutions. DLS is for example more robust at low volume fractions and correspondingly low values of ηr, as the resulting high tracer particle mobility only allows for short-time tracking in MPT, leading to decreased statistics and larger error bars. On the other hand, and more importantly, for proteins that exhibit liquid–liquid phase separation the significantly increased protein scattering due to critical fluctuations close to the critical point and the spinodal line causes major problems for DLS-based microrheology, as the extraction of the particle signal becomes significantly less reliable. Naturally, no such effects are visible with MPT, thus when studying systems displaying critical behavior, MPT is strongly recommended over DLS at higher concentrations c ≈ ccrit. In this context, using a 3D cross-correlation DLS scheme that suppresses contributions from multiple scattering also is highly advantageous and extends the range of applicability of DLS-based microrheology considerably.
4. Materials and Methods
4.1. γ B-Crystallin extraction
The procedure for obtaining and extracting γB-crystallin has been described in detail elsewhere.17,27 Briefly, the filtered cellular contents of bovine eye-lenses were passed through a size exclusion chromatography column, yielding a mixture of γ-crystallins. This mixture was further separated using a fast flow ion exchange column where a salt gradient was used to elute the individual components with γB-crystallin being collected. The final sample was added to a 52.4 mM phosphate buffer corresponding to pH 7.1 in D2O with the addition of 20 mM DL-dithiothreitol (DTT, Sigma Aldrich D9779), 1 mM ethylenediaminetetraacetic acid disodium salt dehydrate (EDTA, Sigma Aldrich E5134) and 0.02 wt% sodium azide (NaN3, Sigma Aldrich S2002). Amicon Ultra centrifugal filter units with a volume of 15 mL (cutoff 3 kDa) or 0.5 mL (cutoff 10 kDa) were used to concentrate the samples. The final protein volume fraction was determined from UV-absorption using an extinction coefficient (0.1%, 1 cm, 280 nm) of 2.1827 and converted to a volume fraction using a voluminosity of 0.71 mL g−1.224.2. Dynamic light scattering-based microrheology
The first microrheology method follows the motion of tracer particles within the protein sample via dynamic light scattering (DLS) and has been thoroughly described earlier.31,50 Polystyrene particles with a diameter of 0.3 μm stabilized with covalently-bound 20 kDa poly(ethylene) glycol were then used as tracer particles when mixed with protein samples. DLS measurements at a scattering angle of 90° were performed at 20, 25, 30, and 35 °C. The tracer diffusion coefficient, D, was determined from a first order cumulant analysis by fitting a single exponential, when possible, to the field correlation function (g1), assuming that the scattering intensity was dominated by the tracer contribution and that g1 directly reflected the tracer motion. In the case when the protein contribution is too significant, the entire correlation function was instead analyzed by simultaneously fitting the combined protein and tracer contribution. Measurements of protein samples without tracers were also performed to verify the result and to make sure that there was no significant long-time protein contribution that may interfere with the tracer fit. The reduced viscosity, ηr, of the sample was extracted using the Stokes–Einstein relation and by normalizing with tracer measurements without protein. A more detailed description of the analysis approach is provided in the ESI.†4.3. Multiple particle tracking-based microrheology
The second microrheology method, multiple particle tracking (MPT), monitors tracer particle motion using videos from confocal laser scanning microscopy (CLSM) and is described in more detail elsewhere.30 In short, fluorescently labeled polystyrene particles with a diameter of 1.0 μm (ThermoFisher, F8820) were mixed into samples containing γB-crystallin. A 5 μL droplet was transferred to a (cleaned) glass slide and sealed using a SecureSeal spacer (12 mm thickness, Invitrogen) and coverslip. Videos (512 × 256 pixels, 6000 frames, frame rate 77 Hz, 10 μm away from the cover slide) at five different locations in the sample were recorded using a Leica SP5 confocal microscope with a resonant scanner, which is housed in a temperature controlled box, allowing precise control of the temperature. In accordance with DLS measurements, videos were recorded at 20, 25, 30 and 35 °C. The 2D (〈Δx2 + Δy2〉) mean squared displacement (MSD) of the tracers was calculated using the standard IDL routines51 and converted to 3D MSD for generality.52 The shown MSDs are time and ensemble-averaged. Rather than extracting the diffusion coefficient from the slope of the MSD – which is quite sensitive to statistics – the Van Hove self-correlation function was calculated. The Van Hove function for one dimension is defined as P(Δx,τ) = (4πDτ)−1/2exp(−〈Δx2(τ)〉/4Dτ).52,53 It relates the probability that a tracer moves a distance Δx in a time-step τ. For a purely diffusive system (and with sufficient statistics) this probability density function follows a Gaussian distribution.54 We tested for which time-step a Gaussian distribution with the highest statistics was obtained, and only used the displacement data at that particular time-step to compute a more robust diffusion coefficient.53 The resulting diffusion coefficients in both x- and y-dimensions were averaged and the viscosity, η0, was obtained using the Stokes–Einstein relation. To obtain ηr this viscosity was subsequently normalized using literature values for the viscosity ηs of D2O.554.4. Preparation of solid-like samples
In an effort to reach volume fractions not easily achieved with conventional means we employed the evaporation method described previously.30 In these experiments, a controlled amount of time was left between deposition of the sample on the glass slide and sealing of the sticker cell with the coverslip. The amount of solvent that evaporated was determined gravimetrically which allows for determining the increase in protein volume fraction. The samples were then investigated using CLSM as previously established.4.5. Computer simulations
For all state points we calculated the diffusion coefficient D from the mean squared displacement 〈Δr2〉, since
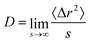 | (1) |
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
PS acknowledges financial support from the European Research Council (ERC-339678-COMPASS) and the Swedish Research Council (VR Grant No. 2019-06075, Röntgen-Ångström Cluster). AS acknowledges financial support from the Swedish Research Council (VR grants No. 2016-03301 and No. 2022-03142) and the Faculty of Science at Lund University. C. D. M. acknowledges financial support from the European Union-Next Generation EU (Grant No. MUR-PRIN2022 TAMeQUAD CUP: B53D23004500006) and from ICSC-Centro Nazionale di Ricerca in High Performance Computing, Big Data, and Quantum Computing, funded by the European Union-NextGenerationEU. PS acknowledges helpful and insightful discussions with Johan Bergenholtz and Håkan Wennerström. This work is dedicated to Stefan U. Egelhaaf, a wonderful friend, outstanding scientist and sorely missed colleague whose contributions to the field have been a constant inspiration to us.References
- J. Berry, C. P. Brangwynne and M. Haataja, Rep. Prog. Phys., 2018, 81, 046601 CrossRef PubMed.
- A. Klosin, F. Oltsch, T. Harmon, A. Honigmann, F. Jülicher, A. A. Hyman and C. Zechner, Science, 2020, 367, 464–468 CrossRef CAS PubMed.
- A. Stradner and P. Schurtenberger, Soft Matter, 2020, 16, 307–323 RSC.
- F. Cardinaux, T. Gibaud, A. Stradner and P. Schurtenberger, Phys. Rev. Lett., 2007, 99, 1–4 CrossRef PubMed.
- G. B. Benedek, Invest. Ophthalmol. Visual Sci., 1997, 1911–1921 CAS.
- J. D. Gunton, A. Shiryayev and D. L. Pagan, Protein Condensation, Cambridge University Press, Cambridge, 2007 Search PubMed.
- F. Platten, N. E. Valadez-Pérez, R. Castañeda-Priego and S. U. Egelhaaf, J. Chem. Phys., 2015, 142, 05B602 CrossRef PubMed.
- S. Bucciarelli, N. Mahmoudi, L. Casal-Dujat, M. Jéhannin, C. Jud and A. Stradner, J. Phys. Chem. Lett., 2016, 7, 1610–1615 CrossRef CAS PubMed.
- M. G. Noro and D. Frenkel, J. Chem. Phys., 2000, 113, 2941–2944 CrossRef CAS.
- J. Hansen, C. J. Moll, L. López Flores, R. Castañeda-Priego, M. Medina-Noyola, S. U. Egelhaaf and F. Platten, J. Chem. Phys., 2023, 158, 024904 CrossRef CAS PubMed.
- A. Lomakin, N. Asherie and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 9465–9468 CrossRef CAS PubMed.
- C. Gögelein, G. Nägele, R. Tuinier, T. Gibaud, A. Stradner and P. Schurtenberger, J. Chem. Phys., 2008, 129, 08B615 CrossRef PubMed.
- M. Kastelic, Y. V. Kalyuzhnyi, B. Hribar-Lee, K. A. Dil and V. Vlachy, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 6766–6770 CrossRef CAS PubMed.
- M. Kastelic and V. Vlachy, J. Phys. Chem. B, 2018, 122, 5400–5408 CrossRef CAS PubMed.
- N. Skar-Gislinge, M. Ronti, T. Garting, C. Rischel, P. Schurtenberger, E. Zaccarelli and A. Stradner, Mol. Pharmaceutics, 2019, 16, 2394–2404 CrossRef CAS PubMed.
- J. Weimar, F. Hirschmann and M. Oettel, Soft Matter, 2024, 20, 8455–8467 RSC.
- S. Bucciarelli, L. Casal-Dujat, C. De Michele, F. Sciortino, J. Dhont, J. Bergenholtz, B. Farago, P. Schurtenberger and A. Stradner, J. Phys. Chem. Lett., 2015, 6, 4470–4474 CrossRef CAS PubMed.
- S. Bucciarelli, J. S. Myung, B. Farago, S. Das, G. A. Vliegenthart, O. Holderer, R. G. Winkler, P. Schurtenberger, G. Gompper and A. Stradner, Sci. Adv., 2016, 2, e1601432 CrossRef PubMed.
- G. Nawrocki, P.-h Wang, I. Yu, Y. Sugita and M. Feig, J. Phys. Chem. B, 2017, 121, 11072–11084 CrossRef CAS PubMed.
- S. von Bülow, M. Siggel, M. Linke and G. Hummer, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 9843–9852 CrossRef PubMed.
- J. A. Thomson, P. Schurtenberger, G. M. Thurston and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 7079 CrossRef CAS PubMed.
- P. Schurtenberger, R. A. Chamberlin, G. M. Thurston, J. A. Thomson and G. B. Benedek, Phys. Rev. Lett., 1989, 63, 2064–2067 CrossRef CAS PubMed.
- E. Héon, M. Priston, D. F. Schorderet, G. D. Billingsley, P. O. Girard, N. Lubsen and F. L. Munier, Am. J. Hum. Genet., 1999, 65, 1261 CrossRef PubMed.
- A. Pande, J. Pande, N. Asherie, A. Lomakin, O. Ogun, J. King and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 6116–6120 CrossRef CAS PubMed.
- M. S. Kosinski-Collins and J. King, Protein Sci., 2003, 12, 480–490 CrossRef CAS PubMed.
- A. Stradner, G. M. Thurston and P. Schurtenberger, J. Phys.: Condens. Matter, 2005, 17, S2805–S2816 CrossRef CAS.
- G. M. Thurston, J. Chem. Phys., 2006, 124, 134909 CrossRef PubMed.
- A. Stradner, G. Foffi, N. Dorsaz, G. M. Thurston and P. Schurtenberger, Phys. Rev. Lett., 2007, 99, 198103 CrossRef CAS PubMed.
- B. M. Fine, J. Pande, A. Lomakin, O. O. Ogun and G. B. Benedek, Phys. Rev. Lett., 1995, 74, 198–201 CrossRef CAS PubMed.
- M. J. Bergman, T. Garting, P. Schurtenberger and A. Stradner, J. Phys. Chem. B, 2019, 123, 2432–2438 CrossRef CAS PubMed.
- T. Garting and A. Stradner, Colloids Surf., B, 2019, 181, 516–523 CrossRef CAS PubMed.
- A. P. R. Eberle, R. Castañeda-Priego, J. M. Kim and N. J. Wagner, Langmuir, 2012, 28, 1866–1878 CrossRef CAS PubMed.
- G. Foffi and F. Sciortino, J. Phys. Chem. B, 2007, 111, 9702–9705 CrossRef CAS PubMed.
- N. Dorsaz, L. Filion, F. Smallenburg and D. Frenkel, Faraday Discuss., 2012, 159, 9 RSC.
- D. Quemada, Rheol. Acta, 1977, 16, 82–94 CrossRef.
- I. M. Krieger and T. J. Dougherty, Trans. Soc. Rheol., 1959, 3, 137–152 CAS.
- M. Mooney, J. Colloid Interface Sci., 1951, 6, 162–170 CrossRef CAS.
- G. Brambilla, D. El Masri, M. Pierno, L. Berthier, L. Cipelletti, G. Petekidis and A. B. Schofield, Phys. Rev. Lett., 2009, 102, 085703 CrossRef CAS.
- A. Pal, M. A. Kamal, P. Holmqvist and P. Schurtenberger, Phys. Rev. Res., 2021, 3, 023254 CrossRef CAS.
- A. M. Puertas, C. De Michele, F. Sciortino, P. Tartaglia and E. Zaccarelli, J. Chem. Phys., 2007, 127, 1–10 CrossRef.
- A. M. Puertas, M. Fuchs and M. E. Cates, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 1–13 CrossRef.
- G. Foffi, G. Savin, S. Bucciarelli, N. Dorsaz, G. M. Thurston, A. Stradner and P. Schurtenberger, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 16748–16753 CrossRef CAS PubMed.
- J. Luettmer-Strathmann, J. V. Sengers and G. A. Olchowy, J. Chem. Phys., 1995, 103, 7482–7501 CrossRef CAS.
- S. Roy and S. K. Das, J. Chem. Phys., 2013, 139, 064505 CrossRef PubMed.
- J. S. Myung, F. Roosen-Runge, R. G. Winkler, G. Gompper, P. Schurtenberger and A. Stradner, J. Phys. Chem. B, 2018, 122, 12396–12402 CrossRef CAS PubMed.
- C. De Michele, R. Schilling and F. Sciortino, Phys. Rev. Lett., 2007, 98, 265702 CrossRef PubMed.
- I. Martchenko, J. J. Crassous, A. M. Mihut, E. Bialik, A. M. Hirt, C. Rufier, A. Menzel, H. Dietsch, P. Linse and P. Schurtenberger, Soft Matter, 2016, 12, 8755–8767 RSC.
- C. J. Roberts and M. A. Blanco, J. Phys. Chem. B, 2014, 118, 12599–12611 CrossRef CAS PubMed.
- C. W. Wahle, K. M. Martini, D. M. Hollenbeck, A. Langner, D. S. Ross, J. F. Hamilton and G. M. Thurston, Phys. Rev. E, 2017, 96, 0324151 CrossRef.
- T. Garting and A. Stradner, Small, 2018, 14, 1801548 CrossRef PubMed.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- T. Moschakis, Curr. Opin. Colloid Interface Sci., 2013, 18, 311–323 CrossRef CAS.
- L. L. Josephson, E. M. Furst and W. J. Galush, J. Rheol., 2016, 60, 531–540 CrossRef CAS.
- M. T. Valentine, P. D. Kaplan, D. Thota, J. C. Crocker, T. Gisler, R. K. Prud'homme, M. Beck and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 061506 CrossRef CAS PubMed.
- R. C. Hardy and R. L. Cottington, J. Chem. Phys., 1949, 17, 509–510 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01275e |
| This journal is © The Royal Society of Chemistry 2025 |