Open Access Article
Open Access ArticleImpact of cross-linking on the time–temperature superposition of creep rupture in epoxy resins†
Atsuomi Shundo *a,
Mika Aokib,
Satoru Yamamoto
*a,
Mika Aokib,
Satoru Yamamoto b and
Keiji Tanaka
b and
Keiji Tanaka *abc
*abc
aDepartment of Automotive Science, Kyushu University, Fukuoka 819-0395, Japan. E-mail: a-shundo@cstf.kyushu-u.ac.jp; k-tanaka@cstf.kyushu-u.ac.jp; Tel: +81-92-802-2880 Tel: +81-92-802-2878
bCenter for Polymer Interface and Molecular Adhesion Science, Kyushu University, Fukuoka 819-0395, Japan
cDepartment of Applied Chemistry, Kyushu University, Fukuoka 819-0395, Japan
First published on 1st April 2025
Abstract
Epoxy resins are an important class of thermosetting resins, and their network structure, formed by the curing reaction of epoxy and amine compounds, plays a crucial role in determining material properties, including creep behavior. We here applied the time–temperature superposition (TTS) principle to analyze the creep behavior of epoxy resins with well-defined network structures that were systematically varied based on the length of the n-alkyl diamine used. The superposition of isothermal creep curves under small stress was achieved through horizontal and vertical shifting, regardless of the length of the n-alkyl diamine. The temperature dependence of the horizontal shift factor was well described by the Williams–Landel–Ferry equation. Creep rupture measurements under large stress conditions revealed specimen rupture, and the time to rupture was plotted against the imposed stress. These plots, acquired at various temperatures, could be superimposed through horizontal shifting. As the diamine length decreased—namely, the distance between cross-linking points—the temperature dependence of the horizontal shift factors deviated from the WLF equation and exhibited Arrhenius-type behavior. The deviation was associated with differences in the fracture process involving chain scission, which became more pronounced as the diamine length decreased. The insights gained in this study should be valuable for controlling creep response and predicting the long-term durability of epoxy resins.
1. Introduction
Epoxy resins, obtained by the curing reaction of epoxies with amine compounds, are an important class of thermosetting polymers used in a wide range of applications, including adhesives,1–10 coatings,11–15 and composite materials.16–24 They possess an internal three-dimensional network, where the segmental mobility is frozen in a glassy state at room temperature.25–30 When polymeric materials in a glassy state are subjected to stress, such as tensile stress, they slowly elongate. This phenomenon, known as creep behavior, has been systematically studied in thermoplastic polymers.31–35 In thermosetting resins, including epoxy resins, creep behavior is equally critical for applications requiring long-term shape stability.36–40 Consequently, the relationship between the network structure, particularly cross-linking density, and creep behavior in epoxy resins has been extensively investigated.41–50From a practical application perspective, it is crucial to understand not only creep behavior but also material durability.51–53 To address durability, establishing a method of predicting long-term behavior from short-term tests is highly desirable. The time–temperature superposition (TTS) principle is one of the most promising methods for this purpose.54–58 A series of isothermal curves for creep compliance, J(t), defined as the strain divided by the stress applied to a sample, can be obtained as a function of time. These curves can be superimposed onto one another through horizontal and/or vertical shifts. This operation generates a master curve that represents creep behavior over a wide time range, which cannot be achieved with individual isothermal measurements.31,59 Consequently, the TTS principle has been widely used to predict the long-term response of material properties.60–64 For instance, short-term (10 h) creep measurements at various temperatures make it possible to access a time scale of up to 106 h (more than 50 years).61
We recently studied the TTS principle based on the dynamic viscoelastic functions of epoxy resins, in which the network was well defined and systematically varied in terms of cross-linking density.65 For these epoxy resins, an increase in cross-linking density led to a higher glass transition temperature (Tg) with an associated reduction in the spatial size scale of the cooperative rearranging region (CRR).66 The superimposition of isothermal curves in the frequency domain required not only horizontal, but also vertical shifts, regardless of the cross-linking density. The temperature dependence of the horizontal shift factor was well described by the Williams–Landel–Ferry (WLF) equation. Fitting analyses of the parameters C1 and C2, combined with full-atomistic molecular dynamics (MD) simulations, revealed that an increase in cross-linking density resulted in a lower thermal expansion coefficient of free volume, accompanied by the suppression of entropic elasticity at high temperatures.65 However, it is noteworthy that the shape of the master curve was slightly distorted for resins with higher cross-linking densities. This distortion is likely due to the increasing importance of cross-linking points, which cannot be ignored as the spatial length scale of the dynamics grows, even though the TTS principle assumes that the mode of dynamics remains unchanged with temperature variations.65,66 These findings motivated us to apply the TTS principle to creep behaviors, which involve chain motions over longer timescales and larger spatial scales.
In this study, we examined how cross-linking density, which is related to all of the aforementioned factors, affects the horizontal and vertical shifts of the isothermal creep curves. Three different epoxy resins with varying cross-linking densities based on the length of n-alkyl diamine were studied. Creep tests were conducted under two distinct stress levels: small stress within the linear response regime and larger stress beyond it.
2. Experimental
2.1. Materials and preparation of epoxy resins
Panel (a) of Fig. 1 shows the chemical structures of diglycidyl ether of bisphenol A (DGEBA) with a purity greater than 99% and n-alkyl diamines with methylene group numbers (n) of 12, 6 and 2, each with a purity exceeding 99%. These compounds were purchased from New Japan Chemical Co., Ltd, Osaka, Japan, and Tokyo Chemical Industry Co., Ltd, Tokyo, Japan. DGEBA and n-alkyl diamines were mixed thoroughly at a molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, corresponding to the stoichiometric ratio of epoxy to amino groups. The mixture, heated to 353 K, was placed onto an aluminum substrate using a silicon rubber mold and pre-cured for 12 h. Subsequently, all samples underwent post-curing at 453 K for an additional 12 h, ensuring the apparent completion of the reactions, as confirmed by Fourier transform infrared (FT-IR) spectroscopy (FT/IR 6700 spectrometer, JASCO Co., Tokyo, Japan).67–69 The resulting epoxy resins are hereafter referred to as ER12, ER6 and ER2, where the number corresponds to the methylene group number of the n-alkyl diamines.
1, corresponding to the stoichiometric ratio of epoxy to amino groups. The mixture, heated to 353 K, was placed onto an aluminum substrate using a silicon rubber mold and pre-cured for 12 h. Subsequently, all samples underwent post-curing at 453 K for an additional 12 h, ensuring the apparent completion of the reactions, as confirmed by Fourier transform infrared (FT-IR) spectroscopy (FT/IR 6700 spectrometer, JASCO Co., Tokyo, Japan).67–69 The resulting epoxy resins are hereafter referred to as ER12, ER6 and ER2, where the number corresponds to the methylene group number of the n-alkyl diamines.
 | ||
| Fig. 1 Chemical structures of (a) DGEBA and (b) n-alkyl diamines with varying numbers of methylene groups (n), where n = 12, 6, and 2. | ||
2.2. Characterizations
The mass density (ρ) of the cured epoxy resins was examined using a gas pycnometer (ULTRAPYC 1200e, Anton Paar QuantaTec Inc., Florida, USA) with helium as the probing gas. The helium pressure was set at 117 kPa, and measurements were taken 100 times to obtain an average value. Dynamic mechanical analysis (DMA) was conducted using a Rheovibron DDV-01FP (A&D Co., Ltd, Tokyo, Japan) on samples with a thickness of 300 μm, width of 3 mm, and length of 30 mm. A sinusoidal strain of 0.3%, within the linear response regime, was applied. Measurements were taken under a dry nitrogen purge with a heating rate of 2 K min−1 at a frequency of 1 Hz. The average cross-linking density (ν) of the network was estimated based on the storage modulus (E′) in the rubbery plateau region.66Before conducting creep and rupture tests, the mechanical properties of the epoxy resins were characterized through tensile testing using a TENSILON RTF-1310 (A&D Co., Ltd, Tokyo, Japan). The specimens were prepared according to Japanese Industrial Standards (JIS) K6251-7, with a gauge length of 12 mm and a width of 2 mm. Tensile tests were conducted at various temperatures ranging from 358 to 438 K, controlled by a thermostatic chamber (TKC-R3-C, A&D Co., Ltd, Tokyo, Japan). The crosshead speed was set at 1 mm min−1.
Creep and rupture tests were performed using the same instrument as the tensile testing setup. For the creep tests, a stress (σ) in the range of 0.7–1.3 MPa, within the linear response regime, was applied to the specimen at a specified temperature (T). J(t), defined as the strain divided by σ, was recorded as a function of time (t). Measurements were taken at different Ts within the range of 358–473 K, at 5 K intervals. For the creep rupture tests, higher σs in the range of 2–25 MPa were applied to the specimens at given Ts, and the time to macroscopic rupture (trp) was recorded. These measurements were taken at various T values within the range of 358–473 K, also at 5 K intervals, to establish the relationship between trp and σ.
After the creep rupture tests, changes in the ν of the specimens were assessed using a swelling test. Specimens were weighed (W0) and immersed in THF at 313 K for 12 days. The equilibrium weight (Weq) was recorded after collecting the fractured pieces and gently blotting THF from the sample surface. The swelling ratio was calculated as (Weq − W0)/W0.
3. Results and discussion
3.1. Creep behavior under small strain
Table 1 summarizes the characterization data for ν, ρ and Tg for ER12, 6 and 2, as reported in our previous study.65 The ν value was estimated based on the rubbery plateau modulus using the equation of ν = E′/3RT, where R is the gas constant.65,66,70,71 The Tg value was dynamically defined at an α-relaxation time (τ) of 100 s, determined through the DMA measurements.65,66 The ν, ρ and Tg values were higher in the order of ER2, 6 and 12. This indicates that the cross-linking density of the products increased as the length of n-alkyl diamine decreased, resulting in a glassy state with higher mass density, which effectively suppressed the segmental motion in between the cross-linking points.72 Notably, the Tg values for ER12, ER6, and ER2 remained unchanged even after a heating and cooling cycle in the range of 293–453 K, suggesting thermal stability during the subsequent creep (rupture) tests.| ν 10−3/mol m−3 | ρ/g cm−3 | Tg/K | |
|---|---|---|---|
| ER12 | 1.70 ± 0.04 | 1.120 ± 0.008 | 357 |
| ER6 | 2.14 ± 0.05 | 1.159 ± 0.004 | 379 |
| ER2 | 2.39 ± 0.04 | 1.180 ± 0.013 | 395 |
The creep test was conducted on the three epoxy resins by applying σ, which was within the linear response regime, as confirmed by the tensile test (see Fig. S1 in the ESI†). This resulted in the time dependence of J(t) being examined at various Ts ranging from Tg to Tg + 35 K (see Fig. S2 in the ESI†). When the TTS principle is applied to the creep tests, the horizontal and vertical shift factors (aT and bT) are expressed as follows:31,54
 | (1) |
Fig. 2 shows the master curves for ER12, ER6 and ER2, with Tr set to their respective Tg values listed in Table 1. For all epoxy resins, the value of J(t) scaled with bT−1 (J(t)·bT−1) increased with increasing scaled time (t·aT−1) before reaching a plateau. However, notable differences were observed in the master curves among the three samples. The speed of increase in J(t)·bT−1 was slower in the order of ER2, ER6 and ER12. Consequently, the t·aT−1 value at which J(t)·bT−1 reached the plateau was longer in the same order, indicating that deformation occurs more slowly as the diamine length decreases. Also, the plateau J(t)·bT−1 values were lower in the order of ER2, ER6 and ER12. This indicates that the magnitude of the deformation over long timescales decreases as the diamine length decreases. Assuming that cross-linking points in the network suppress deformation,45,48 the observed differences in the master curves based on diamine length can be reasonably explained.
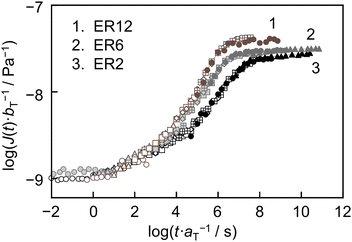 | ||
| Fig. 2 Master curves of J(t) for ER12, ER6 and ER2, constructed through vertical and subsequent horizontal shifting. The reference temperature was set to Tg. | ||
Fig. 3 shows the aT data as a function of inverse temperature for ER12, 6 and 2. Closed symbols represent the aT data obtained from the superposition of J(t) curves in the creep test. The temperature dependence of aT can be well described by the Williams–Landel–Ferry (WLF) equation;31,54,74–76
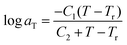 | (2) |
 | ||
| Fig. 3 Temperature dependence of aT for ER12, ER6 and ER2. Closed symbols represent experimental data obtained from the creep test, while open symbols correspond to data from DMA measurements. Solid curves indicate the best fit of the WLF equation to the DMA data. (The DMA data are reproduced from ref. 65 with permission. Copyright 2021 American Chemical Society). | ||
3.2. Creep rupture behavior under large strain
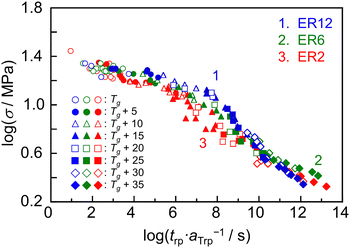
For the creep rupture test, σ larger than the stress levels used previously was applied to the specimen at a constant T. Fig. 4 shows the time dependence of J(t) for a representative sample, ER12, under σ values of 14, 15 and 16 MPa at 368 K. Regardless of the applied σ, the J(t) value increased over time, eventually reaching a plateau. After a certain period, the specimens ruptured. The time required for rupture (trp) decreased as σ increased. To construct master curves, the relationship between trp and σ was obtained at various T values ranging from Tg to Tg + 35 K (see Fig. S3 in the ESI†). The trp–σ plots at different T were horizontally shifted to align with the data at Tg, using a horizontal shift factor (aTrp). Assuming that vertical shifting in the creep rupture test is negligible,77–81 the value of vertical shift factor was set to unity. Fig. 5 shows the master curves for ER12, ER6 and ER2. All samples exhibited the trend where trp·aTrp−1 was inversely proportional to σ, indicating that the specimen ruptured more easily as the stress increased. Notably, the shapes of the master curves for ER12, ER6 and ER2 differed around σ = 10 MPa. Specifically, the trp·aTrp−1 values were shorter in the order of ER2, ER6 and ER12. This suggests that the temperature dependence of aTrp varies with the methylene group number of the diamine. It is also interesting to consider the differences in behavior before and after the threshold σ of 10 MPa. A possible explanation is a transition in the failure mode around this stress level, for σ > 10 MPa, the fracture behavior resembles brittle fracture, whereas for σ < 10 MPa, it appears more ductile-like. However, to draw a definitive conclusion, direct observations of the fracture surfaces would be necessary.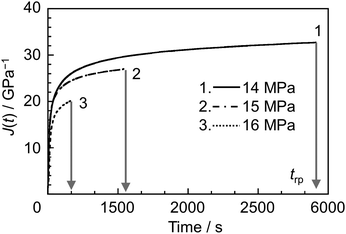 | ||
| Fig. 4 Representative time dependence of J(t) for ER12 under σ values of 14, 15, and 16 MPa at 368 K. | ||
Panel (a) of Fig. 6 shows the temperature dependence of aTrp for ER12, ER6, and ER2. Closed symbols denote experimental data, while solid curves indicate the best-fit results using the WLF equation applied to the aT–T−1 relationship from the creep test under small strain (Fig. 3). For all samples, the aTrp values were close to their respective WLF curves in the low-temperature region. However, as the temperature increased, the aTrp values began to deviate from the WLF curves. This deviation can be quantified as the difference between aTrp and the WLF curve (ΔaTrp). Panel (b) of Fig. 6 shows the correlation between ΔaTrp and T–Tr (ΔT) for ER12, ER6, and ER2. For ER12, ΔaTrp values remained near zero at all ΔT, indicating that the temperature dependence of aTrp was well described by the WLF equation. In contrast, for ER6 and ER2, ΔaTrp increased with increasing ΔT, reflecting greater deviations from the WLF curve in the high-temperature region. Here, it should be noted that the increase in ΔaTrp was more pronounced in the order of ER2, ER6, and ER12. Thus, it is most likely that, as the diamine length decreases, the temperature dependence of aTrp transitions from WLF-type behavior to Arrhenius-type behavior, where the logarithm of aTrp scales linearly with the inverse temperature. The potential reasons for this transition will be discussed in the following section.
3.3. Cross-linking density effect on rupture behavior
To explore the reason for the differences in the temperature dependence of aTrp among the three resins, we examined rupture strain (εrp) as an alternative to trp in the creep rupture test. Fig. 7 shows double logarithmic plots of σ against εrp for ER12, ER6, and ER2. For each sample, the rupture points obtained at the different temperatures were superimposed, resulting in a master curve. As temperature increased, the points moved clockwise around the curve and eventually passed through the maximum. This behavior is consistent with the failure envelope observed in tensile tests, where failure strain is plotted against failure stress while varying temperature and tensile rate.77,78,82–84 It indicates that, for a given applied stress, rupture occurs when the strain exceeds a certain limit. Similarly, in experiments where strain is fixed, the material ruptures when subjected to stress beyond a specific threshold. A particular interesting aspect is that, when failure is analyzed at a fixed strain, two distinct stress limits emerge. These correspond to brittle and ductile failure modes, as mentioned earlier. The data associated with higher failure stress correspond to brittle fracture, whereas those at lower failure stress correspond to ductile fracture. At relatively low temperatures, brittle failure dominates, placing the corresponding data points in the upper region of the plot. Notably, the shapes of the master curves differed markedly among the three resins, particularly at relatively low σ, corresponding to high T. In this region, εrp was smaller in the order of ER2, ER6, and ER12. Thus, it is obvious that the macroscopic rupture occurred more easily as the diamine length decreased. This effect became more pronounced at higher Ts, suggesting that the fracture mechanism depends on the diamine length, and consequently, the cross-linking density. | ||
| Fig. 7 Double logarithmic plots of σ against εrp for ER12, ER6, and ER2. Blue, green, and red-colored symbols denote data for ER12, ER6, and ER2, respectively. | ||
In general, the rupture behavior of polymer materials, including epoxy resins, involves crazing and/or void formation, which lead to crack generation and propagation.85–88 These processes are often accompanied by chain scissions.89–93 If chain scission occurs in epoxy resins, the cross-linking density of the network structure should decrease. To verify this, we examined changes in cross-linking density during the creep rupture test using a swelling test.94–96 Epoxy resin specimens were subjected to a σ of 2.5 MPa at Tg + 35 K and left undisturbed until just before rupture. The stretched portion of each specimen was immersed in a good solvent, THF, for a specific period, and the swelling ratio (ϕ) was obtained based on weight changes. For comparison, neat specimens without creep treatment were also tested.
Fig. 8 shows ϕ as a function of immersion time for ER12, ER6, and ER2, with and without creep treatment. For all samples, ϕ increased over time and reached equilibrium, regardless of the creep treatment. However, specimens subjected to creep exhibited steeper slopes and higher equilibrium ϕ values, with the effect being most pronounced for ER2. The equilibrium ϕ for ER2 increased markedly upon creep treatment. Given that equilibrium ϕ is inversely proportional to cross-linking density,94–96 it can be claimed that the cross-linking density of ER2 decreased due to chain scission during the creep test. As the cross-linking density increases, that is, as the distance between cross-linking points decreases, the proportion of chains in an extended state increases. This is equivalent to our previous finding that a shorter distance between cross-linking points results in a smaller entropic elasticity contribution to bT. Consequently, these chains become more susceptible to scission.89,91 This scenario explains why the temperature dependence of aTrp transitions from the WLF-type to Arrhenius-type behavior as cross-linking density increases (Fig. 6). That is, a two-state approximation, representing the states before and after chain scission, likely underpins the observed Arrhenius-type behavior.
Finally, we discuss the applicability of the TTS principle, which assums that a molecular motion mode remains unchanged with temperature, allowing for the horizontal (time-axis) shifting of viscoelastic data. However, as molecular motion becomes increasingly active at higher temperatures, localized network disruptions occur, leading to a breakdown in cooperative segmental motion. This shift alters the dominant relaxation mechanism, transitioning to one governed by activation energy, characteristic of Arrhenius-type behavior. Thus, when applying the TTS principle to cross-linked polymer networks, including thermosetting polymers, it is crucial to consider these fundamental limitations and recognize the potential transition in temperature dependence as the system undergoes structural changes at elevated temperatures.
4. Conclusions
We examined how cross-linking points affect the time–temperature scaling of creep (rupture) behavior in epoxy resins, obtained from the curing reaction of a DGEBA epoxy base with n-alkyl diamine hardeners containing varying numbers of methylene groups. In creep tests under relatively small σs, time-domain curves of J(t) were successfully superimposed within the temperature region from Tg to at least Tg + 35 K by horizontally and vertically shifting the curves. The resulting master curves indicated that, as the diamine length—namely, the distance between cross-linking points—decreased, deformation became slower and more suppressed. The temperature dependence of aT was well described by the WLF equation, consistent with our previous results obtained by DMA. For creep rupture behavior under relatively large σ, trp–σ plots obtained at various temperatures could also be superimposed through horizontal shifting. However, as the diamine length decreased, the temperature dependence of aTrp deviated from the WLF equation, resulting in Arrhenius-type behavior. This deviation was likely linked to differences in the fracture process, depending on the diamine length, particularly at higher temperatures, as suggested by variations in the master curves of the εrp–σ plots. Solvent swelling tests further revealed that cross-linking density decreased due to chain scission, which became more marked as the diamine length decreased. These findings highlight the impact of cross-linking density on the fracture mechanism and provide valuable insights for the improved design and development of thermosetting polymer materials. In particular, the insights gained from this study is useful for predicting the long-term durability for structural adhesives and composites, which are subjected to a constant stress during their usage leading to the failure via the creep deformation.Author contributions
A. S. conducted the data analysis and drafted the original manuscript. M. A. performed the experiments and contributed to the data analysis. S. Y. provided insights into the deformation mechanism, and K. T. supervised the entire study, reviewed and edited the manuscript, and oversaw its finalization.Data availability
The data that support the findings of this study are available from the corresponding author upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for support from the JST-Mirai Program (JPMJMI18A2) (K. T.) and the JSPS KAKENHI for Scientific Research (B) (no. JP20H02790) (K. T.) and (no. JP22H01795) (A.S.).References
- T. Vidil, F. Tournilhac, S. Musso, A. Robisson and L. Leibler, Control of reactions and network structures of epoxy thermosets, Prog. Polym. Sci., 2016, 62, 126–179 CAS.
- A. Shundo, S. Yamamoto and K. Tanaka, Network formation and physical properties of epoxy resins for future practical applications, JACS Au, 2022, 2, 1522–1542 CAS.
- A. T. Sunny, P. Vijayan, R. Adhikari, S. Mathew and S. Thomas, Copper oxide nanoparticles in an epoxy network: Microstructure, chain confinement and mechanical behaviour, Phys. Chem. Chem. Phys., 2016, 18, 19655–19667 CAS.
- K. Chen, X. Kuang, V. Li, G. Kang and H. J. Qi, Fabrication of tough epoxy with shape memory effects by UV-assisted direct-ink write printing, Soft Matter, 2018, 14, 1879–1886 CAS.
- S. Yamamoto and K. Tanaka, Entropy-driven segregation in epoxy-amine systems at a copper interface, Soft Matter, 2021, 17, 1359–1367 CAS.
- Y. Sumiya, Y. Tsuji and K. Yoshizawa, Shear adhesive strength between epoxy resin and copper surfaces: A density functional theory study, Phys. Chem. Chem. Phys., 2022, 24, 27289–27301 CAS.
- Y. Liu, N. Miyata, T. Miyazaki, A. Shundo, D. Kawaguchi, K. Tanaka and H. Aoki, Neutron reflectometry analysis of condensed water layer formation at a solid interface of epoxy resins under high humidity, Langmuir, 2023, 39, 10154–10162 CAS.
- Y. Jin, Z. Wang, C. Hu, J. Wang, K. Yan, J. He, Z. Wang, Z. Wang and L. Yuan, Chemically debondable, high-strength and tough adhesives from sulfur-modified epoxy networks, Green Chem., 2023, 25, 1157–1168 CAS.
- T. Hoshino, Y. Okamoto, A. Yamamoto and H. Masunaga, Dynamic behaviours of epoxy resin thin films during the curing process, Soft Matter, 2023, 19, 3267–3272 CAS.
- R. A. H. Bayomi, C.-W. Chu, K. Obayashi, Y. Ando, C.-H. Cheng, A. Takahara and K. Kojio, Influences of amine/epoxide ratio on cross-linking structure and mechanical properties of cured hydrogenated epoxy resin sheets and single-lap joints, Polymer, 2024, 298, 126882 CAS.
- H. Wei, J. Xia, W. Zhou, L. Zhou, G. Hussain, Q. Li and K. Ostrikov, Adhesion and cohesion of epoxy-based industrial composite coatings, Composites, Part B, 2020, 193, 108035 CrossRef CAS.
- X. Shi, T. A. Nguyen, Z. Suo, Y. Liu and R. Avci, Effect of nanoparticles on the anticorrosion and mechanical properties of epoxy coating, Surf. Coat. Technol., 2009, 204, 237–245 CrossRef CAS.
- C. Chen, Y. He, G. Xiao, F. Zhong, H. Li, Y. Wu and J. Chen, Synergistic effect of graphene oxide@phosphateintercalated hydrotalcite for improved anti-corrosion and self-healable protection of waterborne epoxy coating in salt environments, J. Mater. Chem. C, 2019, 7, 2318–2326 RSC.
- S. Verma, S. Mohanty and S. K. Nayak, Preparation of hydrophobic epoxy-polydimethylsiloxane-graphene oxide nanocomposite coatings for antifouling application, Soft Matter, 2020, 16, 1211–1226 RSC.
- K. B. Riad, M. R. Kholghy and P. M. Wood-Adams, Photo-polymerization using quantum dots for stable epoxy coatings, Ind. Chem. Mater., 2024, 2, 644–650 RSC.
- N. Domun, H. Hadavinia, T. Zhang, T. Sainsbury, G. H. Liaghat and S. Vahid, Improving the fracture toughness and the strength of epoxy using nanomaterials - A review of the current status, Nanoscale, 2015, 7, 10294–10329 RSC.
- V. Mittal, R. Saini and S. Sinha, Natural Fiber-mediated epoxy composites - A review, Composites, Part B, 2016, 99, 425–435 CrossRef CAS.
- T. Kusunose, T. Yagi, S. H. Firoz and T. Sekino, Fabrication of epoxy/silicon nitride nanowire composites and evaluation of their thermal conductivity, J. Mater. Chem. A, 2013, 1, 3440 RSC.
- L.-Z. Guan, Y.-J. Wan, L.-X. Gong, D. Yan, L.-C. Tang, L.-B. Wu, J.-X. Jiang and G.-Q. Lai, Toward effective and tunable interphases in graphene oxide/epoxy composites by grafting different chain lengths of polyetheramine onto graphene oxide, J. Mater. Chem. A, 2014, 2, 15058 RSC.
- E. Chabert, J. Vial, J.-P. Cauchois, M. Mihaluta and F. Tournilhac, Multiple welding of long fiber epoxy vitrimer composites, Soft Matter, 2016, 12, 4838–4845 RSC.
- H. Hou, W. Dai, Q. Yan, L. Lv, F. E. Alam, M. Yang, Y. Yao, X. Zeng, J.-B. Xu, J. Yu, N. Jiang and C.-T. Lin, Graphene size-dependent modulation of graphene frameworks contributing to the superior thermal conductivity of epoxy composites, J. Mater. Chem. A, 2018, 6, 12091–12097 RSC.
- M. Kuroyanagi, A. Yamaguchi, T. Hashimoto, M. Urushisaki, T. Sakaguchi and K. Kawabe, Novel degradable acetal-linkage-containing epoxy resins with high thermal stability: Synthesis and application in carbon fiber-reinforced plastics, Polym. J., 2022, 54, 313–322 CrossRef CAS.
- P. Wang, R. Maeda, M. Aoki, T. Kubozono, D. Yoshihara, A. Shundo, T. Kobayashi, S. Yamamoto, K. Tanaka and S. Yamada, In situ transmission electron microscopy observation of the deformation and fracture processes of an epoxy/silica nanocomposite, Soft Matter, 2022, 18, 1149–1153 RSC.
- H. K. Nguyen, A. Shundo, X. Liang, S. Yamamoto, K. Tanaka and K. Nakajima, Unraveling nanoscale elastic and adhesive properties at the nanoparticle/epoxy interface using bimodal atomic force microscopy, ACS Appl. Mater. Interfaces, 2022, 14, 42713–42722 CrossRef CAS PubMed.
- G. M. Odegard and A. Bandyopadhyay, Physical aging of epoxy polymers and their composites, J. Polym. Sci., Part B:Polym. Phys., 2011, 49, 1695–1716 CrossRef CAS.
- V. Bellenger, J. Verdu and E. Morel, Effect of structure on glass transition temperature of amine crosslinked epoxies, J. Polym. Sci., Part B:Polym. Phys., 1987, 25, 1219–1234 CrossRef CAS.
- J. K. Lee and J. Y. Hwang, Erasure behavior of isothermal physical aging effect below glass transition temperature in a fully cured epoxy resin. differential scanning calorimetry measurement, Polym. J., 2003, 35, 191–196 CrossRef CAS.
- C. Higuchi, D. Horvath, G. Marcou, K. Yoshizawa and A. Varnek, Prediction of the glass-transition temperatures of linear homo/heteropolymers and cross-linked epoxy resins, ACS Appl. Polym. Mater., 2019, 1, 1430–1442 CrossRef CAS.
- A. Hanafusa, S. Ando, S. Ozawa, M. Ito, R. Hasegawa, K. Mayumi and K. Ito, Viscoelastic relaxation attributed to the molecular dynamics of polyrotaxane confined in an epoxy resin network, Polym. J., 2020, 52, 1211–1221 CrossRef CAS.
- A. Tokunaga, A. Shundo, R. Kuwahara, S. Yamamoto and K. Tanaka, Effect of number density of epoxy functional groups on reaction kinetics for epoxy resin, Macromolecules, 2024, 57, 10530–10538 CrossRef CAS.
- J. D. Ferry, Viscoelastic Properties of Polymers, John Wiley and Sons, Inc., New York, 1961 Search PubMed.
- J. M. Hutchinson, Physical aging of polymers, Prog. Polym. Sci., 1995, 20, 703–760 CrossRef CAS.
- M. A. Wilding and I. M. Ward, Tensile creep and recovery in ultrahigh modulus linear polyethylenes, Polymer, 1978, 19, 969–976 CrossRef CAS.
- P. A. O’Connell, S. A. Hutcheson and G. B. McKenna, Creep behavior of ultra-thin polymer films, J. Polym. Sci., Part B:Polym. Phys., 2008, 46, 1952–1965 Search PubMed.
- Y. Jia, K. Peng, X. Gong and Z. Zhang, Creep and recovery of polypropylene/carbon nanotube composites, Int. J. Plast., 2011, 27, 1239–1251 CAS.
- G. M. Odegard and A. Bandyopadhyay, Physical aging of epoxy polymers and their composites, J. Polym. Sci., Part B:Polym. Phys., 2011, 49, 1695–1716 CrossRef CAS.
- H. Otani, S. L. Phoenix and P. Petrina, Matrix effects on lifetime statistics for carbon fiber-epoxy microcomposites in creep rupture, J. Mater. Sci., 1991, 26, 1955–1970 CrossRef CAS.
- A. Zandiatashbar, C. R. Picu and N. Koratkar, Control of epoxy creep using graphene, Small, 2012, 8, 1676–1682 CrossRef CAS.
- Y. Li, R. Umer, A. Isakovic, Y. A. Samad, L. Zheng and K. Liao, Synergistic toughening of epoxy with carbon nanotubes and graphene oxide for improved long-term performance, RSC Adv., 2013, 3, 8849–8856 RSC.
- N. Mattar, F. Hübner, M. Demleitner, A. Brückner, V. Langlois, E. Renard, H. Ruckdäschel and A. Rios De Anda, Multiscale characterization of creep and fatigue crack propagation resistance of fully bio-based epoxy-amine resins, ACS Appl. Polym. Mater., 2021, 3, 5134–5144 CrossRef CAS.
- W. N. Findley and R. M. Reed, Effect of cross-linking on hydrostatic creep of epoxy, Polym. Eng. Sci., 1977, 17, 837–841 CrossRef CAS.
- R. J. Crowson and R. G. C. Arridge, Linear viscoelastic properties of epoxy-resin polymers in dilatation and shear in the glass-transition region. 1. Time-temperature superposition of creep data, Polymer, 1979, 20, 737–746 CrossRef CAS.
- S. Vleeshouwers, A. M. Jamieson and R. Simha, Effect of physical aging on tensile-stress relaxation and tensile creep of cured EPON-828 epoxy adhesives in the linear viscoelastic region, Polym. Eng. Sci., 1989, 29, 662–670 CrossRef CAS.
- I. Choy and D. J. Plazek, The physical-properties of bisphenol-A-based epoxy-resins during and after curing, J. Polym. Sci., Part B:Polym. Phys., 1986, 24, 1303–1320 CrossRef CAS.
- D. J. Plazek and I. C. Choy, The physical properties of bisphenol-A-based epoxy resins during and after curing. II. Creep behavior above and below the glass transition temperature, J. Polym. Sci., Part B:Polym. Phys., 1989, 27, 307–324 CrossRef CAS.
- D. J. Plazek and I. Chay, The evolution of the viscoelastic retardation spectrum during the development of an epoxy resin network, J. Polym. Sci., Part B:Polym. Phys., 1991, 29, 17–29 CrossRef CAS.
- C. A. Bero and D. J. Plazek, Volume-dependent rate processes in an epoxy resin, J. Polym. Sci., Part B:Polym. Phys., 1991, 29, 39–47 CrossRef CAS.
- C. M. Roland, K. L. Ngai and D. J. Plazek, The viscoelastic behaviour of networks, Comput. Theor. Polym. Sci., 1997, 7, 133–137 CrossRef CAS.
- M. Demleitner, F. Hübner, A. Mainz, H. Ruckdäschel, V. Altstädt, L. Michely and A. Rios De Anda, Influence of network structure determined by time-domain 1H double quantum NMR on the creep properties of non-stoichiometric epoxy-amine resins aimed for chemical anchoring applications, Polymer, 2023, 286, 126373 CrossRef CAS.
- G. Daissè, B. E. Abali and R. Wan-Wendner, Tensile and shear creep behavior of structural adhesives: Experiments and modeling, Appl. Compos. Mater., 2024, 31, 739–764 CrossRef PubMed.
- C. L. Schutte, Environmental durability of glass-fiber composites, Mater. Sci. Eng. R: Rep., 1994, 13, 265–323 CrossRef.
- N. Guermazi, A. Ben Tarjem, I. Ksouri and H. F. Ayedi, On the durability of FRP composites for aircraft structures in hygrothermal conditioning, Composites, Part B, 2016, 85, 294–304 CrossRef CAS.
- Y. Ge, X. Zhang, Y. Shi, Y. Cai, S. Zhou, M. Liang and H. Zou, A multifunctional epoxy structural adhesive with superior flexibility, damping and durability, Mater. Chem. Front., 2021, 5, 8387–8396 RSC.
- F. Schwarzl and A. J. Staverman, Time-temperature dependence of linear viscoelastic behavior, J. Appl. Phys., 1952, 23, 838–843 CrossRef CAS.
- A. V. Tobolsky, Stress relaxation studies of the viscoelastic properties of polymers, J. Appl. Phys., 1956, 27, 673–685 CrossRef CAS.
- Y. Huang and A. J. Kinloch, The use of time−temperature superpositioning in studying the fracture properties of rubber-toughened epoxy polymers, J. Adhes., 1993, 41, 5–22 CrossRef CAS.
- N. B. Olsen, T. Christensen and J. C. Dyre, Time-temperature superposition in viscous liquids, Phys. Rev. Lett., 2001, 86, 1271–1274 CrossRef CAS PubMed.
- R. Gupta, B. Baldewa and Y. M. Joshi, Time temperature superposition in soft glassy materials, Soft Matter, 2012, 8, 4171 RSC.
- J. Dealy and P. Donald, Time-temperature superposition-A users guide, Rheol. Bull., 2009, 78, 16–31 Search PubMed.
- C.-W. Feng, C.-W. Keong, Y.-P. Hsueh, Y.-Y. Wang and H.-J. Sue, Modeling of long-term creep behavior of structural epoxy adhesives, Int. J. Adhes. Adhes., 2005, 25, 427–436 CrossRef CAS.
- M. Pohl, R. Kupfer, I. Koch, N. Modler and W. A. Hufenbach, Determination of the long-term properties in laminate-thickness direction of textile-reinforced thermoplastic composites under compression using time−temperature superposition, Adv. Eng. Mater., 2016, 18, 369–375 CrossRef CAS.
- H. Li, Y. S. Luo and D. L. Hu, Long term creep assessment of room-temperature cured epoxy adhesive by time-stress superposition and fractional rheological mode, Appl. Rheol., 2018, 28, 64796 Search PubMed.
- A. Anand, P. Banerjee, R. K. Prusty and B. C. Ray, Lifetime prediction of nano-silica based glass fibre/epoxy composite by time temperature superposition principle, IOP Conf. Ser.: Mater. Sci. Eng., 2018, 338, 012020 Search PubMed.
- S. K. Ghosh, P. Rajesh, B. Srikavya, D. K. Rathore, R. K. Prusty and B. C. Ray, Creep behaviour prediction of multi-layer graphene embedded glass fiber/epoxy composites using time-temperature superposition principle, Composites, Part A, 2018, 107, 507–518 CrossRef CAS.
- A. Shundo, M. Aoki, S. Yamamoto and K. Tanaka, Effect of cross-linking density on horizontal and vertical shift factors in linear viscoelastic functions of epoxy resins, Macromolecules, 2021, 54, 9618–9624 CrossRef CAS.
- A. Shundo, M. Aoki, S. Yamamoto and K. Tanaka, Cross-linking effect on segmental dynamics of well-defined epoxy resins, Macromolecules, 2021, 54, 5950–5956 CrossRef CAS.
- Z. He, W. Lv, G. Gao and Q. Yin, Investigation of the chemical changes and mechanism of the epoxy-amine system by in situ infrared spectroscopy and two-dimensional correlation analysis, Polym. J., 2022, 54, 1445–1452 CrossRef CAS.
- Y. Yokoyama, T. Yasui, A. Takeda, K. Ogino and S. Kanehashi, Novel bio-based flexible bisphenol epoxy resin derived from cashew nut shell liquid, Polym. J., 2023, 55, 859–867 CrossRef CAS.
- A. Shundo, N. Thao Phan, M. Aoki, A. Tokunaga, R. Kuwahara, S. Yamamoto and K. Tanaka, Exploring the impact of molecular structure on curing kinetics: A comparative study of diglycidyl ether of bisphenol a and f epoxy resins, J. Phys. Chem. B, 2024, 128, 4846–4852 CrossRef CAS PubMed.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, New York, 1953 Search PubMed.
- L. W. Hill, Calculation of crosslink density in short chain networks, Prog. Org. Coat., 1997, 31, 235–243 CrossRef CAS.
- C.-S. Wu, Influence of post-curing and temperature effects on bulk density, glass transition and stress-strain behaviour of imidazole-cured epoxy network, J. Mater. Sci., 1992, 27, 2952–2959 CrossRef CAS.
- K. S. Khare and F. R. Phelan, Integration of atomistic simulation with experiment using time−temperature superposition for a cross-linked epoxy network, Macromol. Theory Simul., 2020, 29, 1900032 CrossRef CAS.
- H. Vogel, The law of the relation between the viscosity of liquids and the temperature, Phys. Z., 1921, 22, 645–646 CAS.
- G. S. Fulcher, Analysis of recent measurements of the viscosity of glasses, J. Am. Ceram. Soc., 1925, 8, 339–355 CrossRef CAS.
- G. Tammann and W. Z. Hesse, The Dependancy of viscosity on temperature in hypothermic liquids, Z. Anorg. Allg. Chem., 1926, 156, 245–257 CrossRef CAS.
- T. L. Smith, Ultimate tensile properties of elastomers II. Comparison of failure envelopes for unfilled vulcanizates, J. Appl. Phys., 1964, 35, 27–36 CrossRef.
- T. L. Smith and J. E. Frederick, Ultimate tensile properties of elastomers. IV. Dependence of the failure envelope, maximum extensibility, and equilibrium stress-strain curve on network characteristics, J. Appl. Phys., 1965, 36, 2996–3005 CrossRef CAS.
- T. L. Smith, Deformation and failure of plastics and elastomers, Polym. Eng. Sci., 1965, 5, 270–279 CrossRef.
- T. L. Smith and W. H. Chu, Ultimate tensile properties of elastomers VII. Effect of crosslink density on time-temperature dependence, J. Polym. Sci., Part A:Polym. Phys., 1972, 10, 133–150 CrossRef CAS.
- F. Zhou, S. Hou, X. Qian, Z. Chen, C. Zheng and F. Xu, Creep behavior and lifetime prediction of PMMA immersed in liquid scintillator, Polym. Test., 2016, 53, 323–328 CrossRef CAS.
- T. L. Smith, Ultimate tensile properties of elastomers I. Characterization by a time and temperature independent failure envelope, J. Polym. Sci., Part A: Gen. Pap., 1963, 1, 3597–3615 CrossRef.
- T. L. Smith, Relations between ultimate tensile properties of elastomers and their structure, Proc. R. Soc. London, Ser. A, 1964, 282, 102–113 Search PubMed.
- K. Nitta and T. Ishiburo, Ultimate tensile behavior of linear polyethylene solids, J. Polym. Sci., Part B:Polym. Phys., 2002, 40, 2018–2026 CrossRef CAS.
- J. P. Bell, Mechanical properties of a glassy epoxide polymer: Effect of molecular weight between crosslinks, J. Appl. Polym. Sci., 1970, 14, 1901–1906 CrossRef CAS.
- H.-J. Sue, Craze-like damage in a core-shell rubber-modified epoxy system, J. Mater. Sci., 1992, 27, 3098–3107 CrossRef CAS.
- K. Cho, D. Lee, C. E. Park and W. Huh, Effect of molecular weight between crosslinks on fracture behaviour of diallylterephthalate resins, Polymer, 1996, 37, 813–817 CrossRef CAS.
- A. Shundo, M. Aoki, P. Wang, T. Hoshino, S. Yamamoto, S. Yamada and K. Tanaka, Effect of a heterogeneous network on the fracture behavior of epoxy resins, Macromolecules, 2023, 56, 3884–3890 CrossRef CAS.
- B. Crist, J. Oddershede, J. R. Sabin, J. W. Perram and M. A. Ratner, Polymer fracture - A simple-model for chain scission, J. Polym. Sci., Polym. Phys. Ed., 1984, 22, 881–897 CrossRef CAS.
- D. Wang, A. A. K. Klaassen, G. E. Janssen, E. De Boer and R. J. Meier, The detection of radicals in strained, high-modulus polyethylene fibers, Polymer, 1995, 36, 4193–4196 CrossRef CAS.
- J. C. L. Hageman, G. A. De Wijs, R. A. De Groot and R. J. Meier, Bond scission in a perfect polyethylene chain and the consequences for the ultimate strength, Macromolecules, 2000, 33, 9098–9108 CrossRef CAS.
- R. Puthur and K. L. Sebastian, Theory of polymer breaking under tension, Phys. Rev. B:Condens. Matter Mater. Phys., 2002, 66, 024304 CrossRef.
- Y. Mao, B. Talamini and L. Anand, Rupture of polymers by chain scission, Extreme Mech. Lett., 2017, 13, 17–24 CrossRef.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, New York, 2003 Search PubMed.
- W. Xue, S. Champ and M. B. Huglin, Network and swelling parameters of chemically crosslinked thermoreversible hydrogels, Polymer, 2001, 42, 3665–3669 CrossRef CAS.
- M. Aoki, A. Shundo, S. Yamamoto and K. Tanaka, Effect of a heterogeneous network on glass transition dynamics and solvent crack behavior of epoxy resins, Soft Matter, 2020, 16, 7470–7478 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: experimental detail and characterization data on stress–strain curves from tensile testing at various temperatures, time-domain curves of creep compliance, rupture time plotted against imposed stress. See DOI: https://doi.org/10.1039/d4sm01540a |
| This journal is © The Royal Society of Chemistry 2025 |