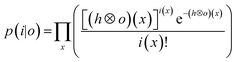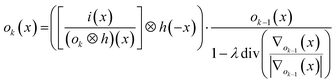Development of a fast laser ablation-inductively coupled plasma-mass spectrometry cell for sub-μm scanning of layered materials

Abstract

Performance data are reported for a commercially available laser ablation-inductively coupled plasma-mass spectrometry (LA-ICP-MS) setup, equipped with a custom-made cell. The low dispersion ablation cell and the connecting tubing achieve a 99% washout of the aerosol in ∼6 ms, enabling separated pulse responses at frequencies up to 200–300 Hz. In addition, the cell employed supports a post-acquisition methodology for the deconvolution of overlapping ablation positions in scanning mode by an iterative Richardson–Lucy algorithm. This enables correction of the distortion in the scan profile upon traversing layers with dimensions below the physical size of the laser beam. By overlapping the ablation positions of a 1 μm diameter laser beam, a lateral resolution in the order of 0.3 ± 0.1 μm was demonstrated for scanning of μm-sized layers in high capacitance multi-layer ceramic capacitors.

---

Introduction

Laser ablation (LA) as a means of sample introduction permits the direct analysis of solid materials using inductively coupled plasma-mass spectrometry (ICP-MS) and was introduced by Gray¹ in 1985. LA-ICP-MS offers spatially resolved information for large sample areas at a lateral resolution in the order of a few micrometers and high detection power, whilst retaining a quantitative character in a wide linear range. The ability to visualize the distribution of major, minor and trace nuclides has led to numerous applications in a wide variety of fields (geology, mineralogy, archaeology, forensics, materials research, environmental studies, biochemistry, and biology).^2–8 We aim to extend this application field by enhancing the lateral resolution capabilities beyond those of current state-of-the-art LA-ICP-MS and by accelerating sample throughput substantially. Particle dispersion generated within the cell and the transfer tubing of most configurations of the hyphenated LA-ICP-MS setup results in an inevitable overlap of the pulse responses generated by sequential laser pulses when these setups are operated at laser repetition rates above 1–2 Hz, as washout times are typically in the range of 1–2 seconds. The extent of the negative effects thus exerted on the spatial resolution of the elemental map generated is governed by this washout time, as well as by other experimental parameters, such as the ICP-MS dwell and settling time, the diameter of the laser beam and the speed at which this beam traverses the sample surface. For example, the effective lateral resolution when scanning a surface at 20 μm s⁻¹ with a laser beam of 5 μm in diameter, firing at 20 Hz, could amount to 20–40 μm. This shortcoming can be compensated for by operating at low sampling rates, effectively separating the pulse responses within one or more sequences of pulses,⁹ or by operating at high sampling rates and low scanning speeds, thereby mixing the dispersion of multiple overlapping signal peaks over a short scanning range.¹⁰ Both options lead to a decreased sample throughput and thus, increased costs. Efforts within the laser ablation community have been directed to the development of ablation cell types^11–16 permitting the impact of dispersion processes to be reduced, as these affect both sensitivity and spatial resolution in a detrimental way. These efforts have resulted in a number of ablation cell geometries capable of achieving washout times of approximately 100 ms (full peak width at 1% maximum). A recent design of a low-dispersion cell by Wang et al.¹² was reported to offer a washout time of ∼30 ms. To achieve such a short washout time, a specially designed low-volume cell was located not more than ca. ∼500 mm away from the ICP. Owing to the improved sensitivity, this cell permits imaging at the μm-level. Nevertheless, numerous analytical applications would still benefit from higher lateral resolutions, as nuclide distributions at the nm-level within μm-sized features could reveal essential information on trace element patterns in geological samples,^17,18 biomarker distributions on subcellular levels¹⁰ and surface layer phenomena in solid samples.^9,10 Strategies for sub-μm focusing of the laser beam such as near-field (NF) laser ablation^19,20 or the use of high-numerical aperture objectives²¹ have been proposed, however, up to this point, to the best of the authors' knowledge, none of them have been demonstrated to be a viable option for sub-μm scanning using LA-ICP-MS. Plotnikov et al.²² presented a strategy for the deconvolution of continuous scan data composed of overlapping signal peaks based on the regularization of a system of linear equations, and on Fredholm integral equations of the first kind. This approach enhanced edge resolution whilst scanning in a single direction considerably, however, did not demonstrate lateral resolution below the beam width. This work reports on the performance of a custom-made low-dispersion cell, integrated into currently available commercial instrumentation, and demonstrates its potential for high spatial resolution scanning by LA-ICP-MS. The analysis of multi-layer ceramic capacitors serves as a proof-of-principle for a post-acquisition deconvolution procedure aimed at achieving a substantial boost in lateral resolution. The deconvolution procedure includes a method to derive the line spread function (LSF) from a crater damage model based on known properties of the laser beam intensity profile.

Theoretical section

The scanning and numerical deconvolution methodologies are aimed at spatially resolving the elemental response within every overlapping zone between overlapping ablation positions. The target zone is oversampled by scanning the sample – i.e. 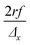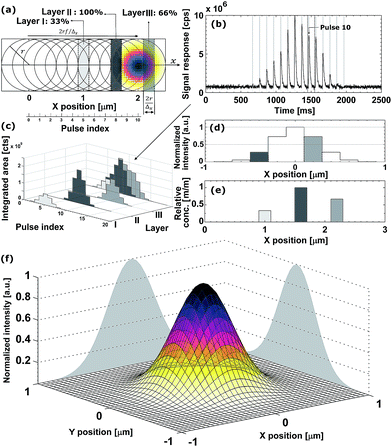by lateral translation of the sample stage – at a scanning speed dx equal to with f the pulse repetition rate of the laser, r the radius of the laser spot, and Δ_x the desired number of pulses overlapping in the x⃑ direction. Hence, ablation positions are projected at an interspacing of 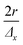, producing artificially convolved data, analogous to the approach of Plotnikov et al.²² in this aspect. A simulation of a 1 μm laser beam spot traversing three closely-spaced layers with Δ_x = 5 and the corresponding detector signal response are shown in Fig. 1a and b, respectively. In Fig. 1c, it can be seen how each individual layer contributes cumulatively to the total integrated signal peak area at each ablation position. This superimposed response is deconvolved to obtain the spatiotemporal response at a virtual lateral resolution of 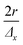. The isotropic kernel for deconvolution, the theoretical LSF (Fig. 1d), was derived from the ablation damage inflicted, modeled as an inverted two-dimensional Gaussian distribution of the space-invariant intensity profile (Fig. 1f) of the beam from a laser operated in the fundamental transverse mode. When considering a beam of 1 μm diameter (as determined by the two points at 1/e² of the maximum intensity), a two-dimensional Gaussian model reflects crater damage more accurately than a binary cylinder would. Despite the presence of beam homogenizer optics, round, flat-top beam profiles cannot be obtained due to the fundamental limitations of a UV laser beam at these beam dimensions, as diffraction effects will distort the uniformity of the beam profile.²³ A Gaussian beam profile is the default net system spread function of the lateral energy distribution as it is the result of multiple convolutions of all component spread functions. The theoretical LSF of the system is extracted from the convolution of the two-dimensional Gaussian model with a binary line, perpendicular to the direction of travel, x⃑. In essence, the model is downsampled virtually in the direction of travel to the dimensions and step size associated with the setup, whilst being projected onto the yz plane. Conventional non-iterative deconvolution approaches, e.g., Fourier deconvolution in combination with Wiener filtering, are not well suited to handle the deconvolution in LA-ICP-MS due to the formation of artifacts in the spatial frequency domain as a result of typical S/N levels. Deconvolution approaches in confocal imaging via 3D fluorescence microscopy include Tikhonov–Miller inverse filtering,²⁴ Wavelet denoising,²⁵ Carrington²⁶ and Richardson-Lucy^27,28 (RL) with Total Variation (TV) regularization.^29,30 In this work, the RLTV algorithm was preferred to process the data, as it computes a maximum likelihood estimation robust to Poisson noise, which dominates the noise statistics in ICP-MS at low count rates,³¹ whilst counteracting noise amplification by regularization constraints based on TV.^30,32 The regularizing constraint performs smoothening of oscillations while preserving feature edges, and provides stable convergence onto a solution. The RL algorithm is based on a general image formation model from the LSF and the spread of the detector noise:

i = [scr p, script letter p] (o ⊗ h)

where i is the observed image, o the distribution of the nuclide, h the LSF and [scr p, script letter p] the Poisson noise. The multiplicative gradient-based RL algorithm with TV regularization constraints minimizes 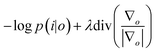, with λ the regularization parameter and p(i|o) the maximum likelihood probability, which can be written as:

Fig. 1 (a) Schematic of a line scan over three layers (indicated by different shades of gray), containing the nuclide of interest in different concentrations. (b) Simulation of the signal response for the experiment in (a). (c) Integrated peak areas of the response, as well as the individual contribution of each layer to the cumulative signal. (d) LSF after virtual downsampling with Δ_x = 5. The layer locations relative to the ablation position of pulse 10 are indicated by their grayscale. (e) Result of the deconvolution of the integrated peak areas based on the LSF. (f) Simulated two-dimensional normalized Gaussian beam intensity distribution profile.

The estimate o_k(x) at iteration k is given by:³⁰

The DeconvolutionLab software package by Vonesch and Unser³³ implements the RLTV algorithm and was used for our purposes for the deconvolution of the integrated areas associated with overlapping ablation positions within the Java-based ImageJ image processing software. The algorithm retrieves the original concentration distribution within the set of layers (Fig. 1e). A positive constraint on the values at each iteration was enabled to further stabilize the RLTV algorithm. The strategy proposed is not limited to the minimum beam waist size of a diffraction-limited, highly collimated, TEM₀₀ (transverse electro-magnetic) mode (X) UV laser beam, as it is not based on focusing the beam to dimensions beyond the physical diffraction barrier, but on the statistical likelihood of the presence of a nuclide within the targeted zone and its detection. At a certain level, the statistics of this strategy will break down; however, this level can be further decreased by improving the sensitivity of ICP-MS instrumentation and optimizing the design of the introduction system assembly. It could be argued that decreasing the beam waist size would be a superior option for achieving higher lateral resolutions, as no deconvolution would be required, and scanning time would remain identical. The methodological strategy proposed should, however, still operate when more advanced focusing techniques are deployed in the field, and beam radii decrease. The beam radius achievable for an ideal Gaussian beam is determined by the constant beam parameter product, the product of the divergence half-angle θ and the radius of the beam waist w₀, equal to λ/π. The minimum theoretical spot size diameter achievable for the ablation cell employed, together with a 193 nm ArF* laser, using refractive lenses, is ca. 265 nm (as determined by the two points at 1/e² of the maximum intensity, and based on the paraxial approximation). Since excimer lasers are characterized by poor spatial and temporal coherence, and the beam quality degrades at higher divergence angles, this theoretical beam waist w₀ and the dimensions of the PSF model are underestimated.²³ Apart from fundamental focusing limits in the far field, the minimum spot size is typically restricted by the sensitivity of the setup for the nuclides targeted. The main advantage of the methodology proposed is that the sampling takes place at a relatively large spot size, thus, a higher S/N ratio can be upheld than when sampling directly at the level of the desired lateral resolution. Rectangular slits can be used in this procedure to increase S/N ratios even further. The deconvolution protocol operates at its highest spatial resolution when employed in a setup equipped with a low-dispersion ablation chamber.

Experimental section

Ablation cell

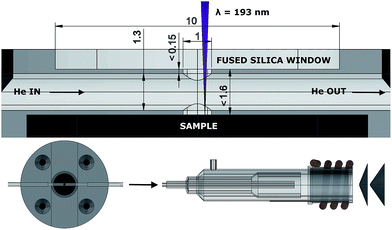
A half-open cell in contact with the surface was machined out of a 40 mm Ø PMMA (poly(methyl methacrylate)) cylinder (Fig. 2). The incident laser beam enters through a 1 mm Ø aperture, which is sealed with a fused silica glass window.

Fig. 2 Technical drawing of the ablation cell and the torch. All dimensions are provided in mm.

The aerosol formed upon ablation enters the central chamber through a cylindrical 1 mm Ø aperture, perpendicular to the central chamber, a 1.3 mm Ø cylinder, in which the aerosol expands, and is transported by a high-velocity, compressed stream of He through the PTFE (polytetrafluoroethylene) tubing (1.3 mm inner Ø, 372 mm in length), incorporated into the cell and the injector of the torch. The pressure of the background gas and the reflected plasma shockwave spatially confine the expanding plume.^34,35 Particles, non-condensed clusters and micro-droplets ejected and accelerated³⁶ tangentially relative to the momentum of the He flow are likely to be trapped in this flow as momentum is transferred. The occurrence of plasma breakdown will alter the velocity vector along which particles are ejected. The expanding aerosol only fills part of the central chamber, it is therefore challenging to define a finite volume in which the aerosol expands. When regarding the ablation as a uniform hemispherical point source explosion, a model which is far too simple to accurately describe the dynamics of the ablation-induced expansion front, the aerosol can expand initially into a ∼1.5 μl volume.

Experimental parameters for performance evaluation

The cell was mounted inside a purpose-built bracket fixed onto the translation stage of an Analyte G2 (Photon Machines Inc., Bozeman, Montana, USA) 193 nm ArF* excimer laser system (pulse duration <5 ns, ∼1% energy stability, 5.45 J cm⁻² energy density) coupled to an Agilent 7900 quadrupole-based ICP-MS instrument (Agilent Technologies Inc., Tokyo, Japan), and evaluated by drilling NIST SRM 610 in sequences of 50 pulses under optimized conditions. The ICP-MS unit was operated at an RF power of 1500 W, the flow rates tuned to 15 l min⁻¹ for the Ar plasma gas, 0.2 l min⁻¹ for the Ar auxiliary gas, and 1.65 l min⁻¹ for the He carrier gas. The objective of tuning the gas flow rates was to achieve a balance between drag and slipping effects on all particle sizes simultaneously, whilst keeping turbulence, radial and longitudinal diffusion, and plasma cooling at a reasonable level. The read time in the performance evaluation was set to 200 μs. The dual mode discrete dynode detector employed is capable of recording the signal modulation of a single mass-to-charge (m/z) ratio down to 100 μs intervals. Studies focusing on multiple nuclides can acquire the temporal resolution required by full-spectrum time- or mass-division inverse multiplexing via pseudo-parallel detection by time-of-flight (TOF) ICP-MS and simultaneous ion detection instruments of Mattauch–Herzog (MH) geometry.

Multi-layer ceramic capacitor (MLCC)†

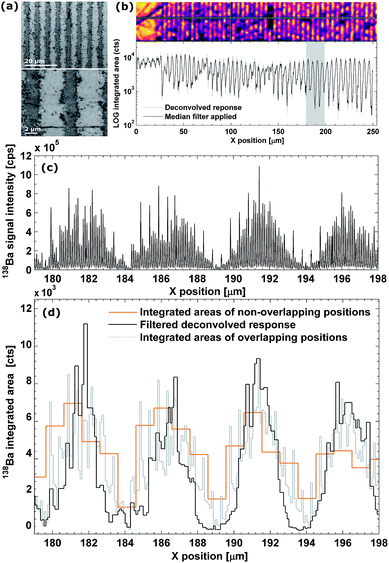
For proof-of-concept purposes, the LA-ICP-MS setup was used for mapping of a high capacitance MLCC (10 μF ± 10%, rated at 25 V), of X5R architecture (class II), 0805 case style, manufactured by AVX (Kyocera, Japan). This capacitor is characterized by a highly regular, layered architecture of alternating planar Ni electrodes and dielectric BaTiO₃ layers. The granular structure of the BaTiO₃ layer gives rise to a coarse transition between the electrodes and BaTiO₃ layers within the MLCC. A laser beam of 1 μm in diameter (the mask uses a circular aperture), set to a pulse repetition rate of 25 Hz, was scanned over 47 electrode end connections, traversing 250 μm perpendicular to the direction of the electrodes at 2.5 μm s⁻¹ (Δ_x = 10). The theoretical virtual lateral resolution that can be achieved, given the amount of overlap between ablation positions, is 100 nm. The response for ¹³⁸Ba was monitored at a read time of 500 μs. The setup was operated at a low scanning speed to eliminate potential inaccuracy associated with rapid acceleration and high speeds of the positioning stage.

Automated peak integration

The integration of individual pulse responses resulting in a discrete number of counts, as opposed to the use of continuous scan data, contributes to the spatial resolution obtained as it limits intermixing of the aerosol from a pulse with the aerosol generated by preceding pulses at different ablation positions. Thus, overlap of peak profiles is preferably avoided. Temporal displacements in peak positions are generated by small firing frequency shifts in the solid state pulse power module and flow fluctuations in the mass flow controllers. To correct for this gradual peak position drift, which becomes apparent at high frequencies, integration intervals were based on the peak maxima detected. In regions where no peaks were present, integration intervals were inter- and extrapolated via the base frequency of the laser. The integration intervals of major elements could be propagated to minor and trace elements. The data reduction process was automated in MATLAB® 8.1. The integrated areas were stored in a multi-dimensional array containing the response for each nuclide recorded and the spatial coordinates of the ablation location in a user-defined Cartesian coordinate system, associated with each peak.

Results and discussion

Cell performance evaluation

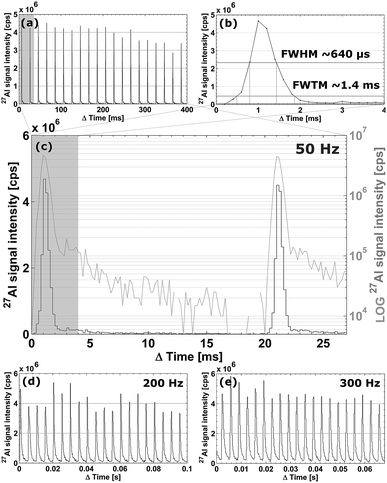
In a configuration of the setup whereby the cell is located ∼400 mm away from the plasma, the cell achieves aerosol washout for ²⁷Al (NIST SRM 612, 5 μm square spot, 50 Hz, 5.45 J cm⁻²) in <4.7 ± 0.4 ms (sequence of 20 pulses; full width at 1% of the maximum) under optimized conditions. More than 99% of the aerosol is removed in ∼6 ms. Secondary processes can be observed at the base of each peak (below 3% of the maximum), preventing the signal to drop exponentially. Inherent limitations may be imposed on the dispersion by these secondary processes as they may originate from differential transport of fractal aggregates of mesoscopic particles (<100 nm) and larger particles formed by coalescence and aggregation.^37–39 A potential supplemental source of dispersion is turbulence within the tubing and the plasma. For setups such as ours, in which the cell is mounted externally, the total contribution of radial (gas flow rotational motion) and co-axial mixing inside the transport tubing to the dispersion increases with tube length. The physical limits for the transfer-induced dispersion of any setup consisting of an external ablation cell a considerable distance away from the plasma can be put into perspective by comparing it to the aerosol washout time of 1–3 ms for in-torch ablation,^40–42 in which the sample is located in very close proximity to the ICP. As the cell performs similarly to in-torch ablation with respect to the dispersion generated, we advance towards the physical limits of LA-ICP-MS in its current mode of operation. In Fig. 3a, a sequence of 20 sequential pulses (NIST SRM 612, 5 μm square spot, drilling at 50 Hz, 5.45 J cm⁻²) is displayed (further zoomed in versions in Fig. 3b and c); the average peak area is (3.4 ± 0.6) × 10³ counts (1.7 ± 0.04% [m/m] Al, RSD on sequential pulses ∼5%); the average peak height is (4.0 ± 0.2) × 10⁶ counts per second (RSD on sequential pulses ∼10%). The signal peak in Fig. 3b drops down to the background level in ∼15 ms. The limits of detection based on the abundance-normalized peak height sensitivities for ¹¹⁵In, ¹⁴⁰Ce, ²³²Th and ²³⁸U, are ∼0.25 ppm. The necessity for these fast cells becomes clear when considering that if the aerosol is transported towards the ICP in a much shorter timeframe, the sensitivity as well as sample throughput times are substantially improved, allowing for smaller beam diameters and their accompanying higher spatial resolution. In Fig. 3d and e, the spatiotemporal signal profile at high pulse repetition rates is shown; it is evident that pulse responses remain separated at repetition rates up to 200–300 Hz. Computational fluid dynamics simulations were used to replicate the conditions within the cell and the connecting tubing.† The Reynolds number (R_e) remains just below the turbulent flow regime (R_e ∼ 1900 for 1.650 l min⁻¹ He). The average He residence time within the introduction system was 24.1 ± 0.4 ms. Preliminary experimental results of a cell and the tubing approximately 30% smaller in diameter indicate that further miniaturization offers slightly better washout characteristics.

Fig. 3 (a–c) Temporal signal intensity profiles for ²⁷Al when ablating NIST SRM 612 at 50 Hz (with various time axes). (d) Pulse repetition rate increased to 200 Hz. (e) Pulse repetition rate increased to 300 Hz.

Scanning and numerical deconvolution methodologies

The deconvolution procedure implies the assumption that homogeneity exists on a depth scale (optical slice thickness) of Δ_x times the ablation depth per pulse, which varies depending on the coupling efficiency and density of the material ablated, the wavelength of the laser, fluence, and the pulse duration, between a few 10 and a few 100 nm.^9,43–45

This assumption is often valid for layered structures, crystallographic domains as well as μm-sized volumes containing liquids. Failure to comply with this premise will result in a deterioration of spatial resolution. The spatial resolution may be compounded further by beam energy inhomogeneity variation, astigmatism, non-linear signal response, spatially variant fluid dynamic effects, temporal aberrations in the definition of the beam profile, non-flat sample topography, re-ablation of the deposited material, sample vibration and local thermal effects, such as melting at the target zone (zone heating), which provokes a rearrangement of particles within the crater walls, and topographical change. Melting effects at the crater walls and elemental fractionation are preferably reduced by operating at fluence levels just above the ablation threshold or by using a ps or fs laser system. The majority of concerns remaining can be addressed by polishing the sample surface and by upgrading to a higher quality laser and a high resolution stabilized positioning stage. Some samples, such as thin sections of biological samples obtained by (cryo-)microtoming may not even require deconvolution of the scan data if single pulses are capable of quantitatively removing the material from the targeted ablation zone and the concentrations of the nuclide of interest in the substrate are negligible relative to the concentrations in the sample.¹⁰ Sequential pulses remove the material from the new non-overlapping edge of the ablation position and the substrate material from the zone overlapping to the preceding pulses. The sensitivity may, however, suffer in this procedure as only small segments of the sample surface, depending on the amount of overlap dictated by the beam diameter, the repetition rate and the scanning speed, are ablated. In any case, the sampling frequency has to be high enough to enable spatial resolutions at which the targeted features can be distinguished. Failure to do so will result in spatial aliasing effects due to undersampling. Hence, the critical sampling distance determined by the Nyquist rate has to be respected if possible. Too much overlap between successive pulses could also negatively influence the quality of the deconvolved data, as the modulation transfer function (MTF) and the data in the Fourier transform space are very sensitive to noise; the artefacts in the spatial frequency domain produced by high S/N ratios in LA-ICP-MS result in severe defects in the deconvolved data. Overlaying of ablation positions introduces defocusing effects as well, thus, the evolution of the ablation rate and crater radius could be taken into account. This factor is, however, of minimal importance due to the good correlation between crater depth and a limited (<20) number of pulses.⁹ Residual variation within the integrated area may originate from laser fluence instability (typically <1%), plasma shielding by inverse Bremsstrahlung and photoionization, changing transport properties (temporal variation in the particle size distribution), target zone lateral inhomogeneity on a micrometer scale, and instability and stochastic noise within the ICP-MS unit.

MLCC

As can be observed from the scanning electron microscopy (SEM) and optical images of the MLCC in Fig. 4a and b, the dielectric layer thickness is ca. 3.5–4.5 μm, while the Ni electrodes are ca. 1.7–2.5 μm thick. The raw signal modulation upon scanning perpendicular to the electrodes (Fig. 4c), and the resulting integrated areas (Fig. 4d) show an aliasing effect due to the layered pattern. This effect becomes more pronounced after deconvolution (RLTV, 5 iterations, λ = 0.01), as the concentration gradient between the electrodes and dielectric material is reflected more accurately due to an increase in lateral resolution (Fig. 4b and d). The width of the negative space at half of the maximum response (1.7 ± 0.4 μm), as well as the normalized average concentrations gradient (∼0.6 μm⁻¹), has increased ∼100% relative to the traditional approach of scanning using non-overlapping pulses (∼1 μm and ∼0.25 μm⁻¹, respectively). A sharp concentration gradient in the transition zone between the electrode and the dielectric material would be in accordance with the SEM and optical images, which indicate a well-defined pattern. The effective lateral resolution obtained in this scan was estimated to be 0.3 ± 0.1 μm.†

Fig. 4 (a) SEM (5 kV accelerating voltage, BSE, Phenom, Phenom-World, Eindhoven, the Netherlands) images of the polished MLCC surface. (b) Enhanced optical image of the target zone (not the actual color) and the aligned deconvolved response. (c) Temporal signal intensity profiles for ¹³⁸Ba within a selected target zone. (d) Detail of the spatiotemporal change of pulse response areas in a selected target zone; the deconvolved response from the procedure proposed here, and the response from the edge-to-edge scanning procedure (Δ_x = 1, non-overlapping pulses, no deconvolution) are displayed.

Conclusion

A newly developed low-dispersion ablation cell assembly permits separation of individual signal peaks generated at pulse repetition rates up to 200–300 Hz. This allows for fast and sensitive line scanning with high lateral resolution, circumventing issues related to peak broadening due to impaired aerosol washout as generally encountered in ablation cells in use for continuous laser ablation. A further boost in lateral resolution was obtained by a laser ablation methodology involving oversampling (overlapping ablation spots) and the use of a post-acquisition iterative deconvolution procedure using the RLTV algorithm, providing lateral resolutions up to 0.3 ± 0.1 μm and thus below the laser beam diameter. These findings open up new fields of application for LA-ICP-MS and for other methods based on laser plasma spectrochemistry. Further research will be directed towards improving the performance of this setup, as well as deconvolution in multimodal 2D and 3D imaging.

Acknowledgements

The authors acknowledge financial and logistic support from the Flemish Research Foundation (FWO-Vlaanderen) and the National Institute of Chemistry (NIC, Slovenia). The authors would like to thank Davy De Pauw (Department of Analytical Chemistry, Ghent University, Belgium) for machining the parts for the ablation cell and Dr Vid Šelih (Analytical Chemistry Laboratory, NIC, Slovenia) for technical assistance. The anonymous reviewers are acknowledged for their efforts in improving the manuscript. The first author is a PhD fellow of FWO-Vlaanderen.

Notes and references

1. A. L. Gray, Analyst, 1985, 110, 551–556.
2. B. Jackson, S. Harper, L. Smith and J. Flinn, Anal. Bioanal. Chem., 2006, 384, 951–957.
3. H. A. O. Wang, D. Grolimund, L. R. Van Loon, K. Barmettler, C. N. Borca, B. Aeschimann and D. Guenther, Anal. Chem., 2011, 83, 6259–6266.
4. D. J. Hare, J. K. Lee, A. D. Beavis, A. van Gramberg, J. George, P. A. Adlard, D. I. Finkelstein and P. A. Doble, Anal. Chem., 2012, 84, 3990–3997.
5. J. S. Becker, M. V. Zoriy, C. Pickhardt, N. Palomero-Gallagher and K. Zilles, Anal. Chem., 2005, 77, 3208–3216.
6. C. Giesen, L. Waentig, T. Mairinger, D. Drescher, J. Kneipp, P. H. Roos, U. Panne and N. Jakubowski, J. Anal. At. Spectrom., 2011, 26, 2160.
7. A. Izmer, D. Gholap, K. De Houwer, F. Cuyckens and F. Vanhaecke, J. Anal. At. Spectrom., 2012, 27, 413–418.
8. D. Gholap, A. Izmer, B. De Samber, J. T. van Elteren, V. S. Selih, R. Evens, K. De Schamphelaere, C. Janssen, L. Balcaen, I. Lindemann, L. Vincze and F. Vanhaecke, Anal. Chim. Acta, 2010, 664, 19–26.
9. J. T. Van Elteren, A. Izmer, M. Sala, E. F. Orsega, V. S. Selih, S. Panighello and F. Vanhaecke, J. Anal. At. Spectrom., 2013, 28, 994–1004.
10. D. Drescher, C. Giesen, H. Traub, U. Panne, J. Kneipp and N. Jakubowski, Anal. Chem., 2012, 84, 9684–9688.
11. E. L. Gurevich and R. Hergenroder, J. Anal. At. Spectrom., 2007, 22, 1043–1050.
12. H. A. Wang, D. Grolimund, C. Giesen, C. N. Borca, J. R. Shaw-Stewart, B. Bodenmiller and D. Gunther, Anal. Chem., 2013, 85, 10107–10116.
13. H. Lindner, D. Autrique, J. Pisonero, D. Gunther and A. Bogaerts, J. Anal. At. Spectrom., 2010, 25, 295–304.
14. D. Asogan, B. L. Sharp, C. J. P. O'Connor, D. A. Green and R. W. Hutchinson, J. Anal. At. Spectrom., 2009, 24, 917.
15. A. M. Leach and G. M. Hieftje, Appl. Spectrosc., 2002, 56, 62–69.
16. W. Müller, M. Shelley, P. Miller and S. Broude, J. Anal. At. Spectrom., 2009, 24, 209.
17. P. Nadoll and A. E. Koenig, J. Anal. At. Spectrom., 2011, 26, 1872.
18. B. Rusk, A. Koenig and H. Lowers, Am. Mineral., 2011, 96, 703–708.
19. M. V. Zoriy, M. Kayser and J. S. Becker, Int. J. Mass Spectrom., 2008, 273, 151–155.
20. M. V. Zoriy, D. Mayer and J. S. Becker, J. Am. Soc. Mass Spectrom., 2009, 20, 883–890.
21. R. E. Russo, T. W. Suen, A. A. Bol'shakov, J. Yoo, O. Sorkhabi, X. Mao, J. Gonzalez, D. Oropeza and V. Zorba, J. Anal. At. Spectrom., 2011, 26, 1596–1603.
22. A. Plotnikov, C. Vogt, K. Wetzig and A. Kyriakopoulos, Spectrochim. Acta, Part B, 2008, 63, 474–483.
23. R. Voelkel and K. J. Weible, Laser beam homogenizing: limitations and constraints, SPIE Conference proceedings, 2008, 71020J.
24. G. M. P. Van Kempen, L. J. Van Vliet, P. J. Verveer and H. T. M. Van Der Voort, J. Microsc., 1997, 185, 354–365.
25. J. B. de Monvel, S. Le Calvez and M. Ulfendahl, Biophys. J., 2001, 80, 2455–2470.
26. W. A. Carrington, R. M. Lynch, E. D. W. Moore, G. Isenberg, K. E. Fogarty and F. S. Fredric, Science, 1995, 268, 1483–1487.
27. W. H. Richards, J. Opt. Soc. Am., 1972, 62, 55–59.
28. L. B. Lucy, Astron. J., 1974, 79, 745–754.
29. P. J. Verveer, M. J. Gemkow and T. M. Jovin, J. Microsc., 1999, 193, 50–61.
30. N. Dey, L. Blanc-Feraud, C. Zimmer, P. Roux, Z. Kam, J. C. Olivo-Marin and J. Zerubia, Microsc. Res. Tech., 2006, 69, 260–266.
31. M. Tanner, J. Anal. At. Spectrom., 2010, 25, 405.
32. M. Laasmaa, M. Vendelin and P. Peterson, J. Microsc., 2011, 243, 124–140.
33. C. Vonesch and M. Unser, IEEE transactions on image processing: a publication of the IEEE signal processing society, 2008, 17, 539–549.
34. A. Bogaerts, Z. Y. Chen, R. Gijbels and A. Vertes, Spectrochim. Acta, Part B, 2003, 58, 1867–1893.
35. D. Bleiner and T. Lippert, J. Appl. Phys., 2009, 106, 123301.
36. A. Lorusso, V. Nassisi, L. Velardi and M. V. Sicilano, J. Phys.: Conf. Ser., 2010, 227, 012037.
37. R. Hergenroder, J. Anal. At. Spectrom., 2006, 21, 1016–1026.
38. J. Koch, M. Waelle, R. Dietiker and D. Gunther, Anal. Chem., 2008, 80, 915–921.
39. J. Koch, I. Feldmann, N. Jakubowski and K. Niemax, Spectrochim. Acta, Part B, 2002, 57, 975–985.
40. M. Tanner and D. Gunther, J. Anal. At. Spectrom., 2007, 22, 1189–1192.
41. M. Tanner and D. Gunther, J. Anal. At. Spectrom., 2006, 21, 941–947.
42. M. Tanner and D. Gunther, Microsc. Res. Tech., 2008, 391, 1211–1220.
43. D. Bleiner, F. Belloni, D. Doria, A. Lorusso and V. Nassisi, J. Anal. At. Spectrom., 2005, 20, 1337.
44. P. K. Diwakar, J. J. Gonzalez, S. S. Harilal, R. E. Russo and A. Hassanein, J. Anal. At. Spectrom., 2014, 29, 339.
45. B. Hattendorf, J. Pisonero, D. Gunther and N. Bordel, Anal. Chem., 2012, 84, 8771–8776.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ja00137k

---