Photocatalytic activity of exfoliated graphite–TiO₂ nanoparticle composites

Abstract

We investigate the photocatalytic performance of composites prepared in a one-step process by liquid-phase exfoliation of graphite in the presence of TiO₂ nanoparticles (NPs) at atmospheric pressure and in water, without heating or adding any surfactant, and starting from low-cost commercial reagents. These show enhanced photocatalytic activity, degrading up to 40% more pollutants with respect to the starting TiO₂-NPs, in the case of a model dye target, and up to 70% more pollutants in the case of nitrogen oxides. In order to understand the photo-physical mechanisms underlying this enhancement, we investigate the photo-generation of reactive species (trapped holes and electrons) by ultrafast transient absorption spectroscopy. We observe an electron transfer process from TiO₂ to the graphite flakes within the first picoseconds of the relaxation dynamics, which causes the decrease of the charge recombination rate, and increases the efficiency of the reactive species photo-production.

---

1. Introduction

Air and water pollution are major environmental risks to human health.¹ According to the World Health Organization (WHO),¹ in the last decade one out of every nine deaths was related to air pollution,² while at least 1.8 bn people used a contaminated drinking-water source.³ For air pollution remediation, environmental contaminants⁴ (e.g. NO, NO₂, SO₂, suspended organic particulate, volatile organic compounds, aromatic hydrocarbons, etc.) must be turned into harmless compounds. This can be achieved exploiting photocatalysts to absorb light and produce reactive holes (h) and electrons (e) that degrade the pollutants via redox processes.⁵ The photocatalytic quantum efficiency (PQE) is defined as the ratio between the rate at which the target molecules undergo photo-degradation (moles of molecules per unit time) [mol s⁻¹], and the rate of photon absorption (moles of absorbed photons per unit time) [mol s⁻¹].^6,7 Since photocatalytic degradation relies on the Sun and on the photocatalyst, not consumed during the process,^4,8 this is a potentially low-cost and environment friendly approach for pollution abatement.⁴

Amongst oxide semiconductor photocatalysts⁴ (such as ZnO, FeO₃, WO₃), titanium dioxide nanoparticles (TiO₂-NPs) have a wide range of applications, including self-cleaning,⁹ sterilization of surfaces,¹⁰ air¹¹ and water¹² purification. TiO₂-NPs have the advantages of stability in water,⁴ biocompatibility¹³ and low cost (∼1900 USD per ton at 2016 prices ¹⁴). Due to its wide band gap (3.25 eV (ref. 4)), TiO₂ absorbs only the UV part of the solar spectrum.¹⁵ TiO₂-NPs with diameter >10 nm (ref. 7) do not display quantum confinement effects, which would result in a blue shift of the absorption spectra.⁶ Hence, TiO₂-NPs exploit just the UV part (∼4% ¹⁶) of the solar radiation to perform photodegradation,^4,15,17,18 wasting ∼96% of the usable spectrum. Even considering only the UV component, TiO₂-NPs have a modest PQE ∼ 10%,⁷ limited by the recombination of the photo-generated e–h pairs that occurs with 90% quantum efficiency.¹⁹ The PQE increases with the number of generated e–h pairs per absorbed photon, i.e. the photo-generation yield,¹⁹ and with the carriers’ lifetime.⁷ Integration with materials able to accept e or h may slow down charge recombination, leading to a PQE increase.

The integration of TiO₂ with carbon materials, such as nanotubes,²⁰ dots,²¹ graphene oxide (GO)²² and reduced graphene oxide (RGO),²³ was pursued to enhance PQE.^22–61 The e–h pair generation and evolution in TiO₂/carbon composites, such as TiO₂/RGO^62,63,61 and TiO₂/graphene quantum dots (GQD),⁶⁴ was investigated by transient absorption (TA) spectroscopy.⁶⁵ In TiO₂/GQD,⁶⁴ TiO₂/RGO⁶² and Ti_0.91O₂/RGO,⁶³ TiO₂ acts as e acceptor when excited with visible light below the TiO₂ optical gap. In TiO₂/GQD, the e-injection occurs with a time constant <15 fs.⁶² In Ti_0.91O₂/RGO with 0.1 wt% RGO, RGO was found to act as e acceptor, decreasing the recombination rate in TiO₂.⁶¹ Thus, when excited with UV photons above the TiO₂ gap, RGO acts as e-acceptor causing the decrease of the charge carriers’ recombination rate, resulting in PQE enhancement. However, ref. 61 did not quantify the lifetime of the photo-generated carriers, because of the limited time resolution used (∼μs). Ref. 66 theoretically investigated the charge transfer processes, predicting that charge and energy transfer in TiO₂/single layer graphene (SLG) would proceed in both directions, depending on the energy of the excited charges. Here, we apply ultrafast transient absorption spectroscopy to investigate charge separation in exfoliated graphite/TiO₂. Our results explain the mechanism responsible for the increased PQE in TiO₂/carbon composites.

Our TiO₂/exfoliated graphite (TiO₂/Gr) photocatalyst is prepared by sonication-assisted exfoliation of graphite in presence of TiO₂-NPs, using commercial starting materials suitable for large scale production. Liquid-phase exfoliation (LPE) of graphite typically exploits surfactants,^67,68 such as sodium deoxycholate⁶⁹ and pluronics.⁷⁰ Here we use the TiO₂-NPs themselves to exfoliate graphite in water and produce the photocatalytic composite. The exfoliation process is investigated varying both sonication time and concentration of TiO₂-NPs and comparing the chemical composition and crystal structure by high-resolution powder X-ray diffraction (HR-PXRD). The photocatalytic activity is evaluated by measuring the rate of degradation of a model organic compound (Rhodamine B) in water under UV irradiation. An increase up to ∼40% of the degradation rate, with respect to the TiO₂-NPs used as starting material, is observed.

We also study photodegradation of nitrogen oxides, NO_x. These pollutants are extremely relevant to society since NO_x produced by anthropogenic emissions, in large part by on-road diesel vehicles, are key precursors of fine particulate matter (particle pollution smaller than 2.5 μm) and tropospheric ozone air pollution, that affect human health, crop yields and climate worldwide.^71,72 We find a 70% increase in the photocatalytic activity with respect to TiO₂. The photophysical mechanism underlying this enhanced photocatalytic activity is investigated by ultrafast TA spectroscopy with sub-200 fs time resolution and broad spectral coverage (430–1400 nm). We compare the decays of photo-generated e–h pairs in the composite with those in pristine TiO₂ and we observe that TiO₂-NPs inject e into the graphite flakes. The increased photo-production of reactive species explains the photocatalytic activity improvement, with exfoliated graphite acting as e-acceptor.

2. Results and discussion

The preparation of the photo-catalysts for environmental remediation needs to be as simple as possible, low-cost and easily scalable (e.g. photocatalyst in concrete is used up to 3% w/w, hence 70 kg m⁻³, see ref. 81). As discussed in ref. 82, processes based on hydrothermal synthesis and the use of autoclaves (as, e.g., in ref. 83 and 84) are expensive (because of the cost of the equipment), difficult to control (the morphology and activity of the final product is affected by minimal changes in the process) and hazardous, because of the use of high pressures (>2 atm) and high temperatures (>120 °C). Since these risks are proportional to the scale of production, these methods are not suitable for production of tons of photocatalyst, as required considering that in 2018, 30k tons of TiO₂ NPs were used for photocatalytic applications.⁸⁵ More generally, since the photocatalytic process is needed to clean the environment, the production of the catalyst itself has to be environmentally friendly and hazardous reagents and high temperatures or pressures should be avoided. State-of-the-art carbon/TiO₂ photocatalytic materials do not meet these requirements, since: (i) they are prepared in multi-step processes (ref. 83); (ii) at high temperatures (>120 °C) and high pressures (>2 atm), such as in ref. 73, 83 and 84; (iii) with toxic reagents, such as in ref. 73; (iv) they cannot be prepared on the multi-ton scale, such as in ref. 73, 83 and 84.

Here we use a one-pot process exploiting sono-chemical reactions at room temperature and atmospheric pressure. This is not disturbed by oxygen and can be scaled up. The process starts from low-cost (∼1900 USD per ton at 2016 prices for TiO₂ NPs¹⁴ and ∼1000 USD per ton for graphite platelets at 2018 prices⁸⁶) safe reactants, such as graphite and pre-formed TiO₂ NPs, combining all the characteristics required for environmental remediation.

The composites are prepared by ultra sonication of graphite in a 2 mg ml⁻¹ aqueous dispersion of TiO₂-NPs for 4 hours (ELMATransonicT460/H-35 kHz) at 40 °C. The exfoliation is performed in Millipore ultrapure water (resistivity 18.2 MΩ cm at 25 °C). We use flakes from Sigma-Aldrich with size ∼150 μm and TiO₂-NPs in the anatase form from HOMBIKAT AHP 200, Sachtleben Chemie GmbH (purity of the crystalline phase ≥94% w/w, average surface area ∼193 m² g⁻¹). Two sets of samples are prepared starting from a different mass ratio of TiO₂ NPs and graphite. Samples having a mass ratio 1 : 1 of TiO₂ with respect to graphite are labelled TiO₂-Gr1:1. Those with a mass ratio 10 : 1 are labelled TiO₂-Gr10:1. TiO₂ NPs are labelled TiO₂.

In order to study the effect of TiO₂-NPs during liquid-phase sonication, we perform HR-PXRD measurements as a function of sonication time. Samples are loaded into 1 mm borosilicate glass capillaries and diffraction patterns collected at ambient temperature with an incident X-ray wavelength of 0.319902 Å. The full width at half maximum (FWHM) of the (002) graphite diffraction peak is deduced by the Rietveld refinement method,⁸⁷ using the General Structure Analysis System (GSAS) program and EXPGUI interface.^88,89

Diffraction patterns collected after 30 min sonication are shown in Fig. 1. For longer time, up to 4 h, further structural changes are not observed. Thus samples sonicated for 30 min can be considered as the final products. Fig. 1 confirms the presence of TiO₂ anatase (as for The Joint Committee on Powder Diffraction Standards, JCPDS 21-1272⁹⁰) and graphite (JCPDS 75-2078).⁹¹ Moreover, the basal reflection shifts towards higher d-spacings (d₀₀₂ = 3.357 Å) with respect to graphite (JCPDS 75-2078, d₀₀₂ = 3.347 Å (ref. 91)). This suggests that TiO₂-NPs assisted exfoliation increases the interplanar spacing of the resulting flakes. The (002) diffraction peak of TiO₂-Gr10:1 has lower intensity than in TiO₂-Gr1:1. This indicates that an increase in TiO₂-NPs concentration leads to a decrease in the number of planes oriented along (002).⁹¹ As the concentration of TiO₂-NPs increases, the 002 reflection broadens and the corresponding FWHM increases. The broadened FWHM is due to a smaller crystallite size^91,92 (∼195 nm, ∼241 nm and ∼255 nm for TiO₂-Gr10:1, TiO₂-Gr1:1 and graphite, respectively) as determined by the Rietveld method⁸⁷ using the software GSAS-II of ref. 93.

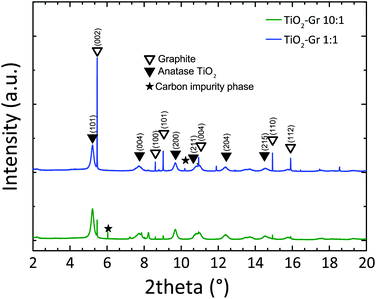Fig. 1 HR-PXRD diffraction profiles of TiO₂-Gr1:1 and TiO₂-Gr10:1 sonicated for 30 min, with peak assignment.

We then investigate the photo-physical properties of the samples by UV-visible (UV-Vis) diffuse reflectance spectrometry with a PerkinElmer Lambda45 UV-Vis spectrophotometer with Harricks praying mantis diffuse reflectance. For each sample, 10 mg is mixed with a 500 mg NaCl matrix. We use a quartz cuvette with 0.5 cm optical path. The reflectance background of NaCl (reference) is taken as baseline for each measurement. The diffuse reflectance can be linked to the absorption coefficient through the Kubelka–Munk (KM) function⁹⁴F(R). For a sample thickness >3 mm,^95,96 with no light transmission, F(R) can be written as:⁹⁷

F(R) = (1 − R)²/2R = K/s = 2.303ε·c/s (1)

where R is the absolute reflectance, K [cm⁻¹] is the absorption coefficient, s [cm⁻¹] is the scattering coefficient, ε is the absorptivity [mol L⁻¹ cm⁻¹] and c is the concentration[M]. Since the samples are dispersed into a non-absorbing matrix (NaCl), s in eqn (1) can be assumed to be that of NaCl and constant.⁹⁸ As a consequence, F(R) is proportional to K. Fig. 2a plots the spectra of pristine TiO₂, TiO₂-Gr10:1 and TiO₂-Gr1:1. A transition from the valence to the conduction band of TiO₂ can be seen at ∼340–360 nm in all samples, as expected for anatase based composites.^99,100 The presence of exfoliated graphite gives rise to absorption from 400 to 800 nm,¹⁰¹ and F(R) is higher with respect to pristine TiO₂. An estimation of the band gap can be obtained applying the Tauc equation, which relates absorption edge, energy of incident photons hν and Tauc gap E_T:¹⁰²

Khν = A(hν − E_T)ⁿ (2)

where A is a proportionality constant and the index n depends on the interband transitions dominating the absorption. In TiO₂n = 2 is applied¹⁰² because the interband transitions are indirect. E_T can be determined by a linear extrapolation of (F(R)hν)^1/2versus hν, Fig. 2. We get E_T ∼ 3.25 eV for pristine TiO₂ decreasing to ∼3.20 and ∼3.02 eV for TiO₂-Gr10:1 and TiO₂-Gr1:1.

Fig. 2 (a) F(R) elaborated and normalized with KM;⁹⁴ (b) Tauc plot of the modified KM function. Dotted lines show the linear extrapolation of the Tauc gap.

The photocatalytic activity is investigated by measuring the photo-degradation of a molecular non-azo-dye (rhodamineB; RhB). This compound is taken as model for organic volatile pollutants, since its molecular structure is close to that of the environmental contaminants used in industry and agriculture.¹⁰³ This test follows the same procedures used to characterize other TiO₂–carbon composites.^28,37 TiO₂, TiO₂-Gr10:1 and TiO₂-Gr1:1 are dispersed in an aqueous solution and sonicated for 4 h. In order to understand the effect of the graphite flakes on PQE, the amount of TiO₂-Gr10:1 and TiO₂-Gr1:1 is chosen to guarantee the same concentration of TiO₂ (2 mg ml⁻¹) inside each suspension. We test 10 ml mixtures comprising 2.86%ml of an aqueous solution of RhB (0.05 mg ml⁻¹, 1 × 10⁻⁴ M), 2.14% ml H₂O and 50% suspension of TiO₂-Gr10:1 or TiO₂-Gr1:1. Considering the affinity of graphitic flakes, due to the π–π stacking of their aromatic systems, for polycyclic aromatic and cationic compounds like RhB,¹⁰⁴ the suspensions are magnetically stirred for 40 min in the dark, in order to attain adsorption–desorption equilibrium between composite and dye. Ref. 104 reported that, when RhB is adsorbed onto 2–3 layers graphene flakes, there is a ground state interaction that leads to a decrement in the intensity of UV/Vis absorption and photoluminescence (PL) of the dye independent of photodegradation. It is thus necessary to determine the fraction of RhB that remains free inside the solution, since this is required to discriminate whether the change in the dye concentration under irradiation is due to a photoreaction or to adsorption. To obtain the adsorption, after stirring in the dark, 0.75 ml of the RhB-composite suspension is taken and centrifuged at 9000 rpm for 10 min at T = 25 °C in order to separate the sample from the RhB solution. The upper 0.5 ml is collected and diluted with water (1 : 6 ratio) to reach the 3 ml volume of analysis of a standard cuvette for a UV/Vis spectrophotometer. The concentration C_D (mol L⁻¹) of free RhB after incubation in the dark is derived from UV/Vis absorption spectra (λ_max = 554 nm) recorded at 25° with a Cary300 UV-Vis spectrophotometer and a 180 μm path-length cuvette. The percentage of RhB adsorbed, Ads, is calculated starting from the initial concentration C₀ (mol L⁻¹) of the used dye, as:¹⁰⁵

Ads = [(C₀ − C_D)/C₀] × 100 (3)

The photoreactivity after photoexcitation of TiO₂ is investigated by exposing each sample to a lamp emitting in the UVA/UVB range (280–400 nm), matching the absorption spectra of the composites, Fig. 2. The lamp has irradiance, i.e. emitted power per unit area, I ∼ 3 W m⁻² in the UVA (280–315 nm) and ∼13.6 W m⁻² in UVB (315 nm–400 nm), at 0.5 m from the source. The samples are placed 35 cm from the lamp. We use 1 mW UVA/UVB for 60 min, sampling 0.75 ml every time interval t of 10 min. The collected volumes are centrifuged, diluted and analyzed with the same procedure used for the determination of C_D, detecting the concentration C(t) of RhB not degraded after t from the beginning of the irradiation. The percentage of RhB photodegraded, P(t), is:¹⁰⁶

P(t) = [(C_D − C(t))/C₀] × 100 (4)

Using this approach, the photocatalytic activity is assessed independently of the possible adsorption of the dye onto the surface of the photoactive material, since the concentration of the dye after pre-equilibration is taken as a reference. For TiO₂-Gr10:1, Table 1 shows an increment of P(t) with respect to TiO₂ of ∼16% after 20 min and ∼21% after 40 min. For TiO₂-Gr1:1, the increment is ∼7% after 20 min while a decrement ∼2% occurs after 40 min. The adsorption of RhB increases from ∼5% in TiO₂-Gr10:1 to ∼35% in TiO₂-Gr1:1. These results indicate that TiO₂-Gr1:1 does not show improvement in photocatalytic activity with respect to TiO₂. The reason for this is the presence of a residual of graphite that is not electronically interacting with TiO₂ in TiO₂-Gr1:1. The excess of graphite is demonstrated by the broad absorption in the 400–800 nm region in Fig. 2. Graphite adsorbs RhB as demonstrated by the increase of the adsorbed fraction from 5% to 35%, but it is not photocatalyically active. As a result, the fraction of light absorbed by this non-photochemically active component is dissipated without giving photodegradation of RhB, causing a decrease of P. We thus identify TiO₂-Gr10:1 as a promising photocatalytic compound since it gives an enhanced P(t) with respect to TiO₂, for a similar RhB adsorption. The observed lack of improvement in photocathalytic activity of TiO₂-Gr1:1 with respect to TiO₂ is in agreement with ref. 28, 48, 51 and 107, where the adsorption and photocatalytic activity of TiO₂ composites with GO and RGO was reported: a GO/TiO₂ or RGO/TiO₂ weight ratio >10% was associated with a decrease of photocatalytic activity. Hence, we focus on TiO₂-Gr10:1 hereafter.

Table 1 Percentage of photodegraded RhB after 20 and 40 min irradiation and adsorption of RhB after incubation in the dark

	TiO2	TiO2-Gr10:1	TiO2-Gr1:1
P(20 min)	38%	54%	45%
P(40 min)	66%	87%	64%
Ads	5%	5%	35%

---

Fig. 3 compares the concentration of RhB during photodegradation upon UV irradiation for: (i) TiO₂-Gr10:1, (ii) reference TiO₂, (iii) graphite, (iv) no photocatalyst, (v) TiO₂-Gr10:1R which is not ultrasonicated. The trends indicate that the dye's degradation temporal profile is a combination of a zero-order and a first-order kinetics. In zero-order kinetics, the rate is independent of reactant concentration and the RhB concentration decreases linearly with time,¹⁰⁸ while in first order, the rate is proportional to the dye concentration.

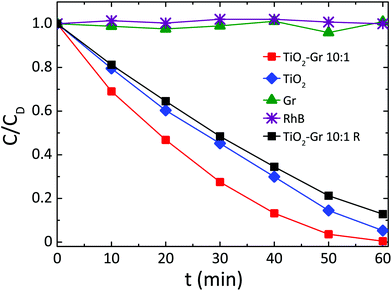Fig. 3 Photocatalytic degradation of RhB under UV light irradiation in the presence of TiO₂-Gr10:1 ultra-sonicated and not ultra-sonicated (TiO₂-Gr10:1R), TiO₂ and Gr.

Since neither zero-order nor first order models fit the data of Fig. 3, we use a pseudo-zero-order kinetic model commonly adopted in the case of organic dye photodegradation in heterogeneous systems:¹⁰⁹

1 − C(t)/C_D = kt (5)

where k(min⁻¹) is the kinetic constant. Fig. 4 fits the data with eqn (5). This gives k(min⁻¹) ∼ 0.018 and ∼0.025 for TiO₂ and TiO₂-Gr10:1, again indicating that TiO₂-Gr10:1 has higher photoactivity than TiO₂. In order to demonstrate the key role of ultra-sonication in enhancing the photocatalytic activity of TiO₂-Gr10:1, we analyze the photocatalytic degradation of RhB for reference samples, with the same composition but not ultra-sonicated (TiO₂-Gr10:1R). The percentage of photodegraded RhB after 20 minutes P(20 min) is ∼36% and after 40 minutes P(40 min) is ∼64%, while the fraction of adsorbed RhB after incubation in the dark is ∼5%. This performance is similar to that of pristine TiO₂, with no significant improvement, thus demonstrating that ultra-sonication is a key step in order to enhance the photocatalytic performance.

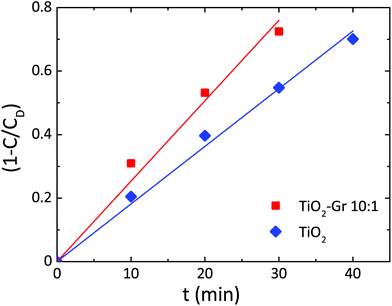Fig. 4 Photodegradation kinetics of RhB for TiO₂, TiO₂-Gr10:1. Lines are fits to the data with eqn (5).

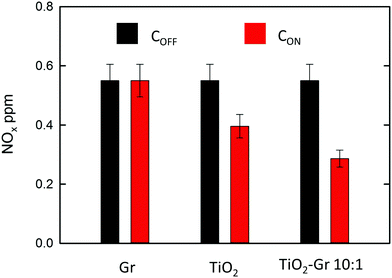
NO_x abatement tests are performed according to the UNI 11247 standard for determination of the degradation of NO_x in air by inorganic photocatalytic materials.¹¹⁰ (1) An artificial atmosphere generator system with a NO_x source, to provide a continuous flow with a constant NO_x concentration. (2) A reaction chamber containing the sample with a UV lamp (irradiance between 300 and 400 nm, 300 Watt power at 365 nm) providing an accurate light intensity (20 W m⁻²) on the sample surface. The chamber (3 liters) is sized in order to test samples with a defined exposed surface area (65 cm²). (3) The NO_x concentration at the outlet is measured with a chemiluminescence NO_x meter, as follows: (1) The sample is placed inside the reaction chamber with the polluted air flow (3 l min⁻¹) and the UV lamp switched off. This phase lasts ∼ one hour and is necessary to equalize the adsorption processes and assure a constant NO_x concentration (i.e. gas flow stabilization) in the air supply flow. This initial value is noted as C_OFF. (2) The UV lamp is switched on and the system is allowed to equalize for a certain time (normally ∼ one hour). The irradiated equilibrium concentration is noted as C_ON. (3) The UV lamp is switched off and the NO_x concentration is checked to its initial value. The samples are prepared as follows: (i) mixing the composite with 2-propanol, (ii) bath sonication of the mixture for 10 min, (iii) drying at room temperature in a Petri glass to make a thin (1 mm) deposit of the photocatalyst on the bottom of a Petri glass. A fixed incoming flow of air ∼1.5 l min⁻¹ is used, with a 0.55 ppm concentration of NO_x, including 0.15 ppm NO₂ and 0.4 ppm NO, corresponding to atmospheric pollution as for ref. 111. The NO_x concentrations at the outlet of the reaction chamber measured in stationary flow conditions, either under UV illumination, C_ON, or without illumination, C_OFF, are shown in Fig. 5 for Gr, TiO₂ and TiO₂-Gr10:1. The NO_x photocatalytic decomposition percentage under UV radiation is calculated as Q = 100(C_OFF − C_ON)/C_OFF. Fig. 5 indicates no NO_x photodegradation for Gr, 28% for TiO₂ and 48% for Gr-TiO₂ 10 : 1, with an increase 70% of photodegradation yield of NO_x with respect to TiO₂.

Fig. 5 NO_x concentration measured in stationary flow conditions either under UV illumination (C_ON, black bars) or without illumination (C_OFF, red bars) at the outlet of the reaction chamber for samples Gr, TiO₂ and Gr-TiO₂ 10 : 1.

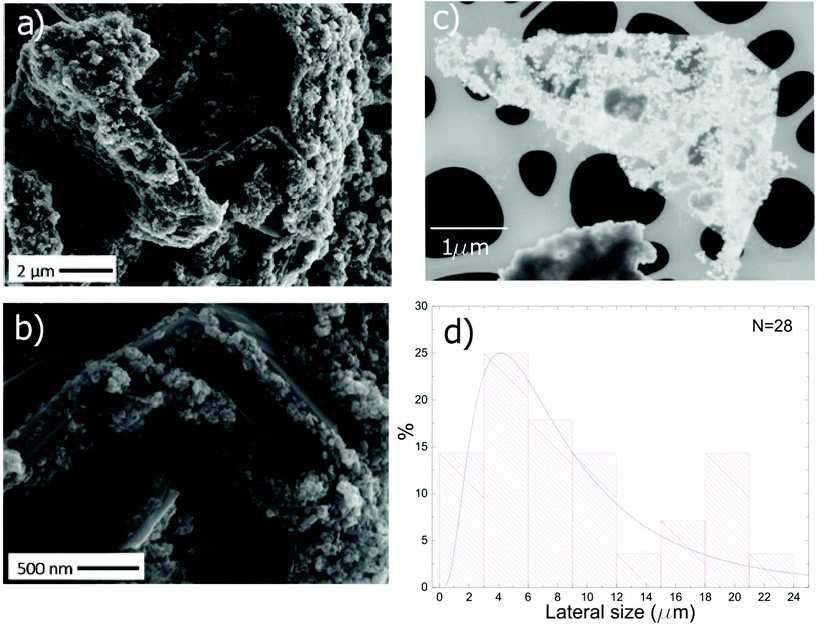
The morphology of TiO₂-Gr10:1 is investigated by scanning electron microscopy (SEM, Quanta3D, FEI Company). Fig. 6a shows graphitic flakes covered by TiO₂-NPs. The higher magnification image Fig. 6b indicates that the flakes edges are decorated by NP agglomerates. The lateral size of the flakes is evaluated by Scanning Transmission Electron Microscopy (STEM, Magellan 400L FEI) depositing ∼20 μl TiO₂-Gr10:1 on a holey carbon Cu grid (300 mesh). From a statistical analysis of isolated flakes similar to that in Fig. 6c, an average lateral size ∼5 μm is estimated, Fig. 6d.

Fig. 6 (a) SEM image of TiO₂-Gr10:1. (b) Higher magnification of (a) showing flakes decorated with NPs. (c) Representative STEM image of a TiO₂-Gr10:1 flake. (d) Distribution of flakes lateral size as determined by STEM of 28 flakes.

To exclude that the TiO₂-NPs adhesion to the flakes is due to the drying of the TiO₂-Gr10:1 suspension, we perform Cryo-TEM (CRyoTitan FEI) experiments. 20 μl TiO₂-Gr10:1 is deposited on a holey carbon grid (Quantifoil R2/2 200 mesh), then loaded into the chamber of a FEI Vitrobot™ Mark III, that maintains 100% humidity at 4 °C. Inside the chamber there are two blotting papers on either side of the sample, which close on the grid and leave a layer of suspension ∼ hundreds nm thick.¹¹² The sample is then plunged into liquid ethane at −183.3 °C, which avoids the formation of ice crystals,¹¹³ creating a vitreous ice (amorphous solid form of water).¹¹³ This allows us to investigate themorphology of TiO₂-Gr10:1 in the liquid phase, confirming that TiO₂-NPs adhere to the flakes, both on the surface (red rectangle) and at the edges (blue rectangle), Fig. 7.

Fig. 7 Cryo-TEM of TiO₂-Gr10:1 in suspension with TiO₂-NPs decorating the flake surface (red rectangle) and the edges (blue rectangle).

TiO₂-Gr10:1 and the starting graphite are also characterized by Raman spectroscopy. 60 μl is drop cast onto a Si/SiO₂ substrate, then heated at 100 °C for 20 min, to ensure water evaporation. Raman spectra are acquired at 514.5 nm using a Renishaw InVia spectrometer with a Leica DM LM microscope and a 50× objective. The power is kept below 1 mW to avoid any possible damage and heating. The spectral resolution is ∼1 cm⁻¹. A statistical analysis is performed as follows: the substrate is divided into 4 regions ∼500 × 500 μm² and in each 5 points are acquired. Fig. 8 plots representative Raman spectra of the starting graphite (black line) and of TiO₂-Gr10:1 (blue line) both on Si/SiO₂. The peaks at 144, 397, 518 and 639 cm⁻¹ are the E_g, B_1g, A_1g and E_g modes of anatase TiO₂.¹¹⁴ The TiO₂ peak at 518 cm⁻¹ is very close to the first order peak of silicon ∼521 cm⁻¹ (ref. 115) and they are partially overlapping. The crystallite size of TiO₂-NPs can be estimated from the position Pos(E_g@144 cm⁻¹) and FWHM(E_g@144 cm⁻¹).¹¹⁶ In our case Pos(E_g@144 cm⁻¹) ∼ 147 cm⁻¹ and FWHM ∼ 20 cm⁻¹ correspond to a NPs size ∼7 nm,¹¹⁶ in agreement with an estimate from TEM images, as in Fig. 7, of ∼5–10 nm. Fig. 9a and b show no significant difference between Pos(G) and FWHM(G) of graphite and TiO₂-Gr10:1. The 2D peak shape for TiO₂-Gr10:1 still resembles that of graphite¹¹⁷ with two components (2D₁, 2D₂), but their intensity ratio I(2D₂)/I(2D₁) is reduced from 2.4 to ∼1.4, Fig. 9c. This indicates that the bulk flakes have undergone exfoliation.¹¹⁸

Fig. 8 Representative Raman spectra at 514.5 nm for graphite (black curve) and TiO₂-Gr10:1 (blue curve) both recorded on a Si/SiO₂ substrate.

Fig. 9 Distribution of: (a) Pos(G), (b) FWHM(G), (c) I(2D₂)/I(2D₁) and (d) I(D)/I(G).

When compared to the initial graphite, TiO₂-Gr10:1 has a higher I(D)/I(G) and FWHM(G). I(D)/I(G) varies inversely with the crystal size, L_a, according to the Tuinstra and Koenig (TK) relation:^118,119I(D)/I(G) ∼ 4.4 nm/L_a. Alternatively, this can be seen as proportional to the average interdefect distance,¹²¹L_D: I(D)/I(G) ∼ 130 nm/L_D². I(D)/I(G) can also be affected by doping.¹²⁰ The lack of up shift of Pos(G) and of FWHM(G) narrowing in TiO₂-Gr10:1 when compared to graphite suggests a level of doping similar to the starting graphite, with a negligible effect on I(D)/I(G). We thus derive L_D ∼ 31 nm and L_a ∼ 33 nm for TiO₂-Gr10:1, and for the starting graphite we get L_D ∼ 43 nm and L_a ∼ 63 nm. Given the average flakes lateral size in Fig. 7, these numbers reflect the defective nature of the starting graphite, and show that defects increase after sonication. L_a determined by Raman is consistent with that derived from HR-PXRD, although lower. Hence, the Raman spectra in Fig. 8 and their fitting parameters in Fig. 9 indicate that our material has changed with respect to the starting flakes, thus graphite itself is not involved in the photo-catalytic activity.

Fig. 10a plots the UV-Vis absorbance, −log₁₀(T), with T the transmittance of TiO₂ and TiO₂-Gr10:1. These have two bands in the UV region at 270 and 306 nm, characteristic of TiO₂-NPs,¹²² assigned to the first allowed vertical transitions that occur at the center of the Brillouin zone of TiO₂-NPs.⁷ The PL spectra of TiO₂ and TiO₂-Gr10:1 in the liquid phase, following excitation at 266 nm, are reported in Fig. 10b. While the shape of the spectra is similar, the PL intensity quenching in TiO₂-Gr10:1 points to an interaction between the excited TiO₂ and the exfoliated graphite, which prevents radiative recombination of the photogenerated e–h pairs.

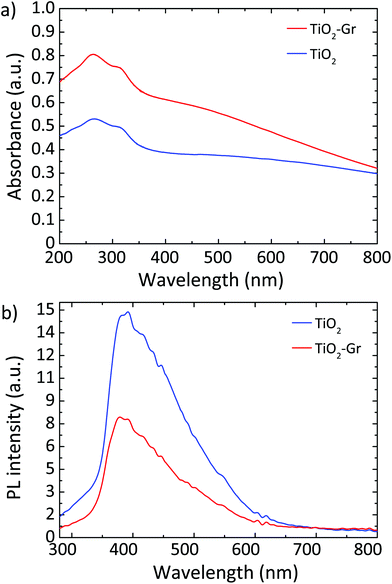Fig. 10 (a) UV-Vis absorbance of TiO₂ and TiO₂-Gr10:1. (b) PL spectra for 266 nm excitation of TiO₂ and TiO₂-Gr10:1.

In order to investigate the photodegradation mechanism, we perform singlet oxygen detection experiments by monitoring the NIR luminescence with an Edinburgh FLS 980 Spectrofluorimeter equipped with a InGaAs detector and a 450 W xenon excitation lamp. Excitation is performed at 350 nm, above the bandgap of TiO₂.⁴ No luminescence, hence no singlet oxygen formation, is detected. We thus rule out formation of singlet oxygen during rhodamine photo-degradation, in contrast to ref. 123, and suggest that degradation occurs via photogeneration of hydroxyl radicals, as for ref. 84.

The generation of reactive oxygen species⁵ (ROS) was identified as the photodegradation mechanism of organic pollutants⁵⁵ and RhB.³¹ The presence of exfoliated graphite in TiO₂-Gr10:1 may result in a higher ROS generation, due to e-transfer from TiO₂ to graphite, allowing a more stable charge separation in TiO₂. The first step of the photocatalytic degradation reaction is the photo-excitation of e–h pairs in TiO₂-NPs by absorption of UV photons with energy exceeding the TiO₂ gap. The ROS generation depends on the competition between charge recombination, either radiative or non-radiative, and the separation of the photo-excited charges required to initiate the oxidative (reductive) pathways.⁵ Accordingly, the enhancement of photocatalytic activity may be traced back to modifications of the relaxation channels of photoexcited e–h in TiO₂, induced by graphite flakes.

In order to identify these channels, we perform a comparative study of charge-carriers dynamics in pristine TiO₂ and TiO₂-Gr10:1 using broadband TA spectroscopy with sub-200 fs time-resolution. We use an amplified Ti:sapphire laser (Coherent, Libra) with 100 fs, 500 μJ pulses at 800 nm and 1 kHz. The 266 nm-pump pulse is generated by frequency tripling the laser output and it is modulated with a chopper at 500 Hz. The broadband probe pulse is obtained by white light continuum generation in a plate of sapphire, for the visible, or yttrium aluminium garnet (YAG), for the near-infrared (NIR). The probe spectrum is detected by an optical multichannel analyzer with a wavelength resolution ∼1 nm. The parallel linearly polarized pump and probe pulses are focused on the sample in a non-collinear geometry with spot sizes ∼180 and ∼80 μm, in order to guarantee homogeneous excitation of the detected sample region. The pump power is 1.6 mW, corresponding to an incident fluence ∼3 mJ cm⁻² (∼10¹⁶ photons per cm²). The measured signal is the delay-dependent differential transmission spectrum,⁶⁵ defined as ΔT/T(λ,τ) = T_on(λ,τ)/T_off(λ) − 1, where T_on and T_off are the probe spectra transmitted through the excited and the unexcited sample, respectively, λ is the probe wavelength and τ the pump–probe delay, controlled with a motorized translation stage. The temporal resolution is ∼180 fs. We excite with UV pulses at 266 nm, well above the band gap of TiO₂,⁴ and measure ΔT/T from 430 to 1400 nm.

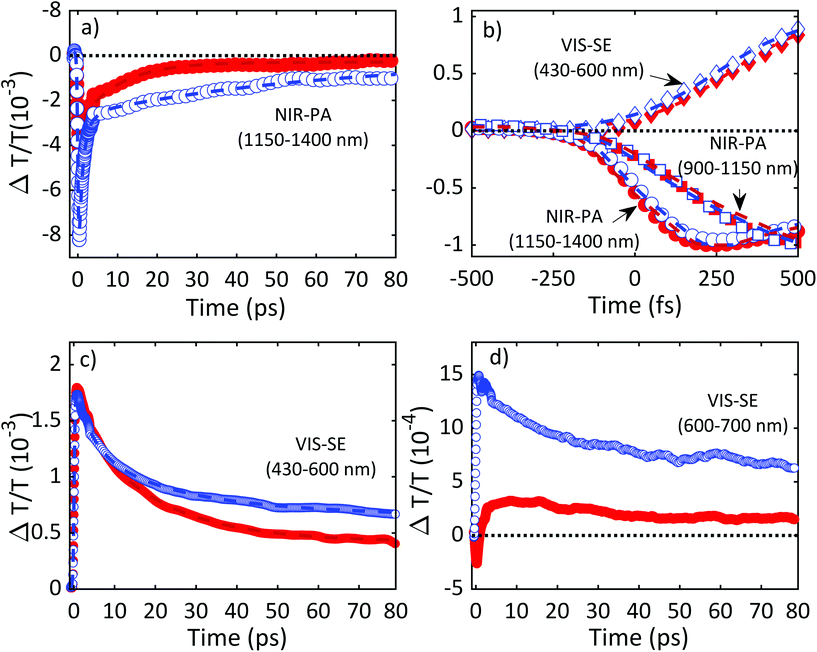
Fig. 11 plots ΔT/T (λ,τ) maps as a function of λ and τ. In the NIR, Fig. 11a and b, both TiO₂ and TiO₂-Gr10:1 exhibit broad photo-induced absorption (PA, ΔT/T < 0) from 900 to 1400 nm. We assign it to intraband transitions of the photo-excited free e from the conduction band (CB) edge, as reported for anatase TiO₂-NPs.^124–127 An additional source of PA in the NIR comes from the transition of trapped e to the CB.¹²⁸ A large variety of trapping states is expected in TiO₂, with energy distribution dependent on sample preparation.¹²⁹ According to ref. 125 and 130 the contribution of trapped e to the PA signal should dominate in the range 900–1150 nm, while the free e absorption, which scales as λⁿ with n = 1.7,¹²⁵ dominates at longer wavelengths. In the NIR, both SLG¹³¹ and multilayer graphene¹³² show a positive ΔT/T, corresponding to photo-bleaching (PB) due to Pauli blocking^131,132 from the hot e distribution in the CB.^133,134 Since the TA spectrum of TiO₂-Gr10:1 in the NIR consists of a PA band, we conclude that its optical response is dominated by TiO₂, due both to the higher intensity of the transient signal from TiO₂ and higher concentration of TiO₂ with respect to graphite flakes.

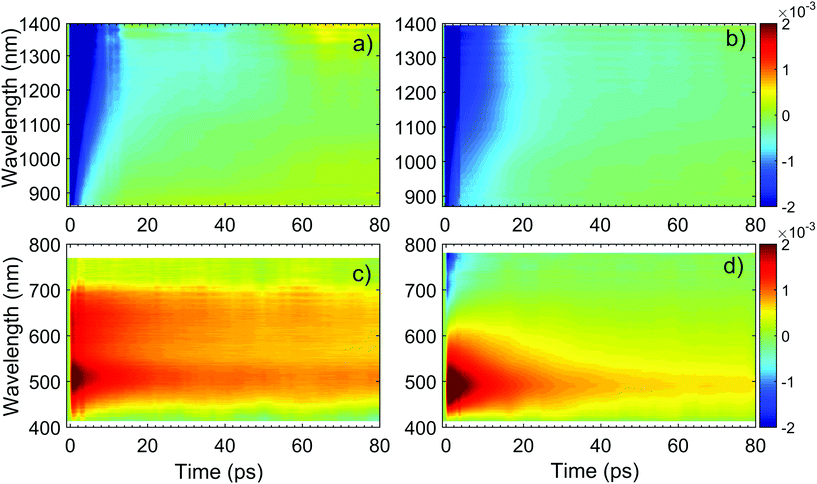Fig. 11 ΔT/T maps as a function of probe wavelength and pump–probe delay of TiO₂ in (a) NIR (c) visible. ΔT/T maps of TiO₂-Gr10:1 in (b) NIR and (d) visible.

The TA maps of TiO₂-Gr10:1 and TiO₂ in the NIR differ for their time decay, as shown in Fig. 12a. The portion of the PA band in the range 1150–1400 nm can be attributed to free e, as confirmed by the resolution limited formation of the signal in Fig. 12b, and by the monotonic increase of the signal with probe wavelength. For TiO₂, this PA relaxes following a bi-exponential decay with time constants τ_1TiO2/PA = 500 fs, τ_2TiO2/PA = 45 ps. In the presence of exfoliated graphite, the relaxation dynamics is best fit by a three-exponential decay with time constants τ_1G/PA = 500 fs, τ_2G/PA = 4 ps, τ_3G/PA = 20 ps. In both TiO₂ and TiO₂-Gr10:1, the first sub-ps decay component is associated to the trapping of free e.^130,135,136 The appearance of an additional decay channel, and the overall shortening of the PA bands lifetime observed in the composite with respect to the pristine TiO₂-NPs can be explained by ultrafast charge transfer from TiO₂ to the graphite flakes, which act as e scavengers. The PA dynamics in the range 900–1150 nm, mainly related to absorption from trapped e,^125,130 appears almost unperturbed by the presence of exfoliated graphite, suggesting that e transfer mostly involves free e. In both samples, this PA band shows a build-up with a 400–500 fs time constant (Fig. 12b), related to e trapping. This rise time, consistent with the ∼200 fs time constant measured in Pt-loaded TiO₂ particles,¹³⁷ matches the sub-ps decay component (indicated as τ_1TiO2/PA, τ_1G/PA) of PA in the range 1150–1400 nm, observed in both TiO₂ and TiO₂-Gr10:1, which we attribute to free e trapping. Further evidence of e transfer from TiO₂ to flakes can be found in the out-of-equilibrium optical response in the visible range, Fig. 11c and d. In the TiO₂ sample we observe an increase in transmission (ΔT/T > 0) in the visible which, considering the vanishing ground state absorption in this spectral range, can be assigned to stimulated emission (SE), i.e. amplification of the probe beam due to optical gain.⁶⁵ We identify two overlapping SE bands: the first, in the range 430–600 nm, due to the recombination of free e with trapped h. The second, in the range 600–700 nm, due to recombination of trapped e with free h. In TiO₂-Gr10:1 the second, red shifted SE band is strongly quenched and a residual component appears few ps after excitation, Fig. 12d. The SE band in the range 430–600 nm, related to trapped h recombination can be observed in both samples, but in TiO₂-Gr10:1 it decreases faster to equilibrium, see Fig. 12c. This band has a single exponential build up with 400–500 fs time constant, possibly due to h trapping, Fig. 12b. The SE relaxation dynamics can be fit by a bi-exponential decay on top of a long-lasting component related to the emission on the ns timescale.¹²⁷ In TiO₂, we get τ_1TiO2/SE = 5 ps, τ_2TiO2/SE = 45 ps, while in TiO₂-Gr10:1 we have τ_1G/SE = 4 ps, τ_2G/SE = 20 ps (Fig. 12c). While τ_1TiO2/SE could depend on the lifetime of the trapped h, the other three relaxation components τ_2TiO2/SE, τ_1G/SE and τ_2G/SE, match those observed for the PA decay in the NIR (equal to τ_2TiO2/PA, τ_2G/PA, τ_3G/PA) indicating that the SE band at 430–600 nm and the PA band at 1150–1400 nm decay with similar dynamics. These components can be associated to the population dynamics of free e, whose lifetime in TiO₂-Gr10:1 is limited by the charge transfer to graphitic flakes, which occurs on a time-scale ∼4–20 ps. Previous ultrafast spectroscopy studies^136,137 on Pt loaded TiO₂-NPs suggested a similar e transfer time of several ps. In our case, e transfer to the graphitic flakes increases the trapped h lifetime, because it inhibits one of their recombination channels, enhancing the oxidative photocatalytic reactivity of the composite.

Fig. 12 Relaxation dynamics of TiO₂ and TiO₂-Gr10:1. For all time traces, the empty blue symbols refer to TiO₂ and the filled red ones refer to TiO₂:Gr10:1. (a) NIR-PA in the range 1150–1400 nm together with best fit functions using bi-exponential decay for TiO₂ (blue dashed line) and three-exponential decay for TiO₂-Gr10:1 (red dashed line), both convoluted to the instrumental response. (b) Normalized signal build-up dynamics for TiO₂ and TiO₂-Gr10:1 together with best fit functions. Dashed blue/red lines are fits to the data for TiO₂/TiO₂-Gr10:1 using an exponential build-up convoluted with the instrumental response. The time traces correspond to VIS-SE in the ranges 430–600 nm (diamonds), NIR-PA 1150–1400 nm (circles) and 900–1150 nm (squares). (c) VIS-SE in the range 430–600 nm together with best fits using a biexponential decay function convoluted to the instrumental response (blue/red dashed lines for TiO₂/TiO₂-Gr10:1). (d) VIS-SE dynamics in the range 600–700 nm for TiO₂ (blue open circles) and TiO₂-Gr10:1 (red full circles).

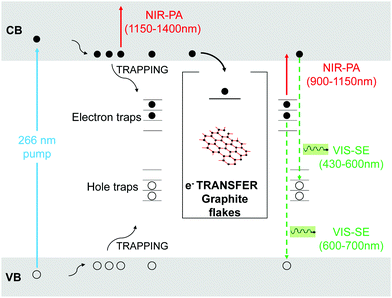
Fig. 13 summarizes the photoexcitation and relaxation pathways of TiO₂ and TiO₂-Gr10:1 derived from our ultrafast TA experiments. In pristine TiO₂, the free e and h photo-excited into CB and VB by the UV-pump pulse (blue arrow), can either be excited by the probe pulse into higher energy states via intraband transitions responsible for the instantaneous PA band in the range 1100–1500 nm, or they can relax into intragap trapped states. The trapped charge carriers can radiatively recombine with free charges giving rise to the SE bands in the range 430–600 nm and 600–700 nm. Trapped e can also be photo-excited into CB as indicated by the PA bands in the range 900–1150 nm. All the bands related to the relaxation of trapped charge carriers share the same build-up dynamics due to the trapping. The interaction with graphitic flakes influences the optical properties of TiO₂-Gr, when compared to TiO₂, by opening an additional relaxation channel for the free e, which can efficiently transfer to the graphite flakes, thus slowing down e–h recombination, enhancing the photocatalytic activity.

Fig. 13 Schematic illustration of the optical transitions contributing to the TA signals of TiO₂ and TiO₂-Gr10:1. The UV-pump pulse (ciano arrow) photo-excites free-e (full black circles) and -h (empty circles) into CB and VB respectively. Photo-excited charge carriers thermalize to the bands edges and may also get trapped inside-gap states. Photo-excited free-e are monitored by the probe pulse through the PA band in the range 1150–1400 nm (red arrow), and the SE band in the range 430–600 nm (green dashed arrow), related to the recombination with trapped holes. In TiO₂-Gr10:1, free-e can also transfer to graphitic flakes (inset box). The trapped e can radiatively recombine with free h giving rise to the SE band in the range 600–700 nm (green dashed arrow) or be photo-excited into CB as indicated by the PA bands in the range 900–1150 nm.

3. Conclusions

We reported TiO₂/Gr composites with enhanced photocatalytic activity with respect to pristine TiO₂-NPs. These are produced via liquid phase exfoliation of graphite in presence of TiO₂-NPs, without surfactants which could prevent the energy or charge transfer between TiO₂ and graphite flakes. The observed photo-degradation kinetics consists of a combination of zero-order and first-order processes. We assigned the increase in photocatalytic activity to electron transfer from TiO₂ to the graphite flakes, which occurs within the first ps of the relaxation dynamics.

Our 40% improvement of photocatalytic performance with respect to TiO₂ NPs is almost 400% larger that reported for state of the art RGO-TiO₂.⁷³ A similar result was achieved in ref. 74, but using carbon nanotubes in combination to RGO. This approach is not suitable for environmental remediation since, due to concerns on toxicity,⁷⁵ the dispersion of carbon nanotubes in the environment as a result, e.g., of progressive release from the photocatalytic surfaces, should be avoided. Ref. 76 and 77 showed that water phase exfoliated graphite does not produce environmental concerns. Thus, our composite is designed to fit the requirements for environmental remediation: to treat water (or air) containing pollutants at low concentration (<ppm). Thus, material costs and environmental impact are the main issues. Materials used for environmental remediation, if not properly designed, may become themselves pollutants if dispersed in the environment.⁷⁸ It is hence fundamental they are biocompatible. The environmental impact of photocatalyst production also needs to be considered in the assessment of the environmental sustainability of photocatalytic processes for air and water remediation.⁷⁹ For different applications, such as fuel photo-production, see e.g.ref. 80, different features are required, in particular the value of the photo-product justifies the use of expensive elements such as Pt, Au or Ag.

Due to the simplicity and cost effectiveness of the preparation procedure of our samples, and the enhanced photocatalytic activity in the photodegradation of relevant environmental contaminants such as NO_x, with respect to pristine TiO₂-NPs, we anticipate applications to smart photoactive surfaces for environmental remediation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank G. Grancini for useful discussions. We acknowledge funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No. 785219 (GrapheneCore2), EU Neurofibres, ERC Minegrace and Hetero2D, EPSRC Grants EP/509K01711X/1, EP/K017144/1, EP/N010345/1, EP/M507799/5101, and EP/L016087/1.

References

1. http://www.who.int/topics/en .
2. http://www.who.int/mediacentre/news/releases/2016/air-pollution-estimates/en .
3. https://www.unicef.org/publications/files/Progress_on_Drinking_Water_Sanitation_and_Hygiene_2017.pdf .
4. M. R. Hoffmann, S. T. Martin, W. Y. Choi and D. W. Bahnemann, Chem. Rev., 1995, 95, 69.
5. T. Hirakawa and Y. Nosaka, Langmuir, 2002, 18, 3247.
6. N. Serpone, D. Lawless, R. Khairutdinov and E. Pelizzetti, J. Phys. Chem., 1995, 99, 16655.
7. N. Serpone, D. Lawless and R. Khairutdinov, J. Phys. Chem., 1995, 99, 16646.
8. Q. Zhang, Q. An, X. Luan, H. Huang, X. Li, Z. Meng, W. Tong, X. Chen, P. K. Chu and Y. Zhang, Nanoscale, 2015, 7, 14002.
9. Y. Lai, J. Huang, Z. Cui, M. Ge, K. Zhang, Z. Chen and L. Chi, Small, 2016, 12, 2203.
10. S. Nishimoto and B. Bhushan, RSC Adv., 2013, 3, 671.
11. A. Mamaghani, F. Haghighat and C. S. Lee, Appl. Catal., B, 2017, 203, 247.
12. C. Yu, W. Zhou, H. Liu, Y. Liu and D. D. Dionysiou, Chem. Eng. J., 2016, 287, 117.
13. T. Xia, M. Kovochich, J. Brant, M. Hotze, J. Sempf, T. Oberley, C. Sioutas, J. I. Yeh, M. R. Wiesner and A. E. Nel, Nano Lett., 2006, 6, 1794.
14. http://www.cnchemicals.com/Press/88893-CCM .
15. A. L. Linsebigler, G. Q. Lu and J. T. Yates, Chem. Rev., 1995, 95, 735.
16. I. Foyo-Moreno, I. Alados, F. J. Olmo and L. Alados-Arboledas, Agric. For. Meteorol., 2003, 120, 101.
17. X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891.
18. A. Fujishima, X. Zhang and D. A. Tryk, Surf. Sci. Rep., 2008, 63, 515.
19. N. Serpone, J. Photochem. Photobiol., A, 1997, 104, 1.
20. K. Dai, T. Peng, D. Ke and B. Wei, Nanotechnology, 2009, 20, 125603.
21. M. Sun, X. Ma, X. Chen, Y. Sun, X. Cui and Y. Lin, RSC Adv., 2014, 4, 1120.
22. K. R. Reddy, M. Hassan and V. G. Gomes, Appl. Catal., A, 2015, 489, 1.
23. L. Han, P. Wang and S. Dong, Nanoscale, 2012, 4, 5814.
24. R. Leary and A. Westwood, Carbon, 2011, 49, 741.
25. W. Tu, Y. Zhou and Z. Zou, Adv. Funct. Mater., 2013, 23, 4996.
26. H. X. Wang, Q. Wang, K. G. Zhou and H. L. Zhang, Small, 2013, 9, 1266.
27. N. Zhang, M. Q. Yang, S. Liu, Y. Sun and Y. J. Xu, Chem. Rev., 2015, 115, 10307.
28. N. Zhang, Y. Zhang and Y. J. Xu, Nanoscale, 2012, 4, 5792.
29. C. Chen, W. Cai, M. Long, B. Zhou, Y. Wu, D. Wu and Y. Feng, ACS Nano, 2010, 4, 6425.
30. J. Du, X. Lai, N. Yang, J. Zhai, D. Kisailus, F. Su, D. Wang and L. Jiang, ACS Nano, 2011, 5, 590.
31. Y. Gao, X. Pu, D. Zhang, G. Ding, X. Shao and J. Ma, Carbon, 2012, 50, 4093.
32. J. Guo, S. Zhu, Z. Chen, Y. Li, Z. Yu, Q. Liu, J. Li, C. Feng and D. Zhang, Ultrason. Sonochem., 2011, 18, 1082.
33. B. Jiang, C. Tian, Q. Pan, Z. Jiang, J. Q. Wang, W. Yan and H. Fu, J. Phys. Chem. C, 2011, 115, 23718.
34. C. H. Kim, B. H. Kim and K. S. Yang, Carbon, 2012, 50, 2472.
35. I. Y. Kim, J. M. Lee, T. W. Kim, H. N. Kim, H. I. Kim, W. Choi and S. J. Hwang, Small, 2012, 8, 1038.
36. N. Li, G. Liu, C. Zhen, F. Li, L. Zhang and H. M. Cheng, Adv. Funct. Mater., 2011, 21, 1717.
37. Y. Liang, H. Wang, H. S. Casalongue, Z. Chen and H. Dai, Nano Res., 2010, 3, 701.
38. Y. T. Liang, B. K. Vijayan, K. A. Gray and M. C. Hersam, Nano Lett., 2011, 11, 2865.
39. Y. T. Liang, B. K. Vijayan, O. Lyandres, K. A. Gray and M. C. Hersam, J. Phys. Chem. Lett., 2012, 3, 1760.
40. J. Liu, Z. Wang, L. Liu and W. Chen, Phys. Chem. Chem. Phys., 2011, 13, 13216.
41. S. Liu, H. Sun, S. Liu and S. Wang, Chem. Eng. J., 2013, 214, 298.
42. X. Pan, Y. Zhao, S. Liu, C. L. Korzeniewski, S. Wang and Z. Fan, ACS Appl. Mater. Interfaces, 2012, 4, 3944.
43. L. M. Pastrana-Martinez, S. Morales-Torres, V. Likodimos, J. L. Figueiredo, J. L. Faria, P. Falaras and A. M. T. Silva, Appl. Catal., B, 2012, 123, 241.
44. M. S. A. S. Shah, A. R. Park, K. Zhang, J. H. Park and P. J. Yoo, ACS Appl. Mater. Interfaces, 2012, 4, 3893.
45. J. Shen, M. Shi, B. Yan, H. Ma, N. Li and M. Ye, Nano Res., 2011, 4, 795.
46. N. P. Thuy-Duong, P. Viet Hung, E. W. Shin, P. Hai-Dinh, S. Kim, J. S. Chung, E. J. Kim and S. H. Hur, Chem. Eng. J., 2011, 170, 226.
47. P. Wang, J. Wang, T. Ming, X. Wang, H. Yu, J. Yu, Y. Wang and M. Lei, ACS Appl. Mater. Interfaces, 2013, 5, 2924.
48. Y. Wang, R. Shi, J. Lin and Y. Zhu, Appl. Catal., B, 2010, 100, 179.
49. G. Williams, B. Seger and P. V. Kamat, ACS Nano, 2008, 2, 1487.
50. N. Yang, Y. Liu, H. Wen, Z. Tang, H. Zhao, Y. Li and D. Wang, ACS Nano, 2013, 7, 1504.
51. H. Zhang, X. Lv, Y. Li, Y. Wang and J. Li, ACS Nano, 2010, 4, 380.
52. J. Zhang, Z. Xiong and X. S. Zhao, J. Mater. Chem., 2011, 21, 3634.
53. L. W. Zhang, H. B. Fu and Y. F. Zhu, Adv. Funct. Mater., 2008, 18, 2180.
54. P. Zhang, C. Shao, Z. Zhang, M. Zhang, J. Mu, Z. Guo and Y. Liu, Nanoscale, 2011, 3, 2943.
55. Y. Zhang, Z. R. Tang, X. Fu and Y. J. Xu, ACS Nano, 2010, 4, 7303.
56. Y. Zhang, Z. R. Tang, X. Fu and Y. J. Xu, ACS Nano, 2011, 5, 7426.
57. Y. Zhang, N. Zhang, Z. R. Tang and Y. J. Xu, Phys. Chem. Chem. Phys., 2012, 14, 9167.
58. D. Zhao, G. Sheng, C. Chen and X. Wang, Appl. Catal., B, 2012, 111, 303.
59. N. Yang, J. Zhai, D. Wang, Y. Chen and L. Jiang, ACS Nano, 2010, 4, 887.
60. T. F. Yeh, J. Cihlaář, C. Y. Chang, C. Cheng and H. Teng, Mater. Today, 2013, 16, 78.
61. A. Morais, C. Longo, J. R. Araujo, M. Barroso, J. R. Durrant and A. F. Nogueira, Phys. Chem. Chem. Phys., 2016, 18, 2608.
62. P. Wang, N. M. Dimitrijevic, A. Y. Chang, R. D. Schaller, Y. Liu, T. Rajh and E. A. Rozhkova, ACS Nano, 2014, 8, 7995.
63. K. K. Manga, Y. Zhou, Y. Yan and K. P. Loh, Adv. Funct. Mater., 2009, 19, 3638.
64. K. J. Williams, C. A. Nelson, X. Yan, L. S. Li and X. Zhu, ACS Nano, 2013, 7, 1388.
65. S. De Silvestri, C. Manzoni, R. Borrego-Varillas, A. Oriana and G. Cerullo, Riv. Nuovo Cimento, 2017, 41, 1.
66. R. Long, N. J. English and O. V. Prezhdo, J. Am. Chem. Soc., 2012, 134, 14238.
67. Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. McGovern, B. Holland, M. Byrne and Y. K. Gun'Ko, et al. , Nat. Nanotechnol., 2008, 3, 563.
68. F. Bonaccorso, A. Lombardo, T. Hasan, Z. Sun, L. Colombo and A. C. Ferrari, Mater. Today, 2012, 15, 564.
69. M. Lotya, P. J. King, U. Khan, S. De and J. N. Coleman, ACS Nano, 2010, 4, 3155.
70. A. C. Ferrari, F. Bonaccorso, V. Fal'ko, K. S. Novoselov, S. Roche, P. Boggild, S. Borini, F. H. L. Koppens, V. Palermo and N. Pugno, et al. , Nanoscale, 2015, 7, 4598.
71. S. C. Anenberg, J. Miller, R. Minjares, L. Du, D. K. Henze, F. Lacey, C. S. Malley, L. Emberson, V. Franco, Z. Klimont and C. Heyes, Nature, 2017, 545, 467.
72. J. Lelieveld, J. S. Evans, M. Fnais, D. Giannadaki and A. Pozzer, Nature, 2015, 525, 367.
73. Á. Tolosana-Moranchel, A. Manassero, M. L. Satuf, O. M. Alfano, J. A. Casas and A. Bahamonde, Appl. Catal., B, 2019, 246, 1.
74. Y. Huang, D. Chen, X. Hu, Y. Qian and D. Li, Nanomaterials, 2018, 8, 431.
75. N. Kobayashi, H. Izumi and Y. Morimoto, J. Occup. Health, 2017, 59, 394.
76. C. Martín, K. Kostarelos, M. Prato and A. Bianco, Chem. Commun., 2019, 55, 5540.
77. S. Gurunathan and J.-H. Kim, Int. J. Nanomed., 2016, 11, 1927.
78. D. M. Mitrano, S. Motellier, S. Clavaguera and B. Nowack, Environ Int, 2015, 77, 132.
79. J. Luo, S. Zhang, M. Sun, L. Yang, S. Luo and J. C. Crittenden, ACS Nano, 2019, 13, 9811–9840.
80. K. Wenderich and G. Mul, Chem. Rev., 2016, 116, 14587.
81. J. Jiang, X. He, J. Du, X. Pang, H. Yang and Z. Wei, Mater. Lett., 2019, 244, 178.
82. A. Tayel, R. A. Ramadan and A. O. El Seoud, Catalysts, 2018, 8, 491.
83. Á. Tolosana-Moranchel, A. Casasa, A. Bahamonde, L. Pascual, L. I. Granone, J. Schneider, R. Dillert and D. W. Bahnemann, Appl. Catal., B, 2019, 241, 375.
84. G. Luna-Sanguino, Á. Tolosana-Moranchel, C. Duran-Valle, M. Faraldos and A. Bahamonde, Catal. Today, 2019, 328, 172.
85. http://www.42teknanomaterials.com/ .
86. http://www.northerngraphite.com/ .
87. R. A. Young, The Rietveld method, International union of crystallography, 1993.
88. O. Tanaike and M. Inagaki, Carbon, 1997, 35, 831.
89. A. N. Fitch, J. Res. Natl. Inst. Stand. Technol., 2004, 109, 133.
90. W. Li, R. Liang, A. Hu, Z. Huang and Y. N. Zhou, RSC Adv., 2014, 4, 36959.
91. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210.
92. C. E. Holcombe, Report Y 1887, USAEC Oak Ridge Y 12 Plant, 1973.
93. B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544.
94. P. Kubelka and F. Munk, Z. Tech. Phys., 1931, 12, 593.
95. G. Kortüm, Reflectance spectroscopy: principles, methods, applications, Springer Science & Business Media, 2012.
96. J. Workman Jr. and A. Springsteen, Applied spectroscopy: a compact reference for practitioners, Academic Press, 1998.
97. A. A. Christy, O. M. Kvalheim and R. A. Velapoldi, Vib. Spectrosc., 1995, 9, 19.
98. S. D. Jackson and J. S. J. Hargreaves, Metal Oxide Catalysis, John Wiley & Sons, 2009.
99. K. M. Reddy, S. V. Manorama and A. R. Reddy, Mater. Chem. Phys., 2003, 78, 239.
100. A. Murphy, Sol. Energy Mater. Sol. Cells, 2007, 91, 1326.
101. T. Smausz, B. Kondász, T. Gera, T. Ajtai, N. Utry, M. D. Pintér, G. Kiss-Albert, J. Budai, Z. Bozóki and G. Szabo, et al. , Appl. Phys. A, 2017, 123, 633.
102. S. Ngamta, N. Boonprakob, N. Wetchakun, K. Ounnunkad, S. Phanichphant and B. Inceesungvorn, Mater. Lett., 2013, 105, 76.
103. R. Jain, M. Mathur, S. Sikarwar and A. Mittal, J. Environ. Manage., 2007, 85, 956.
104. G. Guidetti, A. Cantelli, R. Mazzaro, L. Ortolani, V. Morandi and M. Montalti, Nanoscale, 2016, 8, 8505.
105. S. P. Patil, B. Bethi, G. H. Sonawane, V. S. Shrivastava and S. Sonawane, J. Ind. Eng. Chem., 2016, 34, 356.
106. T. S. Natarajan, M. Thomas, K. Natarajan, H. C. Bajaj and R. J. Tayade, Chem. Eng. J., 2011, 169, 126.
107. P. Zhu, A. S. Nair, S. Peng, S. Yang and S. Ramakrishna, ACS Appl. Mater. Interfaces, 2012, 4, 581.
108. F. Zhou, C. Yan, T. Liang, Q. Sun and H. Wang, Chem. Eng. Sci., 2018, 183, 231.
109. K. Rajeshwar, M. Osugi, W. Chanmanee, C. Chenthamarakshan, M. Zanoni, P. Kajitvichyanukul and R. Krishnan-Ayer, J. Photochem. Photobiol., C, 2008, 9, 171.
110. http://www.fotocatalisis.org/assets/doc497.pdf .
111. R. Zouzelka and J. Rathousky, Appl. Catal., B, 2017, 217, 466.
112. http://www.fei.com/products/vitrobot .
113. H. Friedrich, P. M. Frederik, G. de With and N. A. Sommerdijk, Angew. Chem., Int. Ed., 2010, 49, 7850.
114. T. Ohsaka, F. Izumi and Y. Fujiki, J. Raman Spectrosc., 1978, 7, 321.
115. P. A. Temple and C. E. Hathaway, Phys. Rev. B, 1973, 7, 3685.
116. V. Swamy, A. Kuznetsov, L. S. Dubrovinsky, R. A. Caruso, D. G. Shchukin and B. C. Muddle, Phys. Rev. B, 2005, 71, 184302.
117. A. C. Ferrari, et al. , Phys. Rev. Lett., 2006, 97, 187401.
118. A. C. Ferrari and J. Robertson, Phys. Rev. B, 2000, 61, 14095.
119. F. Tuinstra and J. L. Koenig, J. Chem. Phys., 1970, 53, 1126.
120. M. Bruna, A. K. Ott, M. Ijaes, D. Yoon, U. Sassi and A. C. Ferrari, ACS Nano, 2014, 8, 74327441.
121. L. G. Cancado, A. Jorio, E. H. Martins Ferreira, F. Stavale, C. A. Achete, R. B. Capaz, M. V. O. Moutinho, A. Lombardo, T. S. Kulmala and A. C. Ferrari, Nano Lett., 2011, 11, 3190.
122. D. E. Gu, Y. Lu and B. C. Yang, Chem. Commun., 2008, 21, 2453.
123. T. Takizawa, T. Watanabe and K. Honda, J. Phys. Chem., 1978, 82, 1391.
124. S. H. Szczepankiewicz, J. A. Moss and M. R. Hoffmann, J. Phys. Chem. B, 2002, 106, 2922.
125. T. Yoshihara, R. Katoh, A. Furube, Y. Tamaki, M. Murai, K. Hara, S. Murata, H. Arakawa and M. Tachiya, J. Phys. Chem. B, 2004, 108, 3817.
126. A. Yamakata, T. A. Ishibashi and H. Onishi, Chem. Phys. Lett., 2001, 333, 271.
127. A. Yamakata, T. A. Ishibashi and H. Onishi, J. Phys. Chem. B, 2001, 105, 7258.
128. F. J. Knorr, C. C. Mercado and J. L. McHale, J. Phys. Chem. C, 2008, 112, 12786.
129. J. Schneider, M. Matsuoka, M. Takeuchi, J. Zhang, Y. Horiuchi, M. Anpo and D. W. Bahnemann, Chem. Rev., 2014, 114, 9919.
130. Y. Tamaki, A. Furube, R. Katoh, M. Murai, K. Hara, H. Arakawa and M. Tachiya, C. R. Chim., 2006, 9, 268.
131. M. Breusing, S. Kuehn, T. Winzer, E. Malic, F. Milde, N. Severin, J. P. Rabe, C. Ropers, A. Knorr and T. Elsaesser, Phys. Rev. B, 2011, 83, 153410.
132. D. Sun, Z. K. Wu, C. Divin, X. Li, C. Berger, W. A. de Heer, P. N. First and T. B. Norris, Phys. Rev. Lett., 2008, 101, 157402.
133. D. Brida, A. Tomadin, C. Manzoni, Y. J. Kim, A. Lombardo, S. Milana, R. R. Nair, K. S. Novoselov, A. C. Ferrari, G. Cerullo and M. Polini, Nat. Commun., 2013, 4, 1987.
134. A. Tomadin, D. Brida, G. Cerullo, A. C. Ferrari and M. Polini, Phys. Rev. B, 2013, 88, 035430.
135. K. Iwata, T. Takaya, H. O. Hamaguchi, A. Yamakata, T. A. Ishibashi, H. Onishi and H. Kuroda, J. Phys. Chem. B, 2004, 108, 20233.
136. Y. Tamaki, A. Furube, M. Murai, K. Hara, R. Katoh and M. Tachiya, Phys. Chem. Chem. Phys., 2007, 9, 1453.
137. A. Furube, T. Asahi, H. Masuhara, H. Yamashita and M. Anpo, Chem. Phys. Lett., 2001, 336, 424.

---