Open Access Article
Open Access ArticleVisual kinetic analysis†
Christian D.-T.
Nielsen
 a and
Jordi
Burés
a and
Jordi
Burés
 *b
*b
aImperial College London, White City Campus, 80 Wood Lane, London, W12 0BZ, UK
bSchool of Chemistry, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: jordi.bures@manchester.ac.uk; Tel: +44 (0)161 275 4634
First published on 13th December 2018
Abstract
Visual kinetic analyses extract meaningful mechanistic information from experimental data using the naked-eye comparison of appropriately modified progress reaction profiles. Basic kinetic information is obtained easily and quickly from just a few experiments. Therefore, these methods are valuable tools for all chemists working in process chemistry, synthesis or catalysis with an interest in mechanistic studies. This minireview describes the visual kinetic analyses developed in the last fifteen years and provides answers to the most common queries of new users. Furthermore, a video tutorial is attached detailing the implementation of both VTNA and RPKA.
Visual kinetic analyses extract kinetic information from the naked-eye comparison of original or modified progress reaction profiles. These analyses are becoming a popular tool in chemistry and related disciplines, even replacing traditional kinetic analyses focused on the measurement of initial rates. This increasing popularity is due to the combination of recent advances in both reaction monitoring technology and the development of new kinetic analyses. This minireview is focused on the most recent analyses developed in the last fifteen years. Also, it highlights the main differences between the most traditional kinetic analyses and answers the most frequently asked questions by new users of visual kinetic analyses.
In the past, visual analyses of the slope and interception of linearized plots (Lineweaver–Burk,1 Eadie–Hofstee2,3 and Hanes–Woolf4 plots) have been used to quickly identify different types of inhibition and concentration dependences of substrates. However, the simplest comparison of two reaction curves is to visually discern whether they are identical, that is if they overlay. These visual analyses transform the axes to achieve the overlay of the progress reaction profiles. The transformations required to achieve this overlay provide information about the relationship between the different progress reaction profiles.
The strategy of overlaying reaction profiles was first used by Michaelis and Davidsohn in 1911,5 although it was surprisingly omitted until Selwyn formalised a simple test to detect enzyme inactivation in 1965 that is still used nowadays.6 The Selwyn method plots [product] against t[enzyme]o for a set of progress curves of reactions run with different concentrations of enzyme but the same concentration of all other reaction components. If all the points fall on one curve, it is deduced that there is no enzyme denaturalisation during the reaction. In fact, as it will be shown in this minireview, this is a specific case of the Variable Time Normalisation Analysis (VTNA).
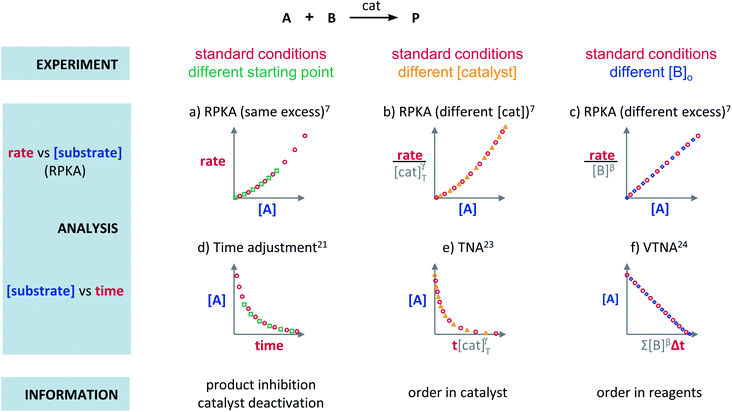
Plots using rate profiles – RPKA
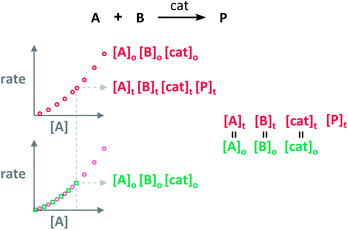
Blackmond exploited the overlay of progress reaction profiles in the Reaction Progress Kinetic Analysis (RPKA).7,8 This analysis uses entire reaction profiles of rate against concentration to visually interrogate the kinetic data. It comprises three kinds of analyses for three sets of experiments in order to identify: product inhibition or catalyst deactivation (Fig. 1a), the order in catalyst (Fig. 1b) and the order in any other component of the reaction (Fig. 1c).The analysis to check for product inhibition or catalyst deactivation compares curves of rate against [substrate] for reactions started at different points (Fig. 1a). This means that the initial concentration of starting materials are different, but they are such that the reaction started at higher concentrations will, at some point, have the same concentration of all the starting materials as the reaction started at lower concentrations (Fig. 2). As both experiments have the same difference between the concentration of reactants, they are called “same excess”‡ experiments. As a consequence, for any given concentration of substrate, both reactions will have the same concentration of starting materials, but different concentration of product and different number of turnovers completed by the catalyst. Therefore, overlay of the reaction profiles indicates the lack of product inhibition and, in the case of catalytic reactions, the absence of significant catalyst deactivation. If the curves don't overlay, product inhibition or catalyst deactivation can be inferred. To discern between these two options, a third experiment with product added is required. This experiment should have the same initial concentrations of starting materials as the experiment started at lower concentrations (i.e. the green experiment in Fig. 2) plus the amount of product generated by the other reaction until this reaction point ([P]t in Fig. 2). These two reactions are identical by composition but vary in the number of turnovers that the catalyst has completed. As such, overlay of these two reactions progress curves indicates product inhibition while no overlay is indicative of catalyst deactivation.
To elucidate the order in catalyst utilising RPKA (Fig. 1b), the profiles of reactions run with different catalyst loadings plotted as rate/[cat]Tγ against [substrate] are compared. The “γ” value that makes all the curves overlay is the correct order in catalyst.
The RPKA “different excess” analysis (Fig. 1c) elucidates the order in a given substrate by comparison of rate profiles with different concentrations of that specific substrate but identical concentration of other reaction components.§ To elucidate the order in B (Fig. 3), profiles are plotted as rate/[B]β against [A] and the value of “β” is changed until all the curves overlay, which indicates the correct order in component B.
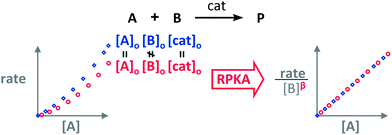 | ||
| Fig. 3 The order in [B], “β”, can be found by applying the RPKA to two reaction profiles of reactions with the same concentrations of all the substances except [B]. | ||
RPKA has been applied by academic and industrial research groups for a diverse range of reactions including precious metal-catalysed reactions,8–12 first row metal catalysis13–15 and organocatalysis.16–20
Plots using concentration profiles
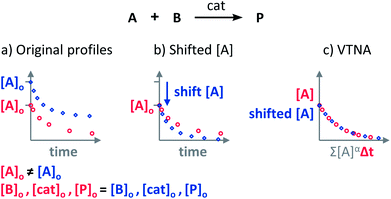
The Variable Time Normalisation Analysis (VTNA) uses ubiquitously accessible concentration-against-time reaction profiles. These profiles are directly obtained by almost any reaction monitoring technique currently available, such as NMR, FTIR, UV, Raman, GC and HPLC. The comparison of concentration against time profiles can identify: product inhibition or catalyst deactivation (Fig. 1d), the order in catalyst (Fig. 1e) and the order in any other component of the reaction (Fig. 1f).To identify product inhibition or catalyst deactivation (Fig. 1d), the profiles of two (or more) reactions started at different points are examined.21,22 In order to facilitate the visual comparison of both profiles, the profile of the reaction started at lower concentration of starting materials must be shifted to the right on the time scale until the first point of the profile overlays with the second reaction profile (Fig. 4). The overlay of the progress concentration profiles evidences the absence of catalyst deactivation and product inhibition. Conversely, lack of overlay indicates catalyst deactivation or product inhibition and a third experiment with product added is necessary to discern between these two possibilities. Again, the overlay of the original curve and a curve with product added indicates the presence of product inhibition, while the absence of overlay proves catalyst deactivation.
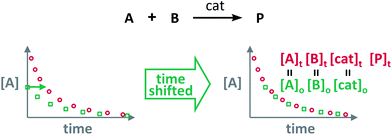 | ||
| Fig. 4 The comparison of the sections of reaction profiles with identical concentrations of starting materials and catalyst allows the identification of product inhibition and catalyst deactivation. | ||
To elucidate the order in catalyst (Fig. 1e), the time scale of two (or more) reactions run with different catalyst loadings is substituted by Σ[cat]γΔt (eqn (1)). When the concentration of active catalyst is constant during the entire reaction, the equation is simplified to t[cat]oγ.23 If the order in catalyst is assumed to be 1, this plot can instead be used to assess the stability of the catalyst, which is known as the Selwyn method. On the other hand, when the concentration of active catalyst changes during the reaction, for example due to catalyst deactivation, it is necessary to know the amount of remaining active catalyst and apply the variable time normalisation analysis (eqn (1)). In both cases, the value of “γ” that produces the overlay of the curves is the order in catalyst.
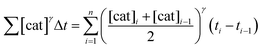 | (1) |
To elucidate the order in a component of the reaction, such as B, whose concentration changes during the progress of reaction (Fig. 1f), the time scale must be substituted by Σ[B]βΔt (eqn (2)). The value of “β” that produces the overlay of the reaction profiles is the order in component B.24
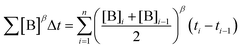 | (2) |
VTNA has already been used successfully by academic and industrial research groups in metal-catalysed25–38 and organocatalytic reactions.39–43
Pros and cons of visual kinetic analysis
While the root of these analyses is still highly mathematical, visual kinetic analyses depend on the subjective analysis of the user. This unusual characteristic for scientific analyses causes some advantages and disadvantages with respect to other classic kinetic analyses.+ Simple analysis
The main advantage of visual kinetic analyses is their simplicity. Minimal mathematical treatment and visual comparison make it quick to perform. Also, by avoiding counter-intuitive mathematical transformations, such as log–log plots, the results are easy to interpret.+ Information about the entire reaction
Visual kinetic analyses use the comparison of entire reaction profiles and therefore provide information on the entire course of the reactions. The analysis of the full profiles enables the detection of catalyst activation and deactivation, product inhibition and changes of order throughout the reaction. Initial rate measurements are totally blind to all these effects.+ Fewer experiments required
The comparison of entire reaction profiles involves all the experimental points of each trace and the effect of measurement errors at single points is minimised. Therefore, fewer experiments are necessary compared to the analysis using initial rates.+ Better way to report data
Plots using visual kinetic analyses include all the experimental data collected and facilitate their direct reinterpretation by other researchers. On the contrary, initial rates are the result of the analysis of experimental data usually not provided or only partially shown in the ESI.− Low precision
Although visual kinetic analyses are accurate, they lack high precision. Therefore, visual kinetic analyses are inadequate to obtain the precise values of kinetic constants. However, this is not a problem to elucidate kinetic parameters that usually don't require high precision, such as the orders of reaction in the reaction components.FAQs about RPKA and VTNA
How similar must the progress reaction curves be in order to be considered as overlaid?
The definition of what overlaid curves are can be, up to some extent, subjective. Experience has proven that, in some cases, slightly different solutions can lead to reasonable overlay, but generally it is easy to define a small range of valid values. Visual kinetic analyses provide accurate, although not always precise, solutions. Usually, less noisy and smoother traces lead to a smaller range of solutions. Since overlay is a qualitative property, no traditional error analysis such as standard deviation may be applied.Can VTNA be performed by monitoring any reactant of the reaction?
Yes, any parameter that correlates to the progress of the reaction can be used. If the initial concentration of the monitored substrate is the same for all reactions, the comparison is direct because the starting point will be the same. If the initial concentration of the monitored substrate is different for the reactions being compared (Fig. 5a), the curves have to be shifted vertically until the starting points of the profiles meet (Fig. 5b) before applying the VTNA (Fig. 5c).How to design “same” and “different excess” experiments in reactions with more than two reactants?
The objective of “same excess” experiments is to compare the kinetic profile of two identical reactions starting at different initial concentrations to find out if there is catalyst deactivation or product inhibition. Therefore, in the “same excess” experiments, the concentrations of all the reactants must be modified to match the concentrations of the original reaction at a given conversion. Additional experiments also adjusting the concentration of product (and byproducts) can be performed to discern between catalyst activation/deactivation and product or byproduct acceleration/inhibition.The “different excess” experiments aim to elucidate the effect of one of the reactants by comparing reaction profiles with identical reaction conditions except for the concentration of the analysed reactant. If the reactant to be investigated is in fact the product of an initial reaction (i.e. it is formed in situ), then the concentration of preceding starting components must be modified simultaneously.
How separate must the initial concentrations in “same excess” experiments be? And how different the excess, in “different excess” experiments?
Larger differences in initial concentrations for “same excess” experiments and in excess for “different excess” experiments increase the sensitivity of the analyses. However, larger differences also reduce the range of reaction profile to be compared. Therefore, it is necessary to find an adequate balance for each case. Ultimately, the sensitivity of the parameter analysed and the range of reaction profile available for comparison will dictate the appropriate initial concentrations and excess.What does it mean when the reaction profiles become straight lines?
When reaction profiles are not straight lines it is because some driving forces – the concentration of reactants or products – change during the progress of the reaction. In the case of RPKA plots, the reaction profiles will become straight lines when all the changing kinetic driving forces are raised to the correct power and either dividing the rate in the ordinate axis or multiplying in the abscises axis (Fig. 6a). In VTNA plots, the reaction profiles will become straight when the time scale is normalised by all the driving forces changing during the reaction raised to the correct order (Fig. 6b).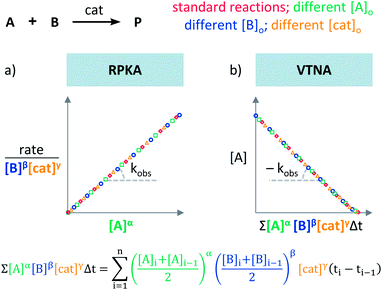 | ||
| Fig. 6 Straight lines appear in (a) RPKA and (b) VTNA plots when all the changing driving forces are raised to their order of reaction. | ||
Interestingly, if the kinetic effect of all the reaction components that affect the rate of the reaction is removed, the slope of the straight line is the kobs of the reaction. It is advisable to perform this analysis after all the orders have been independently elucidated, instead of attempting to directly find the combination of orders for each substance that leads to the straightest line.
Conclusions
Visual kinetic analyses are very powerful tools to qualitatively assess the presence of product inhibition and catalyst deactivation, as well as to elucidate the order of reaction in any component. Currently, analyses for rate data profiles (RPKA) as well as for concentration temporal profiles (e.g. VTNA) are available. These analyses should be the first choice of non-kinetic experts wanting to obtain basic kinetic data to refine their mechanistic proposals. These analyses could also inspire the development of new methods to visually extract additional kinetic information from reaction profiles.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. D.-T. N. thanks the Pharmacat Consortium (Syngenta) for a PhD studentship. J. B. thanks The University of Manchester for a generous starting package.Notes and references
- H. Lineweaver and D. Burk, J. Am. Chem. Soc., 1934, 56, 658–666 CrossRef CAS.
- B. H. J. Hofstee, J. Biol. Chem., 1952, 199, 357–364 CAS.
- G. S. Eadie, J. Biol. Chem., 1942, 146, 85–93 CAS.
- C. S. Hanes, Biochem. J., 1932, 26, 1406–1421 CrossRef CAS.
- L. Michaelis and H. Davidsohn, Biochem. Z., 1911, 35, 386–412 Search PubMed.
- M. J. Selwyn, Biochim. Biophys. Acta, Enzymol. Biol. Oxid., 1965, 105, 193–195 CrossRef CAS.
- D. G. Blackmond, Angew. Chem., Int. Ed., 2005, 44, 4302–4320 CrossRef CAS PubMed.
- J. S. Mathew, M. Klussmann, H. Iwamura, F. Valera, A. Futran, E. A. C. Emanuelsson and D. G. Blackmond, J. Org. Chem., 2006, 71, 4711–4722 CrossRef CAS PubMed.
- S. Shekhar, P. Ryberg, J. F. Hartwig, J. S. Mathew, D. G. Blackmond, E. R. Strieter and S. L. Buchwald, J. Am. Chem. Soc., 2006, 128, 3584–3591 CrossRef CAS PubMed.
- P. Dydio, R. J. Detz and J. N. H. Reek, J. Am. Chem. Soc., 2013, 135, 10817–10828 CrossRef CAS PubMed.
- J. R. Coombs, F. Haeffner, L. T. Kliman and J. P. Morken, J. Am. Chem. Soc., 2013, 135, 11222–11231 CrossRef CAS.
- P. Ruiz-Castillo, D. G. Blackmond and S. L. Buchwald, J. Am. Chem. Soc., 2015, 137, 3085–3092 CrossRef CAS PubMed.
- J. Streuff, M. Feurer, G. Frey, A. Steffani, S. Kacprzak, J. Weweler, L. H. Leijendekker, D. Kratzert and D. A. Plattner, J. Am. Chem. Soc., 2015, 137, 14396–14405 CrossRef CAS PubMed.
- L. Mesas-Sanchez and P. Diner, Chem.–Eur. J., 2015, 21, 5623–5631 CrossRef CAS PubMed.
- Q. A. Lo, D. Sale, D. C. Braddock and R. P. Davies, ACS Catal., 2018, 8, 101–109 CrossRef CAS.
- S. Liu and E. N. Jacobsen, Nat. Chem., 2012, 4, 817–824 CrossRef.
- D. D. Ford, D. Lehnherr, C. R. Kennedy and E. N. Jacobsen, J. Am. Chem. Soc., 2016, 138, 7860–7863 CrossRef CAS PubMed.
- K. A. D'Angelo and M. S. Taylor, J. Am. Chem. Soc., 2016, 138, 11058–11066 CrossRef PubMed.
- R. S. Klausen, C. R. Kennedy, A. M. Hyde and E. N. Jacobsen, J. Am. Chem. Soc., 2017, 139, 12299–12309 CrossRef CAS PubMed.
- A. E. Wendlandt, P. Vangal and E. N. Jacobsen, Nature, 2018, 556, 447–451 CrossRef CAS PubMed.
- R. D. Baxter, D. Sale, K. M. Engle, J.-Q. Yu and D. G. Blackmond, J. Am. Chem. Soc., 2012, 134, 4600–4606 CrossRef CAS.
- D. G. Blackmond, J. Am. Chem. Soc., 2015, 137, 10852–10866 CrossRef CAS.
- J. Burés, Angew. Chem., Int. Ed., 2016, 55, 2028–2031 CrossRef PubMed.
- J. Burés, Angew. Chem., Int. Ed., 2016, 55, 16084–16087 CrossRef PubMed.
- D. Whitaker, J. Burés and I. Larrosa, J. Am. Chem. Soc., 2016, 138, 8384–8387 CrossRef CAS PubMed.
- H. Noda, F. Amemiya, K. Weidner, N. Kumagai and M. Shibasaki, Chem. Sci., 2017, 8, 3260–3269 RSC.
- L.-J. Cheng, A. P. N. Brown and C. J. Cordier, Chem. Sci., 2017, 8, 4299–4305 RSC.
- H. Lundberg, F. Tinnis, J. Zhang, A. G. Algarra, F. Himo and H. Adolfsson, J. Am. Chem. Soc., 2017, 139, 2286–2295 CrossRef CAS PubMed.
- R. E. Plata, D. E. Hill, B. E. Haines, D. G. Musaev, L. Chu, D. P. Hickey, M. S. Sigman, J. Q. Yu and D. G. Blackmond, J. Am. Chem. Soc., 2017, 139, 9238–9245 CrossRef CAS PubMed.
- Z. Liu, Y. Wang, Z. Wang, T. Zeng, P. Liu and K. M. Engle, J. Am. Chem. Soc., 2017, 139, 11261–11270 CrossRef CAS PubMed.
- S. Ibáñez, M. Poyatos and E. Peris, Organometallics, 2017, 36, 1447–1451 CrossRef.
- C. Weatherly, J. M. Alderson, J. F. Berry, J. E. Hein and J. M. Schomaker, Organometallics, 2017, 36, 1649–1661 CrossRef CAS.
- Z. W. Davis-Gilbert, X. Wen, J. D. Goodpaster and I. A. Tonks, J. Am. Chem. Soc., 2018, 140, 7267–7281 CrossRef CAS PubMed.
- R. J. Somerville, L. V. A. Hale, E. Gómez-Bengoa, J. Burés and R. Martin, J. Am. Chem. Soc., 2018, 140, 8771–8780 CrossRef CAS PubMed.
- T. C. Malig, D. Yu and J. E. Hein, J. Am. Chem. Soc., 2018, 140, 9167–9173 CrossRef CAS PubMed.
- V. Vasilenko, C. K. Blasius and L. H. Gade, J. Am. Chem. Soc., 2018, 140, 9244–9254 CrossRef CAS PubMed.
- C. Colletto, A. Panigrahi, J. Fernández-Casado and I. Larrosa, J. Am. Chem. Soc., 2018, 140, 9638–9643 CrossRef CAS PubMed.
- S. Aikonen, M. Muuronen, T. Wirtanen, S. Heikkinen, J. Musgreave, J. Burés and J. Helaja, ACS Catal., 2018, 8, 960–967 CrossRef CAS.
- C. M. Young, D. G. Stark, T. H. West, J. E. Taylor and A. D. Smith, Angew. Chem., Int. Ed., 2016, 55, 14394–14399 CrossRef CAS.
- D. A. DiRocco, Y. Ji, E. C. Sherer, A. Klapars, M. Reibarkh, J. Dropinski, R. Mathew, P. Maligres, A. M. Hyde, J. Limanto, A. Brunskill, R. T. Ruck, L.-C. Campeau and I. W. Davies, Science, 2017, 356, 426–430 CrossRef CAS PubMed.
- A. Matviitsuk, M. D. Greenhalgh, D. J. B. Antúnez, A. M. Z. Slawin and A. D. Smith, Angew. Chem., Int. Ed., 2017, 56, 12282–12287 CrossRef CAS PubMed.
- S. M. Banik, A. Levina, A. M. Hyde and E. N. Jacobsen, Science, 2018, 358, 761–794 CrossRef PubMed.
- L. Schreyer, P. S. J. Kaib, V. N. Wakchaure, C. Obradors, R. Properzi, S. Lee and B. List, Science, 2018, 362, 216–219 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Microsoft Excel files with tutorials for VTNA and RPKA and a video available at https://youtu.be/5ORFRB4U10s. See DOI: 10.1039/c8sc04698k |
| ‡ The term “excess” is defined as the difference in the initial concentrations of two substrates (e.g. A and B: [excess] = [B]o − νB/νA[A]o = [B]t − νB/νA[A]t (where νA and νB are the stoichiometric coefficients for A and B)).7 |
| § The “different excess” analysis can also use experiments with different [A]o and [B]o, but the analysis will only occur from the point where both reaction profiles have the same [A]o or [B]o. |
| This journal is © The Royal Society of Chemistry 2019 |