Before Förster. Initial excitation in photosynthetic light harvesting

Abstract

Electronic 2D spectroscopy allows nontrivial quantum effects to be explored in unprecedented detail. Here, we apply recently developed fluorescence detected coherent 2D spectroscopy to study the light harvesting antenna 2 (LH2) of photosynthetic purple bacteria. We report double quantum coherence 2D spectra which show clear cross peaks indicating correlated excitations. Similar results are found for rephasing and nonrephasing signals. Analysis of signal generating quantum pathways leads to the conclusion that, contrary to the currently prevailing physical picture, the two weakly coupled pigment rings of LH2 share the initial electronic excitation leading to quantum mechanical correlation between the two clearly separate absorption bands. These results are general and have consequences for the interpretation of initially created excited states not only in photosynthesis but in all light absorbing systems composed of weakly interacting pigments where the excitation transfer is commonly described by using Förster theory. Being able to spectrally resolve the nonequilibrium dynamics immediately following photoabsorption may provide a glimpse to the systems' transition into the Förster regime.

---

Introduction

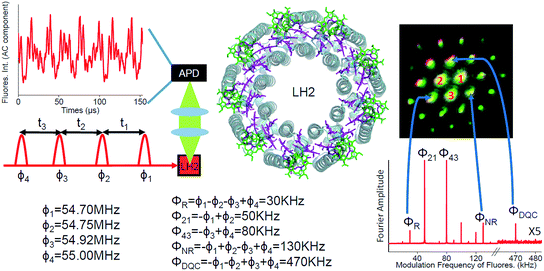
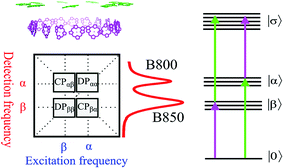
Photosynthesis is the amazing outcome of long evolutionary optimization. Life on earth and most of the energy currently consumed by mankind is based on this process – also fossil fuel is the result of past photosynthesis. Even though, the power conversion efficiency of today's photovoltaic solar cells surpasses the best photosynthesis systems by a good margin¹ the initial stages of photosynthesis are very efficient – almost every absorbed photon leads to a charge separation event despite often highly disordered structures and noisy thermal environments. How such high efficiency is achieved and the possible role of quantum processes in it are currently at the center of active scientific research.^2–5 One of the possible functional elements of such quantum behavior and optimization in photosynthesis is delocalization – the spatial domain coherently covered by the excited state after light absorption.⁶

The peripheral light harvesting antenna 2 (LH2) of photosynthetic purple bacteria consists of two rings of bacteriochlorophyll (BChl) a molecules embedded into a protein scaffold forming a barrel-like structure (see Fig. 1).⁷ The rings are responsible for two absorption bands which in most of the LH2s are at 800 nm and 850 nm. Correspondingly, both the rings and the absorption bands are called B800 and B850. In the LH2 of Rhodopseudomonas (Rps.) acidophila the B800 ring has 9 BChl a molecules and the B850 ring 18 BChl a molecules. While the B800 BChls are well separated from each other and from the BChls of the B850 ring, the latter forms a closely packed aggregate where inter-pigment excitonic interactions are significant (300–400 cm⁻¹).

Fig. 1 Schematic diagram of the FD2D experiment. Four collinear 8–10 fs pulses have tunable delays and different phase modulation frequencies ϕ_i. The avalanche photodiode (APD) detects fluorescence from the LH2 sample. The structure of the LH2 is also given with BChl a from different rings shown in green and purple. An example of the oscillatory component of the detected fluorescence signal is provided at the upper left corner. In the lower right the Fourier transformed signal is shown. The rephasing, the nonrephasing and the DQC signals appear at Φ_R = 30 kHz, Φ_NR = 130 kHz and Φ_DQC = 470 kHz, respectively. The other peaks correspond to other possible pulse combinations which exhibit fluorescence. For example, 80 kHz is excited by pulses 3 and 4. Also shown is the image of the phase-matched signals in conventional 3-pulse photon echo spectroscopy. 1, 2 and 3 are the three laser beams which have passed through the sample. All other spots are phase-matched coherently generated photon echo type signals. The correspondence between the three signals used in the current work and the phase-matched coherent signals is indicated by arrows.

In coherent two-dimensional (2D) spectroscopy the spectral information is spread over multiple dimensions revealing features that are otherwise hidden behind broad one-dimensional spectra. Furthermore, since the spectral resolution of the method is obtained by temporal scanning of the laser pulses and taking the Fourier transform over the delay time, simultaneous high energy and time resolution beyond the usual Fourier relation between the spectral bandwidth and the pulse length, can be achieved. Therefore, the technique enables ultrafast processes triggered by absorption of light to be followed in detail that is not possible in other more conventional time-resolved methods. Various types of 2D spectroscopy have emerged. In the original implementation, the third order polarization generated by three laser pulses emits a coherent signal which is mixed with a fourth pulse for phase sensitive heterodyne detection.⁸ The signal depends on the timing of the pulses and is measured in a certain phase-matched direction, which is related to the k-vectors of the incoming laser beams. In the third order nonlinear response one can distinguish rephasing (R), nonrephasing (NR) and double quantum coherence (DQC) signals.⁹

Earlier, 2D spectroscopy has been applied to study the excited states and energy transfer in LH2.^10,11 A generic 2D spectrum of a system like LH2, has two diagonal peaks corresponding to the two linear absorption bands and possibly also two cross peaks reflecting the correlations between the two bands (see Fig. 2). The 2D lineshape of the B800 diagonal peak at 77 K suggests that the ring has a significant excitonic character¹² despite the weak electronic couplings between the BChl a molecules giving support to earlier theoretical suggestions.¹³ In another study, oscillations of the 2D signal as a function of the population time between the excitation pulses and the detection pulse were studied.¹⁴ The 90° shift between oscillations recorded in different areas of the 2D spectra was taken as evidence for coherent exciton dynamics between B800 and B850. Indeed, coherent dynamics would lead to such a phase shift. However, the phase shift of the oscillations of 2D spectra can have many other origins.^15,16

Fig. 2 (Upper left) Arrangement of BChl a pigments in the LH2 structure. The purple and green molecules are commonly related to the B850 and B800 bands, respectively. (Lower left) The generic 2D spectrum with two diagonal peaks DP_ββ and DP_αα corresponding to the B850 and B800 bands, respectively (see also the absorption spectrum of the LH2 to the right from the 2D panel). The cross peaks CP_αβ and CP_βα are shown too. At the right hand side a schematic electronic level diagram of LH2 is shown to describe third order optical experiments like 2D spectroscopy. The one-exciton bands α and β correspond to the B800 and B850 bands, respectively, while the two-exciton band σ corresponds to all possible combinations of double excitations (including intramolecular double excitation) in the system. The purple and green arrows correspond to the transitions which mainly involve the β and α transitions, respectively.

In a more recent development, various incoherent action signals have been applied to measure coherent spectra. Photocurrent detected 2D spectroscopy has provided valuable information about photoinduced processes in quantum well and quantum dot based materials.^17,18 Photo-electron detection has been used to achieve spatial resolution beyond the diffraction limit of the optical beams in 2D spectroscopy.¹⁹ Fluorescence detected 2D (FD2D) spectroscopy was used to investigate the conformation of molecular dimer complexes²⁰ and spatial differences of the micro-distribution of the LH2 antenna composition due to growth condition variations.²¹ In all these approaches four collinear laser pulses bring the system to an excited state, which can generate the signals as photocurrent, photoelectrons or fluorescence. Such incoherent signals do not carry the directionality of the phase matching. Instead phase cycling²² or phase modulation²³ of the pulses is used to separate the different signal contributions. For example separating DQC using FD2D has been proposed,²⁴ and recently demonstrated in a dye molecule.²⁵

Here, we apply FD2D spectroscopy with phase modulation and use the generalized lock-in method²⁶ to record the rephasing, nonrephasing and double quantum coherence signals reporting properties of the initially created excited states directly after light absorption in LH2 complexes from Rps. acidophila (see Fig. 1). This gives access to the dynamical regime that precedes incoherent Förster energy transfer.

Experimental

The details of the FD2D setup are shown in Fig. 1 and S1.† A special feature of the setup is that we have phase locked all the beams and the full modulated signal is recorded in real time. These two features provide simultaneous phase synchronous access to all third order nonlinear signals – rephasing, nonrephasing and DQC. We point out that nonresonant signals from the environment (protein or solvent) which are known to seriously distort conventional coherent heterodyne detected 2D (HD2D) experiments during pulse overlaps (population time comparable to the pulse duration), do not contribute to fluorescence. This makes FD2D particularly suitable for recording the rapidly decaying DQC signals (FD2D_DQC) and also for the NR and R 2D spectra (FD2D_R+NR) at very short population times.

Results and discussion

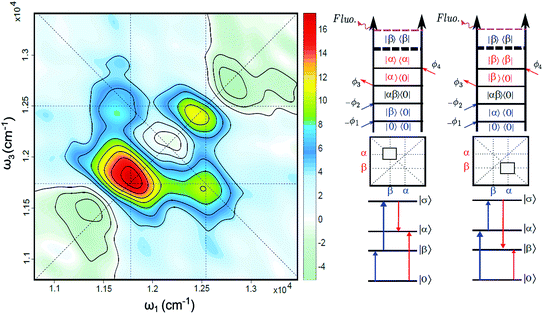
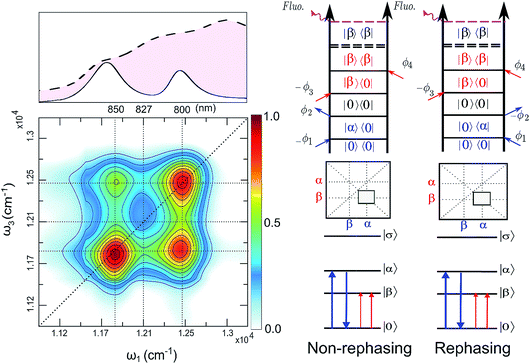
The FD2D_DQC spectra of LH2 are presented in Fig. 3. We use the conventional 2D Fourier scanning protocol²⁷ and not the double-frequency scanning as in earlier coherently detected DQC implementations.²⁸ Besides the diagonal peaks, distinct cross peaks are observed. In the Liouville pathway analyses one can pair up most of the double-sided Feynman diagrams so that they cancel out each other (see ESI†). Only two diagrams which can contribute to the cross peaks remain. These two FD2D_DQC diagrams are in a |αβ〉〈0| double quantum coherence during the t₂ evolution while evolving during t₁ and t₃ in |α〉〈0| and |β〉〈0| coherences (cf. right panel of Fig. 3). The presence of such cross peaks means that in absorption of light B800 and B850 act collectively; otherwise the B800 and B850 coherences would not be correlated and the signal would not appear.

Fig. 3 (Left) Fluorescence detected 2D double quantum coherence spectrum (FD2D_DQC), color scale in arbitrary units. (Right) Two Liouville space pathways which lead to the nondiagonal bands (crosspeaks). Here the doubly excited state corresponds to the configuration where both B800 and B850 are excited: |σ〉 = |αβ〉.

An important feature of all previous HD2D results²⁹ is that the B800–B850 cross peaks at very early population times are weak if not absent. This agrees with multi-color pump probe spectroscopy experiments where the B850 bleach signal grows from low levels after B800 excitation and the bleach dynamics has been interpreted as excitation transfer from one ring to the other.³⁰ Why do the prominent cross peaks signaling inter-band correlations appear in fluorescence detected DQC but not in rephasing and/or nonrephasing HD2D and the transient absorption experiments? Do these experiments give complementary information? In order to address these issues we present also the FD2D_R+NR spectra, see Fig. 4. In agreement with the earlier results²¹ prominent crosspeaks are present at zero population time. In the following we first explain the origin of the differences between the HD2D and FD2D signals and then discuss the conceptual consequences of the findings.

Fig. 4 (Left): Total (rephasing + nonrephasing) FD2D_R+NR of LH2, at t₂ = 0 fs, color scale normalized to one. Upper panel shows the absorption spectrum and the spectrum of the pulses (dashed) used in the experiment. (Right) Non-rephasing and rephasing GSB diagrams of the lower cross peak are shown.

The argumentation is analogous to earlier work^31–33 and follows the analyses of the third order optical response and the corresponding Liouville pathways represented here as double-sided Feynman diagrams.³⁴ The different pathways of the rephasing and nonrephasing signals can be classified as ground state bleach (GSB), stimulated emission (SE) and excited state absorption (ESA). There is a one-to-one correspondence between all possible GSB and SE pathways in HD2D and the pathways in FD2D_R+NR.²⁰ However, for each ESA pathway in the conventional HD2D signal there are two possible ESA pathways in FD2D_R+NR. One of the pathways ends at a singly excited level |α〉 or |β〉 while the other at the doubly excited level |σ〉. According to the Feynman diagram rules³⁴ the signals from these two pathways have opposite signs while the strength of them only depends on the yield of fluorescence from the doubly excited state |σ〉 relative to the singly excited state. The doubly excited state in antenna complexes is known to rapidly relax to a singly excited state via nonradiative exciton–exciton annihilation. In LH2 this process is faster than 1 ps³⁵ and should not be confused with the diffusion-driven slow annihilation in larger molecular systems. Since the singly excited state lifetime is about 1 ns, the difference of the amount of fluorescence while starting from |σ〉〈σ| and from |α〉〈α| is negligible. This means that the signals from these two pathways cancel out each other. Therefore, in FD2D of light harvesting complexes and in any other excitonic system with efficient annihilation the ESA signal completely vanishes. On the other hand, in the HD2D spectra of weakly coupled systems with significant energy gap such as B800–B850, the ESA contribution coincides with the GSB at the cross peaks while having opposite signs; therefore they largely cancel each other (see ESI†). This cancellation is the main reason why in HD2D measurements no significant B800–B850 cross peak is visible at zero population time. This also means that the pump–probe signal of the B850 band after B800 excitation has to be seen as decay of the ESA contribution due to the B800 to B850 transfer while at the moment of excitation the bleach appears but is almost entirely canceled by the opposite ESA.

A rigorous theory and discussion of the above cancellation effect based on nonlinear response functions can be found in ref. 33. An interesting and somewhat unintuitive conclusion is that in a heterodimer with parallel transition dipole moments, the initial cross peak amplitude is not proportional to the coupling. This effect is due to the weakening of the cancellation of one of the exciton components upon decreasing the coupling. However, in the limit when the coupling is so small that even annihilation does not occur, the ESA cancellation does not take place and thereby even the cross peaks vanish as in usual HD2D. To sum up this discussion, in contrast to the HD2D, FD2D_R+NR provides access to ESA-free cross peaks and confirms the findings of the DQC measurements.

An obvious conclusion from our DQC experiments is that the B800 and B850 transitions are correlated. This is to say that, at the moment of excitation, the LH2 pigments act as a collective state, even though the subsequent B800 to B850 transfer is considered to be an incoherent generalized Förster type rate process.³⁶ The cross peaks of DQC and of the early time FD2D measurements give a glimpse of a transient regime, before the incoherent rate process sets in, which is usually neglected in the description. Interestingly, recent theoretical studies of the coherent properties and entanglement of various excitation scenarios in LH2 also found that the B800 excitonic excitation has delocalization that extends to the B850 ring.³⁷ Significant delocalization-related transition strength redistribution from antenna to the RC has been predicted despite very weak interaction between the two.³⁸

The parameter regime where instead of efficient fast annihilation like in the individual LH2 we are reporting here, a slower diffusion-related annihilation takes place, also deserves attention. Action-detected 2D signals from such systems have recently been discussed in the literature.³⁹ The action signal is recorded over a much longer timescale than the four-pulse sequence which is exciting the sample. If during that time the second order populations generated by pulse pairs at different molecules undergo a nonlinear process such as a bimolecular reaction, the so-called incoherent mixing can take place providing a signal which carries the same modulation components as the fourth-order signal.³⁹ In the context of large light harvesting antenna arrays containing tens, possibly hundreds of complexes like LH2, diffusion-driven excitation annihilation⁴⁰ can lead to such mixing.

We also point out that it has been theoretically predicted that even without incoherent mixing, two independent molecules can provide fluorescence with the modulation combination frequencies where both excited molecules contribute.⁴¹ By comparing the signals at ϕ₂₁ = ϕ₂ − ϕ₁ and 2ϕ₂₁ we demonstrate that our experimental results cannot be explained by such a mechanism (for the details see ESI†).

Conclusions

Many conceptual discussions have suggested that exciton delocalization may be an important factor in optimizing energy transfer over large distances.^2,42 From the point of view of photosynthesis, the energy transfer within a single LH2 complex is clearly of secondary importance compared to the transfer between LH2s and from LH2 to the core antenna linked further to the reaction center (RC). The coupling between the B800 and B850 electronic transitions is about 20–30 cm⁻¹.⁴³ Using novel FD2D spectroscopy we have unequivocally detected B800–B850 DQC crosspeaks, which lead to the conclusion that B800 and B850 transitions are initially correlated despite the rather weak coupling between them. The coupling between LH2s and between LH2 and the core antenna is estimated to be even weaker.⁴⁴ Is such coupling, far smaller than the ambient thermal energy kT, enough to create inter-complex delocalization and where is the boarder-line from where the complexes can be considered electronically independent? How these findings do relate to the standard Förster theory, which assumes independence of the weakly coupled complexes and an incoherent energy transfer? What can FD2D spectroscopy tell us about the nonequilibrium dynamics immediately after photoabsorption, where the system transitions into the Förster regime? Answers to these questions may call for rethinking of the ways how the primary energy transfer in photosynthesis works and the current study is the first step in this direction. Furthermore, it should be pointed out that the present discussion is also relevant for other systems, see e.g., the recent article where evidence is provided for delocalized states between very weakly interacting atoms of a dilute gas.⁴⁵ It has been argued that delocalization can allow sensing of the energy funnel towards the RC providing biased motion in the right direction thereby making energy harvesting more efficient.⁴² Such a biased random walk can reach significantly larger distances than a Brownian walk.⁴⁶ In this context the coherent supercomplex character of light harvesting systems may be key for efficient energy transfer towards the RC.

Data availability

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

Author contributions

T. P. coordinated the project, K. J. K. implemented the experimental setup, A. S., J. S. and K. J. K. performed the experiments and data analyses. A. T. G. and R. J. C. prepared the light harvesting complexes, Q. S. and T. P. performed the Feynman diagram analyses, and T. P., K. J. K. and O. K. formulated the conceptual conclusions. All authors contributed to discussion of the data and writing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financed by the Swedish Research Council (VR), the Knut and Alice Wallenberg Foundation, the Swedish Energy Agency, NanoLund, the Crafoord Foundation, and a Laserlab-Europe EU-H2020 654148 grant. QS acknowledges scholarship support from the China Scholarship Council. ATG and RJC gratefully acknowledge funding from the Photosynthetic Antenna Research Center, an Energy Frontier Research Center funded by the DOE, Office of Science, Office of Basic Energy Sciences under Award Number DE-SC 0001035. AS acknowledges the Scandinavia-Japan Sasakawa Foundation (No. 14-22) and the Grant-in-Aid for JSPS Research Fellow (16J04694). TP and OK acknowledge financial support from the NPRP grant # NPRP7-227-1-034 from the Qatar National Research Fund (a member of Qatar Foundation). JC acknowledges Lundbeck Foundation grant R303-2018-3237.

References

1. R. E. Blankenship, D. M. Tiede, J. Barber, G. W. Brudvig, G. Fleming, M. Ghirardi, M. R. Gunner, W. Junge, D. M. Kramer, A. Melis, T. A. Moore, C. C. Moser, D. G. Nocera, A. J. Nozik, D. R. Ort, W. W. Parson, R. C. Prince and R. T. Sayre, Science, 2011, 332, 805–809.
2. G. D. Scholes, G. R. Fleming, L. X. Chen, A. Aspuru-Guzik, A. Buchleitner, D. F. Coker, G. S. Engel, R. Van Grondelle, A. Ishizaki, D. M. Jonas, J. S. Lundeen, J. K. McCusker, S. Mukamel, J. P. Ogilvie, A. Olaya-Castro, M. A. Ratner, F. C. Spano, K. B. Whaley and X. Zhu, Nature, 2017, 534, 647–656.
3. F. D. Fuller, J. Pan, A. Gelzinis, V. Butkus, S. S. Senlik, D. E. Wilcox, C. F. Yocum, L. Valkunas, D. Abramavicius and J. P. Ogilvie, Nat. Chem., 2014, 6, 706–711.
4. E. Romero, R. Augulis, V. I. Novoderezhkin, M. Ferretti, J. Thieme, D. Zigmantas and R. Van Grondelle, Nat. Phys., 2014, 10, 676–682.
5. G. D. Scholes, G. R. Fleming, A. Olaya-Castro and R. Van Grondelle, Nat. Chem., 2011, 3, 763–774.
6. T. Pullerits, M. Chachisvilis and V. Sundström, J. Phys. Chem., 1996, 100, 10787–10792.
7. G. McDermott, S. M. Prince, A. A. Freer, A. M. Hawthornthwaite-Lawless, M. Z. Papiz, R. J. Cogdell and N. W. Isaacs, Nature, 1995, 374, 517–521.
8. D. M. Jonas, Annu. Rev. Phys. Chem., 2003, 54, 425–463.
9. S. Mukamel, D. Abramavicius, L. Yang, W. Zhuang, I. V. Schweigert and D. V. Voronine, Acc. Chem. Res., 2009, 42, 553–562.
10. E. Harel and G. S. Engel, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 706–711.
11. M. Schröter, M. J. P. Alcocer, R. J. Cogdell, O. Kühn and D. Zigmantas, J. Phys. Chem. Lett., 2018, 9, 1340–1345.
12. D. Zigmantas, E. L. Read, T. Mančal, T. Brixner, A. T. Gardiner, R. J. Cogdell, G. R. Fleming, T. Mancal, T. Brixner, A. T. Gardiner, R. J. Cogdell and G. R. Fleming, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12672–12677.
13. Y. C. Cheng and R. J. Silbey, Phys. Rev. Lett., 2006, 96, 028103.
14. E. Harel and G. S. Engel, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 706–711.
15. V. Butkus, D. Zigmantas, L. Valkunas and D. Abramavicius, Chem. Phys. Lett., 2012, 545, 40–43.
16. J. Seibt and T. Pullerits, J. Chem. Phys., 2014, 141, 09B613_1.
17. G. Nardin, Semicond. Sci. Technol., 2015, 117, 112804.
18. K. J. Karki, J. R. Widom, J. Seibt, I. Moody, M. C. Lonergan, T. Pullerits and A. H. Marcus, Nat. Commun., 2014, 5, 5869.
19. M. Aeschlimann, T. Brixner, A. Fischer, C. Kramer, P. Melchior, W. Pfeiffer, C. Schneider, C. Strüber, P. Tuchscherer and D. V. Voronine, Science, 2011, 333, 1723–1726.
20. G. A. Lott, A. Perdomo-Ortiz, J. K. Utterback, J. R. Widom, A. Aspuru-Guzik and A. H. Marcus, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16521–16526.
21. V. Tiwari, Y. A. Matutes, A. T. Gardiner, T. L. C. Jansen, R. J. Cogdell and J. P. Ogilvie, Nat. Commun., 2018, 9, 4219.
22. P. Tian, D. Keusters, Y. Suzaki and W. S. Warren, Science, 2003, 300, 1553–1555.
23. P. F. Tekavec, G. A. Lott and A. H. Marcus, J. Chem. Phys., 2007, 127, 214307.
24. A. Perdomo-Ortiz, J. R. Widom, G. A. Lott, A. Aspuru-Guzik and A. H. Marcus, J. Phys. Chem. B, 2012, 116, 10757–10770.
25. S. Mueller, S. Draeger, X. Ma, M. Hensen, T. Kenneweg, W. Pfeiffer and T. Brixner, J. Phys. Chem. Lett., 2018, 9, 1964–1969.
26. S. Fu, A. Sakurai, L. Liu, F. Edman, T. Pullerits, V. Öwall and K. J. Karki, Rev. Sci. Instrum., 2013, 84, 115101.
27. F. A. Damtie, A. Wacker, T. Pullerits and K. J. Karki, Phys. Rev. A, 2017, 96, 053830.
28. A. Nemeth, F. Milota, T. Mančal, T. Pullerits, J. Sperling, J. Hauer, H. F. Kauffmann and N. Christensson, J. Chem. Phys., 2010, 133, 094505.
29. M. Ferretti, R. Hendrikx, E. Romero, J. Southall, R. J. Cogdell, V. I. Novoderezhkin, G. D. Scholes and R. van Grondelle, Sci. Rep., 2016, 6, 20834.
30. T. Pullerits, S. Hess, J. L. Herek and V. Sundström, J. Phys. Chem. B, 1997, 101, 10560–10567.
31. T. Kunsel, V. Tiwari, Y. A. Matutes, A. T. Gardiner, R. J. Cogdell, J. P. Ogilvie and T. L. C. Jansen, J. Phys. Chem. B, 2019, 123, 394–406.
32. P. Malý and T. Mančal, J. Phys. Chem. Lett., 2018, 9, 5654–5659.
33. M. Schröter, T. Pullerits and O. Kühn, J. Chem. Phys., 2018, 149, 114107.
34. S. Mukamel, Principles of nonlinear optical spectroscopy, Oxford University Press, Oxford, 1995.
35. B. Brüggemann, J. L. Herek, V. Sundström, T. Pullerits and V. May, J. Phys. Chem. B, 2001, 105, 11391–11394.
36. G. D. Scholes and G. R. Fleming, J. Phys. Chem. B, 2002, 104, 1854–1868.
37. C. Smyth, D. G. Oblinsky and G. D. Scholes, Phys. Chem. Chem. Phys., 2015, 17, 30805–30816.
38. F. Caycedo-Soler, C. A. Schroeder, C. Autenrieth, A. Pick, R. Ghosh, S. F. Huelga and M. B. Plenio, J. Phys. Chem. Lett., 2017, 8, 6015–6021.
39. P. Grégoire, A. R. Srimath Kandada, E. Vella, C. Tao, R. Leonelli and C. Silva, J. Chem. Phys., 2017, 147, 114201.
40. A. Schubert, A. Stenstam, W. J. D. Beenken, J. L. Herek, R. Cogdell, T. Pullerits and V. Sundström, Biophys. J., 2004, 86, 2363–2373.
41. S. Mukamel, J. Chem. Phys., 2016, 145, 041102.
42. J. L. Brédas, E. H. Sargent and G. D. Scholes, Nat. Mater., 2016, 16, 35–44.
43. B. P. Krueger, G. D. Scholes and G. R. Fleming, J. Phys. Chem. B, 1998, 102, 5378–5386.
44. X. Hu, T. Ritz, A. Damjanović and K. Schulten, J. Phys. Chem. B, 1997, 101, 3854–3871.
45. L. Bruder, A. Eisfeld, U. Bangert, M. Binz, M. Jakob, D. Uhl, M. Schulz-Weiling, E. R. Grant and F. Stienkemeier, Phys. Chem. Chem. Phys., 2019, 21, 2276–2282.
46. E. Codling, M. J. Plank and S. Benhamou, J. R. Soc., Interface, 2008, 5, 813–834.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc01888c

‡ These authors contributed equally to this work.

§ Current affiliation: Nano-Science Center & Department of Chemistry, University of Copenhagen, Universitetsparken 5, 2100 Copenhagen, Denmark.

---